空间汇交力系和空间力偶系
合集下载
第4章空间力系分解
合力的大小
FR ( Fx )2 ( Fy )2 ( Fz )2
Fx 方向余弦 cos( FR , i ) FR
Fy Fz cos( FR , j ) cos( FR , k ) FR FR
7
空间汇交力系的合力等于各分力的矢量和，合力的作用 线通过汇交点.
M 为合力偶矩矢，等于各分力偶矩矢的矢量和。
25
力偶系的合成（与汇交力系的计算完全相同）
合力偶矩矢
M Mi
M x Mix M y Miy Mz Miz
M M xi M y j Mzk
合矢量投影定理：Βιβλιοθήκη 合力偶矩矢的大小和方向余弦:
M
M M M
2 2 ix iy iz
2
M ix cos M
cos
M iy M
M iz cos M
26
空间力偶系平衡的充分必要条件是：合力偶矩矢等于零。
为代数量
z
即：力对轴之矩，等于力在垂直于
该轴的平面上的投影对轴与平面交 点之矩。 O x
y
特殊情况：
1、力与轴平行，矩为零。 2、力与轴相交，矩为零。
即： 力与轴位于同一平面内时，力对轴之矩为零。 16
合力矩定理
空间任意力系的合力对于任一轴的矩等于力系中所有各 力对于该轴的矩的代数和。（用于求力矩）
B
F
F
rBA rA
A
M rBA F
rB
O
23
2、空间力偶等效定理
作用在同一刚体上的两个力偶，如果力偶矩矢相等， 则它们彼此等效。
第六章 重心
S
S
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
6.3确定刚体重心的几种方法
1 对于匀质、具有对称性的刚体,重心在对称 轴、对称面、或对称中心上.采用查表法
(参见书中简单几何形体的形心,注意坐标轴向)
2 求形状复杂的物体的重心时，可采用 组合法或实验法。 (1)分割法：可将物体分割为几个简单形状 的物体，而这些简单形状物体的重心是易于 确定或是已知的，则整个物体重心可用坐标 公式求出。
在力学和工程技术问题中，物体的重心位 置具有重要意义，例如高速旋转机械的均衡运 转．飞机的稳定飞行都会涉及重心的问题．因 此，在机械、航空、水利或土建等的设计中， 以及有些静力学计算中都常需确定物体重心的 位置。
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
6.1 平行力系中心
第6节 空间汇交力系和空间力偶系
例6· 2 半径为R的圆面有一圆孔,孔的半径为r， 两圆中心的距离OO1＝a，求图形的重心位置。 解: 将图形看作由两部分组成，取坐标系OXY 如图所示，它们的面积和重心坐标分别为:
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
第六章 重心
内容:
⑴ 本章首先从平行力系中心导出重心 和形心坐标的普遍公式． ⑵ 然后着重从工程应用的角度来讨论 重心和形心的求法．
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
重心的概念: 在地球表面附近的物体，每一 微小部分都受到重力的作用，由于物体与地球 中心间的距离远大于物体各部分间的距离，因 而各部分所受的重力,通常可认为组成空间平行 力系。这个由物体各部分重力组成的空间平行 力系的合力的作用点就是物体的重心。
S
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
6.3确定刚体重心的几种方法
1 对于匀质、具有对称性的刚体,重心在对称 轴、对称面、或对称中心上.采用查表法
(参见书中简单几何形体的形心,注意坐标轴向)
2 求形状复杂的物体的重心时，可采用 组合法或实验法。 (1)分割法：可将物体分割为几个简单形状 的物体，而这些简单形状物体的重心是易于 确定或是已知的，则整个物体重心可用坐标 公式求出。
在力学和工程技术问题中，物体的重心位 置具有重要意义，例如高速旋转机械的均衡运 转．飞机的稳定飞行都会涉及重心的问题．因 此，在机械、航空、水利或土建等的设计中， 以及有些静力学计算中都常需确定物体重心的 位置。
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
6.1 平行力系中心
第6节 空间汇交力系和空间力偶系
例6· 2 半径为R的圆面有一圆孔,孔的半径为r， 两圆中心的距离OO1＝a，求图形的重心位置。 解: 将图形看作由两部分组成，取坐标系OXY 如图所示，它们的面积和重心坐标分别为:
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
第六章 重心
内容:
⑴ 本章首先从平行力系中心导出重心 和形心坐标的普遍公式． ⑵ 然后着重从工程应用的角度来讨论 重心和形心的求法．
理论力学电子教案：张建辉制作
理论力学：第一章 静力学
第6节 空间汇交力系和空间力偶系
重心的概念: 在地球表面附近的物体，每一 微小部分都受到重力的作用，由于物体与地球 中心间的距离远大于物体各部分间的距离，因 而各部分所受的重力,通常可认为组成空间平行 力系。这个由物体各部分重力组成的空间平行 力系的合力的作用点就是物体的重心。
空间力系
第三章 空间力系一、空间汇交力系（一）空间汇交力系的合成 1．空间力在坐标轴上的投影 （1）一次投影法如图3-1所示,若已知力F 与三个坐标轴x,y,z 间的夹角分别为θ、β和γ，则力F 在三个坐标轴上的投影分别为⎪⎭⎪⎬⎫===γβθcos cos cos z y x F F F （3.1）图3-1相应的，若已知力F 的三个投影，可以求出力F 的大小和方向，即大小为 222z y x F F F F ++=（3.2）方向 ⎪⎪⎪⎭⎪⎪⎪⎬⎫===F FF F F F z yx γβθcos cos cos（3.3）（2）二次投影法如图3-2所示,若已知力F 与坐标轴Oxy 的仰角γ以及力F 在Oxy 平面上的投影xy F 与x 轴间的夹角ϕ，则力F 在三个坐标轴上的投影分别为γϕλϕγsin sin in cos in F F Fs F Fs F z y x ===，，图3-22．合力投影定理 合力在某轴上的投影，等于各分力在同一坐标轴上投影的代数和。
即∑=+++=xixn x x Rx FF F F F 21 同理 ∑∑==ziRz yi RyF F F F ，3．空间共点力系的合成空间共点力系可以合成为一个合力，该合力的作用线通过力系的公共作用点，合力的大小和方向为()()()222∑∑∑++=zyxR F F F F （3.4）()()()⎪⎪⎪⎭⎪⎪⎪⎬⎫===∑∑∑R z R R yRR xRF F F F F F k F j F i F ,cos ,cos ,cos（3.5）（二）空间汇交力系的平衡 1．空间汇交力系的平衡条件空间汇交力系平衡的充要条件是合力等于零，即()()()0222=++=∑∑∑zyxR F F F F2．空间汇交力系的平衡方程根据平衡条件，得到空间汇交力系的平衡方程为⎪⎪⎭⎪⎪⎬⎫===∑∑∑000y x zFFF（3.6）利用上述三个方程，可以求解3个未知量。
工程力学
M O ( F ) M x ( F ) i M y ( F ) j M z ( F )k Fb sin i Fa sin j ( Fb sin sin Fa sin cos ) k
例 题 3
已知： P 、 a、b、c 求： 力P 对OA轴之矩
z
解：（1）计算 MO(P)
已知：在工件四个面上同时钻5个孔，每个孔所受切削 力偶矩均为80N· m. 求：工件所受合力偶矩在 x, y, z 轴上的投影
解：把力偶用 力偶矩矢表示， 平行移到点A .
M x M ix M 3 M 4 cos 45 M 5 cos 45 193.1N m
M y M iy M 2 80N m M z M iz M 1 M 4 cos 45 M 5 cos 45 193.1N m
a 2 b2 c2
例4 6.2
如图所示，长方体棱长为 a、 b、c，力 F 沿BD，求力 F 对AC 之矩。 解： mAC (F ) mC (F ) AC
B
F
c
a
C
D
b
A
mC ( F ) F cosa
Fba a 2 b2
mAC ( F ) mC ( F ) cos
Fabc a 2 b2 a 2 b2 c 2
§4–3
空间力偶
1、力偶矩以矢量表示－－力偶矩矢
F1 F2 F1 F2
空间力偶的三要素 （1） 大小：力与力偶臂的乘积；
（2） 方向：转动方向；
（3） 作用面：力偶作用面。
（1） 大小
（2） 方向
第三章理论力学
因此，其平衡的解析条件为：
F
x
0
x
F
y
0
y
F
z
0
z
M
0
M
0
M
0
------ 平衡方程
共六个方程，可以求解空间任意力系中的六个未知约束力． 3、空间任意力系的两种特殊情况： 1）空间平行力系的平衡方程
Fy F cos
，
方向：＋、－号；
Fz F cos
2）间接投影法（二次投影法） 如果只已知与一根轴的夹 角 ，则通常的做法是：先将 该力向z 轴及其垂面分解（与 垂面的夹角为 90 )，而位于 垂面内的分力，其平面几何关
系比空间几何关系要容易寻找得多，因此只要在该垂面内
找出其与该平面内的两根轴之一的夹角（与另一根轴的夹
第三章
空间力系
注意：本章不作为重点，主要介绍一些基本概念、基本原理 和一些基本方法的应用，但不作为重点练习；个别需 要掌握的内容设有标注，望大家掌握．
一、空间力系：当力系中各分力的作用线分布于 三维空间时，该力系称为空间力 系． 二、空间力系又可根据力系中各分力的作用线的 分布情况划分为：空间汇交力系、空间力偶 系、空间平行力系和空间 任意力系． 三、本章研究的主要问题：力系的简化、合成及 平衡问题．
M x ( F ) M x ( Fx ) M x ( Fy ) M x ( Fz ) Fz y Fy z M y ( F ) M y ( Fx ) M y ( Fy ) M y ( Fz ) Fx z Fz x M z (F ) M z (Fx ) M z (Fy ) M z (Fz ) Fy x Fx y
理论力学 chap4
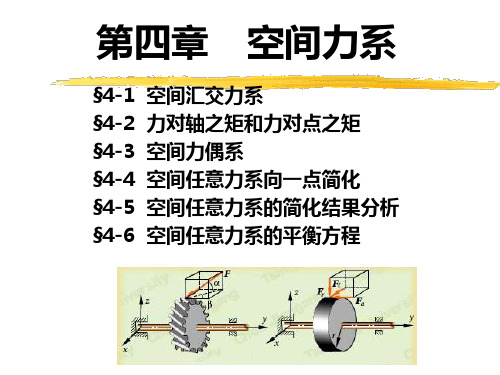
M y M iy M 2 80 N m
M z M iz M 1 M 4 cos 45 M 5 cos 45 193 .1N m
M M ix i M iy j M iz k
例 已知: F1 = 10kN，F2 = 16kN， F3 = 20kN，a=10cm .求力系的合力偶。
2 2 2
力F 对原点O之矩方向余弦：
Mx cos( M O , i ) 0.845 MO
My cos( M O , j ) 0.531 MO Mz cos( M O , k ) 0.064 MO
M O M x M y M z 124 .3 N m
§4-3 空间力偶系 1 空间力偶的概念
F Fx Fy Fz
2 2 2
cos( F , i )
Fx F
解题时究竟用哪种 方法求力的投影？
例1 半径r的斜齿轮，其上作用力F，如图所示。求力在坐标 轴上的投影。
解： Fx Ft F cos sin
FY Fa F cos cos
Fz Fr F sin
Fxy Fxy
F
o d
M z ( F ) M O ( Fxy )
(1)定义
M z dFxy
力对轴之矩的绝对值等于该力在与轴垂直的 平面上的投影对轴与平面交点之矩。
如何求力对轴之矩？
力对轴之矩是代数量，并按右手规则 确定其正负号。
力与轴平行或相交时力对该轴的矩等于零
（1）合力之矩定理
合力对任一点之矩矢等于力系中各力 对该点之矩矢的矢量和；合力对任一轴之 矩等于力系中各力对该轴之矩的代数和。
空间汇交力系和空间力偶系
=
=
=
) rBA FR rBA ( F1 F2 ) M ( FR , FR rBA F1 rBA F2 rBA F1 M ( F1 , F1)
(4) 只要保持力偶矩不变，力偶可从其所在平面移至另 一与此平面平行的任一平面，对刚体的作用效果不变.
M O ( F ) (r F ) ( xi yj zk ) ( Fxi Fy j Fz k ) ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
力对点 O 的矩在三个坐标轴上的投影为
第4章空间汇交力系与空间力偶系41空间汇交力系41空间汇交力系42力对点的矩和力对轴的矩43空间力偶直接投影法1力在直角坐标轴上的投影直接投影法1力在直角坐标轴上的投影?cosff?41空间汇交力系cosyff??coszff???cosffx?间接二次投影法sinxyff??sincosxff???xsinsinyff???coszff??合矢量力投影定理2空间汇交力系的合力与平衡条件合矢量力投影定理2空间汇交力系的合力与平衡条件合力的大小???空间汇交力系的合力??iff??r????xixxfffr????yiyyfffr????zizzfffr合力的大小222rxyzffff??????方向余弦rrcosffifx????rrcosffjfy????rrcosffkfz????空间汇交力系平衡的充分必要条件是
M O ( F ) yFz zFy
x
r xi yj zk
F Fx i Fy j Fz k
M O ( F ) zFx xFz
工程力学：第三章 空间问题的受力分析
。CDB平面与水平
面间的夹角
，物重
。如起重杆的重量不计，试求
起重杆所受的压力和绳子的拉力。
解：取起重杆AB与 重物为研究对象。
取坐标轴如图所示。 由已知条件知：
列平衡方程 解得
§3-3 力对轴的矩 力F对z轴的矩就是分力Fxy 对点O的矩， 即
力对轴的矩是力使刚体绕该 轴转动效果的度量、是一个 代数量。
空间力偶系平衡的必要和充分条件是：该力偶系的合力偶矩等 于零，亦即所有力偶矩矢的矢量和等于零，即
由上式，有 欲使上式成立，必须同时满足
空间力偶系未知量）
空间力偶系平衡的必要和充分条件为：该力偶系中所有各力偶 矩矢在三个坐标轴上投影的代数和分别等于零。
§3-5 空间任意力系的平衡方程
可将上述条件写成空间任意力系的平衡方程
注：1.与平面力系相同，空间力系的平衡方程也有其它的形式。 2.六个独立的平衡方程，求解六个未知量。 3.可以从空间任意力系的普遍平衡规律中导出特殊情况的 平衡规律，例如空间平行力系、空间汇交力系和平面任意 力系等平衡方程。
例：设物体受一空间平行力系作用。 令z轴与这些力平行，则
绝对值： 该力在垂直于该轴的平面上的投影对于 这个平面与该轴的交点的矩的大小。
正负号： 从z轴正端来看，若力的这个投影使物体绕该轴 按逆时针转向转动，则取正号，反之取负号。
也可按右手螺旋规则来确定其正负号，如图所 示，姆指指向与z轴一致为正，反之为负。
当力与轴在同一平面时，力对该轴的矩等于零：
(1)当力与轴相交时 (此时h＝0)；
（三个方程，可 求解三个未知量）
空间汇交力系平衡的必要和充分条件为：该力系中所有各力 在三个坐标轴上的投影的代数和分别等于零。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M O ( F ) (r F ) ( xi yj zk ) ( Fxi Fy j Fz k ) ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
力对点 O 的矩在三个坐标轴上的投影为
z
2.力对轴的矩
M z ( F ) M O ( Fxy ) Fxy h
力与轴相交或与轴平行（力与轴在同一平面内）， 力对该轴的矩为零.
4、力对点的矩与力对过该点的轴的矩的关系 M x ( F ) M x ( Fx ) M x ( Fy ) M x ( Fz ) Fz y Fy z M y ( F ) M y ( Fx ) M y ( Fy ) M y ( Fz ) Fx z Fz x M z ( F ) Fy x Fx y
5月16日 5月21日 5月21日 5月11日
6-9
6-9 2-5 6-9 6-9
10建筑学①
10建筑学② 10城建建筑 ① 10城建建筑 ② 10城规①
25
25 30 30 25
六
三 三
5月28日
5月18日 5月25日
2-5
6-9 6-9
10城规②
10城建城规 ① 10城建城规 ②
25
32 33
8：20或14： 11：30或 00在北 17：10 校区校 在南校 车停车 区校车 场 停车场
1、力偶矩以矢量表示——力偶矩矢
F1 F2 F1 F2
空间力偶的三要素 （1） 大小：力与力偶臂的乘积； （2） 方向：转动方向；
（4） 作用面：力偶作用面。
M rBA F
2、力偶的性质
(1)力偶中两力在任意坐标轴上投影的代数和为零 . (2)力偶对任意点取矩都等于力偶矩，不因矩心的改变而改变。
合力偶矩矢的大小和方向余弦
M ( M x ) 2 ( M y ) 2 ( M z ) 2
Mx cos M
cos
My M
Mz cos M
空间力偶系平衡的充分必要条件是 :合力偶矩矢等于零，即
M 0
M
x
0
M
y
0
M
z
0
--称为空间力偶系的平衡方程.
第4章
空间汇交力系与空间力偶系
§4–1 空间汇交力系 §4–2 力对点的矩和力对轴的矩
§4–3 空间力偶
§4–1
空间汇交力系
1、力在直角坐标轴上的投影
直接投影法
Hale Waihona Puke Fx F cos Fy F cos
Fz F cos
间接（二次）投影法
Fxy F sin
Fx F sin cos
=
=
=
) rBA FR rBA ( F1 F2 ) M ( FR , FR rBA F1 rBA F2 rBA F1 M ( F1 , F1)
(4) 只要保持力偶矩不变，力偶可从其所在平面移至另 一与此平面平行的任一平面，对刚体的作用效果不变.
方向余弦
cos( FR , i )
Fx
FR
cos( FR , j )
Fy
FR
cos( FR , k )
Fz
FR
空间汇交力系的合力等于各分力的矢量和，合力的作用 线通过汇交点. 空间汇交力系平衡的充分必要条件是： 该力系的合力等于零，即 FR 0
30
0
求：杆受力及绳拉力 解：画受力图，列平衡方程
F
x
0
F1 sin 45 F2 sin 45 0
F
F
y
0
0
FA sin 30 F1 cos 45 cos 30 F2 cos 45 cos 30 0
z
F1 cos 45 sin 30 F2 cos 45 sin 30 FA cos 30 P 0
Fz 0
FOA sin 45 P 0
FOA 1414N FOB FOC 707N（拉）
例4-4 已知： F , l , a, 求： Mx F ,My F ,Mz F
解：把力 F 分解如图
Mx My
F Fl cos
例4-1
已知： Fn , , 求：力 Fn 在三个坐标轴上的投影.
解：
Fz Fn sin
Fxy Fn cos
Fx Fxy sin Fn cos sin Fy Fxy cos Fn cos cos
例4-2
已知：物重P=10kN，CE=EB=DE；
F
x
0
F
y
0
--称为空间汇交力系的平衡方程 空间汇交力系平衡的充要条件：该力系中所有各力在三 个坐标轴上的投影的代数和分别为零.
§4–2
力对点的矩和力对轴的矩
1、力对点的矩以矢量表示 ——力矩矢
(1）大小:力 F 与力臂的乘积
三要素：
（2）方向:转动方向 （4）作用面：力矩作用面.
MO ( F ) r F
M O ( F , F ) M O ( F ) M O ( F ) rA F rB F
F F
MO (F , F ) (rA rB ) F M
（4）只要保持力偶矩不变，力偶可在其作用面内任意移转， 且可以同时改变力偶中力的大小与力偶臂的长短，对刚体的 作用效果不变.
• 尽快到教材科去买实验指导 书和实验报告书．
M y M iy M 2 80N m M z M iz M 1 M 4 cos 45 M 5 cos 45 193.1N m
例4-6 已知：两圆盘半径均为200mm，AB =800mm，圆盘面O1垂直于 z 轴，圆盘面 O2 垂直于 x 轴，两盘面上作用有力偶， F1=4N ， F2=5N，构件自重不计. 求:轴承A,B处的约束力. 解：取整体，受力图如图所示.
F F l a cos
M z F F l a sin
例4-5 已知：在工件四个面上同时钻5个孔，每个孔所受切削 力偶矩均为80N· m. 求：工件所受合力偶矩在 x, y, z 轴上的投影 解：把力偶用力偶 矩矢表示，平行移 到点A .
M x Mix M3 M 4 cos45 M5 cos45 193.1N m
4．力偶系的合成与平衡条件
=
=
M1 r1 F1, M2 r2 F2 ,......, M n rn Fn
M Mi
M 为合力偶矩矢，等于各分力偶矩矢的矢量和.
Mx Mx , M y M y , M z M z
F1 F2 3.54kN
FA 8.66kN
例4-3 已知：P=1000N ,各杆重不计. 求：三根杆所受力.
解：各杆均为二力杆，取球铰O，画受 力图。
Fx 0
FOB sin 45 FOC sin 45 0
F 0
y
FOB cos 45 FOC cos 45 FOA cos 45 0
Fy F sin sin
Fz F cos
2、空间汇交力系的合力与平衡条件
空间汇交力系的合力
合矢量（力）投影定理
FR Fi
FRx Fix Fx FRy Fiy Fy FRz Fiz Fz
合力的大小 FR ( Fx )2 ( Fy )2 ( Fz )2
M O ( F ) yFz zFy
x
r xi yj zk
F Fx i Fy j Fz k
M O ( F ) zFx xFz
y
M O ( F ) xFy yFx
M O ( F ) yFz zFy M x ( F ) x M O ( F ) zFx xFz M y ( F ) y M O ( F ) xFy yFx M z ( F ) z
§4-3 空间力偶
(2) 滑移矢量：这种矢量有大小、有方向，但不与一固定的
位置有关，而且需指明这种矢量的基线即可。作用在刚体上 的力不是滑移矢量。 -----只对刚体成立 (3) 自由矢量：这种矢量只有大小、方向作为其特征。只要 保持其大小、方向，该矢量可以在空间任意移动，不仅可以
沿其方向滑移，而且可以平行搬移，如力偶。
=
=
F1 F1 F2
F2 F3 F3 =
=
定位矢量 滑移矢量 自由矢量 力偶矩矢是自由矢量 力偶矩相等的力偶等效 (5)力偶没有合力，力偶只能由力偶来平衡.
根据各类矢量的不同特点，可以把力学中的矢量分为三类。 (1)定位矢量: 如速度、加速度和力等，它们不仅有大小、有 方向，而且这些矢量都与空间中某一确定的位置有关。速度 矢量，必须明确说明在空间哪一点的速度的大小和方向。
M x 0 F2 400 FBz 800 0
M z 0 F1 400 FBx 800 0
FAx FBx 1.5N
FAz FBz 2.5N
星期
实验日 期
节次
实验班级
实验人 数
校车接人 地点、 时间
校车送返 地点、 时间
六
一 六 六 三
5月28日