信号与系统第3章习题

合集下载

信号系统(第3版)习题解答

文档《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。

](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S RS LS C题1-4图解系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

第3章习题解答

第三章习题解答(部分)［1］求以下序列)(n x 的频谱()j X e ω，其中0a >。

(2)()an e u n - (5)0sin()()an e n u n ω-解：对题中所给的)(n x 先进行z 变换，再求其频谱。

(2)由于111)]([)(----==ze n u e Z z X a an ，所以ωωωj a ez j e e z X e X j --=-==11)()(。

(5)由于aa a ane z e z e z n u n eZ z X 2201010cos 21sin )]()sin([)(-------+-==ωωω，所以ωωj e z j z X e X ==)()(aj a j a j e e e e e e 2200c o s 21s i n ------+-=ωωωωω ［2］设()j X e ω和()j Y e ω分别是()x n 和()y n 的傅里叶变换，试求下面序列的傅里叶变换。

(7)(2)x n (8)(),()20n x n g n n ⎧⎪=⎨⎪⎩＝偶，＝奇解：(7)2)()2()]2([ωωn jn n jn en x en x n x DTFT -∞∞-∞=-∑∑==为偶数　2)]()1()([21ωn j nn e n x n x -∞-∞=-+=∑)(21)(21)(21)(212222⎪⎭⎫⎝⎛+∞-∞=⎪⎭⎫⎝⎛+-∞-∞=-+=+=∑∑πωωπωωj j n n j n n j e X e X e n x e n x(8))()'()2/()]([2''2ωωωj n n j n jn e X en x en x n g DTFT ===∑∑∞-∞=-∞-为偶数［3］求出下面序列的傅里叶变换(1))5(2)(-δ=n n x (4))3()2()(--+=n u n u n x解：由DFT 定义有：(1)ωωωδ52)5(2)(j n jn j e en e X -∞-∞=-=-=∑(4)ωωωωωωj j j n jn n jn j ee e een u n u e X ---=-∞-∞=---==--+=∑∑1)]3()2([)(3222⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--=------ωωωωωωωωωωωω21sin 25sin 11222225252525j j j j j j j j j j e e e e e e e e e e ［5］已知001,()0,j X e ωωωωωπ⎧≤⎪=⎨<≤⎪⎩，求()j X e ω的傅里叶逆变换()x n 。

【信号与系统(郑君里)课后答案】第三章习题解答

3-1 解题过程：（1）三角形式的傅立叶级数（Fourier Series ，以下简称 FS ）f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π，n 为正整数，T 1 为信号周期T 11 t +T（a ）直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T（b ）余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T（c ）正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t（2）指数形式的傅立叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn =其中复数频谱F n= F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e − jn ω1t dt T 1 t 0F n =1( a n − jb n ) F − n = 1 ( a n + jb n ) 2 2由图 3-1 可知， f ( t ) 为奇函数，因而a 0 = a n = 04 Tb n = T ∫02= 2Eπ n4TE−2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 − cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以，三角形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5T指数形式的 FS 的系数为1n = 0, ±2, ±4,F n = − jb n jE=2 n = 0,−± 1, ±3,n π1所以，指数形式的 FS 为f ( t ) = − jE π ej ω1t+ πjE e − j ω1t − 3jE π e j 3ω1t + 3jEπ e − j 3ω1t +3-15 分析：半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅立叶变换有如下两种方法。

《信号与系统》奥本海姆第三章

周期性方波序列的频谱
N1 2 N 10
N1 2 N 20
k
k
N1 1 N 10
k
Generated by Foxit PDF Creator © Foxit Software For evaluation only.

x ( r )e
j
2 kr N
1 ak m
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
4. Paseval定理
DFS x(n) ak
成谐波关系的复指数信号集:
k (n) {e
j (k 2 )n N
}, k 0, 1, 2,...
公共周期为N，集合中只有 N 个信号是彼此独立。一个周期为N的序列有：
x[ n ] ak e
k j(k 2 )n N

k N

ak e
j (k
2 )n N
,其中 k 为N个相连的整数
2 rn N
N ar
1 N
即
1 ar N
2 rn N

n N
n N

x ( n ) e jr 0 n , 0
2 N
一个周期为N的序列有：
x(n)
ak 1 N
k N

ak e
j
2 kn N
DFS
j 2 kn N
n N
Wang Zhengyong
Generated by Foxit PDF Creator © Foxit Software For evaluation only.

信号与线性系统题解第三章

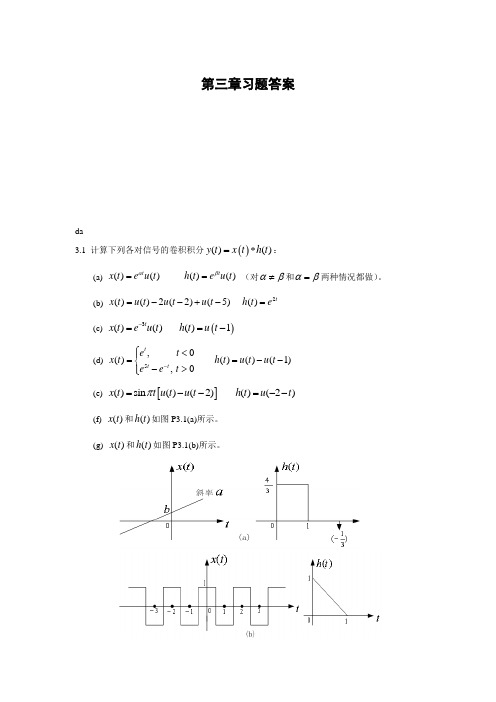
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*：(a) ()()()()t tx t e u t h t e u t αβ==（对αβ≠和αβ=两种情况都做）。

(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。

(g) ()x t 和()h t 如图P3.1(b)所示。

图P3.1 解：(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时，()1()()ttey t e u t αβββα----=-当αβ=时，()()t y t te u t α-=(b) 由图PS3.1(a)知，当1t ≤时，252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时，252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时，52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时，()0y t =(c) 由图PS3.1(b)知，当1t ≤时，()0y t = 当1t >时，133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知：当0t ≤时，11()tt t t y t e d e eττ--==-⎰当01t <≤时，055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时，555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示：(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦，则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知，11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号，由此可推知()()()y t x t h t =*也是周期的，且周期也为2。

信号与系统第三章答案1

时移性
Q 根据傅里叶变换的线性性质可得： 1 U (t ) « p d (w ) + jw 1 U (t - 3) « e - j 3w (p d (w ) + ) 时移性 jw 1 1 = e - j 3wp d (w ) + e - j 3w = p d (w ) + e - j 3w jw jw 1 1 \ U (t ) - U (t - 3) « p d (w ) + - p d (w ) - e - j 3w jw jw 1 = (1- e - j 3w ) jw
2p 5p t ) + 4sin( t ) ，将其表示成复指数信号形 3 3
式，求 Fn ( jnw0 ) ，并画出双边幅度谱和相位谱。
p 解：由三角关系式 sin(a ) = cos(a - ) 可将原式化为： 2 2p 5p p f (t ) = 2 + cos( t ) + 4 cos( t - ) 3 3 2
f (-t ) « F (- jw ) f (t )e ± jw0t « F ( j (w m w0 ) 可得： f (t + 3) « e jw 3 F ( jw ) 1 jw 3 w f (3 + 2t ) « e 2 F ( j ) 2 2 1 - jw 3 w f (3 - 2t ) « e 2 F (- j ) 2 2 (w -1) 1 - j3 (w - 1) jt e f (3 - 2t ) « e 2 F (- j ) 2 2
3.7 一连续周期信号 f (t ) ，周期 T=8，已知其非零傅里叶复系数是：F1 = F-1 = 2 ，
F3 = F-*3 = 4 j ，试将 f (t ) 展开成三角型傅里叶级数，求 An 并画出单边幅度谱和相

信号与系统第三章周期信号的傅里叶级数展开

1 T
2 n 2

T1
f (t ) dt

F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1

三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E

T1

t
2 2
T1
脉冲为，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集

信号与系统第3章(xin ) 信号的频域分析

3 信号的频域分析
2.基本形式（三角形式）
满足狄氏条件的任一周期信号都是由cos，sin组成。连续周期信号的基本形式可以表示为：
a0 f ( t ) ( ak cos k0 t bk sin k0 t ) 2 k 1
2 T 其中：a0 2T f (t )dt T 2
a0 f ( t ) An cos( k0 t n ) 2 t
2 其中：a0 f ( t )dt 是 k 的偶 T

An ak bk
2
2
函数
bk n arctan ak
是k的奇函数
3 信号的频域分析
2.基本形式
满足狄氏条件的任一周期信号都是由cos，sin组成。离散周期信号的基本形式可以表示为：
1 n
f1 (t )
(t nT )
n

重复性、定义域、n、周期等四个要素
3 信号的频域分析
§3.1.1 周期信号的展开（ expansion ）
离散周期信号：
f (n) f (n iN ); n (, ); i 0, 1, 2, ; N C f (n iN )
jk0 t0 jk
有 fT ( t -t0 ) e
C( jk0 ) 2 C( jk ) N
f N ( n n0 ) e
2 n N 0
3 信号的频域分析
§3.1.3 离散频谱的性质
3. 比例特性
若
2 fT ( t ) / f N ( n ) C( jk0 ) / C( jk ) N jk t 0 1 T 2 a
3 信号的频域分析
§3.1.3 离散频谱的性质

信号与系统郑君里第三章连续系统频域分析

编辑状态下，图形演示平移T1/2再翻转。
第3章连续时间信号频域分析
1.三角型傅里叶级数
让· 巴普蒂斯· 约瑟夫· 傅立叶(Jean
Baptiste Joseph Fourier，1768 –1830)，法国著名数学家、物理学家，1817年当选为科学院院士，1822年任该院终身秘书，后又任法兰西学院终身秘书和理工科大学校务委员会主席，主要贡献是在研究热的传播时创立了一套数学理论。小行星10101号傅里叶星、他是名字被刻在埃菲尔铁塔的七十二位法国科学家与工程师其中一位、约瑟夫.傅立叶大学 1807年向巴黎科学院呈交《热的传播》论文，推导出著名的热传导方程，提出任一函数都可以展成三角函数的无穷级数。
��=−1
�� 1 ej��1��
因此得到指数形式的傅里叶级数
∞
��(��) =
��=−∞
��(��1 )ej��1��
第3章连续时间信号频域分析
2.指数型傅里叶级数
��=1
�� = ��0 +
��0 = ��0 = ��0
�� = �� =
2 2 �� + ��
�� = �� cos �� = �� sin ��
第3章连续时间信号频域分析
（1）三角型傅里叶级数系数的计算

信号与系统(第3章)_例题

1 a0 = T
∫
t0 + T
t0
x (t ) dt
直流分量余弦分量幅度正弦分量幅度
2 an = T 2 bn = T
∫ ∫
t0 + T
t0 t0 + T
x ( t ) cos n tdt x ( t ) sin n tdt
t0
(1)x(t) = a0 + ∑( an cos nt + bn sin nt )
周期信号傅立叶级数展开周期信号傅立叶级数展开
三角形式傅立叶级数: 一. 三角形式傅立叶级数: 周期信号x(t)=X(t+nT) ,满足狄氏条件时,可展成: 满足狄氏条件时,可展成: 周期信号
x(t) = a0 + ∑( an cos nt + bn sin nt )
n=1 ∞
2π ( = ) T
其中: 其中:
| F ( jω ) |~ ω :幅度频谱
1 T2 a0 = ∫T x(t)dt =0 T 2
对称于坐标原点
an = 0
2 T bn = ∫ x(t ) sin ntdt T 0
4 T2 = ∫ x(t ) sin ntdt ≠ 0 T 0
奇函数展开成傅立叶级数后, 奇函数展开成傅立叶级数后,直流分量和余弦项为零,正弦项不为零. 弦项为零,正弦项不为零.
π ≤ t ≤ π
tdt = 0
-
π π
-
∫π
π
2 an = ∫ t cos ntdt = 0 T π 其中:T = 2π 2 π 2 bn = ∫ t sin n tdt = ( 1) n +1 n = 1, 2,3, L n T π

信号与系统第3章(陈后金)1

齐次解yh(t)的形式由齐次方程的特征根确定
特解yp(t)的形式由方程右边激励信号的形式确定
一、系统的零输入响应
定义：系统的零输入响应是输入信号为零，仅由系统的初始状态单独作用而产生的输出响应。数学模型:
y ( n) (t ) an1 y ( n1) (t ) a1 y ' (t ) a0 y(t ) 0 求解方法：根据微分方程的特征根确定零输入响应的形式
y ( n ) (t ) an 1 y ( n 1) (t ) a1 y ' (t ) a0 y (t ) bm x ( m ) (t ) bm 1 x ( m 1) (t ) b1 x ' (t ) b0 x(t )
ai 、 bj为常数。
离散LTI系统用n阶常系数线性差分方程描述
则
dx(t ) dy (t ) T{ } dt dt
离散时间系统，若 T{x[k]}= y[k] 则 T{ x[k] -x[k-1]}= y[k] - y[k-1]
线性非时变(LTI)系统的特点
4．积分（求和）特性
连续时间系统，若 T{x(t)}=y(t) 则
T {
t
x( )d }
2
非线性系统非线性系统线性系统线性系统
(3) y(t ) 4 y(0) x(t ) 3x(t )
dx(t ) (4) y(t ) 4 y(0) 2 sin t dt
不满足可分解性
(5) y[k ] ky[0]

i 0
k
x[i]
线性非时变(LTI)系统的特点
2．非时变特性
1
0
1
t
0

信号与线性系统分析 (吴大正第四版)第三章习题答案精编版

第三章习题3.1、试求序列k01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩，的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。

3.6、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。

1）()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3）()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5）1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求下列差分方程所描述的离散系统的单位序列响应。

2）()-(-2)()=y k y k f k5）()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。

（a）（c）3.10、求图所示系统的单位序列响应。

3.11、各序列的图形如图所示，求下列卷积和。

（1）12()()f k f k *（2）23()()f k f k *（3）34()()f k f k *（4）[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。

3.14、求图所示系统的单位序列响应和阶跃响应。

3.15、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=，求其单位序列响应。

3.16、如图所示系统，试求当激励分别为（1）()()f k k ε= （2）()()0.5()kf k k ε=时的零状态响应。

3.18、如图所示的离散系统由两个子系统级联组成，已知()1=2cos4k h k π，()()2=k h k k a ε，激励()()()=--1f k k a k δδ，求该系统的零状态响应()zs k y 。

（提示：利用卷积和的结合律和交换律，可以简化运算。

）3.22、如图所示的复合系统有三个子系统组成，它们的单位序列响应分别为()()1=h k k ε，()()2=-5h k k ε，求复合系统的单位序列响应。

信号与系统课后答案第三章作业答案

u(t1)]
（4） f (t) sin t h(t) u(t1)
f (t) h(t) h '(t)
t
sin
w0
u
(
)
d
(t1)
t 0
sin
w0
d

(t1)
[
1 w0
(1
cos
w0t )] u(t)

1 w0
[1
cos
w0 (t

1 4
(et

e3t
)u(t)

1 2
t
e3tu(t)

[
1 4
et

(
1 2
t

1 4
)e3t
]u
(t)
3-19 一个 LTI 系统，初始状态不祥。当激励为 f (t) 时其全响应为
(2e3t sin 2t)u(t) ；当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
3-1 已知系统微分方程、起始条件以及激励信号分别为
dy(t dt
)

3
y(t
)

4
x(t
),
y
(0
)

2,
x(t
)

e2t
u(t
)
试求解该系统的全响应。
解：由题可知：
dy(t) dt

3
y(t)

4x(t)
的特征方程为

3=0；
=-3
（1）零输入响应：
yx (t) C1e3tu(t)

郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第3章傅里叶变换【圣才出品】

表 3-1-4 时域及频域抽样
4 / 111
圣才电子书

十万种考研考证电子书、题库视频学习平台
2．周期信号和抽样信号的特性（见表 3-1-5）表 3-1-5 周期信号和抽样信号的特性对比
五、雷达测距原理，雷达信号的频谱设雷达的射频脉冲的持续时间为 T0，发送信号的周期为 T1，目标与雷达之间的距离为 d（以 m 为单位），光速为 c，τ 代表往返时间，则有 τ＝2d/c。为考察测距精度质量给出以下两个指标数据：
圣才电子书
十万种考研考证电子书、题库视频学习平

台
且 f＝5kHz，得：T＝1/f＝200μs
所以
a0
1 T
T
2 T
2
f (t)dt
1 T
2 2
Edt
T
E
20 10 200
1V
an
2 T1
t0 T1 f (t) cos(nt)dt 2
t0
T
2
E
cos(nt)dt
π
π
3π
3π
其中 ω＝2π/T。
3-2 周期矩形信号如图3-2-2所示。若重复频率 f＝5kHz，脉宽 τ＝20μs，幅度 E＝10V，求直流分量大小以及基波、二次和三次谐波的有效值。
图 3-2-2 解：由图 3-2-2 可知，f（t）为偶函数，其傅里叶级数不含正弦项，因此 bn＝0。
7 / 111
3.2 课后习题详解
3-1 求图 3-2-1 所示对称周期矩形信号的傅里叶级数（三角形式与指数形式）。
图 3-2-1
解：（1）三角形式
由图 3-2-1 可知，f（t）为奇函数且无直流分量，故有 a0＝an＝0。

信号与系统课后习题与解答第三章

3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1解由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示；（2）)(2t f 的谱线间隔和带宽；（3）)(1t f 与)(2t f 的基波幅度之比；（4）)(1t f 基波与)(2t f 三次谐波幅度之比。

[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案

[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案第一章习题-t1-1 画出下列各信号的波形:(1) f(t)=(2-e)U(t); (2) 1-tf(t)=ecos10πt×[U(t-1)-U(t-2)]。

2答案f(t)1 (1)的波形如图1.1(a)所示.,2T,,0.2sf(t)cos10,t,102(2) 因的周期,故的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案f(t),t[u(t),u(t,1)]，u(t,1)1f(t),,(t,1)[u(t),u(t,1)]2f(t),(t,2)[u(t,2),u(t,3)]31-3 写出图题1-3所示各信号的函数表达式。

答案11,(t，2),t，1,2,t,0,22f(t),,1110,t,2,(,t，2),,t，122,f(t),u(t)，u(t,1)u(t,2)2,f(t),,sint[u(t，2),u(t,2)]32f(t),u(t，2),2u(t，1)，3u(t,1),4u(t,2)，2u(t,3)421-4 画出下列各信号的波形:(1) f(t)=U(t-1); (2) f(t)=(t-1)U(t-1); 1222(3) f(t)=U(t-5t+6); (4)f(t)=U(sinπt)。

34答案f(t),u(t,1)，u(,t,1)1 (1) ,其波形如图题1.4(a)所示.f(t),(t,1)[u(t,1)，u(,t,1)],(t,1)u(t,1)，(t,1)u(,t,1)2(2)其波形如图题1.4(b)所示.f(t),u(,t，2)，u(t,3)3(3) ,其波形如图1.4(c)所示.f(t),u(sin,t)4(4) 的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T。

,,2(1)f(t),2cos(2t,)(1)f(t),[sin(t,)]1246; ; (3) f(t),3cos2,tU(t)3。

郑君里《信号与系统》(第3版)(上册)(章节题库傅里叶变换)【圣才出品】

(0 )]
1
[e e ] j(0 )t0
j ( 0 )t0
2
1
(e e )e j0t0
j0t0 jt0
2
1
e
jt0
cos(0t0 )
5．设 f（t）的频谱函数为 F（jω），则【答案】2F（-2ω）ej2ω
的频谱函数等于（）。
【解析】
可写为 f[-1/2（t+2）],根据傅里叶变换的尺度变换性质，
图 3-1 【答案】
【解析】由图可以得出 f2 (t) 和 f1(t) 的关系， f2 (t) f1(t) f1(t 1) ，故 f2 (t) 的
傅里叶变换为。
4 / 133
圣才电子书

十万种考研考证电子书、题库视频学习平台
7．信号
的傅里叶变换为（）。
【答案】
j
【解析】将原式分解，t
e4t
e
2u(
t
1 2
)
，
u(
t
1 2
)
对应信号频域为
e2 j
， e4t 对应频
j 4
j
域频移
e j
2
4
， e2 为常数，直接乘上后频谱变为，
e j
2
4 ，由频域微分特性知，乘以
t
j 4
e2 对应频域求导，即对 j 4 求导，最后得到答案。
8．已知 f（t）的傅里叶变换为 F（jω），则
【答案】Y ( j)
1 2
(e j0t0
e j0t0 )e jt0
1
e jt0
cos(0t0 )
【解析】对于 x1(t) ，傅立叶变换为 e jt0 ，所以

信号与系统第三章习题部分参考答案

↔ 2π e−a⎜−ω⎜
（4）单边指数信号 ∵ e−atu(t) ↔ 1 a + jw
∴ 1 ↔ 2π e−a(−w)u(−w) a + jt
即 1 ↔ 2π eawu(−w) a + jt
3.20 求下列各傅里叶变换的原函数
（1） F (ω) = δ (ω − ω0 ) （2） F (ω) = u(ω + ω0 ) − u(ω − ω0 )；
2π
（2）[1 + mf (t)]cos(w0t) = cos(w0t) + mf (t) cos(w0 (t)
↔
π [δ
(w
+
w0
)
+
δ
(w
−
w0
)]
+
m 2
{F[
j(w
+
w0
)
+
F[
j(w
−
w0
)]}
（3） f (6 − 3t) = f [−3(t − 2)] ↔ 1 F (− 1 jw)e− j2w
−τ τ
w
方法二利用时域微分性质
对 f(t)求一阶导数得到
f
′(t)
=
1 τ
G2τ
(t)
−
δ
(t
+
τ
)
−
δ
(t
−
δ
)
F1 (w) = 2sa(wτ ) − 2 cos(wτ )
F1 (0) = 0
F (w) =
F1 (w) jw
+
πF1
(0)δ
(w)
=
j
2 [cos(wτ ) − sa(wτ )] w

信号与系统第3章傅里叶变换

3.11 抽样定理
傅里叶生平

1768年生于法国 1807年提出“任何周期信号都可用正弦函数级数表示” 1829年狄里赫利第一个给出收敛条件拉格朗日反对发表 1822年首次发表“热的分析理论”中
傅里叶的两个最主要的贡献——

―周期信号都可表示为成谐波关系的正弦信号的加权”—— 傅里叶的第一个主要论点 “非周期信号都可用正弦信号的加权积分表示”——傅里叶的第二个主要论点
cos（α＋β）＝cosαcosβ－sinαsinβ
cos（α－β）＝cosαcosβ＋sinαsinβ
3.3 典型周期信号的傅里叶级数
本节以周期矩形脉冲信号为例进行分析主要讨论：频谱的特点，频谱结构，频带宽度，能量分布。其他信号: 周期锯齿脉冲信号周期三角脉冲信号周期半波余弦信号
周期全波余弦信号请自学。
六．周期信号的功率
周期信号平均功率=直流、基波及各次谐波分量有效值的平方和；也就是说，时域和频域的能量是守恒的。
证明
对于三角函数形式的傅里叶级数平均功率
对于指数形式的傅里叶级数
总平均功率=各次谐波的平均功率之和
三角函数公式 sin（α＋β）＝sinαcosβ＋cosαsinβ
sin（α－β）＝sinαcosβ－cosαsinβ
例1
不满足条件1的例子如右图所示，这个信号的周期为8，它是这样组成的：后一个阶梯的高度和宽度是前一个阶梯的一半。可见在一个周期内它的面积不会超过8，但不连续点的数目是无穷多个。
f (t ) 1
1 2
L 8 O 8
L t
例2
不满足条件2的一个函数是
f (t ) 1 L L O 1 t