信号与系统第一章习题和重点(精)
信号与系统第一章(重点)
－1
图 1.2-1 连续时间信号
离散时间信号：亦称序列， 其自变量n是离散的， 通常为整数。 若是时间信号 （可为非时间信号）， 它只在某些不连续的、 规定的瞬时给出确定的函数值， 其它 时间没有定义， 其幅值可以是连续的也可以是离散的， 如图1.2-2所示。
x1(n) 2
1
只能取－1,0,1,2
0
t
－1
6. 单位冲激偶函数δ′(t)
单位冲激函数的导数。
(t)
1 lim
0
u(t
)
2
u(t
2)
(t)
d(t)
dt
1 lim
0
(t
)
2
(t
2)
(1.3-30) (1.3-31)
式（1.3-31）取极限后是两个强度为无限大的冲激函数，
0
t
－k
3. 复指数信号
f(t)=kest
s=σ+jω为复数， σ为实部系数， ω为虚部系数。 借用欧拉公式： kest=ke(σ+jω)t=keσt e jωt=keσt cosωt+jkeσt sinωt 复指数信号可分解为实部与虚部。 实部为振幅随时间变化的余弦函数， 虚部为振幅随时间变化的正弦函数。
第1章 信号与系统
1.1 信号与系统概述 1.2 信号及其分类 1.3 典型信号 1.4 连续信号的运算 1.5 连续信号的分解 1.6 系统及其响应 1.7 系统的分类 1.8 LTI系统分析方法
1.1 信号与系统概述
人们每天都与载有信息的信号密切接触:
听广播、看电视是接收带有信息的消息； 发短信、打电话是传送带有信息的消息。
信号与线性系统分析习题答案
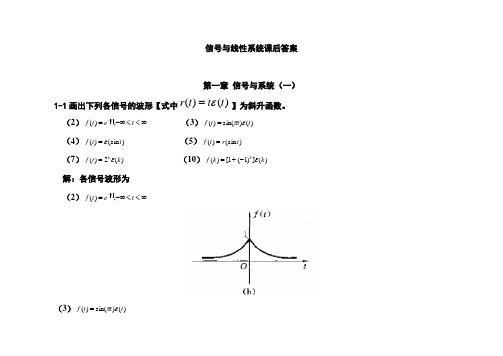
信号与线性系统课后答案第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)tf=r(sin)(t（7）)tf kε(k=(2)（10）)f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
信号与系统第一章习题及作业(1,2)
(2)（余弦序列是否为周期信号，取决于2л/Ω0是正整 （余弦序列是否为周期信号，取决于 Ω 有理数还是无理数。） 数、有理数还是无理数。） 因此， 因此， 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7； 所以基波周期为N=7； N=7
因为2л/Ω =16л 为无理数， (4) 因为 Ω0=16л,为无理数，则此信号不是周期 信号． 信号． (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统？为什么？ 、判断是否为线性系统？为什么？
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的？非时变的？因果的？ 试确定系统是否为线性的？非时变的？因果的？
解：积分系统是线性的，因此系统是线性系统。 积分系统是线性的，因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
《信号与系统》第一章知识要点+典型例题
y() 表示系统的输出。
1、线性系统与非线性系统 若系统满足下列线性性质： （1）可分解性 全响应 y () 可分解为零输入响应 y zi () 与零状态响应 y zs () 之和，即
y() y zi () y zs ()
（2）齐次性 零输入响应 y zi () 满足齐次性，零状态响应 y zs () 满足齐次性，即
( t ) 、 ( t ) 的重要性质
1
( t )dt 1 ，
t
( t )dt 0 ， ( t )dt ( t ) ( k ) (k )
f ( k ) ( k ) f (0) ( k ) f ( k ) ( k k 0 ) f ( k 0 ) ( k k 0 )
f ( t ) ( t a )dt f (a )
k
f ( k ) ( k ) f (0)
(at )
5
1 (t ) a
1 b (at b) ( t ) a a f ( t ) ( t ) f (0) ( t ) f (0) ( t ) f ( t ) ( t ) f (0) ( t ) f (0) ( t )
2
。
而对离散的正弦（或余弦）序列 sin( k ) [或 cos( k ) ]( 称为数字角频率，单位为 rad )， 只有当
2
为有理数时才是周期序列，其周期 N M
2
， M 取使 N 为整数的最小整数。
如对信号 cos(6 k ) ，由于
2
2 1 为有理数，因此它是周期序列，其周期 N 1 。 6 3
信号与系统课后习题与解答第一章
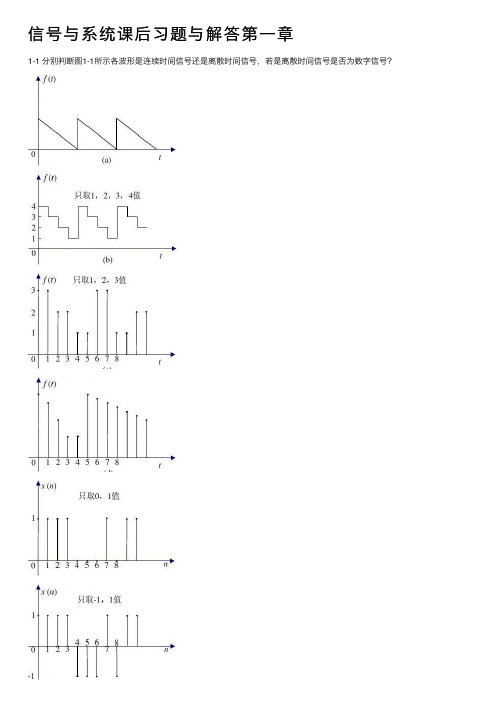
信号与系统课后习题与解答第⼀章1-1 分别判断图1-1所⽰各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解信号分类如下：--???--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所⽰信号分别为（a ）连续信号（模拟信号）；（b ）连续（量化）信号；（c ）离散信号，数字信号；（d ）离散信号；（e ）离散信号，数字信号；（f ）离散信号，数字信号。
1-2 分别判断下列各函数式属于何种信号？（重复1-1题所⽰问）（1）)sin(t e at ω-；（2）nT e -；（3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）221。
解由1-1题的分析可知：（1）连续信号；（2）离散信号；（3）离散信号，数字信号；（4）离散信号；（5）离散信号。
1-3 分别求下列各周期信号的周期T ：（1）)30t (cos )10t (cos -；（2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解判断⼀个包含有多个不同频率分量的复合信号是否为⼀个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为⾮周期信号。
（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15T 2π=。
由于5π为21T T 、的最⼩公倍数，所以此信号的周期5T π=。
（2）由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
（3）因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-?=所以周期8162T ππ==。
信号与系统课后习题答案
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(应自炉)习题答案第1章 习题解重点
(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数，令1k =，则基波周期为2π。
1-2．
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解：cos(101 t +的基波周期为15
π，s i n (4
1-8．
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解：（a）((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--（b）([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π，故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3．
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
（1）(t f -1（2）((t f t f -+-21（3）((t f t f --21（4）(t f 3（5）(f
信号与系统课后题解第一章
（6） f (2 − t ) （8） f (− 2 − t )ε (− t )
图 1.14
【知识点窍】本题考察信号的绘制及自变量变换导致信号变换的概念 【逻辑推理】本题用到信号的时域运算与变换。 解： （1） f (2t ) 信号的波形如图 1.15 所示。 （2） f (t )ε (t ) 信号的波形如图 1.16 所示。
t
ε [sin π t ]
1 … -2 -1 1 2 3 …
t
（b） 图 1.8 （9） 2 −n ε [n ] 函数式的信号的波形如图 1.9（c ）所示. 。
ε [n]
1 0 1 … 2 1
2−n
-1
n
-1 （a） 0 1 2
…
n
（b）
2 −n ε [n ]
1 … -1 0 1 2 （c ）
7
n
4
cos ω (t − t 0 )
1 … …
t0பைடு நூலகம்
-1 （a）
t
cos [ω (t − t 0 )]ε (t )
1 …
t0
-1
t
（b） 图 1.3
cos ω (t − t 0 )
1 …
t0
-1
t
图 1.4 （5） ε (t 0 − t ) （6） ε (t 0 − 2t )
t 0 > 0 函数式的信号的波形如图 1.5（b）所示. 。 t 0 > 0 函数式的信号的波形如图 1.6 所示. 。
T
2
（4） 3 cos (ω 0t + θ ) 是功率信号，其平均功率为：
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
， 与模拟
以 q' y ' 1x 代入前式
y ' q' 1x
y (t )
( y'1x)' 0 x 0 y 1( y'1x)
整理，得：
与原方程对照，有 《信号与系统》SIGNALS AND SYSTEMS
q" 画系统 x(t ) q ( 3) 模拟图：
5
11
q'
q
15
y (t )
15 《信号与系统》SIGNALS AND SYSTEMS
ZB
1-23 已知某系统的数学模型为 其模拟图如下，试导出微分方程中的系数 图中的系数 的关系。 解：设辅助函数 q" x(t ) 如图所示，则 q" 0 x 0 y 1q' q' q"
f (t ) 2
(2)
2
f ( t 2)
2
0
1
t f( ) 2
t
0
3
f (t 2)
t
(4)
(3)
2
2
4
《信号与系统》SIGNALS AND SYSTEMS
0
2 t
0
1
4 t
ZB
1-14 试判别下列系统是否为线性系统，并说明理由。其 中x(t)为激励，q(0)为初始状态，y(t)为响应。
SIGNALS AND SYSTEMS
信号与系统
第一章 信号与系统的基本概念 习题
南京邮电大学 信号分析与信息处理教学中心
2006.1
《信号与系统》SIGNALS AND SYSTEMS
ZB
1-1 下列信号中哪些是周期信号，哪些是脉冲信号？哪 些是能量信号？哪些是功率信号它们的平均功率各为多 少？ 0t 0t j ( t )
1 T 1 1 lim dt 1 T 2T T 2 2
T
所以,该信号为
dt
周期功率信号。
另 解：对 于 不 同 频 率 的 正 弦 信 号，其平均功率可以叠 加， 2 2 2 2 所以 P( ) ( ) 1 2 2 《信号与系统》SIGNALS AND SYSTEMS
1-21 某系统的数学模型如下，初始状态为0，试画出该系 统的模拟图。 解： 设： q(3) (t ) 5q" (t ) 11q' (t ) 15q(t ) x(t ) 则： y(t ) q" (t ) 15q(t ) 对所假设系统，有：
(3)
q
(t ) x(t ) 5q" (t ) 11q' (t ) 15q(t )
解：因为零输入响应是非线性的，所以该系统为非线性 系统。 1-15 试判别下列零状态系统是否为线性系统，是否为时 不变系统。
解：（5）为非线性（取函数的绝对值为非线性运算） 时不变系统 （10）为非线性（取函数的平方为非线性运算）时 变（两个函数相乘）系统 《信号与系统》SIGNALS AND SYSTEMS ZB
ZB
ZB
1-3 试绘出下列各信号的波形，注意它们的区别。 解： (6) (t 1) (t 1) (4) (t 1) (t )
0 1
1
t
0
1
2
t
(8) t[ (t 1) (t 2)]
t
0
1
2
《信号与系统》SIGNALS AND SYSTEMS
2
ZB
1-7 信号 f (t ) 的波形如图所示，绘出 f ' (t )， f ( )d 的波形。
《信号与系统》SIGNALS AND SYST8) P lim f (t )dt T 2T T
1 lim 2T
0t 0t 2 0t 2 0t 2 cos sin sin cos dt 4 4 5 5 T T 20t 0t 1 cos 1 cos 1 T t t 5 2 2 cos 0 sin 0 lim 2 4 5 2 T 2T T
1-16 试判别下列零状态系统是否为线性系统，是否为时 不变系统。
解：（5）为非线性时不变系统 1-17 试判别下列零状态系统是否为线性系统，是否为时 不变系统，是否为因果系统。
解：（1）为线性、时不变、因果系统 （6）为非线性、时变、非因果[y(0)与x(5)有关]系统 《信号与系统》SIGNALS AND SYSTEMS
ZB
1-20 某系统的框图如图所示，试求
解：
x1(t )
x1 x2
( )2
( x1 x2 )2
x2 ( t )
1
x1 x2
( )2
( x1 x2 )2
1 4
y (t )
1
1 y (t ) {[[ x1(t ) x2 (t )]2 [[ x1(t ) x2 (t )]2 } 4 x1(t ) x2 (t ) 《信号与系统》SIGNALS AND SYSTEMS ZB
(2) (t ) (t 1) (5) 3e
0
(8) cos
解：
4
sin
5
( 2) E lim
T T
T
f (t ) dt
2
1
12dt 1
0
所以，该信号为脉冲能 量信号。
1 1 2 (5) P lim f (t ) dt lim 32dt 9 T 2T T T 2T T 所以，该信号为周期功 率信号。
t
f (t )
f (t )
1 1 0 1 1 2 t
1 1 0 1 2
(1)
1
f ( 1) (t )
2
t
解：
f ' (t )
(1)
1 t 1 0 1 2
ZB
1 0
《信号与系统》SIGNALS AND SYSTEMS
1 2 ( 2)
t
1-9 信号f (t )的波形如图所示 , 绘出下列各函数对 t 的波形。 解：