信号与系统课后习题与解答第一章
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与线性系统分析习题答案
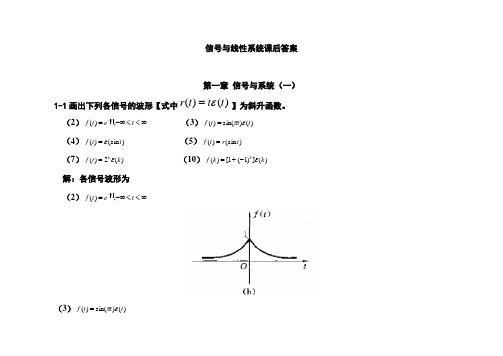
信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统(第1章)上册课后习题答案

0, 0 等幅 0, 0 增幅振荡 0, 0 衰减
第 21 页
4.抽样信号(Sampling Signal)
O
2
2
第 37 页
c.表示符号函数 符号函数:(Signum)
1 sgn( t ) 1
1 u( t ) [sgn( t ) 1] 2
sgnt
t 0 t0
O
t
sgn( t ) u( t ) u( t ) 2u( t ) 1
第 38 页
e
j t
cost j sint
第 20 页
3.复指数信号
f ( t ) Ke st
Ke t cos t jKe t sin t
为复数,称为复频率
( t )
s j
, 均为实常数
的量纲为1 /s , 的量纲为rad/s 讨论
瞬态信号:除准周期信号外的 一切可以用时间函数描述的非 周期信号。
第 10 页
3.连续信号和离散信号
连续时间信号:信号存在的 时间范围内,任意时刻都有定 义(即都可以给出确定的函数 值,可以有有限个间断点)。 用t表示连续时间变量。 离散时间信号:在时间上是 离散的,只在某些不连续的规 定瞬时给出函数值,其他时间 没有定义。 用n表示离散时间变量。
f t f at a 0 波形的压缩与扩展,尺度变换
f (t ) f t 2
f t
2
1
t f 2
2
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统教程习题解析(前七章)
3-19 一线性时不变 变系统,在 在某起始状态 态下,已知 知当输入f t 响应 应y t 3e ε t ;当 当输入f t ε t 时,全响应 时 y t e 系统 统的冲激响应h t 。 解 因为零状态响应 应 ε t → s t , 故有 有 y t y t 从而 而有 y t
10
8
3-10 试用算子法求 求下列系统 的冲激响应 应h t 。 a y 解 t 3y t 2y t p 从而 而有 H p 利用 用公式(3-3 31) K 可得 得K 于是 是 H p
5f t 3p 2 y t
7f 7 t 5p 7 f t K p 1 p K 2
d y t
试判断该系统是否为线性时不变系统? 解
(a) 线性;(b) 线性时不变;(c) 线性时变;(d) 非线性时不变。
1-7 若有线性时不变系统的方程为 y′ t 若在非零f t 作用下其响应y t y′ t 的响应。 解 因为f t ↔ y t 1 e ,由线性关系,则 2 1 e e e 2 e e 1 ay t 2f t f t f′ t
i
0 ⇒ u 0
du dt 2V
u R C
i C
i 0 1A 1 u 0 1 R C
2 V
1 1V
3-5 设有 有一阶系统方程 y t 因方 方程的特征根 根λ δ t 时,则冲激 时 响应 h t g t ∗ δ t 3e
3 3y t 3, 故有 g t
f t
f t
试求 求其冲激响应 h t 和阶 阶跃响应 s t 。 解 当f t e ε t g t ε t
解
因为 t , |t| f t τ 0, |t| t e τ j2 τ
为奇 奇数,故 F ω f t e dt dt tsin nωtdt
信号与系统课后题解第一章

(6) f (2 − t ) (8) f (− 2 − t )ε (− t )
图 1.14
【知识点窍】本题考察信号的绘制及自变量变换导致信号变换的概念 【逻辑推理】本题用到信号的时域运算与变换。 解: (1) f (2t ) 信号的波形如图 1.15 所示。 (2) f (t )ε (t ) 信号的波形如图 1.16 所示。
t
ε [sin π t ]
1 … -2 -1 1 2 3 …
t
(b) 图 1.8 (9) 2 −n ε [n ] 函数式的信号的波形如图 1.9(c )所示. 。
ε [n]
1 0 1 … 2 1
2−n
-1
n
-1 (a) 0 1 2
…
n
(b)
2 −n ε [n ]
1 … -1 0 1 2 (c )
7
n
4
cos ω (t − t 0 )
1 … …
t0பைடு நூலகம்
-1 (a)
t
cos [ω (t − t 0 )]ε (t )
1 …
t0
-1
t
(b) 图 1.3
cos ω (t − t 0 )
1 …
t0
-1
t
图 1.4 (5) ε (t 0 − t ) (6) ε (t 0 − 2t )
t 0 > 0 函数式的信号的波形如图 1.5(b)所示. 。 t 0 > 0 函数式的信号的波形如图 1.6 所示. 。
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期8162T ππ==。
(4)由于原函数⎩⎨⎧+<≤+-+<≤=2)T(2n t T )12n (,11)T(2n t 1,2nT n 为正整数其图形如图1-3所示,所以周期为2T 。
图1-31-4对于教材例1-1所示信号,由f (t )求f (-3t-2),但改变运算顺序,先求f (3t )或先求f (-t ), 讨论所得结果是否与原例之结果一致。
解 原信号参见例1-1,下面分别用两种不同于例中所示的运算顺序,由f (t )的波形求得f (-3t-2)的波形。
两种方法分别示于图1-4和图1-5中。
方法一:倍乘32左移方法二:32左移图1-4图1-51-5 已知f (t ),为求)(0at t f -应按下列那种运算求得正确结果(式中a t ,0都为正值)? (1))(at f -左移0t ;(2))(at f 右移0t ;(3))(at f 左移a t0;(4))(at f -右移at0。
解 (1)因为)(at f -左移0t ,得到的是[])()(00at at f t t a f --=+-,所以采用此种运算不行。
(2)因为)(at f 右移0t ,得到的是[])()(00at at f t t a f -=-,所以采用此运算不行。
(3)因为)(at f 左移a t 0,得到的是)()(00t at f a t t a f +=⎥⎦⎤⎢⎣⎡+,所以采用此运算不行。
(4)因为)(at f -右移a t 0,得到的是)()(00at t f a t t a f -=⎥⎦⎤⎢⎣⎡--,所以采用此运算不行。
1-6 绘出下列各信号的波形:(1))8sin()sin(211t t Ω⎥⎦⎤⎢⎣⎡Ω+;(2)[])8sin()sin(1t t ΩΩ+。
解 (1)波形如图1-6所示(图中)8sin()sin(211)(t t t f Ω⋅⎥⎦⎤⎢⎣⎡Ω+=)。
(2)波形如图所示1-7(图中[1)(t f +=1-7 绘出下列各信号的波形:(1)[])4sin()()(t TT t u t u π--;(2)[])4sin()2()(2)(t TT t u T t u t u π-+--。
解 )4sin(t Tπ的周期为2T。
(1)波形如图1-8(a )所示(图中[])4sin()()(t TT t u t u π--)。
在区间[]T ,0,内,包含有)4sin(t Tπ的两个周期。
图1-8(2)波形如图1-8(b )所示(图中[])4sin()2()(2)(t TT t u T t u t u π-+--)。
在区间[]T T 2,内是)4sin(t T π-,相当于将)4sin(t Tπ倒像。
1-8 试将教材中描述图1-15波形的表达式(1-16)和(1-17)改用阶越信号表示。
解 表达式(1-16)为⎩⎨⎧-==---)(0)(t t a atate e e tf ()()∞<≤<<t t t t 000当当 这是一个分段函数。
若借助阶越信号,则可将其表示为[])()()(][)()(e )(0)(0)(000t t u e t u e t t u e e t t u t u t f t t a at t t a at at --=--+--=-------] 表达式(1-17)为⎪⎩⎪⎨⎧∞<≤---<<-=----∞-⎰)()1(1)1(1)0()1(1)(0)(00t t e a e at t e a d f t t a at at t ττ 借助阶越信号,可将其表示为 )(]1[1)()(1)(]1[1)1(1)]()()[1(1)(0)(0)(000t t u e a t u e a a t t u e a e a t t u t u e a d f t t a at t t a atat t ----=-⎭⎬⎫⎩⎨⎧---+---=-------∞-⎰ττ1-9 粗略绘出下列各函数式的波形图: (1))()2()(t u e t f t --=; (2))()63()(2t u e e t f t t --+=; (3))()55()(3t u e e t f t t ---=;(4))]2()1()[10cos()(---=-t u t u t e t f t π。
解图1-9(1)信号波形如图1-9(a )所示。
(2)信号波形如图1-9(b )所示。
(3)信号波形如图1-9(c )所示。
(4)信号波形如图1-9(d )所示。
在区间[1,2]包含)10cos(t 的5个周期。
1-10 写出如图所示各波形的函数式。
(a)(b)(c)图1-10解 (a )由图1-10(a )可写出⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤≤-+=)(0)20(211)02(211)(其它t t t t t f于是)]2()2([21)(--+⎪⎪⎭⎫ ⎝⎛-=t u t u t t f (b )由图1-10(b )可写出⎪⎪⎩⎪⎪⎨⎧>≤<≤<≤=23)21(2)10(1)0(0)(t t t t t f于是)2()1()()2(3)]2()1([2)]1()([)(-+-+=-+---+--=t u t u t u t u t u t u t u t u t f 实际上,可看作三个阶越信号)2()1()(--t u t u t u ,,的叠加,见图1-11,因而可直接写出其函数表达式为图1-11)2()1()()(-+-+=t u t u t u t f (c )由图1-10(a )可写出⎪⎩⎪⎨⎧<≤⎪⎭⎫⎝⎛=)(0)0(sin )(其它T t t T E t f π于是)]()([sin )(T t u t u t T E t f --⎪⎭⎫⎝⎛=π1-11绘出下列各时间函数的波形图: (1))(t u te t -;(2))]2()1([)1(-----t u t u e t ; (3))]2()()][cos(1[--+t u t u t π;(4))2()1(2)(-+--t u t u t u ;(5)[])()(sin 00t t a t t a --; (6))](sin [t tu e dtdt -。
解 (1)信号波形如图1-12(a)所示,图中)()(t u te t f t -=。
图1-12(b )(c )(2)信号波形如图1-12(b)所示,图中)]2()1([)()1(---=--t u t u et f t 。
(3)信号波形如图1-12(c)所示,图中)]2()()][cos(1[)(--+=t u t u t t f π。
(4)信号波形如图1-12(d)所示,图中)2()1(2)()(-+--=t u t u t u t f 。
(5)信号波形如图1-12(e)所示,图中[])()(sin )(00t t a t t a t f --=,信号关于0t t = 偶对称。
(6)因为 )(4cos 21)(cos )(sin )(sin )(cos )(sin )](sin [t u e t t tu e t tu e t t e t tu e t tu e t tu e dtd t t t t t t t-------⎪⎭⎫⎝⎛+=+-=++-=πδ所以该信号是衰减正弦波。
其波形如图1-12(f)所示,图中)](sin [)(t tu e dtd t f t-=。
1-12 绘出下列各时间函数的波形图,注意它们的区间: (1))]1()([--t u t u t ; (2))1(-⋅t u t ;(3))1()]1()([-+--t u t u t u t ; (4))1()1(--t u t ;(5))]1()()[1(----t u t u t ; (6))]3()2([---t u t u t ;(7))]3()2()[2(----t u t u t 。
解 (1)信号波形如图1-13(a)所示,图中)]1()([)(--=t u t u t t f 。
图1-13(b )(c )(e )(2)信号波形如图1-13(b)所示,图中)1()(-⋅=t u t t f 。
(3)信号波形如图1-13(c)所示,图中)1()]1()([)(-+--=t u t u t u t t f 。
(4)信号波形如图1-13(d)所示,图中)1()1()(--=t u t t f 。
(5)信号波形如图1-13(e)所示,图中)]1()()[1()(----=t u t u t t f 。
