信号与系统西安邮电习题答案
信号与系统习题部分参考答案
信号与系统第三章习题部分参考答案3-2 已知连续时间周期信号()⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=35sin 432cos 2t t t f ππ。
将其表示成复指数傅立叶级数形式，求n F ，并画出双边幅度谱和相位谱。
解：由于()t f 为连续的时间周期信号。
由于题易知T=61ω=3π又()⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=35sin 432cos 2t t t f ππ即有2=a 12=a 45=b 200==a F ()2121222=−=jb a F ()221555j jb a F −=−=431F F F ==故()53322212t j tj jee tf ππ−+=又nn F F −=其双边幅度谱如图 3-2-1所示易知43210ϕϕϕϕϕ====25πϕ−=25πϕ=−其相位谱如图 3-2-2所示15w −12w −012w 15w wnF 0F 2 15−F 2−F 2F 5F 图 3-2-115w −015w wnϕ2π2π−图3-2-2 相位谱3-4 如题图3-4所示信号，求指数形式和三角形式的傅里叶级数。
所示信号，求指数形式和三角形式的傅里叶级数。
()t f 1EE −T2/T 题图3－4t()t f 21T t()t f 31TT−00T−T 24T 4T −t()t f 61TT−04T 4T −2T 2T −()t f 5()t f 4A TT2T−A TT−4T 4T−00()a ()b ()c()d()e ()f ttt解：（a ） 由于)(1t f 为奇函数故有为奇函数故有 00=a })sin()sin([2202∫∫+=−TT n dt nwt dt nwt T E b=]1)[cos(2−ππn n E0 n=2k N k ∈πn E4− n=2k+1 N k ∈∴ ]))12sin((121)5sin(51)3sin(31)[sin(4)(1⋅⋅⋅++++⋅⋅⋅⋅+++−=wt k k wt wt wt E t f π=)sin(]1)[cos(121nwt n nEn −−∑∞=ππ]1)[cos()(21−−=−=ππn n E j jb a F n n njnwt jnwt n e n n E j e F t f }1)[cos(1)(1−−==∑∑+∞∞−+∞∞−ππ3-8：设()()ωF t f ↔，试用()ωF 表示下列各信号的频谱。
西安邮电大学2012年824信号与系统考研真题及答案
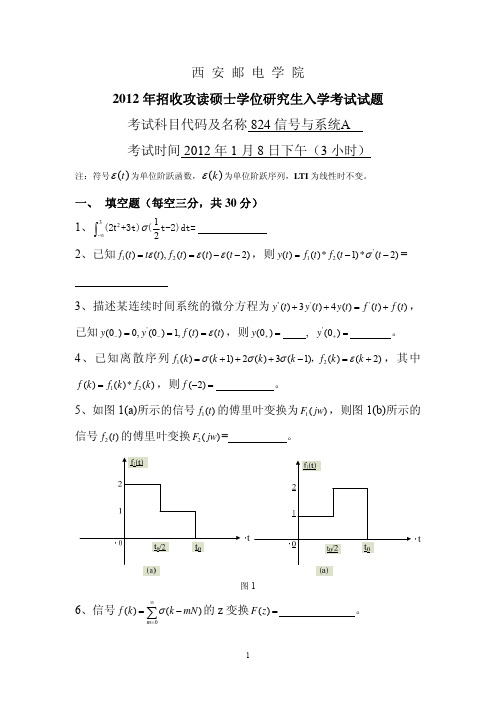
6
西 安 邮 电 学 院 2012 年招收攻读硕士学位研究生入学考试试题答案 考试科目代码及名称 824 信号与系统A
一、填空题 1、0； 3、 0 ； 2 ； 5、 F1 j e jt 0 ； 7、 te t t ； 二、选择题 2、 t 3 t 3 t 5 t 5 ； 4、 3 ； 6、
n
ห้องสมุดไป่ตู้
6、 f (k ) 2 (k ) 的 z 变换为 (A) F ( z )
2z z 1
(B) F ( z )
2 z 1
(C) F ( z )
2 z z 1
(D) F ( z )
2 z 1
7、设离散时间系统的频率响应为 H (e j ) H (e j ) e j ( ) ，些列叙述正确 的是 (A) H (e j ) 是周期信号，周期为 2π； (B) H (e j ) 是θ的奇函数； (C) ( ) 是θ的偶函数； (D)任何系统的频率响应 H (e j ) 都存在。 8、如果一连续时间系统的系统函数 H(s)只有一对在虚轴上的共轭极 点，则它的 h(t)应是 (A)指数增长信号 (B)指数衰减振荡信号 (C)常数 (D)等幅振荡信号
1 g 2 5 5 2 2 sin t （4）求其傅里叶逆变换可得系统的输出信号为 y t cos5t t
Y j
2
1 2 3s 2 2 s 3 3s 2 3 六、解： （1） H ( s ) Pi i 1 2 i 1 1 3s 2 s s 3s 2 2 s
（2）系统的冲激响应为
ht 1 e t 2e 2t t
西安邮电大学信号与系统习题册答案(一)
Sa (
2
0t
2
) F ( j ) A 0 2
2
2
据时移特性得
即 f (t ) A 0 2
Sa [
0 (t t0 )
2
] F ( j ) e
j t 0
= F ( j )
Sa [
0 (t t0 )
2
]
第3-19页
■
西安邮电大学
信号与系统 4.10（b）
F ( 0 ) ( ) e
F ( j 2 ) j
第3-14页
■
西安邮电大学
信号与系统
4.7（5）
sgn( t ) 2 2
j
jt
2 sgn( )
1
1 t
j 2
2 s g n ( ) j s g n ( )
4 t
j
4
sgn( )
f ( at b )
2,b 3
1
j
b a
a
e
F (j
a
)
( jt )f (t )
dF ( j ) d
1 2
j 3 2
tf (t ) j
dF ( d( j 2 ) )
dF ( j ) d
j 3 2
(3 2 t ) f (3 2 t ) j
0
F ( j ) e
j ( )
F ( j ) 是一个三角波，对它乘
得到的 A F ( j ) 可以看成 的两个门函数卷积得到的，即
A
0
F ( j ) e
j t 0
0
通信原理习题答案-西安邮电
第一章绪论学习要求：✧常用通信术语；✧模拟信号与数字信号的定义；✧通信系统的组成、分类、和通信方式；✧数字通信系统的优缺点；✧离散消息的信息量、平均信息量（信源熵）的计算；✧衡量模拟通信系统和数字通信系统的性能指标；✧传码率、传信率、频带利用率、平均传信率和最大传信率的计算及其关系；✧误码率和误信率的定义及计算。
一、简答题1．消息、信息、信号，通信的含义是什么？通信系统至少包含哪几部分？2．试画出模拟和数字通信系统的模型图，并指出各组成部分的主要功能，说明数字通信系统有什么特点？3．举例说明单工、半双工及全双工的工作方式及其特点。
4．举例说明如何度量信息量。
5．通信系统的性能指标是什么？这些性能指标在模拟和数字通信系统中指的是什么？二、综合题1.设有四个符号，其中前三个符号出现的概率分别为1/4，1/8，1/8，且各符号的出现是相对独立的。
试计算该符号集的平均信息量。
H x 1.75 bit/符2.一个由字母A、B、C、D组成的字，对于传输的每一个字母用二进制脉冲编码，00代替A、01代替B、10代替C，11代替D，每个二进制脉冲宽度为5ms。
（1）不同字母是等可能出现时，试计算传输的平均信息速率；（2）若每个字母出现的可能性分别为1 1 1 3P A P B ，P C ，P D5 4 4 10 试计算传输的平均信息速率。
R b max 200 bit/sR b 198.5 bit/s3.国际莫尔斯电码用“点”和“划”的序列发送英文字母，“划”用持续3单位的电流脉冲表示，“点”用持续1单位的电流脉冲表示；且“划”出现的概率是“点”出现概率的1/3。
（1）计算“点”和“划”的信息量；（2）计算“点”和“划”的平均信息量。
I 2 bit I. 0.415 bitH x 0.81 bit/符4.设一信息源的输出由128个不同的符号组成，其中16个出现的概率为1/32，其余112出现的概率为 1/224。
《信号与系统》课后习题参考答案
《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。
又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值 又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。
信号与系统--完整版答案--纠错修改后版本
1）
3）
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2）5）
3.9、求图所示各系统的单位序列响应。
（a）
（c）
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示，求下列卷积和。
（1）（2）（3）（4）
4.34 某LTI系统的频率响应，若系统输入，求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入，求该系统的输出。
4.39 如图4-35的系统，其输出是输入的平方，即（设为实函数）。该系统是线性的吗？
（1）如，求的频谱函数（或画出频谱图）。
（2）如，求的频谱函数（或画出频谱图）。
（1） （2） （3） （4） （5）
4.19 试用时域微积分性质，求图4-23示信号的频谱。
图4-23
4.20 若已知，试求下列函数的频谱：
（1）（3） （5）
（8）（9）
4下列方式求图4-25示信号的频谱函数 （1）利用xx和线性性质（门函数的频谱可利用已知结果）。
（1）
5-18 已知系统函数和初始状态如下，求系统的零输入响应。
（1），
（3），
5-22 如图5-5所示的复合系统，由4个子系统连接组成，若各子系统的系统函数或冲激响应分别为，，，，求复合系统的冲激响应。
5-26 如图5-7所示系统，已知当时，系统的零状态响应，求系数a、b、c。
5-28 某LTI系统，在以下各种情况下起初始状态相同。已知当激励时，其全响应；当激励时，其全响应。
（7）（8）
1-7 已知序列的图形如图1-7所示，画出下列各序列的图形。
西安电子考研 信号与系统第四版 答案
专业课习题解析课程西安电子科技大学信号与系统第二章2-12-22-42-82-122-16波形图如图2-9(a)所示。
波形图如图2-9(b)所示。
波形图如图2-9(c)所示。
波形图如图2-9(d)所示。
波形图如图2-9(e)所示。
2-202-222-282-29第三章习题3.1、3.63.8、3.9、3.10、3.11、3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、若LTI离散系统的阶跃响应，求其单位序列响3.16、如图所示系统，试求当激励分别为（1）（2）3.18、3.22、第四章习题4.64.74.104-114.174.184.194.204.214.254.234.274.284.294.314.334.34某LTI 系统的频率响应ωωωj j j H +-=22)(，若系统输入)2cos()(t t f =，求该系统的输出)(t y 。
4.35 一理想低通滤波器的频率响应⎪⎩⎪⎨⎧><-=s rad srad j H /3,0/3,31)(ωωωω4.36 一个LTI 系统的频率响应4.394.45 如图4-42(a)的系统，带通滤波器的频率响应如图(b)所示，其相频特性0)(=ωϕ，若输入图4-424.484.50图4-47图4-48图4-49 4.53 求下列离散周期信号的傅里叶系数。
第五章5-2 求图5-1所示各信号拉普拉斯变换，并注明收敛域。
5-35-45-65-75-85-9其波形如下图所示：其波形如下图所示：其波形如下图所示：5-105-125-135-15。
信号与系统课后习题参考答案
1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。
题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。
信号与系统课后习题答案汇总
第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为：(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列，周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率，其功率为1/2。
西安邮电大学824信号与线性系统综合2006-2018考研真题答案
2
01
3t
图4
40
西安邮电大学 824 信号与系统 研究生入学考试题
四、（5 分）已知信号 F j 1，
3 ，计算
2
f t dt 的值。
五 、（ 20 分 ） 如 图 5 所 示 LTI 系 统 ， 已 知 输 入 f (t) cos1000t 1 e j2nt ， n 1
（D） 1 cos 3t 45 2
10、序列 f (k) k 的 z 变换为
（A）F (z)
z
z 1
（B）F (z)
1 z 1
（C）F
(z)
z
z
1
（D）F
(
z)
z
1 1
三、（5 分）已知信号 f t的波形如图 4 所示，试画出 f 1 2t的波形。 f t
西安邮电大学 824 信号与系统 研究生入学考试题
西安邮电大学
2018 年招收攻读硕士学位研究生入学考试试题
一、填空题（每空 3 分，共 30 分）
1、
t 0
2
2 2
d
。
2、已知某离散 LTI 系统的阶跃响应 g(k) 1 k (k) ，则该系统的单位序列响应 4
， 。
7、因果信号
f
(t) 的单边拉普拉斯变换为
F (s)
3s
ss
1
1
，则
f
()
。
8、某线性时不变离散系统，其单位阶跃响应为 1 k k ，则该系统的系统函数
2
Hz
信号与系统 西安邮电 习题答案
第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
(1) ()()()t t t f εsin = 解：正弦信号周期ππωπ2122===T 1-12ππt()f t(2) ()()sin f t t επ=解：()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩，正弦信号周期22==ππT10-1-1-212-1-2121()f t tt()sin t π(3) ()()cos f t r t =解：()0 cost 0cos cos 0f t t t <⎧=⎨>⎩，正弦信号周期221T ππ== 10-1t()cos t π2ππ-2π-1()f t 0tπ2ππ-2π-(4) ()()k k k f ε)12(+=-1-212k3135()f k …………(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦-2-412k312()f k …………45-1-31.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
信号与系统课后习题答案汇总
第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为：(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为：(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列，周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知，在),(∞-∞区间上n 4sin π的功率为1/2，因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sin n n επ在),0(∞区间上的功率，其功率为1/2。
信号与系统课后习题与解答第三章
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。
图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统课后答案（ＰＤＦ）
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2（b）所示。
故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3（b）所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。
信号与系统考试题及答案
信号与系统考试题及答案一、单项选择题（每题2分，共20分）1. 信号与系统中，信号的分类不包括以下哪一项？A. 确定性信号B. 随机信号C. 离散信号D. 连续信号答案：C2. 以下哪个选项不属于线性时不变系统的属性？A. 线性B. 时不变性C. 因果性D. 稳定性答案：C3. 傅里叶变换的主要应用不包括以下哪一项？A. 信号频谱分析B. 滤波器设计C. 信号压缩D. 信号加密答案：D4. 拉普拉斯变换与傅里叶变换的主要区别是什么？A. 拉普拉斯变换适用于所有信号B. 傅里叶变换适用于周期信号C. 拉普拉斯变换适用于非周期信号D. 拉普拉斯变换是傅里叶变换的特例答案：D5. 以下哪个选项不是信号与系统中的卷积定理？A. 卷积定理将时域的卷积转换为频域的乘法B. 卷积定理适用于连续信号和离散信号C. 卷积定理只适用于线性时不变系统D. 卷积定理可以简化信号处理中的计算答案：C6. 信号的采样定理是由哪位科学家提出的？A. 奈奎斯特B. 香农C. 傅里叶D. 拉普拉斯答案：A7. 以下哪个选项是信号的时域表示？A. 傅里叶级数B. 拉普拉斯变换C. 傅里叶变换D. 时域图答案：D8. 以下哪个选项是信号的频域表示？A. 时域图B. 傅里叶级数C. 傅里叶变换D. 拉普拉斯变换答案：C9. 信号的希尔伯特变换主要用于什么？A. 信号滤波B. 信号压缩C. 信号解析D. 信号调制答案：C10. 信号与系统中，系统的稳定性是指什么？A. 系统对所有输入信号都有输出B. 系统对所有输入信号都有有限输出C. 系统对所有输入信号都有零输出D. 系统对所有输入信号都有无限输出答案：B二、填空题（每题2分，共20分）1. 信号与系统中，信号可以分为______信号和______信号。
答案：确定性；随机2. 线性时不变系统的最基本属性包括线性、时不变性和______。
3. 傅里叶变换的公式为：X(f) = ∫x(t)e^(-j2πft)dt，其中j是______。
(完整版)信号与系统练习及答案
信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（ ）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（ ） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（ ）4．周期矩形脉冲的谱线间隔与（ ）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（ ） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（ ） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（ ） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（ ） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。
2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。
3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。
信号与系统第1至8章习题参考解答
《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章（无） (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号，由f (t )求f (−3t − 2)，但改变运算顺序，先求f (3t )或先求f (−t )，讨论所得结果是否与原例之结果一致。
解：(1). 例1-1的方法： f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二：f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三：f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三：1-5 已知()f t ，为求0()f t at −应按下列哪种运算求得正确结果（式中0t ，a 都为正值）？（1）()f at −左移0t （2）()f at 右移0t （3）()f at 左移0t a （4）()f at −右移0ta解：（4）()f at −右移t a：故（4）运算可以得到正确结果。
注：1-4、1-5 题考察信号时域运算：1-4 题说明采用不同的运算次序可以得到一致的结果； 1-5 题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。
1-9 粗略绘出下列各函数式的波形图： （1）()(2)()t f t e u t −=− （2）2()(36)()t t f t e e u t −−=+ （3）3()(55)()t t f t e e u t −−=−（4）()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解：（1）()(2)()tf t e u t −=−（2）2()(36)()ttf t e eu t −−=+（3）3()(55)()ttf t e eu t −−=−（4）()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图，注意它们的区别：（1）[()(1)]−−；t u t u t（2）(1)�；t u t−（3）[()(1)](1)−−+−；t u t u t u t（4）(1)(1)−−；t u t（5）(1)[()(1)]−−−−；t u t u t（6）[(2)(3)]−−−；t u t u t（7）(2)[(2)(3)]t u t u t−−−−。
信号与系统西安邮电习题答案
信号与系统西安邮电习题答案第一次1.1画出下列各个信号的波形[式中为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法： 首先考虑各信号中普通函数的波形特点，再考虑与或结合时的变化情况；若只是普通信号与阶跃信号相乘，则可利用或的性质直接画出或部分的普通函数的波形；若是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
(1)解：正弦信号周期(2)解：，正弦信号周期(3)解：，正弦信号周期(4)(5)1.2画出下列各信号的波形[式中为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法： 首先考虑各信号中普通函数的波形特点，再考虑与或结合时的变化情况；若只是普通信号与阶跃信号相乘，则可利用或的性质直接画出或部分的普通函数的波形；若是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
(1)(2)(3)解：(4)(5)1.3写出下图所示各波形的表达式(1)解：(2)解：1.4写出下图所示各序列的闭合形式的表示式(a)解：(b)解：(课堂已讲)1.5判别下列各序列是否为周期性的，如果是，确定其周期(1)解：周期序列(2)解：，，m取3，；，，；故(3)解：，，故非周期；，，；故非周期 1.6已知信号的波形如下图所示，画出下列各函数的波形(1)(2)(3)1.7已知序列的图形如图所示，画出下列各序列的图形(1)(2)1.8信号的波形图如下所示，试画出和的波形解：由图可知：，则当时，；当时，当时，(课堂已讲)1.9已知信号的波形如图所示，分别画出和的波形解：第二次1.10计算下列各题，(1)解：(2)解：(3)解：(4)解：(5)解：(6)解：(7)解：(8)解：(课堂已讲)1.11设系统的初始状态为，激励为，各系统的全响应与激励和初始状态的关系如下，试分析各系统是否是线性的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
(1) ()()()t t t f εsin = 解：正弦信号周期ππωπ2122===T(2) ()()sin f t t επ=解：()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩，正弦信号周期22==ππT(3) ()()cos f t r t =解：()0 cost 0cos cos 0f t t t <⎧=⎨>⎩，正弦信号周期221T ππ==(4) ()()k k k f ε)12(+=(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦1.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。
(1) ()()()()315122f t t t t εεε=+--+-(2) ()()()12f t r t t ε=--tt)1t-t (3)()()()()sin13f t t t tπεε=---⎡⎤⎣⎦解：22Tππ==(4) ()()()()25f k k k k εε=+--⎡⎤⎣⎦(5) ()()()241k f k k k εε=---⎡⎤⎣⎦1.3 写出下图所示各波形的表达式 (1)解：()()()()()()()()()()()2111223 211223f t t t t t t t t t t t εεεεεεεεεε=+--+-------⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=+----+-(2)解：24T πω==2πω∴=⇒10cos 2t π⎛⎫⎪⎝⎭()()()10cos 112f t t t t πεε⎛⎫=+--⎡⎤ ⎪⎣⎦⎝⎭1.4 写出下图所示各序列的闭合形式的表示式 (a)解：()()3f k k ε=+ (b)解：()()()38f k k k εε=---(课堂已讲)1.5 判别下列各序列是否为周期性的，如果是，确定其周期(1) ()2cos 5f k k π⎛⎫= ⎪⎝⎭解：25πβ=25252ππβπ=⨯= 5N ∴= 周期序列(2) ()⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+=632cos 443sin ππππk k k f 解：431πβ=，3834221=⨯=ππβπ，∴m 取3，81=∴N ； 322πβ=，323222=⨯=ππβπ，32=∴N ； 故24=N(3) ()⎪⎭⎫⎝⎛+=k k k f 2sin 2cos 3π解：11=β，ππβπ21221=⨯=，故非周期；22πβ=，42222=⨯=ππβπ，42=∴N ；故非周期1.6 已知信号的波形如下图所示，画出下列各函数的波形(1) ()()t2ε-2tf-)(2) ()12f t -(3)() dd f tt1.7 已知序列的图形如图所示，画出下列各序列的图形(1) ()()()24f k k k εε---⎡⎤⎣⎦(2) ()()21f k k ε-+-+1.8 信号()t f 22-的波形图如下所示，试画出()t f 和()ττd ⎰∞-t f 的波形解：由图可知：()()()()222+---=t t t t f δεε，则 当0<t 时，()()()22d 2)2(d +-=+-=⎰⎰∞-∞-t t f ttετδττ；当20≤≤t 时，()()()()()2d 22d 1 d ]222[d -=+-⋅=+---=⎰⎰⎰⎰∞-∞-∞-∞-t t t t f tttt ττδττδεεττ当2>t 时，()()()()022 2d 1 2d 1 d ]222[d 2=-=-⋅=-⋅=+---=⎰⎰⎰⎰∞-∞-∞-ττττδτετεττt ttf(课堂已讲)1.9 已知信号的波形如图所示，分别画出()f t 和()d d f t t的波形解：第二次1.10 计算下列各题()001t at t t a a δδ⎛⎫-=- ⎪⎝⎭，()()0001t t f t at t f t a a a δδ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭(1)()()01sin d 2t t t t πδδ-∞⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎰ 解：()()()()()()00001sin d 21 sin d sin d 2 sin 0t f t t t t tt t t t t t t πδδπδπδπ---∞∞∞=⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=++ ⎪⎝⎭==⎰⎰⎰(2)()()2[2]d t e t t t δδ∞--∞'+⎰解：()()()()()()()()()()()22220[2]d [2]d [22]d [22]d 044t t t tt f t e t t te t e t tt e t t t t t t t δδδδδδδδδδ∞--∞+∞---∞+∞-=-∞+∞-∞'=+'=+'=++'=++=+=⎰⎰⎰⎰(3)()2sin 3d 4t t t t πδ∞-∞⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎰ 解：()()2232 sin 3d 4sin 433sin 439sin492t t t t t t t πδπππ∞-∞=-⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=+ ⎪⎝⎭⎛⎫=-+- ⎪⎝⎭=-=-⎰(4)()()2d t x x x δ-∞'-⎰解：()()()()()()()() 2d 2d 2d d 2ttttx x xx x x x x x xt t δδδδδδε-∞-∞-∞-∞'-'=+⎡⎤⎣⎦'=+=+⎰⎰⎰⎰(5)()()()6236224d t t t t δδ--++⎡⎤⎣⎦⎰ 解：()()()()()()()()()()()()6236622336223623226224d 6d 2624d 16262d 2662d 66628t t t t t tt t t t t tt t t tt t tt δδδδδδ---=--=--++⎡⎤⎣⎦=-+-+=-+-⋅+=+-+=+-=+=⎰⎰⎰⎰⎰(6)()20(2)2d tτδττ+-⎰解：()()()20202022(2)2d (2)[(2)]d (2)2d 2| ,2 (42)(2) 6(2)tttt f t t t t t τδτττδτττδττεε==+-=+--=+-=+≥=+-=-⎰⎰⎰(7)()()55342d t t t δ---⎰解：()()()()()()()()()555555552 342d 324d 132d 2132d 213212t t t t t t tt t t t t t t δδδδ----=--=--=-⋅-=--=-=-⎰⎰⎰⎰ (8)()02d 3tτδττ-⎛⎫- ⎪⎝⎭⎰解：()()()()()()()00002d 332d 32d 32,06t ttt t ττδττδττττδτττε---=⎛⎫- ⎪⎝⎭=-=-=-≥=-⎰⎰⎰(课堂已讲)1.11 设系统的初始状态为()0x ，激励为()f ⋅，各系统的全响应()y ⋅与激励和初始状态的关系如下，试分析各系统是否是线性的。
根据线性系统的定义，依次判断系统是否具有分解特性、零输入线性、零状态线性()()()()11221122T f f T f T f αααα⋅+⋅=⋅+⋅⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦。
(1) ()()()200cos d t ty t e x xf x x π-=+⎰解：()()20t zi y t e x -=()()0cos d tzs y t xf x x π=⎰∴()()()zi zs y t y t y t =+ 满足可分解性()()211110t zi y t e x αα-= ()()212220t zi y t e x αα-=∴()()()()()()2221122112211220000t t t zi zi y t y t e x e x e x x αααααα---+=+=+⎡⎤⎣⎦ 线性()()11110cos d tzs y t xf x x ααπ=⎰()()22220cos d tzs y t xf x x ααπ=⎰∴()()()()()()1122112211220cos d cos d cos d t t tzs zs y t y t xf x x xf x x x f x f x xαααπαππαα+=+=+⎡⎤⎣⎦⎰⎰⎰线性(2) ()()()()()10.5012k y k x f k f k +=+-- 解：()()()10.50k zi y t x +=()()()12zs y k f k f k =--∴()()()zi zs y k y k y k =+ 满足可分解性()()()111110.50k zi y k x αα+= ()()()122220.50k zi y k x αα+=()()()()()()()()()1111122112211220.500.500.500k k k zi zi y k y k x x x x αααααα++++=+=+⎡⎤⎣⎦线性()()()11111112zs y k f k f k ααα=--()()()22222212zs y k f k f k ααα=--∴()()()()()()()()()()112211112222112211221212 1122zs zs y k y k f k f k f k f k f k f k f k f k αααααααααα+=--+--≠-+--+-⎡⎤⎡⎤⎣⎦⎣⎦非线性∴系统非线性(课堂已讲)1.12 下列微分或差分方程所描述的系统，是线性的还是非线性的？是时变的还是不变的？(1) ()()()()()322y t y t y t f t f t ''''++=- 解：常系数、线性、微分方程 故为，线性时不变系统(2) ()()()()2111y k k y k f k +--=- 解：变系数、线性、差分方程 故为，线性时变系统1.13 设激励为()f ⋅，下列等式是各系统的零状态响应()zs y ⋅，判断各系统是否是线性的、时不变的、因果的、稳定的？ (1) ()()1+=t f t y zs解：()()111+=t f t y zs αα，()()122+=t f t y zs ββ，()()()()()()111212121++≠+++=+t f t f t f t f t y t y zs zs βαβαβα，∴非线性()()1+-=-d d zs t t f t t y ，∴时不变当0t t <，有()0=t f ，则()()11=+=t f t y zs ，∴非因果 若()∞<t f ，则()∞<t y zs ，∴稳定 (2) ()()2zs y t f t =- 解：()()11112zs y t f t αα=-()()22222zs y t f t αα=-()()()()1122112222zs zs y t y t f t f t αααα+=-+-，∴线性()()()22zs d d d y t t f t t f t t -=--=-+⎡⎤⎣⎦若延迟输入为()d f t t -，则系统输出为()2d f t t --∴()()22d d f t t f t t --≠-+，时变 若0t t <，有()0f t =若()()20zs y t f t =-=，则02t t -<⇒02t t >-，∴非因果若()f t <∞，则()()2zs y t f t =-<∞，∴稳定。