西安邮电大学信号与系统48学时总复习2014版
《信号与系统》第一章 信号与系统

第1-6页
西安邮电大学通信与信息工程学院
信号与系统
第一章 信号与系统
信号的定义及分类 信号的基本运算 阶跃函数和冲激函数 系统的描述和特性
第1-7页
西安邮电大学通信与信息工程学院
信号与系统
1.1 信号与系统基本概念
什么是信号?什么是系统?为什么把这两个概念 连在一起?
一、信号的概念
1. 消息(message):
1.1 信号与系统基本概念
二、系统的概念
系统:由若干相互作用和相互依赖的事物组合而成
的,具有稳定功能的整体。如通信系统、控制系统
和经济系统等。
系统的基本作用:是对输入信号进行加工和处理, 将其转换为所需要的输出信号。
输入信号
系统
输出信号
激励
响应
系统的描述:在数学上系统用微分方程和差分方程
来描述,其功能就是通过由怎样的激励产生怎样的
为随机信号或不确定信号。电子系统中的起伏热噪声、
雷电干扰信号就是两种典型的随机信号。
研究确定信号是研究随机信号的基础。本课程只
讨论确定信号。
第1-13页
西安邮电大学通信与信息工程学院
信号与系统
1.2 信号的分类
2. 连续信号和离散信号 :根据信号定义域划分
(1)连续时间信号: 在信号存在的时间范围内,任意时刻都有定义
的信号称为连续时间信号,简称连续信号。
这里的“连续”指函数的定义域—时间是连续
的,但可含间断点,至于值域可连续也可不连续。
值域连续
f1(t) =sin(πt)
1
o1 -1
2t
第1-14页
f2(t) 1
o1 2 t -1
值域不 连续
西安邮电大学通信系统概论复习

传输介质
▪ 按照传输方式介质分为有线介质(双绞线、同轴
电缆、光纤)和无线介质(无线电、微波、红外 线)
纤包
保
芯层
护
套
通信网的定义和构成
▪ 定义:通信网是由一定数量的节点和连接这些节
点的传输系统有机地结合在一起,按约定信令和 协议完成任意用户间信息交换的通信体系。
▪ 构成要素
软件设施:信令、协议、控制、管理、计费 硬件设施:终端节点
在数字信道中传送数字信号的一个波形符号,它 可能是二进制的,也可能是多进制的。
▪ 比特:是信息的度量单位。一位二进制数所携
带的信息量即为一比特(bit,缩写为b)。例如, 10010110,八位二进制数字,所携带的信息量 为8比特。
1.2 信息和信息量
例 求下图1-2-1所示分别为二进制和四进制码元 序列的信息量
第一章 基本概念
1.1通信系统与通信网
21世纪,计算机和通信技术在飞速发展,它们的结合 具有划时代的意义。以计算机为代表的IT产业和以语音、 数据通信为代表的CT产业,融合为了ICT(Information and Communication Technology)产业。
:将内容转换成文字、声音、标识,通过某种装置变 成电磁信号,通过光纤、铜线、无线等传送方式(信道), 从地球的某个角落传送到另一角落。
通信的传输方式
通信的传输方式
按消息传送的方向与时间,通信方式可分为单工通信、半双工通信 及全双工通信三种。 单工通信
是指消息只能单方向进行传输的一种通信工作方式。 单工通信的例子很多,如广播、遥控、无线寻呼等。这里,信号(消息
)只从广播发射台、遥控器和无线寻呼中心分别传到收音机、遥控对象 和 BP 机上。
西安邮电大学信号与系统习题册答案(一)

Sa (
2
0t
2
) F ( j ) A 0 2
2
2
据时移特性得
即 f (t ) A 0 2
Sa [
0 (t t0 )
2
] F ( j ) e
j t 0
= F ( j )
Sa [
0 (t t0 )
2
]
第3-19页
■
西安邮电大学
信号与系统 4.10(b)
F ( 0 ) ( ) e
F ( j 2 ) j
第3-14页
■
西安邮电大学
信号与系统
4.7(5)
sgn( t ) 2 2
j
jt
2 sgn( )
1
1 t
j 2
2 s g n ( ) j s g n ( )
4 t
j
4
sgn( )
f ( at b )
2,b 3
1
j
b a
a
e
F (j
a
)
( jt )f (t )
dF ( j ) d
1 2
j 3 2
tf (t ) j
dF ( d( j 2 ) )
dF ( j ) d
j 3 2
(3 2 t ) f (3 2 t ) j
0
F ( j ) e
j ( )
F ( j ) 是一个三角波,对它乘
得到的 A F ( j ) 可以看成 的两个门函数卷积得到的,即
A
0
F ( j ) e
j t 0
0
(完整版)信号与系统复习知识点

第一章
1.信号的运算:时移、反褶、尺度变换、微分、积分等;
2.LTI系统的基本性质:叠加性、时不变特性、微分特性、因果性、可分解线性;
3.阶跃型号与冲激信号及其特性。
单位冲激信号的性质:
1.
2.
3.
4.
5.
6.
7.
例、求下列积分
例、已知信号 的波形如下图1所示,试画出下列各信号的波形
抽样信号的拉氏变换
求半波整流和全波整流周期信号的拉氏变换
(1)
(2)
4-29求下列波形的拉氏变换
(1)
解题思路:单对称方波 ——周期方波——乘
—— ——
(2)
第一周期:
周期信号的拉氏变换:
第五章
1.频域系统函数 ,理想低通滤波器频谱特性;
2.无失真传输条件:幅频特性为常数,相频特性是过原点的直线;
3.系统的物理可实现性判断(1)佩利-维纳准则;(2)系统可实现性的本质是因果性。
被理想抽样信号的傅立叶变换:
被非理想抽样信号傅立叶变换:
第四章
1.典型信号的拉氏变换及拉氏变换的基本性质;
2.S域元件模型、系统函数、系统函数与激励信号极点分布与电响应的关系、系统函数与输入输出方程的关系(利用拉氏变换求解电系统响应);
3.线性系统的稳定性分析。
周期信号的拉氏变换
为信号第一个周期 的拉氏变换;整个周期信号 的拉氏变换为:
第七章
1.离散系统和信号的描述方法、基本性质
2.差分方程的经典解法
3.卷积和定义及其求解方法
第八章
1. z变换的定义、收敛域和基本性质,常用序列的z变换
2.逆z变换的求解方法
3. 的定义、零极点分布与信号/系统性质的关系
信号与系统西安邮电习题答案

信号与系统西安邮电习题答案第一次1.1画出下列各个信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)解:正弦信号周期(2)解:,正弦信号周期(3)解:,正弦信号周期(4)(5)1.2画出下列各信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)(2)(3)解:(4)(5)1.3写出下图所示各波形的表达式(1)解:(2)解:1.4写出下图所示各序列的闭合形式的表示式(a)解:(b)解:(课堂已讲)1.5判别下列各序列是否为周期性的,如果是,确定其周期(1)解:周期序列(2)解:,,m取3,;,,;故(3)解:,,故非周期;,,;故非周期 1.6已知信号的波形如下图所示,画出下列各函数的波形(1)(2)(3)1.7已知序列的图形如图所示,画出下列各序列的图形(1)(2)1.8信号的波形图如下所示,试画出和的波形解:由图可知:,则当时,;当时,当时,(课堂已讲)1.9已知信号的波形如图所示,分别画出和的波形解:第二次1.10计算下列各题,(1)解:(2)解:(3)解:(4)解:(5)解:(6)解:(7)解:(8)解:(课堂已讲)1.11设系统的初始状态为,激励为,各系统的全响应与激励和初始状态的关系如下,试分析各系统是否是线性的。
西安邮电大学2013-2014-01学期课程表

关于2013级课表以及F段教室
情况说明
各位任课教师:
因13级新生第七周开始上课,为按时完成教学计划,经研究决定,从第七周到第十八周每周六进行补课。
补课规则为从第七周周六开始,每周六按照周一至周五的教学计划依次进行补课,即第七周周六补周一的课程,第八周周六补周二的课程,依次顺延循环。
课表中教室号以F开头的教室,为东区新盖实验楼教室。
例如F0208:代表东区实验楼二楼208教室。
教务处
2013-07-01
新校区2013-2014学年第二学期电子工程学院本科课程表(十)
新校区2013-2014学年第一学期电子工程学院本科课程表(十三)
新校区2013-2014学年第一学期通信与信息工程学院本科课程表(二十二)。
信号与系统期末复习材料

信号与系统期末复习材料信号与系统期末复习一、基础知识点:1.信号的频带宽度(带宽)与信号的脉冲宽度成反比,信号的脉冲宽度越宽,频带越窄;反之,信号脉冲宽度越窄,其频带越宽。
2. 系统对信号进行无失真传输时应满足的条件:①系统的幅频特性在整个频率范围(∞<<∞-ω)内应为常量。
②系统的相频特性在整个频率范围内应与ω成正比,比例系数为-0t3.矩形脉冲信号的周期与频谱线的间隔存在着倒数的关系。
4.零输入响应(ZIR )从观察的初始时刻(例如t=0)起不再施加输入信号(即零输入),仅由该时刻系统本身具有的初始状态引起的响应称为零输入响应,或称为储能响应。
5.零状态响应(ZSR )在初始状态为零的条件下,系统由外加输入(激励)信号引起的响应称为零状态响应,或称为受迫响应。
6.系统的完全响应也可分为:完全响应=零输入响应+零状态响应7.阶跃序列可以用不同位移的单位阶跃序列之和来表示。
8.离散信号)(n f 指的是:信号的取值仅在一些离散的时间点上才有定义。
9.信号的三大分析方法:①时域分析法②频域分析法③复频域分析法10.信号三大解题方法⑴傅里叶:①研究的领域:频域②分析的方法:频域分析法⑵拉普拉斯:①研究的领域:复频域②分析的方法:复频域分析法⑶Z 变换:主要针对离散系统,可以将差分方程变为代数方程,使得离散系统的分析简化。
11.采样定理(又称为奈奎斯特采样频率)如果)(t f 为带宽有限的连续信号,其频谱)(ωF 的最高频率为m f ,则以采样间隔ms f T 21≤对信号)(t f 进行等间隔采样所得的采样信号)(t f s 将包含原信号)(t f 的全部信息,因而可()()()zi zs y t y t y t =+利用)(t f s 完全恢复出原信号。
12.设脉冲宽度为1ms ,频带宽度为KHz ms111=,如果时间压缩一半,频带扩大2倍。
13.在Z 变换中,收敛域的概念:对于给定的任意有界序列)(n f ,使上式收敛的所有z 值的集合称为z 变化的收敛域。
信号与系统 西安邮电 习题答案
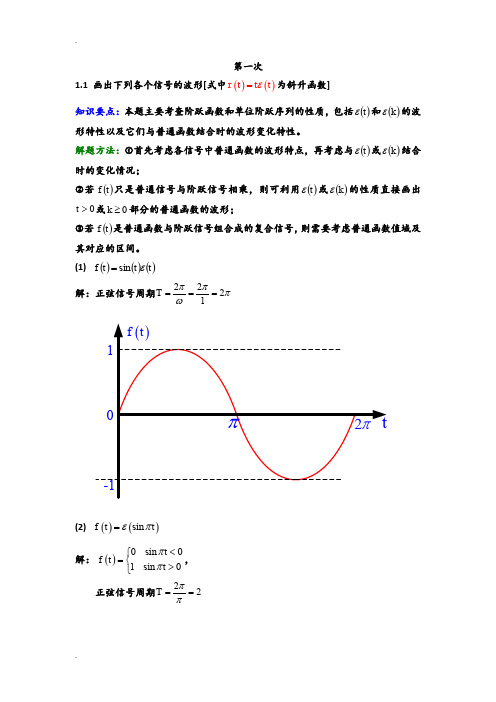
第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法:①首先考虑各信号中普通函数的波形特点,再考虑与()t ε或()k ε结合时的变化情况;②若()t f 只是普通信号与阶跃信号相乘,则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形;③若()t f 是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1) ()()()t t t f εsin = 解:正弦信号周期ππωπ2122===T 1-12ππt()f t(2) ()()sin f t t επ=解:()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩,正弦信号周期22==ππT10-1-1-212-1-2121()f t tt()sin t π(3) ()()cos f t r t =解:()0 cost 0cos cos 0f t t t <⎧=⎨>⎩,正弦信号周期221T ππ== 10-1t()cos t π2ππ-2π-1()f t 0tπ2ππ-2π-(4) ()()k k k f ε)12(+=-1-212k3135()f k …………(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦-2-412k312()f k …………45-1-31.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法:①首先考虑各信号中普通函数的波形特点,再考虑与()t ε或()k ε结合时的变化情况;②若()t f 只是普通信号与阶跃信号相乘,则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形;③若()t f 是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 拉普拉斯变换、 连续时间系统的s域分析
定义:
单边拉氏变换、双边、收敛域、常用函数的拉氏变换
拉氏变换的性质
线性、原函数微分、原函数积分、时域平移、s域平移、
尺度变换、初值、终值
卷积特性 拉氏逆变换
部分分式展开法(求系数)
系统函数H(s)
定义(两种定义方式)
求解(依据两种定义方式)
jn t n T n n
1 2 jn t Fn T f T (t ) e dt T 2
T
位置:ω=nΩ(谐波频率) 强度:2πFn, 与成Fn正比,离散谱
2 谱线的幅度不是有限值, 因为F F ( j )表示的是频谱密度。 Ω 处, )只存在于 nn 周期信号的F F(j 1
关于冲激信号
1 (at ) (t ) a
尺度变换特性
(t ) f (t ) f (0) (t )
(t t0 ) f (t ) f (t0 ) (t t0 )
(t ) f (t )dt f (0)
(t t0 ) f (t )dt f (t0 )
o
2
T(t)的频谱密度函数仍是冲激序列;
强度和间隔都是Ω。
2
24
时域取样定理: 一个频谱在区间(-m,m)以外为0的带限信号f(t), 可唯一地由其在均匀间隔Ts [Ts<1/(2fm)] 上的样值点 f(nTs)确定。 注意:为恢复原信号,必须满足两个条件: (1)f(t)必须是带限信号; (2)取样频率不能太低,必须fs>2fm,或者说,取样 间隔不能太大,必须Ts<1/(2fm);否则将发生混叠。 通常把允许的最低取样频率fs=2fm称为奈奎斯 特频率,把最大允许的取样间隔Ts=1/(2fm)称为奈奎斯 特间隔。
2T T
t
1 1 解: Fn F0 j n T T
2 T (t ) T
n n
Fnቤተ መጻሕፍቲ ባይዱ1 T
o
( n)
2
2
( n) ( )
F j
各章典型复习题
第一章
-0.5
1 (at ) (t ) a 1 2 原式 cos 2 t 2(t 0.5) dt cos 2 t (t 0.5)dt 4 2 4 1 1 cos 2 (0.5) cos 0.5 2 2
2
第一章
信号的平移:
f(t)的 右 边。 信号基本运算的画图表示法(例题) 冲激函数的理解
f ( t )时移后成为 f (t t0 ) 当 t0>0时 f (t t0 ) 是在
信号基本运算
已知f (t),画出 f (– 4 – 2t)。 三种运算的次序可任意。 但一定要注意始终对时间 t 进行。 f (t -4)
求导,得g(t)
(4) -2
g(t) = f '(t)
2
t
o -1
t
压缩,得g(2t)
(2) -1 o -1
g(2t)
1
t
33
冲激信号的性质 抽样性(筛选性)
若f(t) 在t=0处连续,处处有界,则有
(t ) f (t ) f (0) (t )
(t t0 ) f (t ) f (t0 ) (t t0 )
三大变换
傅立叶变换 拉普拉斯变换 z变换
第一章 绪论
1、信号的概念 2、分类:典型的连续时间信号:
指数、正弦、复指数、eat, sin(ω0t), Sa(t)
3、信号的运算:
移位、反转、尺度变换、微分运算、相加、相乘
4、奇异信号:
阶跃、冲激(特性)、冲激偶,δ(t), ε(t), δ’(t)
第五章 拉普拉斯变换、 连续时间系统的s域分析
收敛域:实际上就是拉氏变换存在的条件;
lim f (t ) e
t
σ t
0
σ σ0
三.一些常用函数的拉氏变换
1.阶跃函数
L (t ) 1 e st d t
0
1 st 1 e 0 s s
α s t
偶函数 (t ) (t ) f (t ) * (t ) f (t ); f (t ) * (t t0 ) f (t t0 )
系统分析过程
列写方程 : 根据元件约束,网络拓扑约束 齐次解:yh (t )满足高阶微分方程中右端激励f (t ) 及其各阶导数都为零的齐次方程 经典法 特解:y (t )的函数形式与激励函数形式有关 p 零输入 : 可利用经典法求 解方程 双零法 零状态 : 利用卷积积分法求解 变换域法 : s变换,在s域求解微分方程
2 正弦分量 bn T 系数
T 2 T 2
f (t ) sin(nt ) d t
指数形式傅立叶级数的傅里叶系数
称为指数形式 的傅立叶级数
T
f (t )
n
jnt F e n
1 2 jn t Fn T f (t ) e dt T 2
n = 0, ±1, ±2,…
5、系统模型及其分类 6、线性时不变系统的基本特性:
线性(叠加性、均匀性)、时不变特性、微分特性、因果特性
7、系统分析方法:
输入输出描述法、状态变量描述法
周期信号 ①连续正弦信号一定是周期信号,而正
弦序列不一定是周期序列。 ②两连续周期信号之和不一定是周期信 号,而两周期序列之和一定是周期序列。 线性时不变系统直观判断方法: 若函数与函数f (· )与y(· )乘积,则非线性 若 f (· )前出现变系数,或有反转、展缩 变换,则系统为时变系统。
1 则 f1(t) f2(t) ←→ 2
F1(jω)*F2(jω)
卷积定理揭示了时间域与频率域的运算关系,在通信 系统和信号处理研究领域中得到大量应用。
一般周期信号的傅里叶变换
f T (t ) fT (t )
n
n
F
n
e
jn t
F e F ( j) 2 F ( n) 1 fT t 的频谱由冲激序列组成 ;
(t ) f (t )dt f (0)
(t t 0 ) f (t )dt f (t 0 )
23
频率范围无限小, 幅度为。
T (t )
周期为T的单位冲激序列T(t)的傅里叶变换 T t
m
(t mT )
n
n
1 1 1 1 1
o
T 2T
fT (t ) FT ( j ) 2
F ( n)
f ( ) (t ) d f ( ) d
t
ε(t) *ε(t) = tε(t)
第三章 离散时间系统的时域分析
序列的概念、离散时间信号的运算 常系数线性差分方程的求解
时域经典法:齐次解+特解
零输入响应+零状态响应
离散时间系统的冲激响应与阶跃响应
2.指数函数
Le
α t
0
e
α t st
3.单位冲激信号
0
1 e e dt α s 0 α s
σ α
L t t e std t 1
0
全s域平面收敛
L t t0 t t0 e std t e st0
f(t) 1 -2 o
f (-2t -4) 1 -3 -1 o t
右移4,得f (t – 4)
2 t
o
1 2 4 6 t
压缩,得f (2t – 4)
反转,得f (– 2t – 4)
o f (2t -4) 1 1 2 3 t
32
已知f(t),画出g(t) = f ’(t)和 g(2t)
f (t)
4 -2 o 2
第四章 傅立叶变换
周期信号的傅立叶级数
a0 f (t ) a n cos(nt ) bn sin(nt ) 2 n1 n 1
称为f (t)的傅立叶级数(三角形式)
三角形式傅立叶级数的傅里叶系数:
2 余弦分量 an T 系数
T 2 T 2
f (t ) cos(nt ) d t
第二章
连续时间系统的时域分析
微分方程式的建立与求解
零输入响应与零状态响应
冲激响应与阶跃响应
关系!
卷积及其性质(方便求零状态响应)
(一)冲激响应 h (t)
1)定 义
系统在单位冲激信号δ(t) 的激励下产生 的零状态响应。
2)求 解 形式与齐次解相同
第二章
卷积定义:
f t
单位样值响应h(k)的定义与求解
离散卷积(卷积和)
定义、性质、计算
离散卷积(卷积和)定义
f (k )
i
f (i) f
1
2
(k i )
yzs (k )
i
f (i)h(k i) f (k )* h(k )
利用卷积和求系统的零状态响应
