《一笔画里的数学秘密》
小学三年级奥数-一笔画问题
1727年在欧拉20岁的时候，被俄国请去在圣彼得堡（原列宁格勒）的科学院做研究。他的德国朋友告诉了他这个曾经令许多人困惑的问题。 欧拉并没有跑到哥尼斯堡去走走。他把这个难题化成了这样的问题来看：把二岸和小岛缩成一点，桥化为边，于是“七桥问题”就等价于下图中所画图形的一笔画问题了， 这个图如果能够一笔画成的话，对应的“七桥问题”也就解决了。
画一画，找一找
下面的图形，哪些能一笔画出？哪些不能一笔画出
根据今天学习知识，先判断下列图形能不能一笔画成？再想一想该从哪里开始画？最后再动手画画看。
练习
一辆洒水车要给某城市的街道洒水，街道地图如下：你能否设计一条洒水车洒水的路线，使洒水车不重复地走过所有的街道，再回到出发点？
菜市场
小广场
园林工人张大伯为花园浇花，怎样走才能不重复地走遍图中的每条小路？
演讲完毕，感谢观看
邮递员叔叔向10个地点送信一次走完，不走重 复路，应该怎样走合适?(看下图)
文具店
超市
电器城
服装城
甲乙两个邮递员去送信，两人以同样的速度走遍所有的街道，甲从A点出发，乙从B点出发，最后都回到邮局（C）。如果要选择最短的线路，谁先回到邮局？
甲
邮局
乙
下面的图能不能一笔画成？如果能，应怎样画？ 2、3、4、5、6六个点都是两条线的交点，是偶点，7是四条线的交点，，也是偶点，没有奇点，能一笔画成。
两条相交的线处都有一个交点。
数一数下列图形各有几个交点？
（ ）个
（ ）个
（ ）个
（ ）个
我们刚才画的图形都有几个交点？几个双数点？几个单数点？
判断下列图形能否一笔画
不连通的图形不能一笔画
连通的图形有可能一笔画
《有趣的小学数学—一笔画》
【知识点】1、七桥问题：18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如右上图）。
有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。
这个问题在很长一段时间里，都没有解决。
后来大数学家欧拉证明了这个问题的不可能性，把它转化成一个几何问题，即一笔画问题。
2、奇点与偶点：凡是从一个点出发有奇数条线的点，叫做奇点；凡是从一个点出发有偶数条线的点，叫做偶点。
3、欧拉定理：（1）凡是由偶点组成的连通图，一定可以一笔画成。
画时可以任一偶点为起点，最后一定能以这个点为终点画完此图。
（2）凡是只有两个奇点（其余均为偶点）的连通图，一定可以一笔画完。
画时必须以一个奇点为起点，另一个奇点为终点。
（3）奇点的个数一定为偶数，奇点个数超过两个的图形不能一笔画，所需的最少笔数等于奇数点的个数除以2。
例题1：下面这些图形是否能一笔画？能一笔画的打“√”，不能画的打“×”。
（）（）（）（）（）【答案】×，×，√，√，√例题2：用标数法判断下图是否能一笔画，如果哪个图形可以一笔画，就请并标出它的起点和终点。
【答案】前两个图形，以任一偶点为起点，最后以这个点为终点；后两个图形以任意一个奇点为起点，另一个奇点为终点。
例题3：（1）下面两个图形均不能一笔画成，你能将原图形中的某一线段去掉，使它可以一笔画吗？【解析】（1）去掉AC、AD、AE任意一个即可；（2）去掉AB（答案不唯一）；（3）去掉AG（答案不唯一）（2）下列各图形能不能一笔画成，如果不能，至少添上几笔，就能使整个图形一笔画完？【答案】（1）不能，至少添加1笔；（2）不能，至少添加2笔。
【解析】图（1）共有4个奇点，留下两个奇点，这样只要将其中两个奇点之间连一条线段，就把4个奇点变成2个奇点了，这样就能使整个图形一笔画完，所以至少需要添加1笔，就能使整个图形一笔画完；图（2）共有6个奇点这样只要将其中4个奇点之间连两条线段，就把6个奇点变成2个奇点了，这样就能使整个图形一笔画完了，所以至少只需要添加2笔，就能使整个图形一笔画完。
让学生学会“数学地想”--《好玩的一笔画》教学实录及解析
让学生学会“数学地想”*——《好玩的一笔画》教学实录及解析□李铁安张惠云这节课是以数学家欧拉解决“哥尼斯堡七桥问题”为史料背景展开的。
本节课不仅要让学生探究一笔画图形的规律，还要让学生经历一个发现提出问题和分析解决问题的完满的过程，并在探索的过程中引导学生“用数学的眼光观察世界，用数学的思维分析世界，用数学的语言描述世界”。
【教学过程】环节一：创作及判断图形能否一笔画——明确何为一笔画教师在屏幕上动态展示一笔写出“好玩”两个字的过程（如图1）。
师：同学们请看！这两个字认识吗？生：认识！是“好玩”两个字。
生：我发现“好玩”这两个字是一笔写出来的。
师：一笔连着写出“好玩”两个字，确实挺好玩。
今天让我们一起来学习“好玩的一笔画”。
大家请看，我用一笔创作了一个图形，这是什么？（生答，略）师：是的，老师用一笔画出了一个向上指的箭头。
你们能用一笔画出怎样的图形呢？自己试一试！（学生交流各自的作品，如图2）图2师：哦！这么多图案都能用简单的一笔就画出来，你们的想象和创意都很独特。
下面同学们再认真看看这些图形（出示图3）。
想一想，试一试，能一笔画吗？①②③④⑤⑥图3生：第①个图形能一笔画，我是这样画的（从圆点处起笔）。
生：我还有其他的画法，这样画也是可以的（从圆点处起笔）。
生：我再试试其他两个点，都不行。
师：你们是从每个点开始尝试一笔画的，这个想法挺好。
生：第②个图形和第⑤个图形从哪个点开始画都行，只要绕着所有的线走一圈就可以啦！师：从哪个点画都行！你的发现太美妙了！生：第③个图形也能一笔画，从这两个点开始都是可以的。
师：是啊，这个图形能一笔画，也确实只有这两个点能走通。
生：第④个图形我尝试了所有的点，无论从哪个点开始都不能一笔画，大家看。
（展示图片，如图4）图4图1*本文系中国教育科学研究院2019年基本科研业务费专项资金项目“推进数学文化进课堂的实践研究”（项目批准号：GYI2019041）的阶段成果。
生：第⑥个图形也不能一笔画，怎么画都少一条线。
一笔画
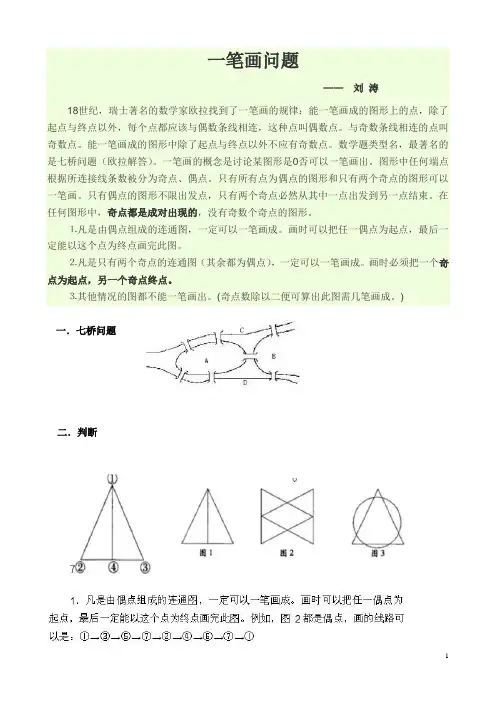
一笔画问题
—— 刘 涛
18世纪，瑞士著名的数学家欧拉找到了一笔画的规律：能一笔画成的图形上的点，除了起点与终点以外，每个点都应该与偶数条线相连，这种点叫偶数点。
与奇数条线相连的点叫奇数点。
能一笔画成的图形中除了起点与终点以外不应有奇数点。
数学题类型名，最著名的是七桥问题（欧拉解答）。
一笔画的概念是讨论某图形是0否可以一笔画出。
图形中任何端点根据所连接线条数被分为奇点、偶点。
只有所有点为偶点的图形和只有两个奇点的图形可以一笔画。
只有偶点的图形不限出发点，只有两个奇点必然从其中一点出发到另一点结束。
在任何图形中，奇点都是成对出现的，没有奇数个奇点的图形。
⒈凡是由偶点组成的连通图，一定可以一笔画成。
画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。
⒉凡是只有两个奇点的连通图（其余都为偶点），一定可以一笔画成。
画时必须把一个奇点为起点，另一个奇点终点。
⒊其他情况的图都不能一笔画出。
(奇点数除以二便可算出此图需几笔画成。
)
二．判断
一．七桥问题
三．生活应用
【题目】：下图是一个公园的道路平面图，要使游客走遍每条路而又不重复，出、人口应该设在哪里？
【解析】：
要使游客走遍每一条路而又不重复，也就是一笔画出上图，公园的出入口就是一笔画的起点和终点。
观察图形，图中只有I 和E 两个奇点（每个点连接3条线），因此公园的出入口应设在这两个点上，以其中一个点为入口，以另一个点为出口。
四．小试牛刀。
世界数学难题——一笔画
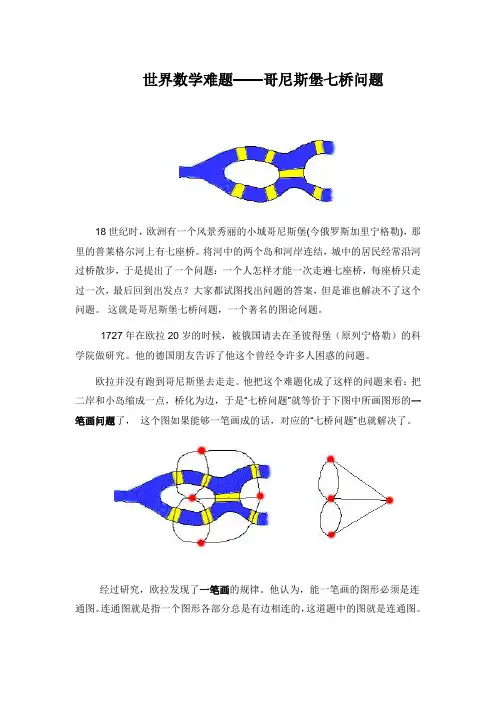
世界数学难题——哥尼斯堡七桥问题18世纪时，欧洲有一个风景秀丽的小城哥尼斯堡(今俄罗斯加里宁格勒)，那里的普莱格尔河上有七座桥。
将河中的两个岛和河岸连结，城中的居民经常沿河过桥散步，于是提出了一个问题：一个人怎样才能一次走遍七座桥，每座桥只走过一次，最后回到出发点？大家都试图找出问题的答案，但是谁也解决不了这个问题。
这就是哥尼斯堡七桥问题，一个著名的图论问题。
1727年在欧拉20岁的时候，被俄国请去在圣彼得堡（原列宁格勒）的科学院做研究。
他的德国朋友告诉了他这个曾经令许多人困惑的问题。
欧拉并没有跑到哥尼斯堡去走走。
他把这个难题化成了这样的问题来看：把二岸和小岛缩成一点，桥化为边，于是“七桥问题”就等价于下图中所画图形的一笔画问题了，这个图如果能够一笔画成的话，对应的“七桥问题”也就解决了。
经过研究，欧拉发现了一笔画的规律。
他认为，能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的，这道题中的图就是连通图。
但是，不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
那么什么叫奇、偶点呢？与奇数（单数）条边相连的点叫做奇点；与偶数（双数）条边相连的点叫做偶点。
如下图中的①、④为奇点，②、③为偶点。
1．凡是由偶点组成的连通图，一定可以一笔画成。
画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。
例如下图都是偶点，画的线路可以是：①→③→⑤→⑦→②→④→⑥→⑦→①2．凡是只有两个奇点的连通图（其余都为偶点），一定可以一笔画成。
画时必须把一个奇点为起点，另一个奇点终点。
例如下图的线路是：①→②→③→①→④3．其他情况的图都不能一笔画出。
有趣的一笔画问题
精心整理有趣的一笔画问题一笔画问题的提出：我们从生活提出一笔画问题。
为了更好的解决这个问题，一笔画是一个大问题，希望在这他为了检查几个城市之间的若干公路，我们先看一个公路检查员的问题：使他能不重复地恰好通过每条公路些城市和公路组成的公路系统中找出一条路线一次，而经过每个城市的次数不限。
这就是拓扑学中的数学问题一笔画的含这种图形就叫一笔画如果用笔在纸上连续不断又不重复一笔画成某种图形下面的画能一笔画成，你也试着描一描，画一画吧那么是不是所有的图形都能一笔画成呢？那我们就要一起学习一笔画的规律。
传统意义上的几何学其实一笔画是一个几何问题，一个图形由一笔构成叫一笔画。
通常的几而对于平面图形的一笔画与多笔画问题，是研究图形的形状大小等性质，何方法是无能为力的，因为一个图形能否一笔画，与图形的大小、形状和线段的长我们可以随而是与图形中线段的数目及连接关系有关，短等几何概念都没有关系，意地将图形拉伸、压缩或弯曲，甚至在保持端点不动的前提下，还可以将某些线段“搬家”，只要图形的整体结构不变，能否一笔画的性质也就不会改变。
即平面上由曲线段构成的一个图形能不能一笔画问题是一个简单的数学游戏，使得在每条线段上都不重复？例如汉字‘日'和‘中'字都可以一笔画一笔画成，在日本动画片一休中，是采用对折纸张的方法画的，而‘田'和‘目'则不能。
( 出‘田'和‘目'的一笔画）也是可取之处。
一笔画图形的规律和判别：精心整理欧拉最终证明了这个图著名的哥尼斯堡七桥问题实质上就是一个一笔画问题。
并在关于七桥问题的报告中得到了任一网络图能否一笔画的形是不能一笔画成的，判别法则。
连通图就是指一个图形各部分总是欧拉认为，能一笔画的图形必须是连通图。
有边相连的．但是，不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
数学家欧拉找到一笔画的规律是：1．凡是由偶点组成的连通图，一定可以一笔画成。
小学奥数—奇妙的一笔画
知识点拨
所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次， 不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？ 下面，我们就来探求解决这个问题的方法．
什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏． 我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点． 一笔画问题： (1)能一笔画出的图形必须是连通的图形； (2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题： 我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于 任意的连通图来说，如果有 2n 个奇点(n 为自然数)，那么这个图一定可以用 n 笔画成．
【例 17】 下图中不能一笔画成，请你在下图中添加最少的线段，将其改成一笔画的图形，并画出路线图．
A
E
D
G
H
B
C
F
【例 18】 如图所示，某小区花园的道路为一个长 480 米，宽 200 米的长方形；一个边长为 260 米的菱形和十 字交叉的两条道路组成．一天，王大爷 A 处进入花园，走遍花园的所有道路并从 A 处离开．如果
【巩固】如下图所示，两条河流的交汇处有两个岛，有七座桥连接这两个岛及河岸．问：一个散步者能否一 次不重复地走遍这七座桥？
【例 21】 一个邮递员投递信件要走的街道如右图所示，图中的数字表示各条街道的千米数，他从邮局出发， 要走遍各街道，最后回到邮局．怎样走才能使所走的行程最短？全程多少千米？
数学人教版六年级下册微课教案：《一笔画里的数学秘密》
微课教案：《一笔画里的数学秘密》一、教学内容人教版《义务教育课程标准实验教科书数学》六年级下册，解决七桥问题中的“一笔画”规律。
二、教学目标1．通过“一笔画”问题及其结论的了解，使学生对点、线有进一步的认识，来解决一些实际问题。
2．通过探究“一笔画”规律的活动，扩大学生知识视野，激发学生学习兴趣。
三、教学流程设计及意图1、导语：同学们，今天老师跟你们分享一个画画里的数学秘密，下面请同学们跟老师一起画一画吧！2、讲述“一笔画”的含义a.下笔后笔尖不能离开纸。
b.每条线都只能画一次而不重复、不遗漏。
3、探究“一笔画”的规律a.不连通的图形不可以一笔画b.连通的图形有可能可以一笔画（1）画一画9个连通的图形能否都一笔画成？发现图2、3、7可以一笔画成，图4、5、8不能一笔画成，但是图1、6、9有的同学可以一笔画成，有的同学不能一笔画成。
（2）“一笔画”与奇、偶点的关系通过以图1为例，继续探究能否一笔画成与出发点的位置有关，引出奇、偶点概念。
a.奇点：有奇数条边相连的点b.偶点：有偶数条边相连的点（3）填表格老师让学生自己完成两个表格的奇、偶个数。
同时，让学生观察“一笔画”与奇偶点个数之间的关系。
（4）总结“一笔画”的规律老师引导学生一起总结出“一笔画”的规律。
如下：规律1：凡能一笔画的图形必须是一个连通图；规律2：凡能一笔画的图形，与偶点个数无关，与奇点个数有关，其个数是0或2.规律3：如果有0个奇点，那么每个点都能作为起点；如果有2个奇点，那其中一个必为起点，另一个必为终点。
4、“一笔画”的历史和应用介绍数学家欧拉解决“七桥问题”发现的“一笔画”规律。
同时，介绍了现在生活中“一笔画”的影子。
用“一笔画”规律设计出来的唯美图画。
5、结束语世界是美的，只要有一双发现美的眼睛；数学是美的，只要有一颗发现美的心灵。
同学们，这就是老师今天要告诉大家画画里的数学秘密，你学会了吗？谢谢大家观赏！四、教学设计流程图课题：一笔画里的数学秘密1、导语2、讲述“一笔画“的含义连通图3、探究“一笔画”的规律画一画填一填总结“一笔画”的规律4、“一笔画”的历史和应用5、结束语。
小学奥数教程-奇妙的一笔画 (含答案)
所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点． 一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】 同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要 种颜色的旗子，如果贝贝从某营地出发，不走重复路线就 （填“能”或“不能”）完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛，六年级，初赛，第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。
一笔画数学原理
一笔画数学原理嘿，朋友们！今天咱来聊聊这神奇的一笔画数学原理呀！你说这一笔画，咋就这么有意思呢？就好像我们走路，得一口气走到底，中间不能断，不能停。
这多像我们的人生啊，一路向前，不能半途而废！想象一下，一张纸上那些弯弯绕绕的线条，就等着我们用一支笔去征服它们。
有时候看着那些复杂的图形，心里还真有点犯嘀咕：这能一笔画出来吗？但当你静下心来，仔细琢磨，嘿，还真就找到那奇妙的路径了。
就好比我们遇到困难，乍一看觉得没法解决，可只要我们不放弃，慢慢摸索，总能找到出路。
一笔画不也是这样嘛，别被那些看似杂乱的线条给唬住了，只要有耐心，就能发现其中的奥秘。
咱再说说那些能一笔画成的图形。
它们可都有自己的特点呢，什么奇点啦，偶数点啦。
这奇点就好像是路上的绊脚石，要是奇数个奇点，那可就麻烦喽，一般就不能一笔画成啦。
但要是偶数个奇点呢，那就有戏！这不就跟我们做事一样嘛，得找到关键所在，避开那些难搞的地方。
我记得小时候玩连线游戏，不就是一笔画的雏形嘛。
那时候可认真了，就想着一定要一笔连成，不然就觉得不甘心。
现在想想，这也是对一笔画原理的一种早期探索呀！你说数学这东西，有时候真的很神奇。
一个小小的一笔画原理，就能让我们琢磨半天，还乐在其中。
而且在生活中也能找到它的影子呢。
比如我们规划一天的行程，要合理安排，不能走冤枉路，这是不是也有点像一笔画呀？还有啊，那些艺术家们创作的画作，线条流畅自然，说不定也是在遵循着一笔画的原理呢！他们用画笔在画布上一笔一笔地勾勒出美妙的图案，不也是一种对一笔画的完美诠释嘛。
总之呢，这一笔画数学原理可真是个宝呀！它让我们看到了数学的趣味和实用，也让我们在生活中多了一份思考和乐趣。
大家可别小瞧了它，多去研究研究，说不定能发现更多的惊喜呢！咱就好好享受这神奇的一笔画带给我们的乐趣吧！。
一笔画问题例题加解析
一笔画问题例题加解析一、什么是一笔画问题。
一笔画问题呀，就像是一个超有趣的小谜题呢。
简单来说，就是在一个图形里，能不能一笔就把这个图形画出来，而且笔不能离开纸，也不能重复画已经画过的线。
这就像是在走迷宫，但是这个迷宫是用线条画出来的。
比如说，一个圆形，那肯定能一笔画出来，就顺着圆的边画一圈就好啦，简单得很。
二、一笔画问题的小规则。
这里面可是有小秘密的哦。
有个叫欧拉的超级聪明的人发现了一些规律。
对于一个连通图（就是这个图里的各个部分都是连着的，没有分开的小块），如果这个图里的奇点（就是从这个点出发的线的数量是奇数条的点）个数是0或者2的时候，这个图就能一笔画出来。
要是奇点个数是0呢，就可以从任何一个点开始画，最后还能回到这个点；要是奇点个数是2呢，就得从其中一个奇点开始画，然后到另一个奇点结束。
三、例题来啦。
1. 比如说这个三角形，我们来看看它能不能一笔画出来呢。
三角形的每个顶点，都有两条线连着，那就是说，它的奇点个数是0。
按照我们刚刚说的规则，它肯定能一笔画出来啦。
怎么画呢？就从三角形的一个顶点开始，顺着边画，绕一圈就画好啦，是不是很容易呢？2. 再看这个正方形加上一条对角线的图形。
这个图形的四个顶点本来都是有两条线连着的，但是加上对角线之后呢，对角线的两个端点就变成了奇点，这时候奇点个数是2。
那按照规则，我们从其中一个奇点开始，沿着边画，就能一笔画出来啦。
四、解析例题。
1. 对于三角形那个例子，因为每个顶点都是偶点（从这个点出发的线的数量是偶数条的点），所以我们在画的时候，就可以很顺畅地绕着图形走一圈，不会出现画不下去或者必须重复的情况。
这就像是在一个没有障碍的小路上散步，一路畅通无阻。
2. 在正方形加对角线的例子里，由于有两个奇点，这就像是两个特殊的出入口。
我们从一个奇点这个特殊的入口进去，然后沿着图形的边和线走，最后到达另一个奇点这个出口，就刚好把整个图形一笔画完了。
如果我们不按照这个规则，从别的点开始画，就会发现画到一半就会走不下去，或者必须要重复画某些线了。
[实用]趣味数学一笔画PPT文档
![[实用]趣味数学一笔画PPT文档](https://img.taocdn.com/s3/m/4b279ae16c85ec3a86c2c507.png)
图1
图2
你能用一笔画出下列图形吗？
趣味数学一笔画趣味数学一笔画 “一笔画”是一种有趣的数学游戏，那么什么样的图形可以一笔画成呢？试一试，画一画，发挥你的想象力，发现一笔画的规律。 “一笔画”是一种有趣的数学游戏，那么什么样的图形可以一笔画成呢？试一试，画一画，发挥你的想象力，发现一笔画的规律。 试试看。 “一笔画”是一种有趣的数学游戏，那么什么样的图形可以一笔画成呢？试一试，画一画，发挥你的想象力，发现一笔画的规律。 试试看。 趣味数学一笔画趣味数学一笔画 趣味数学一笔画趣味数学一笔画 你能笔尖不离纸，一笔画出下面的每个图形吗？ 你能笔尖不离纸，一笔画出下面的每个图形吗？ “一笔画”是一种有趣的数学游戏，那么什么样的图形可以一笔画成呢？试一试，画一画，发挥你的想象力，发现一笔画的规律。 你能笔尖不离纸，一笔画出下面的每个图形吗？ 趣味数学一笔画趣味数学一笔画 通过阅读报刊，我们能增长见识，扩大自己的知识面。 通过阅读报刊，我们能增长见识，扩大自己的知识面。 通过阅读报刊，我们能增长见识，扩大自己的知识面。 通过阅读报刊，我们能增长见识，扩大自己的知识面。
趣味数学一笔画
一笔画之绵羊 一笔画之猩猩
不重复的路
——一笔画
“一笔画”是指笔不 离开纸，而且每条线 都只画一次不准重复 而画成的图形。
“一笔画”是一种有趣 的数学游戏，那么什么 样的图形可以一笔画成 呢？试一试，画一画， 发挥你的想象力，发现 一笔画的规律。
你能笔尖不“一离纸笔，一画笔”画出的下规面的律每个图形吗
谢谢？趣味数学一笔画趣味来自学一试笔画试看。（不走重复线路）
你能笔尖不离纸，一笔画出下面的每个图形吗？ 通过阅读报刊，我们能增长见识，扩大自己的知识面。 趣味数学一笔画趣味数学一笔画 趣味数学一笔画趣味数学一笔画 “一笔画”是一种有趣的数学游戏，那么什么样的图形可以一笔画成呢？试一试，画一画，发挥你的想象力，发现一笔画的规律。 通过阅读报刊，我们能增长见识，扩大自己的知识面。 你能笔尖不离纸，一笔画出下面的每个图形吗？ 趣味数学一笔画趣味数学一笔画 你能用一笔画出下列图形吗？ “一笔画”是指笔不离开纸，而且每条线都只画一次不准重复而画成的图形。 趣味数学一笔画趣味数学一笔画
266揭秘数学中的魔法：一笔成画的神秘理论
揭秘数学中的魔法：一笔成画的神秘理论在数学的世界里，有一种令人着迷的理论，它能让一条连续的线条在纸面上自由穿梭，最终形成一幅美丽的图案。
这种理论被称为“一笔成画”，它不仅是数学家的宠儿，也吸引了无数艺术爱好者和探索者的目光。
今天，就让我们一起走进这个神秘的世界，揭开一笔成画的神秘面纱吧！一、一笔成画的起源与定义一笔成画，顾名思义，就是用一笔连续不断地画出整个图形。
这种绘画方式看似简单，实则蕴含着深刻的数学原理。
在数学上，一笔成画被称为“一笔画问题”，它是图论中的一个重要分支。
一笔画问题的研究起源于著名的哥尼斯堡七桥问题，当时的人们试图找到一种方法，能够不重复、不遗漏地走过城市的七座桥。
这个问题最终由数学家欧拉解决，他通过将实际问题抽象为图形，并运用数学方法进行分析，为一笔画问题奠定了坚实的基础。
二、一笔成画的原理与分类一笔成画的原理主要基于图论中的“欧拉路径”和“欧拉回路”概念。
简单来说，如果一个图形中的每个节点（即交叉点或端点）都有偶数条边相连，那么这个图形就可以一笔画成，且起点和终点相同，这种路径被称为欧拉回路；如果一个图形中有且仅有两个节点具有奇数条边相连，那么这个图形也可以一笔画成，但起点和终点不同，这种路径被称为欧拉路径。
根据欧拉路径和欧拉回路的原理，我们可以将一笔成画的图形分为两类：封闭图形和开放图形。
封闭图形是指起点和终点重合的图形，如圆形、正方形等；开放图形是指起点和终点不重合的图形，如直线、折线等。
这两种图形在一笔成画的过程中有着不同的特点和规律。
三、一笔成画的技巧与实例掌握了一笔成画的原理后，我们就可以尝试运用一些技巧来画出各种美丽的图案。
首先，我们需要选择合适的起点和终点，以确保图形能够一笔画成。
其次，我们需要合理规划线条的走向和交叉点的位置，以使得最终形成的图案既美观又符合数学原理。
例如，我们可以尝试用一笔画出一个五角星。
首先，我们选择一个合适的起点，然后沿着五角星的轮廓连续不断地画出线条，直到回到起点。
奇妙的一笔画(含详细解析)
所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点． 一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画． 多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】 同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要 种颜色的旗子，如果贝贝从某营地出发，不走重复路线就 （填“能”或“不能”）完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【考点】一笔画问题【难度】2星【题型】填空【关键词】华杯赛，六年级，初赛，第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一笔画图片欣赏
一笔画图片欣赏
世界是美的， 只要有一双发现美的眼睛； 数学是美的， 只要有一颗发现美的心灵。
规律1：凡能一笔画的图形必须是一个连通图； 规律2：凡能一笔画的图形，与偶点个数无关， 与奇点个数有关，其个数是0或2.
18世纪时风景秀丽的小城哥尼斯堡中有一 条河，河的中间有两个小岛，河的两岸与两 岛之间共建有七座桥（如图），当时小城的 居民中流传着一道难题：一个人怎样才能不 重复地走过所有七座桥，再回到出图5
让我们先来了解两个新概念
1、奇点：有单数条边相连的点
● ●
●
2、偶点：有双数条边相连的点
● ● ●
图形与点的关系
图形 奇点个数 偶点个数
能一笔画的图形
图形 奇点个数 偶点个数
2个 2个
3个 4个
0个 0个
10个
8个
判断下面图形是不是一笔画的图形？
“一笔画图”的规律
人教版小学数学六年级下册七桥问题
《一笔画里的数学秘密》 一笔画里的数学秘密
北京师范大学厦门海沧附属学校 录制者：苏洪霞
一笔画：
1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不重复、不遗漏。
和老师一起画
1、老师可以一笔画出来， 你们能做到吗？
2、动脑筋！这个图形可 以一笔画出来吗？
不连通的图形不能一笔画