基于最大熵的直方图阈值分割算法
二维最大熵阈值分割法

二维最大熵阈值分割算法[引用]杜峰,施文康,邓勇等:《一种快速红外图像分割方法》1. 二维最大熵阈值分割熵是平均信息量的表征。
二维最大熵法是基于图像二维直方图。
图像二维直方图定义如下:NM n P j i j i ⨯=,,其中N M ⨯表示图像大小,j i n ,表示图像灰度值为i ,邻域灰度平均值为j 的像素个数。
通常二维直方图的平面示意图可以用下图1表示:其中区域1和2表示背景和目标像素,区域3和4通常表示边界和噪声信息。
阈值向量(t ,s ),t 表示灰度值,s 表示像素邻域均值(通常是8邻域)。
对于L 个灰度级的图像,设在阈值(t,s)定义区域1和2的概率P1,P2:∑∑-=-==101,1s i t j ji PP ,∑∑-=-==11,2L s i L tj j i P P定义二维离散熵H 的一般表示:∑∑-=ijji ji P PH ,,lg对各区域概率j i P ,进行归一化处理可得区域1的二维熵:11)1lg(1lg 1)1(101,,P H P P P P P H s i t j j i ji +=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=∑∑-=-= 同理区域2的二维熵:22)2lg()2(P H P H +=其中,H 1,H 2为:∑∑-=-=-=101,,lg 1s i t j ji ji P PH ,∑∑-=-=-=11,,lg 2L s i L tj j i j i P P H那么整个图像中目标和背景熵之和的函数)2()1(),(H H t s +=φ根据最大熵原则,存在最佳的阈值向量满足条件:图1 二维直方图平面示意图灰阶)},(max{),(t s t s φφ=**图2显示了一幅图像的二维直方图说明了背景和目标的主要分布情况,其中图2(b)横坐标表示邻域的均值,纵坐标表示灰度值分布:2. 微粒群寻优算法(PSO )PSO 最早由Kenredy 和Eberhart 于1995年提出。
python最大熵阈值分割

python最大熵阈值分割摘要:1.最大熵阈值分割简介2.最大熵阈值分割原理3.最大熵阈值分割在Python 中的实现4.结论正文:1.最大熵阈值分割简介最大熵阈值分割是一种基于熵的图像分割方法。
熵是信息论中的一个重要概念,用于衡量一个事件的不确定性。
在图像分割中,最大熵阈值分割算法通过计算图像的熵来确定最佳阈值,使得分割后的前景和背景两部分熵之和最大。
这种方法可以用于二值图像、灰度图像和彩色图像的分割。
2.最大熵阈值分割原理最大熵阈值分割的原理如下:(1) 计算图像的直方图,得到像素值的概率分布。
(2) 计算图像的熵,表示为各像素值概率分布的加权熵之和。
(3) 设定一个阈值,将图像分为前景和背景两部分。
(4) 计算分割后前景和背景的熵之和。
(5) 求解使熵之和最大的阈值,即为最佳阈值。
3.最大熵阈值分割在Python 中的实现在Python 中,可以使用OpenCV 库实现最大熵阈值分割。
以下是一个简单的示例代码:```pythonimport cv2# 读取图像image = cv2.imread("image.jpg", cv2.IMREAD_GRAYSCALE)# 计算直方图hist, _ = cv2.calcHist([image], [0], None, [256], cv2.HIST_GRAYSCALE) # 计算熵entropy = -np.sum(hist * np.log2(hist + 1e-5))# 设定阈值threshold = 128# 进行最大熵阈值分割_, binary_image = cv2.threshold(image, threshold, 255,cv2.THRESH_BINARY)# 显示结果cv2.imshow("Original Image", image)cv2.imshow("Binary Image", binary_image)cv2.waitKey(0)cv2.destroyAllWindows()```4.结论最大熵阈值分割是一种基于熵的图像分割方法,可以用于二值图像、灰度图像和彩色图像的分割。
基于熵的图像二值化算法设计-二维最大熵分割

1设计目的与要求1.1 设计目的(1)熟悉和掌握MATLAB程序设计方法。
(2)学习和掌握MATLAB图像处理工具箱。
(2)了解图像分割和图像二值化的原理。
(3)掌握图像二值化技术阈值的选取。
(4)将原彩色图像变为二值化后的图像,通过二维最大熵图像分割法对图像进行分割达到预期目的。
1.2 设计要求(1)了解图像变换的意义和手段。
(2)熟悉最大熵和二值化的基本性质。
(3)通过本实验掌握利用MATLAB编程实现数字图像处理。
(4)理解图像分割的原理,了解其应用,掌握最大熵和二值化分割的方法。
2 设计方案2.1 图像二值化图像二值化是数字图像处理技术中的一项基本技术,二值化图像的显示与打印十分方便,存储与传输也非常容易,在目标识别、图像分析、文本增强、字符识别等领域得到广泛应用。
图像二值化是将灰度图像转化为只有黑白两类像素的图像,大多采用阈值化算法处理。
在不同的应用中,阈值的选取决定着图像特。
征信息的保留。
因此,图像二值化技术的关键在于如何选取阈值。
2.2 最大熵原理最大熵原理:最大熵原理是在1957 年由E.T.Jaynes 提出的,其主要思想是,在只掌握关于未知分布的部分知识时,应该选取符合这些知识但熵值最大的概率分布。
因为在这种情况下,符合已知知识的概率分布可能不止一个。
我们知道,熵定义的实际上是一个随机变量的不确定性,熵最大的时候,说明随机变量最不确定,换句话说,也就是随机变量最随机,对其行为做准确预测最困难。
图像分割中最大熵的引入:在图像分割中若假定以灰度级T 分割图像,则图像中低于灰度级T 的像素点构成目标物体,高于灰度级T 的像素点构成背景那么各个灰度级在图像分割后的两区域中的概率如下:O :ti N N (0<=i<=t) (3.2.1)B :ti N N N - (t+1<=i<=255) (3.2.2)其中Ni 为图像中灰度级为i 的像素点个数,Nt 为灰度级从0~t 的像素点总和,N 为图像总像素点,t 为假定灰度阈值T 。
二维最大熵阈值分割

二维最大熵阈值分割
二维最大熵阈值分割算法
若一幅图像的灰度级数为L,总的象素点数为N(m×n),设f i,j 为图像中点灰度为i及其区域灰度均值为j的象素点数,p i,j为点灰度-区域灰度均值对(i,j)发生的概率,即:p i,j=f i,j/N,其中N (m×n)为图像的总象素数,则{p i,j,i,j=1,2,…,L}是该图像关于点灰度-区域灰度均值的二维直方图。
图1为二维直方图的xoy平面图。
沿对角线分布的A区和B区分别代表目标和背景,远离对角线的C区和D区代表边界和噪声,所以应该在A区和B区上利用点灰度-区域灰度均值二维最大熵法确定最佳阈值,可使真正代表目标和背景的信息量最大。
于是,定义离散二维熵为:
3 二维最大熵阈值分割递推算法
在上述二维阈值化方法中,对于每个(s,t)对,都要从头开始计算P A(s,t)和H A(s,t),运算过程是一个4重循环,计算复杂性为,计算比较耗时。
实际应用中,为了提高运算速度,减少重复计算,必须对二维最大熵进行进一步优化。
对于一个固定的s,当t取1-L时,计算Φ(s,t)已经不存在重复计算,但同样s也要从1取到L,这样
这样通过优化,该递推算法可将计算的复杂性减至O(L2),大大减少了计算的复杂性,提高了计算速度。
具体算法实现如下:(1)计算原始图像中各个象素点的灰度值以及各个象素点的4邻域平均灰度值,并计算统计灰度信息P[i][j];
(2)相关计算
(3)求出最佳阈值(s*,t*),分割图像。
二维直方图区域斜分的最大熵阈值分割算法

维直方图区域划分成图 1 ( c) 所示的 4个矩形区域.
假设图像的暗 (亮 ) 像素属于目标 (背景 ) , 则区域 0
和目标对应 ,区域 1和背景对应 ,而区域 2和 3则表
示边缘和噪声. 计算时仅考虑区域 0和 1, 而假设区
域 2和 3的概率近似为零. 最后采用与灰度级轴垂直
的直线将灰度级小于 t的部分分成目标 ,大于 t的则
A BSTRAC T
The obvious w rong segmentation is pointed out in the existing two2dimensional histogram vertical segm entation method. A two2dimensional histogram oblique segm entation method is p roposed. Then the formula and its fast recursive algorithm of the maximum Shannon entropy thresholding are deduced based on the two2dim ensional histogram oblique segm entation. Finally, the threshold images and the p rocessing tim e are given in the experimental results and analysis. The results are compared w ith those of the original m axim um Shannon entropy algorithm and its fast algorithm s based on the two2dim ensional histogram vertical segmentation. The experimental results show that the p roposed method makes the inner part uniform and the edge accurate in the threshold image, and it has a better anti2noise p roperty. The p rocessing tim e of the fast recursive algorithm of the p roposed method is about 2% of that of the original two2dim ensional maximum Shannon entropy algorithm , and it is less than one third of that of two fast recursive algorithm s of the maximum Shannon entropy thresholding based on the two2dim ensional histogram vertical segmentation.
快速最大熵多阈值图像分割算法

s n f a t mp o e o a e t o v n in lma i m nr p t o n sa l c o i i c nl i r v d c mp r d wi c n e t a x mu e to y meh d a d i e t a c mmo ae g n r l印 p iai n r q i me t . g i y h o b o d t e e a l t e u r c o e ns
0 引 言
图像分 割就是依据图像 的性质 , 将一 幅 图像 划分 不 同区域
大小 的影 响小 , 可用于小 目标 分割 。但 因为传统 的最大熵 算 法是使用穷举法选取使 目标 函数 取得最 大值 的阈值 , 并且 目标
的过 程。图像 分割是图像处 理 和计 算机 视觉 中的基本 技术 , 是 图像 分析 、 理解 和描 述的关 键步骤 。阈值方 法是一 种重要 的 图 像分 割方法 , 由于其算法 简单 和易于执行 , 图像分 割中得到 了 在 广泛的应用 。如果只是将 图像分 为 目标 和背景 两类 , 么就只 那 需要选取 一个阈值 , 图像 中每个 像素的灰度值与 阈值 比较 , 将 灰 度值 大于阈值的像素为一类 , 度值小 于 阈值 的像 素则为 另一 灰 类 。如果要将 图像 分为多个 目标 , 就需要 选取多个阚值 , 图像 将 中每个像 素的灰度值与 阈值 比较 , 得到分割结果 。
推公式提 出了快速选 取 阈值 的方法 ; 文献 [ ] 7 提出 了一种利 用
粒子群优化算 法提 高选取 阈值速 度 的方法 ; 文献 [ ] 出了一 8提 种利用增量学 习法 ( L 提高选取 阈值 速度 的方法 。本 文 的研 R)
究 目的就是要提 高最大熵算 法 的运算 速度 。文献 [ ] 2 针对 Os t u 算法利用代数运算 的递 推公式 , 出了一种快速 Os 法。受 提 t u算 其思想启发 , 本文针对选取阈值的最大熵算法 , 出了一 种基 于 提 最大熵算法 的快速 阙值 选取算 法 , 能够实 现对图像 的多 阈值 快
基于最大信息熵原理的显微细胞图像多阈值分割算法
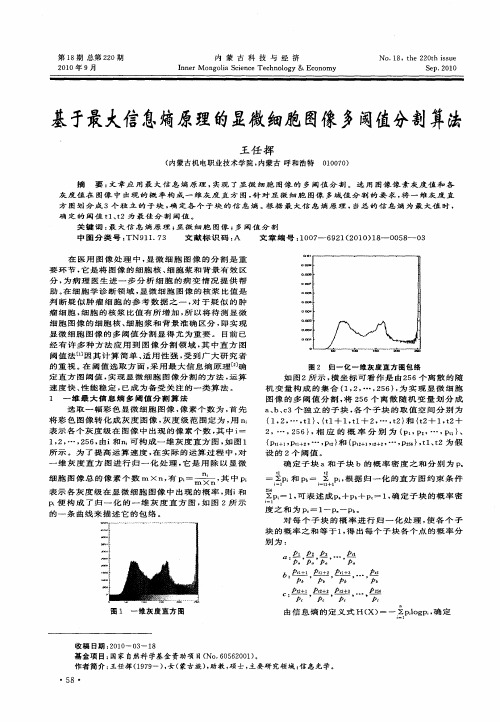
细 胞 图像 的 细 胞 核 、 胞 浆 和 背 景 准 确 区 分 , 实 现 细 即 显 微 细 胞 图 像 的 多 阈 值 分 割 显 得 尤 为 重 要 。 目前 已 经 有 许 多 种 方 法 应 用 到 图 像 分 割 领 域 , 中 直 方 图 其 阈 值 法 n因 其 计 算 简 单 、 用 性 强 , 到 广 大 研 究 者 ] 适 受 的 重 视 。 阈 值 选 取 方 面 , 用 最 大 信 息 熵 原 理 [确 在 采 2
定 直 方 图 阈 值 , 现 显 微 细胞 图像 分 割 的方 法 , 算 实 运 速度快 、 能稳定 , 成 为备受关 注的一类算 法 。 性 已 1 一 维 最 大 信 息 熵 多 阈 值 分 割 算 法
图 2 归一 化 一 维 灰 度 直方 图包 络
如 图 2所 示 , 坐 标 可 看 作 是 由 2 6个 离 散 的 随 横 5 机 变 量 构 成 的集 合 { 2 … , 5 )为 实 现 显 微 细 胞 1, , 26,
2 56
P 便 构 成 了 归 一 化 的 一 维 灰 度 直 方 图 , 图 2所 示 . 如 的一 条 曲 线 来 描 述 它 的 包 络 。
∑p一 1 可 表 述 成 p + p + p一 1, 定 子 块 的 概 率 密 i , 。 b 确 度 之 和 为 p 一1 p-p 。 。 一 。 b 对 每 个 子 块 的 概 率 进 行 归 一 化 处 理 , 各 个 子 使 块 的概率 之和等 于1得 出每个子块 各个点 的概率分 ,
在 医 用 图 像 处 理 中 , 微 细 胞 图 像 的 分 割 是 重 显
要 环 节 , 是 将 图 像 的 细 胞 核 、 胞 浆 和 背 景 有 效 区 它 细 分 , 病 理 医 生 进 一 步 分 析 细 胞 的 病 变 情 况 提 供 帮 为 助 。 细 胞 学 诊 断 领 域 , 微 细 胞 图 像 的 核 浆 比值 是 在 显 判 断 疑 似 肿 瘤 细 胞 的 参 考 数 据 之 一 , 于 疑 似 的 肿 对 瘤 细 胞 , 胞 的 核 浆 比值 有 所 增 加 , 以将 待 测 显 微 细 所
基于遗传算法的最佳直方图熵图像分割算法研究

上式中 A g a 是求使 函数 H f rm x f j最大的那个值 t ,即所求 得 的最佳分割 阈值 。因此采用公式 ()作 为适度 函数 ,满足 1 最 大熵 即最高适 应度值 的个 体为所求 的最佳 阈值 。利用 公式 ()计算初始群体中每个个体 的适应度 。 1 第 四步 :依据遗 传策略 ,选用遗 传算子 ,产生下 一代群 体。 第五步 :直到找到最 大值 ,否则继续执行第三步。 第六步 :用找到的最佳阈值分割 图像 。 ( 下转到
值分割法的关Leabharlann ,利 用遗传算 法的特点来快速准确地确定灰度 图像直方 图熵的最佳分割 阈值 ,实现 图像分割。通过
仿真试验 验证 ,分割效果明显 ,该算法具有很好的应用前景。 关键词 : 遗传 算法 ; 直方 图熵 ; 图像 分割
Th g rt m fI a e S g e t t n f r Be tHit g a t o y e Al o i h o m g e m n a i o s so r m En r p o Ba e n Ge e i g rt m s d o n tc Al o ih
阈值为 :
T = Ar g
m x a
憾
l
佳分割 阈值 ,实现图像分割 。
( f )
() 2
2 图像分割算法
图像分割 中如何求解最 佳的 阈值 ,寻找 出最优 分割参量 , 以保 证有效 的分割效果是 研究 的 目标 。为了使设计 出的算法 更有 效地搜索 到全局最优 解 ,寻找 出最佳 阈值 ,利 用遗传算 法 的特点来快 速准确地确 定灰度 图像直方 图熵 的最 佳分割 阈 值 ,实现 图像分割 。
数为 2 6 5。
作者简介 :扶晓 ( 7一 , , 师 , 1 8) 女 讲 9 研究 方向 :图像处理 、 计算 机仿真及人工 智能 ;刘劲 ( 7一 ,女 , 师 ,研 究方 1 8) 9 讲
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于最大熵的直方图阈值分割算法苏茂君1 陈锐1 马义德1*1兰州大学信息科学与工程学院,兰州 (730000)Email: ydma@摘 要:本文对图像阈值化分割算法进行了研究,提出了一种基于最大熵的直方图阈值分割算法,并通过几种常用的评价准则对本文算法和几种典型的图像分割算法进行了客观而定量的评价和比较,实验结果表明:基于最大熵的图像自动阈值选取分割算法分割效果良好,要优于常用的直方图分割算法。
关键词:图像分割 直方图 分割评价 信息熵1. 引 言图像的二值分割是数字图像处理中的一个很重要的研究领域。
图像的二值化在计算机图像处理技术中的应用非常广泛,可以应用于目标识别、图像分析、文本增强、字符识别、牌照识别等各种应用领域,因此对其进行深入研究具有很重要的实际意义。
图像的二值分割就是把一幅图像分成目标和背景两大类,传统的二值分割方法主要是根据目标和背景的灰度分布差异选取适当的阈值进行分割,因此如何来选取阈值是图像分割的关键问题。
本文中我们首先研究和分析了三种典型的图像阈值分割算法:直方图谷点阈值选取算法[1]、最大类间方差法(OSTU)[2]、基于灰度期望值的图像分割算法[3]。
并在此基础上,通过对常用直方图谷点阈值选取算法以及信息熵的研究,提出了一种基于最大熵的直方图阈值分割算法,该算法不依赖于人的主观参与,利用计算机自动选取最佳阈值。
为了将本文提出的图像分割算法与常用的经典分割算法进行比较,我们运用了几种典型的并且通用性较强的图像分割评价准则[4、5、8]:区域内部均匀性准则(UM),形状测度准则(SM)和区域对比度准则(GC),对不同分割算法下的分割结果进行了比较和评价,实验结果表明:本文提出的基于最大熵的自动图像阈值选取分割算法分割效果要明显优于传统基于直方图的阈值分割算法,分割效果良好。
2. 常用图像二值分割算法2.1直方图谷点阈值选取算法这是最简单的一种图像阈值分割算法,一般是根据图像的直方图来进行的。
基本原理是:如果图像的目标和背景区域的灰度差异较大,则该图像的灰度直方图包络线就呈现双峰一谷的曲线,那么选取两峰之间的谷值就可以作为阈值来分割图像的目标和背景[1]。
这种方法在图像的目标和背景之间的灰度差异较为明显时,可以取得良好的分割效果,通常可以满足我们的分割要求。
虽然由于该方法对图像直方图的特殊要求和依赖,使其在图像分割中具有一定的局限性,但其操作简单运算量低,因此也被经常使用。
2.2基于灰度期望值的图像分割算法在对随机变量的统计过程中,期望值是一个十分重要的统计特征,它反映了随机变量的平均取值,类似于物体的质量中心,因此从灰度“中心”进行分割应当是最佳的分割平衡点。
灰度图像的数学期望值[3]可以按下式计算得到: 1()Nthreshold n n n L P L µ==∑ (1)其中为图像的灰度级,为灰度级出现的概率。
n L ()n P L n L上式是一种基于全局的阈值分割法,分割效果要优于灰度差直方图法、微分直方图法以及非等同熵法[3],并且该算法的复杂度较低且处理速度较快。
2.3最大类间方差法(OSTU)最大类间方差法[2]也称大律法,其基本原理是:对一幅图像,记T为目标与背景的分割阈值,T的取值范围是从最小灰度值到最大灰度值;目标点数占图像像素点数的比例为,平均灰度为A W A µ;背景点数占图像像素点数的比例为, 平均灰度为B W B µ。
图像的总平均灰度为µ。
则两类间方差的计算公式为: 2σ22()()()A A B B T W W 2σµµµµ=−+− (2)即阈值T将图像分成目标和背景两部分,使得两类总方差取最大值的T即为最佳分割阈值。
因为方差是图像灰度分布均匀性的一种度量,方差越大说明构成图像的两部分差别越大,而部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小,因此使类间方差最大的分割意味着错分概率最小)(T 2σ[ 6 ]。
大量实验结果表明OSTU算法对图像的分割质量通常都有一定的保障,对各种情况的表现都较为良好,可以说是比较好的一种分割算法。
3. 常用图像分割效果评价准则3.1 区域内部均匀性(Uniformity Measure)分割就是要把一个原始图像f(x,y)分成若干个内部具有相似特性的区域,所以可用分割图像中各区域内部均匀的程度来描述分割图像的质量。
如用Ri表示第i个区域,Ai表示其面积,则分割图像的均匀性测度[4]UM为: 2(,)(,)111{[(,)(,)i i n i x y R x y R iUM f x y f x y C A ∈∈=−−∑∑∑]} (3) C 为归一化系数,在二值图像中i 即为2,UM 的值越大,分割效果就越好,所用的算法性能也就越好。
3.2形状测度准则(Shape Measure)一个好的图像分割结果应该有一个好的目标轮廓,区域形状测度就是来衡量目标轮廓光滑程度的一个指标,其形状测度计算公式[4]为: (,)1()gn[(,)(,)](,)sgn[(,)]N x y SM t S f x y f x y x y f x y t C =−⋅∆⋅∑− (4) 其中,(,)N f x y 为邻域N(x,y)的灰度均值,t 为灰度阈值,∆(x,y)为广义梯度,C 为归一化因子,而。
{11()x x Sgn x ≥−<=003.3 区域对比度(Gray-Level Contrast)图像二值分割是按照目标和背景的灰度差异将图像分割成两个不同区域,如果这两部分区域的灰度分布特性差别比较大,也就是说灰度对比度较大,也可以推断出所用分割算法的性能优劣。
对于目标和背景这两个区域来说,如果它们各自的平均灰度分别为:fo和fb,则它们之间的灰度对比度计算公式[5]GC为:||()o b o bf f GC t f f −=+ (5) 由上述分析可知灰度对比GC 越大,则分割效果就越好。
4. 本文算法和实验结果讨论4.1 本文算法灰度直方图在图像分割技术中得到了广泛应用, 通常情况下, 当图像的目标和背景之间的灰度分布具有明显差别时,显示在直方图上大致就是两个峰值,通常选取较明显的波谷位置即可得到较佳的阈值。
但实际情况一般要比这复杂的多:首先由于图像的灰度分布往往不是很均匀,并且图像背景也很有可能受到噪声影响,从而使图像的直方图存在多个且不明显的谷值, 在这种情况下要得到合理的图像分割阈值是十分困难的;另外,常用的确定谷值的方法是先做直方图,然后人工找谷点,因为直方图往往参差不齐,很难找出理想的谷值。
众所周知,熵是图像统计特性的一种表现形式,反映了图像包含信息量的大小。
因为对于绝大多数图像来说,不管采用何种分割算法,一般分割后图像熵值越大,说明分割后从原图得到信息量越大,分割图像细节越丰富,因而总体分割效果也应越好[7]。
这一点进一步得到了我们实验的验证,如图1和图2所示:图1是lena 图像的灰度分布直方图,文中我们特意取了直方图中的七个明显的谷值作为分割阈值(见表1),图4是我们对lena 图像取上述阈值时所得到的对应的分割图像,图2是从不同阈值下的分割结果得到的“阈值—熵”关系曲线图,从图2和图4的对应关系中很容易得知,信息熵是一个上凸函数,并且当熵值较大时所对应的分割效果也较好,如:在T=110和134时熵值较大,曲线处于峰值附近,且他们所对应的分割效果如图4所示也优于其他几幅。
因此我们得出结论:熵值最大时所对应的阈值即可当作最佳阈值。
香农熵公式为:H S p p p p=−− (6)()1ln10ln0其中P1和P0分别表示分割图像二值输出为1和0的概率。
上式即为一幅图像分割后的二值序列中输出值为1和值为0的像素所含信息量的统计平均值。
T=54 T=105 T=110 T=134 T=149图4 lena图像在不同谷值处分割所得到的结果因此,我们对常用的直方图阈值选取算法进行了改进并提出了如下算法,算法流程图如图3所示:当图像的目标和背景对比并不是很强烈,并且存在多个不明显的波谷时,我们首先计算出图像的直方图,然后按照迭代算法(下文将讲到)求出其中所有的谷值,并取各个谷值作为阈值分别对图像进行分割,最后求出所有分割图像的信息熵,则所求熵值最大的一个谷值即可作为图像的最佳分割阈值。
本算法中谷值的迭代寻找过程为:在图1所示的直方图中每三个连续点为一组寻找一个最小值做为谷值,得到谷值序列P={p1,p2,p3……};在第二次迭代过程中,将P序列再按照第一次迭代过程所采用方法再求取谷值;继续迭代直到谷点个数较少为止,此时得到最终谷点序列PT,一般情况迭代三四次即可得到少数几个谷点。
4.2 实验结果我们将本文的改进算法与上文提到的几种典型图像分割算法进行了比较,图5是lena 图像在不同分割算法下的分割结果:(a)图是采用常用的直方图谷点阈值选取算法所得到的分割结果,选取的阈值是在直方图上人工寻找到的最佳谷值作为阈值,很明显由于lena图像的直方图(图1)是多峰的,很难人工找出最佳的分割阈值;而其他三幅分割结果从主观上看,分割效果都较好,差别不是很明显:(a)常用直方图谷点阈值分割 (b)最大熵阈值选取算法 (c)数学期望法 (c)OSTU图5 不同分割算法下得到的分割结果但为了从客观上对分割结果进行比较,我们采用了三种通用性较强的评价准则:区域内部均匀性准则(UM),形状测度准则(SM)和区域对比度准则(GC),对图5得到的四幅分割结果进行了客观和定量的评价,评价结果如表1所示:表1 不同算法下的分割结果比较区域均匀性形状参数区域对比度综合指标常用直方图谷点阈值分割0.9838 0.9149 0.3640 0.7542 最大熵直方图分割算法0.9862 0.8960 0.4267 0.7696 数学期望法0.9859 0.9014 0.4075 0.7649 OSTU 0.9862 0.8946 0.4338 0.7715由于一种图像分割评价准则是无法对分割结果做准确评价[8]的,因此我们综合三种评价准则得到了一个综合指标。
从上表实验中得到的综合指标数据可以看出,本文提出的最大熵阈值分割算法要优于常用的直方图阈值选取算法,并且分割结果要好于采用数学期望法得到的结果,这主要是由于数字图像处理是离散数值操作,在离散域里求取数学期望本质上就是求取了图像的灰度平均值,因此该方法本身具有自身的不足。
但与经典的OSTU分割算法相比,本文算法又有所不及,但本文所提的方法运算复杂度稍低,且运算时间较短。
5.结论本文通过对常用直方图分割算法的研究和改进,提出了一种基于最大熵的直方图阈值选取分割算法,该算法不仅能够自动获取最佳阈值,而且克服了因灰度分布复杂,灰度直方图呈现多峰以致难以获取最佳阈值的缺陷,实验取得了良好的分割效果。
