理论力学第八章题解
理论力学课后习题答案-第8章--动量定理及其应用

论力学课后习题答案-第8章--动量定理及其应用第8章 动量定理及其应用8-1 计算下列图示情况下系统的动量。
(1) 已知OA =AB =l ,θ=45°,ω为常量,均质连杆AB 的质量为m ,而曲柄OA 和滑块B 的质量不计(图a )。
(2) 质量均为m 的均质细杆AB 、BC 和均质圆盘CD 用铰链联结在一起并支承如图。
已知AB = BC = CD = 2R ,图示瞬时A 、B 、C 处于同一水平直线位置,而CD 铅直,AB 杆以角速度ω转动(图b )。
(3) 图示小球M 质量为m 1,固结在长为l 、质量为m 2的均质细杆OM 上,杆的一端O 铰接在不计质量且以速度v 运动的小车上,杆OM 以角速度ω绕O 轴转动(图c )。
解:(1)p = mv C =ωm l 25,方向同Cv (解图(a ));(2)p = mv C 1 + mv C 2 = mv B = 2Rm ω,方向同Bv ,垂直AC (解图(b )); (3)j i p )60sin 260sin ()]60cos 2()60cos ([2121︒+︒+︒-+︒-=ωωωωlm l m l v m l v m j i 423]42)[(212121m m l l m m v m m +++-+=ωω(解图(c ))。
习题8-1图ABOθω ABCDωOMvω 60˚(a)(b)(c)8-2 图示机构中,已知均质杆AB 质量为m ,长为l ;均质杆BC 质量为4m ,长为2l 。
图示瞬时AB 杆的角速度为ω,求此时系统的动量。
解:杆BC 瞬时平移,其速度为v Bωωωm l m l l m p p p BCAB 2942=+=+= 方向同v B 。
8-3 两均质杆AC 和BC 的质量分别为m 1和m 2,在C 点用铰链连接,两杆立于铅垂平面内,如图所示。
设地面光滑,两杆在图示位置无初速倒向地面。
问:当m 1= m 2和m 1= 2m 2时,点C 的运动轨迹是否相同。
理论力学 第八章

x o ' = x o ' (t ) 牵连运动方程 y o ' = y o ' ( t ) = ( t )
动系与定系之间的坐标变换关系
x = xO′ + x′ cos y′sin y = yO′ + x′ sin + y′ cos
沿半径为r的圆 例8-1 点M相对于动系 Ox′y′ 沿半径为 的圆 相对于动系 周以速度v作匀速圆周运动 圆心为O 作匀速圆周运动(圆心为 周以速度 作匀速圆周运动 圆心为 1 ) ,动系x′y′ O Oxy 以匀角速度ω绕点 作定轴转动, 相对于定系 以匀角速度 绕点O作定轴转动, 绕点 作定轴转动 如图所示。 重合, 重合。 如图所示。初始时x′y′ 与 与 重合 O Oxy 重合,点M与O重合。 的绝对运动方程。 求:点M的绝对运动方程。 的绝对运动方程
. 已知: 已知 ω, OA, = r, OO1 = l, OA水平 求: ω1 = ?
解:
1.动点:滑块A . 动系:摇杆AB 2. 运动分析 绝对运动:绕O点的圆周运动
相对运动:沿O1B的直线运动 牵连运动:绕O1轴定轴转动
√ √ √
3.
ve = va sin = ωr
r
2 2
l +r ve r2ω ∴ω1 = = 2 2 O A l +r 1
4. 绝对运动方程 vt vt x = x′ cos y′ sin = r1 cos r cosωt r sin r sin ωt y = x′ sin + y′ cos = r1 cos vt sin ωt + r sin vt co-3 用车刀切削工件的直径端面,车刀刀尖 M沿水平轴 作往复运动,如图所示。设oxy为定坐 沿水平轴x作往复运动 沿水平轴 作往复运动,如图所示。 为定坐 标系,刀尖的运动方程为 x = bsin (ωt ) 。工件以 标系, 逆时针转向转动。 等角速度 ω逆时针转向转动。 求:车刀在工件圆端面上切出的痕迹。 车刀在工件圆端面上切出的痕迹。
理论力学第8章习题解答

第八章 质点系动力学:矢量方法 习题解答8-1 一个质量为5 kg 弹头M 以水平速度v = 60 m/s 飞行,在D 处爆炸成位于同一水平面内如图示速度方向的两块碎片A 和B 。
已知碎片A 的速度大小v A = 90 m/s 。
试求:(1) 碎片A 的质量m A ;(2) 碎片B 的速度大小v B 。
解:取弹头M 为研究对象,弹头爆炸前后动量守恒 () 30cos B A v m M Mv -= () 30sin 0B A A A v m M v m --=解得M v vm A A 33=,AA B v v vv v 32--=, 代入数据得:kg 92.1=A m ,m/s 64.112=B v .8-2 一个质量为m 1的人手里拿着质量为m 2的物体,以仰角θ,速度v 0向前跳起。
当他到达最高点时将物体以相对速度u 水平地向后抛出。
如果不计空气阻力,问由于物体的抛出,跳远距离增加了多少?解:取m 1和m 2物体系统为研究对象,人跳至最高点时只有水平速度 ϑc o s 01v v =,所费时间 gv t ϑsin 0=。
抛物前后系统水平动量守恒,即 ()()u v m v m v m m -+=+1211021c o s ϑ,式中1v 为抛物后人的速度。
解得21201c o s m m um v v ++=ϑ,可见,人的速度增量为2121Δm m um v +=,从而跳远距离增加()gm m uv m v t s 21021sin ΔΔ+==ϑ.8-3质量为m 1的平台AB 放在水平面上,平台与水平面间的滑动摩擦因数为f 。
质量为m 2的小车D 由绞车拖动,相对平台的运动规律为221bt s =,其中b 为已知常数。
不计绞车质量,求平台的加速度。
解:1)设平台与水平面间的滑动摩擦因数比较小,当小车D 相对平台运动时,平台AB 的有速度1v (向左),小车D 的相对速度bt s v == r ,(向右),小车D 的绝对速度bt v v v v +-=+-=1r e a ,(向右), 滑动摩擦力为 N fF F =题8-3图题8-3受力图题8-1图由动量定理,()[]F v bt m v m t=-+-1211d d()021=++-N F g m m解得()212121m m g m m f b m a ++-=, ()g m m bm f 212+≤.当()gm m bm f 212+>时,01=a .8-4 质量为m 1的矩形板可在如图所示的光滑水平面上运动。
理论力学

两个坐标系
定坐标系(定系) 动坐标系(动系)
三种运动
绝对运动:动点相对于定系的运动。 相对运动:动点相对于动系的运动。 牵连运动:动系相对于定系的运动。
定参考系
牵连运动
动参考系
动点
一点、二系、三运动
相对轨迹
相对速度 v r
相对加速度 a r
绝对轨迹
绝对速度 绝对加速度
va
aa
牵连速度 v e 和牵连加速度 a e
在动参考系上与动点相重合的那一点(牵连点)的 速度和加速度称为动点的牵连速度和牵连加速度。
(1) 动点相对于定参考系的速度、加速度和轨迹, 称为动点的绝对速度va、绝对加速度aa和绝对轨迹。
(2) 动点相对于动参考系的速度、加速度和轨迹, 称为动点的相对速度vr、相对加速度ar和相对轨迹 。
由于动参考系的运动是刚体的运动而不是一个点 的运动,所以除非动参考系作平动,否则其上各点的 运动都不完全相同。因为动参考系与动点直接相关的 是动参考系上与动点相重合的那一点(牵连点),因此 定义:
rO xi ' yj 'zk '
v a d d r M t r O x i' y j ' z k ' x i' y j ' z k '
得
vavevr
点的速度合成定理:动点在某瞬时的绝对速度等于
它在该瞬时的牵连速度与相对速度的矢量和。
处理具体问题时应注意: (1) 选取动点、动参考系和定参考系。
练习:已知 ,,小球的相对速度u,OM=l。 求:牵连速度和牵连加速度
y x'
y'
M
O
φ
x
实例一:车刀的运动分析
08-理论力学-第二部分运动学第八章刚体的平面运动

形S在该瞬时的位置也就确定了。
88
运动学/刚体的平面运动
四、平面运动的分解 ——平移和转动
当图形S上A点不动时,则
刚体作定轴转动 。
当图形S上 角不变时,
则刚体作平移。
故刚体平面运动可以看成是 平移和转动的合成运动。
例如:车轮的平面运动可以看成: 车轮随同车厢的平移 和相对车厢的转动的合成。
99
2121
如图示平面图形,某瞬时速度瞬心为P点, 该瞬时平面图形内任一点B速度大小
vB vP vBP vBP
B
大小:vB BP
方向:BP,指向与 转向相一致。
vB
S
vA
C
vC
同理:vA=ω·AP, vC=ω·CP
由此可见,只要已知图形在某一瞬时的速度瞬心 位置和角速度 ,就可求出该瞬时图形上各点的速度。
的平面Ⅱ内的运动。
66
运动学/刚体的平面运动
二、平面运动的简化 刚体的平面运动可以简化为
平面图形S在其自身平面内的运动。 即在研究平面运动时,不需考虑 刚体的形状和尺寸,只需研究平 面图形的运动,确定平面图形上 各点的速度和加速度。
三、平面运动方程 为了确定代表平面运动刚体的
平面图形的位置,我们只需确定平 面图形内任意一条线段的位置。
vBA
s
B
vB vA
A
vA
方向: AB, 指向与 转向一致。
即:平面图形上任一点的速度等于基点的速度与该点随
平面图形绕基点转动的速度的矢量和。 ——基点法
基点法是求解平面图形内一点速度的基本方法。 1414
运动学/刚体的平面运动
二、速度投影法
由于A, B点是任意的,因此
理论力学习题解答第八章
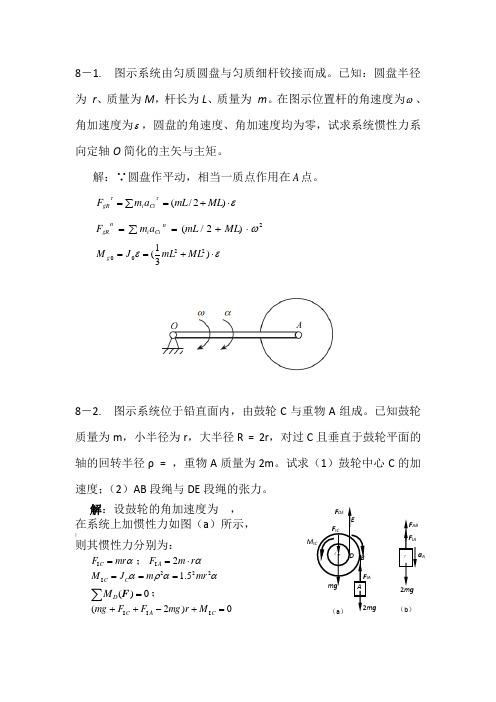
8-1. 图示系统由匀质圆盘与匀质细杆铰接而成。
已知:圆盘半径为 r 、质量为M ,杆长为L 、质量为 m 。
在图示位置杆的角速度为ω、角加速度为ε,圆盘的角速度、角加速度均为零,试求系统惯性力系向定轴O 简化的主矢与主矩。
解:∵圆盘作平动,相当一质点作用在A 点。
εττ⋅+==∑)2/(ML mL a m F Ci i gR 2)2/(ω⋅+==∑ML mL a m F n Ci i ngR εε⋅+==)31(2200ML mL J M g8-2. 图示系统位于铅直面内,由鼓轮C 与重物A 组成。
已知鼓轮质量为m ,小半径为r ,大半径R = 2r ,对过C 且垂直于鼓轮平面的轴的回转半径ρ = ,重物A 质量为2m 。
试求(1)鼓轮中心C 的加速度;(2)AB 段绳与DE 段绳的张力。
解:设鼓轮的角加速度为, 在系统上加惯性力如图(a )所示, |则其惯性力分别为:αmr F C =I ;αr m F A ⋅=2I ααρα222I 5.1mr m J M C C === ∑=0)(F D M ;0)2(I I I =+-++C A C M r mg F F mg?AM I CF I Cm g F DE (a )A B 《D E2gF A F I A F AB (b )g g r a C 2145.132=+==α ∑=0y F ;02I I =--+-mg mg F F F A C DE ;mg mr mg F DE 21593=-=α 取重物A 为研究对象,受力如图(b )所示,∑=0y F ;02I =-+mg F F A AB ;mg mg mr mg F AB 2134)2141(222=-=-=α:8-3. 11-15重力的大小为100N 的平板置于水平面上,其间的摩擦因数f = ,板上有一重力的大小为300N ,半径为20cm 的均质圆柱。
圆柱与板之间无相对滑动,滚动摩阻可略去不计。
理论力学第三版课后答案第8章
(9)
代入式(3)得 aCx = 1.03m/s 2 ,将其与式(9)第 1 式代入式(7)可解出端 B 加速度
aB = 2.65m/s 2
aB 为正,表明原假定正确,端 B 的确向左滑动。
课
后 答
案
网
ww w
.k hd
aw .
8-5C 质量为 m 半径为 R 的半圆柱体在图示位置静止释放。 图中,点 C 为质心, OC =
洪嘉振等《理论力学》第 3 版习题详解
2
1 R 5 R R J C = mR 2 + m( ) 2 + m( ) 2 + m( ) 2 = mR 2 4 2 2 4 4
系统惯性力系的主矩方向如图 8-1Cb 所示,其大小为为
M * = J Cα =
5 mR 2α 4
课
后 答
案
网
ww w
.k hd
aw .
可解得此瞬时质心速度为
vC = gl
由于杆作瞬时平移,故有点 B 的速度
vB = v A = vC = gl
r (2)对于连体基 A − e 1 ,定义该基的角加速度的正向如图 8-4Cb 不所示。基点 A 作圆 周运动,令其加速度为
课
T − T0 = mg xC0 − xC
后 答
(
1 2 mvC 。由动能定理 2
r r r r r r 其中 a1C = aC = aCx + aCy , a1etC = a A , a1eωC = lω12 = 0 , a1eαC = lα1 。上式变为
即
后 答
r x : aCx = − aωA + a1eαC cos θ
理论力学8
求曲柄在水平位置瞬时,摇杆O1B绕O1轴的角速度1及滑块A相
对摇杆O1B的相对速度。
运动学/点的合成运动
解:
选取动点: OA 上的A点 动系: O1B 定系: 基座
运 绝对运动:圆周运动 动 分 相对运动:直线运动 析 牵连运动:定轴转动 :
运动学/点的合成运动
另一方面,在实际问题中,不仅要在固联在地面上
的参考系上还要在相对于地面运动着的参考系上观察和
研究物体的运动。下面先看几个例子。
沿直线轨道纯滚动 的圆轮,研究轮缘上A 点的运动,对于地面上 的观察者,是旋轮线轨 迹,对站在轮心上的观 察者是圆。
A点的运动可看成随轮心的平移与绕轮心转动的合成。
运动学/点的合成运动
MM MM1 M1M 将上式两边同时除以t并取 t0得
lim MM lim MM1 t 0 t t 0 t
lim
M1M
t 0 t
va ve vr
即:在任一瞬时动点的绝对速度等于牵连速度与相对速
度的矢量和,这就是点的速度合成定理。
点的速度合成定理是瞬时矢量式,共包括大小‚方向 六个元素,已知任意四个元素,就能求出其它两个。
运动学/点的合成运动
例如,直管OB以匀角速度绕定轴O转动,小球M
以速度u在直管OB中作相对的匀速直线运动,如图示。 将动坐标系固结在OB管上,以小球M为动点。随着动 点M的运动,牵连点在动坐标系中的位置在相应改变。 设小球在t1、t2瞬时分别到达M1、M2位置,则动点的 牵连速度分别为
ve1 OM1
运动学/点的合成运动
第八章
点的合成运动
在前两章中研究点和刚体的运动时,认为地球( 参考体)固定不动,将坐标系(参考系)固连于地面。 因此,点和刚体的运动是相对固定参考系而言的。
08第八章习题解答
第八章习题解答8-1匀质杆AB 长l ,重G ,沿光滑的圆弧轨道运动如图示。
设当OA 在水平位置时,3arcisn =θ,125gl v A =,求此时轨道对于杆AB 的约束力。
题8-1图解:以杆AB 为研究对象,受力分析A F N 、B F N、G 如图示,杆AB 作定轴转动。
∵53arcsin =θ 53sin =∴θ 54cos =θ 25242sin =θ 2572cos =θ ∵ l R 85=、125gl v A = l g R v A 1516==∴ω l OC 83=AB 杆的质心加速度为OC a ⋅=21ω,OC a ⋅=α2 惯性力主矢*F和主矩*M 方向如图所示,大小为mg l l g m a m F 528315161*1=⋅⋅=⋅=l m a m F 832*2⋅⋅=⋅=ααα222*19243])83(121[ml l m ml M =+=题8-1答案图列平衡方程式∑=0)(F m zO 01924353832=−⋅⋅αml l mg l g 215216=α 0=∑ixF 0sin cos 2cos N *1*2N =−++⋅A B F F F F θθθ 0=∑iyF0cos sin 2sin *1*2N =−−+⋅mg F F F B θθθ mg l g ml F 2158121521683*2=⋅=代入上式得:mg F B4349N =,mg F A 4337N =8-2 匀质杆AB 长l ,重G ,用两根软绳悬挂如图示。
求当其中一根软绳切断,杆AB 开始运动时,另一根软绳中的拉力。
题8-2图解:建立参考基e C−,连体基1e O −和2e B −设当AO 被切断时,BO 的角加速度为1α,AB 杆的角加速度为2α题8-2答案图以杆AB 为研究对象,受力分析如图示重力G ,绳中张力T F 。
杆AB 作平面运动,惯性力主矢*F 和主矩*M 方向如图所示,大小为:C ma F =*,2*αC J M =e C e C e tC C a a a a αω222 ++= , 02=eC a ω e B e B e tC a a a αω112 +=, 01=e B a ω , B e B a a=α1 e C e B C a a a αα21 +=, eC e B C a m a m a m αα21 += 11*122ααl m ma F e B ==∴ 22*22ααl m ma F e C == 22*121αml M =0)(=∑F m Dz0121442222=+⋅−⋅ααml lmg l ml lg 562=α0)(=∑F m Cz012122222T =−⋅⋅αml l Fmg F 52T =8-3 匀质杆AB 长2l ,重G ,一端A 用长l 的软绳OA 拉住,一端B 放在光滑地面上如图示。
理论力学第八章
?
几个有意义的实际问题
偏心转子 为什么要 固定,如 果不固定 会怎样
几个有意义的实际问题
偏心转子 电动机工作 时为什么会 左右运动;
这种运动有 什么规律; 会不会上 下跳动; 利弊得失。
?
几个有意义的实际问题
偏心转子 没有跳起 时,质心 运动情况
几个有意义的实际问题
偏心转子 有跳起时, 质心运动 情况
工程实际中的动力学问题
v1
F
v2
棒球在被球棒 击打后,其速度 的大小和方向发 生了变化。如果 已知这种变化即 可确定球与棒的 相互作用力。
工程实际中的动力学问题
载人飞船的交会与对接
v2 v1
B A
工程实际中的动力学问题
航空航天器 的姿态控制
工程实际中的动力学问题
高速列车的振动问题
ቤተ መጻሕፍቲ ባይዱ
工程实际中的动力学问题
1. 直角坐标系投影式
z
ma F
O x
M
r z y
a
y
x
v
F
d r m 2 dt
2
F
直角坐标形式
d2x m 2 Fx ma x m x dt d2y m 2 Fy ma y m y dt d 2z m 2 Fz ma z m z dt
牛顿及其在力学发展中的贡献
牛顿出生于林肯郡伍尔索朴城的一个中等农户家中。 在他出生之前父亲即去世,他不到三岁时母亲改嫁了, 他不得不靠他的外祖母养大。
1661年牛顿进入了剑桥大学的三一学院,1665年获文 学学士学位。在大学期间他全面掌握了当时的数学和光 学。1665-1666的两年期间,剑桥流行黑热病,学校暂 时停办,他回到老家。这段时间中他发现了二项式定律, 开始了光学中的颜色实验,即白光由7种色光构成的实 验,而且由于一次躺在树下看到苹果落地开始思索地心 引力问题。在30岁时,牛顿被选为皇家学会的会员,这 是当时英国最高科学荣誉。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学题解第八章 思考题8.1. 8.2.8.3. 拉格朗日函数是系统的特征函数,与系统的运动状态有关,而运动状态由αq 、αq 描述,与αq 、αq 无关,所以拉格朗日函数不含αq 、αq 。
8.4.8.5.第八章 习题8.1. 以滑轮、绳子和重物作为系统,滑轮角坐标ϕ为广义坐标,mg R h R m m L )()21(210221ϕϕ+++=(0h 为重物的初始位置坐标),将L 代入拉氏方程,得0)21(21=-+mgR R m m ϕ,R m m mg )2(21+=ϕ 。
重物加速度为mm mgR a 221+==ϕ8.2. 将小圆柱质心和所在的大圆柱截面中心的连线与竖直直线的夹角θ作为广义坐标,逆时针方向为θ正方向。
设小圆柱角坐标正方向为顺时针方向,坐标变换方程为ϕθr r R =-)(,系统拉氏函数为)cos 1)(()(4322θθ----=r R mg r R m L ,将L 代入拉氏方程后得θθsin )(32r R g --= ,当θ很小时θθ)(32r R g --= 。
小圆柱质心的运动周期为gr R T 2)(32-=π。
8.3. 以小球的r 为广义坐标,20222)(21)(21l r k r r m L --+=ϖ ,代入拉氏方程得)()(02l r k r rm --=-ϖ 。
8.4. 选择题8.4图中θ角为广义坐标,拉氏函数为]cos )()sin [(])[(2122θθθθθr l r l mg l r m L +-+-+=,代入拉氏方程后得到质点的运动微分方程0sin )(2=+++θθθθg r l r 。
8.5. 以定滑轮中心作为坐标原点,建立Oxy 直角坐标系,Ox 轴竖直向下,以重物A 和B 的坐标A x 、B x 为系统(定滑轮和物体A 、B 、C ,以及连接重物的绳)的广义坐标,经过坐标变换,拉格朗日函数为)2(2)(21)4(213213232231B A B A B A B A x x C g m gx m gx m x x m x m m xm m L --+++++++=,C 是在坐标变换中出现的常量的总和,将L 代入拉氏方程,且将32135.1m m m ==代入,得027=-+g x x B A ,032=-+g xx B A ,A 、B 两物体的加速度分别为:g x A 171= ,g x B 175= 。
故 g xx x B A C 1772-=--= 。
8.6. 选择弧坐标s 为广义坐标,221s m T =,28s a mg V =,V T L -=,代入拉氏方程得04=+s a g s ,质点的振动周期gaT π4=。
(旋轮线方程见教材65页3.5题) 8.7. 建立原点O 在定滑轮中心的正下方地面上一点,Ox 轴通过滑轮中心向上,以重物1m 的坐标x 为广义坐标。
系统(由滑轮、重物、绳、弹簧组成)的221)(21xm m T +=,201)(21l x k gx m V A -+=,A 点为弹簧上端点,通过约束条件,知x C x A -=(C 是常量),则221)(21xm m L +=201)(21l x C k gx m ----,代入拉氏方程得,0)(21='+++C kx xm m (C '是常量),可知重物作简谐振动,周期为km m T 212+=π。
8.8. 以滑块到斜面底端的坐标x 和摆的摆角ϕ作为广义坐标,)cos(21)(212222221ϕαϕϕ-+++=x l m l m xm m T ,)cos sin (sin 21ϕααl x g m gx m V -+=,V T L -=,将L 代入拉氏方程得系统的运动微分方程:⎩⎨⎧=--+-+=++-+-++0sin )sin()cos(0sin )()sin()cos()(2122221ϕϕαϕϕαϕαϕαϕϕαϕg x x l g m m l m l m xm m 8.9. 以滑块的坐标x 和轻杆摆角ϕ为广义坐标,(1)ϕϕϕϕcos cos 21)(2122222221gl m x l m l m x m m L ++++= ,因0=∂∂tL,且2T T =所以ϕϕϕϕcos cos 21)(2122222221gl m x l m l m x m m E H -+++== =常量。
又因0=∂∂xL,所以ϕϕcos )(221 l m x m m x Lp x ++=∂∂==常数。
(2)选择ϕ为广义坐标,ϕϕϖϕϖϕϖϖcos cos cos 21cos )(212222222221gl m t lA m l m t A m m L ++++= 。
系统不存在初积分。
8.10. 以OA 杆和转轴的夹角θ和绕转轴转动的转角ϕ为广义坐标,θϕθθθcos )(2sin )sin 2(21222122122gl m m l m l m m L ++++= ,因0=∂∂ϕL,故 ==ϕθϕ 221sin 2l m p 常量;又因0=∂∂tL,且2T T =,故=+==V T E H =+-++θϕθθθcos )(2sin )sin 2(21222122122gl m m l m l m m 常量。
8.11. 以小环为研究对象,选择题8.11图中的角ϕ为广义坐标,)2cos 42cos 4(21)(212222222222ϕϕϖϕϖϕθ a a a m r rm T ++=+=,0=V ,将L 代入拉氏方程0sin 2=+ϕϖϕ。
由于0=∂∂tL,所以V T T H +-=02=)2cos 4(2122222ϕϖϕa a m - 。
8.12. 选择ϕ和θ为两圆柱组成的系统的广义坐标,ϕ 为圆柱体P 的转角,θ是两圆柱体连心线与竖直方向的夹角,相对直角坐标系Oxy ,系统的动能为ψϕ S scsc P pc I y x m I x m T 21)(212121221222++++=,S I 、P I 分别是S 、P 相对自身对称轴的转动惯量,ψ 是圆柱体S 的角速度。
坐标变换方程为pc x ϕR =,)(θψ-r )(ϕθ-=R ,θθϕθθϕϕcos )()1cos 2()(21)(43434311221221222r R g m r R R m r R m R m R m L +--+++++=,因0=∂∂ϕL ,所以存在)1cos 2()(21)(231221-+++=θθϕϕ r R R m R m m p =常量。
根据初始条件:0=t 时,0=ϕ ,0=θ ,得0)1cos 2()()(31221=-+++θθϕ r R R m R m m ,经积分,得ϕR )(3)sin 2)((211m m r R m +-+=θθ(注意此方程是通过求解运动微分方程得出的ϕ与θ的关系,不是约束方程)。
将此式代入几何关系式:θϕsin )(r R R x sc ++=,θcos )(r R y sc +=8.13. 以杆和甲虫为系统,以θ为广义坐标。
T杆22222)](31[2121θθ l R m ml I -+==,22222222])[(2121l R mu t u l R m mu T -++-+=θθ 虫,=L =T T 杆+T 虫22222222)352(2121l R mu t u l R m mu -++-+=θθ 。
因0=∂∂θT ,所以=∂∂=θθ T p 常量,又根据初始条件,0θθ =,得022222235656θθ tu l R l R +--=。
8.14. 选择滑块A 的水平轴坐标x 和杆的摆角θ为广义坐标,,61)cos 2(2122222θθθθ ma x a a x m T +++=广义力为θθθcos 2sin aF mga Q +-=,F Q x =。
将T 、θQ 、x Q 代入拉氏方程,得θθθθθθcos 2sin sin 34cos F mg x m ma xm +-=-+ ,F ma ma x m =-+2sin cos θθθθ ,当摆角很小时,1cos ,sin ≈≈θθ,结果为:m F x g a x234=-++θθθθ ,2θθθ a a x-+mF =。
8.15. 以曲柄和齿轮2S 为系统,选择曲柄对称轴与过齿轮1S 中心的固定直线的夹角ϕ(固定直线与两齿轮中心在同一平面上)为广义坐标。
根据对系统动能的计算与坐标变换方程ϕθ)(R r r +=(θ是齿轮2S 的角坐标),T 222221)(43)(61ϕϕr R m r R m +++=,广义力M Q =ϕ,代入拉氏方程,结果是221))(92(6r R m m M++=ϕ。
8.16. 系统的动能)sin sin 2cos cos 2(2121212122121222212212θθθθθθθθθθθ l l l l m ml T ++++=,势能为1cos θmgl V -=)cos (cos 21θθ+-mgl 作近似计算,使212221221θθθθ ml ml ml T ++=,其中忽略了二阶以上小量;2221213θθmgl mgl mgl V ++-=,其中只保留1cos θ、2cos θ作级数展开的二阶小量。
V T L -=,代入拉氏方程得 ⎪⎩⎪⎨⎧=++=++0022221121θθθθθθg l l g l l 设方程的解的形式为:⎩⎨⎧+=+=)cos()cos(2211ϕϖθϕϖθt A t A 代入方程后得⎪⎩⎪⎨⎧=+-+-=-+-0)(0)22(22122212A g l A l A l A g l ϖϖϖϖ 得简正频率 l g )22(1+=ϖ lg )22(2-=ϖ 进而得到分别与1ϖ、2ϖ对应得的两式:11212A A -=,12222A A =,前者两摆振动反相,后者同相,其运动方程分别为:⎩⎨⎧+-=+=)cos(2)cos(111121111111ϕϖθϕϖθt A t A ⎩⎨⎧+=+=)cos(2)cos(221222221212ϕϖθϕϖθt A t A ),(2111A A 、(2212,A A )组成两个二维矢量本征矢量1A 、2A,它确定了系统简正模式--反对称模式和对称模式。
8.17. 以1ϕ、2ϕ为广义坐标,考虑到系统做小振动并用近似计算,可得动能)(2122212ϕϕ +=ml T ,势能)(21)(2121222122ϕϕϕϕ++-=mgl kl V ,V T L -=,代入拉氏方程得⎩⎨⎧=+++-=-++0022212111ϕϕϕϕϕϕϕϕkl mg ml kl kl mg kl ml 设解的形式为⎩⎨⎧+=+=)cos()cos(2211θϖϕθϖϕt A t A 代入方程中求出简正频率l g =1ϖ,lgm k +=22ϖ,进一步求出1121A A =,1222A A -=,由分别与21,ωϖ对应的两本征矢量),(2111A A 、(2212,A A )确定该系统的本征模式。
