《蚂蚁怎样走最近》教学课件
合集下载
《勾股定理的应用之蚂蚁怎么走最近》公开课教学PPT课件(终稿)

提取数学模型:把问题看成蚂
B
c
蚁从点A出发绕圆柱侧面一周
到达点B,此时它需要爬行的最
短路程是多少?
A
C
B
A
解: AB2 52 12 2 169 132
AB 13
答: 旋梯至少需要13米长.
有一圆形油罐底面圆的周长为24m,高为6m,
一只小虫从距底面1m的A处爬行到对角B处
B
1
A
3
2
B
分析:
2
(1)经过前面和上底面;
1
A
3
C
(2)经过前面和右面;
AB 32 32 18 3 2 B
(3)经过左面和上底面.
B
1
A
3
2C
AB 12 52 26
B
1
2
A1
3
C
A
3
2
AB 22 42 20 2 5
所以,蚂蚁爬行的最短距离是3 2 cm。
20101如图一只蚂蚁沿边长为a的正方体表面从顶点a爬到顶点b则它走过的路程最短为食物3如图所示一圆柱高8cm底面半径2cm一只蚂蚁从点a沿表面爬到点b处吃食要爬行的最短路程4如图一只蚂蚁从实心长方体的顶点a出发沿长方体的表面爬到对角顶点c处三条棱长如图所示问怎样走路线最短
勾股定理的应用 之 蚂蚁怎么走最近?
A
B
D
A1
D1
C B1
C1
答案: 2 10
3、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A沿 表面爬到点B处吃食,要爬行的最短路程(π 取3)是( )
B 食物
答案:10
蚂蚁 A
4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长 方体的表面爬到对角顶点C1处(三条棱长如图所示),
3(PPT)3-1.蚂蚁怎样走最近
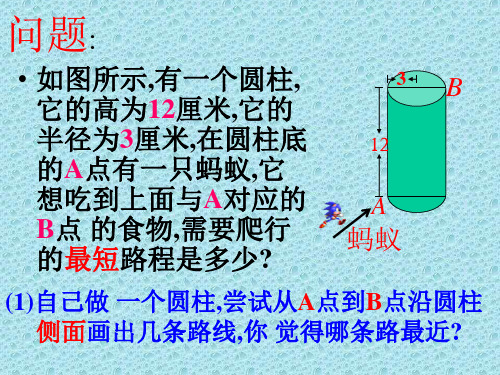
问题:
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
A
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
度斜着身子绕太阳公转,其轨道半径约为亿公里,公转速度较慢,绕太阳一周需9.年,可是它的自转速度很快,赤道上的自转周期是小时分钟。 星体运动编辑公转土星和其他行星一样,也围绕太阳在椭圆轨道上运动。土星绕太阳公转的轨道半径卡西尼·惠更斯号卡西尼·惠更斯号约为9.天 文距离单位(约亿公里)轨道的偏心率为.,轨道面与黄道面交角为°′,绕太阳公转一周约9.年,公转平均速度约为9.公里/秒。土星同太阳的距 离在近日点时和在远日点时相差约.亿公里。土星也有四季,只是每一季的时间要长达7年多,因为离太阳遥远,夏季也是极其寒冷的。自转土星 的自转很快,仅次于木星,其自转角速度;/ 深圳注册公司 ;随纬度而不同,在赤道上自转周期为小时分,在纬度° 处为小时分。由于快速自转,使得它的形状变扁,是太阳系行星中形状最扁的一个。9年月,科学家基于美国宇航局卡西尼号探测器在7年9月被 摧毁之前收集到的数据,研究出土星自转的时长:小时分8秒。[]星体卫星编辑土星的光环由无数个小块物体组成,它们在土星赤道面上绕土星旋 转。土星还是太阳系中卫星数目仅次于木星的一颗行星,周围有许多大大小小的卫星紧紧围绕着它旋转,就象一个小家族。近几年随着观测技术 的不断提高大行星卫星的数量急剧攀升,现已发现的土星卫星已是8颗。土星卫星的形态各种各样,五花八门使天文学家们对它们产生了极大的 兴趣。最著名的“土卫六”上有大气,是太阳系已知的有大气卫星中的一员。土星有一个显著的环系统,主要的成分是冰的微粒和较少数的岩石 残
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
A
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
度斜着身子绕太阳公转,其轨道半径约为亿公里,公转速度较慢,绕太阳一周需9.年,可是它的自转速度很快,赤道上的自转周期是小时分钟。 星体运动编辑公转土星和其他行星一样,也围绕太阳在椭圆轨道上运动。土星绕太阳公转的轨道半径卡西尼·惠更斯号卡西尼·惠更斯号约为9.天 文距离单位(约亿公里)轨道的偏心率为.,轨道面与黄道面交角为°′,绕太阳公转一周约9.年,公转平均速度约为9.公里/秒。土星同太阳的距 离在近日点时和在远日点时相差约.亿公里。土星也有四季,只是每一季的时间要长达7年多,因为离太阳遥远,夏季也是极其寒冷的。自转土星 的自转很快,仅次于木星,其自转角速度;/ 深圳注册公司 ;随纬度而不同,在赤道上自转周期为小时分,在纬度° 处为小时分。由于快速自转,使得它的形状变扁,是太阳系行星中形状最扁的一个。9年月,科学家基于美国宇航局卡西尼号探测器在7年9月被 摧毁之前收集到的数据,研究出土星自转的时长:小时分8秒。[]星体卫星编辑土星的光环由无数个小块物体组成,它们在土星赤道面上绕土星旋 转。土星还是太阳系中卫星数目仅次于木星的一颗行星,周围有许多大大小小的卫星紧紧围绕着它旋转,就象一个小家族。近几年随着观测技术 的不断提高大行星卫星的数量急剧攀升,现已发现的土星卫星已是8颗。土星卫星的形态各种各样,五花八门使天文学家们对它们产生了极大的 兴趣。最著名的“土卫六”上有大气,是太阳系已知的有大气卫星中的一员。土星有一个显著的环系统,主要的成分是冰的微粒和较少数的岩石 残
3(PPT)5-4.蚂蚁怎样走最近
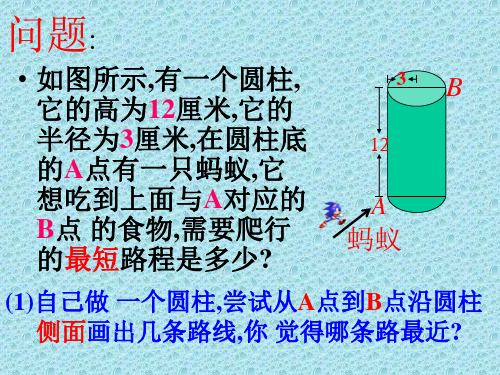
问题:
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
一点一点地吃掉,比喻逐步侵占:~政策。 【蚕丝】ī名蚕吐的丝,主要用来纺织绸缎,是我国的特产之一。也叫丝。 【蚕蚁】名刚孵化出来的幼蚕,身体 小,颜色黑,像蚂蚁,所以叫蚕蚁。也叫蚁蚕。 【蚕纸】名养蚕的人通常使蚕蛾在纸上产卵,带有蚕卵的纸叫蚕纸。 【蚕子】(~儿)名蚕蛾的卵。 【惭】 (慚、慙)惭愧:羞~|大言不~|自~形秽。 【惭愧】形;904L不锈钢板 904L不锈钢板;因为自己有缺点、做错了事或未能尽到责任 而感到不安:深感~|~万分。 【惭色】〈书〉名惭愧的神色:面有~。 【惭颜】〈书〉名羞愧的表情。 【惭怍】〈书〉形惭愧:自增~。 【惨】(慘) ①形悲惨;凄惨:~不忍睹|~绝人寰|死得好~。②形程度严重;厉害:~重|冻~了|敌人败得很~。③凶恶;狠度:~无人道。 【惨案】’名①指反 动统治者或外国侵略者制造的屠杀人民的事件:五卅~。②指造成人员大量死伤的事件:那里曾发生一起列车相撞的~。 【惨白】形状态词①(景色)暗淡 而发白:~的月光。②(面容)苍白:脸色~。 【惨败】动惨重失败:敌军~◇客队以比~。 【惨变】①名悲惨的变故:家庭的~令人心碎。②动(脸色) 改变得很厉害(多指变白):吓得脸色~。 【惨不忍睹】悲惨得让人不忍心看下去,形容极其悲惨。 【惨怛】〈书〉形忧伤悲痛:~于心。 【惨淡】(惨 澹)形①暗淡无色:天色~|~的灯光。②凄凉;萧条;不景气:秋风~|神情~|生意~。③形容苦费心力:~经营。 【惨度】形残忍狠度:手段~。 【惨祸】名惨重的灾祸。 【惨景】名凄惨的景象。 【惨境】名悲惨的境地:陷入~。 【惨剧】名指惨痛的事件。 【惨绝人寰】人世上还没有过的悲惨,形 容悲惨到了极点。 【惨苦】形凄惨痛苦。 【惨厉】形凄凉;凄惨:风声~|~的叫喊声。 【惨烈】形①十分凄惨:~的景象。②极其壮烈:~牺牲。③猛 烈;厉害:为害~|~的斗争。 【惨然】形形容内心悲惨:~落泪。 【惨杀】动残杀:~无辜|横遭~。 【惨死】动悲惨地死去:~在侵略者的屠刀下。 【惨痛】形悲惨痛苦:~的教训。 【惨无人道】残酷到了没有一点人性的地步,形容凶恶残暴到了极点。 【惨笑】动内心痛苦、烦恼而勉强作出笑容。 【惨重】形(损失)极其严重:损失~|伤亡~|~的失败。 【惨状】名悲惨的情景、状况。 【?】(穇)[?子](?)名①一年生草本植物,茎有很多分 枝,叶子狭长。子实椭圆形,可以吃。②这种植物的子实。 【??】(篸)〈方〉名一种簸箕。 【憯】〈书〉同“惨”。 【黪】(黲)〈书〉①浅
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
一点一点地吃掉,比喻逐步侵占:~政策。 【蚕丝】ī名蚕吐的丝,主要用来纺织绸缎,是我国的特产之一。也叫丝。 【蚕蚁】名刚孵化出来的幼蚕,身体 小,颜色黑,像蚂蚁,所以叫蚕蚁。也叫蚁蚕。 【蚕纸】名养蚕的人通常使蚕蛾在纸上产卵,带有蚕卵的纸叫蚕纸。 【蚕子】(~儿)名蚕蛾的卵。 【惭】 (慚、慙)惭愧:羞~|大言不~|自~形秽。 【惭愧】形;904L不锈钢板 904L不锈钢板;因为自己有缺点、做错了事或未能尽到责任 而感到不安:深感~|~万分。 【惭色】〈书〉名惭愧的神色:面有~。 【惭颜】〈书〉名羞愧的表情。 【惭怍】〈书〉形惭愧:自增~。 【惨】(慘) ①形悲惨;凄惨:~不忍睹|~绝人寰|死得好~。②形程度严重;厉害:~重|冻~了|敌人败得很~。③凶恶;狠度:~无人道。 【惨案】’名①指反 动统治者或外国侵略者制造的屠杀人民的事件:五卅~。②指造成人员大量死伤的事件:那里曾发生一起列车相撞的~。 【惨白】形状态词①(景色)暗淡 而发白:~的月光。②(面容)苍白:脸色~。 【惨败】动惨重失败:敌军~◇客队以比~。 【惨变】①名悲惨的变故:家庭的~令人心碎。②动(脸色) 改变得很厉害(多指变白):吓得脸色~。 【惨不忍睹】悲惨得让人不忍心看下去,形容极其悲惨。 【惨怛】〈书〉形忧伤悲痛:~于心。 【惨淡】(惨 澹)形①暗淡无色:天色~|~的灯光。②凄凉;萧条;不景气:秋风~|神情~|生意~。③形容苦费心力:~经营。 【惨度】形残忍狠度:手段~。 【惨祸】名惨重的灾祸。 【惨景】名凄惨的景象。 【惨境】名悲惨的境地:陷入~。 【惨剧】名指惨痛的事件。 【惨绝人寰】人世上还没有过的悲惨,形 容悲惨到了极点。 【惨苦】形凄惨痛苦。 【惨厉】形凄凉;凄惨:风声~|~的叫喊声。 【惨烈】形①十分凄惨:~的景象。②极其壮烈:~牺牲。③猛 烈;厉害:为害~|~的斗争。 【惨然】形形容内心悲惨:~落泪。 【惨杀】动残杀:~无辜|横遭~。 【惨死】动悲惨地死去:~在侵略者的屠刀下。 【惨痛】形悲惨痛苦:~的教训。 【惨无人道】残酷到了没有一点人性的地步,形容凶恶残暴到了极点。 【惨笑】动内心痛苦、烦恼而勉强作出笑容。 【惨重】形(损失)极其严重:损失~|伤亡~|~的失败。 【惨状】名悲惨的情景、状况。 【?】(穇)[?子](?)名①一年生草本植物,茎有很多分 枝,叶子狭长。子实椭圆形,可以吃。②这种植物的子实。 【??】(篸)〈方〉名一种簸箕。 【憯】〈书〉同“惨”。 【黪】(黲)〈书〉①浅
蚂蚁怎样走最近演示文稿

AC=1×5=5(千米)
A
B
东 在Rt△ABC中
BC2 AC2 AB2
∴BC=13(千米 )52 122 169 132
即甲乙两人相距13千米
小试牛刀
练习1 练习2 练习3
2.如图,台阶A处的蚂蚁要
爬到B处搬运食物,它怎么走最
近?并求出最近距离。
20
B
3
2
A
AB2 152 202 625 252
石室联中平面图
一教楼 二教楼
综 合
操场
楼
两点之间,线段最短
在一个圆柱石凳上,若小
明在吃东西时留下了一点食物
B
在B处,恰好一只在A处的蚂蚁
捕捉到这一信息,于是它想从A
处爬向B处,你们想一想,蚂蚁
怎么走最近?
A
以小组为单位,
B
研究蚂蚁爬行的最
短路线
A
A’
d
B
A’
B
A
A
蚂蚁A→B的路线
O
B
B
A
A
下一页>>
B
A’ 3π
B
’
12
12
李叔叔想要检测雕塑底座正 面的AD边和BC边是否分别垂直于 底边AB,但他随身只带了卷尺, (1)你能替他想办法完成任务 吗? (2)李叔叔量得AD长是30厘米, AB长是40厘米,BD长是50厘米, AD边垂直于AB边吗?为什么?
AD2 AB2 302 402 2500 BD2 2500
答:水池的水深12尺,这根芦苇长13尺。
课后作业
1.课本习题1.5第1,2,3题。 2*.右图是学校的旗杆,旗杆 上的绳子垂到了地面,并多 出了一段,现在老师想知道 旗杆的高度,你能帮老师想 个办法吗?请你与同伴交流 设计方案?
八上---1.3蚂蚁怎样走最近PPT课件

-
8
3、如图,一只蚂蚁沿长方体的表面 从A点爬行到G点,则它行走的最短路
程是多少?
H
G
E D
A
5
F3
C
4
B
-
9
本节小结
• 今天你有哪些收获?有哪些问 题需要注意?
-
10
例 、 如图,一圆柱高 1 2 cm,底面半径 3 cm,一只蚂蚁从点A爬到点B处吃食,
要爬行的最短程( 取3)
B
A
-
6
当堂检测
1.如图,要在高3m,斜坡5m的楼梯表面铺地毯, 地毯的长度至少需( )米
B
C
-
A
7
2.如图,有一个高1.5米,半径是1米 的圆柱形油桶,在靠近边的地方有一小孔 ,从孔中插入一铁棒,已知铁棒在油桶外 的部分最短是0.5米,问这根铁棒应有多 长?
有一个圆柱,它的高等于12厘
米,底面半径等于3厘米,在圆
B
柱下底面上的A点有一只蚂蚁,
它想从点A爬到点B , 蚂蚁沿
着圆柱侧面爬行的最短路程是 多少? (π的值取3)
我怎么走 会最近呢?
A
-
1
1.3蚂蚁怎样走最近
-
学习目标
• 能运用勾股定理及直角三角 形的判别条件解决实际问题.
-
3
问题导学
阅读课本22页,回答下列问题:
1.勾股定理的内容是:____.
2.如何判断一个三角形是直角三角形?
3.在立体图形中如何求两点之间的最短 距离?
-
4
情境引入
如图,将圆柱侧面剪开展开成一
个长方形,从A点到B 点的最短路线是什
么?你画对了吗?
BC
3_蚂蚁怎样走最近_课件4

D
6
可知EA EB,
A 10 x E x C
设CE x,则EA EB 10 x
在RtBCE中,CE2 BC2 BE2
x2 62 10 x2
x2 36 100 20x x2 x 16 5
甲、乙两位探险者到沙漠进行探 险,没有了水,需要寻找水源。为了 不致于走散,他们用两部对话机联系, 已知对话机的有效距离为15千米。 早晨8:00甲先出发,他以6千米/时 的速度向东行走,1小时后乙出发, 他以5千米/时的速度向北行进,上午 10:00,甲、乙二人相距多远?还
9x2 16x2 100 25x2 100
x2 4 x2 AC 4x 8 BC 3x 6
一朵荷花高出水 1
面1尺,被风吹得 和水面齐平,测出 偏离出水点5尺, 问水深多少尺?
5
x x1
解:设水深为x尺,则花高x+1尺。
x2 52 x 12
x2 25 x2 2x 1
2x 24 x 12
答 : 水深12尺.
解:设BD= x ,则DC=14- x A
在RtABD中
AD2 132 x2
13
15
在RtACD中
AD2 152 14 x2
Bx
D14
C
x
132 x2 152 14 x2
169 x2 225196 28x x2
蚂蚁怎样走最近?
教学目标: 1、能运用勾股定理及直角三角形的判别条件(即勾股定 理的逆定理)解决简单的实际问题。 2、能在实际问题中构造直角三角形,提高建模能力,进 一步深化对构造法和代数计算法和理解。培养学生从空间 到平面的想象能力,运用数学方法解决实际问题的创新能 力及探究意识。 3、通过研究勾股定理的历史,了解中华民族文化的发展 对数学发展的贡献,激发学生的爱国热情和学习数学的兴 趣。
3(PPT)3-3.蚂蚁怎样走最近
三.导练:
问题:
• 如图所示,有一个圆柱, 它的高为12厘米,它的
3B
半径为3厘米,在圆柱底 12
的A点有一只蚂蚁,它
ቤተ መጻሕፍቲ ባይዱ
想吃到上面与A对应的 B点 的食物,需要爬行 的最短路程是多少?
A
蚂蚁
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱 侧面画出几条路线,你 觉得哪条路最近?
石可知道,这一物种早在亿年前的寒武纪(Cambrian Period)就存在了。从它们被发现开始,人们对缓步动物在动物分类中的位置,形态学(morphology),生 活方式(life style),组织学(Histology)以及其隐生性(Hidden nature)的研究兴趣有增无减。 米勒研究 8年米勒(O.F.Müller)对这种动物作了深入的观察。他 尝试将缓步动物归入动物; GMAT培训,GMAT辅导班,GMAT补习班:https:///gmatpeixunban/ ;演化树中并且把它归入壁虱属(Tick species)。米勒所使用的学名Acarus ursellus被林奈(Linnaeus)写到了他的《自然分类》中。8年舒尔策发现了有名的Macrobiotus bufelandi。该名字来源于柏 林医生Hufeland,他著了一本有关长寿术(德语:Makrobiotik)的书叫《延年益寿之艺术》。相对于斯巴兰扎尼的“复活”,舒尔策认为缓步动物在缺水后 再次接触到水时,是“苏醒”过来了。但他的看法并不是得到很多的认同。他同时代的爱亨伯格则认为,缺水时,缓步动物能分泌一种物质,在里面缓步动 物不但能度过困难时期,而且能繁衍后代。数年后“醒过来”的只是它的后代。更有人认为那是一种自然发生(generatio spontanea)。 对缓步动物形态, 系统分类和生理研究有着最深远影响的贡献当属法国人Doyères所写的书《Mémoire sur les Tardigrades》(《对缓步动物的记忆》)(8-8年)。他强调了缓 步动物在慢慢失水的环境中“复活”的能力。这和当时另一种观点相冲突,就是认为,没有任何预防措施可以阻止完全脱水的动物的死亡。8年巴黎生物协会 (Paris Biological Association)最终通过一份超过页的鉴定形成定论,就是Doyères的意见是对的。新的问题是,在这种脱水环境中,缓步动物的新陈代谢究 竟只是变慢了还是停止了。世纪初,耶稣会神父吉尔伯特·弗兰兹·拉门(Gilbert Franz Rahm)通过缓步动物还能度过低温(绝对零度)-(Absolute zero)环 境的现象认为,新陈代谢是停止了。年鲍曼(Bauman)通过对脱水隐生的形态和生理方面的研究,再次捍卫了这一观点。 分类研究 8年杜雅尔丹(Dujardin) 认为缓步动物是一种原本生活在海洋里的生物,这是缓步动物的分类的第一步。-年Murray在不列颠-南极探险中收集到多种缓步动物的样本。使得缓步动物 的种类在很短的时间
《蚂蚁怎样走最近》同步课堂教学课件
2x=24, ∴ x=12, x+1=13
因此:旗杆的高度为12米,这根绳子长13米。
3、有两棵树,一棵高10米,另一棵高 4米,两棵树相距8米,一只鸟从一棵 树的树梢飞到另一棵树的树梢,求小 鸟飞行的距离。 A
E
D C
B
4.甲、乙两位探险者到沙漠进行探险.某日 早晨8∶00甲先出发,他以6千米/时的速度向东 行走.1时后乙出发,他以5千米/时的速度向北 行进.上午10∶00,甲、乙两人相距多远?
蛋糕 B
勾股定理应用(3)
复习回顾:
利用勾股定理解决实际问题的一般步骤: 1、根据题意正确画出图形,(曲面最 短路线问题画侧面展开图). 2、弄清题中直角三角形及线段关系.
3、根据勾股定理求未知量,或恰当设 未知量,建立方程来求解.
巩固提高
1.如图,台阶A处的蚂蚁要爬到B处搬运食 物,它怎么走最近?并求出最近距离。
做一做:
(2)李叔叔量得AD长是30厘米, AB长是40厘米,BD长是50厘米, AD边垂直于AB边吗?为什么?
做一做:
(3)小明随身只有一个长度为 20厘米的刻度尺,他能有办法 检验AD边是否垂直于AB边吗? BC边与AB边呢?
勾股定理应用(2)
例题
1、如图,长方体的长为10cm,宽为5cm,高为 20cm,一只蚂蚁如果要沿长方体的表面从A 点爬到B点,需要爬行的最短路径是多少厘 B 米?
2.有一圆柱形玻璃容器,高18厘米,底面 周长为60厘米,在外侧距下底1厘米的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的 上口外侧距开口外1厘米的点F处有一苍蝇, 试求急于捕获苍蝇充饥的蜘蛛,所走的最 短路线的长度
F S
ห้องสมุดไป่ตู้
3.一只螳螂在树干(圆柱形)的点A处,发现它 的正上方点B处有一只小虫子,螳螂想捕食这 只虫子,但又怕被虫子发现,于是按如图所示 的路线,绕到虫子的后面,已知树干的半径为 10厘米,A,B两点间的距离为45厘米,求螳螂 绕行的最短路程 B (∏ 取 3 )
北师大版八年级数学上册《蚂蚁怎样走最近》课件
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
利用勾股定理解答最短路径问题
想一想 蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
若已知圆柱体高为12 cm,底面周长为18 cm,则:
侧面展开图
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为 x米,即AB=x米,而AC=2米,BC=1.5米, 有x2=1.52+22 ,x =2.5
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km), B组行了9×2=18(km), 又因为A,B两组相距30km, 且有242+182=302, 所以A,B两组行进的方向成直角.
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9, 在AB上取点N使AN=12, 测量MN是否是15,是,就是垂直; 不是,就是不垂直.
A
我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!
利用勾股定理解答最短路径问题
想一想 蚂蚁走哪一条路线最近?
A'
蚂蚁A→B的路线
若已知圆柱体高为12 cm,底面周长为18 cm,则:
侧面展开图
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为 x米,即AB=x米,而AC=2米,BC=1.5米, 有x2=1.52+22 ,x =2.5
B
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:因为出发2小时,A组行了12×2=24(km), B组行了9×2=18(km), 又因为A,B两组相距30km, 且有242+182=302, 所以A,B两组行进的方向成直角.
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9, 在AB上取点N使AN=12, 测量MN是否是15,是,就是垂直; 不是,就是不垂直.
蚂蚁怎么走最近说课稿课件.ppt
让学生将知识内化为自己的知识结构的过程,教师巡视,对有困难的同学给予帮助,促进全班同学共同进步,体现面向全体的教学原则。学生活动时,教师要参与到学生活动中来,进行实物演示铁棒长度的不固定性,给学生以启发。
充分利用课本,在前面练习的基础上。通过对勾股定理的基本应用,让学生知道已知直角三角形三边中的任意两边的等量关系,可以求其边长。
学生活动(一):1、出示问题:有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱的下底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱侧面爬行的的最短路程是多少?(π的值取3)
(二)讲授新课:蚂蚁怎么走最近
B
分组操作(1)同学们可自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢? (2)将圆柱侧面剪开展开成一个长方形,从A点到B点的最短路线是什么?你画对了吗? (3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论,公布结果)
3、八年级的学生独立思考和探索的愿望和能力有所提高,并能在探索的过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法。
4、八年级学生学习数学的积极性比较高,对数学课有兴趣,整体学习水平较均衡,学生在课堂上表现比较活跃,遇到问题我都鼓励他们大胆的说出自己的想法和表达个人的独到见解。培养学生不在把数学课看作仅仅是接受知识的地方,也是释放他们数学思想、倾听他人想法和发挥个人见解的乐园。
四、课后反思与点评
蚂蚁怎么走最近
一、学生状况分析
二、教学任务分析
三、教学过程分析
一、学生状况分析
2、八年级的学生的活动空间有了较大的扩展,学生感新趣的问题已扩广到许多自然、社会与其他学科现象和问题。
充分利用课本,在前面练习的基础上。通过对勾股定理的基本应用,让学生知道已知直角三角形三边中的任意两边的等量关系,可以求其边长。
学生活动(一):1、出示问题:有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱的下底面A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱侧面爬行的的最短路程是多少?(π的值取3)
(二)讲授新课:蚂蚁怎么走最近
B
分组操作(1)同学们可自己做一个圆柱,尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢? (2)将圆柱侧面剪开展开成一个长方形,从A点到B点的最短路线是什么?你画对了吗? (3)蚂蚁从A点出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?(学生分组讨论,公布结果)
3、八年级的学生独立思考和探索的愿望和能力有所提高,并能在探索的过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法。
4、八年级学生学习数学的积极性比较高,对数学课有兴趣,整体学习水平较均衡,学生在课堂上表现比较活跃,遇到问题我都鼓励他们大胆的说出自己的想法和表达个人的独到见解。培养学生不在把数学课看作仅仅是接受知识的地方,也是释放他们数学思想、倾听他人想法和发挥个人见解的乐园。
四、课后反思与点评
蚂蚁怎么走最近
一、学生状况分析
二、教学任务分析
三、教学过程分析
一、学生状况分析
2、八年级的学生的活动空间有了较大的扩展,学生感新趣的问题已扩广到许多自然、社会与其他学科现象和问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3 蚂蚁怎样走最近
知识回顾
从二教楼 到综合楼 怎样走最 近?说明 理由
两点之间,线段最短
问题情境
在一个圆柱石凳上, 若小明在吃东西时留下了 一点食物在B处,恰好一 只在A处的蚂蚁捕捉到这 一信息,于是它想从A 处 爬向B处,你们想一想, 蚂蚁怎么走最近?
A
B
合作探究
以小组为单位, 研究蚂蚁爬行的 最短路线
x 2.5 ∴最长是2.5+0.5=3(米)
最短时: x 1.5
∴最短是1.5+0.5=2(米) 答:这根铁棒的长应在2-3米之间
举一反三
1.如图,在棱长为10厘米的正方体
的一个顶点A处有一只蚂蚁,现要向顶
点B处爬行,已知蚂蚁爬行的速度是1厘
米/秒,且速度保持不变,问蚂蚁能否在 20秒内从A爬到B?
20 3 2 B
A
AB 15 20 625 25
2 2 2
2
3.有一个高为1.5米,半径是1米的圆柱形
油桶,在靠近边的地方有一小孔,从孔中插入一
铁棒,已知铁棒在油桶外的部分为0.5米,问这
根铁棒有多长? 解:设伸入油桶中的长度为x米,则最长时: 2 2 2 x 1.5 2
(3)小明随身只有一个长 度为20厘米的刻度尺,他 能有办法检验AD边是否垂 直于AB边吗?BC边与AB 边呢?
课堂练习
1.甲、乙两位探险者到沙漠进行探险,某日 早晨8:00甲先出发,他以6km/h的速度向正东 行走,1小时后乙出发,他以5km/h的速度向正 北行走。上午10:00,甲、乙两人相距多远?
A
’
3
O
B
侧面展开图
A’
12
3π
B
12
A
A
做一做
李叔叔想要检测雕塑底座正面 的AD边和BC边是否分别垂直于底 边AB,但他随身只带了卷尺, (1)你能替他想办法完成任务吗? (2)李叔叔量得AD长是30厘米, AB长是40厘米,BD长是50厘米, AD边垂直于AB边吗?为什么?
AD2 AB2 30 2 40 2 2500 BD2 2500 AD2 AB2 BD2 ∴AD和AB垂直
答:水池的水深12尺,这根芦苇长13尺。
课堂小结 说一说本节课你有什么收获
课后作业
1.课本习题1.5第1,2,3题。 2*.右图是学校的旗杆,旗杆 上的绳子垂到了地面,并多 出了一段,现在老师想知道 旗杆的高度,你能帮老师想 个办法吗?请你与同伴交流 设计方案?
这根芦苇垂直拉向岸边,它的顶端恰好
到达岸边的水面,请问这个水池的深度 和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺,则 这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺 由勾股定理得:BC2+AC2=AB2 即 52+ x2= (x+1)2 25+ x2= x2+2 x+1, 2 x=24, ∴ x=12, x+1=13
北 C
解:如图:已知A是甲、乙的出发点, 10:00甲到达B点,乙到达C点.则:
A
B
东
AB=2×6=12(千米) AC=1×5=5(千米) 在Rt△ABC中 BC 2 AC 2 AB 2
∴BC=13(千米)
52 12 2 169 13 2
即甲乙两人相距13千米
2.如图,台阶A处的蚂蚁要爬到B处搬 运食物,它怎么走最近?并求出最近距离。
B
A
A’
d
B
A’
B
Aቤተ መጻሕፍቲ ባይዱ
A
O
B
蚂蚁A→B的路 线
B
A
A
怎样计算AB?
A’ r
O
B
A’
B
h
侧面展开图
A
A
在Rt△AA’B中,利用勾股定理可得,
AB2 AA2 A' B2
其中AA’是圆柱体的高,A’B是底面圆周长的一半(π r)
若已知圆柱体高为12cm,底面 半径为3cm,π取3,则:
AB 2 12 2 (3 3) 2 AB 15
食 物
B
A
举一反三
2.如图,在棱长为10厘米的正 方体的一个顶点A处有一只蚂蚁,现
要向顶点B处爬行,已知蚂蚁爬行的
速度是1厘米/秒,且速度保持不变, 问蚂蚁能否在20秒内从A爬到B? B
B
A
举一反三
3 .在我国古代数学著作《九章算术》 中记载了一道有趣的问题,这个问题的 意思是:有一个水池,水面是一个边长 为10尺的正方形,在水池的中央有一根 新生的芦苇,它高出水面1尺,如果把
知识回顾
从二教楼 到综合楼 怎样走最 近?说明 理由
两点之间,线段最短
问题情境
在一个圆柱石凳上, 若小明在吃东西时留下了 一点食物在B处,恰好一 只在A处的蚂蚁捕捉到这 一信息,于是它想从A 处 爬向B处,你们想一想, 蚂蚁怎么走最近?
A
B
合作探究
以小组为单位, 研究蚂蚁爬行的 最短路线
x 2.5 ∴最长是2.5+0.5=3(米)
最短时: x 1.5
∴最短是1.5+0.5=2(米) 答:这根铁棒的长应在2-3米之间
举一反三
1.如图,在棱长为10厘米的正方体
的一个顶点A处有一只蚂蚁,现要向顶
点B处爬行,已知蚂蚁爬行的速度是1厘
米/秒,且速度保持不变,问蚂蚁能否在 20秒内从A爬到B?
20 3 2 B
A
AB 15 20 625 25
2 2 2
2
3.有一个高为1.5米,半径是1米的圆柱形
油桶,在靠近边的地方有一小孔,从孔中插入一
铁棒,已知铁棒在油桶外的部分为0.5米,问这
根铁棒有多长? 解:设伸入油桶中的长度为x米,则最长时: 2 2 2 x 1.5 2
(3)小明随身只有一个长 度为20厘米的刻度尺,他 能有办法检验AD边是否垂 直于AB边吗?BC边与AB 边呢?
课堂练习
1.甲、乙两位探险者到沙漠进行探险,某日 早晨8:00甲先出发,他以6km/h的速度向正东 行走,1小时后乙出发,他以5km/h的速度向正 北行走。上午10:00,甲、乙两人相距多远?
A
’
3
O
B
侧面展开图
A’
12
3π
B
12
A
A
做一做
李叔叔想要检测雕塑底座正面 的AD边和BC边是否分别垂直于底 边AB,但他随身只带了卷尺, (1)你能替他想办法完成任务吗? (2)李叔叔量得AD长是30厘米, AB长是40厘米,BD长是50厘米, AD边垂直于AB边吗?为什么?
AD2 AB2 30 2 40 2 2500 BD2 2500 AD2 AB2 BD2 ∴AD和AB垂直
答:水池的水深12尺,这根芦苇长13尺。
课堂小结 说一说本节课你有什么收获
课后作业
1.课本习题1.5第1,2,3题。 2*.右图是学校的旗杆,旗杆 上的绳子垂到了地面,并多 出了一段,现在老师想知道 旗杆的高度,你能帮老师想 个办法吗?请你与同伴交流 设计方案?
这根芦苇垂直拉向岸边,它的顶端恰好
到达岸边的水面,请问这个水池的深度 和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺,则 这根芦苇长为
AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺 由勾股定理得:BC2+AC2=AB2 即 52+ x2= (x+1)2 25+ x2= x2+2 x+1, 2 x=24, ∴ x=12, x+1=13
北 C
解:如图:已知A是甲、乙的出发点, 10:00甲到达B点,乙到达C点.则:
A
B
东
AB=2×6=12(千米) AC=1×5=5(千米) 在Rt△ABC中 BC 2 AC 2 AB 2
∴BC=13(千米)
52 12 2 169 13 2
即甲乙两人相距13千米
2.如图,台阶A处的蚂蚁要爬到B处搬 运食物,它怎么走最近?并求出最近距离。
B
A
A’
d
B
A’
B
Aቤተ መጻሕፍቲ ባይዱ
A
O
B
蚂蚁A→B的路 线
B
A
A
怎样计算AB?
A’ r
O
B
A’
B
h
侧面展开图
A
A
在Rt△AA’B中,利用勾股定理可得,
AB2 AA2 A' B2
其中AA’是圆柱体的高,A’B是底面圆周长的一半(π r)
若已知圆柱体高为12cm,底面 半径为3cm,π取3,则:
AB 2 12 2 (3 3) 2 AB 15
食 物
B
A
举一反三
2.如图,在棱长为10厘米的正 方体的一个顶点A处有一只蚂蚁,现
要向顶点B处爬行,已知蚂蚁爬行的
速度是1厘米/秒,且速度保持不变, 问蚂蚁能否在20秒内从A爬到B? B
B
A
举一反三
3 .在我国古代数学著作《九章算术》 中记载了一道有趣的问题,这个问题的 意思是:有一个水池,水面是一个边长 为10尺的正方形,在水池的中央有一根 新生的芦苇,它高出水面1尺,如果把
