概率论与数理统计模拟题 重庆大学
重庆大学学年(秋)数理统计试题及答案

重庆大学全日制学术型硕士研究生 《数理统计》(A )课程试卷2013-2014学年第一学期(秋)请保留四位小数,部分下侧分位数为:0.95 1.65u =,0.99 2.33u =,20.95(1) 3.841χ=,0.95(3,6)9.78f =一、(18分)设1X ,2X ,…,64X 是来自总体N (0,2σ)的样本,X ,2S 分别是样本均值和样本方差:(1)求参数c 满足{}0.1P X S c >⋅=;(2)求概率22122234{1}X X P X X +>+;(3)求322321(2)i i i D X X X +=⎡⎤+-⎢⎥⎣⎦∑。
(请写出计算过程)解:(1)~(1)t n-{}}0.1P X S c P c ∴>⋅=>=得0.95(63)c t = 故 1.650.20638c ==(2)2~(0,)X N σ22212(/)(/)~(2)X X σσχ∴+ 同理22234(/)(/)~(2)X X σσχ+2222223412122234(/)(/)(/)(/)/~(2,2)22X X X X X X F X X σσσσ+++∴=+ 22122234{1}{(2,2)1}X X P P F X X +>=>+ 且0.50.50.51(2,2)(2,2)1(2,2)F F F =⇒= 得2222121222223434{1}1{1}0.5X X X X P P X X X X ++>=-≤=++ (3)令2~(2,2)i i n i Y X X N μσ+=+,112n i i Y Y X n ===∑ 221()(1)ni Y i T Y Y n S =∴=-=-∑3232223211(2)[()]i i i i i D X X X DT D Y Y +==⎡⎤+-==-⎢⎥⎣⎦∑∑2~(0,2(11/))i Y YN n σ-+~(0,1)YN=3222422421[2(11/)4(11/)((32))256(11/32)i Y D n n D σσχσ=+=+=+∑二、(26分)设1X ,2X ,…,n X 是来自总体2~(2,)(0)X N σσ>的样本,{}0.95P X A <=。
重庆大学概率论习题三

Y
0 25/36 5/36
1 5/36 1/36
X
0 45/66 5/33
1 5/33 1/66
0 1
0 1
(1) (2) 2.盒中装有 3 只黑球,2 只红球,2 只白球,现从盒中任取 4 只球,用 X 表示黑球数,用 Y 表示红球数,求 ( X , Y ) 的联合分布律。 解: X 的可能取值:0,1,2,3, Y 的可能取值:0,1,2
y x e dy x 0 e f ( x, y )dy x 0 0 x 0 x0 x0
;
(2) f X ( x)
fY ( y )
y y y e dx y 0 ye f ( x, y )dx 0 0 0 y0
0 x 1 其他
fY ( y )
1 3 xdx 1 y 0 y 2 3 2 1 3 (1 y ), | y | 1 f ( x, y )dx xdx 0 y 1 4 y 2 0 其他 0 其他
(2)X、Y分别可能取值为0、1,于是(X,Y)的分布律如下:
P{ X 0, Y 0} P{ X 1, Y 0}
即
Y X
1 1 1 1 C10 C9 C10 C2 45 5 , P { X 0 , Y 1 } 1 1 1 1 C12 C11 66 C12 C11 33 1 1 1 1 C2 C10 C2 C1 5 1 , P { X 1 , Y 1 } 1 1 1 1 C12 C11 33 C12 C11 66
X
0
1
P 计算: (X,Y) P Max(X,Y) Min(X,Y) X+Y (0,0) 1/4 0 0 0 (0,1) 1/4 1 0 1
重庆大学数理统计试题3

n Xi
i 1 m n m
( 1 ) Y1
m
2
i m 1
X
; ( 2 ) Y2
2 i
n X i 2 m Xi
i m 1 i 1 mn 2
n n 2 i 1 2 1 e 2 ) ( 2 2 ) 2 e 2 2 n xi2
xi2
n
L( 2 , X 1 , X 2 ,
Xn) (
i 1
ln( L( 2 , X 1 , X 2 , ln( L( 2 , X 1 , X 2 , d 2
xi2 n X n )) ln( 2 ) ln 2 i 1 2 2 2 X n )) n 1 n 1 n 2 i 1 ( xi 2 ) 2 2 2 4 2 2( ) 2 n i 1
s
2
c1
1 1 2 (n 1), c2 2 (n 1) n 1 2 n 1 1 2 s2
k0 :{
2
c2或
s2
2
c1}
(2) H0 : 2 1, H1 : 2 2
2 拒绝域 k0 : (n 1)s 2 12 (n 1);22s 2 0.95 (22) 33.92; :
m
2 i m1
X
n X i 2 m Xi
i m 1 i 1 mn 2
Y2 ~ F (m, n)
2 i
n
Xi
(3)
i 1
m
m n
m
~ N (0,1),
重庆理工大学概率论与数理统计_学习指导与练习册习题答案

1 / 24习题一一.填空题一.填空题1.ABC 2、50× 3、20× 4、60× 二.单项选择题二.单项选择题 1、B 2、C 3、C 4、A 5、B 三.计算题三.计算题 1.(1)略)略 (2)A 、321A A AB 、321A A A ÈÈC 、321321321A A A A A A A A A ÈÈD 、321321321321A A A A A A A A A A A A ÈÈÈ 2.解.解)()()()(AB P B P A P B A P -+=È=85812141=-+83)()()()(=-=-=AB P B P AB B P B A P87)(1)(=-=AB P AB P21)()()])([(=-È=ÈAB P B A P AB B A P3.解:最多只有一位陈姓候选人当选的概率为531462422=-C C C 4.)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++=ÈÈ=855.解:(1)n Nn A P !)(=(2)nn NNn C B P !)(=、 (3)nmn m n N N C C P --=)1()(习题二一.填空题一.填空题1.0.8 2、50× 3、32 4、735、43 二.单项选择题二.单项选择题 1、D 2、B 3、D 4、B 三.计算题三.计算题1. 解:设i A :分别表示甲、乙、丙厂的产品(i =1,2,3) B :顾客买到正品:顾客买到正品)/()()(11A B P A P B P =)/()(22A B P A P +)/()(33A B P A P +=83.065.05185.0529.052=´+´+´ 8334)()/()()/(222==B P A B P A P B A P2.解:设iA :表示第i 箱产品(i =1,2)i B :第i 次取到一等品(i =1,2) (1))/()()(1111A B P A P B P =)/()(212A B P A P +=4.0301821501021=´+´ (2)同理4.0)(2=B P(3))/()()(121121A B B P A P B B P =)/()(2212A B B P A P +=19423.02917301821499501021=´´+´´ 4856.04.019423.0)()()/(12112===B P B B P B B P (4)4856.04.019423.0)()()/(212121===B P B B P B B P 3. 解:设i A :表示第i 次电话接通(i =1,2,3)101)(1=A P 10191109)(21=´=A A P1018198109)(321=´´=A A A P所以拨号不超过三次接通电话的概率为3.0101101101=++如已知最后一位是奇数,则如已知最后一位是奇数,则51)(1=A P 514154)(21=´=A A P51314354)(321=´´=A A A P 所以拨号不超过三次接通电话的概率为60515151=++ 4.解:)()()(1)(1)(C P B P A P C B A P C B A P -=ÈÈ-=ÈÈ=6.04332541=-5.解:设21,B B 分别表示发出信号“A ”及“B ” 21,A A 分别表示收到信号“A ”及“B ”)/()()(1111B A P B P A P =)/()(212A A P B P +=30019701.031)02.01(32=+- 197196)()/()()()()/(111111111===A P B A P B P A P B A P A B P第一章 复习题一.填空题一.填空题1.0.3,0.5 2、0.2 3、2120 4、153,1535、158,32,31 6.4)1(1p --二.单项选择题二.单项选择题1、B2、B3、 D4、D5、A 三.计算题三.计算题1. 解:设i A :i 个人击中飞机(i =0,1,2,3) 则09.0)(0=A P 36.0)(1=A P 41.0)(2=A P 14.0)(3=A PB :飞机被击落:飞机被击落)/()()(11A B P A P B P =)/()(22A B P A P +)/()(33A B P A P ++)/()(00A B P A P +=458.0009.0114.06.041.02.036.0=´+´+´+´ 2.解:设i A : i 局甲胜(i =0,1,2,3)(1)甲胜有下面几种情况:)甲胜有下面几种情况: 打三局,概率36.0打四局,概率12136.06.04.0××C打五局,概率122246.06.04.0××CP (甲胜)=36.0+11221136.06.04.0××C +1122222246.06.04.0××C =0.68256 (2)93606.06.0*4.0*6.06.0*4.0*6.06.0)()()()()/(2222321321212121=++===A A P A A A P A A P A AA P A A A P3.解:设A :知道答案:知道答案 B :填对:填对)/()()(A B P A P B P =475.0417.013.0)/()(=´+´=+A B P A P197475.0417.0)()/()()()()/(=´===B P A B P A P B P B A P B A P 4.解:设iA :分别表示乘火车、轮船、汽车、飞机(i =1,2,3,4)B :迟到:迟到)/()()(11A B P A P B P =)/()(22A B P A P +)/()(33A B P A P ++)/()(44A B P A P +=203052121101315141103=´+´+´+´2120341103)()/()()()()/(11111=´===B P A B P A P B P B A P B A P同理94)/(2=B A P 181)/(3=B A P5.解:A :甲袋中取红球;B :乙袋中取红球:乙袋中取红球)()()()()()()(B P A P B P A P B A P AB P B A AB P +=+=È =40211610106166104=´+´习题三 第二章 随机变量及其分布一、填空题一、填空题1、19272、23、134、0.85、010.212()0.52313x x F x x x <ìï£<ï=í£<ïï³î6、113~0.40.40.2X -éùêúëû二、单项选择题二、单项选择题1、B2、A3、B4、B 三、计算题三、计算题1、解:由已知~(15,0.2)X B ,其分布律为:1515()0.20.8(0,1,2,...,15)kk kP X k C k -===至少有两人的概率:(2)1(2)1(0)(1)0.833P X P X P X P X ³=-<=-=-==多于13人的概率:(13)(14)(15)P X P X P X >==+==02、解、解 设击中的概率为p ,则X 的分布率为的分布率为 X123456k p p (p p )1- (p p 2)1- (p p 3)1- (p p 4)1- (p p 5)1-+(6)1p -3、解:X 的分布律为:的分布律为:X34 5 k p0.10.30.6X 的分布函数为:0,30.1,34()0.4,451,5x x F x x x <ìï£<ï=í£<ïï³î4、解:由已知,X 的密度函数为:1,33()60,x f x ì-££ï=íïî其它此二次方程的22(4)44(2)16(2)x x x x D =-××+=--(1)当0D ³时,有实根,即2(2)021x x x x --³Þ³£-或 所以{}{21}{2}{1}P P X X P X P X =³£-=³+£-方程有实根或3123111662dx dx --=+=òò(2)当0D =时,有重根,即2(2)021x x x x --=Þ==-或所以{}{21}{2}{1}0P P X X P X P X ===-==+=-=方程有重根或 (3)当0D <时,无实根,1{}1{}2P P =-=方程有实根无实根 5、解:设X 为元件寿命,Y 为寿命不超过150小时的元件寿命。
重庆大学概率与数理统计课后答案第八章

习题八A 组1.假设总体X ~)1,(μN ,从中抽取容量为25的样本,对统计假设0:,0:10≠=μμH H ,拒绝域为X 0={}392.0≥x 。
(1)求假设检验推断结果犯第Ⅰ类错误的概率。
(2)若3.0:1=μH ,求假设检验推断结果犯第Ⅱ类错误的概率。
解:(1){}{}001H H P P α==犯第I 类错误拒绝成立={}0392.0=>μX P{}{}96.10392.0>==>=n XP X P μ,所以05.01=α(2){}{}00H H P P β==犯第II 类错误接受不成立{}3.0392.0=≤=μX P{}6769.046.0)3.0(46.3=<-<-=n X P2.已知某厂生产的电视机显像管寿命(单位:小时)服从正态分布。
过去,显像管的平均寿 命是15000小时,标准差为3600小时。
为了提高显像管寿命采用了一种新技术,现从新生 产的显像管中任意抽取36只进行测试,其平均寿命为15800=x 小时。
若用假设检验方 法推断新技术是否显著提高了显像管的寿命,试指出:(1)假设检验中的总体;(2)统计假设;(3)检验法、检验统计量、拒绝域;(4)推断结果。
解:(1)假设检验中的总体是新生产的显像管的寿命,用X 表示,由题意知:X ~),(2σμN )90000,5000(N(2)统计假设:15000:0≤μH ,15000:1>μH(3)假设σ与过去一样为3600小时,那么检验方法为U 检验法,检验统计量为:nX U σ15000-=显著水平05.0=α时的拒绝域为:X 0 ={}α->1u u ={}645.1>u(4)推断:因为U 的样本值为1.333不在X 0 内,所以接受原假设,即在显著水平05.0=α下,认为新技术没有提高显像管的寿命。
3.某计算机公司使用的现行系统,运行通每个程序的平均时间为45秒。
现在使用一个新系统运行9个程序,所需的计算时间(秒)分别是:30,37,42,35,36,40,47,48,45。
第二学期概率论与数理统计试卷 参考答案
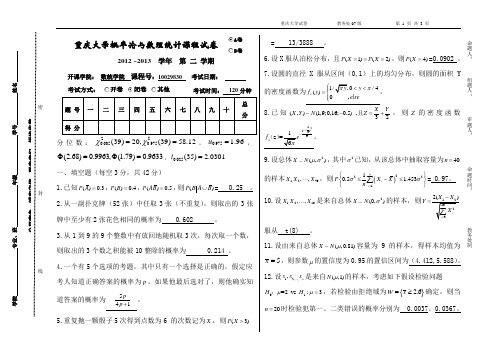
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
2.从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
3.从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为6 的次数记为X ,则(3)P X >= 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Z f --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
重庆大学概率统计试题(A上期解答)

2002级重大概率论和数理统计试题(A )一、 填空题(每空3分,共45分)1、已知P(A) = 0.92, P(B) = 0.93, P(B|A ) = 0.85, 则P(A|B ) = 0.8286 。
P( A ∪B) = 0.988 。
2、设事件A 与B 独立,A 与B 都不发生的概率为19,A 发生且B 不发生的概率与B发生且A 不发生的概率相等,则A 发生的概率为: 2/3 ;3、一间宿舍内住有6个同学,求他们之中恰好有4个人的生日在同一个月份的概率:14212661112C C ⨯ ,没有任何人的生日在同一个月份的概率61266!12C ;4、已知随机变量X 的密度函数为:,0()1/4,020,2x Ae x x x x ϕ⎧<⎪=≤<⎨⎪≥⎩, 则常数A= 1/2 , 分布函数F (x )= 1,021,02241,2xe x xx x ⎧≤⎪⎪⎪+<≤⎨⎪>⎪⎪⎩, 概率{0.51}P X -<<= 0.53142e --;5、设随机变量X~ B(2,p)、Y~ B(1,p),若{1}5/9P X ≥=,则p = 1/3 ,若X与Y 独立,则Z=max(X,Y)的分布律: Z 0 1 2P 8/27 16/27 3/27;6、设~(200,0.01),~(4),X B Y P 且X 与Y 相互独立,则D(2X-3Y)= 43.92 , COV(2X-3Y , X)= 3.96 ;7、设125,,,X X X 是总体~(0,1)X N 的简单随机样本,则当k =~(3)Y t =;8、设总体~(0,)0X U θθ>为未知参数,12,,,n X X X 为其样本,11ni i X X n==∑为样本均值,则θ的矩估计量为: 2X 。
9、设样本129,,,X X X 来自正态总体(,1.44)N a ,计算得样本观察值10x =,求参数a 的置信度为95%的置信区间: [9.216,10.784] ;二、 计算题(35分)1、 (12分)设连续型随机变量X 的密度函数为:1,02()20,x x x ϕ⎧≤≤⎪=⎨⎪⎩其它求:1){|21|2}P X -<;2)2Y X =的密度函数()Y y ϕ;3)(21)E X -; 1) 9{|21|2}{0.5 1.5}16P X P X -<=-<<=2)(0()0,01,0440,X X Y y y y y ϕϕϕ+>=≤⎩⎧≤≤⎪=⎨⎪⎩其它3)45(21)212133E X E X -=-=⨯-=2、(12分)设随机变量(X,Y)的密度函数为1/4,||,02,(,)0,y x x x y ϕ<<<⎧=⎨⎩其他1) 求边缘密度函数(),()X Y x y ϕϕ; 2) 问X 与Y 是否独立?是否相关? 3) 计算Z = X + Y 的密度函数()Z z ϕ;解:1)1,02,02()(,)420,0,x X x x dy x x x x y dy ϕϕ+∞--∞⎧⎧<<<<⎪⎪===⎨⎨⎪⎪⎩⎩⎰⎰其它其它2||1,||22||,||24()(,)0,0,y Y dx y y y y x y dx ϕϕ+∞-∞⎧<-<⎧⎪===⎨⎨⎩⎪⎩⎰⎰其它其它2)显然,(,)()()X Y x y x y ϕϕϕ≠,所以X 与Y 不独立。
第二学期概率论与数理统计试卷 参考答案

重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为 6 的次数记为X ,则(3)P X > = 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Zf --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453n i i P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.填空题
1.设,2.0)(,4.0)(,3.0)(===B A P B P A P 则=)(B A P ,B A ,中至少一个不发生的概率为
2.设在一个学生宿舍某房间内住有6个同学,恰有4个同学生日是星期天的概率为 3.设随机变量X 在区间[2,5]上服从均匀分布,对X 进行三次独立的观测中,刚好有两次的观测值大于3的概率为 4.设X 分布如下:
则关于λ的一元二次方程02
=-+X X λλ有实根的概率为 5.设随机变量X ~)10,0(2
N ,则}{
=>6.19X P
6.设随机变量X ~)001.0,5000(B ,根据泊松定理,则{}≈=2X P
7.设随机变量Y X ,独立并且具有相同分布)4.0,1(B ,则),max(Y X Z =的分布律为
8.设随机变量X ~⎪⎩
⎪
⎨⎧<-≤≤>=-0,120,02,1],3,1[X X X Y U ,则=EY
9.设)5.0;9,0;4,1(~),(N Y X ,则____~332-+Y X
10.设621,,,X X X 是来自正态总体),0(2
σN 的一个样本,则~)(2
6
25242
321X X X X X X Y ++++=
11.设21,X X 为来自正态总体),(2
σμN 的一个样本,若212008
1
X cX +是参数μ的一个无偏估计量,则____=c
12.设正态总体~X ),(2
σμN ,若2
σ已知,n X X X ,,,21 为样本,X 为样本均值,μ的
置信度为α-1的置信区间为
),n
X n
X σ
λ
σ
λ+-(,那么____=λ
13.设投篮比赛中,甲,乙两人每次投中的概率分别为0.6和0.75,那么甲,乙两人各
独立地投1次,恰有1人投中的概率是
14.已知一批产品的次品率为4%,而非次品中有75%的优等品。
从这批产品中任取一件产品,则取到优等品的概率为
15.已知测量某一距离时的随机误差X (单位:cm )的密度函数为
R x e
x f x ∈=
--
,2401)(3200
)20(2π
,则误差的绝对值不超过30cm 的概率为
._____]1600
)20([____,~4020___2
=--X D X ,
16.已知连续型随机变量X 的密度函数为⎩⎨
⎧≤-=其它
,01
,1)(x x x f ,则X 的分布函数__________)(=x F ,概率.______}10{=<<X P 17.利用概率知识计算∑+∞
=-=+0
4
._______!4)1(k k e k k 18.设随机变量)5.0,1(~],6,0[~ΓY U X ,则._______)2,2cov(=+-Y X Y X
19.设4321,,,X X X X 为总体)1,0(N 的样本,则.______)255.19(2
3
222
1=>+X X X P 20.设一批零件的长度(cm )服从正态分布)5.1,(2
μN 。
为了以95%的置信度保证样本均值对零件的平均长度的估计误差不超过.80,则至少需要抽取 个零件。
21.当作出拒绝被择假设的决策时,这个决策可能犯第 类错误。
二.计算题。
1.设随机变量X 的密度函数为+∞<<-∞=-x Ae x f x
,)(
⑴求系数A 的值; ⑵X 的分布函数);(x F ⑶};11{<<-X P ⑷2
4
1X Y =
的密度函数).(y f Y 2.设二维连续型随机变量),(Y X 的密度为:1,01,02(1)
(,)0,x y x f x y ≤≤≤≤-⎧=⎨⎩
其他
⑴求边缘密度函数)(x f X 和);(y f Y ⑵判断X 和Y 是否相互独立; ⑶Y X Z +=的密度函数);(z f Z ⑷).(X Y P <
3.轰炸机轰炸某目标,它能飞到距目标400m ,200m ,100m 的概率分别为0.5,0.3,0.2,
又设它在距离目标400m ,200m ,100m 的命中率分别为0.01,0.02,0.1。
⑴求目标被击中的概率;
⑵当目标被击中时,求飞机是在400m 处轰炸的概率。
4.设随机变量),(Y X 的联合密度函数为
⎩⎨
⎧≥≤≤=-其它,00
,10,),(y x e y x f y
⑴求),(Y X 的边缘密度函数)(x f X ,);(y f Y
⑵判断X 和Y 是否相关,是否独立;
⑶求Y X Z +=的密度函数);(z f Y X +
⑷令,3,2Y V X U ==求),(V U 的联合密度函数).,(v u h
5.假设随机变量X 和Y 相互独立,同服从区间]2,0[上的均匀分布。
随机变量
⎩⎨
⎧≥+<+=⎩⎨⎧≥+<+=2,12,0;1,11,0Y X Y X V Y X Y X U
⑴求),(V U 的联合分布律及边缘分布律; ⑵求);(V U D +
⑶求),(V U ρ.
6.设总体X 的密度函数为
⎪⎩
⎪⎨⎧≤>=-0,00,)(2
21x x e
x x f x ββ其中)0(>β是未知参数。
⑴求β的矩估计量;ˆ1
β ⑵求β的极大似然估计量.ˆ2
β 7.设总体X 具有密度函数
⎩⎨
⎧<<+=+其它
,010,)3()()2(x x x f θθ n X X X ,,,21 为来自X 的样本,求参数θ的极大似然估计量。
8.两台车床加工同样的零件,第一台出现不合格品的概率是0.03,第二天出现不合格品
的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍。
求
⑴任取一个零件是合格品的概率;
⑵如果取出的零件是不合格品,求它是由第二台车床加工的概率。
9.一水果店为了要提前贮备某种秋季出售的应时商品,已知该商品每出售一千克获利润1000元,如到秋季末尚有剩余商品未能售完,则每千克将亏损500元。
设在任一秋季内,该商品的总销售量为X 千克,它的密度函数为
,0
,00,)(⎩⎨⎧≤>=-x x e x f x 如贮备0y 千克,求该商品的期望利润值。
10.根据去年的调查,某城市一个家庭每月的耗电量服从正态分布),10,32(2
N ,今年随机调查100个家庭,统计得到他们每月的耗电量的平均值为5.234,能否确定今年家庭平均每月耗电量是否有所提高?)05.0(=α。
