特级教师彭海燕精编高考数学全国卷基本不等式
2015年高考数学总复习(人教A版,理科)配套教案:第七章 不等式 7.5
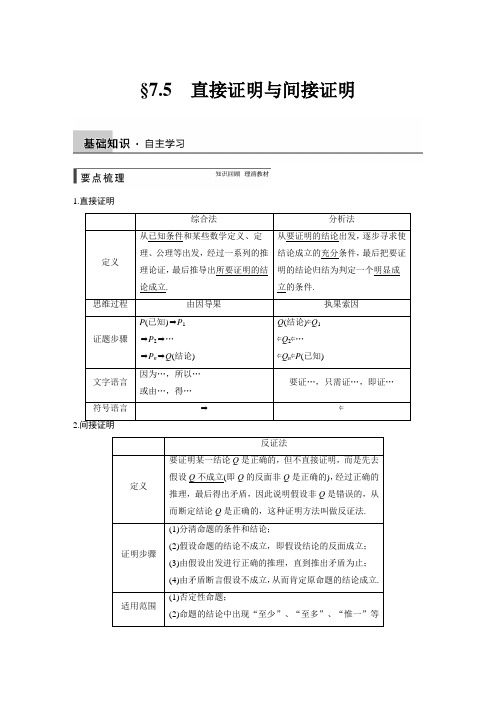
§7.5直接证明与间接证明1.直接证明综合法分析法定义从已知条件和某些数学定义、定理、公理等出发,经过一系列的推理论证,最后推导出所要证明的结论成立.从要证明的结论出发,逐步寻求使结论成立的充分条件,最后把要证明的结论归结为判定一个明显成立的条件.思维过程由因导果执果索因证题步骤P(已知)⇒P1⇒P2⇒…⇒P n⇒Q(结论)Q(结论)⇐Q1⇐Q2⇐…⇐Q n⇐P(已知)文字语言因为…,所以…或由…,得…要证…,只需证…,即证…符号语言⇒⇐2.反证法定义要证明某一结论Q是正确的,但不直接证明,而是先去假设Q不成立(即Q的反面非Q是正确的),经过正确的推理,最后得出矛盾,因此说明假设非Q是错误的,从而断定结论Q是正确的,这种证明方法叫做反证法.证明步骤(1)分清命题的条件和结论;(2)假设命题的结论不成立,即假设结论的反面成立;(3)由假设出发进行正确的推理,直到推出矛盾为止;(4)由矛盾断言假设不成立,从而肯定原命题的结论成立.适用范围(1)否定性命题;(2)命题的结论中出现“至少”、“至多”、“惟一”等词语的;(3)当命题成立非常明显,而要直接证明所用的理论太少,且不容易说明,而其逆否命题又是非常容易证明的; (4)要讨论的情况很复杂,而反面情况很少.1.判断下面结论是否正确(请在括号中打“√”或“×”) (1)综合法是直接证明,分析法是间接证明.( × ) (2)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件. ( × ) (3)用反证法证明结论“a >b ”时,应假设“a <b ”. ( × ) (4)反证法是指将结论和条件同时否定,推出矛盾.( × )(5)在解决问题时,常常用分析法寻找解题的思路与方法,再用综合法展现解决问题的过程.( √ )(6)证明不等式2+7<3+6最合适的方法是分析法. ( √ ) 2.若a ,b ,c 为实数,且a <b <0,则下列命题正确的是( )A.ac 2<bc 2B.a 2>ab >b 2C.1a <1bD.b a >a b答案 B解析 a 2-ab =a (a -b ),∵a <b <0,∴a -b <0,∴a 2-ab >0,∴a 2>ab . ① 又ab -b 2=b (a -b )>0,∴ab >b 2,②由①②得a 2>ab >b 2.3.设a =lg 2+lg 5,b =e x (x <0),则a 与b 的大小关系为( )A.a >bB.a <bC.a =bD.a ≤b答案 A解析 a =lg 2+lg 5=1,b =e x ,当x <0时,0<b <1, ∴a >b .4.用反证法证明某命题时,对结论:“自然数a ,b ,c 中恰有一个偶数”正确的反设为( ) A.a ,b ,c 中至少有两个偶数B.a ,b ,c 中至少有两个偶数或都是奇数C.a ,b ,c 都是奇数D.a,b,c都是偶数答案 B解析自然数a,b,c中为偶数的情况为a,b,c全为偶数;a,b,c中有两个数为偶数;a,b,c全为奇数;a,b,c中恰有一个数为偶数,所以反设为a,b,c中至少有两个偶数或都是奇数.5.如果a a+b b>a b+b a,则a、b应满足的条件是________.答案a≥0,b≥0且a≠b解析∵a a+b b-(a b+b a)=a(a-b)+b(b-a)=(a-b)(a-b)=(a-b)2(a+b).∴当a≥0,b≥0且a≠b时,(a-b)2(a+b)>0.故a a+b b>a b+b a成立的条件是a≥0,b≥0且a≠b.题型一综合法的应用例1对于定义域为[0,1]的函数f(x),如果同时满足:①对任意的x∈[0,1],总有f(x)≥0;②f(1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立,则称函数f(x)为理想函数.(1)若函数f(x)为理想函数,证明:f(0)=0;(2)试判断函数f(x)=2x(x∈[0,1]),f(x)=x2(x∈[0,1]),f(x)=x(x∈[0,1])是否是理想函数.思维启迪(1)取特殊值代入计算即可证明;(2)对照新定义中的3个条件,逐一代入验证,只有满足所有条件,才能得出“是理想函数”的结论,否则得出“不是理想函数”的结论.(1)证明取x1=x2=0,则x1+x2=0≤1,∴f(0+0)≥f(0)+f(0),∴f(0)≤0.又对任意的x∈[0,1],总有f(x)≥0,∴f(0)≥0.于是f(0)=0.(2)解对于f(x)=2x,x∈[0,1],f(1)=2不满足新定义中的条件②,∴f(x)=2x,(x∈[0,1])不是理想函数.对于f(x)=x2,x∈[0,1],显然f(x)≥0,且f(1)=1.任意的x1,x2∈[0,1],x1+x2≤1,f(x1+x2)-f(x1)-f(x2)=(x1+x2)2-x21-x22=2x1x2≥0,即f(x1)+f(x2)≤f(x1+x2).∴f(x)=x2(x∈[0,1])是理想函数.对于f(x)=x,x∈[0,1],显然满足条件①②.对任意的x1,x2∈[0,1],x1+x2≤1,有f2(x1+x2)-[f(x1)+f(x2)]2=(x1+x2)-(x1+2x1x2+x2)=-2x1x2≤0,即f2(x1+x2)≤[f(x1)+f(x2)]2.∴f(x1+x2)≤f(x1)+f(x2),不满足条件③.∴f(x)=x(x∈[0,1])不是理想函数.综上,f(x)=x2(x∈[0,1])是理想函数,f(x)=2x(x∈[0,1])与f(x)=x(x∈[0,1])不是理想函数.思维升华用综合法证题是从已知条件出发,逐步推向结论,综合法的适用范围:(1)定义明确的问题,如证明函数的单调性、奇偶性,求证无条件的等式或不等式.(2)已知条件明确,并且容易通过分析和应用条件逐步逼近结论的题型.在使用综合法证明时,易出现的错误是因果关系不明确,逻辑表达混乱.定义:若数列{A n}满足A n+1=A2n,则称数列{A n}为“平方递推数列”.已知数列{a n}中,a1=2,点(a n,a n+1)在函数f(x)=2x2+2x的图象上,其中n为正整数,证明:数列{2a n+1}是“平方递推数列”.证明∵点(a n,a n+1)在函数f(x)=2x2+2x的图象上,∴a n+1=2a2n+2a n,∴2a n+1+1=4a2n+4a n+1=(2a n+1)2,∴{2a n+1}是“平方递推数列”.题型二 分析法的应用例2 已知m >0,a ,b ∈R ,求证:(a +mb 1+m )2≤a 2+mb 21+m .思维启迪 将要证分式化成整式,再合并同类项. 证明 ∵m >0,∴1+m >0. 所以要证原不等式成立,只需证(a +mb )2≤(1+m )(a 2+mb 2), 即证m (a 2-2ab +b 2)≥0, 即证(a -b )2≥0, 而(a -b )2≥0显然成立, 故原不等式得证.思维升华 分析法的特点和思路是“执果索因”,即从“未知”看“需知”,逐步靠拢“已知”或本身已经成立的定理、性质或已经证明成立的结论等,运用分析法必须考虑条件的必要性是否成立.通常采用“欲证—只需证—已知”的格式,在表达中要注意叙述形式的规范.已知a ,b ∈(0,+∞),求证:(a 3+b 3)31<(a 2+b 2)21.证明 因为a ,b ∈(0,+∞),所以要证原不等式成立,只需证[(a 3+b 3)31]6<[(a 2+b 2)21]6,即证(a 3+b 3)2<(a 2+b 2)3,即证a 6+2a 3b 3+b 6<a 6+3a 4b 2+3a 2b 4+b 6, 只需证2a 3b 3<3a 4b 2+3a 2b 4. 因为a ,b ∈(0,+∞), 所以即证2ab <3(a 2+b 2).而a 2+b 2≥2ab,3(a 2+b 2)≥6ab >2ab 成立, 以上步骤步步可逆,所以(a 3+b 3)31<(a 2+b 2)21.题型三 反证法的应用例3 已知数列{a n }的前n 项和为S n ,且满足a n +S n =2. (1)求数列{a n }的通项公式;(2)求证:数列{a n }中不存在三项按原来顺序成等差数列.思维启迪 (1)先利用S n -S n -1=a n (n ≥2)两式相减得a n 和a n +1的关系,再求a n ; (2)用反证法证明.(1)解 当n =1时,a 1+S 1=2a 1=2,则a 1=1. 又a n +S n =2,所以a n +1+S n +1=2, 两式相减得a n +1=12a n ,所以{a n }是首项为1,公比为12的等比数列,所以a n =12n -1.(2)证明 反证法:假设存在三项按原来顺序成等差数列,记为a p +1,a q +1,a r +1(p <q <r ,且p ,q ,r ∈N *),则2·12q =12p +12r ,所以2·2r -q =2r -p +1.①又因为p <q <r ,所以r -q ,r -p ∈N *.所以①式左边是偶数,右边是奇数,等式不成立. 所以假设不成立,原命题得证.思维升华 (1)当一个命题的结论是以“至多”、“至少”、“唯一”或以否定形式出现时,可用反证法来证,反证法关键是在正确的推理下得出矛盾,矛盾可以是与已知条件矛盾,与假设矛盾,与定义、公理、定理矛盾,与事实矛盾等.(2)用反证法证明不等式要把握三点:①必须否定结论;②必须从否定结论进行推理;③推导出的矛盾必须是明显的.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若a 、b 、c 三边的倒数成等差数列,求证:∠B <90°.证明 假设∠B <90°不成立,即∠B ≥90°,从而∠B 是△ABC 的最大角,∴b 是△ABC 的最大边, 即b >a ,b >c . ∴1a >1b ,1c >1b,相加得1a +1c >1b +1b =2b ,这与1a +1c =2b 矛盾. 故∠B ≥90°不成立,即∠B <90°.混淆特殊值检验和一般性证明致误典例:(12分)设f (x )=ax 2+bx +c (a ≠0),若函数f (x +1)与f (x )的图象关于y 轴对称,求证:f (x +12)为偶函数. 易错分析 在证明f (x +12)是偶函数时,用特殊值f (32+12)=f (-32+12)成立来判断f (x +12)是偶函数. 规范解答证明 由函数f (x +1)与f (x )的图象关于y 轴对称, 可知f (x +1)=f (-x ).[4分] 将x 换成x -12代入上式可得f (x -12+1)=f [-(x -12)],即f (x +12)=f (-x +12),[10分]由偶函数的定义可知f (x +12)为偶函数.[12分]温馨提醒 在证明数学命题时,必须通过严格的推理来证明对任意满足题意的条件,命题的结论都成立,特殊值的检验不能代替一般性的证明.方法与技巧1.分析法的特点:从未知看需知,逐步靠拢已知.2.综合法的特点:从已知看可知,逐步推出未知.3.分析法和综合法各有优缺点.分析法思考起来比较自然,容易寻找到解题的思路和方法,缺点是思路逆行,叙述较繁;综合法从条件推出结论,较简捷地解决问题,但不便于思考.实际证题时常常两法兼用,先用分析法探索证明途径,然后再用综合法叙述出来. 失误与防范1.用分析法证明数学问题时,要注意书写格式的规范性,常常用“要证(欲证)…”“即要证…”“就要证…”等分析到一个明显成立的结论.2.利用反证法证明数学问题时,要假设结论错误,并用假设命题进行推理,没有用假设命题推理而推出矛盾结果,其推理过程是错误的.A 组 专项基础训练 (时间:40分钟)一、选择题1.若a ,b ∈R ,则下面四个式子中恒成立的是( )A.lg(1+a 2)>0B.a 2+b 2≥2(a -b -1)C.a 2+3ab >2b 2D.a b <a +1b +1答案 B解析 在B 中,∵a 2+b 2-2(a -b -1)=(a 2-2a +1)+(b 2+2b +1)=(a -1)2+(b +1)2≥0, ∴a 2+b 2≥2(a -b -1)恒成立.2.在△ABC 中,sin A sin C <cos A cos C ,则△ABC 一定是( )A.锐角三角形B.直角三角形C.钝角三角形D.不确定答案 C解析 由sin A sin C <cos A cos C 得, cos A cos C -sin A sin C >0, 即cos(A +C )>0,∴A +C 是锐角, 从而B >π2,故△ABC 必是钝角三角形.3.已知m >1,a =m +1-m ,b =m -m -1,则以下结论正确的是( )A.a >bB.a <bC.a =bD.a ,b 大小不定答案 B 解析 ∵a =m +1-m =1m +1+m,b =m -m -1=1m +m -1.而m +1+m >m +m -1,∴1m +1+m <1m +m -1,即a <b .4.已知a >0,b >0,则1a +1b +2ab 的最小值是( )A.2B.2 2C.4D.5答案 C解析 因为1a +1b +2ab ≥21ab+2ab =2(1ab+ab )≥4. 当且仅当1a =1b且1ab=ab , 即a =b =1时,取“=”.5.用反证法证明命题“若a ,b ∈N ,ab 能被3整除,那么a ,b 中至少有一个能被3整除”时,假设应为( )A.a ,b 都能被3整除B.a ,b 都不能被3整除C.b 不能被3整除D.a 不能被3整除答案 B解析 由反证法的定义可知,否定结论,即“a ,b 中至少有一个能被3整除”的否定是“a ,b 都不能被3整除”,故选B. 二、填空题6.6+7与22+5的大小关系为________. 答案6+7>22+ 5解析 要比较6+7与22+5的大小, 只需比较(6+7)2与(22+5)2的大小, 只需比较6+7+242与8+5+410的大小, 只需比较42与210的大小, 只需比较42与40的大小, ∵42>40,∴6+7>22+ 5.7.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是________. 答案 (5,7)解析 依题意,把“整数对”的和相同的分为一组,不难得知每组中每个“整数对”的和为n +1,且每组共有n 个“整数对”,这样的前n 组一共有n (n +1)2个“整数对”,注意到10(10+1)2<60<11(11+1)2,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).8.凸函数的性质定理:如果函数f (x )在区间D 上是凸函数,则对于区间D 内的任意x 1,x 2,…,x n ,有f (x 1)+f (x 2)+…+f (x n )n ≤f (x 1+x 2+…+x n n ),已知函数y =sin x 在区间(0,π)上是凸函数,则在△ABC 中,sin A +sin B +sin C 的最大值为________. 答案332解析 ∵f (x )=sin x 在区间(0,π)上是凸函数,且A 、B 、C ∈(0,π). ∴f (A )+f (B )+f (C )3≤f (A +B +C 3)=f (π3),即sin A +sin B +sin C ≤3sin π3=332,所以sin A +sin B +sin C 的最大值为332. 三、解答题9.已知非零向量a ⊥b ,求证:|a |+|b ||a -b |≤ 2. 证明 ∵a ⊥b ,∴a ·b =0.要证|a |+|b ||a -b |≤2,只需证:|a |+|b |≤2|a -b |, 平方得:|a |2+|b |2+2|a ||b |≤2(|a |2+|b |2-2a ·b ),只需证:|a |2+|b |2-2|a ||b |≥0,即(|a |-|b |)2≥0,显然成立.故原不等式得证.10.已知四棱锥S -ABCD 中,底面是边长为1的正方形,又SB =SD =2,SA =1.(1)求证:SA ⊥平面ABCD ;(2)在棱SC 上是否存在异于S ,C 的点F ,使得BF ∥平面SAD ?若存在,确定F 点的位置;若不存在,请说明理由.(1)证明 由已知得SA 2+AD 2=SD 2,∴SA ⊥AD .同理SA ⊥AB .又AB ∩AD =A ,∴SA ⊥平面ABCD .(2)解 假设在棱SC 上存在异于S ,C 的点F ,使得BF ∥平面SAD .∵BC ∥AD ,BC ⊄平面SAD .∴BC ∥平面SAD .而BC ∩BF =B ,∴平面SBC ∥平面SAD .这与平面SBC 和平面SAD 有公共点S 矛盾,∴假设不成立.故不存在这样的点F ,使得BF ∥平面SAD .B 组 专项能力提升(时间:30分钟)1.已知函数f (x )=(12)x ,a ,b 是正实数,A =f (a +b 2),B =f (ab ),C =f (2ab a +b),则A 、B 、C 的大小关系为 ( )A.A ≤B ≤CB.A ≤C ≤BC.B ≤C ≤AD.C ≤B ≤A答案 A 解析 ∵a +b 2≥ab ≥2ab a +b,又f (x )=(12)x 在R 上是减函数. ∴f (a +b 2)≤f (ab )≤f (2ab a +b),即A ≤B ≤C . 2.若a 、b 、c 是不全相等的正数,给出下列判断:①(a -b )2+(b -c )2+(c -a )2≠0;②a >b 与a <b 及a =b 中至少有一个成立;③a ≠c ,b ≠c ,a ≠b 不能同时成立.其中判断正确的个数是( ) A.0 B.1 C.2D.3 答案 C解析 ①②正确,③中,a ≠c ,b ≠c ,a ≠b 可能同时成立,如a =1,b =2,c =3.3.a 2+2+2a 2+2与22的大小关系是________. 答案 a 2+2+2a 2+2>2 2 解析 利用基本不等式,但不能取等号.4.已知二次函数f (x )=ax 2+bx +c (a >0)的图象与x 轴有两个不同的交点,若f (c )=0,且0<x <c 时,f (x )>0.(1)证明:1a是函数f (x )的一个零点; (2)试用反证法证明1a>c . 证明 (1)∵f (x )图象与x 轴有两个不同的交点,∴f (x )=0有两个不等实根x 1,x 2,∵f (c )=0,∴x 1=c 是f (x )=0的根,又x 1x 2=c a ,∴x 2=1a (1a≠c ), ∴1a 是f (x )=0的一个根.即1a是函数f (x )的一个零点.(2)假设1a <c ,又1a>0,由0<x <c 时,f (x )>0, 知f (1a )>0与f (1a )=0矛盾,∴1a≥c , 又∵1a ≠c ,∴1a>c . 5.已知数列{a n }满足:a 1=12,3(1+a n +1)1-a n =2(1+a n )1-a n +1,a n a n +1<0(n ≥1),数列{b n }满足:b n =a 2n +1-a 2n (n ≥1).(1)求数列{a n },{b n }的通项公式;(2)证明:数列{b n }中的任意三项不可能成等差数列.(1)解 由题意可知,1-a 2n +1=23(1-a 2n ). 令c n =1-a 2n ,则c n +1=23c n. 又c 1=1-a 21=34,则数列{c n }是首项为c 1=34, 公比为23的等比数列,即c n =34·(23)n -1, 故1-a 2n =34·(23)n -1⇒a 2n =1-34·(23)n -1. 又a 1=12>0.a n a n +1<0, 故a n =(-1)n -11-34·(23)n -1. b n =a 2n +1-a 2n =[1-34·(23)n ]-[1-34·(23)n -1] =14·(23)n -1. (2)证明 用反证法证明.假设数列{b n }存在三项b r ,b s ,b t (r <s <t )按某种顺序成等差数列,由于数列{b n }是首项为14,公比为23的等比数列, 于是有b r >b s >b t ,则只能有2b s =b r +b t 成立.∴2·14(23)s -1=14(23)r -1+14(23)t -1,两边同乘以3t-121-r,化简得3t-r+2t-r=2·2s-r3t-s. 由于r<s<t,∴上式左边为奇数,右边为偶数,故上式不可能成立,导致矛盾.故数列{b n}中任意三项不可能成等差数列.。
高考一轮复习全国卷本不等式公开课

解析:∵a b 0 ∴ab 0,a b 0,
a2 1 1 ab a(a-b)
=a(a-b) ab 1 1 ab a(a-b)
=
a(a-b)
1 a(a-b)
ab
1 ab
22=4
等号成立时,应有
a(a-b)=
1 a(a-b)
ab=
1 ab
∴a= 2,b= 2 . 2
总结:应用基本不等式求两个式子最值的和时, 等号必须同时成立.
备用练习
1.(2015·株洲联考)“a>0 且 b>0”是
“a+2 b≥ ab”成立的(
).
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析 a>0 且 b>0⇒a+2 b≥ ab,但a+2 b≥ ab a>0 且 b>0,只能推出 a≥0 且 b≥0.
1 基本不等式成立的条件:__a_≥_0_,__b_≥_0 .
2 等号成立的条件:当且仅当 _a_=_b__ 时取等号.
3其中称 a b 为正数a,b的 __算_术__平__均__值__,称 ab为
2 正数a,b的 __几__何__平_均__值___.
2.利用基本不等式求最值 已知x>0,y>0,则
∴x 1 2(当且仅当x 1时取等号) x
∴ x2
x 3x
1
=
x
1 1
3
2
1
3
1 5
,
x
即 x 的最大值为1,
x2 3x 1
高考数学一轮复习第一章第五讲基本不等式及其应用课件

(a2+b2) 2
图 1-5-2
解析:∵△ACD∽△CBD,∴CADD=CBDD, 即 CD= AD·BD= ab. ∵OC=A2B=AD+2 BD=a+2 b, ∴ ab≤a+2 b.故选 B.
答案:B
考点二 利用基本不等式求最值 考向 1 通过配凑法求最值
[例 2]设 0<x<23,则函数 y=4x(3-2x)的最大值为________.
2-x x·2-x x+2=2,
当且仅当2-x x=2-x x,即 x=1 时取等号,所以 y 的最小值为
2.故选 B.
答案:B
2.(考向 2)(2023 年罗湖区校级期中)已知 x>0,y>0,且 2x+ y=xy,则 x+2y 的最小值为( )
A.8
B.8 2
C.9
D.9 2
解析:x>0,y>0,且 2x+y=xy,可得:1x+2y=1,则 x+2y
错误. (3)连续使用基本不等式求最值,要求每次等号成立的条件一
致. (4)若 a≥b>0,则 a≥ a2+2 b2≥a+2 b≥ ab≥a2+abb≥b.
考点一 基本不等式的证明 [ 例 1](1)(2023 年广西一模) 《几何原本》中的“几何代数 法”(以几何方法研究代数问题)是西方数学家处理问题的重要依 据,通过这一原理,很多代数的公理或定理都能够通过图形实现
【变式训练】
如图1-5-2所示,线段AB为半圆的直径,O为
圆心,点 C 为半圆弧上不与 A ,B 重合的点. 作 CD⊥AB于点D,设 AD=a,BD=b,则下列不等
式中可以直接表示 CD≤OC 的是( )
A.a2+abb≤ ab
B. ab≤a+2 b
C.a+2 b≤
旧教材适用2023高考数学一轮总复习第七章不等式第4讲基本不等式课件

角度
利用消元法求最值
例 3 (1)(2021·武汉模拟)若正数 x,y 满足 x+4y-xy=0,则x+4 y的最
大值为( )
A.25 B.49 C.12 D.47
答案 B
解析 因为正数 x,y 满足 x+4y-xy=0,所以 y=x-x 4>0,解得 x>4,
所以x+4 y=x+4x-x 4=x+1+4 x-4 4=x-4+4x-4 4+5
(2)(2021·甘 肃 武 威 模 拟 ) 设
x>0 , 则 函 数
y
=x
+
2 2x+1
- 32
的
最
小
值
为
0.
解析 y=x+2x+2 1-32=x+12+x+1 12-2≥2
x+21·x+1 12-2=0,当
且仅当 x+12=x+1 12,即 x=12时等号成立.所以函数的最小值为 0.
通过拼凑法利用基本不等式求最值的策略 拼凑法的实质在于代数式的灵活变形,拼系数、凑常数是关键,利用拼 凑法求解最值应注意以下几个方面的问题: (1)拼凑的技巧,以整式为基础,注意利用系数的变化以及等式中常数的 调整,做到等价变形. (2)代数式的变形以拼凑出和或积的定值为目标. (3)拆项、添项应注意检验利用基本不等式的前提.
1.(2022·岳阳一中月考)已知 a>b>0,则 2a+a+4 b+a-1 b的
最小值为( )
A.6
B.4
C.2 3
D.3 2
答案 A
解析 因为 a>b>0,所以 a+b>0,a-b>0, 所以 2a+a+4 b+a-1 b=a+b+a+4 b+a-b+a-1 b≥2 (a+b)·a+4 b +2 (a-b)·a-1 b=4+2=6,当且仅当 a+b=a+4 b且 a-b=a-1 b, 即 a=32,b=12时等号成立.所以 2a+a+4 b+a-1 b的最小值为 6.
高考理科数学(人教A版)一轮复习课件72基本不等式及其应用

1
∴ + =
2
2
+
当且仅当 =
1
2
2
(x+2y)= +
2
+5≥2·
2
2
· +5=4+5=9.
1
,即 x=y= 时等号成立,
3
1
所以2+ 的最大值为9.
故选 C.
(2)∵正项等比数列{an}的公比为 3,且 aman=922 ,
a2·
3n-2=22 ·3m+n-4=922 ,
∴2x+y=xy.
1
1
1
1
∴ +x+2y= + 2xy≥2
1
1
· = 2.
2
-9-
考点1
考点2
考点3
思考利用基本不等式证明不等式的方法技巧有哪些?
解题心得利用基本不等式证明不等式时,首先要观察题中要证明
的不等式的形式,若不能直接使用基本不等式,则考虑利用拆项、
配凑等方法对不等式进行变形,使之达到能使用基本不等式的条件;
(1)求a的值;
1
2
1
1
(2)若正数 x,y 满足 + =a.证明:+x+2y≥ 2.
-8-
考点1
考点2
考点3
解:(1)由f(x)=|x-1|-|x+a|≤|x-1-x-a|=|a+1|,
又f(x)≤2恒成立,
∴|a+1|≤2.
∴-3≤a≤1.
∵a∈N*,
∴a=1.
2025年高考数学复习核心考点全题型突破(新教材新高考)第03讲 基本不等式(解析版)

A.
f
(x)
x2
1 x2
B. f (x) cos x 1 (0 x )
cos x
2
C. f (x) x2 4 x2 3
D.
f
(x)
3x
4 3x
2
【答案】AD
【详解】对于选项
A:∵x2>0,∴由基本不等式可得 x2
1 x2
2 ,当且仅当
x2
1 x2
,即
x=1
或
x= 1时,
等号成立,故选项 A 正确;
x 23
1 2 ,当且仅当 x2 3
x2 3
1 ,
x2 3
即 x2 2 时,等号成立,显然不可能取到,故选项 C 不正确;
对于选项
D:∵3x>0,∴由基本不等式可得
f
(x)
3x
4 3x
2
2
3x
4 3x
2 2 ,当且仅当 3x
4 3x
,即 x=
log32 时,等号成立,故选项 D 正确. 故选:AD.
D.若
a,
b
Rห้องสมุดไป่ตู้
,且
ab
0
,则
b a
a b
b a
a b
2
b a
a b
2
【答案】D
【详解】对于 A 选项,当 ab 0 时, b a 0 ,所以 A 选项错误. ab
对于 B 选项,如 x 时, cos x 1 2 0 ,所以 B 选项错误. cos x
对于
C
选项,由于
x
精练核心考点
1.(2023·全国·高三专题练习)下列不等式的证明过程正确的是( )
A.若 a,b R ,则 b a 2 b a 2 a b ab
2021年高考数学 第六章 第4课时 基本不等式知能演练轻松闯关 新人教A版

2021年高考数学第六章第4课时基本不等式知能演练轻松闯关新人教A版1.(xx·高考福建卷)下列不等式一定成立的是( )A.lg(x2+14)>lg x(x>0)B.sin x+1sin x≥2(x≠kπ,k∈Z)C.x2+1≥2|x|(x∈R)D.1x2+1>1(x∈R)解析:选C.取x=12,则lg⎝⎛⎭⎪⎫x2+14=lg x,故排除A;取x=32π,则sin x=-1,故排除B;取x=0,则1x2+1=1,故排除D.2.(xx·河北教学质量检测)“a2+b2ab≤-2”是“a>0且b<0”的( )A.必要不充分条件B.充要条件C.充分不必要条件D.既不充分也不必要条件解析:选A.a2+b2ab≤-2⇔a2+b2ab+2=(a+b)2ab≤0⇔ab<0⇔⎩⎨⎧a<0b>0或⎩⎨⎧a>0b<0.3.(xx·江南十校联考)已知a>0,b>0,a,b的等比中项是1,且m=b+1 a ,n=a+1b,则m+n的最小值是( )A.3 B.4 C.5 D.6解析:选B.由已知得ab=1,m+n=a+b+1a+1b=2(a+b)≥4ab=4,当且仅当a=b=1时取等号,m+n取得最小值4.4.(xx·高考福建卷)若2x+2y=1,则x+y的取值范围是( ) A.[0,2] B.[-2,0]C.[-2,+∞) D.(-∞,-2]解析:选D.∵2x+2y≥22x+y,2x+2y=1,∴22x+y≤1,∴2x+y≤14=2-2,∴x+y≤-2,即(x+y)∈(-∞,-2].5.(xx·浙江十校联考)若正数x,y满足4x2+9y2+3xy=30,则xy的最大值是( )A.43B.53C.2 D.5 4解析:选C.由x>0,y>0知4x2+9y2+3xy≥2×(2x)×(3y)+3xy(当且仅当2x=3y时等号成立),∴12xy+3xy≤30,即xy≤2.6.若0<x<25,则y=2x-5x2的最大值为________.解析:y=2x-5x2=x(2-5x)=15·5x·(2-5x).∵0<x<25,∴5x<2,2-5x>0,∴5x(2-5x)≤(5x+2-5x2)2=1,∴y≤15,当且仅当5x=2-5x,即x=15时,y max=15.答案:1 57.某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为y=-x2+18x-25(x∈N*).则当每台机器运转__________年时,年平均利润最大,最大值是__________万元.解析:每台机器运转x年的年平均利润为yx=18-(x+25x),而x>0,故yx≤18答案:5 88.已知函数f (x )=x +p x -1(p 为常数,且p >0),若f (x )在(1,+∞)上的最小值为4,则实数p 的值为________.解析:由题意得x -1>0,f (x )=x -1+p x -1+1≥2p +1,当且仅当x =p+1时取等号,因为f (x )在(1,+∞)上的最小值为4,所以2p +1=4,解得p =94. 答案:949.设a 、b 均为正实数,求证:1a 2+1b2+ab ≥2 2.证明:由于a 、b 均为正实数, 所以1a 2+1b 2≥21a 2·1b 2=2ab, 当且仅当1a 2=1b2,即a =b 时等号成立.又因为2ab+ab ≥22ab·ab =22,当且仅当2ab=ab 时等号成立,所以1a 2+1b 2+ab ≥2ab+ab ≥22,当且仅当⎩⎪⎨⎪⎧1a 2=1b 2,2ab =ab即a =b =42时取等号.10.(1)当x <32时,求函数y =x +82x -3的最大值;(2)设0<x <2,求函数y =x (4-2x )的最大值. 解:(1)y =12(2x -3)+82x -3+32=-⎝⎛⎭⎪⎫3-2x 2+83-2x +32. 当x <32时,有3-2x >0,∴3-2x 2+83-2x≥23-2x 2·83-2x=4, 当且仅当3-2x 2=83-2x ,即x =-12时取等号. 于是y ≤-4+32=-52,故函数的最大值为-52.(2)∵0<x <2, ∴2-x >0,∴y=x(4-2x)=2·x(2-x)≤2·x+2-x2=2,当且仅当x=2-x,即x=1时取等号,∴当x=1时,函数y=x(4-2x)的最大值为 2.[能力提升]1.设a>0,b>0,且不等式1a+1b+ka+b≥0恒成立,则实数k的最小值等于( )A.0 B.4C.-4 D.-2解析:选C.由1a+1b+ka+b≥0得k≥-(a+b)2ab,而(a+b)2ab=ba+ab+2≥4(a=b时取等号),所以-(a+b)2ab≤-4,因此要使k≥-(a+b)2ab恒成立,应有k≥-4,即实数k的最小值等于-4.2.(xx·浙江嘉兴调研)已知正实数a,b满足a+2b=1,则a2+4b2+1 ab 的最小值为( )A.72B.4C.16136D.172解析:选D.因为a>0,b>0,1=a+2b≥22ab,所以ab≤18,当且仅当a=2b=12时取等号.又因为a2+4b2+1ab≥2a·(2b)+1ab=4ab+1ab,令t=ab,所以f(t)=4t+1t,因为f(t)在⎝⎛⎦⎥⎤0,18上单调递减,所以f(t)min=f⎝⎛⎭⎪⎫18=172,此时a=2b=12,故选D.3.规定记号“⊗”表示一种运算,即a⊗b=ab+a+b(a、b为正实数).若1⊗k=3,则k的值为________,此时函数f(x)=k⊗xx的最小值为________.解析:1⊗k=k+1+k=3,即k+k-2=0,∴k=1或k=-2(舍去).∴k=1.f(x)=1⊗xx=x+x+1x=1+x+1x≥1+2=3,当且仅当x=1x,即x=1时等号成立.答案:1 34.(原创题)设a≥b>0,a+b≤22,(a-b)2=4ab,则log(a-1)(b+1)=________.解析:(a +b )2=(a -b )2+4ab =4ab+4ab ≥8,①∴a +b ≥2 2.又a +b ≤22,∴a +b =22,② 由①中等号成立条件得ab =1,③联立②、③得a =2+1,b =2-1,log (a -1)(b +1)=1. 答案:15.正数x ,y 满足1x +9y=1.(1)求xy 的最小值; (2)求x +2y 的最小值. 解:(1)由1=1x +9y ≥21x ·9y ,得xy ≥36,当且仅当1x =9y,即y =9x =18时取等号,故xy 的最小值为36.(2)由题意可得x +2y =(x +2y )⎝⎛⎭⎪⎫1x +9y =19+2y x +9x y ≥19+22yx·9xy=19+62,当且仅当2yx=9xy,即9x 2=2y 2时取等号,故x +2y 的最小值为19+6 2.6.(选做题)某食品厂定期购买面粉,已知该厂每天需用面粉6吨,每吨面粉的价格为1 800元,面粉的保管等其他费用为平均每吨每天3元,购买面粉每次需支付运费900元.(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?(2)某提供面粉的公司规定:当一次购买面粉不少于210吨时,其价格可享受9折优惠,问该厂是否考虑利用此优惠条件?请说明理由.解:(1)设该厂应每隔x天购买一次面粉,其购买量为6x吨,由题意可知,面粉的保管等其他费用为3[6x+6(x-1)+6(x-2)+…+6×1]=9x(x+1).设平均每天所支付的总费用为y1元,则y1=[9x(x+1)+900]x+1 800×6=900x+9x+10 809≥2900x·9x+10 809=10 989,当且仅当9x=900x,即x=10时取等号.即该厂应每隔10天购买一次面粉,才能使平均每天所支付的总费用最少.(2)因为不少于210吨,每天用面粉6吨,所以至少每隔35天购买一次面粉.设该厂利用此优惠条件后,每隔x(x≥35)天购买一次面粉,平均每天支付的总费用为y2元,则y2=1x[9x(x+1)+900]+6×1 800×0.90=900x+9x+9 729(x≥35).令f (x )=x +100x(x ≥35),x 2>x 1≥35,则f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+100x 1-⎝ ⎛⎭⎪⎫x 2+100x 2=(x 2-x 1)(100-x 1x 2)x 1x 2∵x 2>x 1≥35,∴x 2-x 1>0,x 1x 2>0,100-x 1x 2<0, ∴f (x 1)-f (x 2)<0,f (x 1)<f (x 2),即f (x )=x +100x,当x ≥35时为增函数,∴当x =35时,f (x )有最小值,此时y 2<10 989.∴该厂应接受此优惠条件.37396 9214 鈔! 31229 79FD 秽21322 534A 半•Kz;20344 4F78 佸Ms25425 6351 捑%。
2021年高考数学理新课标A版一轮总复习开卷速查必修部分36基本不等式

2021年高考数学理新课标A版一轮总复习开卷速查必修部分36基本不等式1.下列命题正确的是( )A.若x≠kπ,k∈Z,则sin2x+1sin2x≥4B.若a<0,则a+4a≥-4C.若a>0,b>0,则lg a+lg b≥2lg a·lg bD.若a<0,b<0,则ab+ab≥2解析:当sin2x=1时,1+1=2<4,所以A错;若a<0,则a+4a≤-4,B错;因为lg a,lg b可以小于零,C错;由a<0,b<0,所以ba,ab都大于零,D正确.答案:D2.若正实数x,y满足x+y+1x+1y=5,则x+y的最大值是( )A.2 B.3 C.4 D.5解析:∵xy≤x+y24,x>0,y>0,∴1xy≥4x +y2,x +y xy ≥4x +y. ∴x +y +4x +y ≤5.设x +y =t ,即t +4t≤5,得到t 2-5t +4≤0,解得1≤t ≤4,∴x +y 的最大值是4.答案:C3.已知a ,b ∈R ,且ab ≠0,则下列结论恒成立的是( )A .a +b ≥2abB.a b +ba≥2C.⎪⎪⎪⎪⎪⎪a b +b a ≥2 D.a 2+b 2>2ab 解析:当a ,b 都是负数时,A 不成立,当a ,b 一正一负时,B 不成立,当a =b 时,D 不成立,因此只有C 是正确的.答案:C4.若正数a ,b 满足1a +1b =1,则1a -1+9b -1的最小值为( )A .1 B.6 C .9 D.16解析:方法一:因为1a +1b =1,所以a +b =ab ⇒(a -1)(b -1)=1,所以1a -1+9b -1≥21a -1·9b -1=2×3=6.方法二:因为1a +1b =1,所以a +b =ab ,1a -1+9b -1=b -1+9a -9ab -a -b +1=b +9a-10=(b +9a )⎝ ⎛⎭⎪⎫1a +1b -10≥16-10=6.方法三:因为1a +1b =1,所以a -1=1b -1,所以1a -1+9b -1=(b -1)+9b -1≥29=2×3=6. 答案:B5.设a >0,b >0.若3是3a 与32b 的等比中项,则2a +1b的最小值为( )A .8B.4 C .1D.14解析:由题意可知3=3a 32b =3a +2b ,即a +2b =1. 因为a >0,b >0,所以2a +1b =⎝ ⎛⎭⎪⎫2a +1b (a +2b )=a b +4ba+4≥2a b ·4ba+4=8,当且仅当a b =4b a ,即a =2b =12时取“=”. 答案:A6.若x ,y ∈(0,2]且xy =2,使不等式a (2x +y )≥(2-x )(4-y )恒成立,则实数a 的取值范围为( )A .a ≤12B.a ≤2C .a ≥2 D.a ≥12解析:由x ,y ∈(0,2],xy =2,得a ≥2-x 4-y2x +y=10-22x +y2x +y=102x +y-2. 又由2x +y ≥22xy =4,∴a ≥12.答案:D7.已知正数x ,y 满足x +2y =2,则x +8yxy的最小值为__________.解析:由已知得x +2y 2=1,则x +8y xy =1y +8x =⎝ ⎛⎭⎪⎫1y +8x ⎝ ⎛⎭⎪⎫x +2y 2=12⎝ ⎛⎭⎪⎫10+x y +16y x ≥12(10+216)=9,当且仅当x =43,y =13时取等号.答案:98.已知集合A ={x |x 2-2x -3>0},B ={x |ax 2+bx +c ≤0},若A ∩B ={x |3<x ≤4},A ∪B =R ,则b 2a +ac2的最小值为__________.解析:∵x 2-2x -3>0,∴x <-1或x >3. ∵A ∩B ={x |3<x ≤4},A ∪B =R , ∴B ={x |-1≤x ≤4}.∴-1和4是ax 2+bx +c =0的根.∴-1+4=-b a ,(-1)×4=ca .∴b =-3a ,c =-4a ,且a >0.∴b 2a +ac 2≥2b 2c 2=2b c =-6a -4a =32, 当且仅当b 2a =ac 2取等号.答案:329.若实数a ,b ,c 满足2a +2b =2a +b,2a +2b +2c =2a +b +c ,则c 的最大值是__________.解析:由基本不等式得2a +2b ≥22a 2b =2×2a +b 2,即2a +b ≥2×2a +b 2,所以2a +b ≥4.令t =2a +b ,由2a +2b +2c =2a +b +c 可得2a +b +2c =2a +b ·2c ,所以2c =t t -1=1+1t -1,由t ≥4,得1<t t -1≤43,即1<2c ≤43,所以0<c ≤log 243=2-log 23,故答案为2-log 23.答案:2-log 2310.设关于x 的不等式|x -2|<a (a ∈R )的解集为A ,且32∈A ,-12∉A .(1)∀x ∈R ,|x -1|+|x -3|≥a 2+a 恒成立,且a ∈N ,求a 的值;(2)若a +b =1,求13|b |+|b |a的最小值,并指出取得最小值时a 的值. 解析:(1)∵32∈A ,-12∉A ,∴⎪⎪⎪⎪⎪⎪32-2<a ,⎪⎪⎪⎪⎪⎪-12-2≥a ,即12<a ≤52.∵|x -1|+|x -3|≥|(x -1)-(x -3)|=2, ∴a 2+a -2≤0,∴-2≤a ≤1,∴12<a ≤1.又a ∈N ,∴a =1.(2)∵12<a ≤52,∴13|b |+|b |a =a +b 3|b |+|b |a =b 3|b |+a 3|b |+|b |a ≥-13+2a 3|b |×|b |a =23-13.当且仅当⎩⎨⎧ b <0,a 2=3b 2,即⎩⎨⎧a =33-1,b =-13-1时上式取等号.又∵12<33-1=3+32≤52,∴13|b |+|b |a 的最小值是23-13,取最小值时a =3+32. B 级 能力提升练11.已知正实数a ,b 满足a +2b =1,则a 2+4b 2+1ab的最小值为( )A.72 B.4C.16136D.172解析:因为1=a +2b ≥22ab ,所以ab ≤18,当且仅当a =2b =12时取等号.又因为a 2+4b 2+1ab≥2a 2·4b 2+1ab=4ab +1ab .令t =ab ,所以f (t )=4t +1t 在⎝ ⎛⎦⎥⎤0,18单调递减,所以f (t )min =f ⎝ ⎛⎭⎪⎫18=172.此时a =2b =12.答案:D12.已知函数y =x -4+9x +1(x >-1),当x =a 时,y 取得最小值b ,则a +b =( )A .-3 B.2 C .3D.8解析:y =x -4+9x +1=x +1+9x +1-5,由x >-1,得x +1>0,9x +1>0,所以由基本不等式得y =x +1+9x +1-5≥2x +1×9x +1-5=1,当且仅当x +1=9x +1,即(x +1)2=9,所以x +1=3,即x =2时取等号,所以a =2,b =1,a +b =3.答案:C13.[xx·武汉模拟]经观测,某公路段在某时段内的车流量y (万辆/小时)与汽车的平均速度v (千米/小时)之间有函数关系y =92vv 2+3v +1 600(v >0).(1)在该时段内,当汽车的平均速度v 为多少时车流量y 最大?最大车流量为多少?(2)为保证在该时段内车流量至少为1万辆/小时,则汽车的平均速度应控制在什么范围内?解析:(1)y =92vv 2+3v +1 600=92v +1 600v+3≤922v ·1 600v+3=9283≈1.108. 当v =1 600v,即v =40千米/小时,车流量最大,最大值约为1.108万辆/小时.(2)据题意有92vv 2+3v +1 600≥1,化简得v 2-89v +1 600≤0,即(v -25)(v -64)≤0,所以25≤v ≤64.所以汽车的平均速度应控制在[25,64](千米/小时)这个范围内.14.为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y (单位:毫克/立方米)随着时间x (单位:天)变化的函数关系式近似为y =⎩⎪⎨⎪⎧168-x -1,0≤x ≤4,5-12x ,4<x ≤10.若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a (1≤a ≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a 的最小值(精确到0.1,参考数据:2取1.4).解析:(1)因为一次喷洒4个单位的净化剂,所以浓度f (x )=4y =⎩⎨⎧648-x -4,0≤x ≤4,20-2x ,4<x ≤10.则当0≤x ≤4时,由648-x-4≥4,解得0≤x ≤8, 所以此时0≤x ≤4.当4<x ≤10时,由20-2x ≥4,解得x ≤8, 所以此时4<x ≤8.综合得0≤x ≤8,若一次投放4个单位的净化剂,则有效净化时间可达8天. (2)设从第一次喷洒起,经x (6≤x ≤10)天, 浓度g (x )=2⎝ ⎛⎭⎪⎫5-12x +a ⎣⎢⎡⎦⎥⎤168-x -6-1=10-x +16a 14-x -a =(14-x )+16a14-x-a -4≥214-x·16a14-x-a -4=8a -a -4.因为14-x ∈[4,8],a-4.令8a-a-4≥4,解得24-162≤a≤4,所以a的最小值为24-162≈1.6.31124 7994 禔32464 7ED0 绐23618 5C42 层38715 973B 霻Q30678 77D6 矖€23703 5C97 岗^(x .27106 69E2 槢。
