工资问题数学建模
数学建模-聘用方案问题

聘用方案问题问题:(1)某服务部门一周中每天需要不同数目的雇员:周一到周四每天至少50人, 周五和周日每天至少80人, 周六至少90人. 现规定应聘者需连续工作5日, 试确定聘用方案, 即周一到周日每天聘多少人, 使在满足需求条件下聘用总人数最少.(2)上面指的是全时雇员 (一天工作8小时),如果可以用两个临时聘用的半时雇员(一天工作4小时, 不需要连续工作)代替一个全时雇员,但规定半时雇员的工作量不得超过总工作量的四分之一. 又设全时雇员和半时雇员每小时的酬金分别为5元和3元,试确定聘用方案, 使在满足需求的条件下所付酬金总额最小。
问题(1)⏹ 问题分析要求应聘者需连续工作五日,那么,为了模型的建立,我们令每个人工作且仅连续工作五日,且认为每个人都长期工作,则每一周都是等同的。
设从星期i 开始工作的人有x i 个,那么他他将工作到星期(i+4),当i+4>7时则工作到下一周的星期(i-3),这同时意味着他在本周的星期1,…,i-3,也工作了。
例如星期一的x 1个人工作的日子为星期1,2,3,4,5,星期五的x 5个人工作的日子为星期1,2,5,6,7。
其他天的情况同理可知。
那么星期一工作的人有x1+x4+x5+x6+x7个,要求星期一工作的人数至少为50,那么就有x1+x4+x5+x6+x7>=50,其他的日子也可以同样地写出来。
于是就有了下面(模型建立中)的限制条件。
我们要求的是总人数最少,即目标函数z=∑x i 7i=1最小。
设定x i >=0,且为整数。
⏹ 模型建立Min x1+x2+x3+x4+x5+x6+x7 s.t.x1+x4+x5+x6+x7>=50 x1+x2+x5+x6+x7>=50 x1+x2+x3+x6+x7>=50 x1+x2+x3+x4+x7>=50 x1+x2+x3+x4+x5>=80 x3+x4+x5+x6+x7>=80 x2+x3+x4+x5+x6>=90 x1>=0 x2>=0 x3>=0 x4>=0x5>=0x6>=0x7>=0⏹编写程序在lindo软件下编写程序Min x1+x2+x3+x4+x5+x6+x7s.t.1) x1+x4+x5+x6+x7>=502) x1+x2+x5+x6+x7>=503) x1+x2+x3+x6+x7>=504) x1+x2+x3+x4+x7>=505) x1+x2+x3+x4+x5>=806) x3+x4+x5+x6+x7>=807) x2+x3+x4+x5+x6>=908) x1>=0x2>=0x3>=0x4>=0x5>=0x6>=0x7>=0endgin 7⏹运行结果Global optimal solution found.Objective value: 90.00000Objective bound: 90.00000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 5Variable Value Reduced Cost X1 0.000000 1.000000 X2 10.00000 1.000000 X3 30.00000 1.000000 X4 10.00000 1.000000 X5 30.00000 1.000000 X6 10.00000 1.000000 X7 0.000000 1.000000Row Slack or Surplus Dual Price1 90.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.000000 10 10.00000 0.000000 11 30.00000 0.000000 12 10.00000 0.000000 13 30.00000 0.000000 14 10.00000 0.000000 15 0.000000 0.000000⏹ 解释结果使得z=∑x i 7i=1最小且满足限制条件的x i 取值为x 1=0,x 2=10,x 3=30,x 4=10,x 5=30,x 6=10,x 7=0,Min z=90.⏹ 具体方案由以上讨论得,使得周一到周四每天至少50人, 周五和周日每天至少80人, 周六至少90人且聘用人数最少的方案是:周一开始的不聘,周二开始工作的聘10人,周三开始工作的聘30人,周四开始工作的聘10人,周五开始工作的聘30人,周六开始工作的聘10人,周日开始工作的不聘。
数学建模-人员安排问题及参考答案

Reduced Cost 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 19200.00 19200.00 19200.00 19200.00 19200.00 19200.00
目标函数值:203400 元; 费用增加量:203400-198000=5400 元; 当重新安排工程师甲到工期 2 时的损失不超过 5400 元时, 可以将 他的工作重新安排。 5.2 问题三 模型构成: 增加约束条件: (不一起工作可理解为不同时在一个项目中工 作) : 0 x2 jk x3 jk 1 , j 1, 2,3 , k 1, 2,3 ; 求解: 最 优 解 : x123 x131 x132 1 , x213 x222 x231 1 , x313 x331 x332 1 ,
Value 3000.000 3500.000 3200.000 3900.000 3.000000 2.000000 5.000000 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000 1.000000 0.000000 0.000000 1.000000 1.000000 0.000000 0.000000 0.000000 1.000000 0.000000 1.000000 0.000000 0.000000 0.000000 1.000000 0.000000
数学建模模拟本科组题目
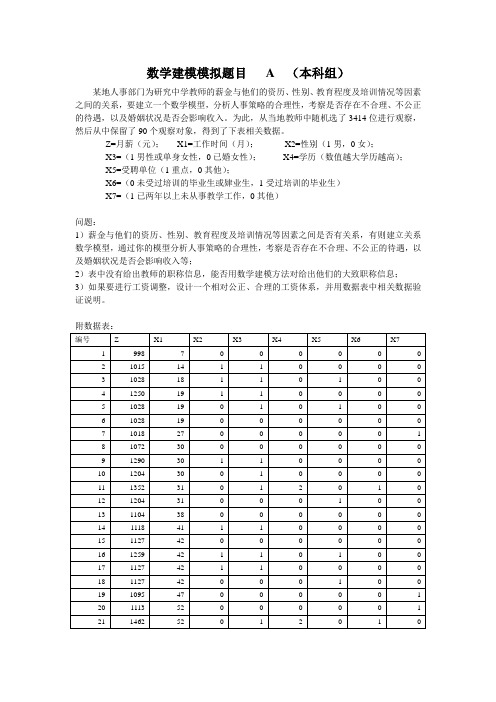
数学建模模拟题目 A (本科组)某地人事部门为研究中学教师的薪金与他们的资历、性别、教育程度及培训情况等因素之间的关系,要建立一个数学模型,分析人事策略的合理性,考察是否存在不合理、不公正的待遇,以及婚姻状况是否会影响收入。
为此,从当地教师中随机选了3414位进行观察,然后从中保留了90个观察对象,得到了下表相关数据。
Z=月薪(元);X1=工作时间(月);X2=性别(1男,0女);X3=(1男性或单身女性,0已婚女性);X4=学历(数值越大学历越高);X5=受聘单位(1重点,0其他);X6=(0未受过培训的毕业生或肄业生,1受过培训的毕业生)X7=(1已两年以上未从事教学工作,0其他)问题:1)薪金与他们的资历、性别、教育程度及培训情况等因素之间是否有关系,有则建立关系数学模型,通过你的模型分析人事策略的合理性,考察是否存在不合理、不公正的待遇,以及婚姻状况是否会影响收入等;2)表中没有给出教师的职称信息,能否用数学建模方法对给出他们的大致职称信息;3)如果要进行工资调整,设计一个相对公正、合理的工资体系,并用数据表中相关数据验证说明。
附数据表:第五次数学建模模拟本科组B题设有一个靶标如下,取1个边长为100mm的正方形,分别以四个顶点(对应为A、C、D、E)为圆心,12mm为半径作圆。
以AC边上距离A点30mm处的B为圆心,12mm为半径作圆,如图1所示。
图 1 靶标示意图用分辨率为1024*768的数码相机对靶标进行拍摄。
图2是某次拍摄得到的图像。
图2 靶标的像靶标的像有5个类似椭圆形状的黑色块,分别在各个黑色块内任取一点,记得到的位置为P1(x1,y1), P2(x2,y2), P3(x3,y3), P4(x4,y4), P5(x5,y5)。
请建立模型设计一个算法,以确定P1,P2,P3,P4,P5的原像分别位于A, B, C, D,。
互付工资数学建模实例

互付工资数学建模实例互付工资,作为一种新型的薪酬支付方式,近年来在我国逐渐受到关注。
它是指两个或多个企业之间,为各自员工提供等值的服务或产品,从而实现工资的互相支付。
这种模式有利于缓解企业资金压力,提高员工福利,促进企业间合作。
本文将通过数学建模的方法,对互付工资进行深入分析,以期为实际操作提供有益的参考。
一、互付工资的数学建模方法互付工资的数学建模,可以从以下几个方面入手:1.确定合作企业数量:根据企业间的合作关系,确定参与互付工资的企业数量。
2.设定工资标准:结合企业规模、行业特点等因素,为每个企业的员工设定合理的工资标准。
3.制定互付规则:明确互付工资的支付方式、周期等,确保各企业间的公平与合理。
4.建立动态模型:根据企业业务发展、市场变化等因素,构建动态的工资互付模型。
二、模型应用与分析以某地区四个企业为例,分别为A、B、C、D。
企业间合作关系如下:A→B:员工工资比例为2:3B→C:员工工资比例为4:5C→D:员工工资比例为6:7D→A:员工工资比例为8:9根据以上关系,可以计算出各企业间的互付工资比例。
以A企业为例,其员工工资分为两部分,一部分来自B企业的支付,另一部分来自D企业的支付。
计算公式如下:A企业员工工资=A企业工资总额×(1+B企业支付比例/D企业支付比例)同理,可以计算出其他企业的员工工资。
在此基础上,对模型进行动态分析,观察企业间互付工资的影响。
三、模型优缺点及改进方向1.优点:互付工资模型有利于缓解企业资金压力,提高员工福利,促进企业间合作。
同时,通过数学建模,可以更加精确地计算出各企业的工资支付比例,保证公平性与合理性。
2.缺点:模型较为复杂,对企业的管理要求较高。
此外,模型的稳定性受企业间合作关系、市场环境等因素影响较大,可能需要定期调整。
3.改进方向:简化模型,降低管理成本;加强企业间的沟通与合作,提高模型的稳定性;根据实际情况,灵活调整互付工资比例。
工资问题数学建模

对工资待遇问题的探讨工资支付,就是工资的具体发放办法。
包括如何计发在制度工作时间内职工完成一定的工作量后应获得的报酬,或者在特殊情况下的工资如何支付等问题。
主要包括:工资支付项目、工资支付水平、工资支付形式、工资支付对象、工资支付时间以及特殊情况下的工资支付等。
工资支付的项目,一般包括计时工资、计件工资、奖金、津贴和补贴、延长工作时间的工资报酬以及特殊情况下支付的工资。
本文我们讨论的是对大学教师工资的分配问题,原工资支付系统导致抱怨的原因大致分为两个方面:1. 称与工龄相同的教师的工资相差太大,则工资低的人会抱怨。
2. 能力高、贡献大的人希望得到更高的收入,否则则会产生抱怨。
我们对两篇获奖论文进行了分析摘要总结。
论文1:摘要:该模型通过选取两个指标作为评价某工资分配方案优劣的标准,并以该指标确定三种不同的评价函数,建立规划模型。
通过对规划问题求解,可以找到较为合理的工资过渡方案。
在年工资总额增长3%,人年工资增长率介于1%~3%间的条件下,通过对工资调整的几个原则的逐步考虑,由较为简化的单一模型发展到较为复杂的分级非线性模型,使模型在符合所有的原则的前提下,做到了过渡过程尽可能平稳有序,达到了较为满意的结果。
知识:最小二乘法:用于直线拟合;偏差平方和:实际值与理论值差的平方和;无序度函数:Entropy 定义为某数列的逆序值。
线性规划假设:工资增长总额为定值,问题转化为:如何将增长额合理地分配到各教员,使其尽可能接近目标方案的优化问题。
原则:1.每年所有教员工资须有所提升。
2.教员应从晋级中获得实质性利益,如果一个人在最短的时间内得到晋级,其工资的增长应大致相当于七年正常(未晋级)工资的增长。
3.按时(每7至8年)得到晋级且工作25年以上的教员在退休时工资应大致相当于刚工作博士工资的两倍。
4.对于相同级别的教员,工作年限长,经验多的应得到更多的报酬,但是这种由工作年限长短导致的工资差异应逐渐变小。
消费与工资模型数学建模

消费与工资模型数学建模
消费与工资模型的数学建模可以使用线性回归模型来实现。
具体步骤如下:
1. 收集数据,包括工资和消费的相关数据。
2. 将数据分成训练集和测试集。
3. 使用训练集数据训练线性回归模型。
4. 使用测试集数据评估模型的准确性和可靠性。
5. 如果模型准确性和可靠性较高,则使用该模型进行预测。
具体地,假设工资是自变量,消费是因变量。
则线性回归模型的公式为:
```
Y = a + bX + ε
```
其中,Y表示消费, X表示工资, a表示截距, b表示斜率, ε表示误差。
线性回归模型可以用最小二乘法拟合数据,并获得线性关系的系数a和b。
系数a表示在工资为0时,预测消费的值。
而系数b表示每增加1元工资,消费会相应增加多少元。
通过建立消费与工资的线性回归模型,我们可以预测消费在不同工资水平下的变化。
进一步应用该模型,可以评估不同消费政策的影响,并制定相应的措施。
数学建模教师薪金问题

数学建模论文题目:教师薪金问题教师薪金问题摘要本文是一个关于建立教师薪金影响因素的回归模型。
在模型中我们考虑到了题目给出的所有因素,通过题目给出的数据,发现这七个变量之间与因变量均呈线性关系,因此我们初步的建立了一般的线性回归模型,然后我们用MATLAB软件求解。
我们首先利用MATLAB软件作出薪金与老师工作时间的散点图,然后假设工作时间与教师薪金为线性关系,通过对解出的数据进行分析,我们发现模型存在缺陷,有些变量对因变量的影响不显著,这也就说明性别和婚姻状况上的差异对所调查的教师的薪金影响较小。
经过对模型的各个变量的逐步回归和作残差图,从影响系数的表图中我们得出了工作时间和学历对教师的薪金的影响最大。
关键词:统计回归模型 MATLAB软件残差分析法逐步回归一、问题提出某地人事部门为研究中学教师的薪金与他们的资历,性别,教育程度及培训情况等因素之间的关系,要建立一个数学模型,分析人士策略的合理,特别是考虑女教师是否受到不公平的待遇,以及他们的婚姻状况是否会影响收入。
为此,从当地教师中随机选了3414位进行观察,然后从中保留了90个观察对象,得到了下表给出的相关数据。
尽管这些数据具有一定的代表性,但是仍有统计分析的必要。
现将表中数据的符号介绍如下:Z~月薪(单位:元);X1~工作时间(以月计);X2=1~男性,X2=0~女性;X3=1~男性或单身女性,X3=0~已婚女性;X4~学历(取值0~6,值越大表示学历越高);X5=1~受雇于重点中学,X5=0~其它;;X6=1~受过培训的毕业生,X6=0~未受过培训的毕业生或受过培训的肄业生;X7=1~以两年以上未从事教学工作,X7=0~其他。
注意组合(X2,X3)=(1,1),(0,1),(0,0)的含义。
(1)进行变量选择,建立变量X1~X7与Z的回归模型(不一定包括每个自变量),说明教师的薪金与哪些变量关系密切,是否存在性别和婚姻状况上的差异。
为了数据处理上的方便,建立对薪金取对数后作为因变量。
工资报酬的数学模型

A题:垃圾分类处理与清运方案设计垃圾分类化收集与处理是有利于减少垃圾的产生,有益于环境保护,同时也有利于资源回收与再利用的城市绿色工程。
在发达国家普遍实现了垃圾分类化,随着国民经济发展与城市化进程加快,我国大城市的垃圾分类化已经提到日程上来。
2010年5月国家发改委、住房和城乡建设部、环境保护部、农业部联合印发了《关于组织开展城市餐厨废弃物资源化利用和无害化处理试点工作的通知》,并且在北京、上海、重庆和深圳都取得一定成果,但是许多问题仍然是垃圾分类化进程中需要深入研究的。
在深圳,垃圾分为四类:橱余垃圾、可回收垃圾、有害垃圾和其他不可回收垃圾,这种分类顾名思义不难理解。
其中对于居民垃圾,基本的分类处理流程如下:在垃圾分类收集与处理中,不同类的垃圾有不同的处理方式,简述如下:1)橱余垃圾可以使用脱水干燥处理装置,处理后的干物质运送饲料加工厂做原料。
不同处理规模的设备成本和运行成本(分大型和小型)见附录1说明。
2)可回收垃圾将收集后分类再利用。
3)有害垃圾,运送到固废处理中心集中处理。
4)其他不可回收垃圾将运送到填埋场或焚烧场处理。
所有垃圾将从小区运送到附近的转运站,再运送到少数几个垃圾处理中心。
显然,1)和2)两项中,经过处理,回收和利用,产生经济效益,而3)和4)只有消耗处理费用,不产生经济效益。
本项研究课题旨在为深圳市的垃圾分类化进程作出贡献。
为此请你们运用数学建模方法对深圳市南山区的分类化垃圾的实现做一些研究,具体的研究目标是:1)假定现有垃圾转运站规模与位置不变条件下,给出大、小型设备(橱余垃圾)的分布设计,同时在目前的运输装备条件下给出清运路线的具体方案。
以期达到最佳经济效益和环保效果。
2)假设转运站允许重新设计,请为问题1)的目标重新设计。
仅仅为了查询方便,在题目附录2所指出的网页中,给出了深圳市南山区所有小区的相关资料,同时给出了现有垃圾处理的数据和转运站的位置。
其他所需数据资料自行解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工资问题数学建模对工资待遇问题的探讨工资支付,就是工资的具体发放办法。
包括如何计发在制度工作时间内职工完成一定的工作量后应获得的报酬,或者在特殊情况下的工资如何支付等问题。
主要包括:工资支付项目、工资支付水平、工资支付形式、工资支付对象、工资支付时间以及特殊情况下的工资支付等。
工资支付的项目,一般包括计时工资、计件工资、奖金、津贴和补贴、延长工作时间的工资报酬以及特殊情况下支付的工资。
本文我们讨论的是对大学教师工资的分配问题,原工资支付系统导致抱怨的原因大致分为两个方面:1.称与工龄相同的教师的工资相差太大,则工资低的人会抱怨。
2.能力高、贡献大的人希望得到更高的收入,否则则会产生抱怨。
我们对两篇获奖论文进行了分析摘要总结。
论文1:摘要:该模型通过选取两个指标作为评价某工资分配方案优劣的标准,并以该指标确定三种不同的评价函数,建立规划模型。
通过对规划问题求解,可以找到较为合理的工资过渡方案。
在年工资总额增长3%,人年工资增长率介于1%~3%间的条件下,通过对工资调整的几个原则的逐步考虑,由较为简化的单一模型发展到较为复杂的分级非线性模型,使模型在符合所有的原则的前提下,做到了过渡过程尽可能平稳有序,达到了较为满意的结果。
知识:最小二乘法:用于直线拟合;偏差平方和:实际值与理论值差的平方和;无序度函数:Entropy定义为某数列的逆序值。
线性规划假设:工资增长总额为定值,问题转化为:如何将增长额合理地分配到各教员,使其尽可能接近目标方案的优化问题。
原则:1.每年所有教员工资须有所提升。
2.教员应从晋级中获得实质性利益,如果一个人在最短的时间内得到晋级,其工资的增长应大致相当于七年正常(未晋级)工资的增长。
3.按时(每7至8年)得到晋级且工作25年以上的教员在退休时工资应大致相当于刚工作博士工资的两倍。
4.对于相同级别的教员,工作年限长,经验多的应得到更多的报酬,但是这种由工作年限长短导致的工资差异应逐渐变小。
建模分析:为了解决该问题,我们建立了三种模型:单一线性模型、分级模型和分级非线性模型。
单一线性模型的建立是假设每个教员每年工资的期望增长率均相同,与级别或工资年限无关。
由原则二可以为每个教员建立单一的工资水平参考分数:7⨯+=rank year score在理想的情况下可以认为工资仅和该参考分数有关,该工资方案下,对数据点()salary score ,运用最小二乘法得到拟合线性方程)(,score fsalary score ,为了得到较为精确的线性方程,我们用偏差平方和无序度指数来衡量线性方程。
目 标 函 数 一:该 组 数 据 点 偏 差 平 方 和T1=()∑∆+-∆+2salary ,)(x f salary salary salary score 。
目标函数二:根据Score 对教员进行排序,计算该序列的无序度T2=()salary score ,Entropy 。
1. 评价该分配方案优劣采取指标一,可建立下列规划模型令目标函数Min:()()∑∆+-∆+=∆2salary ,)(arg score f salary salary salary et t salary score st. LowRate salary salary ⨯≤∆HighRate salary salary ⨯≥∆Total salary ∆=∆∑2. 评价该分配方案优劣采取指标二,可建立下列规划模型:令目标函数Min:()()salary score salary et t ,Entropy arg =∆st. LowRate salary salary ⨯≤∆HighRate salary salary ⨯≥∆Total salary ∆=∆∑3. 从两组结果来看,各指标均能对工资方案进行约束,其中指标一的整体约束效果较好,但在每年调整过程中个体间的有序度并未显著改善;指标二的针对局部有序的调整十分有效,但整体效果欠佳,理想的优化目标应是两者兼顾。
可建立下列规划模型令目标函数Min:()2t⨯+∆λet=arg Tsalary1Tst. LowRate∆≤salary⨯salary≥∆salary⨯salaryHighRate∑∆salary∆Total=所以,今后目标函数均采取()2t⨯+=et∆λ形salaryarg T1T式分级模型:如果考虑实际情况,不同职级的人应该有不同的年限工资,例如一个讲师一年增加的工资应该没有一个副教授一年增加的工资多,这是我们就不能单纯的用以上直线模型来规划,而应分别对不同的职级分开加以讨论,得到一个分级的模型。
由于不同的职级的人有不同的年限工资,由原则二可知,在工作年限相同的情况下,相邻两职级的教员的工资差异应大致等于同在较低一级中工作年限相差七年的两教员的工资差。
这样我们可以对分级模型进行一些改动就可以满足要求。
目标函数T1变为各级偏差平方和的总和,T2变为各级五序度的总和,仍令目标函数Min: ()21arg T T salary et t ⨯+=∆λst. LowRate salary salary ⨯≤∆HighRate salary salary ⨯≥∆Total salary ∆=∆∑分级非线性模型:结合考虑到原则四,在同一职级中,若每年增加的工资都相同,则在同职级的情况下,由工作年限产生的工资差异将不会逐渐消除。
为了达到原则四的要求,则同一职级中,每年增加的工资额应逐渐减少,而前两个模型都没有考虑该原则,为了满足该原则可以假设在同一职级中,每一年所增加的工资随着工作年限呈指数关系递减,在足够后,两个同职级的有丰富经验的教员的工资会很接近。
这样我们可以对分级模型进行一些改动就可以满足要求。
在该工资方案下,首先我们对各数据点以rank 为分类变量将数据点按级别分类,在每一个级别内对数据点()salary year ,以指数函数作为基底运用最小二乘法得到拟合非线性方程year salary year rank b a year f +=)(,,,以此作为各教员期望工资函数,同上可计算各级别内各数据点偏差平方和,再对各级别的偏差平方和求和作为T1=(公式)。
在各级别内根据year 对教员进行排序,计算该序列的无序度()salary year ,Entropy rank ,再对各级别的无序度求和作为T2=(公式)目标函数:Min: ()21arg T T salary et t ⨯+=∆λst. LowRate salary salary ⨯≤∆HighRate salary salary ⨯≥∆Total salary ∆=∆∑单一模型对于原则一、二有较好的体现,并可得到较好的结果。
若要符合原则三,仅使用单一模型是不够的,需要使用分级模型,此外若要顾及原则四,则需要使用分级非线性模型。
限制因素:工资增长总额上限,人员的动态调整(晋级,退休,聘用等),教员间工资增长间差异应保持在一定范围(一定的稳定性)内。
评价方案1. 偏差平方和。
2. 有序度指数。
论文2:摘要: 作者考虑把总工资S 分为由不同因素决定的三部分,列出基本关系式:S=W+A+L级别工资W:由级别(职称)与工龄决定。
级别越高,工龄越长,则级别工资越高。
能力奖金A:由能力和贡献决定。
能力越高,贡献越大,则能力奖金越高。
生活津贴L:由生活指数决定。
随着生活指数的增长,生活津贴也增长。
模型假设:1.经验的丰富由给定的工龄长短决定。
2.级别不同,相同的工龄的重要性不同。
但以前的级别工龄仅由表中数据无法判断,则以前的工龄同等看待,不再区分。
而今后的工龄应分别对待。
3.级别越高,应受的优待越多。
4.正常晋升,即各级别的工龄应大于一最小值,即各级别的最小工龄。
5.在过渡期,教师的晋升均为正常晋升,不存在破格提拔。
模型的建立与求解:对4个等级分别用最小二乘法拟合其工资曲线,发现拟合的曲线与题目要求的有很大的不符。
于是认为原工资体系在公平合理性方面过于脆弱,不能从此数据中得到足够的信息量,从另一方面着手,先根据题目的要求构造出合理的工资体系,在反过头来用数据检验该工资体系。
㈠级别工资w1. 原则四说明随着t 的增长,同级别的W i 的差异趋近于0,即存在W i 的上限k i 使()−−→−→∝t it f 常数k i由此立出下式:()i T t i i t i a m x f i i i +-=-01)(i x 为级别i 的教师的W i 增长工资的上限,即在级别i 工作若干年增长值△W i −−→−→∝t i x a i 为级别i 的起点工资,且a 1=27000 a 2=32000。
m i 为常数,控制增长幅度。
由于各级别工资若干年增长极限值x i 不同。
设各级别工资若干年增长极限值x i 之比分别为一常数c i ,即i i i c x x=+1(c i >1)对c i 的确定如下:Ⅰ 对原工资数据按不同级别分别进行拟合。
Ⅱ 求出级别i 的教师工资的标准差σi ,得到标准差之比。
275.134=σσ 125.134=σσ 546.134=σσⅢ 原工资的标准差σi 之比反映了各级别工资若干年增长极限值x i 之比,设为正比关系,则 11i i i i i c x x c σσ++==c 为比例系数。
特殊情况(t 1<T 10 ,t 2<T 20 ,t 3<T 30 ,t 4<T 40 ):认为工龄不够的教师的级别工资W 为该级的起点工资a i ,其级别工龄补足为该级别的工龄最小值,即在t i <T i0时,令t i =T i0i t i a f i =)(。
㈡能力奖金A定义能力系数αj :教师j 原工资与他应得标准级别工资之差与标准级别工资之比。
00i i ji j W W S -=α,并且由于原工资系统存在不合理性,规定一个修正系数ωj ,表明原工资系统体现的能力水平的可信程度,即原能力奖金偏高还是偏低及偏差的大小。
ωj =1,表明教师j 原工资准确的反映了其能力。
ωj <1, 表明教师j 原能力奖金偏高,即应降低其能力奖金。
ωj >1, 表明教师j 原能力奖金偏低,即应增高其能力奖金。
ωj 的确定应用了概率的相关知识:因为无法从已知中获得,采取仿真模拟,随机产生一组数据,并根据以下原则;1.认为原工资系统在总体上反映出的能力水平应是比较合理的,只是反映个人水平时有偏高偏低,偏差由大有小。
且认为偏差很大的情况发生的几率很小,即认为绝大多数偏差集中在一定范围内。
2.设ωj服从正态分布,其均值μ为1,ωj在1附近波动,标准差σ由偏差集中程度决定。
即满足ωj出现在一个置信区间内的概率不小于p。
变动p及置信区间的位置,可得到不同的标准差σ,从而产生不同组的ωj修正后的能力系数与其应得的标准级别工资之积即为标准能力奖金。
