能量均分定理理想气体内能
合集下载
大学物理第8章第3节-能量均分定理 理想气体的内能
1 2 1 2 1 2 1 mvx mvy mvz k BT 2 2 2 2
在每一个平动自由度上, 分子的每个平 动自由度具有的能量都是 k BT 2 .
可以证明, 平衡态下一个转动自由的平 均能量是 k BT 2 . 能量按自由度均分定理 平衡态下气体分子的每一个自由度的 平均动能都等于 k BT 2 . 一个振动自由度的平均能量是 2(k BT 2) . ( k BT 2 是动能, k BT 2 是势能.)
y
P( x, y, z )
o
x
z
一个刚性分子的自由度
平动: 3 单原子分子 3 个 转动: 0 平动: 3 5 个 双原子分子 转动: 2 平动: 3 6 个 多原子分子 转动: 3
一个刚性分子的自由度
i t r
ikBT 2
(ii) 一摩尔理想气体分子
E N 0 N 0 ikBT 2 i RT 2
(iii) 质量为 M 摩尔质量为 M mo l 的理想气 体ห้องสมุดไป่ตู้子
i M i i RT pV E N N k BT 2 M mol 2 2
CO 2 气体在标 O2 、 例8.2 求1 mol的 He 、 准状态下的内能. O2 、 CO 2 都可看作理想气. 解 He 、 He 是单原子分子, i 3 ,
三. 理想气体的内能 内能: 在热力学系统中, 系统与热现象 有关的能量. 包括: (i) 气体分子热运动所具有动能, (ii) 气体分子之间以及分子内的原子与 原子之间相互作用所具有的势能. 理想气体分子间没有相互作用, 理想气 体的内能只有气体分子作热运动的动能.
理想气体的内能 (i) 一个理想气体分子
在每一个平动自由度上, 分子的每个平 动自由度具有的能量都是 k BT 2 .
可以证明, 平衡态下一个转动自由的平 均能量是 k BT 2 . 能量按自由度均分定理 平衡态下气体分子的每一个自由度的 平均动能都等于 k BT 2 . 一个振动自由度的平均能量是 2(k BT 2) . ( k BT 2 是动能, k BT 2 是势能.)
y
P( x, y, z )
o
x
z
一个刚性分子的自由度
平动: 3 单原子分子 3 个 转动: 0 平动: 3 5 个 双原子分子 转动: 2 平动: 3 6 个 多原子分子 转动: 3
一个刚性分子的自由度
i t r
ikBT 2
(ii) 一摩尔理想气体分子
E N 0 N 0 ikBT 2 i RT 2
(iii) 质量为 M 摩尔质量为 M mo l 的理想气 体ห้องสมุดไป่ตู้子
i M i i RT pV E N N k BT 2 M mol 2 2
CO 2 气体在标 O2 、 例8.2 求1 mol的 He 、 准状态下的内能. O2 、 CO 2 都可看作理想气. 解 He 、 He 是单原子分子, i 3 ,
三. 理想气体的内能 内能: 在热力学系统中, 系统与热现象 有关的能量. 包括: (i) 气体分子热运动所具有动能, (ii) 气体分子之间以及分子内的原子与 原子之间相互作用所具有的势能. 理想气体分子间没有相互作用, 理想气 体的内能只有气体分子作热运动的动能.
理想气体的内能 (i) 一个理想气体分子
理想气体内能 平均自由程
推广：在温度为T 的平衡态下，分子的每一个转动自由度
上也具有相同的平均动能，大小也为kT/2。
能量按自由度均分定理：
在温度为T的平衡态下，气体分子每个自由度 的平均动能都相等，都等于kT/2。这就是能量 按自由度均分定理，简称能量均分定理。
k
i 2
k=3kT/2
说明：
kT
•是统计规律，只适用于大量分 子组成的系统。 •统计物理可给出严格证明。
b A(x,y,z) a
y
x
说明：一般来说，n≥3个原子组成的分子，共有3n个自由度，
其中3个平动自由度，3个转动自由度，(3n-6)个振动自由度。当 气体处于低温状态时，可把分子视为刚体。
二、能量均分定理：
一个分子的平均平动能为
k
2 x
kt
2 y
3 2
kT
1 2
mv
2
1 2
E＝ m i M 2 RT
E E 2 E1
m i M 2
R (T 2 T1 )
在相同的t时间内，分子由A到 B的位移大小比它的路程小得多
A
B
(路程/时间) (位移量/时间)
扩散速率 平均速率 气体分子两次相邻碰撞之间自由通过的路程。
分子自由程: 分子碰撞频率:
在单位时间内一个分子与其他分子碰撞的次数。
y
q
x
z
自由刚体
三个独立的坐标 x,y,z 决定转轴上一点 两个独立的a， b 决定转轴空间位置
一个坐标q 决定刚体转过的角度
i=6 3个平动 3个转动
b A(x,y,z) a
y
刚性杆：
x,y,z,α,β i=5
z
6.4X 能量均分定理 理想气体的内能
刚性近似下, s = 0, i = t + r, 分子的平均总能量：
3 2 kT（单原子分子） i tr 5 E Ek kT kT kT（双原子分子） 2 2 2 6 2 kT 3kT（多原子分子）
当温度极低时，转动自由度 r 也被“冻结”， 任何气体分子都可视为只有平动自由度 , 就如 同单原子分子。这时, r = 0, s = 0, i = t, i t 分子的平均总能量 E Ek kT kT 2 2
1.52102 ( J / m3 )
(4) 0.3 mol气体的内能
i 5 E RT 0.3 8.31 273 1.7 10 3 J 2 2
例2：贮存有氮气的容器以速度100米/秒运动。若该容 器突然停止，问容器中温度将升多少？
已知：u
100m / s, i 5, 28 10 kg / mol
常温下热运动能kt为0026ev故转动状态很容易被激发而振动状态很少被激发因此故转动状态很容易被激发而振动状态很少被激发因此在常温下理想气体分子可近似看成是刚性的在常温下理想气体分子可近似看成是刚性的只需考虑其平动和转动自由度而不必考虑其振动自由度
6.4 能量均分定理 理想气体的内能
引言：前面我们研究气体动能时，把分子看作弹性 小球的集合，人们发现用这一模型去研究单原子气体问 题时，理论与实际符合得很好，但是用这一模型去研究 多原子分子时，理论值与实验值相差甚远。 1857年克劳修斯提出：将理想气体模型稍作修改。 即不能将所有分子都看成质点，对结构复杂的多原子 分子，考虑分子的能量时，要考虑分子各种运动的能 量。即不但要考虑分子的平动，还要考虑其转动和分 子内原子之间的振动。 下面我们来考察包括平动、转动、及振动在内的理 想气体能量。
能量均分定理-推荐精选PPT
分子中的所有原子都在一条联心线上的分子称为线型 分子,它的转动自由度也只有两个。
• 单原子分子只有三个平动自由度，而没有转动自由 度。
• 双原子分子的自由度数最多可以有6个。
• 由此可估计到，N 个原子组成的多原子分子，其自 由度数最多为 3N 个。
在这 3N 自由度中，有三个（整体）平动、三个 （整体）转动及 3N – 6 个振动自由度。
理杜想隆气 -珀体蒂的定总律动: 固能体就摩是位尔内热能置容U 。所需独立坐标数也就不同。
由于固体处于静止状态，它的平动、转动运动不必考虑， 则物体在该过程中的热容C 定义为 粗略地考虑，可不必区分定压热容还是定体热容，而以 C m 表示晶体的摩尔热容。
• 若要解释单原子、双原子、多原子理想气体热容的
• 双原子分子、多原子分子及单原子分子之间的差
别在于它们的分子结构各不相同 大家知道，确定一个质点的空间位置需 x、y、z 三个独立坐标，故自由度数是3个。 ，描述它们的空间
由于分子中的原子所进行的振动都是振幅非常小的微振动，可把它看作简谐振动。 本节将在此基础上，通过与实验测量值的比较，得到能量均分定理,
• 因为转动惯量与回转半径平方成正比，，所以转动惯 量之比为 10-10 倍。转动角速度相同时的转动能量之 比也是 10-10 倍。
故双原子分子绕中心轴转动自由度不必考虑,
刚性双原子分子的自由度数为三个平动自由度两个转 动自由度。
• 非刚性双原子分子有一个沿两质心联线振动的振动自 由度，其总自由度数为六个。
一个刚性多原子分子既在空间平动又作转动，确定
空间位置就需 x、y、z 及α、β、γ 六个独立坐
标，它的自由度数是六个。 • 而双原子分子本身很像一个哑铃，每个原子的质量
• 单原子分子只有三个平动自由度，而没有转动自由 度。
• 双原子分子的自由度数最多可以有6个。
• 由此可估计到，N 个原子组成的多原子分子，其自 由度数最多为 3N 个。
在这 3N 自由度中，有三个（整体）平动、三个 （整体）转动及 3N – 6 个振动自由度。
理杜想隆气 -珀体蒂的定总律动: 固能体就摩是位尔内热能置容U 。所需独立坐标数也就不同。
由于固体处于静止状态，它的平动、转动运动不必考虑， 则物体在该过程中的热容C 定义为 粗略地考虑，可不必区分定压热容还是定体热容，而以 C m 表示晶体的摩尔热容。
• 若要解释单原子、双原子、多原子理想气体热容的
• 双原子分子、多原子分子及单原子分子之间的差
别在于它们的分子结构各不相同 大家知道，确定一个质点的空间位置需 x、y、z 三个独立坐标，故自由度数是3个。 ，描述它们的空间
由于分子中的原子所进行的振动都是振幅非常小的微振动，可把它看作简谐振动。 本节将在此基础上，通过与实验测量值的比较，得到能量均分定理,
• 因为转动惯量与回转半径平方成正比，，所以转动惯 量之比为 10-10 倍。转动角速度相同时的转动能量之 比也是 10-10 倍。
故双原子分子绕中心轴转动自由度不必考虑,
刚性双原子分子的自由度数为三个平动自由度两个转 动自由度。
• 非刚性双原子分子有一个沿两质心联线振动的振动自 由度，其总自由度数为六个。
一个刚性多原子分子既在空间平动又作转动，确定
空间位置就需 x、y、z 及α、β、γ 六个独立坐
标，它的自由度数是六个。 • 而双原子分子本身很像一个哑铃，每个原子的质量
气体动理论-2
对非刚性的双原子和多原子分子，还须考虑振动自 由度（视温度而定）。
返回 退出
二、能量均分定理
分子的平均平动动能：
kt
1 2
m v2
1 2
m
vx2
1 2
m vy2
1 2
m
vz2
3 kT 2
vx2
v2y
vz2
1 v2 3
1 2
m vx2
1 2
m vy2
1 2
m vz2
1 2
kT
分子的平均平动动能 3kT/2 是均匀地分配在每个
§3-3 能量均分定理 理想气体的内能
一、分子的自由度
自由度 ( i )： 决定某物体在空间的位置所需要的 独立坐标数目。
质点: (x, y, z)
i=3
做直线运动的质点： 做平面运动的质点： 做空间运动的质点：
1个自由度 2个自由度 3个自由度
返回 退出
运动刚体的自由度： 随质心的平动+绕过质心轴的转动 自由刚体有 6个自由度：
(t r 2s) 1 kT
2
返回 退出
三、理想气体的内能
气体的内能：气体中所有分子的热运动能量和分 子间相互作用势能的总和。
理想气体内能：气体中所有分子的平均能量的总和。
1mol 理想气体的内能： （只考虑刚性分子）
Emol
NA
i 2
kT
i 2
RT
质量为m'，摩尔质量为M的理想气体内能：
E
率在 v 附近单位速率区间 的分子数占总
数的百分比 .
f (v)dv 的物理意义：
表示速率在v v dv区间的分 子数占总分子数的百分比.
速率在v v dv内分子数：dN Nf (v)dv
返回 退出
二、能量均分定理
分子的平均平动动能：
kt
1 2
m v2
1 2
m
vx2
1 2
m vy2
1 2
m
vz2
3 kT 2
vx2
v2y
vz2
1 v2 3
1 2
m vx2
1 2
m vy2
1 2
m vz2
1 2
kT
分子的平均平动动能 3kT/2 是均匀地分配在每个
§3-3 能量均分定理 理想气体的内能
一、分子的自由度
自由度 ( i )： 决定某物体在空间的位置所需要的 独立坐标数目。
质点: (x, y, z)
i=3
做直线运动的质点： 做平面运动的质点： 做空间运动的质点：
1个自由度 2个自由度 3个自由度
返回 退出
运动刚体的自由度： 随质心的平动+绕过质心轴的转动 自由刚体有 6个自由度：
(t r 2s) 1 kT
2
返回 退出
三、理想气体的内能
气体的内能：气体中所有分子的热运动能量和分 子间相互作用势能的总和。
理想气体内能：气体中所有分子的平均能量的总和。
1mol 理想气体的内能： （只考虑刚性分子）
Emol
NA
i 2
kT
i 2
RT
质量为m'，摩尔质量为M的理想气体内能：
E
率在 v 附近单位速率区间 的分子数占总
数的百分比 .
f (v)dv 的物理意义：
表示速率在v v dv区间的分 子数占总分子数的百分比.
速率在v v dv内分子数：dN Nf (v)dv
第19讲能量均分定理理想气体的内能
教学要求了解速率分布函数、分子速率的实验测定、麦克斯韦速率分布律。
理解气体分子的方均根速率、刚性分子的自由度。
掌握气体的能量均分定理，理想气体的内能。
7.4 能量均分定理 理想气体的内能前面讨论分子热运动时，把分子视为质点，只考虑分子的平动。
气体的能量是与分子结构有关的，除了单原子分子可看作质点外，一般由两个以上原子组成的分子，不仅有平动，而且还有转动和分子内原子间的振动。
为了确定分子的各种运动形式的能量的统计规律，需要引用力学中有关自由度的概念。
7.4.1自由度完全描述系统在空间位置所需独立坐标的数目，称为系统的自由度。
考察分子运动的能量时，不能再把各种分子都当作质点处理,从而还要考虑其它运动形式(如转动和振动等)的自由度。
气体分子按其结构可分为单原子分子、双原子分子和三原子或多原子分子。
当分子内原子间距离保持不变（不振动）时，这种分子称为刚性分子，否则称为非刚性分子，对于非刚性双原子分子或多原子分子，由于在原子之间相互作用力的支配下，分子内部还有原子的振动，因此还应考虑振动自由度。
但是由于关于分子振动的能量，经典物理不能给出正确的说明，正确的说明需要量子力学；另外在常温下用经典方法认为分子是刚性的也能给出与实验大致相符的结果；所以作为统计概念的初步，下面只讨论刚性分子的自由度。
1 单原子分子如氦(He)、氖(Ne)、氩(Ar)等分子只有一个原子，可看成自由质点，所以有3个平动自图7-3 分子的自由度（a ）单原子分子 （b ）双原子分子（c ）三原子分子zzzααγββθ由度［如图7-3（a ）］。
2 刚性双原子分子如氢 (H 2)、氧( O 2)、氮(N 2)、一氧化碳(CO)等分子，两个原子间联线距离保持不变。
就像两个质点之间由一根质量不计的刚性细杆相连着（如同哑铃），确定其质心C 的空间位置，需3个独立坐标（x ，y ，z ）；确定质点连线的空间方位，需两个独立坐标（如α，β）， 而两质点绕连线的的转动没有意义（因为相对该连线的转动惯量J 是非常小的，从而与该连线相应的转动动能212J ω可以忽略不计）。
7-5 能量均分定理 理想气体内能要点
1 2
m vC2 y
1 2
m vC2 z
分子平均转动动能
kr
1 2
J
2 y
1 2
J
2 z
➢ 刚性分子平均能量
kt kr
7 – 5 能量均分定理 理想气体内能
非刚性双原子分子
y
m2
m1
* C
x
z
刚性分子平均能量
kt kr
非刚性分子平均振动能量
v
1 2
vC2x
1 kx 2 2
非刚性分子平均能量
7 – 5 能量均分定理 理想气体内能
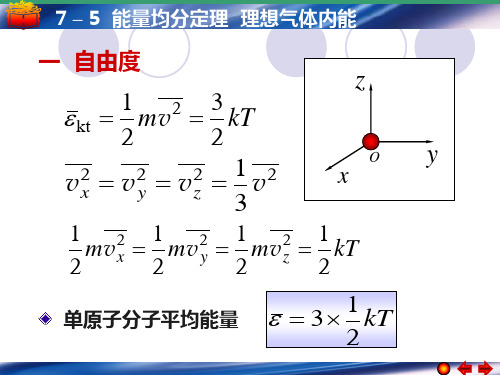
一 自由度
kt
1 mv2 2
3 2
kT
v
2 x
v
2 y
v2z
1 v2 3
z
Oy
x
1 2
mv2x
1 2
mv
2 y
1 2
mv2z
1 kT 2
单原子分子平均能量 3 1 kT
2
7 – 5 能量均分定理 理想气体内能
刚性双原子分子
分子平均平动动能
kt
1 2
m
vC2 x
kt kr v
自由度 分子能量中独立的速度和坐标的二次方
项数目叫做分子能量自由度的数目, 简称自由度，用
符号 表i示.
7 – 5 能量均分定理 理想气体内能
自由度 分子能量中独立的速度和坐标的二次方项
数目叫做分子能量自由度的数目, 简称自由度，用符号
i 表示.
自由度数目
i t r v
平转振 动动动 刚性分子能量自由度
t r i 自由度
分子
平动
转动
总
(完整版)理想气体内能
7－4 能量均分定理 理想气体内能
一、自由度
定义：
确定一个物体的空间位置所需要的独 立坐标数目——自由度。
质点的自由度
直线运动 x 一个自由度 i=1 平面运动 x,y 两个自由度 i=2 空间运动 x,y,z 三个自由度 i=3
自由刚体
三个独立的坐标 x,y,z 决定转轴上一点
两个独立的a， b 决定转轴空间位置
热力学系统的内能是指气体分子各种形态的动能与势能的总 和。即系统所包含的全部分子的能量总和称为系统的内能。
理想气体内能公式
理想气体内能是分子平动动能与转动动能之和
分子的自由度为i，则一个 说明：
分子能量为ikT/2， 1摩尔理 •理想气体的内能与温度和分子的想气体，有个NA分子源自内能 E＝ i 2kT
克劳修斯指出：气体分子的速度虽然很大，但前 进中要与其他分子作频繁的碰撞，每碰一次，分 子运动方向就发生改变，所走的路程非常曲折。
在相同的t时间内，分子由A到
B的位移大小比它的路程小得多
A• •B
扩散速率
平均速率
(位移量/时间) (路程/时间)
分子自由程: 气体分子两次相邻碰撞之间自由通过的路程。
C p,m
i
2 2
R
C p,m CV ,m
i2 i
对于单原子分子与双原子 分子，理论与实验符合得 很好，而对于多原子分子， 理论与实验相差较大。
气体
理论值
CV,m CP,m
γ
实验值
CV,m
CP,m
γ
He
12.61 20.95 1.66
12.47 20.78 1.67
Ne
12.53 20.90 1.67
一个坐标q 决定刚体转过的角度
一、自由度
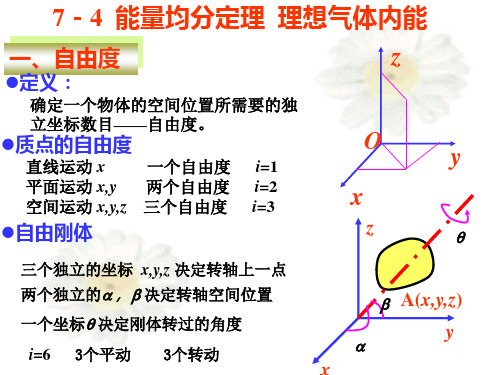
定义：
确定一个物体的空间位置所需要的独 立坐标数目——自由度。
质点的自由度
直线运动 x 一个自由度 i=1 平面运动 x,y 两个自由度 i=2 空间运动 x,y,z 三个自由度 i=3
自由刚体
三个独立的坐标 x,y,z 决定转轴上一点
两个独立的a， b 决定转轴空间位置
热力学系统的内能是指气体分子各种形态的动能与势能的总 和。即系统所包含的全部分子的能量总和称为系统的内能。
理想气体内能公式
理想气体内能是分子平动动能与转动动能之和
分子的自由度为i，则一个 说明：
分子能量为ikT/2， 1摩尔理 •理想气体的内能与温度和分子的想气体，有个NA分子源自内能 E＝ i 2kT
克劳修斯指出：气体分子的速度虽然很大，但前 进中要与其他分子作频繁的碰撞，每碰一次，分 子运动方向就发生改变，所走的路程非常曲折。
在相同的t时间内，分子由A到
B的位移大小比它的路程小得多
A• •B
扩散速率
平均速率
(位移量/时间) (路程/时间)
分子自由程: 气体分子两次相邻碰撞之间自由通过的路程。
C p,m
i
2 2
R
C p,m CV ,m
i2 i
对于单原子分子与双原子 分子，理论与实验符合得 很好，而对于多原子分子， 理论与实验相差较大。
气体
理论值
CV,m CP,m
γ
实验值
CV,m
CP,m
γ
He
12.61 20.95 1.66
12.47 20.78 1.67
Ne
12.53 20.90 1.67
一个坐标q 决定刚体转过的角度
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 1 2 m0 v x kT 2 2
气体分子在每一个平动自由度上具有相等的 平均平动动能，其大小等于二分之一kT。
前页 后页 目录
3
5.4 能量均分定理 理想气体内能
能量按自由度均分定理 在温度为T的平衡态下，气体分子每一个自由 1 度的平均动能为 kT 2
分子平均平动动能Байду номын сангаас kt
t kT 2
r 分子平均转动动能 kr kT 2
前页 后页 目录
4
5.4 能量均分定理 理想气体内能
分子平均振动动能 ks
s kT 2
trs 分子平均动能 k kT 2
分子平均振动势能 ps
s kT 2
i 分子平均能量 kT 2
i =t+r+2s,称为能量自由度
前页 后页 目录
5.4 能量均分定理 理想气体内能
5.4 能量均分定理 理想气体内能
一. 分子自由度 确定分子位置的独立坐标数。 分为平动、转动和振动自由度。 (1)单原子分子 平动自由度t =3
o x
z
( x, y, z )
y
前页 后页 目录
1
5.4 能量均分定理 理想气体内能
(2)刚性双原子分子 平动自由度t =3 转动自由度r =2 振动自由度s =0
5
5.4 能量均分定理 理想气体内能
三. 理想气体的内能 气体分子热运动能量的总和。
m i E N A kT M 2 m i E RT M 2
理想气体的内能只是温度的单值函数。
本节完
前页 后页 目录
6
z
B
A ( x, y, z )
o
x
y
(3)非刚性双原子分子 平动自由度t =3 转动自由度r =2 振动自由度s =1
(4)刚性多原子分子 平动自由度t =3 转动自由度r =3 振动自由度s =0
前页 后页 目录
2
5.4 能量均分定理 理想气体内能
二. 能量均分定理
kt
1 3 2 m0 v kT 2 2 1 3 2 2 2 m0 (v x v y v z ) kT 2 2