MATLAB遗传算法PID大作业.
MATLAB遗传算法PID大作业

遗传算法在调节控制系统参数中的应用【摘要】自动化控制系统多采用PID 控制器来调节系统稳定性和动态性,PID 的Kp,Ki,Kd 参数需要合理选择方能达到目标。
遗传算法是一种模拟生物进化寻求最优解的有效算法,本文通过利用GAbx 工具箱实现对控制电机的PID 进行参数优化,利用matlab 的仿真功能可以观察控制效果。
1. 直流伺服电机模型 1.1物理模型图1 直流伺服电机的物理模型αu ---电枢输入电压(V ) a R ---电枢电阻(Ω) S L ---电枢电感(H ) q u ---感应电动势(V ) g T ---电机电磁转矩(N m ⋅) J---转动惯量(2m kg ⋅)B---粘性阻尼系数(s m N ⋅⋅) g i ---流过电枢的电流(A ) θ---电机输出的转角(rad )1.2传递函数利用基尔霍夫定律和牛顿第二定律得出电机基本方程并进行拉布拉斯变换)()()()()()()()()()()(2s s K s U K s I s T s Bs s Js s T s I s L R s I s U s U e q t a g g a a a a q a θθθ⋅=⋅=⋅+⋅=⋅+⋅=-式中:t K 为电机的转动常数(m N ⋅)A ;e K 为感应电动势常数(s V ⋅)radaa R s L +1S1 BJs +1i KC K)(s U a)(s U q)(s I a )(s T g)(s Ω)(s θ图2 直流伺服电机模型方框图消去中间变量得系统的开环传递函数:sK K B Js R s L K s U s s G C t a d ta ]))([()()()(+++==θ系统参数如下:s m uN B m mg J ⋅⋅=⋅=51.3,23.32A m N K K uH L R e t a a )(03.0,75.2,4⋅===Ω=2. PID 校正图3 PID 校正s K sK K s G d ip c ++=)( Kp,Ki,Kd 为比例,积分,微分系数 令Kp=15、Ki=0.8 、Kd=0.6M 文件:J=3.23E-6;B=3.51E-6; Ra=4;La=2.75E-6; Kt=0.03; num= Kt;den=[(J*La) ((J*Ra)+(La*B)) ((B*Ra)+Kt*Kt) 0]; t=0:0.001:0.2; step(num,den,t); Kp=15; Ki=0.8; Kd=0.6;numcf=[Kd Kp Ki]; dencf=[1 0];numf=conv(numcf,num); denf=conv(dencf,den);[numc,denc]=cloop(numf,denf); t=0:0.001:0.04; step(numc,denc,t);matlab 进行仿真,我们可以看出不恰当的PID 参数并不能使系统达到控制系统的要求,因此需要对PID参数进行优化。
MATLAB实验遗传算法与优化设计(可编辑)

MATLAB实验遗传算法与优化设计遗传算法与优化设计一实验目的1 了解遗传算法的基本原理和基本操作选择交叉变异2 学习使用Matlab中的遗传算法工具箱 gatool 来解决优化设计问题二实验原理及遗传算法工具箱介绍1 一个优化设计例子图1所示是用于传输微波信号的微带线电极的横截面结构示意图上下两根黑条分别代表上电极和下电极一般下电极接地上电极接输入信号电极之间是介质如空气陶瓷等微带电极的结构参数如图所示Wt分别是上电极的宽度和厚度D是上下电极间距当微波信号在微带线中传输时由于趋肤效应微带线中的电流集中在电极的表面会产生较大的欧姆损耗根据微带传输线理论高频工作状态下假定信号频率1GHz电极的欧姆损耗可以写成简单起见不考虑电极厚度造成电极宽度的增加图1 微带线横截面结构以及场分布示意图1其中为金属的表面电阻率为电阻率可见电极的结构参数影响着电极损耗通过合理设计这些参数可以使电极的欧姆损耗做到最小这就是所谓的最优化问题或者称为规划设计问题此处设计变量有3个WDt它们组成决策向量[W D t] T待优化函数称为目标函数上述优化设计问题可以抽象为数学描述2其中是决策向量x1xn为n个设计变量这是一个单目标的数学规划问题在一组针对决策变量的约束条件下使目标函数最小化有时也可能是最大化此时在目标函数前添个负号即可满足约束条件的解X 称为可行解所有满足条件的X组成问题的可行解空间2 遗传算法基本原理和基本操作遗传算法 Genetic Algorithm GA 是一种非常实用高效鲁棒性强的优化技术广泛应用于工程技术的各个领域如函数优化机器学习图像处理生产调度等遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化算法按照达尔文的进化论生物在进化过程中物竞天择对自然环境适应度高的物种被保留下来适应度差的物种而被淘汰物种通过遗传将这些好的性状复制给下一代同时也通过种间的交配交叉和变异不断产生新的物种以适应环境的变化从总体水平上看生物在进化过程中子代总要比其父代优良因此生物的进化过程其实就是一个不断产生优良物种的过程这和优化设计问题具有惊人的相似性从而使得生物的遗传和进化能够被用于实际的优化设计问题按照生物学知识遗传信息基因Gene 的载体是染色体Chromosome 染色体中一定数量的基因按照一定的规律排列即编码遗传基因在染色体中的排列位置称为基因座Locus在同一个基因座上所有可能的基因就称为等位基因Allele生物所持有的基因以及基因的构成形式称为生物的基因型Genotype而该生物在环境中所呈现的相应性状称为该生物的表现型Phenotype在遗传过程中染色体上的基因能够直接复制给子代从而使得子代具有亲代的特征此外两条染色体之间也通过交叉 Crossover 而重组即两个染色体在某个相同的位置处被截断其前后两串基因交叉组合而形成两个新的染色体在基因复制时也会产生微小的变异Mutation从而也产生了新的染色体因此交叉和变异是产生新物种的主要途径由于自然选择在子代群体新产生的物种或染色体当中只有那些对环境适应度高的才能生存下来即适应度越高的被选择的概率也越大然后又是通过遗传和变异再自然选择一代一代不断进化因此生物遗传和进化的基本过程就是选择即复制交叉和变异遗传算法就是通过模拟生物进化的这几个基本过程而实现的①编码编码是设计遗传算法首要解决的问题在生物进化中选择交叉变异这些基本过程都是基于遗传信息的编码方式进行的即基于染色体的基因型而非表现型因此要模拟生物进化过程遗传算法必须首先对问题的可行解X决策向量进行某种编码以便借鉴生物学中染色体和基因等概念在遗传算法中将每一个决策向量X用一个染色体V来表示3其中每一个vi代表一个基因染色体的长度m不一定等于设计变量的数目n取决于染色体上基因的编码方式一般有两种编码方式二进制编码和浮点数编码如果是二进制编码每一个设计变量xi的真实值用一串二进制符号0和1按照一定的编码规则来表示每个二进制符号就代表一个基因因此染色体长度要远大于设计变量的数目这种由二进制编码构成的排列形式V就是染色体也称个体的基因型而基因型经过解码后所对应的决策向量X即可行解就是个体的表现型如果是浮点数编码每个设计变量用其取值范围内的一个浮点数表示构成染色体的一个基因vi因此个体的编码长度m也就等于决策变量的个数n由于这种编码方式使用的是决策变量的真实值所以也称真值编码方法无论哪种编码方式所有可能的染色体个体V构成问题的搜索空间种群遗传算法对最优解的搜索就是在搜索空间中搜索适应度最高的染色体后面叙述适应度的计算因此通过编码将一个问题的可行解从其解空间转换到了遗传算法能够处理的搜索空间经过个体的编码后就可以进行遗传算法的基本操作选择交叉和变异②选择复制操作选择也就是复制是在群体中选择适应度高的个体产生新群体的过程生物的进化是以集团为主体的与此相应遗传算法的运算对象是有M个个体或染色体组成的集合称为种群M也称为种群规模遗传算法在模拟自然选择时以个体的适应度Fitness高低为选择依据即适应度高的个体被遗传到下一代种群的概率较高而适应度低的个体遗传到下一代的概率则相对较低个体适应度由适应度函数计算适应度函数总是和个体表现型 ie X 的目标函数值f X 关联一般是由目标函数经过一定的变换得到一种最简单的方法就是直接使用目标函数f X 作为适应度函数4选定了适应度函数之后个体适应度也随之确定则在选择操作时个体被选中的概率5其中Fi为个体的适应度这种选择方式称为比例选择也称轮盘赌选择除此之外还有多种选择方法如随机竞争选择均匀选择无回放随机选择等不一一介绍③交叉操作所谓交叉就是以一定的概率交叉概率从群体中选择两个个体染色体按照某种方式交换其部分基因从而形成两个新的个体在遗传算法中它是产生新个体同时也是获得新的优良个体的主要方法它决定了遗传算法的全局搜索能力对于不同的编码方式交叉操作的具体方法也不相同对于浮点数编码一般使用算术交叉对于二进制编码有单点交叉和多点交叉等方式不论何种方式在交叉操作时首先应定义交叉概率Pc这个概率表明种群中参与交叉的个体数目的期望值是M 是种群规模通常交叉概率应取较大的值以便产生较多的新个体增加全局搜索力度但是Pc过大时优良个体被破坏的可能性也越大如果Pc 太小则搜索进程变慢影响算法的运行效率一般建议的取值范围是04–099④变异操作遗传算法中的变异操作就是将染色体上某些基因座上的基因以一定的变异概率Pm用其他的等位基因替代从而形成新的个体对于浮点数编码变异操作就是将变异点处的基因用该基因取值范围内的一个随机数替换对于二进制编码则是将变异点处的基因由1变成00变成1变异操作也有多种方法如均匀变异非均匀变异高斯变异等变异操作的概率Pm要比交叉操作的概率Pc小得多变异只是产生新个体的辅助手段但它是遗传算法必不可少的一个环节因为变异操作决定了算法的局部搜索能力它弥补了交叉操作无法对搜索空间的细节进行局部搜索的不足因此交叉和变异操作相互配合共同完成对搜索空间的全局和局部搜索以上简要介绍了遗传算法的基本原理和操作归纳起来基本遗传算法一般可以表示为一个8元组6式中C 个体的编码方法E 个体适应度评价函数P0 初始种群M 种群规模选择操作交叉操作变异操作是进化终止代数进化终止条件其中有4个运行参数需要预先设定M T PcPm 种群规模M一般取为20100 终止代数T一般取100500交叉概率Pc一般取04099 变异概率Pm一般取0000101最后给出遗传算法的基本步骤①选择二进制编码或浮点数编码把问题的解表示成染色体②随机产生一群染色体个体也就是初始种群③计算每一个个体的适应度值按适者生存的原则从中选择出适应度较大的染色体进行复制再通过交叉变异过程产生更适应环境的新一代染色体群即子代④重复第3步经过这样的一代一代地进化最后就会收敛到最适应环境适应度最大的一个染色体即个体上它就是问题的最优解图2给出了基本遗传算法设计流程图其中t代表当前代数T是进化终止代数图2 基本遗传算法设计流程图3 Matlab遗传算法工具箱 gatoolMatlab的遗传算法工具箱有一个精心设计的图形用户界面可以帮助用户直观方便快速地利用遗传算法求解最优化问题在Matlab命令窗口输入命令gatool可以打开遗传算法工具箱的图形用户界面如图3所示GA工具箱的参数设置步骤如下图3 遗传算法工具1 首先使用遗传算法工具箱必须输入下列信息Fitness function 适应度函数这里指的是待优化的函数也即目标函数该工具箱总是试图寻找目标函数的最小值输入适应度函数的格式为fitnessfun其中符号产生函数fitnessfun的句柄fitnessfun代表用户编写的计算适应度函数目标函数的M文件名该M文件的编写方法如下假定我们要计算Rastrigin函数的最小值7M函数文件确定这个函数必须接受一个长度为2的行向量X也即决策向量向量的长度等于变量数目行向量X的每个元素分别和变量x1和x2对应另外M文件要返回一个标量Z其值等于该函数的值下面是计算Rastrigin函数的M文件代码function Z Ras_fun XZ 20X 1 2X 2 2-10 cos 2piX 1 cos 2piX 2M文件编写保存后再在gatool工具箱界面Fitness function栏输入 Ras_funNumber of variable 变量个数目标函数中的变量数目也即适应度函数输入向量的长度在上例中它的值是22 其次设置遗传算法参数即Options设置以下只介绍部分运行参数的设置其他未提及的参数采用默认设置即可①种群参数 PopulationPopulation size 种群规模每一代中的个体数目一般是20-100之间种群规模大算法搜索更彻底可以增加算法搜索全局最优而非局部最优的概率但是耗时也更长Initial range 初始范围其值是两行的矩阵代表初始种群中个体的搜索范围实际上是决策向量X中每个变量xi的初始搜索范围矩阵的列数等于变量个数Number of variable第一行是每个变量的下限第二行是每个变量的上限如果只输入2 1的矩阵则每个变量的初始搜索范围都一样注意初始范围仅限定初始种群中个体或决策向量的范围后续各代中的个体可以不在初始范围之内初始范围不能设置太小否则造成个体之间的差异过小即种群的多样性降低不利于算法搜索到最优解②复制参数 ReproductionCrossover fraction 交叉概率一般取04099默认08③算法终止准则 Stopping Criteria提供了5种算法终止条件Generations最大的进化代数一般取100500默认是100当遗传算法运行到该参数指定的世代计算终止Time limit指明算法终止执行前的最大时间单位是秒缺省是Inf 无穷大Fitness limit 适应度限当最优适应度值小于或等于此参数值时计算终止缺省是-InfStall generation 停滞代数如果每一代的最佳适应度值在该参数指定的代数没有改善则终止计算缺省是50代Stall time 停滞时间如果每一代的最佳适应度值在该参数指定的时间间隔内没有改善则终止计算缺省是20秒3 设置绘图参数即Plots设置绘图参数Plots工作时可以从遗传算法得到图形数据当选择各种绘图参数并执行遗传算法时一个图形窗口在分离轴上显示这些图形下面介绍其中2个参数Best fitness 选择该绘图参数时将绘制每一代的最佳适应度值和进化世代数之间的关系图如图4的上图所示图中蓝色点代表每一代适应度函数的平均值黑色点代表每一代的最佳值Distance 选择此参数时绘制每一代中个体间的平均距离它反映个体之间的差异程度所以可用来衡量种群的多样性图4的下图显示的即是每一代个体间的平均距离图44 执行算法参数设置好了之后点击工具箱界面上的按钮Star 执行求解器在算法运行的同时Current generation当前代数文本框中显示当前的进化代数通过单击Pause按钮可以使计算暂停之后再点击Resume可以恢复计算当计算完成时Status and results窗格中出现如图5所示的情形图5其中包含下列信息算法终止时适应度函数的最终值即目标函数的最优值Fitness function value 0003909079476983379算法终止原因Optimization terminated imum number of generations exceeded 超出最大进化世代数最终点即目标函数的最优解[x1 x2] [-0004 -000193]两个变量的例子三实验内容1 Rastrigin函数的最小值问题函数表达式如 7 式函数图像如下图6所示它有多个局部极小值但是只有一个全局最小值Rastrigin函数的全局最小值的精确解是0出现在[x1 x2] [0 0]处图6 Rastrigin函数图像使用遗传算法工具箱近似求解Rastrigin函数的最小值首先编写计算适应度函数的M文件然后设置运行参数绘图参数Plots勾选Best fitness和Distance两项其它参数可以使用默认值执行求解器Run solver计算Rastrigin函数的最优值观察种群多样性对优化结果的影响决定遗传算法的一个重要性能是种群的多样性个体之间的距离越大则多样性越高反之则多样性越低多样性过高或过低遗传算法都可能运行不好通过实验调整Population 种群的Initial range 初始范围参数可得到种群适当的多样性取Initial range参数值[1 11]观察Rastrigin函数最小值的计算结果取Initial range参数值[1 100]观察Rastrigin函数最小值的计算结果取Initial range参数值[1 2]观察Rastrigin函数最小值的计算结果2 微带电极欧姆损耗的优化微带电极的欧姆损耗公式可由 1 式表示令设计变量[WDt] [x1 x2 x3] X变量的约束条件如下8根据 1 式和 8 式使用遗产算法工具箱优化设计电极的结构参数W 宽度 D 间距 t 厚度使得电极的欧姆损耗最小 1 式中用到的常数提示对约束条件 8 式的处理可以在编写计算适应度函数的M文件中实现方法是在M文件中引入对每个输入变量值范围的判断语句如果任一变量范围超出 8 式的限制则给该个体的适应度施加一个惩罚使得该个体被遗传到下一代的概率减小甚至为0一般可用下式对个体适应度进行调整9其中F x 是原适应度F x 是调整后的适应度P x 是罚函数为简单计本问题中我们可以给个体的适应度 com件的返回值Z 加上一个很大的数即可如正无穷Inf四思考题1 在遗传算法当中个体的变异对结果有何影响如果没有变异结果又将如何试以Rastrigin函数最小值的计算为例说明取变异概率为0即交叉概率Crossover fraction 102 遗传算法工具箱针对的是最小化函数值问题如果要利用该工具箱计算函数的最大值该如何实现。
用遗传算法实现PID参数整定

控制理论与应用Control Theory and Applications《自动化技术与应用》2004年第23卷第7期用遗传算法实现PID 参数整定万佑红1,李新华2(1.南京邮电学院电子工程系,江苏 南京 210003; 2.安徽大学电子工程系,安徽 合肥 230001)摘要:PI D 参数整定一直是控制领域中的重要研究问题。
本文在M AT LAB 平台上将遗传算法应用于PI D 参数的自动整定,算法实例仿真取得了良好的效果,为PI D 参数整定方法提供了一种新的尝试。
关键词:PI D 参数;遗传算法中图分类号:TP27312 文献标识码:A 文章编号:100327241(2004)0720007202PID Tu nin g Bas e d O n Ge netic Alg orit h m sWAN You -hong 1,LI Xin -hua 2(1.E lectronics Department of Nanjing University of P osting T echnology ,Nanjing 210003,China ;2.E lectronics Department of AnHui University ,Hefei 230001,China )Abstract :A new method to s olve the tuning of PI D paramrters is proposed in this paper.I t is showed that g ood control effect can be obtained by usingG enetic Alg orithms (G A ).K ey w ords :PI D paramrters ;G A1 引言PI D 控制无需知道被控对象的数学模型,算法简单,鲁棒性好且可靠性高,因此成为一种获得广泛应用的控制策略。
Matlab遗传算法及实例

Matlab遗传算法及实例Matlab遗传算法工具箱函数及实例讲解转:最近硏究了一下遗传算法,因为要用遗传算法来求解多元非线性模型。
还好用遗传算法的工具箱予以实现了,期间也遇到了许多问题。
借此与大家分享一下。
首先,我们要熟悉遗传算法的基本原理与运算流程。
基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step 1 :对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step 2 :建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step 3 :在Step 2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step 4 :执行比例选择算子进行选择操作。
Step 5 :按交叉概率对交叉算子执行交叉操作。
Step 6 :按变异概率执行离散变异操作。
Step 7 :计算Step 6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step 8 :判断是否满足遗传运算的终止进化代数,不满足则返回Step 4,满足则输出运算结果其次,运用遗传算法工具箱。
运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库。
目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学幵发的遗传算法工具箱GATBXGAOT以及Math Works公司推出的GADS实际上,GAD鉞是大家所看到的Matlab中自带的工具箱。
基于遗传算的PID参数优化及MATLAB实现

引言PID操纵器结构简单且鲁棒性强,在操纵领域一直被普遍应用。
运算机的进展为在线辩识提供了条件,从而也为在线整定PID参数提供了可能。
PID操纵是工业进程中应用最普遍的策略之一,因此PID 操纵器参数的优化成为人们关注的问题,它直接阻碍操纵成效的好坏,并和系统的平安、经济运行有着密不可分的关系。
目前PID参数的优化方式很多,如:间接寻优法,梯度法,登山法等,而在热工系统中单纯形法、专家整定法那么应用普遍。
尽管二者都具有良好的寻优特性,但却存在一些短处,单纯刑法对初值比较灵敏,容易陷入局部最优解,造成寻优失败。
专家整定法那么需要太多体会,不同的目标函数对应不同的体会,而整理知识库是一项长时刻的工程。
因此咱们选取遗传算法来进行参数寻优,该方式是一种不需要任何初始信息并能够寻求全局最优解的高效的优化组合方式。
第一章:遗传算法和PID操纵原理简介一遗传算法简介大体原理遗传算法是依照生物进化的模型提出的一种优化算法。
遗传算法是从代表问题可能潜在解集的一个群组(popuation)开始的,而一个种群那么由通过基因(gene)编码(coding)的必然数量的个体(individual)组成。
每一个个体事实上是染色体(chromosome)带有特点的实体。
染色体作为遗传物质的要紧载体,即多个基因组合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现。
因此,在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,咱们往往进行简化,如二进制编码。
初代种群产生以后,依照适者生存和优胜劣汰的原理,逐代(genetation)演化产生出愈来愈好的近似解。
在每一代,依照问题域中个体的适应度(fitness)大小挑选(selection)个体,并借助于自然遗传学的遗传算子(genetic operator)进行组合交叉.(crossover)和变异(mutation),产生出代表新的解集的种群。
遗传算法在PID控制方面的应用
计算机科学 Consumer Electronics Magazine 2013 年 4 月下
遗传算法在PID控制方面的应用
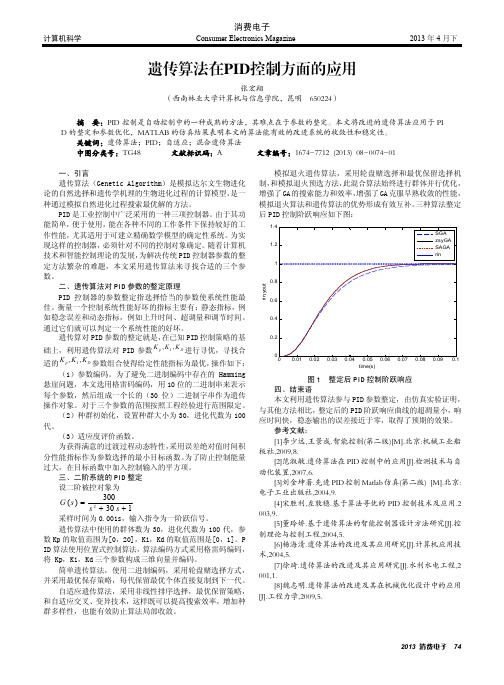
张宏翔 (西南林业大学计算机与信息学院,昆明 650224) 摘 要:PID 控制是自动控制中的一种成熟的方法,其难点在于参数的整定。本文将改进的遗传算法应用于 PI D 的整定和参数优化,MATLAB 的仿真结果表明本文的算法能有效的改进系统的收敛性和稳定性。 关键词:遗传算法;PID;自适应;混合遗传算法 中图分类号:TG48 文献标识码:A 文章编号:1674-7712 (2013) 08-0074-01 一、引言 遗传算法(Genetic Algorithm)是模拟达尔文生物进化 论的自然选择和遗传学机理的生物进化过程的计算模型, 是一 种通过模拟自然进化过程搜索最优解的方法。 PID 是工业控制中广泛采用的一种三项控制器。 由于其功 能简单, 便于使用, 能在各种不同的工作条件下保持较好的工 作性能, 尤其适用于可建立精确数学模型的确定性系统。 为实 现这样的控制器, 必须针对不同的控制对象确定。 随着计算机 技术和智能控制理论的发展, 为解决传统 PID 控制器参数的整 定方法繁杂的难题,本文采用遗传算法来寻找合适的三个参 数。 二、遗传算法对 PID 参数的整定原理 PID 控制器的参数整定指选择恰当的参数使系统性能最 佳。衡量一个控制系统性能好坏的指标主要有:静态指标,例 如稳念误差和动态指标,例如上升时间、超调量和调节时间。 通过它们就可以判定一个系统性能的好坏。 遗传算对 PID 参数的整定就是, 在已知 PID 控制策略的基 础上,利用遗传算法对 PID 参数
1.4 SGA zsyGA SAGA rin
1.2
1
rin,yout
0.8
matlab模拟中央空调pid遗传算法

一、引言中央空调系统在现代建筑中扮演着至关重要的角色,对空调系统的控制效率和性能要求也越来越高。
PID控制器作为一种经典的控制算法,被广泛应用于中央空调系统中。
而遗传算法作为一种全局搜索和优化的方法,具有一定的优势和应用前景。
MATLAB作为一个功能强大的模拟工具,提供了丰富的工具箱和函数,可以用于模拟和优化中央空调系统的PID控制器参数。
二、MATLAB模拟中央空调PID控制器1. 使用MATLAB进行中央空调系统建模在MATLAB环境中,可以利用Simulink工具箱进行中央空调系统的建模。
建立空调系统的传递函数模型,包括室内外温度传感器、风机、制冷剂循环等部件,以及控制器的输入输出。
这一步可以帮助工程师理解系统的动态特性,并为下一步的控制器设计做准备。
2. 设计PID控制器在MATLAB中,可以利用Control System Toolbox设计PID控制器。
根据已建立的系统模型,利用PID Tuner或者手动调节的方式,得到合适的比例、积分和微分系数,使得系统能够快速、稳定地响应温度变化。
3. 仿真系统响应利用Simulink工具箱对设计的PID控制器进行仿真,观察系统的响应特性。
可以通过改变温度变化输入信号,观察系统的温度响应、控制器输出等参数,并评估PID控制器性能的优劣。
三、遗传算法在PID参数优化中的应用1. 遗传算法原理及优化遗传算法是一种模拟生物进化过程的优化方法,其基本思想是通过种群的选择、交叉和变异等操作,实现对问题的全局搜索和优化。
在PID参数优化中,可以利用遗传算法搜索合适的控制器参数,使得系统的性能指标达到最优。
2. MATLAB中的遗传算法工具MATLAB提供了遗传算法工具箱,可以方便地使用遗传算法对问题进行优化。
用户可以自定义适应度函数、遗传算子等参数,也可以选择内置的优化函数进行快速优化。
3. 将遗传算法与PID控制器相结合通过将遗传算法与PID控制器相结合,可以实现对PID参数的优化。
基于遗传算法寻优的PID控制及MATLAB仿真

基于遗传算法寻优的PID控制及MATLAB仿真
牛理想;扈晓利;王高平
【期刊名称】《电子质量》
【年(卷),期】2008(000)012
【摘要】文中介绍了遗传算法和基于遗传算法寻优的PID控制设计,采用误差绝对值时间积分性能指标作为参数选择的最小目标函数,利用遗传算法的全局搜索能力,使得在无须先验知识的情况下实现对全局最优解的寻优.以降低PID参数整定的难度.达到总体上提高系统的控制精度和鲁棒性的目的.通过MATLAB仿真结果表明,根据遗传算法寻优设计的PID控制器其有较强的鲁棒性,即使在外部环境恶劣的条件下,系统的控制性能仍具有较好的动态品质和稳态精度.
【总页数】3页(P7-9)
【作者】牛理想;扈晓利;王高平
【作者单位】河南工业大学,河南,郑州,450001;河南工业大学,河南,郑州,450001;河南工业大学,河南,郑州,450001
【正文语种】中文
【中图分类】TB11
【相关文献】
1.基于遗传算法寻优的PID控制与仿真 [J], 秦国经;任庆昌
2.基于遗传算法的锅炉水温PID控制寻优 [J], 李玉娜
3.基于混合遗传算法的转台PID控制寻优 [J], 杨明
4.基于遗传算法的PID控制及其MATLAB仿真 [J], 赵亮; 付兴武; 徐广明
5.基于非线性模型和遗传算法寻优的无人艇航向PID控制研究 [J], 王亮;向金林;王鸿东
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
遗传算法在调节控制系统参数中的应用【摘要】自动化控制系统多采用PID 控制器来调节系统稳定性和动态性,PID 的Kp,Ki,Kd 参数需要合理选择方能达到目标。
遗传算法是一种模拟生物进化寻求最优解的有效算法,本文通过利用GAbx 工具箱实现对控制电机的PID 进行参数优化,利用matlab 的仿真功能可以观察控制效果。
1. 直流伺服电机模型 1.1物理模型图1 直流伺服电机的物理模型αu ---电枢输入电压(V ) a R ---电枢电阻(Ω) S L ---电枢电感(H ) q u ---感应电动势(V ) g T ---电机电磁转矩(N m ⋅) J---转动惯量(2m kg ⋅)B---粘性阻尼系数(s m N ⋅⋅) g i ---流过电枢的电流(A ) θ---电机输出的转角(rad )1.2传递函数利用基尔霍夫定律和牛顿第二定律得出电机基本方程并进行拉布拉斯变换)()()()()()()()()()()(2s s K s U K s I s T s Bs s Js s T s I s L R s I s U s U e q t a g g a a a a q a θθθ⋅=⋅=⋅+⋅=⋅+⋅=-式中:t K 为电机的转动常数(m N ⋅)A ;e K 为感应电动势常数(s V ⋅)rad图2 直流伺服电机模型方框图消去中间变量得系统的开环传递函数:sK K B Js R s L K s U s s G C t a d ta ]))([()()()(+++==θ系统参数如下:s m uN B m mg J ⋅⋅=⋅=51.3,23.32A m N K K uH L R e t a a )(03.0,75.2,4⋅===Ω=2. PID 校正图3 PID 校正s K sK K s G d ip c ++=)( Kp,Ki,Kd 为比例,积分,微分系数 令Kp=15、Ki=0.8 、Kd=0.6M 文件:J=3.23E-6;B=3.51E-6; Ra=4;La=2.75E-6; Kt=0.03; num= Kt;den=[(J*La) ((J*Ra)+(La*B)) ((B*Ra)+Kt*Kt) 0]; t=0:0.001:0.2; step(num,den,t); Kp=15; Ki=0.8; Kd=0.6;numcf=[Kd Kp Ki]; dencf=[1 0];numf=conv(numcf,num); denf=conv(dencf,den);[numc,denc]=cloop(numf,denf); t=0:0.001:0.04; step(numc,denc,t);matlab 进行仿真,我们可以看出不恰当的PID 参数并不能使系统达到控制系统的要求,因此需要对PID参数进行优化。
图4 系统阶跃响应(Kp=15,Ki=0.8,Kd=0.6)3.遗传算法3.1 遗传算法和工具箱简介遗传算法(GA)是基于自然选择和基因遗传学原理的优化搜索方法。
它借鉴了达尔文的进化论和孟德尔的遗传学说。
其本质上是一种高效、并行、全局搜索的方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优解。
遗传算法操作使用适者生存的原则,在潜在的解决方案种群中逐次产生一个近似最优的方案。
在遗传算法的每一代中,根据个体在问题域中的适应度值和从自然遗传学中借鉴来的再造方法进行个体选择,产生一个新的近似解。
在这个过程导致种群中个体的进化,得到的新个体比原个体更能适应环境,就像自然界中的改造一样。
表3.1遗传学和遗传算法中基本用语对照表英国谢菲尔德大学开发的遗传算法工具箱把参数,选择,交叉,变异等过程封装成函数进行操作,其基本搜索过程不变。
表3.2 遗传算法工具箱常用函数3.2 利用遗传算法优化过程1)根据遗传算法优缺点这里选择遗传代数为100,种群大小为30,变量维数为3其中10≤Kp ≤20,0≤Ki ≤1, 0≤Kd ≤1,要求精度0.0001所以二进制串编码长度为17故Kp 精度为(20-10)/(-1) Ki,Kd 精度为(1-0)/(-1),代沟为0.9,交叉概率为0.6,变异概率为0.01。
2)适应度函数的设计PID 优化设计的目的是使系统某些性能指标最优,然而,单纯的误差性能指标很难同时满足系统对快速性、稳定性和鲁棒性的要求,因此在适应度函数中引入超调量、上升时间和累计绝对误差指标项。
设σ=(|y p -y ref |/y ref )×100%为系统的超调量,y p 和y ref 分别为输出峰值和输入参考值;t *r 为上升时间,将其定义为输出从0第1次达到0.95yref 的时间;e k =y k -y ref 为采样时刻k 的输出误差;w j (j=1,2,3)为权重系数。
则多目标适应度函数为:∑=++=nk k r e w t w w f 13*21σ (5)通过对权重系数的调整,可以改变系统对快速性和稳定性的要求。
如系统要求较小的超调,可以适当增大w 1;若系统要求快速的动态响应,则可以适当增大w 2。
计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用,需要采用离散化方法。
在计算机PID 控制中,使用的是数字PID 控制器。
图3.2 增量式PID 控制系统增量式PID 控制是数字控制器的输出只是控制器的增量△u(k)。
当执行机构需要的是控制量的增量时,应采用增量式PID 控制,采样时刻点kT (T 为采样周期)代表连续时间t 。
做如下近似变换来离散化:()()00()()(1)k tj t kT e t Te j de t e k e k dtT =⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩=≈--≈∑⎰ 可得离散的PID 表达式:1(1)(2)(1)(1)()k pi d j e k e k u k k e k k e j T k T==----=-++∑增量式PID 控制算法: ()2(1)(2)()(()(1))()e k e k e k u k k p e k e k k i e k T k dT--+-∆=--++ 增量式PID 控制算法不需多次累加,控制增量△u(k)仅与最近3次得采样有关,所以误动作时的影响相对较小图3.3 基于GA 算法参数调整的PID 控制系统采样时间取1ms ,为获取满意的过渡过程动态特性,采用误差绝对值时间积分性能指标作为参数选择的目标函数。
为防止控制量过大,在目标函数中加入控制输入的平方项。
选用下式作为参数选取的最优指标20(0.999|()|0.001())2uJ e t u t dt t ∞=++⎰()e t 为系统偏差,()u t 为PID 控制器输出,u t为上升时间。
为避免超调了,采用惩罚功能,一旦产生超调,将超调量作为最优指标的一项,此时最优指标为20()0(0.999|()|0.001()100|()|)2uif e t J e t u t e t dt t ∞<=+++⎰J 值越小,对应的PID 参数越优良。
但是,由于GA 算法用于求解最大值问题,所以需要对J 做一个简单变形,从而得到算法的适应度函数:1f J =3)依据遗传算法的步骤编写程序并仿真图3.4 BestKpKiKd优化值时的阶跃响应图3.5 J随进化代数的变化曲线图3.6 优化得到BestKpKiKd及此时的LeastJ4.程序代码1.GA.m文件%GA(Generic Algorithm) Program to optimize Parameters of PIDclcclear all;close all; %清除命令,变量,关闭窗口global rin yout timef %输入,输出,离散时间%******Initialization******%MAXGEN=100; %遗传代数NIND=30; %种群大小NVAR=3; %变量维数PRECI=17; %变量精度GGAP=0.9; %代沟(Generation gap)Pc=0.6; %交叉概率Pm=0.01; %变异概率FieldD=[PRECI,PRECI,PRECI;10,0,0;20,1,1; 1,1,1;0,0,0;1,1,1;1,1,1]; %区域描述器Chrom=crtbp(NIND,NVAR*PRECI); %初始种群for i=1:1:MAXGENgen(i)=i; %遗传代数%****** Step 1 : Evaluate LeastJ ******KpKiKdlsj=bs2rv(Chrom,FieldD); %各代种群由二进制串转化为实值for j=1:1:NINDJ=0;KpKiKd=KpKiKdlsj(j,:);[KpKiKd,J]=pidf(KpKiKd,J); %计算本代种群中各个个体的目标函数值Lsj(j,1)=J;end[OderLsj,IndexLsj]=sort(Lsj); %本代种群中各个个体的目标函数值升序排列genlstj(i)=OderLsj(1); %升序排列中第一个最小,为本代最优BestKpKiKd=KpKiKdlsj(IndexLsj(1),:);%BestKpKiKdLsj=Lsj+1e-10; %Avoiding deviding zero 1*10^(-10)Msj=1./Lsj; %设置适应度函数[OderMsj,IndexMsj]=sort(Msj); %Arranging fi small to bigger适应度值升序排列genmost=OderMsj(NIND) ; % Let Bestfi=max(fi)升序中最后一个最大,为本代最优moststring=Chrom(IndexMsj(NIND),:); %本代中对应最优的PID参数%****** Step 2 : Select and Reproduct Operation******FitnV = ranking(Lsj); %分配适应度值(Assign fitness values)SelCh=select('sus',Chrom,FitnV,GGAP); %选择%************ Step 3 : Crossover Operation ************SelCh=recombin('xovsp', SelCh,Pc); %交叉%************ Step 4: Mutation Operation **************SelCh=mut(SelCh,Pm); %变异SelCh(NIND,:)=moststring; %保证交叉后的新种群Temp2包含原种群中的最优个体%*************Step 5:Reinsert Operation***************ObjV=FitnV;KpKiKdlsj=bs2rv(SelCh,FieldD); %计算ObjVSelfor j=1:1:NINDJ=0;KpKiKd=KpKiKdlsj(j,:);[KpKiKd,J]=pidf(KpKiKd,J);Lsj(j,1)=J;endLsj=Lsj+1e-10;Msj=1./Lsj;ObjVSel=Msj;[Chrom ObjV] = reins(Chrom, SelCh, 1, 1, ObjV,ObjVSel); %重插入endLeastJ=genlstj(MAXGEN) %最优目标函数值(性能指标)BestKpKiKd %最优PID参数(实值)figure(1);plot(gen,genlstj);xlabel('gen(s)');ylabel('genlstj');figure(2);plot(timef,rin,'r',timef,yout,'b');xlabel('Time(s)');ylabel('rin,yout');2.pidf.m函数文件function [KpKiKd,J]=pidf(KpKiKd,J)global rin yout timeftz=0.001;sys=tf(0.03,[8.8825e-12,1.2920e-05,9.1404e-04,0]);zsys=c2d(sys,tz,'z');[num,den]=tfdata(zsys,'v');rin=1.0;u_1=0.0;u_2=0.0;u_3=0.0;y_1=0.0;y_2=0.0;y_3=0.0;K=[0,0,0]';error_1=0;Tup=1;m=0;final=100;for t=1:1:finaltimef(t)=t*tz;r(t)=rin;u(t)=KpKiKd(1)*K(1)+KpKiKd(2)*K(2)+KpKiKd(3)*K(3);if u(t)>=10u(t)=10;endif u(t)<=-10u(t)=-10;endyout(t)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3; error(t)=r(t)-yout(t);%------------ Return of PID parameters -------------u_3=u_2;u_2=u_1;u_1=u(t);y_3=y_2;y_2=y_1;y_1=yout(t);K(1)=error(t); % Calculating PK(2)=(error(t)-error_1)/tz; % Calculating DK(3)=K(3)+error(t)*tz; % Calculating Ierror_1=error(t);if m==0if yout(t)>0.95&yout(t)<1.05Tup=timef(t);m=1;endendendfor t=1:1:finalJ=J+0.999*abs(error(t))+0.001*u(t)^2; if t>1erry(t)=yout(t)-yout(t-1);if erry(t)<0J=J+100*abs(erry(t));endendendJ=J+2*Tup;。
