旋转倒立摆虚拟仿真模型构建与验证
自动化实验-倒立摆实验-附仿真结果图

一、直线一级倒立摆的仿真(一)直线一级倒立摆的数学建模对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难。
但是忽略掉一些次要的因素后,倒立摆系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
下面我们采用其中的牛顿-欧拉方法和拉格朗日方法分别建立直线型一级倒立摆系统的数学模型.图2 直线一级倒立摆模型φ摆杆与垂直向上方向的夹角;θ摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)。
图3 小车及摆杆受力分析分析小车水平方向所受的合力,可以得到以下方程:由摆杆水平方向的受力进行分析可以得到下面等式:把这个等式代入式1中,就得到系统的第一个运动方程:为了推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:力矩平衡方程如下:注意:此方程中力矩的方向,由于θ=π+φ,cosφ= −cosθ,sinφ= −sin θ,故等式前面有负号。
合并这两个方程,约去P 和N,得到第二个运动方程:设θ=π+φ(φ是摆杆与垂直向上方向之间的夹角),假设φ与1(单位是弧度)相比很小,即φ<〈1,则可以进行近似处理:。
用u 来代表被控对象的输入力F,线性化后两个运动方程如下:对式9进行拉普拉斯变换,得到注意:推导传递函数时假设初始条件为0。
由于输出为角度φ,求解方程组的第一个方程,可以得到:或如果令v = x,则有:把上式代入方程组的第二个方程,得到:整理后得到传递函数:其中设系统状态空间方程为:方程组对解代数方程,得到解如下:整理后得到系统状态空间方程:设则有:实际系统的模型参数如下:M 小车质量1。
096 Kgm 摆杆质量0.109 Kgb 小车摩擦系数0 。
1N/m/secl 摆杆转动轴心到杆质心的长度0。
2 5mI 摆杆惯量0。
0034 kg*m*m把上述参数代入,可以得到系统的实际模型。
摆杆角度和小车位移的传递函数:摆杆角度和小车加速度之间的传递函数为:摆杆角度和小车所受外界作用力的传递函数:以外界作用力作为输入的系统状态方程:(二)倒立摆的PID调节:经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型。
倒立摆系统虚拟样机仿真

第 5 期 ( 第 1 4期 ) 总 4 20 0 7年 1 O月
机 械 工 程 与 自 动 化
M ECHANI CAL ENGI NEERI NG & AUT0M AT1 0N
No. 5 Oc . t
文 章 编 号 :6 26 1 ( 0 7 0 —0 30 1 7—4 3 2 0 )50 5 —3
2 倒 立摆 系统 模糊 控制 器 的设计 [ 2 ]
2 1 变 量 和 隶 属 度 函数 的确 定 .
收 稿 日期 {2 0 —22 ;修 回 日期 :2 0 —42 0 61 —2 0 70 —3
模糊 推理 采 用最 大一 最小 推理 方法 ,解 模糊 采用
中心 法 。
作者简介 ;孟巧荣 (9 4) 女 , 1 7 一 , 山西朔州人 , 讲师 , 博士研究生 , 主要从事岩石显微 C T微观测试研究 。
和初始摆角对其动态特性 的影响 。 关 键 词 :虚 拟 样 机 ; 倒 立 摆 ;仿 真 中 图 分 类 号 :T 3 19 P 9. 文 献 标 识 码 :A
0 引 言
首 先 确定 倒 立 摆 系 统 的输 入 变 量 为 摆 的 角 位 移
、
倒 立摆 系统 的仿 真研 究 一般 都建 立在 数 学模 型的 基础 上 , 由于倒 立摆 系统 本身 是一 高 阶非线 性 系统 , 而 模 型是 建立 在线 性化基 础 之 上的 , 二者 之 间存 在误 差 , 为了使 仿真 能尽 可能 地反 映 实际 系统 的 动态过 程 ,减 小 误差 , 文采用 ADAMS建 立 倒立 摆 系统 的虚拟 样 本 机 模型 , MAT 在 I AB中设计 控 制器 , 将二者 结 合起 来
两轮移动式倒立摆机器人系统结构及模型设计

两轮移动式倒立摆机器人系统结构及模型设计宋昌统【摘要】倒立摆是典型的非线性控制系统,集机器人技术、人工智能技术、计算机控制技术于一体,两轮倒立摆是一种两轮式左右并行布置结构的自平衡系统。
采用DSP最小系统实现控制模块的设计,采用倾角传感器、陀螺仪、编码器等保持系统的自平衡,通过它们测量和计算出小车的状态参数。
进而通过微分计算出小车左、右车轮的角速度,再通过控制系统与PC机之间的通信,得出倒立摆系统的控制规律和运动模型,在平衡点附近对系统进行线性化处理,得到系统的运动仿真曲线,并分析系统的稳定性和能控性。
%Inverted pendulum is a typical nonlinear control system,integrating robot technology,artificial intelli-gence technology and computer control technology.Two-wheel inverted pendulum is a self-balanced system with a structure of two wheels paralleled on the right and left.Design by using DSP minimum system control module is to keep self-balance of the system through the angle sensor Takahashi Ji,multi variable,strong coupling and strong robustness for nonlinear systems,with which to measure and calculate parameters of cars and then calculate the angular velocity of right and left wheels.The communication between the control system and the PC machine is used to decide the control law and the motion model of the inverted pendulum system.Near the equilibrium point,the system is linearized to get the motion simulation curve of the system and analyze the system stability and controllability.【期刊名称】《镇江高专学报》【年(卷),期】2014(000)001【总页数】3页(P56-58)【关键词】倒立摆;自平衡;传感器;指令【作者】宋昌统【作者单位】镇江高等专科学校电子与信息工程系,江苏镇江 212003【正文语种】中文【中图分类】TP242移动机器人是机器人学的重要分支。
基于MATLAB的单级旋转倒立摆建模与控制仿真
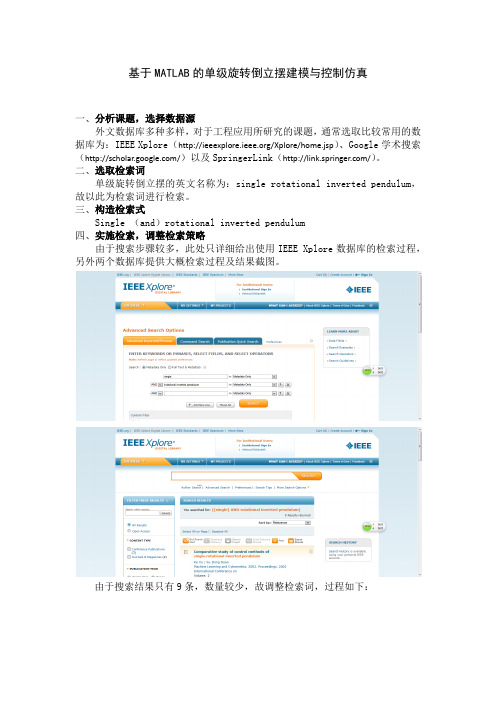
基于MATLAB的单级旋转倒立摆建模与控制仿真一、分析课题,选择数据源外文数据库多种多样,对于工程应用所研究的课题,通常选取比较常用的数据库为:IEEE Xplore(/Xplore/home.jsp)、Google学术搜索(/)以及SpringerLink(/)。
二、选取检索词单级旋转倒立摆的英文名称为:single rotational inverted pendulum,故以此为检索词进行检索。
三、构造检索式Single (and)rotational inverted pendulum四、实施检索,调整检索策略由于搜索步骤较多,此处只详细给出使用IEEE Xplore数据库的检索过程,另外两个数据库提供大概检索过程及结果截图。
由于搜索结果只有9条,数量较少,故调整检索词,过程如下:Google学术搜索:SpringerLink数据库:五、检索结果1、题目:Analysis of human gait using an Inverted Pendulum Model基于倒立摆模型的人体步态分析Zhe Tang ; Meng Joo Er ; Chien, C.-J. Fuzzy Systems, 2008. FUZZ-IEEE 2008. (IEEE World Congress on Computational Intelligence). IEEE International Conference onAbstract: IPM(Inverted Pendulum Model) has been widely used for modeling of human motion gaits. There is a common condition in most of these models, the reaction force between the floor and the humanoid must go through the CoG (Center of Gravity) of the a humanoid or human being. However, the recent bio-mechanical studies show that there are angular moments around the CoG of a human being during human motion. In other words, the reaction force does not necessarily pass through the CoG. In this paper, the motion of IPM is analyzed by taking into consideration two kinds of rotational moments, namely around the pivot and around the CoG. The human motion has been decomposed into the sagittal plane and front plane in the double support phase and single support phase. The motions of the IPM in these four different phases are derived by solving four differential equations with boundary conditions. Simulation results show that a stable human gait is synthesized by using our proposed IPM.摘要:IPM(倒立摆模型)已被广泛用于人体运动步态建模。
现代控制理论大作业-倒立摆模型建立与仿真(深圳大学)

深圳大学实验报告课程名称:现代控制理论实验项目名称:倒立摆模型建立与仿真学院:机电与控制工程学院专业:自动化指导教师:***报告学号:班级:实验时间:实验报告提交时间:教务部制一、 实验目的(1)实验一:增强状态空间表达式的理解和应用,通过直线型一级倒立摆系统的具体对象,展现非线性系统线性化的应用和特点,提高仿真计算和应用Matlab 进行系统分析的能力,并为后续章节的有关系统稳定性提供感性认识。
(2)实验二:了解采用状态反馈改善系统性能的方法,应用状态反馈方法配置直线型一级倒立摆系统的极点,设计控制器,并在倒立摆系统实验平台上实现一级倒立摆系统稳定运行。
二、 实验任务与要求(1)实验一建立倒立摆的非线性状态空间表达式; 建立倒立摆的线性状态空间表达式;在两种模型下,在matlab simulink 平台上通过仿真计算给出摆角和直线位移的运动曲线,位移的初始为零,摆角的初始值分别选取如下:20πθ≤, 20πθ≥, πθ=0(2)实验二针对一级倒立摆系统,对于给定的动态性能指标(调节时间小于3秒,阻尼比0.5)确定闭环极点(参考值,32,32,10,10j j --+---),设计系统状态反馈阵的参数; 在倒立摆系统平台上完成极点配置控制实验。
实验要保持倒立状态,当系统受到扰动后仍保持稳定。
记录控制结果曲线,并进行讨论。
重新选择一组(或多组)期望的闭环极点,设计系统状态反馈阵的参数,在倒立摆系统平台上完成极点配置控制实验,记录控制结果曲线,并和第二条的实验结果进行比较分析。
三、 实验原理(1)实验参见固高《倒立摆与自动控制原理实验》(2)若受控系统(A,B)完全能控,则通过状态反馈可以任意配置闭环极点。
实验设计原理参见固高《倒立摆与自动控制原理实验》第82-89页 。
四、 实验步骤及过程(1) 非线性状态方程系统方程:1/(M+m )=0.82988;1/(I+ml^2)=97.91922;m*g*l=0.26705;m*l=0.02725 将系统模型参数代入,可得以下仿真下载后图片可放大X 和φ输出的响应曲线(红为x ,黄为φ) 当20πθ≤,取40πθ=当20πθ≥,取430πθ=当πθ=0(2)线性状态方程可以看出,在单位阶跃响应作用下,小车位置和摆杆角度都是发散的。
小车倒立摆模型建立及初步仿真

实验名称:小车倒立摆模型建立及初步仿真一、写出模型推导过程下面N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量。
分析小车水平方向所受的合力,可得到方程为:N x b F xM --= (1) 由摆杆水平方向的受力进行分析可以得到下面等式:()θθθθθsin cos sin 222ml ml xm N l x dtd m N -+=+= (2) 把这个等式代入(1)式中,得到系统的第一个运动方程:()F ml ml x b xm M =-+++θθθθsin cos 2 (3) 为了推出系统的第二个运动方程,对摆杆垂直方向的合力进行分析,得到下面的方程:()θcos 22l dtd m mg P =- θθθθcos sin 2 ml ml mg P --=- (4) 力矩平衡方程如下:θθ I Nl Pl =--cos sin (5) 方程中力矩的方向,由于φπθ+=,θφθφsin sin ,cos cos -=-=,故等式前面有负号。
合并这两个方程,约去P 和N ,得到第二个运动方程:()θθθcos sin 2x ml mgl ml I -=++ (6) 假设φ与1(单位是弧度)相比很小,即1〈〈φ,则可进行近似处理:0,sin ,1cos 2=⎪⎭⎫ ⎝⎛-=-=dt d θφθθ 用u 代表被控对象的输入力,线性化后两个运动方程如下:()()⎪⎩⎪⎨⎧=-++=-+u ml x b x m M x ml mgl ml I φφφ 2 (7) 对方程(7)进行拉普拉斯变换,得到:()()⎪⎩⎪⎨⎧=-++=-+)()()()()()()(22222s U s s ml s s bX s s X m M s s mlX s mgl s s ml I φφφ (8) (推到时假设初始条件为0)则,摆杆角度和小车位移的传递函数为:mgl s ml I mls s X s -+=222)()()(φ 摆杆角度和小车加速度之间的传递函数为:()mgl s ml I ml s A s -+=22)()(φ 摆杆角度和小车所受外界作用力的传递函数:22432222()()()()()()ml s s q b I ml M m mgl bmgl F s s s s s q q qq M m I ml m l φ=+++--⎡⎤=++-⎣⎦进行开环响应的仿真:M=0.5 kg m=0.2kg b=0.1 N/m/s l=0.3mI=0.006 kg m 2 T=0.005 s(采样时间)s s s s s s F s 4545.41818.311818.05455.4)()(2342--+=φ二、开环响应的MATLAB仿真程序%reverse_pedulumn_TF.m%倒立摆传递函数、开环极点及开环脉冲响应%transfuction=num/denM=0.5;m=0.2;b=0.1;I=0.006;g=9.8;l=0.3;q=(M+m)*(I+m*l^2)-(m*l)^2;%calculate the poly transfunctionnum=[m*l/q 0 0]den=[1 b*(I+m*l^2)/q -(M+m)*m*g*l/q -b*m*g*l/q 0]my_tf=tf(num,den)%calculate the polars p[r,p,k]=residue(num,den);s=p%the pulse reponse of the transfunction and displayt=0:0.005:5;impulse(num,den,t)%step(num,den,t)%display the field: lateral 0-1,longititudal 0-60axis([0 1 0 60])grid%---------end----------Matleb仿真图像三、摆杆质量m=0.5kg、1kg时,MATLAB传递函数表示、开环极点及脉冲响应曲线图1、m=0.5kg2、m=1kg。
二级倒立摆数学模型的建立与仿真培训资料
二级倒立摆数学模型的建立与仿真二级倒立摆数学模型的建立与仿真专业:控制工程姓名:淡丹学号:1406073摘要本文用分析力学中牛顿力学法及拉格朗日方程建立了二级倒立摆的数学模型。
根据已经建立的倒立摆数学模型,对其进行了可控性,可观测性及稳定性的分析与研究,并对状态反馈及状态观测器进行了仿真模拟,分析研究。
并通过分析比较得出,加状态观测器并不影响系统的输出的结论。
关键词:倒立摆状态空间极点配置状态反馈ABSTRACTNewtonian mechanics analysis method and the Lagrange equation of a mathematical model of double inverted pendulum has been used in this paper. According to the established mathematical model of inverted pendulum on the controllability, observability and stability of the analysis and research, and the state observer and state feedback is carried on the simulation ,analysis and research. And through the analysis and comparison of results, plus state observer does not affect the conclusions of the output of the system.KEY WORDS: inverted pendulum state space pole allocation state feedback一、二级倒立摆系统的组成二级倒立摆主要由以下四部分组成:1.在有限长的轨道L上作直线运动的小车;2.与小车铰接在一起,并能在竖直平面内分别绕q,q点转动的下、上摆;3.驱动小车的直流力矩电机和转轮、钢丝等传动部分;4.使上、下摆稳定在垂直向上的平衡位置,且使小车稳定在轨道中心位置附近的控制器。
倒立摆系统建模及MATLAB仿真
倒立摆系统的建模及MATLAB仿真通过建立倒立摆系统的数学模型,应用状态反馈控制配置系统极点设计倒立摆系统的控制器,实现其状态反馈,从而使倒立摆系统稳定工作。
之后通过MA TLAB 软件中Simulink工具对倒立摆的运动进行计算机仿真,仿真结果表明,所设计方法可使系统稳定工作并具有良好的动静态性能。
倒立摆系统是1个经典的快速、多变量、非线性、绝对不稳定系统,是用来检验某种控制理论或方法的典型方案。
倒立摆控制理论产生的方法和技术在半导体及精密仪器加工、机器人技术、导弹拦截控制系统和航空器对接控制技术等方面具有广阔的开发利用前景。
因此研究倒立摆系统具有重要的实践意义,一直受到国内外学者的广泛关注。
本文就一级倒立摆系统进行分析和研究,建立倒立摆系统的数学模型,采用状态反馈极点配置的方法设计控制器,并应用MA TLAB 软件进行仿真。
1 一级倒立摆系统的建模1. 1 系统的物理模型如图1 所示,在惯性参考系下,设小车的质量为M ,摆杆的质量为m ,摆杆长度为l ,在某一瞬间时刻摆角(即摆杆与竖直线的夹角)为θ,作用在小车上的水平控制力为f 。
这样,整个倒立摆系统就受到重力,水平控制力和摩擦力的3 外力的共同作用。
图1 一级倒立摆物理模型1. 2 系统的数学模型在系统数学模型中,本文首先假设:(1) 摆杆为刚体。
(2)忽略摆杆与支点之间的摩擦。
(3)忽略小车与导轨之间的摩擦。
然后根据牛顿第二运动定律,求得系统的运动方程为:方程(1) , (2) 是非线性方程,由于控制的目的是保持倒立摆直立,在施加合适的外力条件下,假定θ很小,接近于零是合理的。
则sinθ≈θ,co sθ≈1 。
在以上假设条件下,对方程线性化处理后,得倒立摆系统的数学模型:1. 3 系统的状态方程以摆角θ,角速度θ',小车的位移x ,速度x'为状态变量,输出为y 。
即令:则一级倒立摆系统的状态方程为:2 控制器设计及MATLAB 仿真2. 1 极点配置状态反馈的基本原理图2 状态反馈闭环控制系统极点配置的方法就是通过一个适当的状态反馈增益矩阵的状态反馈方法,将闭环系统的极点配置到任意期望的位置。
倒立摆系统的建模及Matlab仿真
倒立摆系统的建模及Mat I ab仿真1o系统的物理模型考虑如图(1)所示的倒立摆系统。
图中,倒立摆安装在一个小车上。
这里仅考虑倒立摆在图面内运动的二维问题.I ©y/ m7I //・____ I _____ ■ I T| L// 符 ._________________ . • ;___________/ / / / / / / / / / / / / / "/ / Z-7 / / /图(1)倒立摆系统假定倒立摆系统的参数如下。
摆杆的质量:m二0. lg摆杆的长度:rim小车的质量:H二lkg重力加速度:g=9. 8m/52摆杆的质量在摆杆的中心.设计一个控制系统,使得当给定任意初始条件(由干扰引起)时,最大超调量§ W10%,调节时间ts W4s ,通过小车的水平运动使倒立摆保持在垂直位置.2o系统的数学模型2。
1建立倒置摆的运动方程并将其线性化。
为简化问题,在数学模型中首先假设:1)摆杆为刚体;2)忽略摆杆与支点之间的摩擦;3)忽略小车与接触面间的摩擦。
设小车瞬时位置为z,摆心瞬时位置为(z + /sin&),在u作用下,小车及摆均产生加速远动,根据牛顿第二定律,在水平直线远动方向的惯性力应与u平衡,于是有• 2,2M+ m(Z + / sin 0) = udr dr即:(M + m)z + mlOcosO - mlO1 sin 0 = u①绕摆轴转动的惯性力矩与重力矩平衡,因而有・ IcosO =Ml y = x \ = [i 0 ojv = Cx代入数据计算得到:_0 1 00 0-1 A =0 0 0 0 0 110 ;,B = [0 1 0 一 lf,C = [l 0 0即:Zcos& + /Qcos? 0-101 sin&cos& = gsin& ②以上两个方程都是非线性方程,为求得解析解,需作线性化处理。
山于控制的LI 的是保持倒立摆直 立,在试驾合适的外力条件下,假定0很小,接近于零时合理的,则Sin% &COS& 2 1,且可忽略026项。
倒立摆仿真及实验报告
最优控制实验报告二零一五年一月目录第1章一级倒立摆实验 (3)1.1 一级倒立摆动力学建模 (3)1.1.1 一级倒立摆非线性模型建立 (3)1.1.2 一级倒立摆线性模型建立 (5)1.2 一级倒立摆t∞状态调节器仿真 (5)1.3 一级倒立摆t∞状态调节器实验 (9)1.4 一级倒立摆t∞输出调节器仿真 (11)1.5 一级倒立摆t∞输出调节器实验 (13)1.6 一级倒立摆非零给定调节器仿真 (14)1.7 一级倒立摆非零给定调节器实验 (16)第2章二级倒立摆实验 (16)2.1 二级倒立摆动力学模型 (16)2.1.1 二级倒立摆非线性模型建立 (17)2.1.2 二级倒立摆线性模型建立 (18)2.2 二级倒立摆t∞状态调节器仿真 (19)2.3 二级倒立摆t∞状态调节器实验 (21)2.4 二级倒立摆t∞输出调节器仿真 (22)2.5 二级倒立摆t∞输出调节器实验 (22)2.6 二级倒立摆非零给定调节器仿真 (23)2.7 二级倒立摆非零给定调节器实验 (24)第1章一级倒立摆实验1.1一级倒立摆动力学建模在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如图所示图1-1 直线一级倒立摆模型M小车质量1.096 kg;m 摆杆质量0.109 kg;b 小车摩擦系数0 .1N/m/sec;l 摆杆转动轴心到杆质心的长度0.25m;I 摆杆惯量0.0034 kg·m2;φ摆杆与垂直向上方向的夹角,规定角度逆时针方向为正;x 小车运动位移,规定向右为正。
1.1.1一级倒立摆非线性模型建立采用拉格朗日方法,系统的拉格朗日方程为:()()()=-(1.1)L q q T q q V q q,,,其中,L为拉格朗日算子,q为系统的广义坐标,T为系统的动能,V为系q和L表示为:统的势能。
拉格朗日方程由广义坐标ii i id L Lf dt q q ∂∂-=∂∂ (1.2)i f 为系统沿该广义坐标方向上的外力,在本系统中,系统的两个广义坐标分别为φ和x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转倒立摆虚拟仿真模型构建与验证作者:任桢林都李静来源:《现代电子技术》2019年第06期关键词:旋转倒立摆; 刚体建模; 虚拟仿真; SimMechanics; 系统辨识; 试验验证中图分类号: TN915.5⁃34; N945.12; TP391.9 ; ; ; ; 文献标识码: A ; ; ; ; ; 文章编号:1004⁃373X(2019)06⁃0060⁃05Abstract: A modeling method based on the combination of the Matlab virtual simulation and test data is proposed, and the validity of model establishment is verified using physical objects, so as to solve the problem of deviation between theoretical modeling and engineering application of the rotary inverted pendulum. The rigid body model of the inverted pendulum is obtained by connecting Solidworks with Matlab, and the electromechanical part is added in the SimMechanics, so as to obtain the ideal model of the system at the unstable equilibrium point by means of linearization. The system parameters are identified on the basis of physical object test, so as to obtain the simulation model. The pendulum swinging and stabilization algorithms are studied for the inverted pendulum on the basis of the model. The test results show that the virtual simulation model can visually display and record the changes of the system variables, and there exists only a small gap in overall response when compared with the physical structure of the actual inverted pendulum.Keywords: rotary inverted pendulum; rigid body modeling; virtual simulation; SimMechanics; system identification; test verification倒立摆是一种经典实验装置,对该系统的稳定控制研究可以推广到四轴飞行器、双足机器人及柔性机械臂等欠驱动控制领域。
当前国内对倒立摆实物控制的研究多基于商业设备的先进算法验证,数学建模过程简化[1⁃4]。
目前国内外关于广义系统的建模方法有三种:通过分析运行过程的机理建模,基于实验数据的数据建模与二者交叉使用的混合建模。
其中机理建模方法由于存在预先设定的假设理想条件,得到的模型与实际过程存在较大偏差。
而数据建模方法不考虑机理过程,通过分析已有过程的输入输出数据,得出模型结构。
该方法简化了建模流程,但对存在非线性特征的系统,数据拟合代价过大,精度上也存在误差。
混合建模综合了二者优点,在理想化的机理模型基础上,配合系统辨识与参数估计,得到较为精确的数学模型。
该过程在工程上应用广泛[5⁃6]。
使用混合建模方法,本文提出一种基于计算机辅助设计软件的旋转倒立摆建模过程,在数学模型基础上设计了控制器,将获得的控制增益部署到嵌入式硬件验证了模型与控制器的有效性。
本文以中北大学电气与控制工程学院现代控制工程研究室自行设计的单级旋转倒立摆实验平台作为研究对象,机械结构使用Solidworks完成,如图1所示。
系统机理建模是在与实物一致的机械结构基础上,通过动力学方程,在不稳定平衡点附近等效近似并线性化得到。
使用文献中的动力学方程近似上有很大误差,采用Solidworks导出刚体模型可以在最大程度上减少近似带来的误差。
物体运动主要由质量定义,在Solidworks中修改参数得到与实际一致的机械结构。
在SimMechanics中,零件需要相對于地面在三维空间设置约束关系。
该约束对应于Solidworks装配体的配合(Mate)属性。
对于单级旋转倒立摆,其活动部分为绕电机轴和绕摆杆轴转动的零件集合,该集合对应于两个绕轴线活动的旋转关节。
为得到与实物一致的虚拟仿真模型,需要在Solidworks装配体结构中定义配合属性。
零件属性如表1所示。
对具有相同转轴的相邻零件采用同心方式配合,转轴位置如图2中Revolute,Revolute1所示。
两关节均绕对应坐标系的Z轴旋转,其中CS坐标系对应悬臂(电机轴)转角,以θ表示;CS1坐标系对应摆杆轴转角,以α表示。
两坐标系使用顺时针为旋转正方向。
通过在Matlab R2014内安装Simscape Multibody Link插件程序,可以实现由Solidworks导出可供仿真的多体模型[7]。
多体模型是描述零件间刚性约束关系的框架结构,结构的驱动需要电机提供动力,对应于对底部与悬臂间的旋转关节Revolute施加激励。
关节激励有转矩或旋转角度输入型两种,由于电机实质是一种输入电压,输出转矩的能量转换媒介,故关节激励使用转矩的形式施加。
施加激励信号的多体模型在Simulink内计算得到旋转动作,动作包含关节的转角与转速信息,在关节感知栏中选中对应选项,整理得到系统刚体结构的仿真模块。
仿真模型如图3所示。
倒立摆使用一台小型直流电机驱动,直流电机与负载电路如图4所示。
图中Vm为控制电压,直流电机输出轴与旋转负载相连,负载包含减速器、固定安装的悬臂及活动的摆杆部件,等效转动惯量为JL。
电机反电动势Ve由转速ω决定,它的方向与电流方向相反,公式如下:本文介紹并实现了一种基于Matlab虚拟仿真的单级旋转倒立摆建模过程。
首先配置导出的装配体结构,得到系统机理模型。
然后通过非线性环节补偿与数据拟合得到较为精确的数学模型。
最后在仿真环境与实物上验证了模型的准确性,确保建模方法的科学性。
参考文献[1] 刘薇,郝彬,王跃灵.基于ESO的旋转倒立摆全局终端滑模控制[J].控制工程,2018,25(1):106⁃111.LIU Wei, HAO Bin, WANG Yueling. Global terminal sliding mode control based on extended state observer for rotary inverted pendulum systems [J]. Control engineering of China,2018, 25(1): 106⁃111.[2] 刘慧博,蔡蕊.直线二级倒立摆基于线性矩阵不等式算法的滑模鲁棒H∞控制[J].科学技术与工程,2014,14(5):270⁃275.LIU Huibo,CAI Rui. Sliding mode and robust h∞ control based on LMI algorithm for linear double inverted pendulum [J]. Science technology and engineering, 2014, 14(5): 270⁃275.[3] 王瑶为,邢科新,马剑,等.直线一级倒立摆的自抗扰控制方法及实现[J].控制工程,2017,24(4):711⁃715.WANG Yaowei, XING Kexin, MA Jian, et al. Implementation and design of active disturbance rejection control for the linear inverted pendulum [J]. Control engineering of China,2017, 24(4): 711⁃715.[4] 聂卓赟,刘瑞娟.复杂条件下倒立摆摆角控制设计与实验研究[J].信息与控制,2016,45(4):506⁃512.NIE Zhuoyun, LIU Ruijuan. Inverted pendulum angle control design and experimental studies under complex conditions [J]. Information and control, 2016, 45(4): 506⁃512.[5] 郭盛,梁艺瀚,王志群,等.基于虚拟仿真的并联构型手控器动力学建模与力反馈控制[J].机器人,2015,37(2):224⁃230.GUO Sheng, LIANG Yihan, WANG Zhiqun, et al. Dynamic modeling and force⁃feedback control of haptic device with parallel structure based on virtual simulation [J]. Robot, 2015, 37(2): 224⁃230.[6] 王英波,黄其涛,郑书涛,等.Simulink和SimMechanics环境下并联机器人动力学建模与分析[J].哈尔滨工程大学学报,2012,33(1):100⁃105.WANG Yingbo, HUANG Qitao, ZHENG Shutao, et al. Dynamic modeling and analysis of a parallel manipulator using Simulink and SimMechanics [J]. Journal of Harbin Engineering University, 2012, 33(1): 100⁃105.[7] 姚太克.一类三自由度并联机构的特性研究与优化设计[D].合肥:中国科学技术大学,2013.YAO Taike. Performance analysis and optimal design of a class of parallel mechanisms with 3 degrees of freedom [D]. Hefei: University of Science and Technology of China, 2013.[8] 丁锋.辅助模型辨识方法(5):最小二乘辨识[J].南京信息工程大学学报(自然科学版),2016,8(5):385⁃403.DING Feng. Auxiliary model based identification methods⁃Part E: Least squares identification [J]. Journal of Nanjing University of Information Science & Technology (Natural science edition), 2016, 8(5): 385?403.[9] OLEJNIK P, AWREJCEWICZ J, FECKAN M. Modeling, analysis and control of dynamical systems with friction and impacts [M]. Geneva: World Scientific Publishing Company,2017.[10] MATHEW N J, RAO K K, SIVAKUMARAN N. Swing up and stabilization control of a rotary inverted pendulum [C]// Proceedings of the 10th IFAC International Symposium on Dynamics and Control of Process Systems. Mumbai: IFAC, 2013: 654⁃659.。
