活性污泥反应动力学及其应用
第四章 (4.3)活性污泥反应动力学

图中的生化反应可以用下式表示:
S yX zP
及
dX dS y dt dt
即
dS 1 dX dt y dt
式中:反应系数 y 又称产率系数,mg(生物量)/mg(降解的 dS 底物)。 该式反映了底物减少速率和细胞增长速率之间的关系,是废水生物处理 中研究生化反应过程的一个重要规律。
(4-29)
V
1 ds X dt
∵
r V max r Vmax Vmax max r
V
V:比降解速率
∴
1 maxS max S S Vmax r r KS S r KS S KS S
(4-30)
∴
有机底物降解速度
XS e ds Vmax dt K S Se
(4-41)
(4-42)
将( 4 42) 代入( 4 40) 式后:
并在等式两边同时除以X得出:
Vmax
XSe Q( S 0 S e ) K S Se V
Vmax
Se Q(S 0 S e ) (S 0 S e ) K S Se XV Xt
的变化
∴动力学是研究讨论下列函数关系:
S V Vmax KS S ds f s, x XS dt ds V max dt KS S
S max KS S dx g(S, X) XS dt dx max dt KS S
S0 Se K 2Se Xt S0 Se K 2Se Xt Se (1 K 2 Xt )
有机物地残留率
去除率
活性污泥反应动力学及其应用26页PPT

2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
活性污泥反应动力学及其应用 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
பைடு நூலகம்
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
活性污泥反应动力学及工艺的设计与计算

主要假设:
曝气池中呈完全混合状态; 活件污泥系统运行条件绝对稳定; 活性污泥在二次沉淀池内不产生微生物代谢
活动,而且其量不变; 处理系统中不含有有毒物质和抑制物质。
莫诺特(Monod)方程式 法国学者Monod于1942年采用纯菌种在培养基稀溶
液中进行了微生物生长的实验研究,并提出了微生物生 长速度和底物浓度间的关系式:
此时,μ ∝S,与底物浓度呈一级反应。
(3)随着底物浓度逐步增加,微生物增长速度和
底物浓度呈μ =μ maxS/Ks+S关系,即不成正比关系,
此时0<n<1为混合反应区的生化反应。
上述研究结果,与米—门方程式十分相近。 米—门方程式为: V=VmaxS/Ks+S monod方程的结论使米一门方程式引入了
∴ µ=YV µmax=YVmax; 带入μ=μmaxS/Ks+S 得: V=VmaxS/Ks+S 即米一门方程式。
劳伦斯—麦卡蒂模式的基础概念
建议的排泥方式 有两种剩余污泥排放方式: 传统的排泥方式; 劳伦斯—麦卡蒂推荐的排泥方式。
第二种排泥方式的主要优点在于减轻二次沉 淀池的负荷,有刊于污泥浓缩,所得回流污泥 的浓度较高。
(2)参数选择 在进行曝气池(区)容积计算时,应在一定的范围内合
理地确定污泥负荷和混合液悬浮固体浓度,此外.还应同 时考虑处理效率、污泥容积指数(SVl)和污泥龄等参数。 污泥负荷的的取值应低于0.2kgBOD/(kgMLVSS d)。
2 需氧量和供气量的计算 (1)需氧量 活性污泥法处理系统的日平均需氧量(Q)和去除每 kgBOD的需氧量(⊿Q)可分别按动力学公式计算.也可 根据经验数据选用。
曝气沉淀池的构造设计
曝气沉淀池多呈圆形并用表面机械曝气装置。在 构造设计方面有下列基本要求。
2.4 活性污泥反应动力学及应用
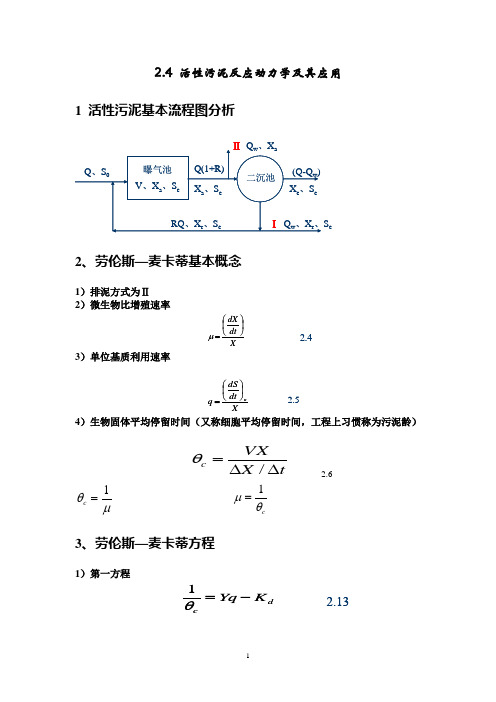
2.4 活性污泥反应动力学及其应用1 活性污泥基本流程图分析S e2、劳伦斯—麦卡蒂基本概念1)排泥方式为Ⅱ2)微生物比增殖速率⎛μXdt dX ⎪⎭⎫ ⎝= 2.43)单位基质利用速率⎛=Xdt dS q u ⎪⎭⎫ ⎝ 2.54)生物固体平均停留时间(又称细胞平均停留时间,工程上习惯称为污泥龄)tX VXc ∆∆=/θ 2.6μθ1=ccθμ1=3、劳伦斯—麦卡蒂方程1)第一方程dcK Yq -=θ12.132)第二方程K =⎫⎛S S X q dt dS s au+⎪⎭ ⎝m ax 2.154、劳伦斯—麦卡蒂基本方程式的应用1)确立处理水基质浓度(S e )与生物固体平均停留时间(θc )之间的关系(1)全混流⎫=K K ⎪⎪⎭⎝⎛+-⎪⎪⎭⎫⎝⎛+dcd c s eYv K S θθ11m ax 2.16(2)推流式S 对推流式deos e o e o cK S K S S S S v Y-+--=ln)()(1m ax θ 2.172)确立微生物浓度(X )与生物固体平均停留时间θc 之间的关系(1)全混流)1()(c d e o c K S S Y t X θθ+-=2.18(2)推流 X对推流式(反应器内微生物浓度采用其平均值)。
)1()(c d e o c K S S Y t X θθ+-=2.193)确立活性污泥回流比(R )与生物固体平均停留时间(θc )之间的关系)1(=++-dt dXV X R Q RQX a r⎪⎪⎭⎫⎝⎛-+=a r c X X R R V Q 11θ 10S V IX r 6m a x)(=4)总产率(Y )与表现产率(Y obs )之间的关系()q X dt dS X dtdX dS dXdt dS dt dXY uu uμ=⎪⎭⎫⎝⎛==⎪⎭⎫⎝⎛=dX ()uobsdS Y '=2.23=11cd d c obs K Y K Y Y θμθ++⨯=2.245)θc 值与Se 值及E 的关系1dc K Yv -=m ax m in)(θ 2.266)(2.32)式便于用以求定曝气池的容积(V )qX S S Q V a e )(0-=5、动力学参数的测定maxmax 011v S v K S S tXe S e +⎪⎪⎭⎫ ⎝⎛∙⎪⎪⎭⎫ ⎝⎛=-dcK Yq -=θ16、例题。
活性污泥法污水处理数学模型的发展和应用

活性污泥法污水处理数学模型的发展和应用活性污泥法污水处理数学模型的发展和应用污水处理是国家和社会发展中的一个重要环节。
随着工业化和城市化进程的加快,污水处理厂的建设和运行愈加重要。
活性污泥法是目前应用最广泛的一种污水处理技术,它通过活性污泥微生物群落的代谢活动来去除水中的有机物质和氮、磷等污染物。
为了更好地设计和运行活性污泥法污水处理系统,科学家们开展了大量的研究,并发展了一系列的数学模型。
本文将探讨活性污泥法污水处理数学模型的发展和应用。
首先,要了解活性污泥法的基本原理。
在活性污泥法污水处理系统中,活性污泥是核心元素。
活性污泥中的微生物以有机物为能源,通过氧化、还原反应分解有机物,从而将污水中的有机物质降解为水和二氧化碳。
此外,活性污泥还可以通过硝化和反硝化过程将水中的氨氮转化为硝酸盐和氮气,并通过磷酸盐的沉淀去除水中的磷。
因此,了解活性污泥的代谢特性和微生物群落结构对于优化污水处理系统非常重要。
由于活性污泥法处理系统的复杂性和实际运行中的不确定性,传统经验模型的优化和改进已经不能满足实际需求。
因此,科学家们开始研究并发展了数学模型,以预测和模拟活性污泥法处理系统的性能。
这些数学模型包括质量平衡模型、动力学模型和群体动力学模型等。
质量平衡模型是最基本的数学模型之一,它基于质量守恒原理,以质量浓度的变化作为变量,描述污水中有机物质和污染物的传输和转化。
质量平衡模型可以用来优化活性污泥污染物的去除效率,提高系统的稳定性和可靠性。
然而,质量平衡模型无法描述微生物群落的动态变化和相互作用。
为了更好地描述活性污泥法处理系统中微生物的动态行为,科学家们发展了动力学模型。
动力学模型以微生物群落的代谢过程为基础,通过微分方程组描述了有机物质和污染物的转化动力学。
这些模型可以用来预测系统的稳态和响应速度,优化供碳、氮和磷源的进料方式,提高活性污泥的处理效率。
群体动力学模型是动力学模型的进一步发展,它考虑了微生物群体内部的异质性和互作。
2活性污泥反应动力学及其应用(二)09

1、活性污泥系统运行条件处于稳定状态 2、活性污泥在二次沉淀池内不产生微生物代谢活动 3、系统中不含有毒性物质和抑制物质 4、进水底物浓度保持恒定 5、全部生物可降解的底物处于溶解状态
Lawrence-McCarty
VX c X / t
反应器内微生物总量
2.6
△X—每天从系统中排出增殖的微生物总量;mg
X—反应器内微生物浓度,mg/l
2.4.3 劳伦斯—麦卡蒂模式的基本概念
针对两种不同的排泥方式 传统方式
Lawrence-McCarty
一般Xe值很低,可以 忽略
VX a c Qw X r (Q Qw ) X e
2.4.2
活性污泥反应动力学基础
假设:微生物比增殖速率(μ)与基质比降解速率(v)呈比例关 系,即
v
基质比降解速率(v),可以用莫诺模式加以描述:
v vmax
S Ks S
2.3
v 式中: -基质比降解速率,d-1 ;
vmax
-基质最大比降解速率,d-1 。
对废水处理来说,有机物的降解是其基本目的,因此,式2.3的实 际意义较大
max
零级 反应 区 混合级反应区 (n=0) (0<n<1)
max S
Ks S
2.2
1 max 2
μ— 微生物比增殖速率,d-1;
μ max—微生物最大比增殖速率,d-1;
S— 溶液中限制微生物生长的基质浓度, mg/L、g/m3;
活性污泥法动力学

浅谈好氧活性污泥法在污水治理中的应用随着城市化程度的不断深化,人口压力的逐步提高。
我国环境污染的情况也越来越严峻。
党和国家已经将环境保护确立为我国的基本国策之一。
目前,按照要素分类,环境污染主要包括大气污染、水体污染和土壤污染。
针对水体污染的治理,直接关系到人民群众的用水健康和环境的可持续发展。
传统的污水处理方法,较难直接分解污染物,残留量较高,容易造成二次污染;同时,成本较高,设备较为复杂。
而欠发达地区通常使用的方法是利用自然水体的自身净化能力对受到污染的水体进行净化,这种方法对自然环境的破坏较大,过多依赖水体的自然净化能力,不符合可持续发展的战略目标。
而新兴的微生物活性污泥法,因为其设备简单,投资较低,污水净化效率高,二次污染少等优势,得到了广泛的应用与认可。
并在实践中不断发展。
一、水体自净和活性污泥法自然界中的水体是存在自我净化的能力的。
当水体中存在一些有机污染物的时候。
水中的浮游生物、紫外线照射等影响因素就可以使有污染性的有机物转变为无害的简单物质。
使水体质量恢复到受到污染之前的水平。
这就是水体自净。
但是,水体自净是存在一个污染浓度的上限的。
也就是说,自然界的水体存在一定的自净容量。
超过自净容量的水体污染就不能被水体的自净能力所消化。
因此,自净容量就是指在水体正常生物循环过程中能够净化有机污染物的最大数量。
基于以上思路,我们可以人为扩大水体的自净容量。
这就引出了活性污泥法在污水处理中的应用。
活性污泥法,是利用活性污泥中的好氧生物,对污水中的污染物进行氧化还原。
使之变为无害化产物的过程。
将曝气池与二次沉淀池进行串联,并且将污泥管与之回联。
使得二次沉淀池中沉淀的污泥回流到曝气池中。
使这些污泥以及其中的活性成分能够在曝气池中起到凝聚、吸附的作用。
同时,其中的微生物能够使曝气池中的有害化学成分进行氧化分解。
这就是活性污泥法的基本原理和概念。
二、活性污泥法的基本原理活性污泥法是利用悬浮生长的微生物絮体处理废水的一类好氧生物处理方法,生物絮体称活性污泥。
13-2活性污泥反应动力学基础水质工程学

生物处理动力学研究新进展
– 近年来,应用数学工具建立数学模型对活性 污泥系统的复杂过程进行模拟。1983年国 际水污染研究和控制协会(IAWPRC)成立 课题组,对已有的悬浮生长反应器的模型进 行评估从中提出切合实际、可以在实践当中 应用的数学模型,专家组经过3年的研究于 1986年推出ASM1,相继于1995年推出 ASM2,1999年推出ASM3。
c
完全混合活性泥 反应器内活性污 泥的浓度X与污 泥龄的关系为:
θcY (S0 − Se ) X= t(1+ Kdθc )
开题报告 — 25
Eckenfelder模式和Lawrence-McCarty模式都 是针对完全混合活性污泥系统得出的一些有 意义的结论,不适用于推流型反应器。 例如在推流式反应器中:污泥龄与衰 减系数有如下关系:
其中q的物理意义是:单位微生物量对有机底 物的降解速率,也即比降解速率。
开题报告 — 22
Hale Waihona Puke 通过对完全混合活性污泥系统进行物料衡算, 通过对完全混合活性污泥系统进行物料衡算 , 结合Lawrence-McCarty方程式得出如下结 结合 方程式得出如下结 论:
由
1 ds = Y (− ) − Kd = Yq − Kd θc X dt 1
活性污泥法的概念开题报告2开题报告3开题报告4活性污泥法的物料平衡开题报告5生物处理动力学和数学建模的意义在废水生物处理系统的功能设计中往往采用经验与半验方法这些方法未能反应生化过验与半经验的方法这些方法未能反应生化过程中各种变量之间的相互关系设计带有一定的盲目性难以经济合理的设计污水处理系统也难以预测和指导处理系统的运行和管理
经整理后得:
开题报告 — 17
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2.2
有机物降解与需氧量
在曝气池内,活性污泥微生物对有机物的氧化分解和其自 身氧化都是需氧过程。这两部分氧化过程所需要的氧量,一般 用下列公式求定 :
△o2 = a QSr
式中 ΔO2 —— a —— b —— kgO2/d 表示;
b XV
(9)
混合液需氧量,其量纲为 [ 质量 ][ 时间 ]-1 ,一般用 活性污泥微生物对有机物氧化分解过程的需氧率,
从活性污泥法处理系统的工程实践要求考虑,对活 性污泥反应动力学的研讨重点在于“确定生化反应速率与各 项主要环境因素之间的关系”,研讨的主要内容是: ( 1 ) 有机物的降解速率与有机物浓度、活性污泥 微生物量等因素之间的关系; ( 2 ) 活性污泥微生物的增殖速率(亦即活性污泥 的增长速率)与有机物浓度、微生物量等因 素之间的关系。 ( 3 ) 微生物的好氧速率与有机物降解、微生物量 等因素之间的关系。
ν
ν ν ν
S KS S
max
ν
( 13 )
—— 底物的比降解速率, [ 时间 ]-1 ,常用 h-l 或 d-1 表示 ; —— 底物的最大比降解速率, [ 时间 ]-1 ,常用 h-l 或 d-1 表 max 示;
对于完全混合式曝气池,底物的比降解速率,按物理 意义考虑,下式成立:
ν
dt t
b q
1
( 11 )
o2
——
去除每 kgBOD 的需氧量, [ 质量 ][ 质量 ]-1[ 时间 ]-1 , 用 kgO2/(kgBOD·d) 表示。
QSr
一般
从上式可看出,当在高 BOD 比降解速率条件下运行时,活 性污泥的污泥龄较短,每降解单位重量( 1kg ) BOD 的需氧量 就较低。这是因为在高负荷条件下,一部分被吸附而未被摄入细 胞体内的有机物随剩余污泥排出。此外,在高负荷条件下,活性 污泥微生物的自身氧化作用很低,因此,需氧量较低。
即活性污泥微生物每代谢 1kgBOD 所需氧量的 kg 数; 每千克活性污泥单位时间进行自身氧化所需的氧的 千克数,即污泥自身氧化需氧速率,其量纲为 [ 时 间 ]-1 ,一般用 d-1 表示。
( 9 )式可改写为下列两种形式
QSr = a XV XV
△o2
b = aq
b
( 10 )
生活污水的 a 值为 0.42 ~ 0.53 , b 值介于 0.10 ~ 0.20 之间
令
Sr= S0 — Se
-1
Sr —— 污水中被利用的有机物浓度,其量纲为 [ 质量 ][ 体积 ] △X XV
,一般用 kg/
m3 表示。将( 5 )式各项以 XV 除之,则上式变为
= Y
Q Sr
XV
Kd
(6)
BOD 比降解速率 q ,其量纲与污泥负荷相同,单位用 kgBOD/ ( kgMLSS· d )表示。
对 活性污 泥反应动 力学进 行研讨 的目的
明确各项因素对反应速率的影响,使人们能够创造更适宜于 活性污泥系统内生化反应进行的环境条件,使反应能够在比较 理想的速率下进行,使活性污泥法处理系统的设计和运行更合 理化和科学化。 对反应机理进行研究,探讨活性污泥对有机物的代谢、降解 过程,揭示这一反应过程的本质,使人们能够更自觉地对反应速 率加以控制和调节。
4.3.3
莫诺 特公式在完全混合曝气池中的应 用
完全混合曝气池内的活性污泥一般处在减衰增殖 期。此外,池内混合液中的有机物浓度是均一的, 并与出水的浓度( Se )相同,其值较低,有 Se<S "。因此,采用式( 19 )是适宜的。
进水
Q , S0
完全混合式活性污泥法处理系统 V , Se , X Q+RQ 曝气池 二沉池 Se , X
Q(S0 Se) XV
根据完全混合曝气池的 特征,式( 15 )可改写, 即以 Se 代入式中之 S , 得:
=
(S0
Xt
Se)
= K Se
2
( 22 )
ds
X Vmax Se = K dt S Se
( 23 )
代入式( 21 )得:
Q(S0 Se) XV
=
(S0
Xt
S e)
Vmax Se = KS Se
ν=ν
ds
dt
max
S
KS
= K2 S
= K2 SX
( 19 )
从式( 18 )可见,底物降解 速率与底物浓度呈一级反应, ( 18 ) 底物浓度已成为底物降解的限 制因素。因为在这种条件下, 混合液中底物浓度已经不高, 微生物增殖处于减衰增殖期或 内源呼吸期,微生物酶系统多 未被饱和,
K2=VMAX/KS, 量纲为 [ 体积 ][ 质量 ]-1[ 时间 ]-1 ,一般用 m3/ ( kg·d ) 或 L/ ( mg·h )表示。
4.4.1 劳伦 斯 - 麦卡蒂( lawrence - McCarty )模型的基本概 念
4.4 劳伦 斯 - 麦卡蒂( lawrence - McCarty ) 模型
微生物比增殖速率
单位重量微生物(活性污泥)的增殖速率,即比增殖速率,仍以 µ
表 示。以
dX
dt
表示微生物的增殖速率,则 µ 值为 :
进水
Q , S0
曝气池
Q+RQ Se , X
二沉池
处理水
Q-QW Se , Xe
回流污泥
RQ , Se , Xr
剩余污泥排放
Qw , Xr
Q—— 污水流量; S0—— 原污水底物浓度; Se—— 处理水底物浓度; X—— 曝气池内活性污泥浓度; R—— 污泥回流比; Xr—— 回流污泥浓度; V—— 曝气池的有效容积; Qw—— 排泥量; Xe—— 处理水中的污泥浓度
4.3
4.3.1
莫诺特( Monod )公 式
莫诺 特公式及其推广应 用
max
max
2
莫诺特于 1942 年和 1950 年曾两次用纯种的微生物在单一 底物的培养基上进行微生物增 殖速率与底物浓度之间关系的试 验。得出了如右图所示的形式。 这个结果和米凯利斯 - 门坦于 1 913 年提出的酶促反应速率与 底物浓度之间的关系是相同的。
△
o2
——
单位重量活性污泥的需氧量, [ 质量 ][ 质量 ]-1[ 时间 ]-1 一般用 kgO2/(kgMLVSS·d) 表示;
XV
,
从上式可以看出,在 BOD 比降解速率高,污泥龄短时, 每 kg 活性污泥的需氧量较大,也就是单位容积曝气池的需氧 量较大。
△o2
QSr
△
= a
XV b = a QSr
活性污泥微生物增殖的基本方程式为:
dX dt
g
= Y
dS dt u
Kd X
(4)
活性污泥微生物每日在曝气池内的净增殖量为:
△X
Y S0-Se ) Q = (
Kd V X
(5)
Se
经活性污泥法处理系统处理后,处理水中残 留的有机物浓度, [ 质量 ][ 体 积 ]-1 一般用 kgBOD/m3 ;
完全混合式活性污泥法处理系统 V , Se , X
概述 第三节
活性污泥反应动力学及其应用
反应动 力学的理论 基础 莫诺 特公式及其推广应 用 劳伦 斯-麦卡蒂(lawrence-McCarty)模型
IWA(国际 水协 会) 的活性污 泥法动 力学模型
4.1 概述
活性污泥反应动力学通过数学式定量或半定量地揭示活 性污泥系统内有机物降解、污泥增长等与设计运行参数、环境因 素之间的关系,对工程设计与优化运行管理有着一定的指导意 义。 有关的动力学模型都是以完全混合式曝气池为基础建立 的,经过修正后再应用到推流式曝气池系统。 ⑴ ⑵ ⑶ ⑷ 在建立活性污泥反应动力学模型时,作了以下假定: 活性污泥系统运行处于稳定状态; 活性污泥在二沉池内不进行代谢活动且泥水分离良好; 进入系统的有毒物质和抑制物质不超过其毒阈浓度; 进入曝气池的原污水中不含活性污泥。
( 24 )
本书提到的动力学参数 K2 、 µmax 、 Vmax 、 Ks 、 Y 、 Kd 、 a 和 b 等各值,在特定条件下,对于特定的污水来说,为一 常数值。本书中的底物一般指有机物,可用 BOD 、 COD 或 TOC 等指标表示;污泥浓度也可用 MLSS 或 MLVSS 等表示。 当采用不同指标时,与其对应的上述动力学参数的数值也有所不 同,因为动力学参数的量纲和单位中包含着不同的指标因素。
ν=ν
max
( 16 )
ds dt
νmax X K1 X
( 17 )
式中 vmax 为常数值,以 K1 表示。
在高底物浓度的条件 下,底物以最大的速率进 行降解,而与底物浓度无 关,呈零级反应关系。即右 图上所表示的底物浓度大 于 S’ 时的情况。底物浓度 进一步提高,比降解速率 也不会提高,因为在这一条 件下,微生物处于对数增 殖期,其酶系统的活性位 置都被底物所饱和。
4.2
4.2.1
反应动 力学的理论 基础
有机物降解与活性污泥微生物增殖
活性污泥微生物的增殖是微生物合成反应和内源代谢两 项生理活动的综合结果。因此,单位曝气池容积内,活性污 泥的净增殖速率为:
dX dt
g
=
dX dt
_
s
dX dt
e
(1)
dX dt s dS dt u
可用下式计算:
dX = dt s
在稳定条件下,对系统中的有机物进行物料平衡,得:
QS0 + RQSe
经整理后,得:
(Q+RQ)Se
V
0 = dt
ds
( 20 )
Q(S0 V
