活性污泥法的反应动力学原理及其应用
活性污泥法

2 活性污泥法有效运行的基本条件
① 废水中含有足够的可溶性易降解有机物; ② 混合液含有足够的溶解氧; ③活性污泥连续回流,使混合液保持一定浓度的活 性污泥,及时排除剩余污泥; ④ 活性污泥在池内呈悬浮状态; ⑤ 无有毒有害的物质流入。
3 活性污泥的基本性质
物理性能:“菌胶团”、“生物絮凝体”; 颜色:褐色、(土)黄色、铁红色; 气味:泥土味(城市污水); 比重:略大于1(1.0021.006); 粒径:0.020.2 mm; 比表面积:20100cm2/ml; 含水率:99.299.8%。
活性污泥微生物增长曲线
内源呼吸期
量
污泥浓度 氧利用率
BOD浓度
对数增长期 减速增长期
时间
四个生长阶段特点
(1)迟缓期:表示细菌适应新环境需要的时间, (2)对数增长期:由于营养物浓度超过细菌的需 要量,生长不受限制,生物量以对数速度增加, (3)减速增长期:由于营养物浓度随细菌的消 耗逐渐下降,细菌繁殖世代时间增长,毒性代 谢产物逐渐增高,当营养物浓度达到生长限度 时,细菌即进入减速生长期。 (4)内源呼吸期:串长阶段到内源呼吸期时, 营养物耗尽,迫使细菌代谢自身的原生质,生 物量逐渐减少。
活性污泥净化反应过程
活性污泥去除水中有机物,主要经历三 个阶段: 吸附阶段 氧化阶段 絮凝体形成与凝聚沉淀阶段
吸附阶段:
污水与活性污泥接触后的很短时间内水中有 机物(BOD)迅速降低,这主要是吸附作用引 起的。 由于絮状的活性污泥表面积很大(约200010000m2/m3混合液),表面具有多糖类粘液 层,污水中悬浮的和胶体的物质被絮凝和吸 附迅速去除。活性污泥的初期吸附性能取决 于污泥的活性。
4 活性污泥中的微生物
活性污泥法的工作原理

活性污泥法的工作原理
活性污泥法是一种常用的废水处理技术,其工作原理如下:
1. 污水进入活性污泥池:废水首先被引导进入活性污泥池,其中含有大量的微生物(活性污泥)。
这些微生物能够通过吸附、吞噬、分解等方式处理废水中的有机物。
2. 微生物降解有机物:活性污泥中的微生物通过与废水中的有机物接触,利用有机物作为能源进行生长和繁殖。
微生物分解有机物的主要过程包括:好氧降解和厌氧降解。
在好氧条件下,微生物需氧进行有机物的分解;在缺氧或无氧条件下,微生物可利用硝酸盐、硫酸盐等物质进行有机物的分解。
3. 混合与搅拌:为了保持污泥颗粒的悬浮状态,活性污泥池通常会进行混合与搅拌。
这有助于提供足够的氧气和营养物质到微生物中,使其能够正常生长和降解有机物。
4. 沉淀和分离:经过一段时间的降解后,污水中的微生物和其它固体悬浮物会逐渐沉淀到底部形成污泥。
然后,通过调节沉淀污泥与水的比例,可以将污泥分离出来,从而使净化后的水体流向下一个处理单元。
5. 污泥处理:将分离出来的活性污泥送入消化池或污泥浓缩池中进行进一步处理。
消化池用于进一步降解活性污泥中的有机物,而污泥浓缩池则用于将污泥的固体含量提高,减少处理所需的体积。
6. 净化水体排放:经过活性污泥法处理后,废水中的有机物质得到了有效去除,达到了排放标准。
因此,净化后的水体可以安全地排放或进一步处理,达到再利用的水平。
2.4 活性污泥反应动力学及应用
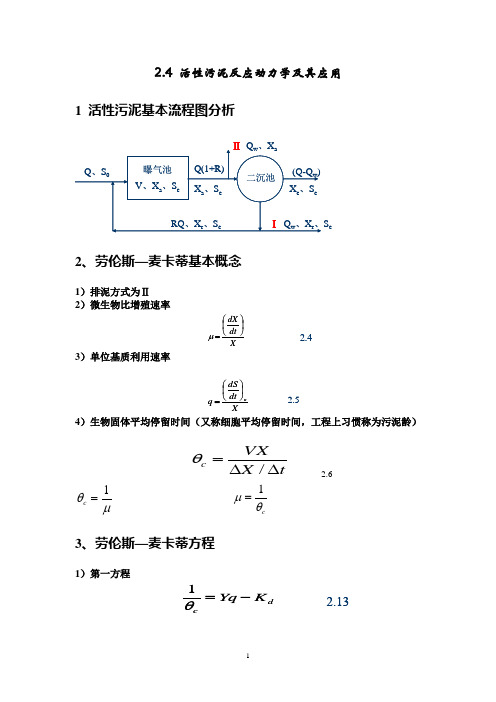
2.4 活性污泥反应动力学及其应用1 活性污泥基本流程图分析S e2、劳伦斯—麦卡蒂基本概念1)排泥方式为Ⅱ2)微生物比增殖速率⎛μXdt dX ⎪⎭⎫ ⎝= 2.43)单位基质利用速率⎛=Xdt dS q u ⎪⎭⎫ ⎝ 2.54)生物固体平均停留时间(又称细胞平均停留时间,工程上习惯称为污泥龄)tX VXc ∆∆=/θ 2.6μθ1=ccθμ1=3、劳伦斯—麦卡蒂方程1)第一方程dcK Yq -=θ12.132)第二方程K =⎫⎛S S X q dt dS s au+⎪⎭ ⎝m ax 2.154、劳伦斯—麦卡蒂基本方程式的应用1)确立处理水基质浓度(S e )与生物固体平均停留时间(θc )之间的关系(1)全混流⎫=K K ⎪⎪⎭⎝⎛+-⎪⎪⎭⎫⎝⎛+dcd c s eYv K S θθ11m ax 2.16(2)推流式S 对推流式deos e o e o cK S K S S S S v Y-+--=ln)()(1m ax θ 2.172)确立微生物浓度(X )与生物固体平均停留时间θc 之间的关系(1)全混流)1()(c d e o c K S S Y t X θθ+-=2.18(2)推流 X对推流式(反应器内微生物浓度采用其平均值)。
)1()(c d e o c K S S Y t X θθ+-=2.193)确立活性污泥回流比(R )与生物固体平均停留时间(θc )之间的关系)1(=++-dt dXV X R Q RQX a r⎪⎪⎭⎫⎝⎛-+=a r c X X R R V Q 11θ 10S V IX r 6m a x)(=4)总产率(Y )与表现产率(Y obs )之间的关系()q X dt dS X dtdX dS dXdt dS dt dXY uu uμ=⎪⎭⎫⎝⎛==⎪⎭⎫⎝⎛=dX ()uobsdS Y '=2.23=11cd d c obs K Y K Y Y θμθ++⨯=2.245)θc 值与Se 值及E 的关系1dc K Yv -=m ax m in)(θ 2.266)(2.32)式便于用以求定曝气池的容积(V )qX S S Q V a e )(0-=5、动力学参数的测定maxmax 011v S v K S S tXe S e +⎪⎪⎭⎫ ⎝⎛∙⎪⎪⎭⎫ ⎝⎛=-dcK Yq -=θ16、例题。
活性污泥法的原理及应用

利用物联网、大数据和人工智能等技术,实现活性污泥法的智能 化控制,提高处理过程的稳定性和可靠性。
资源化利用
将活性污泥中的有用物质提取和利用,实现资源化利用,减少二 次污染。
活性污泥法在未来的应用前景
城市污水处理
随着城市化进程的加速,城市污水处理需求不断增加,活 性污泥法将继续作为主流的污水处理技术得到广泛应用。
VS
详细描述
污泥膨胀的主要原因是污泥中丝状菌过度 繁殖,导致污泥结构松散、沉降性差。此 外,低溶解氧、高碳水化合物负荷、缺乏 营养等也会引起丝状菌过度繁殖。解决污 泥膨胀的对策包括控制溶解氧浓度、调整 营养物质比例、使用药剂抑制丝状菌等。
泡沫问题
总结词
泡沫问题是活性污泥法中另一个常见问题, 会导致处理效率下降、影响出水水质。
营养物质的影响
活性污泥中的微生物需要适量的营养物质,如氮、磷等,以维持正常的代谢活动。缺乏必要的营养物 质会导致微生物的生长受限,从而影响有机污染物的去除效率。
在实际应用中,需要根据具体工艺要求和进水水质情况,合理控制营养物质的投加量,以保证微生物 的正常生长和代谢。
有毒物质的影响
有毒物质的存在会对活性污泥中的微生物产生抑制作用,降低有机污染物的去除效率。常见的有毒物质包括重金属、有毒有 机物等。
02
活性污泥法的应用
在生活污水处理中的应用
去除有机物
活性污泥中的微生物能够吸附和 降解污水中的有机物,将其转化 为无害的物质,达到净化水质的 目的。
去除氮、磷等营养
物质
通过活性污泥的吸附和微生物的 代谢作用,可以有效去除污水中 的氮、磷等营养物质,从而降低 水体富营养化的风险。
改善水体环境
活性污泥法能够降低水体的浊度 、色度等指标,提高水体的透明 度和溶解氧含量,改善水体的环 境质量。
活性污泥法工作原理

活性污泥法工作原理
活性污泥法是一种生物处理技术,主要用于处理废水中的有机物和氮的污染物。
其工作原理如下:
1. 污泥负载:将含有高浓度有机物的废水与活性污泥混合,使污泥中的微生物负载污染物。
活性污泥是由多种细菌和其他微生物组成的混合物,具有高度耐性和能力来降解有机物。
2. 暴露于空气中:将污泥置于暴露在空气中的容器中,以确保供氧和气体交换。
空气中的氧气提供给微生物进行呼吸作用,并促进细菌降解有机污染物的过程。
同时,活性污泥中的微生物通过呼吸作用释放出二氧化碳。
3. 分离固液:在活性污泥容器中,废水中的有机物被降解为二氧化碳和废水中的可溶性化合物。
此外,微生物合成新的细胞物质,因此为维持微生物群体的生长,需要一部分有机物。
4. 沉淀:处理后的废水进入沉淀器,通过重力作用使随废水进入的活性污泥颗粒沉降到底部,形成污泥混合物。
此时,可以将一部分活性污泥用于下一批废水的处理,使系统稳定。
5. 排放水体:处理后的废水经过后处理,满足排放标准后,可以安全地排放到水体中。
通过这一系列过程,活性污泥法能够高效地将有机物和氮的污染物降解为较低的水平,达到净化废水的目的。
活性污泥法及其在污染治理中的应用

活性污泥法及其在污染治理中的应用随着工业化进程的加快,水环境污染已经成为一个全球性的问题。
为了解决水环境污染带来的各种问题,人们开发了一些污染治理技术。
其中活性污泥法是一种常用的污染治理技术,本文将对其原理和应用做简要介绍。
一、活性污泥法的原理活性污泥法是一种生物处理技术,它利用微生物的活性将污染物质降解成无害物质。
活性污泥法的原理是,在恰当的生态环境下,一些微生物通过吞噬、降解、氧化还原等生命活动,可以将水中的有机物质、无机物质及某些重金属成分转化为可接受的物质。
该技术的基本步骤包括污水与活性污泥的接触、生化降解、沉淀和排放。
其中,污水与活性污泥的接触是指将污水和活性污泥充分混合,以便使微生物附着在污水中的有机物上。
生化降解是将有机物质降解成简单的无机物,即二氧化碳、水等。
沉淀是将水中的污泥聚集,使其快速沉淀。
排放是指将清理后的水排放入环境中。
二、活性污泥法的应用活性污泥法在污染治理中有着广泛的应用,下面将从两个方面进行介绍。
1. 工业废水处理工业污染对生态环境和人类健康造成的影响很大,因此对工业废水的处理非常重要。
活性污泥法在工业废水处理中有广泛的应用,可用于石化、纺织、食品、制药等领域。
例如,在造纸工业中,废水通常含有大量有机污染物,包括棉浆、切割废料和涂料等,这些污染物可通过活性污泥法处理。
活性污泥法还可用于金属、半导体以及电子行业的废水处理中,这类废水含有各种金属离子和有机物质。
2. 生活污水处理除了工业废水处理,活性污泥法还可用于生活污水处理。
生活污水包括家庭污水、商业污水、医院污水等,其中污染物质种类繁多,但它们有一个共同点,就是有机物质含量较高。
因此,活性污泥法非常适合处理这类污水。
在生活污水处理中,活性污泥法常常被用于城市污水、农村污水、养殖污水和食品加工废水等方面。
三、活性污泥法的优缺点活性污泥法的优点包括:处理效率高、处理能力强、设备简单、过程稳定、具有良好的降解效果等。
另外,该技术的成本低廉,不需要额外的化学药品等。
污水处理 活性污泥法

污水处理活性污泥法活性污泥法是一种常用的污水处理方法,它可以有效地去除污水中的有机物质和悬浮物。
该方法利用活性污泥微生物群落在充分供氧的条件下进行生化反应,使有机物质转化为无机物质和生物质,从而达到净化污水的目的。
一、活性污泥法的原理在活性污泥法中,通过将污水引入活性污泥容器中,并加入一定量的曝气装置,使污水中的有机物质被微生物群落分解,产生大量生物质。
通过间歇式的曝气,可以使活性污泥中的微生物得到充分的供氧,从而加速生化反应的速度。
处理完毕后,活性污泥会随着出水从反应器中流出,再经过沉淀池等后续处理设备得到回收利用。
二、活性污泥法的优点1. 适用范围广:活性污泥法处理的污水种类包括城市污水、工业废水等各种类型的污水。
2. 净化效果好:活性污泥法处理污水后,可以有效地去除其中的有机物质和悬浮物,净化效果非常明显。
3. 操作简单:一般情况下,活性污泥法的设备比较简单,易于安装和操作维护,能够有效地降低设备维护成本。
4. 可回收利用:通过对处理后的活性污泥进行沉淀,可以得到大量的生物质,并进一步制成肥料等,实现资源的回收利用。
三、活性污泥法的缺点1. 对环境有一定的影响:除了污水本身的影响以外,活性污泥法处理过程中需要使用大量的曝气装置,会产生一定的噪音和振动。
2. 能耗和物料消耗较大:活性污泥法需要大量的能源来驱动曝气装置,同时对周围环境的氧气需求较大,需要消耗大量的物料。
3. 仅针对有机物质有效:活性污泥法只针对有机物质进行处理,对于其他物质的处理效果很有限。
四、活性污泥法的应用活性污泥法已经广泛应用于城市供水、工业废水等领域,其主要作用在于实现长期、可靠、高效的污水处理。
在城市供水领域,活性污泥法被广泛应用于自来水厂污泥处理等领域。
通过对污泥进行生物处理和回收利用,可以实现资源的合理利用和再利用。
在工业废水处理领域,活性污泥法被广泛应用于纺织、印染、造纸等行业的废水处理。
通过对废水进行生化反应,可以实现高效的净化效果和资源回收利用。
活性污泥法原理

活性污泥法原理
活性污泥法是一种常用于废水处理的方法,它基于生物学原理。
该方法利用活性污泥中的微生物来吸附和分解有机物质,从而实现废水的净化。
具体而言,活性污泥法通过将废水与含有活性污泥的反应槽中接触,使污水中的有机物质被微生物吸附到污泥表面。
同时,废水中的有机物质也可被微生物分解为无害的物质,例如水和二氧化碳。
在这个过程中,微生物需要适宜的环境条件来生长和繁殖,包括适宜的氧气、营养物质和温度等。
在活性污泥法中,污泥的颗粒化是非常重要的。
污泥颗粒化可以增加活性污泥的比表面积,提高微生物的吸附和分解能力。
同时,污泥颗粒化还能促进颗粒之间的氧气和废水的接触,加快有机物质的降解速度。
为了保持活性污泥法的稳定性和高效性,需要定期对污泥进行处理。
典型的处理方法包括曝气、混合和污泥回流等。
曝气可以提供污泥所需的氧气,促进微生物的有氧呼吸过程;混合则能均匀分布污泥中的微生物和营养物质;而污泥回流则可以保持活性污泥中微生物的浓度和活性。
总之,活性污泥法通过利用微生物的吸附和分解能力,实现废水的净化。
这种方法在废水处理领域具有广泛的应用和较高的效率,能够有效地去除废水中的有机物质,实现废水的可持续处理和回用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
活性污泥法的反应动力学原理及其应用活性污泥法反应动力学可以定量或半定量地揭示系统内有机物降解、污泥增长、耗氧等作用与各项设计参数、运行参数以及环境因素之间的关系。
它主要包括:① 基质降解的动力学,涉及基质降解与基质浓度、生物量等因素的关系;② 微生物增长动力学,涉及微生物增长与基质浓度、生物量、增长常数等因素的关系;③ 还研究底物降解与生物量增长、底物降解与需氧、营养要求等的关系。
在建立活性污泥法反应动力学模型时,有以下假设:① 除特别说明外,都认为反应器内物料是完全混合的,对于推流式曝气池系统,则是在此基础上加以修正;② 活性污泥系统的运行条件绝对稳定;③ 二次沉淀池内无微生物活动,也无污泥累积并且水与固体分离良好;④ 进水基质均为溶解性的,并且浓度不变,也不含微生物;⑤ 系统中不含有毒物质和抑制物质。
一、活性污泥反应动力学的基础——米—门公式与莫诺德模式1、米—门公式Michaelis—Menton 提出酶的“中间产物”学说,通过理论推导和实验验证,提出了含单一基质单一反应的酶促反应动力学公式,即米—门公式:SK Sv m +=m ax ν式中:v ——酶促反应中产物生成的反应速率; m ax v ——产物生成的最高速率;m K ——米氏常数(又称饱和常数,半速常数);S ——基质浓度。
中间产物学说:P E ES S E +↔↔+米门公式的图示:2、莫诺德模式① 莫诺德模式的基本形式:Monod 于1942年和1950年曾两次进行了单一基质的纯菌种培养实验,也发现了与上述酶促反应类似的规律,进而提出了与米门公式想类似的表达微生物比增殖速率与基质浓度之间的动力学公式,即莫诺德模式:SK Ss +⋅=m ax μμ式中: ()x dtdx/=μ——微生物的比增殖速率,d kgVSS kgVSS ⋅/;m ax μ——基质达到饱和浓度时,微生物的最大比增殖速率, S ——反应器内的基质浓度,mg/l ; s K ——饱和常数,也是半速常数。
随后发现,用由混合微生物群体组成的活性污泥对多种基质进行微生物增殖实验,也取得了符合这种关系的结果。
可以假定:在微生物比增殖速率与底物的比降解速率之间存在下列比例关系:v maxv=v maxOK mv ∝μ则与比增殖速率相对应的比底物降解速率也可以用类似公式表示,即:SK SS +=m axνν式中: x dtdsv )(-=——比底物降解速率(d kgVSS kgBOD ⋅5); m ax v ——底物的最大比降解速率; S ——限制增殖的底物浓度; s K ——饱和常数。
对于废水处理来说,有机物的降解是其基本目的,因此上式的实际意义更大。
② 莫诺德模式的图示:③ 莫诺德方程式的推论:1) 在高底物浓度的条件下,即S >>s K ,呈零级反应,则有:m ax μμ= , m ax νν=X K X dtdS1m ax ==-⇒ν2) 在低底物浓度的条件下,即S <<s K ,则:S K KS 2m ax==νν XS K dtdS2=-⇒ 二、Lawrence—McCarty 模式:1、 有关基本概念:① 微生物比增殖速率: X dtdS)(=μ ② 单位基质利用率: X dtdSq u )(= ③ 生物固体平均停留时间(又称细胞平均停留时间,在工程上习称污泥龄): 在反应系统内,微生物从其生成开始到排出系统的平均停留时间;也可以说是反应系统内的微生物全部更新一次所需要的平均时间;从工程上来说,就是反应系统内微生物总量与每日排放的剩余污泥量的比值,以c θ表示,单位为d ,即: xXV c ∆⋅=θ式中:x ∆——每日增殖的微生物量,稳态运行时,就是每日排放的剩余污泥量。
因此:ie w r w c X Q X Q Q X Q XV ⋅-⋅-+⋅⋅=)(θ简化后,则: rw c X Q XV ⋅⋅=θ④μ与c θ的关系:Xdtdx /=μ ,而 ()()T T c t x x ∆∆=/θ,所以有: μθ1=c或c θμ1=2、L—M 模式的基本方程式:① 第一基本方程式:前面已有:X K dt ds Y dt dx d u-⎪⎭⎫⎝⎛= 式中 Y ——微生物的产率系数,d kgBOD kgVSS ⋅5/;d K ——自身氧化系数,又称衰减常数,1-d ,(d kgVSS kgVSS ⋅/);经整理后: d cK Yq -=θ1表示的是污泥龄(c θ)与产率系数Y 、基质比利用速率(q )及自身氧化系数之间的关系。
② 第二基本方程式:认同莫诺德模式: SK Sv v s +⋅=max认为有机基质的降解速率等于其被微生物的利用速率,即X dt ds q v u⎪⎭⎫⎝⎛== S K S X q dt ds s u+⋅⋅=⎪⎭⎫⎝⎛max 式中: S ——反应器内的基质浓度;m ax q ——单位生物量的最大基质利用速率; s K ——半速常数。
表示的是基质利用速率与反应器内微生物浓度和基质浓度之间的关系。
3、L -M 模式的导出方程式① 第一导出方程——出水水质e S 与污泥龄c θ之间的关系:(对于完全混合式)将 se eu K S S v X dt ds q +==m ax)/( 代入: d cK q Y -⋅=θ1则有: d s e ec K K S S v Y -⎪⎪⎭⎫ ⎝⎛+=m ax 1θ1)()1(m ax --+=⇒d c c d s e K Yv K K S θθLawrence—McCarty 建议的排泥方式:两种排泥方式:I.剩余污泥从污泥回流系统排出; II.剩余污泥从曝气池直接排出。
第二种排泥方式的优点:1)减轻了二沉池的负担;2)可将剩余污泥单独浓缩处理;3)便于控制曝气池的运行。
因此按这种排泥方式的污泥龄的计算就可以变得更简单,如下: ie w w c QX X Q Q X Q VX --+=)(θ简化后, wc Q V =θ 由此可看出这种排泥方式更有利于控制和运行管理。
② 第二导出方程——曝气池内微生物浓度X 与污泥龄c θ的关系 对曝气池作有机底物的物料衡算:底物的净变化率 = 底物进入曝气池的速率 - 底物从曝气池中消失的速率 e u e i T QS R V dt ds RQS QS dt ds V )1()/()/(0+-⋅-+==V S S Q dt ds e i u)(-=⎪⎭⎫ ⎝⎛⇒ 代入第一基本方程有: ()()c d e i c K V S S Q Y X θθ⋅+⋅-⋅⋅⋅=1由于Q V HRT t /==,则有: ()()c d e i c K S S Y t X θθ⋅+-⋅⋅=1 上式说明:曝气池中微生物量浓度是与有机物的浓度、c θ和曝气时间等有关的。
式中c θ=Φ,可以称为污泥循环因子,其物理意义为:活性污泥从生长到被排出系统期间与废水的平均接触次数。
③ 第三导出方程——回流比R 与c θ之间的关系 对曝气池的生物量进行物料衡算:(曝气池内生物量的净变化率)=(生物量进入曝气池的速率)-(生物量离开曝气池的速率)X R Q V X K dtds Y QX RQX V dt dx d ui r )1()(0+-⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛++== 其中 X dt ds q u /)/(=, 所以:X R Q V X K Yq RQXd r)1()(+=⋅⋅-+d cK Yq -=θ1所以:⎥⎦⎤⎢⎣⎡-+⋅=X X R R V Q r c11θ 式中:r X ——回流污泥的浓度,可由下式估算: SVIX r 610=注意:1)是近似值;2)由SVI 算出的是MLSS 值,应再换算成MLVSS 。
④ 产率系数(Y )与表观产率系数(obs Y )之间的关系:产率系数(Y )是指单位时间内,微生物的合成量与基质降解量的比值,即:usdt dS dt dX Y )()(-=表观产率系数(obs Y )是指单位时间内,实际测定的污泥产量与基质降解量的比值,即: uT obs dt dS dt dX Y )/()/(=q Xdt dS Xdt dX Y u T obs //)/(/)/(μ==⇒将cθμ1=,以及d cK Yq -=θ1 代入,则有:)1/(c d obs K Y Y θ+=该式还提供了通过试验求Y 及d K 的方法,将其取倒数后得:c d obs YK Y Y θ⋅+=11以obs Y 1对c θ作图,即可求得Y 及d K 值。
其中)(/e i obs S S Q x Y -∆=⑤ c θ与S e 及E 的关系:(见附图3)c θ 升高 S e 下降 E 升高; c θ 下降 S e 升高 E 下降因此,对于一个活性污泥系统有一个(c θ)min可以通过假定S e = S I 并代入d es ecK S K S v Y-+=m a x 1θ则有:d is i c K S K S v Y -+=m ax m in )(1θ一般,i s S K 〈〈,所以,d c K v Y -⋅=m ax m in)(1θ⑥ 对方程式的推论已有:SK Sv v s +=m ax因 q v =,所以,S K S v q s +=m ax活性污泥处理系统一般为低基质浓度,即e s S K 〉〉,所以, S K S K v q s⋅=⋅=max, 其中sK v K max =又: KS Xdt ds q u==)/( ,所以:KSXdt ds u =)/(在稳态下,V S S Q t S S dt ds e i e i u /)(/)()/(-=-=所以: XVS S Q KS q e i e )(-== Xq S S Q V e i )(-=⇒三、动力学参数的测定动力学参数s K 、)(max max q v 、Y 、d K 是模式的重要组成部分,一般是通过实验来确定的。
① s K 、)(max max q v 的确定:将下式:e s e S K S v v +=max取倒数,得:maxmax 111v S v K v e +⋅= 式中 ()Xdt ds q v u/== 所以eI u S S tXdt ds X q v -===)/(11 取不同的t 值,即可计算出qv 11=值,绘制e S v 11~关系图,图中直线的斜率为m ax v K s 值,截距为max1v 值。
② Y 、d K 值的确定已知d cK q Y -⋅=θ1以及 tXS S X dt ds q ei u -==)/( 取不同的c θ值,并由此可以得出不同的e S 值,代入上式,可得出一系列q 值。
绘制的cq θ1~关系图,图中直线的斜率为Y 值,截距为d K 值。
