追及问题的应用题
追及问题应用题

追及问题应用题追及问题应用题1.甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地的距离是多少千米?2.李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到。
0.5小时后,营地老师闻讯前往迎接,每小时比李华多走 1.2千米。
又过了1.5小时,张明从学校骑车去营地报到。
结果3人同时在途中某地相遇。
问:骑车人每小时行驶多少千米?3快车和慢车分别从甲、乙两地同时开出,相向而行,经过5小时相遇。
已知慢车从乙地到甲地用12.5小时,慢车到甲地停留0.5小时后返回,快车到乙地停留1小时后返回,那么两车从第一次相遇到第二次相遇需要多少时间?4.某校和某工厂之间有一条公路,该校下午2时派车去该厂接某劳模来校作报告,往返需用1小时。
这位劳模在下午1时便离厂步行向学校走来,途中遇到接他的汽车,便立刻上车驶向学校,在下午2时40分到达。
问:汽车速度是劳模步行速度的几倍?5.已知甲的步行的速度是乙的1.4倍。
甲、乙两人分别由A,B两地同时出发。
如果相向而行,0.5小时后相遇;如果他们同向而行,那么甲追上乙需要多少小时?6.猎狗发现在离它10米的前方有一只奔跑着的兔子,马上紧追上去。
兔跑9步的路程狗只需跑5步,但狗跑2步的时间,兔却跑3步。
问狗追上兔时,共跑了多少米路程?7.张、李两人骑车同进从甲地出发,向同一方向行进。
张的速度比李的速度每小时快4千米,张比李早到20分钟通过途中乙地。
当李到达乙地时,张又前进了8千米。
那么甲、乙两地之间的距离是多少千米?8.上午8时8分,小明骑自行车从家里出发;8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他;然后爸爸立刻回家,到家后又立刻回头去追小明,再追上他的时候,离家恰好是8千米。
问这时是几时几分?9.龟兔进行10000米赛跑,兔子的速度是乌龟的速度的5倍。
当它们从起点一起出发后,乌龟不停地跑,兔子跑到某一地点开始睡觉,兔子醒来时乌龟已经领先它5000米;兔子奋起直追,但乌龟到达终点时,兔子仍落后100米。
初一数学追及应用题

初一数学追及应用题一、基础追及问题(1 - 10题)1. 甲、乙两人相距20千米,甲以每小时4千米的速度先走1小时后,乙从同一地点出发,以每小时6千米的速度追赶甲,乙几小时后能追上甲?- 解析:- 甲先走1小时,先走的距离为4×1 = 4千米。
- 此时两人相距20 - 4=16千米。
- 甲乙的速度差为6 - 4 = 2千米/小时。
- 根据追及时间=路程差÷速度差,可得追及时间为16div2 = 8小时。
2. 甲、乙两人在同一条路上,前后相距9千米。
他们同时向同一个方向前进。
甲在前,以每小时5千米的速度步行;乙在后,以每小时6千米的速度骑自行车追赶甲。
几小时后乙能追上甲?- 解析:- 甲乙的速度差为6 - 5=1千米/小时。
- 路程差为9千米。
- 根据追及时间 = 路程差÷速度差,可得追及时间为9div1 = 9小时。
3. 小明和小红在环形跑道上跑步,跑道一圈长400米,小明每秒跑6米,小红每秒跑4米。
如果他们同时同地同向出发,经过多少秒小明第一次追上小红?- 解析:- 小明每秒比小红多跑6 - 4 = 2米。
- 因为是环形跑道同向出发,当小明第一次追上小红时,小明比小红多跑了一圈,即400米。
- 根据追及时间 = 路程差÷速度差,可得追及时间为400div2 = 200秒。
4. 一辆汽车和一辆摩托车同时从相距180千米的两地出发,汽车每小时行40千米,摩托车每小时行60千米,摩托车在汽车后面,几小时后摩托车可以追上汽车?- 解析:- 摩托车与汽车的速度差为60 - 40 = 20千米/小时。
- 路程差为180千米。
- 根据追及时间 = 路程差÷速度差,可得追及时间为180div20 = 9小时。
5. 甲、乙两人分别从A、B两地同时出发,同向而行,乙在前,甲在后。
已知A、B两地相距20千米,甲的速度是每小时15千米,乙的速度是每小时10千米,甲几小时后能追上乙?- 解析:- 甲、乙的速度差为15 - 10 = 5千米/小时。
行程问题:追及问题应用题(小升初专项练习)六年级数学小考总复习(含答案)

行程问题:追及问题应用题(小升初专项练习)六班级数学小考总复习(含答案)一、追及问题常用的公式:追准时间=追及路程÷(快的速度-慢的速度)追及路程=(快的速度-慢的速度)×追准时间追准时间=两者距离差÷两者速度差两者距离差=两者速度差×追准时间两者速度差=两者距离差÷追准时间快的速度=两者速度差+慢的速度慢的速度=快的速度-两者速度差二、简洁的追及问题的解决方法:(1) 依据问题的类型,找到问题适合的方法与公式。
(2) 除了未知数外,要梳理清楚追及问题里的其余两个条件(路程、时间或速度)。
(3)代入已知有关的路程公式,从而进行求解。
【典型例题】1、一辆货车从A地动身开向距离360千米的B地,由于有个小货物落下了没有装上货车,1.2个小时后一辆小汽车装着这个小货物从A地动身,以每小时行驶115千米的速度朝货车追赶。
已知货车每小时行驶75千米,那么小汽车多久后能追上货车?【例题分析】该题是典型的路程追及问题,现已知货车和小汽车的速度,以及两车相距的路程“75×1.2”。
只需运用追及公式:追准时间=两者距离差÷两者速度差然后代入数据,求出追准时间。
【解答】(75×1.2)÷(115-75)=90÷40=2.25(小时)答:小汽车2.25小时后能追上货车。
【培优练习】1、放学后,贺礼和刘超同时从学校动身去往公车站,两人同向而行,贺礼行走的速度是85米/分,刘超的行走速度是70米/分,10分钟后他们两人相距多少米?2、秦叔叔刚好看到前方有一个跑步者掉落了东西,他距离秦叔叔或许135米远。
跑步者正在以每秒2.3米的速度跑步,秦叔叔此时抓紧以每秒3.2米的速度朝他追去,请问秦叔叔多少秒后可以追上跑步者?3、学校有一条长800米的环形跑道,李俊和石林同时从起点动身,朝同一方向竞赛跑步。
李俊每分钟跑240米,石林每分钟跑200米。
五年级奥数追及问题应用题

五年级奥数追及问题应用题一、追及问题应用题20题。
1. 甲、乙两人分别从相距18千米的A村和B村同时向东而行,甲骑车每小时行14千米,乙步行每小时走5千米。
几小时后甲可以追上乙?- 解析:甲、乙两人的路程差是18千米,甲每小时比乙多行14 - 5=9千米(速度差)。
根据追及时间 = 路程差÷速度差,可得追及时间为18÷(14 - 5)=2小时。
2. 一辆汽车和一辆摩托车同时从甲、乙两地出发,向同一个方向前进,摩托车在前,每小时行28千米,汽车在后,每小时行65千米,经过4小时汽车追上摩托车,甲乙两地相距多少千米?- 解析:汽车每小时比摩托车多行65 - 28 = 37千米,经过4小时追上,那么4小时汽车比摩托车多行驶的路程就是甲乙两地的距离,即37×4 = 148千米。
3. 甲、乙两人相距4千米,乙在前,甲在后,两人同时同向出发,2小时后甲追上乙,乙每小时行6千米,甲每小时行多少千米?- 解析:甲2小时比乙多走了4千米,那么甲每小时比乙多走4÷2 = 2千米。
乙每小时行6千米,所以甲每小时行6+2 = 8千米。
4. 甲、乙两架飞机同时从一个机场起飞,向同一方向飞行,甲机每小时行300千米,乙机每小时行340千米,飞行4小时后它们相隔多少千米?这时候甲机提高速度用2小时追上乙机,甲机每小时要飞行多少千米?- 解析:- 开始飞行4小时后,乙机每小时比甲机多行340 - 300 = 40千米,4小时后相隔40×4 = 160千米。
- 甲机要在2小时内追上乙机,这2小时内乙机又飞行了340×2 = 680千米,甲机总共要比乙机多飞行160千米,所以甲机2小时要飞行680 + 160=840千米,那么甲机每小时要飞行840÷2 = 420千米。
5. 小明以每分钟50米的速度从学校步行回家,12分钟后小强从学校出发骑自行车去追小明,结果在距学校1000米处追上小明,求小强骑自行车的速度。
小学奥数趣味学习《追及问题》典型例题及解答

小学奥数趣味学习《追及问题》典型例题及解答两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发,或者在不同地点又不是同时出发)作同向运动,在后面的,行进速度要快些,在前面的,行进速度较慢些,在一定时间之内,后面的追上前面的物体。
这类应用题就叫做追及问题。
数量关系:追及时间=追及路程÷(快速-慢速)追及路程=(快速-慢速)×追及时间解题思路和方法:简单的题目可直接利用公式,复杂的题目变通后再利用公式,利用线段图分析可以让解题事半功倍。
例题1:某警官发现前方100米处有一匪徒,匪徒正以每秒2米的速度逃跑。
警官赶紧以每秒3米的速度追,()秒后警官可以追上这个匪徒。
解:1、从警官追开始到追上匪徒,这就是一个追及过程。
根据公式:路程差÷速度差=追及时间。
2、路程差为100米,警官每秒比匪徒多跑3-2=1(米),即速度差为1米/秒。
所以追及的时间为100÷1=100(秒)。
例题2:甲乙二人同时从400米的环形跑道的起跑线出发,甲每秒跑6米,乙每秒跑8米,同向出发。
那么甲乙二人出发后()秒第一次相遇?解:1、由题可知,甲乙同时出发后,乙领先,甲落后,那么两人第一次相遇时,乙从后方追上甲,所以,乙的路程=甲的路程+一周跑道长度,即追及路程为400米。
2、由追及时间=总路程÷速度差可得:经过400÷(8-6)=200(秒)两人第一次相遇。
例题3:小轿车、面包车和大客车的速度分别为60千米/时、48千米/时和42千米/时,小轿车和大客车从甲地、面包车从乙地同时相向出发,面包车遇到小轿车后30分钟又遇到大客车。
那么甲、乙两地相距多远?解:1、根据题意,将较复杂的综合问题分解为若干个单一问题。
首先是小轿车和面包车的相遇问题;其次是面包车和大客车的相遇问题;然后是小轿车与大客车的追及问题。
最后通过小轿车与面包车共行甲、乙两地的一个单程,由相遇问题可求出甲、乙两地距离。
追及与相遇问题练习题
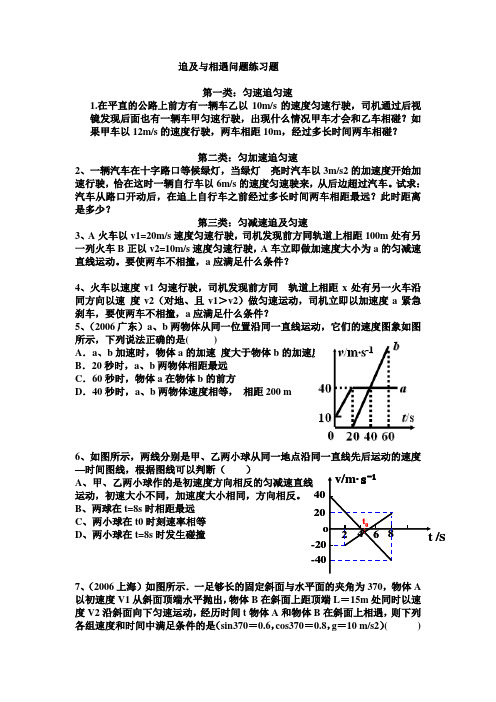
追及与相遇问题练习题第一类:匀速追匀速1.在平直的公路上前方有一辆车乙以10m/s 的速度匀速行驶,司机通过后视镜发现后面也有一辆车甲匀速行驶,出现什么情况甲车才会和乙车相碰?如果甲车以12m/s 的速度行驶,两车相距10m ,经过多长时间两车相碰?第二类:匀加速追匀速2、一辆汽车在十字路口等候绿灯,当绿灯 亮时汽车以3m/s2的加速度开始加速行驶,恰在这时一辆自行车以6m/s 的速度匀速驶来,从后边超过汽车。
试求:汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?第三类:匀减速追及匀速3、A 火车以v1=20m/s 速度匀速行驶,司机发现前方同轨道上相距100m 处有另一列火车B 正以v2=10m/s 速度匀速行驶,A 车立即做加速度大小为a 的匀减速直线运动。
要使两车不相撞,a 应满足什么条件?4、火车以速度v1匀速行驶,司机发现前方同 轨道上相距x 处有另一火车沿同方向以速 度v2(对地、且v1>v2)做匀速运动,司机立即以加速度a 紧急刹车,要使两车不相撞,a 应满足什么条件?5、(2006广东)a 、b 两物体从同一位置沿同一直线运动,它们的速度图象如图所示,下列说法正确的是( )A .a 、b 加速时,物体a 的加速 度大于物体b 的加速度B .20秒时,a 、b 两物体相距最远C .60秒时,物体a 在物体b 的前方D .40秒时,a 、b 两物体速度相等, 相距200 m6、如图所示,两线分别是甲、乙两小球从同一地点沿同一直线先后运动的速度—时间图线,根据图线可以判断( ) A 、甲、乙两小球作的是初速度方向相反的匀减速直线运动,初速大小不同,加速度大小相同,方向相反。
B 、两球在t=8s 时相距最远 C 、两小球在t0时刻速率相等 D 、两小球在t=8s 时发生碰撞7、(2006上海)如图所示.一足够长的固定斜面与水平面的夹角为370,物体A 以初速度V1从斜面顶端水平抛出,物体B 在斜面上距顶端L =15m 处同时以速度V2沿斜面向下匀速运动,经历时间t 物体A 和物体B 在斜面上相遇,则下列各组速度和时间中满足条件的是(sin370=0.6,cos370=0.8,g =10 m/s2)( )S 2040A、V1=16m/s,V2=15m/s,t=3sB、V1=16m/s,V2=16m/s,t=2sC、V1=20m/s,V2=20m/s,t=3sD、V1=20m/s,V2=16m/s,t=2s——匀速追匀加速8、(2007全国)甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。
七年级上册追及问题应用题

七年级上册追及问题应用题一、追及问题基本公式1. 公式追及路程 = 速度差×追及时间速度差=追及路程÷追及时间追及时间 = 追及路程÷速度差2. 解释速度差:是快者速度与慢者速度的差值。
例如,甲的速度是公式,乙的速度是公式(公式),那么速度差公式。
追及路程:在追及过程中,开始时两者相距的距离。
追及时间:从开始追及到追上所花费的时间。
二、典型例题及解析1. 例题1甲、乙两人相距公式米,甲在前,乙在后,甲每分钟走公式米,乙每分钟走公式米,两人同时同向出发,几分钟后乙能追上甲?解析首先确定已知条件:追及路程公式米,甲的速度公式米/分钟,乙的速度公式米/分钟。
根据追及时间公式公式,这里速度差公式米/分钟,追及路程公式米。
则追及时间公式分钟。
2. 例题2一辆汽车和一辆摩托车分别从相距公式千米的A、B两城同时同向出发,汽车在前,摩托车在后,汽车每小时行公式千米,摩托车每小时行公式千米,几小时后摩托车可以追上汽车?解析已知追及路程公式千米,汽车速度公式千米/小时,摩托车速度公式千米/小时。
速度差公式千米/小时。
根据追及时间公式公式,可得追及时间公式小时。
3. 例题3甲、乙两人在周长为公式米的环形跑道上跑步,甲的速度是每秒公式米,乙的速度是每秒公式米,两人同时同地同向出发,经过多少秒甲第一次追上乙?解析在环形跑道上同向出发,甲第一次追上乙时,甲比乙多跑了一圈,即追及路程公式米。
甲的速度公式米/秒,乙的速度公式米/秒,速度差公式米/秒。
根据追及时间公式公式,可得追及时间公式秒。
追及问题应用题及答案

追及问题应用题及答案追及问题应用题及答案「篇一」1、小王、小李同住一楼中,两人从家去上班,小王先走20分钟后小李才出发。
已知小李的速度是小王速度的3倍,则小李出发后多少时间能追上小王?2、甲每分钟行80米,乙每分钟行50米,在下午1:30分时,两人在同地背向而行了6分钟,甲又调转方向追乙,则甲在几点的时候追上乙?3、某学校组织学生去长城春游,租用了一辆大客车,从学校到长城相距150千米。
大客车和学校的一辆小汽车同时从学校出发,当小汽车到长城时,大客车还有30千米。
已知大客车每小时行60千米,则小汽车比大客车快多少千米?4、甲乙两人从周长为800米的正方形水池相对的两个顶点同时出发逆时针行走,乙在前,甲在后。
甲每分钟走50米,乙每分钟走46米,出发多长时间甲和乙在同一点上?5、甲、乙两人同时从东村出发到西村,甲的速度是每小时6千米,乙的速度是每小时4千米,甲中途有事休息了2小时,结果比乙迟到了1个小时,求两村相隔的距离?6、龟兔赛跑,同时出发,全程7000米。
龟以每分钟30米的速度爬行,兔每分钟跑330米,兔跑了10分钟后停下来睡觉了200分钟,醒来后立即以原速往前跑,当兔追上龟时,离中点是多少米?7、学校组织四年级学生春游,包了两辆大面包车从学校出发。
第一辆车速每小时30千米,上午7:00出发,第二辆晚开1小时,速度是每小时40千米。
结果两辆车同时到达,问春游的景区离学校多远?8、甲、乙两人同时从A地去B地,甲每分钟行250米,乙每分钟行90米,甲到达B地后立即返回A地,在离B地1200米处与乙相遇,A、B两地相距多少千米?追及问题应用题及答案「篇二」【含义】两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发,或者在不同地点又不是同时出发)作同向运动,在后面的,行进速度要快些,在前面的,行进速度较慢些,在一定时间之内,后面的追上前面的物体。
这类应用题就叫做追及问题。
【数量关系】1.追及时间=追及路程÷(快速-慢速)2.追及路程=(快速-慢速)×追及时间【解题思路和方法】简单的题目直接利用公式,复杂的题目变通后利用公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
追及问题
1.哥哥和弟弟去人民公园参观菊花展,弟弟每分钟走50米,走了10分钟后,哥哥以每分钟70米的速度去追弟弟,问:经过多少分钟以后哥哥可以追上弟弟?
2.甲乙两地相距160千米,一列快车从甲地开出,每小时行60千米,一慢车从乙地开出,每小时行40千米,两辆车同时同向行驶,快在慢后面,问经过多长时间追上?
3.小红和小明分别从西村和东村同时向西而行,小明骑自行车每小时行16千米,小红步行每小时行5千米,2小时后小明追上小红,求东西村相距多少千米?
4、一列慢车在早晨6:30以每小时40千米的速度由甲城开往乙城,另一列快车在早晨7:30以每小时56千米的速度也由甲城开往乙城。
铁路部门规定,向相同方向的两列火车之间的距离不能小于8千米。
那么,这列慢车最迟应该在什么时候停车让快车超过?
5、一队中学生到某地进行军事训练,他们以每小时5千米的速度前进,走了6小时后,学校派秦老师骑自行车以每小时15千米的速度追赶学生队伍,传达学校通知。
秦老师几小时可追上队伍?追上时队伍已经行了多少路?
6、小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280米的速度去小明,那么爸爸出发后几分钟追上小明?
7、一条环形跑道长400米,小强每分钟跑300米,小星每分钟跑250米,两人同时同地同向出发,经过多长时间,小强第一次追上小星?
8、在一条长300米的环形跑道上,甲乙两人同时从一起点出发,同向而跑,甲每秒跑9米,乙每秒跑7米,现在乙在甲后面100米,问:甲追上乙要多少时间?
9、某学校组织学生去长城春游,租用了一辆大客车,从学校到长城相距150千米。
大客车和学校的一辆小汽车同时从学校出发,当小汽车到长城时,大客车还有30千米。
已知大客车每小时行60千米,则小汽车比大客车快多少千米?
10、甲乙两人从周长为800米的正方形水池相对的两个顶点同时出发逆时针行走,乙在前,甲在后。
甲每分钟走50米,乙每分钟走46米,出发多长时间甲和乙在同一点上?
11、甲、乙两人同时从A地去B地,甲每分钟行250米,乙每分钟行90米,甲到达B地后立即返回A地,在离B地1200米处与乙相遇,A、B两地相距多少千米?。
