第三章 哈密顿图

其中, k(G-V1)为从G中删除V1(删除V1中各顶点及
欧拉圈、欧拉图
定义 图G中的一圈，若它通过G中的每一条 边(或弧)恰好一次，则称该圈为欧拉圈，具 有这种圈的图称为欧拉无向(或有向)图。
定理1 无向图G是欧拉图, 当且仅当G是连通图, 且G中 没有奇度顶点。 证：设G = <V, E>是含有m条边的n阶非平凡无向 图, 其中: V = { v1, v2, …, vn }。 1). 必要性 因为G为欧拉图, 所以, G中存在欧拉圈。设C是G中 的欧拉圈, vi, vj V, vi, vj都在C上, 因此, vi和vj是连 通的, 所以, G为连通图。 又vi V, vi在C上每出现一次获得2度。若出现k 次就获得2k度, 即: d(vi) = 2k, 所以, G中无奇度顶点。
设C为G中一个圈, 删除C上的全部边, 得
G的生成子图G’。设G’有s个连通分支G’1,
G’2, …, G’s, 每个连通分支至多有k条边, 且
无奇度顶点, 并且设G’i与C的公共顶点为vji*(i
= 1..s)。
由归纳假设可知: G’1, G’2, …, G’s都是欧拉图, 因此, 都存在欧拉圈C’i(i = 1..s)。 现在将C还原(即将删除的边重新加上), 并从C上的某 顶点vr开始进行遍历, 每遇到vji*, 就行遍G’i中的欧拉圈 C’i(i=1..s), 最后, 回到vr, 得圈C”: vr… vj1* … vj1* …
有边的闭迹（链，点可以重）。 对于一个图是否存在Euler环游存在一
个非常简洁的判别法。但是到目前为止还没
有找到Hamilton图的充要条件。这是图论 尚未解决的主要问题之一。
图中 (1), (3),不是哈密尔顿图,(2) 为哈密尔顿图.
哈密尔顿图的判定 定理(必要条件1) 设无向图G=<V,E>是哈密尔顿 图,V1是V的任意的非空子集, k(G-V1)≤V1.
变性质的几何学
请大家思考：“串”、“田”两字， 在橡皮膜上可变为什么图形
拓扑学是在19世纪末兴起并在20世纪蓬
勃发展的数学分支，与近世代数、近代分析共
同成为数学的三大支柱。
拓扑学已在物理、化学、生物一些工程技
术中得到越来越广泛的应用。拓扑学主要研究 几何图形在一对一的双方连续变换下不同的性 质，这种性质称为“拓扑性质”
2). 充分性 对m作归纳。
由G为非平凡的连通图可知: G中边数m 1。 (1) m = 1时, 由G的连通性和无奇度顶点可
知: G只能是一个环, 因此, G为欧拉图。 (2) 设m k(k 1)时,。
由G的连通性和无奇度顶点可知: (G) 2。用扩大路径法可以证明G中存在长度大于 或等于3的圈。
设计展览会参观路线
A I K H G L
B J M
C D
A
I K H L
B J
C D N
N
E
M
O
O
F
E
G
F
H,G,O,F,E,N,M,O,L,K,I,L,M,J,N,D,C,J,B,I,A,K,H
M
C B A E F D G
H
I
一人如果从门 M进入，再从 门K走出，他 能否不重复地 走过每一扇门？
国管梅谷教授于1962年首先提出并发表的
例如：观察下列段道图 ● ● ● ● ● ▲ 图2 ●
●
● ▲
●
● ● 图1
●
●
● ●
●
问题：从邮局出发，走遍邮区的所有街道至少一次再回到邮 局，按照什么样的路线投递邮件才能使总的路程最短？
数学模型：
构造无向带权图G，E（G）中每个元素对应
于辖区内的一条街道，V（G）中的元素对应于街
含有2n(n>0)个奇点的脉络，需要n笔划
画成。
橡皮膜上的几何学 在《哥尼斯堡七桥》问题中，大家已
经看到了一种只研究图形各部分位置的相
对次序，而不考虑它们尺寸大小的新几何 学。莱布尼兹(Leibniz，1646～1716)和欧 拉为这种“位置几何学”的发展奠定了基 础。如今这一新的几何学，已经发展成一 门重要的数学分支——拓扑学
欢迎 同学们！
邢台学院数学系
第三章 欧拉图和哈密顿图
欧拉（L.Euler,1707.4.151783.9.18）著名的数学家。 生于瑞士的巴塞尔，卒于彼 得堡。大部分时间在俄国和 德国度过。他早年在数学天
才贝努里赏识下开始学习数
学, 17岁获得硕士学位，毕 业后研究数学,是数学史上最 高产的作家。在世发表论文 700多篇,去世后还留下100多
● ● ▲ 图3
● ● ● 图4
●
●
●
最优投递路线
重复的路最短
添弧的总长度最
短
添弧最短的条件
（1）没有重叠的添弧
（2）每一个圈上添弧的总长度不超过圈长的一半 最短的一组添弧称为最优解。
例2：找出下列段道图的最优解
●
3
●
3
●
3
●
1 ● 3 2
●
1 ● 4
2
●
3
2
▲
3
●
●
3
●
3
●
3
●
1 ● 3 3 2
– –
(1) G的每条边在G*至多重复一次；
(2) G的每个(初级)圈在G*重复边权的和不超过该圈 权的一半。

算法过程
–
1．用Dijstra算法求所有奇度顶点对之间的最短路径。 (若G是欧拉图，直接用Fleury算法) 2．以G中所有奇度顶点构造带权完全图G2k, 每边的 权是两端点间最短路径长度。
●
●
●
●
●
●
●
●
●
关于一笔画问题的生活转化
1、甲乙两个邮递员去送信，两人以同样的速度走遍
所有的街道，甲从A点出发，乙从B点出发，最后 都回到邮局（C点）。如果要选择最短的线路，谁 先回到邮局？
D●
C● B●
●A
E● F●
例2 下图是一个公园的平面图.要使游客走遍
每条路而不重复，问出入口应设在哪里？
●
●
●
● ●
● ●
●
●
●
●
●
●
●
●
①凡是由偶点组成的连通图，一定可以一笔
画成；画时可以任一偶点为起点，最后一定
能以这个点为终点画完此图。
②凡是只有两个奇点（其余均为偶点）的连
通图，一定可以一笔画完；画时必须以一个
奇点为起点，另一个奇点为终点。
③其他情况的图，都不能一笔画出。
“一笔划”问题
？
这是一些平面图形，请你思考图形能 否一笔画出与什么有关？
1
2
20
17
19
18
定义： 图G中的一圈，若它通过G中每个顶 点恰好一次，则该圈称为哈密尔顿圈，具 有哈密尔顿圈的图称为哈密尔顿无向图。 完全图必是哈密尔顿图。
从定义可知，一个图的Hamilton圈与
Euler环游是很相似的，差别在于Hamilton
圈是环游G的所有顶点圈（点不重，当然
边也不重），而Euler环游是环游G的所
●
1 ● 4
● ● ● ●
先分奇偶点，奇点对对连 连线不重叠，重叠要改变 圈上连线长，不得过半圈
2
●
2
3 ▲
●
3
●
2
● ●
●
3 3
●
最优解
2
3 1 3 2
3
需要顺便提到的是：既然可由一笔画画 成的脉络，其奇点个数应不多于两个，那么，
两笔划或多笔划能够画成的脉络，其奇点个
数应有怎样的限制呢？
一般地，我们有：
vj2* … vj2* … vjs* … vjs* … vr。
此圈C”经过G中每条边一次且仅一次。因此, C”是G 中的欧拉圈(如右下图所示)。 故, G为欧拉图。
定理2 连通图G具有欧拉路而无欧拉圈,当且仅当G 恰有两个奇数度顶点.
证:必要性:设连通图G从顶点a到顶点b有欧拉路C,
但不是欧拉圈.在欧拉路C中,除第一边和最后一
E G F D I
H
J
K
A
B
C
例(蚂蚁比赛问题) 甲A
甲、乙两只蚂蚁分别位
于如下图中的结点A，B
处，并设图中的边长度
乙B
C 是相等的。甲、乙进行
比赛：从它们所在的结 点出发，走过图中的所 有边最后到达结点C处。 如果它们的速度相同，
问谁先到达目的地？
例4 下图是某展览厅的平面图，它由五个展室 组成，任两展室之间都有门相通，整个展览 厅还有一个进口和一个出口，问游人能否一 次不重复地穿过所有的门，并且从入口进， 从出口出？
道的交叉点，街道长度用相应边的权表示。 则问题的解对应于G中包含所有边的权最小 的圈，称为最优圈(注意：未必是简单圈)。 当G是欧拉图，则最优圈即欧拉圈。 若G不是欧拉图，则通过加边来消除G中的 奇度顶点，要求使加边得到的欧拉图G'中重复边
的权和最小。
C是带正权无向连通图G中的最优圈当且仅当对 应的欧拉图G*满足：
在拓扑学中人们感兴趣的只是图形的位置而不是它的
大小。有人把拓扑学说成是橡皮膜上的几何学是很恰当的。
因为橡皮膜上的图形，随着橡皮膜的拉动，其长度、曲直、 面积等等都将发生变化。不过，在橡皮膜几何里也有一些
图形的性质保持不变。例如点变化后仍然是点；线变化后
依旧为线；相交的图形绝不因橡皮的拉伸和弯曲而变得不 相交!拓扑学正是研究诸如此类，使图形在橡皮膜上保持不
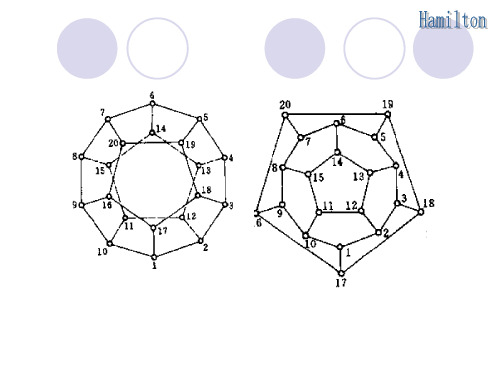
哈密顿图
起源于 1856年英 Hamilton 设计的名为周游 世界的游戏。在一个实心的正十二面体的二十 个顶点上标以世界各地有名的二十座城市的名 字，要求游戏者沿十二面体的棱从一个城市出