辽宁省辽宁师大附中2014届高三上学期期中考试数学文试题及答案

辽宁师大附中2016届高三上学期期中考试数学(文)Word版含答案

2015—2016学年度上学期高三期中考试数学试题（文科）（满分：150分考试时间：120分钟）命题：杨悦一.选择题：（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是最符合题目要求的.）1、对任意的实数，直线与圆的位置关系一定是（）A．相离B．相切C．相交但直线不过圆心D．相交且直线过圆心2、已知直线m、l和平面α、β，则α⊥β的充分条件是( )A．m⊥l，m //α，l//βB．m⊥l，α∩β＝m，lαC．m // l，m⊥α，l⊥βD．m // l，l⊥β，mα3、设是等差数列的前项和，若＝，则＝（）A. B. C. D.4．在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是（）A．B．C．D．5、已知直线的斜率不存在，则的值是（）A．B．或C．D．6. 已知双曲线的一条渐近线的斜率为，且右焦点与抛物线的焦点重合，则该双曲线的方程为（）A．B．C．D．7．ABCD为长方形，AB＝2，BC＝1，O为AB的中点，在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为（）A．B．C．D．8. 设、是两条不同的直线，、是两个不同的平面，则下列命题正确的是( )A. 若，，则B. 若，，，则C. 若，，，则D. 若，，，则9. 等比数列的前n项和为，已知，, 则（）．A．38 B．20 C．10 D．910.为直线上的一动点,过作圆的两条切线,切点分别为,则四边形的面积的最小值是 ( )A．B．C．D．11.在数列中，已知，且，则的值为（）A．2477 B.2427 C.2427.5 D.2477.512.双曲线的左、右焦点分别为为双曲线右支上一点，与圆切于点，且为的中点，则该双曲线的离心率为( )A. B.C．D．二.填空题：(本题共4小题，每小题5分,共20分.)13．若三棱锥的三视图如图，则其表面积为 .14．是圆上固定的一点，在圆上其他位置任取一点，连接，它是一条弦，它的长度小于或等于半径长度的概率是_______．15. 过圆外一点作圆的两条切线，切点为，则的外接圆的方程是_________．16. 在等差数列中，公差，前项和为，若取得最大值，则．三.解答题：(本题共6道大题，共70分.)17.（本题满分10分）如图,四棱锥中,，，，，．(Ⅰ) 求证：；(Ⅱ) 求点到平面的距离．18.（本小题满分12分）袋内装有6个球，这些球依次被编号为1、2、3、4、5、6，设编号为的球重 (单位:克),这些球等可能地从袋里取出（不受重量、编号的影响）.(Ⅰ) 从袋子中任意取出一个球，求其重量大于其编号的概率；(Ⅱ) 如果不放回地任意取出2个球，求它们重量相等的概率.19. （本小题满分12分）各项均为正数的数列{}的前项和为，且点在函数的图象上，(Ⅰ) 求数列{}的通项公式；(Ⅱ) 记求证：20．已知过抛物线的焦点，斜率为的直线交抛物线于（）两点，且．(Ⅰ)求该抛物线的方程；(Ⅱ)为坐标原点，为抛物线上一点，若，求的值．21．（本小题满分12分）如图甲，在平面四边形ABCD 中，已知：, ,现将四边形ABCD 沿BD 折起，使平面ABD 平面BDC （如图乙），设点E 、F 分别为棱D CP B AAC、AD的中点．（Ⅰ）求证：DC平面ABC；（Ⅱ）设，求三棱锥A－BFE的体积．22.（本小题满分12分）已知椭圆.过点作圆的切线交椭圆于两点．（I）求椭圆的焦点坐标和离心率；（II）将表示为的函数，并求的最大值．2015—2016学年度上学期高三期中考试数学试题（文科）(答案)一.选择题：CDAAC DCBCA CB二.填空题：13.14.15. 16. 7或8三.解答题：17. 17.【解】(Ⅰ) 因为，所以，又，，所以，因为，所以．(Ⅱ)设点到平面的距离为，因为，，所以，为直角三角形．又因为，所以．因为，所以三棱锥的高为．．又由(Ⅰ)，则为直角三角形．由及，则，．因为，则，即，．所以点到平面的距离为．18.答案：（1）；（2）19.F EBA.20. 【解】(Ⅰ) 抛物线的焦点为，所以直线的方程为，由消去得．所以，由抛物线定义得，即，所以．所以抛物线方程为．(Ⅱ)由，方程化为．解得，．所以，．则，因为为抛物线上一点，所以，整理得，所以．21．（Ⅰ）证明：在图甲中∵且∴,即在图乙中，∵平面ABD 平面BDC ，且平面ABD 平面BDC ＝BD ∴AB ⊥底面BDC ，∴AB ⊥CD ．又，∴DC⊥BC,且∴DC平面ABC．（Ⅱ）解：∵E、F分别为AC、AD的中点∴EF//CD，又由（Ⅰ）知，DC平面ABC，∴EF⊥平面ABC，∴在图甲中，∵, ∴,由得,∴∴∴.22.解：（Ⅰ）由已知得，所以．所以椭圆的焦点坐标为．离心率为．（Ⅱ）由题意知，．当时，切线的方程，点的坐标分别为，此时．当时，同理可得．当时，设切线的方程为．由得．设两点的坐标分别为，则，．又由与圆相切得，即．所以．由于当时，所以.，．因为．且当时，，所以的最大值为．.。

辽宁省实验中学分校2014届高三上学期期中考试数学(文)试题 Word版含答案

第Ⅰ卷一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若α是第二象限的角，且2sin 3α=，则=αcos （）A. B. 31 D.13- 2．若集合}1|{}2|{2+====-x y y P y y M x ，，则P M ⋂等于（）A ．}0y {y ≥B ．}0y {y >C ． }1y {y ≥D ． }1y {y >3．命题“设a 、b 、c R ∈，若22ac bc >则a b >”以及它的逆命题、否命题、逆否命题中，真命题的个数为（）A. 0B. 1C. 2D. 34. 与函数x y =有相同图象的一个函数是（）A ．2x y =B ．)1,0(log ≠>=a a a y x aC ．xx y 2= D ．)1,0(log ≠>=a a a y x a 5．设α是第三象限角，且|2cosα|=2cos α-，则2α所在象限是（） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限 6. 函数x e x y )3(2-=的单调递增区是（）A. )0,(-∞B. ),0(+∞C. )3,(--∞和),1(+∞D.)1,3(- 7. =⋅+ααααcos2cos cos212sin22 （） A. αtan B. αtan2 C. 1 D.21 8．下列命题错误的是（） A. 命题“若00>>y x 且则0>+y x ”的否命题是假命题；B. 若命题01,:0200≤+-∈∃x x R x p ，则01,:2>+-∈∀⌝x x R x p ； C. ABC ∆中，B A sin sin >是B A >的充要条件；D. 若y x cos sin =，则2π=+y x9．已知函数2()2f x x ax a =-+，在区间(,1)-∞上有最小值，则函数()()f x g x x=在区间(1,)+∞上一定（）A. 是减函数B. 是增函数C. 有最小值D. 有最大值10．已知21)sin(=+απ，则απααπcos )cot()2sin(---的值等于（） A ．2- B ．21- C ．2 D ． 21 11．已知可导函数)()()()(x f x f R x x f >'∈满足，则当0a >时，()(0)a f a e f 和大小关系为（）A ．()(0)a f a e f < B. ()(0)a f a e f > C. ()(0)a f a e f = D. ()()0f e a f a≤ 12．函数1222131)(23++-+=a ax ax ax x f 的图象经过四个象限，则实数a 的取值范围是（）A ．16356<<-a B ．16358-<<-a C ．16158-<<-a D ．16356-<<-a第Ⅱ卷二、填空题(本题共4小题，每小题5分，共20分。

辽宁省师范大学附属中学2018-2019学年高三上期中考试文科数学试题(解析版)

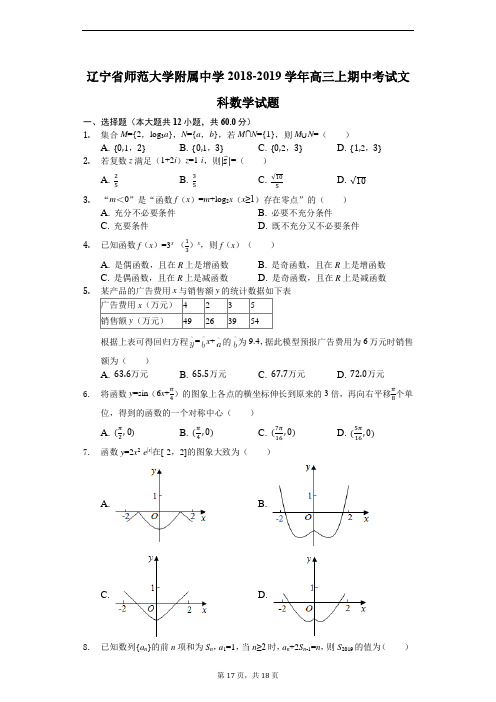
辽宁省师范大学附属中学2018-2019学年高三上期中考试文科数学试题一、选择题（本大题共12小题，共60.0分）1.集合M={2，log3a}，N={a，b}，若M∩N={1}，则M∪N=（）A. {0,1，2}B. {0,1，3}C. {0,2，3}D. {1,2，3}2.若复数z满足（1+2i）z=1-i，则|z−|=（）A. 25B. 35C. √105D. √103.“m＜0”是“函数f（x）=m+log2x（x≥1）存在零点”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件4.已知函数f（x）=3x-（13）x，则f（x）（）A. 是偶函数，且在R上是增函数B. 是奇函数，且在R上是增函数C. 是偶函数，且在R上是减函数D. 是奇函数，且在R上是减函数5.某产品的广告费用x与销售额y的统计数据如下表广告费用x（万元）4235销售额y（万元）49263954根据上表可得回归方程=x+的为9.4，据此模型预报广告费用为6万元时销售额为（）A. 63.6万元B. 65.5万元C. 67.7万元D. 72.0万元6.将函数y=sin（6x+π4）的图象上各点的横坐标伸长到原来的3倍，再向右平移π8个单位，得到的函数的一个对称中心（）A. (π2,0) B. (π4,0) C. (7π16,0) D. (5π16,0)7.函数y=2x2-e|x|在[-2，2]的图象大致为（）A. B.C. D.8.已知数列{a n}的前n项和为S n，a1=1，当n≥2时，a n+2S n-1=n，则S2019的值为（）A. 1008B. 1009C. 1010D. 1011 9. 若不等式x 2-（a +1）x +a ≤0的解集是[-4，3]的子集，则a 的取值范围是（） A. [−4,1] B. [−4,3] C. [1,3] D. [−1,3] 10. 在锐角△ABC 中，B =60°，|AB ⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2，则AB ⃗⃗⃗⃗⃗ •AC⃗⃗⃗⃗⃗ 的取值范围为（） A. (0,12)B. [−14,12)C. (0,4]D. (0,2]11. 在三棱锥S -ABC 中，SA =BC =√41，SB =AC =5，SC =AB =√34，则三棱锥S -ABC 外接球的表面积为（） A. 25π B. 25√2π C. 50π D. 50√2π 12. 已知函数f(x)=e x x 2+2klnx −kx ，若x =2是函数f （x ）的唯一极值点，则实数k 的取值范围是（）A. (−∞,e 24]B. (−∞,e2]C. (0,2]D. [2,+∞)二、填空题（本大题共4小题，共20.0分）13. 已知实数x ，y 满足{2x −y −2≥0x −y +2≥02x +y −2≥0，则z =3x -y 的最小值为______14. 一个几何体的三视图如图所示，且其侧（左）视图是一个等边三角形，则这个几何体的体积为______．15. 数列{a n }为正项等比数列，若a 3=3，且a n +1=2a n +3a n -1（n ≥2，n ∈N *），则此数列的前5项和S 5=______．16. 选做题：若a ，b ，c ＞0，且a 2+ab +ac +bc =4，则2a +b +c 的最小值为______．三、解答题（本大题共7小题，共82.0分）17. D 为△ABC 的边BC 的中点．AB =2AC =2AD =2．（1）求BC 的长；（2）若∠ACB 的平分线交AB 于E ，求S △ACE ．18. 中国神舟十一号载人飞船在酒泉卫星发射中心成功发射，引起全国轰动．开学后，某校高二年级班主任对该班进行了一次调查，发现全班60名同学中，对此事关注的占13，他们在本学期期末考试中的物理成绩（满分100分）如下面的频率分布直方图：（1）求“对此事关注”的同学的物理期末平均分（以各区间的中点代表该区间的均值）．（2）若物理成绩不低于80分的为优秀，请以是否优秀为分类变量，①补充下面的2×2列联表：物理成绩优秀物理成绩不优秀合计对此事关注______ ______ ______对此事不关注______ ______ ______合计______ ______ ______②是否有95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系？，其中n=a+b+c+d．参考公式：k2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)P（K2≥k0）0.150.100.050.0250.0100.0050.001k0 2.0722.7063.8415.0246.6357.87910.82819.如图，正方体ABCDA1B1C1D1的棱长为2，E、F、M分别是C1B1，C1D1和AB的中点．（1）求证：MD1∥平面BEFD．（2）求M到平面BEFD的距离．20. 在等比数列{a n }中，a 1＞0，n ∈N *，且a 3-a 2=8，又a 1、a 5的等比中项为16．（1）求数列{a n }的通公式；（2）设b n =log 4a n ，数列{b n }的前n 项和为S n ，是否存在正整数k ，使得1S 1+1S 2+1S 3+…+1Sn＜k 对任意n ∈N *恒成立．若存在，求出正整数k 的最小值；不存在，请说明理由．21. 已知f （x ）=x lnx ．（Ⅰ）求函数f （x ）在定义域上的最小值；（Ⅱ）求函数f （x ）在[t ，t +2]（t ＞0）上的最小值；（Ⅲ）证明：对一切x ∈（0，+∞），都有ln x ＞1e x −2ex 成立．22. 已知在平面直角坐标系xOy 中，直线l 的参数方程是{y =2t +6x=t（t 是参数），以原点O 为极点，x 轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 的极坐标方程为ρ=2√2cosθ．（Ⅰ）求直线l 的普通方程与曲线C 的直角坐标方程；（Ⅱ）设M （x ，y ）为曲线C 上任意一点，求x +y 的取值范围．23. 已知函数f （x ）=|x -5|+|x +4|．（1）求不等式f （x ）≥12的解集；（2）若关于x 的不等式f （x ）-21-3a -1≥0恒成立，求实数a 的取值范围．答案和解析1.【答案】D【解析】解：由题意知∵M∩N={1}，∴1∈N且1∈M∴log3a=1 即a=3又∵1∈N∴b=1即M={1，2} N={1，3}∴M∪N={1，2，3}故选：D．因为M∩N={1}，所以1∈N且1∈M，即log3a=1，则a=3，那么b=1，故M∪N={1，2，3}．本题主要考查元素的互异性及并集的运算，属于基础题型．2.【答案】C【解析】解：由（1+2i）z=1-i，得z=，∴||=|z|=||=．故选：C．把已知等式变形，再由||=|z|=||，结合商的模等于模的商求解．本题考查复数的基本概念，考查复数模的求法，是基础题．3.【答案】A【解析】解：∵m＜0，函数f（x）=m+log2x（x≥1），又x≥1，log2x≥0，∵y=log2x在x≥1上为增函数，求f（x）存在零点，要求f（x）＜0，必须要求m＜0，∴f（x）在x≥1上存在零点；若m=0，代入函数f（x）=m+log2x（x≥1），可得f（x）=log2x，令f（x）=log2x=0，可得x=1，f（x）的零点存在，∴“m＜0”是“函数f（x）=m+log2x（x≥1）存在零点”充分不必要条件，故选：A．利用特殊值法，令m=0，代入可以求出函数f（x）=m+log2x（x≥1）的零点，从而进行判断；此题以对数函数为载体，考查了必要条件和充分条件的定义及其判断，是一道基础题．4.【答案】B【解析】解：f（x）=3x-（）x=3x-3-x，∴f（-x）=3-x-3x=-f（x），即函数f（x）为奇函数，又由函数y=3x为增函数，y=（）x为减函数，故函数f（x）=3x-（）x为增函数，故选：B．由已知得f（-x）=-f（x），即函数f（x）为奇函数，由函数y=3x为增函数，y=（）x 为减函数，结合“增”-“减”=“增”可得答案．本题考查的知识点是函数的奇偶性，函数的单调性，是函数图象和性质的综合应用，难度不大，属于基础题．5.【答案】B【解析】解：∵=3.5，=42，∵数据的样本中心点在线性回归直线上，回归方程中的为9.4，∴42=9.4×3.5+，∴=9.1，∴线性回归方程是y=9.4x+9.1，∴广告费用为6万元时销售额为9.4×6+9.1=65.5，故选：B．首先求出所给数据的平均数，得到样本中心点，根据线性回归直线过样本中心点，求出方程中的一个系数，得到线性回归方程，把自变量为6代入，预报出结果．本题考查线性回归方程．考查预报变量的值，考查样本中心点的应用，本题是一个基础题，这个原题在2011年山东卷第八题出现．6.【答案】A【解析】解：函数的图象上各点的横坐标伸长到原来的3倍得到图象的解析式为再向右平移个单位得到图象的解析式为=sin2x当x=时，y=sinπ=0，所以是函数y=sin2x的一个对称中心．故选：A．先根据三角函数图象变换规律写出所得函数的解析式，再根据三角函数的性质进行验证：若f（a）=0，则（a，0）为一个对称中心，确定选项．本题考查了三角函数图象变换规律，三角函数图象、性质．是三角函数中的重点知识，在试题中出现的频率相当高．7.【答案】D【解析】解：∵f（x）=y=2x2-e|x|，∴f（-x）=2（-x）2-e|-x|=2x2-e|x|，故函数为偶函数，当x=±2时，y=8-e2∈（0，1），故排除A，B；当x∈[0，2]时，f（x）=y=2x2-e x，∴f′（x）=4x-e x=0有解，故函数y=2x2-e|x|在[0，2]不是单调的，故排除C，故选：D．根据已知中函数的解析式，分析函数的奇偶性，最大值及单调性，利用排除法，可得答案．本题考查的知识点是函数的图象，对于超越函数的图象，一般采用排除法解答．8.【答案】C【解析】解：根据题意，n≥2时，S n-1=S n-a n∴a n+2（S n-a n）=n∴2S n=a n+n ①又n≥2时，2S n-1=a n-1+n-1 ②由①-②知，2a n=a n-a n-1+1∴a n=-a n-1+1∴a2019+a2018=1a2017+a2016=1…a3+a2=1a1=1∴S2019=1×+1=1010故选：C．运用数列的递推公式可解决此问题．本题考查数列的递推公式的应用．9.【答案】B【解析】解：由x2-（a+1）x+a≤0得（x-a）（x-1）≤0，若a=1，不等式等价解为x=1即解集为{1}满足{1}⊆[-4，3]，若a＜1，不等式等价解为a≤x≤1即解集为[a，1]，若满足[a，1]⊆[-4，3]，则-4≤a＜1，若a＞1，不等式等价解为1≤x≤a即解集为[1，a]，若满足[1，a]⊆[-4，3]，则1＜a≤3，综上-4≤a≤3，即实数a的取值范围是[-4，3]，故选：B．求出不等式的等价条件，结合子集关系建立不等式进行求解即可．本题主要考查不等式的应用，结合不等式的解法求出不等式的解集，利用子集关系进行转化是解决本题的关键．10.【答案】A【解析】解：以B为原点，BA所在直线为x轴建立坐标系，∵B=60°，|-|=||=2，∴C（1，），设A（x，0）∵△ABC是锐角三角形，∴A+C=120°，∴30°＜A＜90°，即A在如图的线段DE上（不与D，E重合），∴1＜x＜4，则=x2-x=（x-）2-，∴的范围为（0，12）．故选：A．以B为原点，BA所在直线为x轴建立坐标系，得到C的坐标，找出三角形为锐角三角形的A的位置，得到所求范围．本题考查数量积的应用，根据向量数量积的模长公式，利用解析法建立坐标系，利用坐标法求数量积范围是解决本题的关键．综合性较强，有一定的难度．11.【答案】C【解析】解：如图，把三棱锥S-ABC补形为长方体，设长方体的长、宽、高分别为a、b、c，则a2+b2=41，b2+c2=25，a2+c2=34，∴三棱锥外接球的半径R=．∴三棱锥S-ABC外接球的表面积为S=4πR2=50π．故选：C．由于已知三棱锥的相对棱长相等，可考虑补形为长方体求解．本题考查多面体外接球的求法，关键是补形思想的应用，是中档题．12.【答案】A【解析】解：∵函数f（x）的定义域是（0，+∞）∴f′（x）=+-k=，∵x=2是函数f（x）的唯一一个极值点∴x=2是导函数f′（x）=0的唯一根，∴e x-kx2=0在（0，+∞）无变号零点，即k=在x＞0上无变号零点，令g（x）=，因为g'（x）=，所以g（x）在（0，2）上单调递减，在x＞2 上单调递增所以g（x）的最小值为g（2）=，所以必须k≤，故选：A．由f（x）的导函数形式可以看出，需要对k进行分类讨论来确定导函数为0时的根．本题考查由函数的导函数确定极值问题．对参数需要进行讨论．13.【答案】3【解析】解：由已知的不等式组得到平面区域如图：根据z=3x-y得到y=3x-z，当此直线经过图中A时在y轴截距最大，z最小，由得到A（1，0），所以z的最大值为3×1-0=3；故答案为：3．画出可行域，根据目标函数的几何意义求最小值即可．本题考查了简单线性规划问题；画出可行域，利用目标函数的几何意义求最值．14.【答案】5√33【解析】解：由三视图还原原几何体如图，该几何体为组合体，左边是三棱锥，右边是四棱锥，其中平面PAD⊥底面ABCDE，且△PAD为等边三角形，ED=EA，EO=1，四边形ABCD为正方形，边长是2．∴这个几何体的体积V=．故答案为：．由三视图还原原几何体，可得该几何体为组合体，左边是三棱锥，右边是四棱锥，其中平面PAD⊥底面ABCDE，且△PAD为等边三角形，ED=EA，EO=1，四边形ABCD为正方形，边长是2．再由棱锥体积公式求解．本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．15.【答案】1213【解析】解：根据题意，a n+1+a n=3a n+3a n-1=3（a n+a n-1）∵{a n}为等比数列∴q=3，又a3=3∴a1=∴S5==故答案为．运用数列的递推公式和等比数列的性质可解决此问题．本题考查数列的递推公式和等比数列的性质．16.【答案】4【解析】解：4×4=（a2+ab+ac+bc）×4=4a2+4ab+4ac+4bc≤4a2+4ab+b2+c2+4ca+2bc=（2a+b+c）2，所以2a+b+c≥4．故答案为：4因为（2a+b+c）2=4a2+b2+c2+4ab+2bc+4ca，与已知等式比较发现，只要利用均值不等式b2+c2≥2bc即可求出结果．本小题主要考查均值不等式的有关知识及配方法的有关知识，以及转化与化归的思想方法．解答的关键是利用平方关系4a 2+4ab+b 2+c 2+4ca+2bc=（2a+b+c ）2建立条件与结论之间的联系．17.【答案】解：（1）由题意知AB =2，AC =AD =1．设BD =DC =m ．在△ADB 与△ADC 中，由余弦定理得：AB 2=AD 2+BD 2-2AD •BD cos ∠ADB ，AC 2=AD 2+DC 2-2AD •DC cos ∠ADC ．即：1+m 2-2m cos ∠ADB =4，① 1+m 2+2m cos ∠ADB =1．② 由①+②，得：m 2=32，所以m =√62，即BC =√6．（2）在△ACE 与△BCE 中，由正弦定理得：AE sin∠ACE =EC sin∠EAC ，BE sin∠BCE =ECsin∠CBE ，由于∠ACE =∠BCE ，且BCsin∠BAC =ACsin∠CBA ，所以AE BE =ACBC =√66．所以BE =√6AE ，所以AE =25（√6-1）．又cos ∠BAC =AB2+AC2−BC22AB⋅AC =22+12−(√6)22×2×1=-14，所以sin ∠BAC =√154，所以S △ACE =12AC •AE •sin ∠BAC =12×1×25（√6-1）×√154=3√10−√1520．【解析】（1）由题意知AB=2，AC=AD=1．设BD=DC=m ，在△ADB 与△ADC 中，由余弦定理即可解得m 的值．（2）在△ACE 与△BCE 中，由正弦定理，角平分线的性质可得==．可求BE=AE ，AE=（-1）．利用余弦定理可求cos ∠BAC 的值，根据同角三角函数基本关系式可求sin ∠BAC 的值，利用三角形的面积公式即可计算得解．本题主要考查了余弦定理，正弦定理，角平分线的性质，同角三角函数基本关系式，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．18.【答案】8 12 20 8 32 40 16 44 60【解析】（1）对此事关注的同学的物理期末平均分为（45×0.005+55×0.005+65×0.020+75×0.030+85×0.030+95×0.010）×10=75.5（分）．（2）①补充的2×2列联表如下：物理成绩优秀物理成绩不优秀合计对此事关注 81220对此事不关注 8 32 40合计164460 ②由①中的列联表可得==，∴没有95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系．（1）由频率分布直方图中小矩形中点的横坐标乘以频率，作和得答案；（2）①由题中数据求值填写列联表；②结合列联表中的数据及给出的公式求得K 2的值，与3.841比较的结论．本题考查独立性检验，考查计算能力，训练了频率分布直方图求平均数的估计值，是中档题．19.【答案】（1）证明：连接BF ，∵D 1F ∥A 1B 1，D 1F =12A 1B 1，BM ∥A 1B 1，BM =12A 1B 1， ∴D 1F ∥BM ，D 1F =BM ，∴四边形BMD 1F 是平行四边形， ∴D 1M ∥BF ，又D 1M ⊄平面BEFD ，BF ⊂平面BEFD ， ∴MD 1∥平面BEFD ．（2）解：连接ED ，EM ，DM ，则V E -BDM =13×12×1×2×2=23，又BD =√2AB =2√2，BE =√BB 12+B 1E 2=√5，DE =√D 1C 12+C 1E 2=3，∴cos ∠DBE =BD 2+BE 2−DE 22BD⋅BE =√1010，∴sin ∠DBE =3√1010．∴S △BDE =12×2√2×√5×3√1010=3，设M 到平面BEFD 的距离为d ，则V M -BDE =13×3×d =23， ∴d =23．即M 到平面BEFD 的距离为23．【解析】（1）连接BF ，证明四边形BMD 1F 是平行四边形即可得出D 1M ∥BF ，故MD 1∥平面BEFD ；（2）根据V M-BDE =V E-BDM 求出M 到平面BEFD 的距离．本题考查了线面平行的判定，棱锥的体积计算，属于中档题．20.【答案】解：（1）设数列{a n }的公比为q ，由题意a 1、a 5的等比中项为16可得a 3=16，又a 3-a 2=8，则a 2=8， ∴q =a 3a 2=2， ∴a n =2n +1．（2）∵b n =log 42n +1=n+12，b n +1=n+22，b n +1-b n =12，∴数列{b n }是首项为1，公差为12的等差数列， ∴S n =b 1+b 2+…+b n =(1+n+12)n 2=n(n+3)4，∴1S n=4n(n+3)=43（1n -1n+3），∴1S 1+1S 2+…+1S n=43（1-14+12-15+13-16+…+1n -1n+3）=43（1+12+13-1n+1-1n+2-1n+3） =43×116-43×（1n+1+1n+2+1n+3） =229-43×（1n+1+1n+2+1n+3）当n =1时，1S 1=1＜2＜229，当n ≥2时，1S 1+1S 2+…+1S n=229-43×（1n+1+1n+2+1n+3）＜229．故存在最小的正整数k =3，使得1S 1+1S 2+…+1S n＜3对任意n ∈N *恒成立．【解析】（1）利用等比数列的定义可求其公比q==2，从而可求{a n }的通公式；（2）依题意，可求b n =，从而可求数列{b n }的前n 项和为S n ，继而可得=（-），从而可得++…+＜，于是可求k min ．本题考查数列的求和，考查等比数列的定义及通项公式，突出考查裂项法求和，考查推理与运算能力，属于难题．21.【答案】解：（Ⅰ）由f （x ）=x lnx ，x ＞0得f '（x ）=ln x +1，令f '（x ）=0，得x =1e ．当x ∈(0，1e )时，f '（x ）＜0，f （x ）单调递减；当x ∈(1e ，+∞)时，f '（x ）＞0，f （x ）单调递增．可得最小值为-1e …（3分）（Ⅱ）当0＜t ＜1e ＜t +2，即0＜t ＜1e 时，f(x)min =f(1e )=−1e …（4分）当1e ≤t ＜t +2，即t ≥1e 时，f （x ）在[t ，t +2]上单调递增，此时f （x ）min =f （t ）=t lnt …（6分）所以f(x)min={−1e ，0＜t ＜1etlnt ，t ≥1e…（8分）（Ⅲ）问题等价于证明xlnx ＞xe x −2e (x ∈(0，+∞))．由（1）知f （x ）=x lnx ，x ＞0的最小值是−1e ，当且仅当x =1e 时取到，设m(x)=xe x −2e (x ∈(0，+∞))，则m′(x)=1−x e x ，易知m(x)max =m(1)=−1e ，当且仅当x =1时取到．从而对一切x ∈（0，+∞），都有lnx ＞1e −2ex 成立．…（12分）【解析】（Ⅰ）求出导数，极值点和单调区间，可得极小值和最小值；（Ⅱ）讨论时，时，运用单调性，即可得到所求最小值；（Ⅲ）问题等价于证明．由（1）设，求出导数，求出最大值即可．本题考查导数的运用：求单调区间和最值，注意运用分类讨论的方法和构造函数的方法，考查运算能力，属于中档题．22.【答案】解：（Ⅰ）由直线l 的参数方程是{y =2t +6x=t（t 是参数），转换为直角坐标方程为：y =2x +6，故直线l 的普通方程为2x -y +6=0，曲线C 的极坐标方程为ρ=2√2cosθ．整理得：ρ2=2√2ρcosθ，所以x 2+y 2=2√2x ，即(x −√2)2+y 2=2，故曲线C 的普通方程为(x −√2)2+y 2=2．（Ⅱ）据题意设点M(√2+√2cosθ，√2sinθ)，则x +y =√2+√2cosθ+√2sinθ， =√2+2sin(θ+π4)，所以x +y 的取值范围是[−2+√2，2+√2]．【解析】（Ⅰ）直接利用转换关系式，把参数方程直角坐标方程和极坐标方程之间进行转换．（Ⅱ）利用三角函数关系式的变换和正弦型函数性质的应用求出结果．本题考查的知识要点：参数方程直角坐标方程和极坐标方程之间的转换，三角函数关系式的恒等变变换，正弦型函数的性质的应用，主要考查学生的运算能力和转化能力，属于基础题型．23.【答案】解：（1）原不等式等价于{x −5+x +4≥12x>5或{5−x +x +4≥12−4≤x≤5或{5−x −(x +4)≥12x<−4，解得x ≥132或x ∈∅或x ≤−112．所以不等式的解集为{x|x ≥132或x ≤−112}．（2）不等式f （x ）-21-3a -1≥0恒成立等价于f(x)min ≥21−3a +1，即(|x −5|+|x +4|)min ≥21−3a +1 因为|x -5|+|x +4|≥|（x -5）-（x +4）|=9，所以9≥21-3a +1，得21-3a ≤8，得1-3a ≤3，解得a ≥−23．故实数a 的取值范围是[−23，+∞)．【解析】（1）去掉绝对值符号，转化不等式为不等式组，然后求解即可．（2）不等式f （x ）-21-3a -1≥0恒成立等价于，利用绝对值的几何意义求解函数的最小值，然后求解指数不等式，推出a 的范围即可．本题考查绝对值不等式的解法，函数恒成立条件的应用，考查转化思想以及计算能力．。

辽宁省师范大学附属中学2018-2019学年高三上期中考试文科数学试题含答案

辽宁省师范大学附属中学2018-2019学年高三上期中考试文科数学试题一、选择题（本大题共12小题，共60.0分）1.集合M={2，log3a}，N={a，b}，若M∩N={1}，则M∪N=（）A. {0,1，2}B. {0,1，3}C. {0,2，3}D. {1,2，3}2.若复数z满足（1+2i）z=1-i，则|z−|=（）A. 25B. 35C. √105D. √103.“m＜0”是“函数f（x）=m+log2x（x≥1）存在零点”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件4.已知函数f（x）=3x-（13）x，则f（x）（）A. 是偶函数，且在R上是增函数B. 是奇函数，且在R上是增函数C. 是偶函数，且在R上是减函数D. 是奇函数，且在R上是减函数5.根据上表可得回归方程=x+的为9.4，据此模型预报广告费用为6万元时销售额为（）A. 63.6万元B. 65.5万元C. 67.7万元D. 72.0万元6.将函数y=sin（6x+π4）的图象上各点的横坐标伸长到原来的3倍，再向右平移π8个单位，得到的函数的一个对称中心（）A. (π2,0) B. (π4,0) C. (7π16,0) D. (5π16,0)7.函数y=2x2-e|x|在[-2，2]的图象大致为（）A. B.C. D.8. 已知数列{a n }的前n 项和为S n ，a 1=1，当n ≥2时，a n +2S n -1=n ，则S 2019的值为（）A. 1008B. 1009C. 1010D. 10119. 若不等式x 2-（a +1）x +a ≤0的解集是[-4，3]的子集，则a 的取值范围是（）A. [−4,1]B. [−4,3]C. [1,3]D. [−1,3]10. 在锐角△ABC 中，B =60°，|AB ⃗⃗⃗⃗⃗ −AC ⃗⃗⃗⃗⃗ |=2，则AB ⃗⃗⃗⃗⃗ •AC⃗⃗⃗⃗⃗ 的取值范围为（） A. (0,12)B. [−14,12)C. (0,4]D. (0,2]11. 在三棱锥S -ABC 中，SA =BC =√41，SB =AC =5，SC =AB =√34，则三棱锥S -ABC 外接球的表面积为（）A. 25πB. 25√2πC. 50πD. 50√2π 12. 已知函数f(x)=e x x 2+2klnx −kx ，若x =2是函数f （x ）的唯一极值点，则实数k 的取值范围是（）A. (−∞,e 24]B. (−∞,e2]C. (0,2]D. [2,+∞)二、填空题（本大题共4小题，共20.0分）13. 已知实数x ，y 满足{2x −y −2≥0x −y +2≥02x +y −2≥0，则z =3x -y 的最小值为______14. 一个几何体的三视图如图所示，且其侧（左）视图是一个等边三角形，则这个几何体的体积为______．15. 数列{a n }为正项等比数列，若a 3=3，且a n +1=2a n +3a n -1（n ≥2，n ∈N *），则此数列的前5项和S 5=______． 16. 选做题：若a ，b ，c ＞0，且a 2+ab +ac +bc =4，则2a +b +c 的最小值为______．三、解答题（本大题共7小题，共82.0分）17. D 为△ABC 的边BC 的中点．AB =2AC =2AD =2．（1）求BC 的长；（2）若∠ACB 的平分线交AB 于E ，求S △ACE ．18.中国神舟十一号载人飞船在酒泉卫星发射中心成功发射，引起全国轰动．开学后，某校高二年级班主任对该班进行了一次调查，发现全班60名同学中，对此事关注的占1，他们在本学期期末考试中的物理3成绩（满分100分）如下面的频率分布直方图：（1）求“对此事关注”的同学的物理期末平均分（以各区间的中点代表该区间的均值）．（2）若物理成绩不低于80分的为优秀，请以是否优秀为分类变量，①补充下面的2×2列联表：物理成绩优秀物理成绩不优秀合计对此事关注______ ______ ______对此事不关注______ ______ ______合计______ ______ ______②是否有以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系？，其中n=a+b+c+d．参考公式：k2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)参考数据：P（K2≥k0）0.150.100.050.0250.0100.0050.001k0 2.0722.7063.8415.0246.6357.87910.82819.如图，正方体ABCDA1B1C1D1的棱长为2，E、F、M分别是C1B1，C1D1和AB的中点．（1）求证：MD1∥平面BEFD．（2）求M到平面BEFD的距离．20.在等比数列{a n}中，a1＞0，n∈N*，且a3-a2=8，又a1、a5的等比中项为16．（1）求数列{a n}的通公式；（2）设b n=log4a n，数列{b n}的前n项和为S n，是否存在正整数k，使得1S1+1S2+1S3+…+1S n＜k对任意n∈N*恒成立．若存在，求出正整数k的最小值；不存在，请说明理由．21.已知f（x）=x lnx．（Ⅰ）求函数f（x）在定义域上的最小值；（Ⅱ）求函数f（x）在[t，t+2]（t＞0）上的最小值；（Ⅲ）证明：对一切x∈（0，+∞），都有ln x＞1e x −2ex成立．22. 已知在平面直角坐标系xOy 中，直线l 的参数方程是{y =2t +6x=t（t 是参数），以原点O 为极点，x 轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 的极坐标方程为ρ=2√2cosθ．（Ⅰ）求直线l 的普通方程与曲线C 的直角坐标方程；（Ⅱ）设M （x ，y ）为曲线C 上任意一点，求x +y 的取值范围．23. 已知函数f （x ）=|x -5|+|x +4|．（1）求不等式f （x ）≥12的解集；（2）若关于x 的不等式f （x ）-21-3a -1≥0恒成立，求实数a 的取值范围．参考答案1.【答案】D2.【答案】C3.【答案】A4.【答案】B5.【答案】B6.【答案】A7.【答案】D8.【答案】C9.【答案】B10.【答案】A11.【答案】C12.【答案】A13.【答案】3【解析】解：由已知的不等式组得到平面区域如图：根据z=3x-y得到y=3x-z，当此直线经过图中A时在y轴截距最大，z最小，由得到A（1，0），所以z的最大值为3×1-0=3；故答案为：3．画出可行域，根据目标函数的几何意义求最小值即可．本题考查了简单线性规划问题；画出可行域，利用目标函数的几何意义求最值．14.【答案】5√33【解析】解：由三视图还原原几何体如图，该几何体为组合体，左边是三棱锥，右边是四棱锥，其中平面PAD⊥底面ABCDE，且△PAD为等边三角形，ED=EA，EO=1，四边形ABCD为正方形，边长是2．∴这个几何体的体积V=．故答案为：．由三视图还原原几何体，可得该几何体为组合体，左边是三棱锥，右边是四棱锥，其中平面PAD⊥底面ABCDE，且△PAD为等边三角形，ED=EA，EO=1，四边形ABCD为正方形，边长是2．再由棱锥体积公式求解．本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．15.【答案】1213【解析】解：根据题意，a n+1+a n=3a n+3a n-1=3（a n+a n-1）∵{a n}为等比数列∴q=3，又a3=3∴a1=∴S5==故答案为．运用数列的递推公式和等比数列的性质可解决此问题．本题考查数列的递推公式和等比数列的性质．16.【答案】4【解析】解：4×4=（a2+ab+ac+bc）×4=4a2+4ab+4ac+4bc≤4a2+4ab+b2+c2+4ca+2bc=（2a+b+c）2，所以2a+b+c≥4．故答案为：4因为（2a+b+c ）2=4a 2+b 2+c 2+4ab+2bc+4ca ，与已知等式比较发现，只要利用均值不等式b 2+c 2≥2bc 即可求出结果．本小题主要考查均值不等式的有关知识及配方法的有关知识，以及转化与化归的思想方法．解答的关键是利用平方关系4a 2+4ab+b 2+c 2+4ca+2bc=（2a+b+c ）2建立条件与结论之间的联系． 17.【答案】解：（1）由题意知AB =2，AC =AD =1．设BD =DC =m ．在△ADB 与△ADC 中，由余弦定理得：AB 2=AD 2+BD 2-2AD •BD cos ∠ADB ，AC 2=AD 2+DC 2-2AD •DC cos ∠ADC ．即：1+m 2-2m cos ∠ADB =4，① 1+m 2+2m cos ∠ADB =1．② 由①+②，得：m 2=32，所以m =√62，即BC =√6．（2）在△ACE 与△BCE 中，由正弦定理得：AE sin∠ACE =EC sin∠EAC ，BE sin∠BCE =ECsin∠CBE ，由于∠ACE =∠BCE ，且BCsin∠BAC =ACsin∠CBA ，所以AE BE =ACBC =√66．所以BE =√6AE ，所以AE =25（√6-1）．又cos ∠BAC =AB2+AC2−BC22AB⋅AC =22+12−(√6)22×2×1=-14，所以sin ∠BAC =√154，所以S △ACE =12AC •AE •sin ∠BAC =12×1×25（√6-1）×√154=3√10−√1520．【解析】（1）由题意知AB=2，AC=AD=1．设BD=DC=m ，在△ADB 与△ADC 中，由余弦定理即可解得m 的值．（2）在△ACE 与△BCE 中，由正弦定理，角平分线的性质可得==．可求BE=AE ，AE=（-1）．利用余弦定理可求cos ∠BAC 的值，根据同角三角函数基本关系式可求sin ∠BAC 的值，利用三角形的面积公式即可计算得解．本题主要考查了余弦定理，正弦定理，角平分线的性质，同角三角函数基本关系式，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题． 18.【答案】8 12 20 8 32 40 16 44 60【解析】（1）对此事关注的同学的物理期末平均分为（45×0.005+55×0.005+65×0.020+75×0.030+85×0.030+95×0.010）×10=75.5（分）．（2）①补充的2×2列联表如下：物理成绩优秀物理成绩不优秀合计对此事关注 81220对此事不关注 8 32 40合计164460 ②由①中的列联表可得==，∴没有95%以上的把握认为“对此事是否关注”与物理期末成绩是否优秀有关系．（1）由频率分布直方图中小矩形中点的横坐标乘以频率，作和得答案；（2）①由题中数据求值填写列联表；②结合列联表中的数据及给出的公式求得K 2的值，与3.841比较的结论．本题考查独立性检验，考查计算能力，训练了频率分布直方图求平均数的估计值，是中档题． 19.【答案】（1）证明：连接BF ，∵D 1F ∥A 1B 1，D 1F =12A 1B 1，BM ∥A 1B 1，BM =12A 1B 1， ∴D 1F ∥BM ，D 1F =BM ，∴四边形BMD 1F 是平行四边形， ∴D 1M ∥BF ，又D 1M ⊄平面BEFD ，BF ⊂平面BEFD ， ∴MD 1∥平面BEFD ．（2）解：连接ED ，EM ，DM ，则V E -BDM =13×12×1×2×2=23，又BD =√2AB =2√2，BE =√BB 12+B 1E 2=√5，DE =√D 1C 12+C 1E 2=3，∴cos ∠DBE =BD 2+BE 2−DE 22BD⋅BE =√1010，∴sin ∠DBE =3√1010．∴S △BDE =12×2√2×√5×3√1010=3，设M 到平面BEFD 的距离为d ，则V M -BDE =13×3×d =23， ∴d =23．即M 到平面BEFD 的距离为23．【解析】（1）连接BF ，证明四边形BMD 1F 是平行四边形即可得出D 1M ∥BF ，故MD 1∥平面BEFD ；（2）根据V M-BDE =V E-BDM 求出M 到平面BEFD 的距离．本题考查了线面平行的判定，棱锥的体积计算，属于中档题．20.【答案】解：（1）设数列{a n }的公比为q ，由题意a 1、a 5的等比中项为16可得a 3=16，又a 3-a 2=8，则a 2=8， ∴q =a 3a 2=2， ∴a n =2n +1．（2）∵b n =log 42n +1=n+12，b n +1=n+22，b n +1-b n =12，∴数列{b n }是首项为1，公差为12的等差数列， ∴S n =b 1+b 2+…+b n =(1+n+12)n 2=n(n+3)4，∴1S n=4n(n+3)=43（1n -1n+3），∴1S 1+1S 2+…+1S n=43（1-14+12-15+13-16+…+1n -1n+3）=43（1+12+13-1n+1-1n+2-1n+3） =43×116-43×（1n+1+1n+2+1n+3） =229-43×（1n+1+1n+2+1n+3）当n =1时，1S 1=1＜2＜229，当n ≥2时，1S 1+1S 2+…+1S n =229-43×（1n+1+1n+2+1n+3）＜229．故存在最小的正整数k =3，使得1S 1+1S 2+…+1S n ＜3对任意n ∈N *恒成立．【解析】（1）利用等比数列的定义可求其公比q==2，从而可求{a n }的通公式；（2）依题意，可求b n =，从而可求数列{b n }的前n 项和为S n ，继而可得=（-），从而可得++…+＜，于是可求k min ．本题考查数列的求和，考查等比数列的定义及通项公式，突出考查裂项法求和，考查推理与运算能力，属于难题．21.【答案】解：（Ⅰ）由f （x ）=x lnx ，x ＞0得f '（x ）=ln x +1，令f '（x ）=0，得x =1e ．当x ∈(0，1e )时，f '（x ）＜0，f （x ）单调递减；当x ∈(1e ，+∞)时，f '（x ）＞0，f （x ）单调递增．可得最小值为-1e …（3分）（Ⅱ）当0＜t ＜1e ＜t +2，即0＜t ＜1e 时，f(x)min =f(1e )=−1e …（4分）当1e ≤t ＜t +2，即t ≥1e 时，f （x ）在[t ，t +2]上单调递增，此时f （x ）min =f （t ）=t lnt …（6分）所以f(x)min ={−1e ，0＜t ＜1e tlnt ，t ≥1e…（8分）（Ⅲ）问题等价于证明xlnx ＞x e x −2e (x ∈(0，+∞))．由（1）知f （x ）=x lnx ，x ＞0的最小值是−1e ，当且仅当x =1e 时取到，设m(x)=x e x −2e (x ∈(0，+∞))，则m′(x)=1−xe x ，易知m(x)max =m(1)=−1e ，当且仅当x =1时取到．从而对一切x ∈（0，+∞），都有lnx ＞1e x −2ex 成立．…（12分）【解析】（Ⅰ）求出导数，极值点和单调区间，可得极小值和最小值；（Ⅱ）讨论时，时，运用单调性，即可得到所求最小值；（Ⅲ）问题等价于证明．由（1）设，求出导数，求出最大值即可．本题考查导数的运用：求单调区间和最值，注意运用分类讨论的方法和构造函数的方法，考查运算能力，属于中档题．22.【答案】解：（Ⅰ）由直线l 的参数方程是{y =2t +6x=t（t 是参数），转换为直角坐标方程为：y =2x +6，故直线l 的普通方程为2x -y +6=0，曲线C 的极坐标方程为ρ=2√2cosθ．整理得：ρ2=2√2ρcosθ，所以x 2+y 2=2√2x ，即(x −√2)2+y 2=2，故曲线C 的普通方程为(x −√2)2+y 2=2．（Ⅱ）据题意设点M(√2+√2cosθ，√2sinθ)，则x +y =√2+√2cosθ+√2sinθ，=√2+2sin(θ+π4)，所以x +y 的取值范围是[−2+√2，2+√2]．【解析】（Ⅰ）直接利用转换关系式，把参数方程直角坐标方程和极坐标方程之间进行转换．（Ⅱ）利用三角函数关系式的变换和正弦型函数性质的应用求出结果．本题考查的知识要点：参数方程直角坐标方程和极坐标方程之间的转换，三角函数关系式的恒等变变换，正弦型函数的性质的应用，主要考查学生的运算能力和转化能力，属于基础题型．23.【答案】解：（1）原不等式等价于{x −5+x +4≥12x>5或{5−x +x +4≥12−4≤x≤5或{5−x −(x +4)≥12x<−4，解得x ≥132或x ∈∅或x ≤−112．所以不等式的解集为{x|x ≥132或x ≤−112}．（2）不等式f （x ）-21-3a -1≥0恒成立等价于f(x)min ≥21−3a +1，即(|x −5|+|x +4|)min ≥21−3a +1因为|x -5|+|x +4|≥|（x -5）-（x +4）|=9，所以9≥21-3a +1，得21-3a ≤8，得1-3a ≤3，解得a ≥−23．故实数a 的取值范围是[−23，+∞)．【解析】（1）去掉绝对值符号，转化不等式为不等式组，然后求解即可．（2）不等式f （x ）-21-3a -1≥0恒成立等价于，利用绝对值的几何意义求解函数的最小值，然后求解指数不等式，推出a 的范围即可．本题考查绝对值不等式的解法，函数恒成立条件的应用，考查转化思想以及计算能力．。

辽宁师范大学附属中学高三上学期期末考试数学(文)试题Word版含答案

5 2 3辽宁师范大学附属中学高三上学期期末考试数学（文）试题Word 版含答案2017-2018学年度上学期期末考试高三试题数学（文）第I 卷（共60 分）、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的3.元代数学家朱世杰的数学名著《算术启蒙》是中国古代代数学的通论，其中有关于“松竹5.下列函数中，既是偶函数又在区间（0，1）上单调递减的是（）3x 4y 0和3x 4y 0,则该双曲线A. 5 或 543 C. A. 1 , 2 B，则三的共轭复数为（，则D 1 ,1并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等 .下图是源于C. ” （訓6.某校初三年级有［400名学生，随机抽查了匹|名学生，测试也分钟仰卧起坐的成绩（次数），ln x将数据整理后绘制成如图所示的频率分布直方图 •用样本估计总体，下列结论正确的是B.该校初三年级学生也分钟仰卧起坐的次数的中位数为25次也分钟仰卧起坐的次数的众数为 _24次C.该校初三年级学生D.该校初三年级学生丄分钟仰卧起坐的次数超过 30次的人数约有80人也分钟仰卧起坐的次数少于空次的人数约为人.7.若—，|均为锐角且刁 11 I3cos 二，cos(，sinH 2 )__1 1 14 | 21 C.耳D.丨2丨218.甲乙丙丁四名同学参加某次过关考试，甲乙丙三个人分别去老师处问询成绩,A.老师给每个人只提供了其他三人的成绩 •然后，甲说：我们四个人中至少两人不过关；乙说：我们四人中至多两人不过关；丙说：甲乙丁恰好有一人过关 •假设他们说的都是真的，则下列结论正确的是（）9. 一个正六棱柱的主视图（由两个边长等于［4的正方形组成）如图所示，则该六棱柱的侧视A. 116 B10.已知数列a n是公差不为0的等差数列, 3，且関，离，闔成等比数列，设图的面积为（a2第U 卷(共90 分)、填空题(每题5分，满分20分，将答案填在答题纸上)b 01，点 | A(0 , 0) |在圆 x 2 y 2 2J ax 4 a b 0 的外部，贝|a 2b| 的范围R )，贝U 的最大值为13.若函数 2 f (x )X( x X 2)[1x 1(1 )，则匣14. 已知数列过的前也项和为应，且S n(2)n，则a16.直角梯形ABCD 中,CB CD , AD // BC△ ABD 是边长为［2］的正三角形, |P 是平面b n —1a n an 1的( )A.充分不必要条件 B•必要不充分条件 C.充要条件D.既不充分也不必要条件12.已知三棱锥P ABC 的四个顶点都在同一个球面上,BAC ~~9^1，BC 73，PA 2庐， PA 平面ABC ，则此三棱锥外接球的表面积为() I 1615.若 a 0) B11. “0 m w 1 ，都有 f(Xj f(X 2)-，则数列叵的前mi 项和冋为上的动点，rutw --- tutr ----- t tm-i .__. 设 AP AD AB (口,三、解答题 (本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.)n (\/3sin°, cos2-)，设函数f (x) m n4 4 ----------------(1)求函数f(x)的单调增区间;(2)设△ ABC |的内角［A, B，叵］所对的边分别为叵］，冋，用，且迢，际用成等比数列, 求f(B)的取值范围18. 某中学调查了某班全部匝名同学参加书法社团和演讲社团的情况，数据如下表：(单位:(1)求证：GF //平面IABE (2 )求三棱锥 E ABG 的体积.20. 已知椭圆X 2 y r 1 (|a b 01)，长轴长为丽，冋是左焦点，［M参加书法社团未参加书法社团参加演讲社团西未参加演讲社团(附:2n(ad be)(a b)(e d)(a e)(b d)2 ----------------------------------------------当 3.841时，有95%的把握说事件因与⑥有关；当2 < 3.841，认为事件囚与叵］是无关的)(2)已知既参加书法社团又参加演讲社团的囲名同学中，有制名男同学"A , A , A , A ,A ，囘名女同学包,空,色.现从这国名男同学和3名女同学中各随机选 M 人，求△被选中且B !位被选中的概率•19.如图，在直三棱柱|ABC AB Q ］中，回、［F 分别为I AG |、UC 的中点，［AB BC 2人)是椭圆上一点且在 a b 1—［第二象限，|MF1 国轴，|吋| 76 .(1)求椭圆标准方程;1求实数色的值；(2)若|R(X o , y。

辽宁省辽宁师大附中2014届高三上学期期中考试数学文试题 Word版含答案

v2013-2014学年度上学期高三期中数学(文)试卷命题人:王红校对人：潘巍一选择题：(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求)1.在空间，下列命题正确的是（） A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行2.已知两条直线2-=ax y 和01)2(3=++-y a x 互相平行，则a 等于( ) A ．1或-3 B ．-1或3 C ．1或3 D ． -1或-33.直线l ：x －2y ＋2＝0过椭圆的左焦点F 1和上顶点B ，该椭圆的离心率为( )．A.15B.25C.55 D.2554.设b a ,是两条直线，βα,是两个平面，则b a ⊥的一个充分条件是（）A ．βαβα⊥⊥,//,b aB ．βαβα//,,⊥⊥b aC ．βαβα//,,⊥⊂b aD ．βαβα⊥⊂,//,b a5.过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线（） A ．有且仅有一条 B ．有且仅有两条 C ．有无穷多条 D ．不存在6 .如图，AB 是圆O 的直径，PA 垂直圆O 所在的平面于A ，点C 是圆上的任意一点，图中有（）对平面与平面垂直 A ．1 B ．2 C ．3 D ． 47.过抛物线y 2＝4x 的焦点F 的直线交该抛物线于A ，B 两点，O 为坐标原点．若|AF |＝3，则△AOB 的面积为( )． A.22 B. 2 C.322D ．2 2 8.已知F 1、F 2为双曲线C ：x 2－y 2＝2的左、右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝( )A.14B.35C.34D.459.已知椭圆x 23＋y 24＝1的上焦点为F ，直线x ＋y －1＝0和x ＋y ＋1＝0与椭圆分别相交于点A ，PC BAB 和C ，D ，则AF ＋BF ＋CF ＋DF ＝( )．A ．2 3B ．4 3C ．4D ．810. 已知椭圆C ：x 22＋y 2＝1的右焦点为F ，直线l ：x ＝2，点A ∈l ，线段AF 交C 于点B ，若F A→＝3FB →，则|AF →|＝( )．A. 2 B ．2 C. 3 D ．311.已知双曲线x 2－y 23＝1的左顶点为A 1，右焦点为F 2，P 为双曲线右支上一点，则P A 1→·PF 2→的最小值为( )． A ．－2B ．－8116C ．1D ．012. 棱长为1的正方体ABCD －A 1B 1C 1D 1中，点P 1，P 2分别是线段AB ，BD 1(不包括端点)上的动点，且线段P 1P 2平行于平面A 1ADD 1，则四面体P 1P 2AB 1的体积的最大值是( )A.124B.112C.16D.12二、填空题：(本大题共4小题；每小题5分，共20分，把答案填在题中的横线上.) 13．若双曲线8kx 2－ky 2＝8的一个焦点坐标是(0，3)，则实数k 的值为________． 14．某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．图1－315. 已知＝，＝,＝,…。

辽宁省辽宁师大附中2013-2014学年高二上学期期中考试数学文试卷Word版含答案

2013-2014上学期期中考试高二数学试题（文科）（考试时间：120分钟；总分：150分）命题人:杨悦校对人：袁庆祝一．选择题（共12小题，每题5分，共60分）1．命题“”的否命题．．．是（）A．B．若，则C．D．2.设,若是与的等比中项，则的最小值为（）．A. B. C. D.3.复数满足则等于（）A. B. C. D.4．已知是坐标原点，点，若点为平面区域上的一个动点，则的取值范围是（）．A．B．C．D．5．已知数列的前项和满足：，且，那么( )．A．B．C．D．6.设，则“”是“”的（）．A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件7.下列命题中正确的是( )A．的最小值是2 B．的最小值是2C.的最小值是D．的最大值是8.设满足约束条件，则的取值范围是（）A． B. C. D.9.已知数列为等比数列，是它的前项和,若，且与的等差中项为，则（）．A．B．C．D．10.下列说法错误的是（）A．若命题，则B．命题“若，则”的否命题是：“若，则”C．“”是“”的充分不必要条件D．若命题“”与命题“或”都是真命题，那么命题一定是真命题11.设是等差数列的前n项和，若（）A．B．C．D．12.设.．若关于的不等式的解集中的整数恰有个，则（）．A. B. C. D.二．填空题：(本题共4小题，每小题5分,共20分.)13.复数在复平面上对应的点位于第象限14.设满足约束条件,若目标函数的最大值为8，则的最小值为________．15..若为实数，则“”是“或”的________条件16.已知集合，，则集合．三．解答题：(本题共6小题，17题10分，18--22每题12分，共70分.)17.（本小题满分10分）设为实数，首项为，公差为的等差数列的前项和为，满足．（1）若求及；（2）求的取值范围．18.（本小题满分12分）（1）若不等式的解集是，求不等式的解集.（2），试比较与的大小。

辽宁师大附中高三数学上学期期中试题文(扫描版)新人教A版

辽师附中2014-2015上学期期中考试高三数学（文）试卷一．选择题（每题5分共60分）1．对于非零向量a 、b ，“a＋b ＝0”是“a∥b”的( ) A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 2．设f(x)＝lg 2＋x 2－x ，则f ⎝ ⎛⎭⎪⎫x 2＋f ⎝ ⎛⎭⎪⎫2x 的定义域为( )． A ．(－4,0)∪(0,4) B ．(－4，－1)∪(1,4)C ．(－2，－1)∪(1,2)D ．(－4，－2)∪(2,4)3．设m ，n 是两条不同直线，α，β是两个不同的平面，下列命题正确的是( )．A ．m ∥α，n ∥β，且α∥β，则m ∥nB ．m ⊥α，n ⊥β，且α⊥β，则m ⊥nC ．m ⊥α，n ⊂β，m ⊥n ，则α⊥βD ．m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β 4.已知向量()()()()1,1,2,2,,==+=++⊥-m n m n m n λλλ若则（）A.4-B. 2-C. -3D.-15．函数f(x)＝sin(ωx ＋φ)(x ∈R)(ω＞0，|φ|＜π2)的部分图象如图所示，如果x1，x2∈(－π6，π3)，且f(x1)＝f(x2)，则f(x1＋x2)等于( )A.12B.22C.32D ．1 6.设数列{an}是公差d ＜0的等差数列，Sn 为其前n 项和，若S6＝5a1＋10d ，则Sn 取最大值时，n ＝ ( )．A ．5B ．6C ．5或6D ．6或77．设x ，y ∈R ＋，且x ＋4y ＝40，则lg x ＋lg y 的最大值是( )． A ．40 B ．10 C ．4 D ．28．已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧x －y ＋2≥0，x ＋y －4≥0，2x －y －5≤0，若目标函数z ＝y －ax 取得最大值时的唯一最优解是(1,3)，则实数a 的取值范围为( )．A ．(－∞，－1)B ．(0,1)C ．[1，＋∞)D ．(1，＋∞) 9．一个几何体的三视图如图所示，其中主视图和左视图是腰长为4的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是( )． A ．12π B ．24π C ．32π D ．48π10．在等差数列{an}中，a1＞0，a10·a11＜0，若此数列的前10项和S10＝36，前18项的和S18＝12，则数列{|an|}的前18项和T18的值是（）A ．24B ．48C ．60D ．8411．已知x>0，y>0，且2x ＋1y ＝1，若x ＋2y>m2＋2m 恒成立，则实数m 的取值范围是 ( )．A ．(－∞，－2]∪[4，＋∞)B ．(－∞，－4]∪[2，＋∞)C ．(－2,4)D ．(－4,2)12．设函数f(x)＝sin θ3x3＋3cos θ2x2＋tan θ，其中θ∈⎣⎢⎡⎦⎥⎤0，5π12，则导数f ′(1)的取值范围为( )A ．[2，2]B ．[2，3]C ．[3，2]D ．[－2,2] 二．填空题（每题5分共20分）13.函数的最小正周期T 为_______14．等差数列{an}的前n 项和为Sn ，已知am －1＋am ＋1－a2m ＝0，S2m －1＝38，则m ＝________.15．已知x ＞0，y ＞0，x ＋3y ＋xy ＝9，则x ＋3y 的最小值为________．16.已知,a b 是单位向量，0=∙b a.若向量c 满足1,--=c a b c 则的取值范围是________．三．解答题17．(10分)设函数f(x)＝mx2－mx －1.(1)若对于一切实数x ，f(x)<0恒成立，求m 的取值范围； (2)若对于x ∈[1,3]，f(x)<－m ＋5恒成立，求m 的取值范围．18．(12分)已知向量m ＝⎝ ⎛⎭⎪⎫3sin x 4，1，n ＝⎝ ⎛⎭⎪⎫cos x4，cos2x 4.(1)若∙ ＝1，求cos ⎝⎛⎭⎪⎫2π3－x 的值； (2)记f(x)＝∙,在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且满足(2a －c)cosB ＝bcosC ，求函数f(A)的取值范围．19．(本小题满分12分)已知在等比数列{an}中，a1＝1，且a2是a1和a3－1的等差中项．(1)求数列{an}的通项公式；(2)若数列{bn}满足b1＋2b2＋3b3＋…＋nbn ＝an(n ∈N*)，求{bn}通项公式bn20． (本小题满分12分)设a ＞0，a≠1，t ＞0，比较12logat 与loga t ＋12的大小，并证明你的结论．21．(本小题满分12分)如图，在四棱锥P －ABCD 中，AB ∥ CD ， AB ⊥AD ，CD ＝2AB ，平面PAD ⊥底面ABCD ，PA ⊥AD. E 和F 分别是CD 和PC 的中点．求证：(1)PA ⊥底面ABCD ； (2)BE ∥平面PAD ；(3)平面BEF ⊥平面PCD.22．(本小题满分12分)已知函数kx x f =)(，（1（2）若不等式)()(x g x f ≥在区间（0,+)∞上恒成立，求k 的取值范围；（32014—2015学年第一学期期中考试高三数学（文）试题答案一．选择题1—5 A BBCC 6—10 CDDDC 11—12 DA 二．填空题13. π 14. 10 15. 6 16.⎤⎦ 三．解答题17.[解析] (1)要使mx2－mx －1<0恒成立，若m ＝0，显然－1<0；若m≠0，则⎩⎪⎨⎪⎧m<0，Δ＝m2＋4m<0⇒－4<m<0.所以m 的取值范围是(－4,0]．(2)要使f(x)<－m ＋5在[1,3]上恒成立，就是要使m(x －12)2＋34m －6<0在x ∈[1,3]上恒成立．有以下两种方法：方法一：令g(x)＝m(x －12)2＋34m －6，x ∈[1,3]．当m>0时，g(x)在[1,3]上是增函数，所以g(x)max ＝g(3)＝7m －6<0，所以m<67，则0<m<67；当m ＝0时，－6<0恒成立；当m<0时，g(x)在[1,3]上是减函数，所以g(x)max ＝g(1)＝m －6<0. 所以m<6，所以m<0.综上所述，m 的取值范围是{m|m<67}．方法二：因为x2－x ＋1＝(x －12)2＋34>0，又因为m(x2－x ＋1)－6<0，所以m<6x2－x ＋1.因为函数y ＝6x2－x ＋1＝6－12＋34，在[1,3]上的最小值为67，所以只需m<67即可．所以，m 的取值范围是{m|m<67}．18(2)∵(2a －c)cosB ＝bcosC ，由正弦定理得(2sinA －sinC)cosB ＝sinBcosC. ∴2sinAcosB －cosBsinC ＝sinBcosC ，19.解 (1)由题意，得2a2＝a1＋a3－1，即2a1q ＝a1＋a1q2－1，整理得2q ＝q2.又q≠0，解得q ＝2，∴an ＝2n －1. (2)当n ＝1时，b1＝a1＝1；当n≥2时，nbn ＝an －an －1＝2n －2，即bn ＝2n －2n ，∴bn ＝⎩⎪⎨⎪⎧1，n ＝1，2n －2n，n≥2.20.解：loga t ＋12－12logat ＝loga t ＋12－loga t ＝loga t ＋12t ，∵t ＞0，t ＋1≥2t(当且仅当t ＝1时等号成立)，∴t ＋12t≥1. 当t ＝1时，loga t ＋12＝12logat ；当t≠1时，t ＋12t ＞1.若a ＞1，则loga t ＋12t＞0，即loga t ＋12＞12logat ；若0＜a ＜1，则loga t ＋12t ＜0，即loga t ＋12＜12logat.21.证明 (1)因为平面PAD∩平面ABCD ＝AD.又平面PAD ⊥平面ABCD ，且PA ⊥AD. 所以PA ⊥底面ABCD.(2)因为AB ∥CD ，CD ＝2AB ，E 为CD 的中点，所以AB ∥DE ，且AB ＝DE.所以ABED 为平行四边形．所以BE ∥AD. 又因为BE ⊄平面PAD ，AD ⊂平面PAD ，所以BE ∥平面PAD.(3)因为AB ⊥AD ，且四边形ABED 为平行四边形．所以BE ⊥CD ，AD ⊥CD.由(1)知PA ⊥底面ABCD ，所以PA ⊥CD.所以CD ⊥平面PAD ，从而CD ⊥PD. 又E ，F 分别是CD 和CP 的中点，所以EF ∥PD ，故CD ⊥EF.CD ⊂平面PCD ，由EF ，BE 在平面BEF 内，且EF∩BE＝E ， ∴CD ⊥平面BEF.所以平面BEF ⊥平面PCD.22.解：（1）∵（)0>x∴令0)(>'x g ，得e x <<0 的单调递增区间为),0(e 3分。