2009年上海杨浦区高三数学试卷
2009年全国高考上海数学试题(理科含答案)

2009年全国普通高等学校招生统一考试上海 数学试卷一.填空题 (本大题满分56分)本大题有14题,考生应在答题纸相应编号的空格内直接写结果,每个空格填对得4分,否则一律得零分1. 若复数 z 满足z (1+i) =1-i (i 是虚数单位),则其共轭复数z =__________________ . 2. 已知集合{}|1A x x = ,{}|B x x a = ,且A BR ?,则实数a 的取值范围是______________________ .3. 若行列式417xx 5 3 8 9中,元素4的代数余子式大于0,则x 满足的条件是________________________ .4.某算法的程序框如右图所示,则输出量y 与输入量x 满足的关系式是____________________________ .5.如图,若正四棱柱1111ABC D A B C D - 的底面边长为2,高为4,则异面直线1BD 与AD 所成角的大小是______________(结果用反三角函数表示). 6.函数22cos sin 2y x x =+的最小值是_____________________ .7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望E ξ=____________(结果用最简分数表示).8. 已知三个球的半径1R ,2R ,3R 满足12323R R R +=,则它们的表面积1S ,2S ,3S ,满足的等量关系是___________. 9. 已知1F 、2F 是椭圆2222:1x y C ab+=(a >b >0)的两个焦点,P 为椭圆C 上一点,且12PF PF ^.若12PF F D 的面积为9,则b =____________. 10. 在极坐标系中,由三条直线0q =,3p q =,cos sin 1r q r q +=围成图形的面积是________.11.当01x #时,不等式sin2x kx p ³成立,则实数k 的取值范围是_______________.12.已知函数()sin tan f x x x =+.项数为27的等差数列{}n a 满足22n a p p骣琪?琪桫,,且公差0d ¹.若1227()()()0f a f a f a ++?=,则当k =___________时,()0k f a =.13. 某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点。
2009年上海高考数学试卷
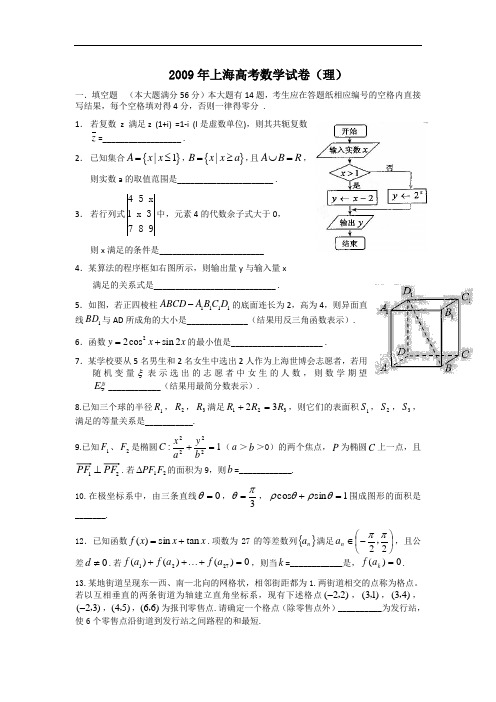
2009年上海高考数学试卷(理)一.填空题 (本大题满分56分)本大题有14题,考生应在答题纸相应编号的空格内直接写结果,每个空格填对得4分,否则一律得零分 .1. 若复数 z 满足z (1+i) =1-i (I 是虚数单位),则其共轭复数z =__________________ .2. 已知集合{}|1A x x =≤,{}|B x x a =≥,且A B R ⋃=, 则实数a 的取值范围是______________________ .3. 若行列式417 5 xx 3 8 9中,元素4的代数余子式大于0,则x 满足的条件是________________________4.某算法的程序框如右图所示,则输出量y 与输入量x满足的关系式是____________________________ .5.如图,若正四棱柱1111ABCD A B C D -的底面连长为2,高为4,则异面直线1BD 与AD 所成角的大小是______________(结果用反三角函数表示).6.函数22cos sin 2y x x =+的最小值是_____________________ .7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望E ξ____________(结果用最简分数表示).8.已知三个球的半径1R ,2R ,3R 满足32132R R R =+,则它们的表面积1S ,2S ,3S ,满足的等量关系是___________.9.已知1F 、2F 是椭圆1:2222=+by a x C (a >b >0)的两个焦点,P 为椭圆C 上一点,且21PF PF ⊥.若21F PF ∆的面积为9,则b =____________.10.在极坐标系中,由三条直线0=θ,3πθ=,1sin cos =+θρθρ围成图形的面积是_______. 12.已知函数x x x f tan sin )(+=.项数为27的等差数列{}n a 满足⎪⎭⎫ ⎝⎛-∈22ππ,n a ,且公差0≠d .若0)()()(2721=+⋯++a f a f a f ,则当k =____________是,0)(=k a f . 13.某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点。
上海市杨浦区2008-2009学年度第二学期高三学科测试数学文科试卷2009.4

上海市杨浦区2008-2009学年度第二学期高三学科测试数学文科试卷 2009.4(满分150分,考试时间120分钟)考生注意:本试卷包括试题纸和答题纸两部分.在本试题纸上答题无效,必须在答题纸上的规定位置按照要求答题.可使用符合规定的计算器答题.一、填空题(本大题满分60分)本大题共有12题,每题5分,考生应在答题纸上相应编号的空格内直接填写结果.1.直线013=+-y x 的倾斜角为 .2.已知全集R U =,集合{}0542>--=x x x M ,{}1≥=x x N ,则)(N C M U ⋂= . 3.若复数z 满足iiz +=3(其中i 是虚数单位),则z = .4.二项式6)21(x -展开式中3x 系数的值是 .5.高三(1)班班委会由3名男生和2名女生组成,现从中任选 2人参加上海世博会的志愿者工作,则选出的人中至少有一名女 生的概率是 .6.如果某音叉发出的声波可以用函数t t f π00.001sin40)(= 描述,那么音叉声波的频率是 赫兹. 7.若抛物线px y 22=的焦点与椭圆12622=+y x 的右焦点重合, 则实数p 的值是 . 8.方程33tan -=x 的解是 . 9.如图是输出某个数列前10项的框图,则该数列第 3项的值是 .10. 若经过点P (-1,0)的直线与圆224230x y x y ++-+=相切,则此直线的方程是 . 11.计算:)11211(lim 222+++++++∞→n nn n n = . 12.在△ABC 中,5=AB ,7=AC ,D 是BC 边的中点,则BC AD ⋅的值是 .第9题二、选择题(本大题满分16分)本大题共有4题,每题4分.每题只有一个正确答案,选择正确答案的字母代号并按照要求填涂在答题纸的相应位置.13.线性方程组⎪⎩⎪⎨⎧=++=++=++78615304z y x z y x z y x 的增广矩阵是………………………………………………( ).A .⎪⎪⎪⎭⎫ ⎝⎛786115130411B .⎪⎪⎪⎭⎫⎝⎛--786115130411 C .⎪⎪⎪⎭⎫ ⎝⎛861513411 D .⎪⎪⎪⎭⎫⎝⎛85461113114.在直角坐标系xoy 中,已知△ABC 的顶点)01(,-A 和)01(,C ,顶点B 在椭圆13422=+y x上,则BCA sin sin sin +的值是…………………………………………………………………( ).A .23B .3C .2D .415.以c b a 、、依次表示方程232212=+=+=+x x x x x x 、、的根,则c b a 、、的大小顺序为…………………………………………………………………………………………( ).A .c b a <<B .c b a >>C .b c a <<D .c a b >>16.如图,下列四个几何体中,它们的三视图(主视图、侧视图、俯视图)有且仅有两个相同,而另一个不同的两个几何体是……………………………………………………………( ).A .(1)(2)B .(1)(3)C .(2)(3)D .(1)(4)三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸上与题号对应的区域写出必要的步骤. 17.(本题满分12分)动物园要建造一面靠墙的2间面积相同的长方形熊猫居室(如图所示).如果可供建造围墙的材料长是30米,那么宽x 为多少米时才能使所建造的熊猫居室面积最大?熊猫居室的最大面积是多少平方米?18. (本题满分14分) 本题共有2个小题,第1小题满分8分,第2小题满分6分. 已知某圆锥的体积是π12cm 3,底面半径等于3cm . (1)求该圆锥的高; (2)求该圆锥的侧面积.19.(本题满分15分) 本题共有3个小题,第1小题满分3分,第2小题满分4分,第3小题满分8分.已知等差数列{}n a 和等比数列{}n b 的通项公式分别为)1(2-=n a n 、nn b )21(=,(其中*N n ∈).(1)求数列{}n a 前n 项的和;(2)底面直径和高均为2的圆柱(1)棱长为2的正方体 (3)底面直径和高均为2的圆锥(4)底面边长为2、高为3的正四棱柱(2)求数列{}n b 各项的和; (3)设数列{}n c 满足⎩⎨⎧=)(.)(为偶数时当为奇数时当,n a n b c n n n ,求数列{}n c 前n 项的和.20.(本题满分15分) 本题共有2个小题,第1小题满分5分,第2小题满分10分.已知a 为实数,函数3sin )(++=a f θθ,1sin )1(3)(+-=θθa g (R ∈θ).(1)若θθcos )(=f ,试求a 的取值范围; (2)若1>a ,求函数)()(θθg f +的最小值.21.(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分7分,第3小题满分7分.已知B A 、是抛物线x y 42=上的相异两点.(1)设过点A 且斜率为-1的直线1l ,与过点B 且斜率1的直线2l 相交于点P(4,4),求直线AB 的斜率;(2)问题(1)的条件中出现了这样的几个要素:已知圆锥曲线Γ,过该圆锥曲线上的相异两点A 、B 所作的两条直线21l l 、相交于圆锥曲线Γ上一点;结论是关于直线AB 的斜率的值.请你对问题(1)作适当推广,并给予解答;(3)线段AB (不平行于y 轴)的垂直平分线与x 轴相交于点)0(0,x Q .若20>x ,试用0x 表示线段AB 中点的横坐标.上海市杨浦区2008学年度第二学期高三学科测试数学文理科试卷参考答案与评分标准2009.4说明1. 本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.3. 第17题至第21题中右端所注分数,表示考生正确做到这一步应得的该题累加分数.4. 给分或扣分均以1分为单位.答案及评分标准1.3π; 2.{}1-<x x ; 3.10; 4.160-; 5.(理)66.8-元;(文)0.7; 6.(理)ααcos cos42⋅; (文)200赫兹; 7.(理)5; (文)p=4.8.(理)858ππ==x x 或; (文)⎭⎬⎫⎩⎨⎧∈-=Z k k x x ,6ππ 9.2113; 10.(理)cos 3ρθ=; (文)方程为01=+-y x . 11.(理)π34; (文)21; 12.12.13——16:A ; C ; C ; 理B 文A17.设熊猫居室的总面积为y 平方米,由题意得:)100()330(<<-=x x x y .… 6分解法1:75)5(32+--=x y ,因为)10,0(5∈,而当5=x 时,y 取得最大值75. 10分所以当熊猫居室的宽为5米时,它的面积最大,最大值为75平方米. …… 12分 解法2:2]2)330(3[31)]330(3[31)330(x x x x x x y -+≤-=-==75,当且仅当x x 3303-=,即5=x 时,y 取得最大值75. …… 10分所以当熊猫居室的宽为5米时,它的面积最大,最大值为75平方米. …… 12分18.理:如图,建立空间直角坐标系,可得有关点的坐标为)0,0,1(A 、)0,0,0(D 、)0,2,0(C 、)1,0,1(A '、)1,2,1(B '、)1,0,0(D '. ……2分设平面AC B '的法向量为),,(w v u n =,则B n '⊥,B '⊥.因为)1,2,0(--='B ,)1,0,1(--='B , ……3分0='⋅A B n ,0='⋅C B n ,所以⎩⎨⎧=+=+.0,02w u w v 解得v w v u 2,2-==,取1=v ,得平面AC B '一个法向量)2,1,2(-=,3=. ……5分 (1)在平面AC B '取一点A ,可得)1,0,1(-=D A ,于是顶点D '到平面AC B '的距离34==d ,所以顶点D '到平面AC B '的距离为34, ……8分(2)因为平面ABC 的一个法向量为)1,0,0(1=n ,设n 与1n 的夹角为α,则32cos -==α, ……12分结合图形可判断得二面角B AC B '--是一个锐角,它的大小为32arccos.……14分文:(1)圆锥底面积为π9 cm 2, ……1分 设圆锥高为h cm ,由体积h V ⋅⋅=π931, ……5分 由π12=V cm 3得4=h cm ; ……8分(2)母线长5=l cm , ……9分 设底面周长为c ,则该圆锥的侧面积=cl 21, ……12分 所以该圆锥的侧面积=π15cm 2. ……14分19.(理)(1)164=a ; ……3分 (2)当k n 2=时,(*N k ∈)k k k k k k k k S S a 22222212222)]12(3412)2([)12(3412)2(=-+--+=-=--, ……6分所以,n n a 42=(*N n ∈). ……8分 (3)与(2)同理可求得:)12(3112-=-n a n , ……10分 设n n a a a a a a a a 212654321-++++ =n T , 则]4)12(45434[3132n n n T ⨯-++⨯+⨯+=,(用等比数列前n 项和公式的推导方法)]4)12(45434[3141432+⨯-++⨯+⨯+=n n n T ,相减得]4)12()444(24[313132+⨯--++++=-n n n n T ,所以94)14(2732491211--⨯-⨯-=-+n n n n T . ……14分(文)(1)设数列前n 项和为n S ,则n n n n S n -=-+=22)220(. ……3分(2)公比121<=q ,所以由无穷等比数列各项的和公式得: 数列{}n b 各项的和为21121-=1. ……7分(3)设数列{}n c 的前n 项和为n T ,当n 为奇数时,n n n b a b a b T +++++=-1321 =2)1())41(1(32221-+-+n n ; ……11分当n 为偶数时,n n n a b b a b T +++++=-1321 =2))41(1(3222n n+-. ……14分即⎪⎪⎩⎪⎪⎨⎧++-+-+-=+为偶数时当,为奇数时当n n n n T n n n 322)21(32,322)1()21(3222)1(. ……15分20.(1)θθcos )(=f 即a --=-3cos sin θθ,又)4sin(2cos sin πθθθ-=-,2分所以232≤+≤-a ,从而a 的取值范围是]23,23[+---. ……5分(2)21sin )1(3)1(sin )()(+++-++=+a a g f θθθθ,令x =+1sin θ,则20≤<x ,因为1>a ,所以)1(32)1(3-≥-+a xa x ,当且仅当)1(3-=a x 时,等号成立,8分 由2)1(3≤-a 解得37≤a ,所以当371≤<a 时,函数)()(θθg f +的最小值是2)1(32++-a a ; ……11分下面求当37>a 时,函数)()(θθg f +的最小值. 当37>a 时,2)1(3>-a ,函数xa x x h )1(3)(-+=在]2,0(上为减函数.所以函数)()(θθg f +的最小值为2)1(522)1(32+=++-+a a a . [当37>a 时,函数xa x x h )1(3)(-+=在]2,0(上为减函数的证明:任取2021≤<<x x ,])1(31)[()()(121212x x a x x x h x h ---=-,因为4012≤<x x ,4)1(3>-a ,所以0)1(3112<--x x a ,0)()(12<-x h x h ,由单调性的定义函数x a x x h )1(3)(-+=在]2,0(上为减函数.]于是,当371≤<a 时,函数)()(θθg f +的最小值是2)1(32++-a a ;当37>a 时,函数)()(θθg f +的最小值2)1(5+a . ……15分21.(1)由⎩⎨⎧==-+.4,082x y y x 解得)8,16(-A ;由⎩⎨⎧==+.4,02x y y x 解得)0,0(B .由点斜式写出两条直线21l l 、的方程,0:;08:21=-=-+y x l y x l ,所以直线AB 的斜率为21-. ……4分 (2)推广的评分要求分三层一层:点P 到一般或斜率到一般,或抛物线到一般(3分,问题1分、解答2分)例:1.已知B A 、是抛物线x y 42=上的相异两点.设过点A 且斜率为-1的直线1l ,与过点B 且斜率为1的直线2l 相交于抛物线x y 42=上的一定点P ),4(2t t ,求直线AB 的斜率;2.已知B A 、是抛物线x y 42=上的相异两点.设过点A 且斜率为-k 1的直线1l ,与过点B 且斜率为k 的直线2l 相交于抛物线x y 42=上的一点P (4,4),求直线AB 的斜率;3.已知B A 、是抛物线)0(22>=p px y 上的相异两点.设过点A 且斜率为-1的直线1l ,与过点B 且斜率为1的直线2l 相交于抛物线)0(22>=p px y 上的一定点P ),2(2t pt ,求直线AB 的斜率; AB 的斜率的值.二层:两个一般或推广到其它曲线(4分,问题与解答各占2分)例:4.已知点P 是抛物线x y 42=上的定点.过点P 作斜率分别为k 、k -的两条直线21l l 、,分别交抛物线于A 、B 两点,试计算直线AB 的斜率.三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)(7分,问题3分、解答4分)例如:5.已知抛物线px y 22=上有一定点P ,过点P 作斜率分别为k 、k -的两条直线21l l 、,分别交抛物线于A 、B 两点,试计算直线AB 的斜率.过点P (00,y x ),斜率互为相反数的直线可设为00)(y x x k y +-=,00)(y x x k y +-=,其中0202px y =。
2009年全国高考文科数学试题及答案-上海卷

上海 数学试卷(文史类)考生注意:1. 答卷前,考生务必在答题纸上将姓名、高考准考证号填写清楚,并在规定的区域内贴上条形码。
2. 本试卷共有23道试题,满分150分,考试时间120分钟。
一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1、函数f(x)=x 3+1的反函数f -1(x)=_____________. 2、已知集合A={x|x ≤1},B={x |≥a},且A ∪B=R ,则实数a 的取值范围是__________________.3、若行列式417 5 xx 3 8 9中,元素4的代数余子式大于0,则x 满足的条件是__________________.4.某算法的程序框如右图所示,则输出量y 与输入量x 满足的关系式是________________.5.如图,若正四棱柱ABC D —A 1B 1C 1D 1的底面边长为2, 高为4,则异面直线BD 1与AD 所成角的大小是___________________(结果用反三角函数值表示).6.若球O 1、O 2表示面积之比421=S S ,则它们的半径之比21R R =_____________. 7.已知实数x 、y 满足223y x y x x ≤⎧⎪≥-⎨⎪≤⎩则目标函数z=x-2y 的最小值是___________.8.若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是 。
9、过点A (1,0)作倾斜角为4π的直线,与抛物线22y x =交于M N 、两点,则MN = 。
10.函数2()2cos sin 2f x x x =+的最小值是 。
11.若某学校要从5名男生和2名女生中选出3人作为上海世博会的志愿者,则选出的志愿者中男女生均不少于1名的概率是 (结果用最简分数表示)。
12.已知12F 、F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点,p 为椭圆C 上的一点,且12PF PF ⊥。
上海市杨浦区2009届高三模拟考试卷数学(文理科)试题参考答案与评分标准2009.04

上海市杨浦区2008学年度第二学期高三学科测试数学文理科试卷参考答案与评分标准2009.4说明1. 本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.3. 第17题至第21题中右端所注分数,表示考生正确做到这一步应得的该题累加分数.4. 给分或扣分均以1分为单位.答案及评分标准1.3π; 2.{}1-<x x ; 3.10; 4.160-; 5.(理)66.8-元;(文)0.7;6.(理)ααcos cos42⋅; (文)200赫兹; 7.(理)5; (文)p=4. 8.(理)858ππ==x x 或; (文)⎭⎬⎫⎩⎨⎧∈-=Z k k x x ,6ππ 9.2113; 10.(理)cos 3ρθ=; (文)方程为01=+-y x .11.(理)π34; (文)21; 12.12.13——16:A ; C ; C ; 理B 文A17.设熊猫居室的总面积为y 平方米,由题意得:)100()330(<<-=x x x y .… 6分解法1:75)5(32+--=x y ,因为)10,0(5∈,而当5=x 时,y 取得最大值75. 10分所以当熊猫居室的宽为5米时,它的面积最大,最大值为75平方米. …… 12分 解法2:2]2)330(3[31)]330(3[31)330(x x x x x x y -+≤-=-==75,当且仅当x x 3303-=,即5=x 时,y 取得最大值75. …… 10分所以当熊猫居室的宽为5米时,它的面积最大,最大值为75平方米. …… 12分18.理:如图,建立空间直角坐标系,可得有关点的坐标为)0,0,1(A 、)0,0,0(D 、)0,2,0(C 、)1,0,1(A '、)1,2,1(B '、)1,0,0(D '. ……2分设平面AC B '的法向量为),,(w v u n =,则A B n '⊥,C B n '⊥.因为)1,2,0(--='A B ,)1,0,1(--='C B , ……3分 0='⋅A B n ,0='⋅C B n ,所以⎩⎨⎧=+=+.0,02w u w v 解得v w v u 2,2-==,取1=v ,得平面AC B '一个法向量)2,1,2(-=n ,3=. ……5分 (1)在平面AC B '取一点A ,可得)1,0,1(-='D A ,于是顶点D '到平面AC B '的距离34==d ,所以顶点D '到平面AC B '的距离为34, ……8分(2)因为平面ABC 的一个法向量为)1,0,0(1=n ,设n 与1n 的夹角为α,则32cos -=⋅=n n α, ……12分结合图形可判断得二面角B AC B '--是一个锐角,它的大小为32arccos.……14分文:(1)圆锥底面积为π9 cm 2, ……1分 设圆锥高为h cm ,由体积h V ⋅⋅=π931, ……5分由π12=V cm 3得4=h cm ; ……8分 (2)母线长5=l cm , ……9分 设底面周长为c ,则该圆锥的侧面积=cl 21, ……12分所以该圆锥的侧面积=π15cm 2. ……14分19.(理)(1)164=a ; ……3分 (2)当k n 2=时,(*N k ∈)kk kk k k k k S S a 22222212222)]12(3412)2([)12(3412)2(=-+--+=-=--, ……6分所以,n n a 42=(*N n ∈). ……8分 (3)与(2)同理可求得:)12(3112-=-n a n , ……10分设n n a a a a a a a a 212654321-++++ =n T , 则]4)12(45434[3132nn n T ⨯-++⨯+⨯+=,(用等比数列前n 项和公式的推导方法)]4)12(45434[3141432+⨯-++⨯+⨯+=n n n T ,相减得 ]4)12()444(24[313132+⨯--++++=-n nn n T ,所以94)14(2732491211--⨯-⨯-=-+n n n n T . ……14分(文)(1)设数列前n 项和为n S ,则n n n n S n -=-+=22)220(. ……3分(2)公比121<=q ,所以由无穷等比数列各项的和公式得:数列{}n b 各项的和为21121-=1. ……7分(3)设数列{}n c 的前n 项和为n T ,当n 为奇数时,n n n b a b a b T +++++=-1321 =2)1())41(1(32221-+-+n n ; ……11分当n 为偶数时,n n n a b b a b T +++++=-1321 =2))41(1(3222nn+-. ……14分即⎪⎪⎩⎪⎪⎨⎧++-+-+-=+为偶数时当,为奇数时当n n n n T n n n 322)21(32,322)1()21(3222)1(. ……15分20.(1)θθcos )(=f 即a --=-3cos sin θθ,又)4sin(2cos sin πθθθ-=-,2分所以232≤+≤-a ,从而a 的取值范围是]23,23[+---. ……5分(2)21sin )1(3)1(sin )()(+++-++=+a a g f θθθθ,令x =+1sin θ,则20≤<x ,因为1>a ,所以)1(32)1(3-≥-+a xa x ,当且仅当)1(3-=a x 时,等号成立,8分由2)1(3≤-a 解得37≤a ,所以当371≤<a 时,函数)()(θθg f +的最小值是2)1(32++-a a ; ……11分下面求当37>a 时,函数)()(θθg f +的最小值. 当37>a 时,2)1(3>-a ,函数x a x x h )1(3)(-+=在]2,0(上为减函数.所以函数)()(θθg f +的最小值为2)1(522)1(32+=++-+a a a .[当37>a 时,函数xa x x h )1(3)(-+=在]2,0(上为减函数的证明:任取2021≤<<x x ,])1(31)[()()(121212x x a x x x h x h ---=-,因为4012≤<x x ,4)1(3>-a ,所以0)1(3112<--x x a ,0)()(12<-x h x h ,由单调性的定义函数xa x x h )1(3)(-+=在]2,0(上为减函数.] 于是,当371≤<a 时,函数)()(θθg f +的最小值是2)1(32++-a a ;当37>a 时,函数)()(θθg f +的最小值2)1(5+a . ……15分21.(1)由⎩⎨⎧==-+.4,082x y y x 解得)8,16(-A ;由⎩⎨⎧==+.4,02x y y x 解得)0,0(B .由点斜式写出两条直线21l l 、的方程,0:;08:21=-=-+y x l y x l ,所以直线AB 的斜率为21-. ……4分(2)推广的评分要求分三层一层:点P 到一般或斜率到一般,或抛物线到一般(3分,问题1分、解答2分)例:1.已知B A 、是抛物线x y 42=上的相异两点.设过点A 且斜率为-1的直线1l ,与过点B 且斜率为1的直线2l 相交于抛物线x y 42=上的一定点P ),4(2t t,求直线AB 的斜率;2.已知B A 、是抛物线x y 42=上的相异两点.设过点A 且斜率为-k 1的直线1l ,与过点B 且斜率为k 的直线2l 相交于抛物线x y42=上的一点P (4,4),求直线AB 的斜率;3.已知B A 、是抛物线)0(22>=p px y 上的相异两点.设过点A 且斜率为-1的直线1l ,与过点B 且斜率为1的直线2l 相交于抛物线)0(22>=p px y 上的一定点P ),2(2t pt,求直线AB 的斜率; AB 的斜率的值.二层:两个一般或推广到其它曲线(4分,问题与解答各占2分)例:4.已知点P 是抛物线x y 42=上的定点.过点P 作斜率分别为k 、k -的两条直线21l l 、,分别交抛物线于A 、B 两点,试计算直线AB 的斜率.三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)(7分,问题3分、解答4分)例如:5.已知抛物线px y 22=上有一定点P ,过点P 作斜率分别为k 、k -的两条直线21l l 、,分别交抛物线于A 、B 两点,试计算直线AB 的斜率.过点P (00,y x ),斜率互为相反数的直线可设为00)(y x x k y +-=,00)(y x x k y +-=,其中0202px y =。
【理数】2009年上海市高三调研试卷

2009年上海市高三数学教学调研试卷(理科)一、填空题:1.方程2log (31)3x -=的解是 。
2.行列式123234345的元素5的代数余子式的值为 。
3.若直线l 过点(1,2)A ,且它的一个方向向量为(1,2)d =,则直线l 的方程为 。
4.若复数Z满足Z =,且(13)i Z -是纯虚数,则复数Z = 。
5.函数()sin 2f x x x =的最小正周期是 。
6.如果()na b +的二项展开式中的第三项与第二项的系数之比为2,那么正整数n = 。
7.若函数()112x f x =-的反函数是()1f x -,则()11f -的值是 。
8.如果执行右面的程序框图,那么输出的S 的值是 。
9.计算:()()()()123lim()1111n nn n n n n n n n →∞++++=++++ 。
10.若正三角形ABC 的边长为1,O 是ABC ∆所在平面内的任意一点,则2OA OB OC +-=。
11.如图,圆锥形量杯的口径(圆锥底面的直径)为d ,高为h ,则圆锥形量杯侧面上刻度V (容积)与页面深度x 的函数关系为 。
12.在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线4cos ρθ=于,A B 两点,则AB = 。
13.在10件产品中有2件次品,连续抽3次,每次抽取一件,且不放回抽取,抽到次品的数学期望E ξ的值是 。
14.已知函数()24(1)3(0)f x ax a x a =+-+>的定义域为[]0,2,若()()m a x 2f x f=,则实数a 的取值范围是 。
二、选择题:15.圆心在直线y x =上,且与x 轴相切于点()1,0的圆的方程为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( ).A ()()22111x y -+-= ; .B ()()22111x y +++=;(第8题图).C ()()22111x y -++=; .D ()()22111x y ++-=16.若,,a b c R ∈,则a b >成立的充分非必要条件为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( ).A 22ac bc > ; .B a c b c +>+; .C a c <且c b <; .D ac bc >17.在直角坐标平面xOy 上,已知点(3,2)A ,点B 在椭圆221168x y +=上运动,动点P 满足AB BP = ,那么点P 的轨迹方程是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( ).A()()223213216x y +++= ; .B()()223216432x y +++=;.C()()223213216x y --+= ; .D()()223216432x y --+=18.已知x 是1,2,3,,5,6,7x 这七个数据的中位数,且21,3,,x y -这四个数据的平均数为1,那么1y x-的最小值是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( ).A 4255; .B 3155; .C 283; .D 不存在三 、解答题: 19.(本题满分12分,第1小题5分,第2小题7分)在直三棱柱111A B C ABC -中,AC BC ⊥,D 为AB 中点,11.CB AC AA ===(1)棱锥1C CDB -的体积;(2)二面角1A AC D --的大小 20.(本题满分14分,第一小题满分6分,第二小题满分8分) 已知函数()2af x x x=+(a 为常数)的图像经过点()1,3。
2009年上海市高考数学试卷(理科)答案与解析

2009年上海市高考数学试卷(理科)参考答案与试题解析一、填空题(共14小题,每小题4分,满分56分)1.(4分)(2009•上海)若复数z满足z(1+i)=1﹣i(I是虚数单位),则其共轭复数=i.【考点】复数的基本概念;复数代数形式的乘除运算.【专题】计算题.【分析】本题考查的知识点是共轭复数的定义,由复数z满足z(1+i)=1﹣i,我们可能使用待定系数法,设出z,构造方程,求出z值后,再根据共轭复数的定义,计算【解答】解:设z=a+bi,则∵(a+bi)(1+i)=1﹣i,即a﹣b+(a+b)i=1﹣i,由,解得a=0,b=﹣1,所以z=﹣i,=i,故答案为i.【点评】求复数的共轭复数一般步骤是:先利用待定系数法设出未知的向量,根据已知条件构造复数方程,根据复数相等的充要条件,转化为一个实数方程组,进而求出求知的复数,再根据共轭复数的定义,求出其共轭复数.2.(4分)(2009•上海)已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是a≤1.【考点】集合关系中的参数取值问题.【专题】集合.【分析】利用数轴,在数轴上画出集合,数形结合求得两集合的并集.【解答】解:∵A={x|x≤1},B={x|x≥a},且A∪B=R,如图,故当a≤1时,命题成立.故答案为:a≤1.【点评】本题属于以数轴为工具,求集合的并集的基础题,也是高考常会考的题型.3.(4分)(2009•上海)若行列式中,元素4的代数余子式大于0,则x满足的条件是x>且x≠4.【考点】三阶矩阵.【专题】计算题.【分析】根据3阶行列式D的元素a ij的余子式M ij附以符号(﹣1)i+j后,叫做元素a ij的代数余子式,所以4的余子式加上(﹣1)1+1即为元素4的代数余子式,让其大于0列出关于x的不等式,求出不等式的解集即可得到x的范围.【解答】解:依题意得,(﹣1)2>0,即9x﹣24>0,解得x>,且x≠4,故答案为:x>且x≠4【点评】此题考查学生掌握三阶矩阵的代数余子式的定义,是一道基础题.4.(4分)(2009•上海)某算法的程序框如下图所示,则输出量y与输入量x满足的关系式是.【考点】程序框图.【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是根据输入x值的不同,根据不同的式子计算函数值.即求分段函数的函数值.【解答】解:根据流程图所示的顺序,程序的作用是分段函数的函数值.其中输出量y与输入量x满足的关系式是故答案为:【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.5.(4分)(2009•上海)如图,若正四棱柱ABCD﹣A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的大小是arctan(结果用反三角函数值表示).【考点】异面直线及其所成的角.【专题】计算题.【分析】先通过平移将两条异面直线平移到同一个起点,得到的锐角或直角就是异面直线所成的角,在直角三角形中求出正切值,再用反三角函数值表示出这个角即可.【解答】解:先画出图形将AD平移到BC,则∠D1BC为异面直线BD1与AD所成角,BC=2,D1C=,tan∠D1BC=,∴∠D1BC=arctan,故答案为arctan.【点评】本题主要考查了异面直线及其所成的角,以及解三角形的应用,属于基础题.6.(4分)(2009•上海)函数y=2cos2x+sin2x的最小值是.【考点】三角函数的最值.【专题】计算题.【分析】先利用三角函数的二倍角公式化简函数,再利用公式化简三角函数,利用三角函数的有界性求出最小值.【解答】解:y=2cos2x+sin2x=1+cos2x+sin2x=1+=1+当=2k,有最小值1﹣故答案为1﹣【点评】本题考查三角函数的二倍角余弦公式将三角函数降幂、利用公式化简三角函数.7.(4分)(2009•上海)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则数学期望Eξ(结果用最简分数表示).【考点】离散型随机变量的期望与方差.【专题】计算题.【分析】用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,结合变量对应的事件写出分布列当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,求出期望.【解答】解:用随机变量ξ表示选出的志愿者中女生的人数,ξ可取0,1,2,当ξ=0时,表示没有选到女生;当ξ=1时,表示选到一个女生;当ξ=2时,表示选到2个女生,∴P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,∴Eξ=0×=.故答案为:【点评】本题考查离散型随机变量的分布列和期望,这是近几年经常出现的一个问题,可以作为解答题出现,考查的内容通常是以分布列和期望为载体,有时要考查其他的知识点.8.(4分)(2009•上海)已知三个球的半径R1,R2,R3满足R1+2R2=3R3,则它们的表面积S1,S2,S3,满足的等量关系是.【考点】球的体积和表面积.【专题】计算题.【分析】表示出三个球的表面积,求出三个半径,利用R1+2R2=3R3,推出结果.【解答】解:因为S1=4πR12,所以,同理:,即R1=,R2=,R3=,由R1+2R2=3R3,得故答案为:【点评】本题考查球的表面积,考查计算能力,是基础题.9.(4分)(2009•上海)已知F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.若△PF1F2的面积为9,则b=3.【考点】椭圆的应用;椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】由已知得|PF1|+|PF2|=2a,=4c2,,由此能得到b的值.【解答】解:∵F1、F2是椭圆C:(a>b>0)的两个焦点,P为椭圆C上一点,且.∴|PF1|+|PF2|=2a,=4c2,,∴(|PF1|+|PF2|)2=4c2+2|PF1||PF2|=4a2,∴36=4(a2﹣c2)=4b2,∴b=3.故答案为3.【点评】主要考查椭圆的定义、基本性质和平面向量的知识.10.(4分)(2009•上海)在极坐标系中,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积等于.【考点】简单曲线的极坐标方程;定积分.【专题】计算题.【分析】三条直线化为直角坐标方程,求出三角形的边长,然后求出图形的面积.【解答】解:三条直线θ=0,,ρcosθ+ρsinθ=1的直角坐标方程分别为:y=0,y=x,x+y=1,所以它们的交点坐标分别为O(0,0),A(1,0),B(,),OB==,由三条直线θ=0,,ρcosθ+ρsinθ=1围成图形的面积S==.故答案为:.【点评】本题考查极坐标与直角坐标的互化,三角形的面积的求法,考查计算能力.11.(4分)(2009•上海)当时,不等式sinπx≥kx恒成立.则实数k的取值范围是k≤2.【考点】函数恒成立问题.【专题】数形结合.【分析】要使不等式sinπx≥kx恒成立,设m=sinπx,n=kx,利用图象得到k的范围即可.【解答】解:设m=sinπx,n=kx,x∈[0,].根据题意画图得:m≥n恒成立即要m的图象要在n图象的上面,当x=时即πx=时相等,所以此时k==2,所以k≤2故答案为k≤2【点评】考查学生利用数形结合的数学思想解决问题的能力,理解函数恒成立时取条件的能力.12.(4分)(2009•上海)已知函数f(x)=sinx+tanx,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,则当k=14时,f(a k)=0.【考点】函数奇偶性的性质.【专题】计算题;压轴题.【分析】本题考查的知识点是函数的奇偶性及对称性,由函数f(x)=sin x+tan x,项数为27的等差数列{a n}满足a n∈(﹣),且公差d≠0,若f(a1)+f(a2)+…f(a27)=0,我们易得a1,a2,…,a27前后相应项关于原点对称,则f(a14)=0,易得k值.【解答】解:因为函数f(x)=sinx+tanx是奇函数,所以图象关于原点对称,图象过原点.而等差数列{a n}有27项,a n∈().若f(a1)+f(a2)+f(a3)+…+f(a27)=0,则必有f(a14)=0,所以k=14.故答案为:14【点评】代数的核心内容是函数,函数的定义域、值域、性质均为高考热点,所有要求同学们熟练掌握函数特别是基本函数的图象和性质,并能结合平移、对称、伸缩、对折变换的性质,推出基本函数变换得到的函数的性质.13.(4分)(2009•上海)某地街道呈现东﹣西、南﹣北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(﹣2,2),(3,1),(3,4),(﹣2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)(3,3)为发行站,使6个零售点沿街道到发行站之间路程的和最短.【考点】两点间距离公式的应用.【专题】直线与圆.【分析】设发行站的位置为(x,y),则可利用两点间的距离公式表示出零售点到发行站的距离,进而求得在(3,3)处z取得最小值.【解答】解:设发行站的位置为(x,y),6个零售点到发行站的距离为Z,则z=|x+2|+|y﹣2|+|x﹣3|+|y﹣1|+|x﹣3|+|y﹣4|+|x+1|+|y﹣3|+|x﹣4|+|y﹣5|+|x﹣6|+|y﹣6|=|x+2|+|x﹣3|+|x﹣3|+|x+1|+|x﹣4|+|x﹣6|+|y﹣2|+|y﹣1|+|y﹣4|+|y﹣3|+|y﹣5|+|y﹣6|x=3,3≤y<4时,取最小值,∴在(3,3)处z取得最小值.故答案为(3,3).【点评】本题主要考查了两点间的距离公式的应用.考查了学生创造性思维能力和逻辑思维能力.14.(4分)(2009•上海)将函数(x∈[0,6])的图象绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则α的最大值为arctan.【考点】旋转变换.【专题】计算题;压轴题.【分析】先画出函数(x∈[0,6])的图象,然后根据由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象,求出此角即可.【解答】解:先画出函数(x∈[0,6])的图象这是一个圆弧,圆心为M(3,﹣2)由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象∴∠MAB=arctan故答案为:arctan【点评】本题主要考查了旋转变换,同时考查了数形结合的思想和分析问题解决问题的能力,属于基础题.二、选择题(共4小题,每小题4分,满分16分)15.(4分)(2009•上海)“﹣2≤a≤2”是“实系数一元二次方程x2+ax+1=0有虚根”的()A.必要不充分条件B.充分不必要条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】实系数一元二次方程x2+ax+1=0有虚根⇒△=a2﹣4<0⇒﹣2<a<2,由此入手能够作出正确选择.【解答】解:∵实系数一元二次方程x2+ax+1=0有虚根,∴△=a2﹣4<0,解得﹣2<a<2,∴“﹣2≤a≤2”是“﹣2<a<2”的必要不充分条件,故选A.【点评】本题考查必要条件、充分条件和充要条件的应用,解题时要认真审题,仔细解答.16.(4分)(2009•上海)若事件E与F相互独立,且P(E)=P(F)=,则P(E∩F)的值等于()A.0 B.C.D.【考点】相互独立事件的概率乘法公式.【分析】本题考查的知识点是相互独立事件的概率乘法公式,由相互独立事件的概率计算公式,我们易得P(E∩F)=P(E)•P(F),将P(E)=P(F)=代入即可得到答案.【解答】解:P(E∩F)=P(E)•P(F)=×=.故选B.【点评】相互独立事件的概率计算公式:P(E∩F)=P(E)•P(F),P(E∪F)=P(E)+P(F).17.(4分)(2009•上海)有专业机构认为甲型N1H1流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是()A.甲地:总体均值为3,中位数为4B.乙地:总体均值为1,总体方差大于0C.丙地:中位数为2,众数为3D.丁地:总体均值为2,总体方差为3【考点】众数、中位数、平均数;极差、方差与标准差.【专题】压轴题.【分析】平均数和方差都是重要的数字特征,是对总体的一种简单的描述,平均数描述集中趋势,方差描述波动大小.【解答】解:假设连续10天,每天新增疑似病例的人数分别为x1,x2,x3,…x10.并设有一天超过15人,不妨设第一天为16人,根据计算方差公式有s2=[(16﹣5)2+(x2﹣5)2+(x3﹣5)2+…+(x10﹣5)2]>12,说明乙地连续10天,每天新增疑似病例的人数都不超过15人.故选:B.【点评】根据题意可知本题主要考查用数字特征估计总体,属于基础题.18.(4分)(2009•上海)过圆C:(x﹣1)2+(y﹣1)2=1的圆心,作直线分别交x、y正半轴于点A、B,△AOB被圆分成四部分(如图),若这四部分图形面积满足S|+S IV=S||+S|||则直线AB有()A.0条B.1条C.2条D.3条【考点】直线与圆的位置关系.【专题】综合题;压轴题;数形结合.【分析】由圆的方程得到圆心坐标和半径,根据四部分图形面积满足S|+S IV=S||+S|||,得到S IV﹣S II=SⅢ﹣S I,第II,IV部分的面积是定值,所以三角形FCB减去三角形ACE的面积为定值即SⅢ﹣S I为定值,所以得到满足此条件的直线有且仅有一条,得到正确答案.【解答】解:由已知,得:S IV﹣S II=SⅢ﹣S I,由图形可知第II,IV部分的面积分别为S正方形OECF﹣S扇形ECF=1﹣和S扇形ECF=,所以,S IV﹣S II为定值,即SⅢ﹣S I为定值,当直线AB绕着圆心C移动时,只可能有一个位置符合题意,即直线AB只有一条.故选B.【点评】此题考查学生掌握直线与圆的位置关系,会求三角形、正方形及扇形的面积,是一道综合题.三、解答题(共5小题,满分78分)19.(14分)(2009•上海)如图,在直三棱柱ABC﹣A1B1C1中,AA1=BC=AB=2,AB⊥BC,求二面角B1﹣A1C﹣C1的大小.【考点】向量在几何中的应用;与二面角有关的立体几何综合题.【专题】计算题;向量法.【分析】建立空间直角坐标系,求出2个平面的法向量的坐标,设二面角的大小为θ,显然θ为锐角,设2个法向量的夹角φ,利用2个向量的数量积可求cosφ,则由cosθ=|cosφ|求出二面角的大小θ.【解答】解:如图,建立空间直角坐标系.则A(2,0,0),C(0,2,0),A1(2,0,2),B1(0,0,2),C1(0,2,2),设AC的中点为M,∵BM⊥AC,BM⊥CC1.∴BM⊥平面A1C1C,即=(1,1,0)是平面A1C1C的一个法向量.设平面A1B1C的一个法向量是n=(x,y,z).=(﹣2,2,﹣2),=(﹣2,0,0),∴令z=1,解得x=0,y=1.∴n=(0,1,1),设法向量n与的夹角为φ,二面角B1﹣A1C﹣C1的大小为θ,显然θ为锐角.∵cosθ=|cosφ|==,解得:θ=.∴二面角B1﹣A1C﹣C1的大小为.【点评】本题考查利用向量求二面角的大小的方法,设二面角的大小为θ,2个平面法向量的夹角φ,则θ和φ相等或互补,这两个角的余弦值相等或相反.20.(16分)(2009•上海)有时可用函数f(x)=,描述学习某学科知识的掌握程度.其中x表示某学科知识的学习次数(x∈N*),f(x)表示对该学科知识的掌握程度,正实数a与学科知识有关.(1)证明:当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降;(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.【考点】分段函数的应用.【专题】应用题;探究型;数学模型法.【分析】(1)x≥7时,作差求出增长量f(x+1)﹣f(x),研究其单调性知,差是一个减函数,故掌握程度的增长量总是下降、(2)学习某学科知识6次时,掌握程度是85%,故得方程由此方程解出a的值即可确定相应的学科.【解答】证明:(1)当x≥7时,而当x≥7时,函数y=(x﹣3)(x﹣4)单调递增,且(x﹣3)(x﹣4)>0故函数f(x+1)﹣f(x)单调递减当x≥7时,掌握程度的增长量f(x+1)﹣f(x)总是下降(2)由题意可知整理得解得(13分)由此可知,该学科是乙学科..(14分)【点评】本题是分段函数在实际问题中的应用,在实际问题中,分段函数是一个很重要的函数模型.21.(16分)(2009•上海)已知双曲线,设直线l过点,(1)当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;(2)证明:当k>时,在双曲线C的右支上不存在点Q,使之到直线l的距离为.【考点】双曲线的简单性质.【专题】计算题;证明题.【分析】(1)先求出双曲线的渐近线方程,进而可得到直线l的斜率,然后根据直线l过点求出直线l的方程,再由平行线间的距离公式可求直线l的方程及l与m 的距离.(2)设过原点且平行于l的直线方程利用直线与直线的距离求得l与b的距离,当k>时,可推断出,利用双曲线的渐近线方程可知双曲线C的右支在直线b的右下方,进而推断出双曲线C的右支上的任意点到直线l的距离大于,进而可知故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【解答】解:(1)双曲线C的渐近线,即∴直线l的方程∴直线l与m的距离.(2)设过原点且平行于l的直线b:kx﹣y=0,则直线l与b的距离d=,当时,.又双曲线C的渐近线为,∴双曲线C的右支在直线b的右下方,∴双曲线C的右支上的任意点到直线l的距离大于.故在双曲线C的右支上不存在点Q(x0,y0)到到直线l的距离为.【点评】本题主要考查了双曲线的简单性质.考查了学生综合分析问题和解决问题的能力.22.(16分)(2009•上海)已知函数y=f(x)的反函数.定义:若对给定的实数a(a≠0),函数y=f(x+a)与y=f﹣1(x+a)互为反函数,则称y=f(x)满足“a和性质”;若函数y=f(ax)与y=f﹣1(ax)互为反函数,则称y=f(x)满足“a积性质”.(1)判断函数g(x)=x2+1(x>0)是否满足“1和性质”,并说明理由;(2)求所有满足“2和性质”的一次函数;(3)设函数y=f(x)(x>0)对任何a>0,满足“a积性质”.求y=f(x)的表达式.【考点】反函数;函数解析式的求解及常用方法.【专题】压轴题;新定义.【分析】(1)先求出g﹣1(x)的解析式,换元可得g﹣1(x+1)的解析式,将此解析式与g (x+1)的作对比,看是否满足互为反函数.(2)先求出f﹣1(x)的解析式,再求出f﹣1(x+2)的解析式,再由f(x+2)的解析式,求出f﹣1(x+2)的解析式,用两种方法得到的f﹣1(x+2)的解析式应该相同,解方程求得满足条件的一次函数f(x)的解析式.(3)设点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,可得ay0=f (x0)=af(ax0),,即,即满足条件.【解答】解(1)函数g(x)=x2+1(x>0)的反函数是,∴,而g(x+1)=(x+1)2+1(x>﹣1),其反函数为,故函数g(x)=x2+1(x>0)不满足“1和性质”.(2)设函数f(x)=kx+b(x∈R)满足“2和性质”,k≠0.∴,∴,而f(x+2)=k(x+2)+b(x∈R),得反函数,由“2和性质”定义可知,对(x∈R)恒成立.∴k=﹣1,b∈R,即所求一次函数f(x)=﹣x+b(b∈R).(3)设a>0,x0>0,且点(x0,y0)在y=f(ax)图象上,则(y0,x0)在函数y=f﹣1(ax)图象上,故,可得ay0=f(x0)=af(ax0),令ax0=x,则,∴,即.综上所述,,此时,其反函数是,而,故y=f(ax)与y=f﹣1(ax)互为反函数.【点评】本题考查反函数的求法,函数与反函数的图象间的关系,体现了换元的思想,属于中档题.23.(16分)(2009•上海)已知{a n}是公差为d的等差数列,{b n}是公比为q的等比数列.(1)若a n=3n+1,是否存在m、k∈N*,有a m+a m+1=a k?说明理由;(2)找出所有数列{a n}和{b n},使对一切n∈N*,,并说明理由;(3)若a1=5,d=4,b1=q=3,试确定所有的p,使数列{a n}中存在某个连续p项的和是数列{b n}中的一项,请证明.【考点】等差数列与等比数列的综合;等差数列的性质;数列递推式.【专题】综合题;压轴题;分类讨论;转化思想.【分析】(1)由a m+a m+1=a k,得6m+5=3k+1,,由m、k∈N*,知k﹣2m为整数,所以不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,由此入手能够导出有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.4m+2p+3+,由p、k∈N*,知p=3s,s∈N.由此入手能导出当且仅当p=3s,s∈N,命题成立.【解答】解:(1)由a m+a m+1=a k,得6m+5=3k+1,整理后,可得,∵m、k∈N*,∴k﹣2m为整数,∴不存在m、k∈N*,使等式成立.(2)设a n=nd+c,若,对n∈N×都成立,且{b n}为等比数列,则,对n∈N×都成立,即a n a n+2=qa n+12,∴(dn+c)(dn+2d+c)=q(dn+d+c)2,对n∈N×都成立,∴d2=qd2(i)若d=0,则a n=c≠0,∴b n=1,n∈N*.(ii)若d≠0,则q=1,∴b n=m(常数),即=m,则d=0,矛盾.综上所述,有a n=c≠0,b n=1,使对一切n∈N×,.(3)a n=4n+1,b n=3n,n∈N*,设a m+1+a m+2++a m+p=b k=3k,p、k∈N*,m∈N.,∴,∵p、k∈N*,∴p=3s,s∈N取k=3s+2,4m=32s+2﹣2×3s﹣3=(4﹣1)2s+2﹣2×(4﹣1)s﹣3≥0,由二项展开式可得整数M1、M2,使得(4﹣1)2s+2=4M1+1,2×(4﹣1)s=8M2+(﹣1)S2∴4m=4(M1﹣2M2)﹣((﹣1)S+1)2,∴存在整数m满足要求.故当且仅当p=3s,s∈N,命题成立.【点评】本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.。
2009年上海杨浦区高三数学试卷及答案-09.1.120数学答题卡

三、解答题
16.1 解:由 2-
1 0 2分 x+ 1
1 4 33 18 --------- --------10 分 2 3 1 1 V 圆锥 S 底 h 9 10 30 ---------12 分 3 3 又因为 30 18
----------------- --------5 分
1 2
2 , 易得 a 1 5
-----------------------------------5 分
2 由1- x- a 0 8分 B 1 a,1 a 10分
由题意得, SAB 90 30 60 在 SAB 中,SA=300,AB=30t,
5.
1+i
8.文 1cm 理 11. (1) 120
0
30
0
9. 8
1 S 球表面积 2
-------------------------------4 分
由余弦定理,
1 10. 4
, (2) 2 3 b c 4
杨浦区学校
2x 1 0 x 1 1 x 1或x - 4分 2 1 A , 1 U , 2 1 CR A 1, 6分 2
√
×
1 a 1 1 11分 1 a 2 3 a ,0 12分 2
17.解 由于半径 R 3cm 高为 h 10cm
B
30
S
A
根据余弦定理,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杨浦区2008学年度高三学科测试
数学试卷 2009.1.12
考生注意: 1、本试卷共有20道题,满分150分,考试时间120分钟.
2、本试卷为文、理合卷,题首标有文科考生做、理科考生做的题目,没有标记的是“文”、“理”考生共同做的题目.
一. 填空题(本大题满分60分)本大题共有11题,考生应在答题纸上相应编号的空格内
直接填写结果,每个空格填对得5分,否则一律得零分. 1.若函数(
)1f x =
的反函数()1f x -,则()11f -=_____.
2.命题“若1x =,则22x
x
-+>2”的逆命题是 .
3.若一元二次不等式2
0ax bx c ++≤的解集为空集φ,则实数a,b,c 应满足的条件是 . 4.若函数()203y sin x πωω⎛
⎫
=+
> ⎪⎝
⎭
的最小正周期为π,则ω= .
5.求满足
2
11z
i i
=+-的复数z 为 .
6.若函数()9
33x
x
f x =+
,若()10f x =,则x 的值为 . 7.根据右边的框图,通过所打印数列的递推关系,可写出这个数列的第3项是 .
8.若正四棱锥的体积为43
cm
,底面边长为cm , (文科考生做) 则正四棱锥的高为 .
(理科考生做)则它的侧面与底面所成的二面角的大小是_____.
9
.若12n
x ⎫+⎪⎭的二项展开式中,前三项系数成等差数列,
则n 的值为 .
10.若将一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),
先后抛掷2次,出现向上的点数分别为a ,b ,集合{
}
2
20A x x ax b x R =-+<∈且 则 A φ≠的概率是 .
11.若A 、B 、C 是ABC ∆的三个内角,其对应边长分别是a ,b ,c
且22A A m cos ,sin ,⎛⎫=- ⎪⎝⎭u r
22A A 1
n cos ,sin ,a m n 2
⎛⎫=== ⎪
⎝
⎭u r u r u r g 且
(1)则角A = ;
(2)则b c +的取值范围为 .
二.选择题(本大题满分16分)本大题共有4题,每题只有一个正确答案,答案必须涂在答题纸上,考生应将代表答案的小方格用铅笔涂黑,注意试题题号与答题纸上相应编号一一对应,不能错位.
12.下列各对矩阵,存在积AB 的是
( )
(
)
A
12A ⎛⎫= ⎪⎝⎭,34B ⎛⎫= ⎪⎝⎭
(
)
B
1243A ⎛⎫= ⎪⎝⎭, 56B ⎛⎫
= ⎪⎝⎭
()C 1
4A ⎛⎫= ⎪⎝⎭,236
5B ⎛
⎫
=
⎪⎝⎭
()D 1352
46A ⎛⎫=
⎪⎝⎭
,78B ⎛⎫
= ⎪⎝⎭ 13.若数列{}n a 为等比数列 ,则3516a a =是44a =的 ( ) ()A 充分非必要条件 ()B 必要非充分条件
()C 充要条件
()D 即非充分也非必要条件
14、已知02a <<,复数z 的实部为a ,虚部为1,则z 的取值范围是 ( )
()A (15),
()B (13),
()C
()
D ()
杨浦区高三数学测试----第3页(共5页)
15.在直角坐标系xOy 中,点()P ,P P x y 和点(
)Q ,
Q Q x y 满足Q P P
Q
P P x y x y y x =+⎧⎪⎨=-⎪⎩,按此
规则由点P 得到点Q ,称为直角坐标平面的一个“点变换”. 若
OQ m OP
=及POQ θ∠=,其中O 为坐标原点,则m 与θ的值 ( )
()A 4
π
θ=
,m 不确定
()B θ
不确定,m =
()
C m =
4
π
θ=
()D 以上答案都不对
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须写在答题纸上与题号对应的区域内,并写出必要的步骤.
16. (本题满分12分) 本题共有2个小题,第1小题满分6分, 第2小题满分6分
为集合B . (1)求 R A ð .
(2)若 A B R =U ,求实数a 的取值范围.
17. (本题满分14分)
一个圆锥形的空杯子,上面放着一个半球形的冰淇淋,形成如图所示的几何体. (1)求该几何体的表面积;(精确到2
01.cm )
(2)如果冰淇淋融化了,会溢出杯子吗?请用有关数据说明.
(杯壁的厚度忽略不计)
18. (本题满分14分)
气象台预报,距离S 岛正东方向300km 的A 处有一台风形成,并以每小时30km 的速度向北偏西︒30的方向移动,在距台风中心处不超过270km 以内的地区将受到台风的影响. (文科考生做) 从台风形成起经过3小时,S 岛是否受到影响?并说明理由.
(理科考生做)从台风形成起经过多少小时,S 岛开始受到台风的影响?持续时间多久? (精确到0.1小时)
19. (本题满分16分)本题共有3个小题,第1小题满分6分,第2小题满分5分. 第3小题满分5分. 已知函数()2
1ax b
f x x
+=
+是定义在()11,-上的奇函数,其中a 、b R ∈且1225
f ⎛⎫= ⎪⎝⎭ (1)求函数()f x 的解析式;
(2)判断函数()f x 在区间()11,-上的单调性, 并用单调性定义证明你的结论; (3)(文科考生做) 解关于t 的不等式()()2
10f t f t
-+< .
(理科考生做)求函数()f x 的值域;
20. (本题满分18分)本题共有3个小题,第1小题满6分,第2小题满分6分,第3小题
杨浦区高三数学测试----第5页(共5页)
满分6分.
在直角坐标平面xOy 上一列点()()()()
112223331n n n P a ,b ,P a ,b ,P a ,b ,,P a ,b ,,⋅⋅⋅⋅⋅⋅都在函数12
y log x =的图像上,其中n a >0 ,n N *
∈.
(I)已知数列{}n b 是等差数列,求证数列{}n a 是等比数列;
(1)(文科考生做) 求n b ;
(理科考生做)设过点1n n P ,P +的直线与两坐标轴所围成的三角形面积为n C , 且n C t ≤对n N *
∈ 恒成立,求实数t 的取值范围;
(2)对于数列{}n d ,假设存在一个常数q ,使得对任意的正整数n 都有n d <q ,且
l i m
n n d q →∞
=,则称{}n d 为“左逼近”数列,q 为该数列的“左逼近”值.
研究:数列{}n
A 是否为“左逼近”数列,如果是,求出“左逼近”值,如果不是,说明理由;受本题的启示,请你设计一个“左逼近”数列,并写出它“左逼近”值.。
