Theis井函数计算方法及井模型参数优化计算研究
抽水试验规范方法及计算公式

观测孔的布置应符合下列要求: (1) 为了计算水文地质参数,在抽水孔的一侧宜垂直地下水的流向布置 2~3 个观测孔。 (2) 为了测定含水层不同方向的非均质性或确定抽水影响半径,可以根据含水层的不同情 况,以抽水孔为中心布置 1~4 条观测线;如有两条观测线,一条垂直地下水流向,另一条宜平行 地下水流向。 (3) 群孔干扰抽水试验和试验性开采抽水试验应在抽水孔组中心布置一个观测孔;为查明相 邻已采水源地的影响,应在连接两个开采中心方向布置观测孔。为确定水位下降漏斗形态和补给 (或隔水)边界,应在边界和外围一定范围内布设一定数量的观测孔。 (4) 多孔抽水孔组的第一个观测孔应尽量避开三维流的影响,相邻两观测孔的水位下降值相 差不小于 0.1 m,最远观测孔的下降值不宜小于 0.2 m,各观测孔应在对数数轴上呈均匀分布。 (5) 在半承压水含水层进行抽水试验时,宜在观测孔附近覆盖层(半透水层或弱含水层)中布 置副观测孔。 (6) 在进行试验性开采抽水试验时,应在水位下降漏斗范围内的重要建筑物附近增设工程地 质、环境地质观测点。
(3) 水温、气温宜 2~4 h 观测一次,读数应准确到 0.5 ℃,观测时间应与水位观测时间相对 应。
4.3.4 恢复水位观测要求
停泵后应立即观测恢复水位,观测时间间隔与抽水试验要求基本相同。若连续 3 h 水位不变, 或水位呈单向变化,连续 4 h 内每小时水位变化不超过 1 cm,或者水位升降与自然水位变化相一 致时,即可停止观测。
注意:①要消除区域水位下降值;②在基岩地区要消除固体潮的影响;③傍河抽水要消除河 水位变化对抽水孔水位变化的影响。
多孔抽水试验、群孔干扰抽水试验和试验性开采抽水试验均应编写试验小结,其内容包括: 试验目的、要求、方法、获得的主要成果及其质量评述和结论。
中国石油大学(北京)现代试井分析-第一章 绪论

现 代 试 井 分 析014一、试井概念¾试井是对油、气、水井进行测试和分析的总称。
在不同工作制度下测量井底压力和温度等信号的工艺。
测试内容包括:产量、压力、温度、取样等。
分析(试井解释):应用渗流力学理论,分析测试数据,反求油层和井的动态参数。
¾试井是一种以渗流力学为基础,以各种测试仪表为手段,通过对油井、气井或水井生产动态的测试来研究和确定油、气、水层和测试井的生产能力、物性参数、生产动态,判断测试井附近的边界情况,以及油、气、水层之间的连通关系的方法。
举例:不稳定试井压力和产量对应关系图二、试井的分类就研究的目的来说⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎧⎧⎨⎨⎪⎪⎩⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎨⎪⎪⎩⎩⎩系统试井等时试井产能试井修正等时试井一点法试井试井压力降落试井单井不稳定试井压力恢复试井不稳定试井干扰试井多井不稳定试井脉冲试井按地层类型分类均质油藏试井非均质油藏试井双孔介质油藏试井双渗介质油藏试井复合油藏油藏试井¾按井类别分类,可分为垂直井、水平井、压裂井、定向井和分支井等试井方法。
¾按流动形态分类,可分为线性流、非线性流的试井。
二、试井的分类常规试井分析按分析方法分现代试井分析数值试井分析压降试井分析压恢试井分析变产量叠加试井分析典型图版手动拟合分析典型图版自动拟合分析针对油气藏和油气井研究的严密的测试设计;应用高精度的仪器设备进行现场测试;压力计精度, 分辨率,在井下高温高压条件下连续记录、存储压力数据量测试过程中要求产油气井配合测试进程反复的开关井,准确计量产气量,并处理好产出的气体;以复杂油气藏为背景的渗流力学理论和方法的研究;以解数理方程中的反问题为基础的试井解释方法及软件;结合地质、物探、测井、油藏及工艺措施的油藏动静态描述。
四、试井的作用2014姚约东2014试井研究贯穿于油气田勘探开发全过程2014四、试井的作用试井的作用总结为以下几点:(1)估算测试井的井底污染情况,判断是否需要采取增产措施(如酸化、 压裂),分析增产措施的效果;(2)估算测试井的地层参数、产能;(3)平均地层压力计算、压力分布;(4)判断和预测油气藏类型,均质、非均质油气藏,边底水等;(5)判断和预测油气藏范围,河道油藏,断层距离,透镜体,油(气)层边界,估算控制储量;(6)判断和评价断层的性质,包括密封性等;(7)判断井间连通性;(8)描述井筒周围油藏特性,包括渗透率、孔隙度、厚度、饱和度分布等。
地下水动力学期末考试复习题(井附近地下水流动)

承压水井的Dupuit(裘布依)公式
(1)假设条件(适用条件)
1)水井布置于均质、各向同性、水平分布、等厚的圆形岛屿状承压含水层的中心,岛屿半径为R,岛屿周围自含水层底面起算的水头H0保持不变;——Dupuit模型(圆岛模型)
21、什么条件下会产生承压-无压井流?推到出承压-无压井流公式?
承压水井中大降深抽水时,如果井中水位低于含水层顶板,井附近含水层中水位也将低于含水层顶板而呈现为无压水流,此时就变为承压—潜水井(承压—无压水井)。
承压—潜水井公式:
22、什么是影响半径?
R—影响半径,即从抽水井开始到实际观测(或可忽略)不到水位降深处的径向距离(Thiem的影响半径的定义),m。
2)计算步骤(以降深-时间距离配线法为例)
在双对数坐标纸上作标准曲线W(u)-1/u;
根据实际观测资料,在另一张同模数透明双对数纸上作s-t/r2实际曲线;
将实际曲线叠放于标准曲线上,保持对应坐标轴平行,平移曲线,直至二曲线最大限度地重合;
任取一匹配点(在曲线上或曲线外均可),记下匹配点对应坐标[W(u)]、[1/u]、[s]、[t/r2],代入Theis公式计算参数:
2)抽水前含水层水位面水平,水头为H0;
3)抽水过程中地下水运动符合Darcy定律。
数学模型:
数学模型的解——Dupuit公式
采用分离变量法求解,在rw至R区间上进行积分,得到方程的通解,再利用边界条件确定通解中的积分常数,便得上述数学模型的解:
或
公式符号含义:
sw—井中水位降深,m;
Q—抽水井流量,m3/d;
Theis解析模型的数值解及其在MatLab中的实现

望
摘要 : 了如何应用数值积分方法求解含水层 中地下水非稳定流抽水试验的解析模型 以获 得含水层 的水文 地质 讨论 参数 , 以 T e 公 式为例讨论求解原理 。引入 了 M ta 并 hi s aLb的数值积 分工具和 优化工具 , 轻松 实现 了对 水文地质参 数 的求解 , 此举既保证 了解 的可靠性和唯一性 , 也大 大提高 了方法 的可操作性 。最后 以一个具 体 的承压水非稳定 流抽水试 验为例验证 了这个方法 , 所得 的结果 与应 用配线 法得 到 的结 果基本 一致 , 而肯定 了方法 的应用 价值 。 从 研究 结果尽管是针对 T e 模型进行 的 , hi s 但求解原理 同样适用于其他各种模型。
1 研究思路
通过 对含水 层进 行地下 水非 稳定 抽水试 验 以求 解水 文地 质参数 是一 种水文 地质基 础研 究 的通用 方
来进 行 , 例如矩 形法 、 梯形 法 、 物线 法等 , 抛 但积 分 区
间无 法 事先 给定 。
②积分区间 [ ,+∞] u 的确定 , 根据 ( ) 可 2 式,
数 值积分 是 通 过 在 有 限 个 采 样 点 上 计 算 f ) ( 的值来 逼 近 ) 区 问 [ , ] 的定 积分 , 据 离 在 ab内 根 散 区间 内引入 的插值 函数 的不 同 , 分 为 ( 可 组合 ) 梯 形 公式 、 组合 辛 普 生 公 式 ( 又称 抛 物 线 公 式 ) 布 尔 、 公 式 、 斯一 勒让 德 公式 等 , 比较 而 言 , 普 生 公 高 相 辛 式 应用较 为广 泛且 只需对 少量 的函数求 解就 能得 到 准 确 的答 案 。文献 [ ] 组 合 辛普 生 公 式 的讨 论 简 4对
关键 词 : ta ; Ma b 数值 积分 ;hi解析模型 ; L Te s 水文地质参数 ; 优化
基于抽水试验的渗透系数计算方法对比与研究
2017年27期科技创新与应用Technology Innovation and Application方法创新基于抽水试验的渗透系数计算方法对比与研究朱保坤,苟联盟,柴永进,张建涛(中设设计集团股份有限公司,江苏南京210014)摘要:以无锡梅梁湖湖区抽水试验为例,对几种常用渗透系数计算方法进行初步的比较和分析。
传统的稳定流公式法计算方法简单,但需对结构进行简化处理,计算结果误差较大;非稳定流配线法计算严谨,准确性高,但通常需借助计算机程序帮助,过程较复杂,对试验数据及 其准确性要求较高。
关键词:抽水试验;稳定流;非稳定流中图分类号:P 641.73 文献标识码:A 文章编号院2095-2945 (2017)27-0071-021概述根据现场抽水试验资料确定含水层渗透系数是查明水文地 质工作中经常采用的有效方法之一 ™。
用抽水试验数据分析水文 ±地质参数的方法已经比较成熟,早在1863年J .Dupuit 就提出了 完整井稳定流的Dupuit 公式,1970年W .C .Walton 提出了承压含 水层完整井有越流、无边界影响时的井流公式,此外还有Theis 公式、Copper-Jacob 法、Boulton 模型及 HantushJacob 法等\ 不 同的计算方法各有优缺点及适用条件,并且存在计算误差,本文 采用稳定流公式法、非稳定流配线法及水位恢复法计算渗透系 数。
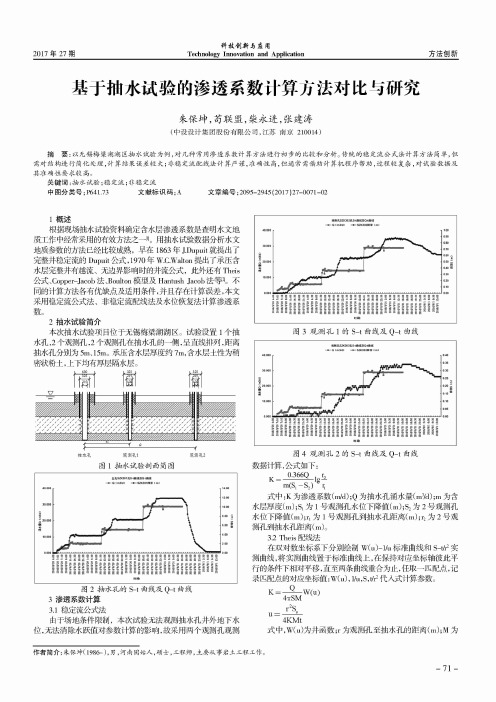
2抽水试验简介本次抽水试验项目位于无锡梅梁湖湖区。
试验设置1个抽 水孔,2个观测孔,2个观测孔在抽水孔的一侧,呈直线排列,距离 抽水孔分别为5m 、15m 。
承压含水层厚度约7m ,含水层土性为稍 密状粉土,上下均有厚层隔水层。
桔水孔 观測孔1 观*孔2图1抽水试验剖面简图40 000-*-S Z X 301»5 <m>140030 0CQ警臓8.00 ^10 000\6 00 g 4 W 2008S S 88S S S 888S 8S 888S 8885S 88S 8S S 888S S 88888«爾图2抽水孔的S -t 曲线及Q -t 曲线3渗透系数计算 3.1 稳定流公式法由于场地条件限制,本次试验无法观测抽水孔井外地下水 位,无法消除水跃值对参数计算的影响,故采用两个观测孔观测4000030 000MHASZK302AS-1lll<ESatatt-m -Q (m 3/d >-*-SZK302K3K <m >100090oeo|o e o «~ 20 0005-/050 s0 40 S 100000300200.10l l l l i i i l l l l i i i i ia 888a «8R a a 88S R R R 888sn »图3观测孔1的S -t 曲线及Q -t 曲线数据计算,公式如下:K = 0.366Q &n H ^-S ,) 5r ,式中:K 为渗透系数(m /d ) ;Q 为抽水孔涌水量(m 3/d ) ;m 为含 水层厚度(m )^为1号观测孔水位下降值(m );S 2S 2号观测孔 水位下降值(m );ri为1号观测孔到抽水孔距离(m );r 2为2号观测孔到抽水孔距离(m )3.2Theis 配线法在双对数坐标系下分别绘制W (u )-1/u 标准曲线和S -t /r 2实 测曲线,将实测曲线置于标准曲线上,在保持对应坐标轴彼此平 行的条件下相对平移,直至两条曲线重合为止,任取一匹配点,记 录匹配点的对应坐标值:W (u ),代人式计算参数。
第四章 地下水向完整井的非稳定运动

第四章 地下水向完整井的非稳定运动§1、承压含水层中的完整井流一、定流量抽水时的Theis(泰斯公式)假定条件:(1)含水层均质各向同性、等厚,侧向无限延伸,产状水平; (2)抽水前天然状态下水力坡度为零; (3)完整井定流量抽水,井径无限小; (4)含水层中水流服从Darcy 定律;(5)水头下降引起的地下水从贮存量中的释放是瞬时完成的。
教学模型的建立和求解:抽水形成以井轴为对称轴的下降漏斗,将坐标原点放在含水层底板抽水井的井轴处,井轴为z 轴,建立坐标系。
则以降深表示的微分方程为:教学模型为: 其解为:其中:s —抽水影响范围内,任一点任一时刻的水位降深;Q —抽水井的流量; T —导水系数;t —自抽水开始导计算时刻的时间; r —计算点到抽水井的距离; u —含水层的贮水系数。
利用上述W(u)和u 的关系制定P 93表,W(u)可查表得。
首先由 计算出u 値,然后查表得相应的W(u),再求r 处的s 値。
tsT urs r rs ∂∂=∂∂+∂∂*221⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=∂∂>=∂∂=∞∞<<=∞<<>∂∂=∂∂+∂∂→∞→T r s r t r s t s r r s r t t s T u rs r r s r r π2Qlim 00,0),(00)0,(0,010*22()()⎰∞-===uy dy y e u W Tt u r u u W T Q s 44*2πTtu r u 4*2=二、流量变化时的计算公式流量随时间的变化,可分为阶梯变化和连续渐变,相应的流量过程线为台阶状和连续光滑的曲线。
连续光滑的曲线应概括成阶梯状折线。
概化的原则:矩形面积等于曲线与横坐标所围成的面积。
每一个阶梯视为定流量,用Theis 公式计算降深,然后将各降深叠加起来,得流量变化的总降深値。
如图,连续抽水,概括为4个阶梯,若求t 时刻的水位降深,则可分解为四个亚问题,第一个亚问题以Q 1流量抽水从t 0→t ;第二个亚问题以Q 2-Q 1流量抽水,从t 1→t ;第三个亚问题以Q 3-Q 2流量抽水从t 2→t ;第四个亚问题以Q 4-Q 3流量抽水从t 3→t 。
渤海Q油田提液井生产规律分析

石油地质与工程2021年11月PETROLEUM GEOLOGY AND ENGINEERING 第35卷第6期文章编号:1673–8217(2021)06–0114–05渤海Q油田提液井生产规律分析张锋利1,高智梁1,李权1,欧阳雨薇1,周日1,张利健2(1.中海石油(中国)有限公司秦皇岛32–6作业公司,天津300450;2.中海油能源发展股份有限公司工程技术分公司,天津300450)摘要:为改善渤海Q油田提液生产效果,对油田实施大泵提液井生产动态参数进行分析,总结出油井提液前后含水率变化、后期递减率变化和含水上升速度与含水阶段、能量补充类型、储层厚度和提液幅度有一定的相关性。
据此确定Q油田提液井筛选及优化方向为:优选能量补充类型为底水油藏、储层厚度超10 m、含水率达到95%的井实施提液。
从理论上对提液井生产的合理性进行分析探讨,并对两口井的提液情况进行了验证,为油田下一步提液井筛选、提液时机优化等提供指导。
关键词:大泵提液;因素分析;提液幅度;提液时机中图分类号: TE2 文献标识码:AAnalysis on production law of liquid extraction wells in Bohai Q oilfieldZHANG Fengli1,GAO Zhiliang1,LI Quan1,OUYANG Yuwei1,ZHOU Ri1,ZHANG Lijian2(1. QHD32-6 Operating Company of CNOOC(China) Co.,Ltd.,Tianjin 300450,China;2. Engineering Technology Company of CNOOC Energy Development Co., Ltd.,Tianjin 300450,China)Abstract: In order to improve the production effect of oilfield liquid extraction, according to the production performance parameters of large pumping liquid extraction wells in the oilfield, it is analyzed and summarized that the change of water cut before and after oil well liquid extraction, the change of decline rate in the later stage and the rising rate of water cut are related to the water cut stage, energy supplement type, reservoir thickness and liquid extraction amplitude. Therefore, the selection and optimization direction of liquid extraction wells in Q oilfield is proposed as follows: the preferred energy supplement type is bottom water reservoir, the reservoir thickness exceeds 10 m, and the water cut reaches 95%. To analyze the rationality of the production law of the liquid extraction wells, the theoretical mechanism has been discussed, and then the liquid extraction conditions of two wells are verified, which provides a good guidance for the selection of liquid extraction wells and the optimization of liquid extraction time in the next step.Key words: large pumping liquid extraction; factor analysis; amplitude of liquid lifting; liquid extraction time 渤海Q油田油藏埋深较浅,为疏松砂岩高孔高渗储层,产液能力高,目前油田平均单井日产液量可达600 m3以上,综合含水接近95%,处于特高含水期。
4-1承压含水层中的完整井流

1 s 当 r一 定 时 , 和e u 起 着 增 、 减 速 度 两 个 向 方的 作 用 , 所 以 不 是 t t t的 单 调 函 数 , s t曲 线 不 能 沿 着 同 一 斜 变 率化 , 存 在 着 拐 点 。
2.拐 点 位 置 : 说 明 st位 置 存 在 拐 点 , v 2 s Q 1 u r 2 μ* 2 2e ( 1 ) 0 t t 4πT t 4Tt r 2 μ* 当u 1, 即 1, 出 现 拐 点 即 最 大 降 速 点 的。 4Tt r
6
(4)确 定 系 数 C dH H Q r ,(当u 0时) du r 2T u 0 dH 上 式 变 为 : 2u 2Ce u,两 边 同 时 求 极 限 , du dH Q u (据 边 界 条 件 ) 2 Ce 2 C ; 2 u lim lim du 2T u 0 u 0 Q Q 方 程 左 边 = 右 边 , 即 2C 所以C , 2T 4T dH Q e u 把C代入(3)得 即 du 4T u H0 Q e u 分离变量积分 : H dH 4T u u du,(当H (u ) H 0时,u ) Q e u Q e u H0 H du,得H H 0 du u u 4T u 4T u 即 为 定 解 问 题 ( 1) 的 解 , 也 是 著 名 的 泰 斯式 公。 lim 2u
r *
19
(2)水位下降速度的变化规律
u s Q e Q 1 v du e u t u 4T u t 4T t 1.当 t一 定 时 , r增 大 v减 小 ; r增 大 , 降 速 越小, r ,v 0;
u r 2 4Tt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于 Theis 井函数为指数积分式, 数学上 无法 直
W (u)=
i -ln(u)+ða• i u i=0 4
5
式 中 :γ =0.5772156649015329, 是 欧拉 常 数 ;N 理论 上 趋近于无穷㊂ 展开 项 N㊂ 国内 绝 大 多数 研究 者 都 是采用的这种方 似 数 值 计算 方法会 因 为 级 数 项 的取 舍 而导 致实际应 5~11 时的 u-W (u)图, 可以很明显地看出当 u 大于 2 时 大,其后果是模型参数最终求解结果出现较大误差㊂
数 W (u)的方法,其替代公式如下: 的误差㊂
2 • (1-G ) ,h = (1-G ) • (G 2-6 • G +12) ɕ G• (2-G ) 3 • G• (2-G )2 • b
如图 2 示,拟合式(6)当 u 大于 2 时 W (u)出现明显 笔者 基 于 最小 二乘原理 , 得出 如 下 井 函 数 W (u)替
⎧ | | | | ⎨ | | | | ⎩
解几乎完全重合: W (u)=
代公式,具体系数见表 2,效果图见图 2,和高精度数值 b 1+b 2 • ub 3+b 4 • ln(u)+b 5 • exp(b 6 • u)
p
系数如表 1㊂
Srivastava 于 1998 年提出的方法如公式(4)示,其
4.156969E-6 -2.624277E-5 4.156478E-6 4.156969E-6 4.156969E-6 4.112166E-6 0.7894027 100.17575
10
9.835525E-11 -52247.83580 4027.53816
程先云 1, 郑凡东 2, 杨
浩 2, 曹大岭 1,杨
勇2
优缺点及对模型最终参数计算的影响, 提出了新的简易计算方法; 以经典实际案例为对象, 对比研究 数优化计算问题, 并可广泛用于其它水文模型参数求解㊂ 关键词:Theis 井模型;Theis 井函数;参数优化;1stOpt 中图分类号:P345 文献标识码: A 应慎用广为采纳的级数展开井函数计算方式;(2)1stOpt 通用优化计算平台可很好处理 Theis 井模型参 文章编号:1000-0852(2015)03-0008-06 即采用该平台进行模型参数优化计算㊂ 了优化软件平台在 Thies 井模型参数计算中的实际应用效果;计算结果表明:(1)Thies 井模型参数估算
2.5 1.5 0.5 -0.5 -1.5 2 1 0 N=5 N=7
(2)
1 • i=0 4 u • exp(u)
ðb•u ðc•u
i=0 i
i
u>1
(4)
实际应用中, 可以根据不同的精度需要选取级数
序号 a b c
法,级数项 N 一般都取 3~5,如文献[1-4]等㊂ 然而该近 用 中 产 生较大 误差 问题 , 如 图 1 为 级 数 项 N 分 别 取 W (u)值 即处于 震荡 发 散 不 稳 定 状态 ,N 值 越 小 误差 越
-0.57722 3.95850 0.2677
0
表1 Srivastava方法系数表 Table1 Coefficient of Srivastava method 0.99999 1 -0.24991 25.63296 18.05902 2 0.05519 3 -0.00976 1 1 4
21.09965
能通过数值计算方法近似求解㊂ 关于井函数 W (u), 在数 称 为 Theis 井 函 数或井 函 数, 其 数 值 求解 方式国内外 学者已进行了众多的探讨和研究, 除了传统的误差较 主要可归纳总结如下㊂ 大且 实施繁琐 的配 线 法和 Jacob 直 线图 解 法外, 其 它
收稿日期:2014-04-26 基金项目:北京市西郊地区地下水战略储备关键技术研究与示范(Z141100003614060);水利部公益性行业科研专项经费项目 山洪灾害监测预警 系统标准化研究 (201201058) 作者简介:程先云 (1965-),男, 四川宜宾人, 工学博士, 高级工程师, 主要从事水信息研究㊂ E-mail:xycheng@
⎞ | | | | | | | | | | | | | ⎠
u>4
﹙
其中:G =exp(-γ),γ=0.5772156649015328606 ;
ɿ 26 1 • q ,q = 20 • h= + hɕ u 1+ q 47 1+u •ɿ u 2.3 Srivastava 方法[6]
31
b=
ɿ
﹙
﹚
﹚
(3)
误差 小 于 1E-10 的 高 精 度 数 值 解 , 以 此 结果 作 为参 表 3㊂ 照 目 标 值 检 验 上 述 不同 井 函 数 计算 方法的 精 度 , 见
u 高精度 级数 展开 W (u) 切比雪夫 Srivastava 拟合 方程 式(6) 式(7) Barry N=5 N=30
表3 不同方法井函数计算精度对比 Table3 Accurate comparsion of various methods for well function 10.9357198 10.9357195 10.9357195 10.9357198 10.9357198 10.9357198 9.46056389 10.9357198 1E-5 4.03792958 4.03792924 4.03792924 4.03783522 4.03792958 4.03787773 4.03792515 4.03793067 0.01 0.21938393 0.21958956 0.21938360 0.21927152 0.21938393 0.21938351 0.21938407 0.221 1
第3期
程先 云等:Theis 井 函数计算方法及井 模型 参数优 化计算研究
⎧ | | | | | | | | | | | ⎨ | | | | | | | | | | | ⎩
9 uɤ1
i i
2.1 级数展开
接得出其积分表达式,为便于数值计算,通常将其以无 穷级数形式展开,如下式: • u W (u)=-γ-ln(u)-ð (-1)n n • n! n=1
-i
2.2 Barry 方法 法,概要如下:
[5]
3,i
-i
Barry 于 2000 年提出了一种估计井函数 W (u)的方 G 1-G exp(-u)ln 1+ u ( h + b • u)2 W (u)= -u G +(1-G ) • exp 1-G
式中:p 1㊁p 2㊁p 3㊁q 1㊁q 2 和 q 3 为常数项系数, 具体值可参 考文献[7]㊂ 2.5 拟合方程替代 巩彦文[8]等提出 了 利用 拟 合 方程 来近 似计算 井 函 W (u)=18.109 • u0.256-31.310 • u0.16+13.482 (6)
2
Theis 井 模 型
表示为:
定流量非稳定流承压水完整井 Thies 井模 型可以 S=
ɕ i
其中:W (u)=
显 而 易 见 , 虽然国内外 还 有不 少 其 它 替 代 计算 方式 , 但都缺乏较为全面和系统的对比介绍㊂ 第二点是模型 参数估算, 虽然自行编程亦 可实现 , 但 由 于涉及 到 优 化和数值算法以及编程技巧, 对一般水文工作者而言 有相当难度, 而随着当今计算 软硬 件 的 快速 发 展 , 利 用成熟优化建模计算平台不失为一可用之道, 这类平 台林林总总㊁ 性能各异, 有的优化能力强但无内置井 函数计算函 数 , 如 Lingo㊁GAMS 等; 有的 井函 数为内 应用效果已被国内外各行业广大研究者认可㊂ 本研究 1stOpt 却可很好满足两者的要求, 使用上也非常简单, 置 函 数 , 但 优 化 能力 却 相对 较 弱 , 如 Matlab 等 ; 而
p 5 p• • p 8) u>1 1 exp(1+p• 2 u 3+p• 4 u +p• 6 ln(u))+p• 7 exp(u
uɤ1
(7)
10
4.3 3.8 3.3 2.8 2.3 1.8 1.3 0.8 0.3 -0.2
水 文
表2 拟合替代公式 (7) 系数表 Table2 The coefficient of regression function 序号 1 2 3 4
契比雪夫有理式逼近可用于高精度计算复杂函数
-ln(u)+
ðp •u ðq •u
i=0 1,i i=0 n1 1,i
n1
i
i
0<uΒιβλιοθήκη 1-1 0 1 2 u 3 4 5
N=9 N=11 N=10 N=8 N=6
• W (u)= exp(-u)
ðp
i=0 n2
⎛ | | | | | | | | | | | | | ⎝
式 中 :S 为 实 测 降 深 (m);Q 为 抽 水 流 量 (m3/d);T 为 承 压含水层导水系数(m2/d);W (u)为 Theis 井函数;us 为承
ʏ
exp(-x) dx,u= r2 • us x 4 • T • t
Q • W (u) 4 • π • T
(1)
压含水层贮水系数;t 为抽水时间(d);r 为观测 孔到抽 水井的距离(m)㊂ T 和 us, 难点之一是公式中的井函数 W (u)无解析解, 只 学上也叫指数积分函数 (ExpInt), 在水文地质中则常 根据抽 水 试 验 资料 和 模 型公式 (1)确定 模 型参数
0.564514611673438
5 6 7 8
Fig.2
图 2 拟合替代公式井函数计算示意图 The regression function for well function
