数列的概念练习题(有答案) 百度文库
高二数学数列专题练习题(含答案)

高二数学数列专题练习题(含答案)高中数学《数列》专题练1.数列基本概念已知数列的前n项和S_n和第n项a_n之间的关系为:a_n=S_n-S_{n-1} (n>1),当n=1时,a_1=S_1.通过这个关系式可以求出任意一项的值。
2.等差数列和等比数列等差数列和等比数列是两种常见的数列类型。
对于等差数列,有通项公式a_n=a_1+(n-1)d,其中d为公差。
对于等比数列,有通项公式a_n=a_1*q^{n-1},其中q为公比。
如果a、G、b成等比数列,那么G叫做a与b的等比中项。
如果a、A、b、B成等差数列,那么A、B叫做a、b的等差中项。
3.求和公式对于等差数列,前n项和S_n=n(a_1+a_n)/2.对于等比数列,前n项和S_n=a_1(1-q^n)/(1-q),其中q不等于1.另外,对于等差数列,S_n、S_{2n}-S_n、S_{3n}-S_{2n}构成等差数列;对于等比数列,S_n、S_{2n}/S_n、S_{3n}/S_{2n}构成等比数列。
4.数列的函数看法数列可以看作是一个函数,通常有以下几种形式:a_n=dn+(a_1-d),a_n=An^2+Bn+C,a_n=a_1q^n,a_n=k*n+b。
5.判定方法对于数列的常数项,可以使用定义法证明;对于等差中项,可以证明2a_n=a_{n-1}+a_{n+1};对于等比中项,可以证明2a_n=a_{n-1}*a_{n+1}。
最后,对于数列的通项公式,可以使用数学归纳法证明。
1.数列基本概念和通项公式数列是按照一定规律排列的一列数,通常用{ }表示。
其中,第n项表示为an,公差为d,公比为q。
常用的数列有等差数列和等比数列。
等差数列的通项公式为an = a1 + (n-1)d,其中a1为首项,d为公差。
等比数列的通项公式为an = a1q^(n-1),其中a1为首项,q为公比。
2.数列求和公式数列求和是指将数列中的所有项加起来的操作。
高二数学数列的概念试题答案及解析

高二数学数列的概念试题答案及解析1.已知数列满足,,且,则【答案】-6【解析】因为,所以由,可依次推得:【考点】数列递推公式2.数列,3,,,,…,则9是这个数列的第()A.12项B.13项C.14项D.15项【答案】C【解析】由数列的前五项可归纳出数列的通项公式为:令,化为:,得,所以,9是这个数列的第14项,故选C.【考点】数列的通项公式.3.已知数列的前n项和,则的值为( )A.80B.40C.20D.10【答案】C【解析】由数列前项和的定义有,所以正确答案选C.【考点】数列前项和概念.4.如果数列的前项和,那么这个数列的通项公式是 ( )A.B.C.D.【答案】D【解析】,,,即:.,解得:,故是以为首项,公比为的等比数列,所以故选D.【考点】数列的通项公式的求法5.已知数列满足(为常数,),若,则.【答案】126【解析】根据已知条件找到数列的特点,再去求解的值.所以是以公比为q的等比数列.又因为,所以应是递减数列.又因为所以所以所以【考点】数列求通项6.用火柴棒摆“金鱼”,如图所示:按照上面的规律,第个“金鱼”图需要火柴棒的根数为()A.B.C.D.【答案】C【解析】本题规律就是:每增加一个金鱼就增加6根火柴棒解:由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为C【考点】数列点评:本题是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律7.已知数列满足若则的值为()A.B.C.D.【答案】C【解析】因为所以,时,由此可以看出,是周期数列,周期为3,所以=,故选C。
【考点】本题主要考查数列的递推公式。
点评:简单题,递推公式随项的取值不同而不同,注意这一特征。
8.下列四个数中,哪一个是数列{}中的一项()A.380B.39C.35D. 23【答案】A【解析】分别让选项中的数值等于n(n+1),求出n是自然数时的这一项,就是符合要求的选项.解:由n(n+1)=380,有n=19.所以A正确; n(n+1)=39,n(n+1)=35,n(n+1)=23均无整数解,则B、C、D都不正确.故选A.【考点】数列的概念点评:数列的概念是高考中的热点,应充分重视.属于基础题.9.在数列1,1,2,3,5,8,x,21,34,55中,x等于()A.B.C.D.【答案】C【解析】从已知数列观察出特点:从第三项开始每一项是前两项的和即可求解∵数列1,1,2,3,5,8,x,21,34,55 设数列为{an }∴(n>3)∴x5+8=13故选C【考点】数列的概念点评:本题考查了数列的概念及简单表示法,是斐波那契数列,属于基础题.10.数列1,2,4,8,16,32,…的一个通项公式是()A.an =2n-1B.an=C.an=D.an=【答案】B【解析】观察此数列是首项是1,且是公比为2的等比数列,根据等比数列的通项公式求出此数列的一个通项公式.由于数列1,2,4,8,16,32,…的第一项是1,且是公比为2的等比数列,故通项公式是,故此数列的一个通项公式,故选B.【考点】数列的通项公式点评:根据数列的前几项归纳猜想其通项公式,这是数列的特点,就是猜想,注意找数字的与项的关系,得到结论。
高中数学选择性必修二 4 1 数列的概念(精练)(含答案)

4.1 数列的概念1.(2020·宜宾市南溪区第二中学校高一月考)已知数列28n na n =+,则数列{}n a 的第4项为( ) A .110B .16C .14 D .13【答案】B【解析】依题意4244148246a ===+.故选:B. 2.(2020·浙江鄞州·宁波诺丁汉附中高一期中)已知数列的通项公式是()()31{22n n n a n n +=-是奇数是偶数,则23⋅a a 等于( ) A .70 B .28C .20D .8【答案】C【解析】因为()()31{22n n n a n n +=-是奇数是偶数,所以,所以23⋅a a =20.故选C.3.(2020·广西田阳高中高一月考)已知数列的一个通项公式为()11312n n n n a +-+=-,则5a = ( ) A .12B .12-C .932D .932-【答案】A 【解析】()11312n n n n a +-+=-,则()51551531122a +-+=-=.故选:A. 4.(2020·广西田阳高中高一月考)已知数列2,5,22,11…,则25是这个数列的( ) A .第六项 B .第七项C .第八项D .第九项【答案】B题组一 根据通项求项【解析】由数列前几项归纳可知通项公式为n a =,=时,7n =,为数列第七项,故选B.5.(2020·浙江鄞州·宁波咸祥中学高一期中)已知数列{}n a 的通项公式为22n a n n =+,则10(a = )A .100B .110C .120D .130【答案】C【解析】数列{}n a 的通项公式为22n a n n =+,则21010210120a =+⨯=.故选:C.6.(2020·四川高一期中)已知数列{}n a 的通项公式是1(2)2n a n n =+,则220是这个数列的( ) A .第19项 B .第20项 C .第21项D .第22项【答案】B【解析】由题意,令1(2)2202n n +=,则(2)440n n +=,解得20n =或22n =-; 因为*n N ∈,所以20n =,即220是这个数列的第20项.故选:B.7.(2020·四川省苍溪实验中学校高一期中)已知数列2,4,……,则8是该数列的第________项 【答案】118=,解得11n =,所以8是该数列的第11项,故答案为:11.8.(2020·上海高二课时练习)在数列{}n a 中,已知()*cos2n n a n N π=∈,则{}n a 的前6项分别为______. 【答案】0,1,0,1,0,1--【解析】易得1cos02a π==,2cos 1a π==-,33cos02a π==,4cos 21a π==,55cos 02a π==,66cos12a π==-.故答案为:0,1,0,1,0,1-- 9.(2020·上海高二课时练习)已知数列{}n a 的通项公式为1(2)n a n n =+,那么199是这数列的第_____项.【答案】9【解析】令11(2)99n n =+,即22990n n +-=,解得9n =或11-(舍去),则199是这数列的第9项,故答案为: 9. 10.(2020·上海高二课时练习)数列{}n a 中,1003n a n =-(*n N ∈),该数列从第_____项开始每项均为负值. 【答案】34【解析】令10030n a n =-<,解不等式得:1003n >,由于*n N ∈,故34n =.故答案为:34.1.(2020·江西高一月考)数列3579,,,24816--,…的一个通项公式为( ) A .()n n n n21a 12+=-⋅ B .()nn n 2n 1a 12+=-⋅C .()n n 1n n 21a 12++=-⋅ D .()n 1n n2n 1a 12++=-⋅【答案】D【解析】根据分子、分母还有正负号的变化,可知,()12112n n nn a ++=-⋅.故选D. 题组二 根据项写通项2.(2020·四川双流·艺体中学)数列2,43,85,167,329…的一个通项公式a n 等于( ) A .221nn -B .2n nC .221nn -D .221nn +【答案】C【解析】数列2,43,85,167,329… 可写成:12211⨯-,22221⨯-,32231⨯-,42241⨯-,52251⨯-… 所以通项公式a n 2=21nn -.故选C. 3.(2020·上海市杨浦高级中学)已知数列1、0、1、0、,可猜想此数列的通项公式是( ).A .()()1*11n n a n N -⎡⎤=+-∈⎣⎦B .()()*1112nn a n N ⎡⎤=+-∈⎣⎦C .()()()()1*111122n n a n n n N +⎡⎤=+-+--∈⎣⎦ D .()()*11cos 2n a n n N π=-∈【答案】D【解析】对于A 选项,()011121a =+-=≠,不合乎题意; 对于B 选项,()1111012a =⨯-=≠,不合乎题意; 对于C 选项,()4311121312a ⎡⎤=⨯+-+⨯=≠⎣⎦,不合乎题意;对于D 选项,当n 为奇数时,cos 1n π=-,此时()11112n a =⨯+=, 当n 为偶数时,cos 1n π=,此时()11102n a =⨯-=,合乎题意. 故选:D.4.(2018·吉林宽城·长春市养正高中高一期中)根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式n a =__________.【答案】54n -【解析】第一图点数是1;第二图点数6=1+5 ;第三图是11=1+25 ;第四图是16=1+35 则第n 个图点数=1+(n-1)554n a n 故答案为:54n -5.(2019·山东东营·)已知数列{}n a 的前4项依次为23,45-,67,89-,试写出数列{}n a 的一个通项公式n a =______.【答案】12(1)21n nn +-+ 【解析】2,4,6,8,的通项公式为2n ,3,5,7,9,的通项公式为21n , 正负交替的通项公式为1(1)n +-,所以数列{}n a 的通项公式12(1)21n n n a n +=-+.故答案为:12(1)21n n n +-+ 6.(2020·全国高一课时练习)写出下列各数列的一个通项公式,使它的前几项分别是下列各数: (1)5784,,2,,,245--⋯(2)246810,,,,,315356399(3)5,55,555,5555,(4)2,0,2,0,2,0,【答案】(1)()131n n n a n ++=-;(2)()2221n n a n =-;(3)()51019n na =-;(4)()111n n a -=+- 【解析】解(1)考虑到第2,4项的分母恰好是所在项的序号, 于是这个数列的前4项可以改写成4567,,,1234--, 这4项的分母都与项的序号相同,分子都恰好是序号加3,且奇数项为正,偶数项为负, 所以它的一个通项公式为()131n n n a n++=-. (2)考虑到分子2,4,6,8,10恰好是序号的2倍,所以分子应为2n .分母22222321,1541,3561,6381,99101=-=-=-=-=-都为分子的平方数减去1,因此它的一个通项公式为()2221n na n =-.(3)这个数列的第n 项可以是n 个5组成的n 位数555n n a ↑=,用代数式替代省略号,可考虑前4项改写成55559,99,999,99999999⨯⨯⨯⨯,其中9999999999,,,又可表示成1234101,101,101,101----, 这里的10的正整数次幂的指数恰好与数列中项的序号相等, 所以它的一个通项公式为()51019n n a =-. (4)211,011=+=-,考虑到其每一项与序号的关系将前几项分别写成:()()()()012311,11,11,11+-+-+-+-, 因此它的一个通项公式为()111n n a -=+-.1.(2020·眉山市东坡区多悦高级中学校高一期中)在数列{}n a 中,已知11a =,25a =,()*21n n n a a a n N ++=-∈,则5a 等于( )A .4-B .5-C .4D .5【答案】B【解析】由()*21n n n a a a n N++=-∈知:3214a a a 4321a a a 5435a a a故选:B2.(2020·自贡市第十四中学校高一期中)数列3,7,11,15,的一个通项公式是( )A .41n a n =+B .21n a n =+C .41n a n =-D .21n a n =-【答案】C【解析】因为数列3,7,11,15⋯的一个通项公式为41n -,故数列3,7,11,15,⋯的一个通项公式是41n a n =-,故选:C . 3.(2019·河北廊坊·高一期末)数列{}n a 的前几项为11121,3,,8,222,则此数列的通项可能是( )A .542n n a -=B .322n n a -=C .652n n a -=D .1092n n a -=【答案】A题组三 根据递推公式求项【解析】数列为16111621,,,,22222其分母为2,分子是首项为1,公差为5的等比数列,故通项公式为542n n a -=. 4.(2020·安徽黄山·高一期末)数列1111,,,,...24816--的一个通项公式是( ) A .1(1)2+-n nB .(1)2-n nC .sin 2nn πD .cos(1)2nn π+【答案】B 【解析】()111122-=-⨯,()2211142=-⨯,()3311182-=-⨯,()44111162=-⨯ 所以其通项公式是:(1)2-nn 故选:B5.(2020·武汉外国语学校高一月考)数列4,6,10,18,34,……的通项公式n a 等于( ) A .12n + B .21n + C .22n + D .22n +【答案】C【解析】234521134522,22,22,22,22a a a a a =+=+=+=+=+22n n a ∴=+故选:C6.(2020·浙江越城·绍兴一中期中)在数列{}n a 中,()1111,1(2)nnn a a n a --==+≥,则5a 等于A .32B .53C .85D .23【答案】D【解析】已知1a 逐一求解2345122323a a a a ====,,,.故选D7.(2020·吉林前郭尔罗斯县第五中学高一期中)数列12-,2,92-,8,252-,…它的一个通项公式可以是( )A .()212nn n a =-B .()2112n n n a +=- C .22n n a =D .1n n a n =-+ 【答案】A【解析】将1n =代入四个选项可得A 为12-,B 为12,C 为12,D 为12-.所以排除B 、C 选项. 将2n =代入A 、D,得A 为2,D 为23-,所以排除D 综上可知,A 可以是一个通项公式故选:A 8.(2019·息县第一高级中学高二月考(文))数列1-,3,7-,15,…的一个通项公式可以是( ) A .()(1)21nnn a =-⋅- B .(1)(21)nn a n =-⋅- C .()1(1)21n n n a +=-⋅-D .1(1)(21)n n a n +=-⋅-【答案】A【解析】将1n =代入四个选项,可知C 中11,a =D 中11,a =所以排除C 、D.当3n =,代入B 可得35,a =-所以排除B ,即A 正确,故选:A.9.(2018·安徽六安一中高一期末(文))已知*n N ∈,给出4个表达式:①0,1,n n a n ⎧=⎨⎩为奇数为偶数,②1(1)2n n a +-=,③1cos 2n n a π+=,④sin 2n n a π=.其中能作为数列:0,1,0,1,0,1,0,1,…的通项公式的是( ) A .①②③ B .①②④C .②③④D .①③④【答案】A【解析】①②③逐一写出为010101,,,,,可以,④逐一写出为1010101,,,,,,不满足,故选A .10.(2020·湖北十堰·高一期末)数列1111,,,57911--,…的通项公式可能是n a =( ) A .1(1)23n n --+B .(1)32nn -+C .1(1)32n n --+D .(1)23nn -+【答案】D【解析】由115a =-,排除A ,C ,由217a =,排除B.故选:D.11.(2020·金华市曙光学校高一开学考试)数列1-,3,5-,7,9-,,的一个通项公式为( )A .21n a n =-B .(1)(12)nn a n =-- C .(1)(21)nn a n =--D .1(1)(21)n n a n +=--【答案】C【解析】∵数列{a n }各项值为1-,3,5-,7,9-,,∴各项绝对值构成一个以1为首项,以2为公差的等差数列,∴|a n |=2n ﹣1 又∵数列的奇数项为负,偶数项为正,∴a n =(﹣1)n (2n ﹣1).故选C .1.(2019·云南东川明月中学高一期中)数列{}n a 的前n 项和21n S n n =++,则{}n a 的通项公式n a = _____.【答案】()()3122n nn ⎧=⎪⎨≥⎪⎩ 【解析】当1n =时,113a S ==;题组四 公式法求通项当2n ≥时,()()()22111112n n n a S S n n n n n -⎡⎤=-=++--+-+=⎣⎦; ∴()()3122n n a n n ⎧=⎪=⎨≥⎪⎩故答案为()()3122n n n ⎧=⎪⎨≥⎪⎩2.(2019·湖南岳阳)已知数列{}n a ,若1222n a a na n +++=,则数列{}1n n a a +的前n 项和为__________. 【答案】41n n + 【解析】因为122++2n a a na n +⋯=所以1212++12n 1n a a n a ()()-+⋯-=- 两式相减得2n na =所以2n a n=设数列{}1n n a a +的前n 项和为S n 则1223342111n n n n n n n S a a a a a a a a a a a a ---+=+++⋅⋅⋅++2222222222221223342111n n n n n n =⨯+⨯+⨯+⋅⋅⋅⨯+⨯+⨯---+ 1111111111141223342111n n n n n n ⎛⎫=-+-+-+⋅⋅⋅-+-+- ⎪---+⎝⎭ 144111n n n ⎛⎫=-= ⎪++⎝⎭3.(2020·上海市金山中学期中)已知数列{}n a 的前n 项和2231n S n n =-+,则n a =__________.【答案】0,145,2n n a n n =⎧=⎨-≥⎩【解析】当1n =时,110a S ==当2n ≥时,由2231n S n n =-+,得212(1)3(1)1n S n n -=---+,两式相减,145n n n a S S n -=-=-,将1n =代入上式,110a =-≠,∴通项公式为0,145,2n n a n n =⎧=⎨-≥⎩故答案为0,145,2n n a n n =⎧=⎨-≥⎩. 4.(2019·黑龙江哈尔滨市第六中学校期中)已知数列{}n a 前n 项和为n S ,且2n S n =,则n a =_______【答案】21n -.【解析】当1n =时,111a S ==当2n ≥且*n N ∈时,()221121n n n a S S n n n -=-=--=-综上所述:21n a n =-,*n N ∈本题正确结果:21n -5.(2020·河北石家庄·辛集中学)在数列{}n a 中,已知其前n 项和为23n n S =+,则n a =__________. 【答案】15,12,2n n n a n -=⎧=⎨≥⎩【解析】当2n ≥时,111(23)(23)2n n n n n n a S S ---=-=+-+=;当1n =时,11235a S ==+=,不满足上式。
高中数学试题含答案-课时规范练28 数列的概念

课时规范练28数列的概念基础巩固组1.已知数列√5,√11,√17,√23,√29,…,则5√5是它的()A.第19项B.第20项C.第21项D.第22项2.记S n为数列{a n}的前n项和.“任意正整数n,均有a n>0”是“数列{S n}是递增数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(多选)已知数列{a n}满足a n+1=1-1a n(n∈N*),且a1=2,则()A.a3=-1B.a2 019=12C.S6=3D.2S2 019=2 0194.(2020河北保定高三期末)在数列{a n}中,若a1=1,a2=3,a n+2=a n+1-a n(n∈N*),则该数列的前100项之和是() A.18 B.8 C.5 D.25.(多选)已知数列{a n}:12,13+23,14+24+34,…,110+210+310+…+910,…,若b n=1a n·a n+1,设数列{b n}的前n项和为S n,则()A.a n=n2B.a n=nC.S n=4nn+1D.S n=5nn+16.(2020湖南益阳高三期末)已知{a n}是等差数列,且满足:对∀n∈N*,a n+a n+1=2n,则数列{a n}的通项公式a n=() A.n B.n-1C.n-12D.n+127.已知数列{a n}的首项a1=21,且满足(2n-5)a n+1=(2n-3)a n+4n2-16n+15,则数列{a n}的最小的一项是()A.a5B.a6C.a7D.a88.已知每项均大于零的数列{a n},首项a1=1且前n项和S n满足S n√S n-1-S n-1√S n=2√S n S n-1(n∈N*且n≥2),则a81=()A.638B.639C.640D.6419.设S n为数列{a n}的前n项和,且a1=4,a n+1=S n,n∈N*,则S4=.10.在数列{a n}中,a1=2,a n+1n+1=a nn+ln1+1n,则a n=.11.已知数列{a n}的通项公式为a n=n+13n-16(n∈N*),则数列{a n}的最小项是第项.12.已知数列{a n}满足a1=3,a n+1=4a n+3.(1)写出该数列的前4项,并归纳出数列{a n}的通项公式;公众号:一枚试卷君(2)证明:a n+1+1a n+1=4.综合提升组13.(2020广东中山期末)设数列{a n}的前n项和为S n,且a1=1,{S n+na n}为常数列,则a n=()A.13n-1B.2 n(n+1)C.1(n+1)(n+2)D.5-2n314.(2020安徽江淮十校第三次联考)已知数列{a n}满足a n+1-a nn =2,a1=20,则a nn的最小值为()A.4√5B.4√5-1C.8D.915.(多选)(2020江西赣州教育发展联盟2月联考)已知数列{a n}的前n项和为S n(S n≠0),且满足a n+4S n-1S n=0(n≥2),a1=14,则下列说法正确的是()A.数列{a n}的前n项和为S n=14nB.数列{a n}的通项公式为a n=14n(n+1)C.数列{a n}为递增数列D.数列1S n为递增数列创新应用组16.已知数列{a n}的前n项和为S n,a1=a,a n+1=S n+3n,若a n+1≥a n对∀n∈N*成立,则实数a的取值范围是.17.已知二次函数f(x)=x2-ax+a(a>0,x∈R)有且只有一个零点,数列{a n}的前n项和S n=f(n)(n∈N*).(1)求数列{a n}的通项公式;(2)设c n=1-4a n (n∈N*),定义所有满足c m·c m+1<0的正整数m的个数,称为这个数列{c n}的变号数,求数列{c n}的变号数.参考答案课时规范练28 数列的概念1.C 数列√5,√11,√17,√23,√29,…,中的各项可变形为√5,√5+6,√5+2×6,√5+3×6,√5+4×6,…,所以通项公式为a n =√5+6(n -1)=√6n -1,令√6n -1=5√5,得n=21.2.A ∵a n >0,∴数列{S n }是递增数列,∴“a n >0”是“数列{S n }是递增数列”的充分条件.如数列{a n }为-1,1,3,5,7,9,…,显然数列{S n }是递增数列,但是a n 不一定大于零,还有可能小于零, ∴数列{S n }是递增数列不能推出a n >0.∴“a n >0”是“数列{S n }是递增数列”的不必要条件. ∴“任意正整数n ,均有a n >0”是“数列{S n }是递增数列”的充分不必要条件.3.ACD 数列{a n }满足a 1=2,a n +1=1-1a n(n ∈N *),可得a 2=12,a 3=-1,a 4=2,a 5=12,…,所以a n+3=a n ,数列的周期为3,a 2 019=a 672×3+3=a 3=-1,S 6=3,S 2 019=2 0192. 4.C ∵a 1=1,a 2=3,a n +2=a n +1-a n (n ∈N *),∴a 3=3-1=2, a 4=2-3=-1, a 5=-1-2=-3, a 6=-3+1=-2, a 7=-2+3=1, a 8=1+2=3, a 9=3-1=2, …∴{a n }是周期为6的周期数列,∴S 100=S 16×6+4=16×(1+3+2-1-3-2)+(1+3+2-1)=5.故选C. 5.AC 由题意得a n =1n+1+2n+1+…+nn+1=1+2+3+…+nn+1=n2,∴b n =1n 2·n+12=4n (n+1)=41n −1n+1,∴数列{b n }的前n 项和S n =b 1+b 2+b 3+…+b n =41-12+12−13+13−14+…+1n −1n+1=41-1n+1=4nn+1.故选AC.6.C 由a n +a n+1=2n ,得a n+1+a n+2=2n+2,两式相减得a n+2-a n =2=2d ,∴d=1,又a n +a n +d=2n ,∴a n =n-12.故选C .7.A ∵4n 2-16n+15=(2n-3)(2n-5),∴(2n-5)a n+1=(2n-3)a n +(2n-3)(2n-5), 等式两边同时除以(2n-3)(2n-5),可得a n+12n -3=a n2n -5+1, 可设b n =a n 2n -5,则b n+1=an+12n -3, ∴b n+1=b n +1,即b n+1-b n =1.∵b 1=a 12×1-5=21-3=-7, ∴数列{b n }是以-7为首项,1为公差的等差数列. ∴b n =-7+(n-1)×1=n-8,n ∈N *.∴a n =(n-8)(2n-5)=2n 2-21n+40.可把a n 看成关于n 的二次函数,则根据二次函数的性质,可知其对称轴n=10.52=5.25. ∴当n=5时,a n 取得最小值.故选A .8.C 已知S n √S n -1-S n-1√S n =2√S n S n -1,数列{a n }的每项均大于零,故等号两边同时除以√S n S n -1,可得√S n −√S n -1=2,∴{√S n }是以1为首项,2为公差的等差数列,故√S n =2n-1,S n =(2n-1)2,∴a 81=S 81-S 80=1612-1592=640.故选C .9.32 因为S n 为数列{a n }的前n 项和,且a 1=4,a n+1=S n ,n ∈N *, ① 则当n ≥2时,a n =S n-1, ②由①-②得a n+1-a n =a n ,∴an+1a n=2,则数列{a n }是从第二项起,公比为2的等比数列,又a 2=S 1=4,∴a n =4·2n-2=2n (n ≥2),故a n ={4(n =1),2n (n ≥2).所以S 4=a 5=25=32.10.2n+n ln n 由题意得a n+1n+1−a n n =ln(n+1)-ln n ,a n n −an -1n -1=ln n-ln(n-1)(n ≥2). ∴a 22−a 11=ln 2-ln 1,a 33−a22=ln 3-ln 2,…,a n n−an -1n -1=ln n-ln(n-1)(n ≥2). 累加得a n n −a 11=ln n ,又a 1=2,∴a nn =2+ln n (n ≥2),当n=1时,a 1=2,上式成立,故a n =2n+n ln n. 11.5 a n =n+13n -16=131+193n -16.当n>5时,a n >0,且单调递减, 当n ≤5时,a n <0,且单调递减. ∴当n=5时,a n 最小.12.(1)解 a 1=3,a 2=15,a 3=63,a 4=255.因为a 1=41-1,a 2=42-1,a 3=43-1,a 4=44-1,…, 所以归纳得a n =4n -1. (2)证明 因为a n +1=4a n +3,所以a n+1+1a n +1=4a n +3+1a n +1=4(a n +1)a n +1=4. 13.B ∵数列{a n }的前n 项和为S n ,且a 1=1,∴S 1+1×a 1=1+1=2.∵{S n +na n }为常数列,∴S n +na n =2.当n ≥2时,S n-1+(n-1)a n-1=2,∴(n+1)a n =(n-1)a n-1,从而a 2a 1·a 3a 2·a 4a 3·…·a n a n -1=13·24·35·…·n -1n+1,∴a n =2n (n+1)(n ≥2),当n=1时上式成立,∴a n =2n (n+1).故选B . 14.C 由a n +1-a n =2n ,知a 2-a 1=2×1,a 3-a 2=2×2,…,a n -a n -1=2(n-1),n ≥2.以上各式相加得a n -a 1=n 2-n ,n ≥2,所以a n =n 2-n+20,n ≥2, 当n=1时,a 1=20符合上式,所以a n n =n+20n-1,n ∈N *, 所以当n ≤4时,a n n单调递减,当n ≥5时,a n n单调递增.因为a 44=a55=8,所以ann 的最小值为8.故选C .15.AD 由题意,可知数列{a n }的前n 项和为S n (S n ≠0),且满足a n +4S n-1S n =0(n ≥2),则S n -S n-1=-4S n-1S n (n ≥2),即1S n−1S n -1=4(n ≥2).又因为a 1=14,所以1S 1=4,所以数列1S n是以4为首项,4为公差的等差数列,所以数列1S n为递增数列,且1S n=4+(n-1)×4=4n ,则S n =14n .又因为当n ≥2时,a n =S n -S n-1=14n −14(n -1)=-14n (n -1),a 1=14,所以数列{a n }的通项公式为a n ={14,n =1,-14n (n -1),n ≥2.故选AD. 16.[-9,+∞) 据题意,得a n+1=S n+1-S n =S n +3n ,∴S n+1=2S n +3n ,∴S n+1-3n+1=2(S n -3n ).又S 1-31=a-3,∴数列{S n -3n }是以a-3为首项,2为公比的等比数列,∴S n -3n =(a-3)·2n-1即S n =3n +(a-3)·2n-1.当n=1时,a 1=a ;当n ≥2时,a n =S n -S n-1=3n +(a-3)×2n-1-3n-1-(a-3)×2n-2=2×3n-1+(a-3)×2n-2,∴a n+1-a n =4×3n-1+(a-3)×2n-2.又当n ≥2时,a n+1≥a n 恒成立,∴a ≥3-12×(32)n -2对∀n ∈N *,且n ≥2成立,∴a ≥-9.又a 2=a 1+3,∴a 2≥a 1成立.综上,所求实数a 的取值范围是[-9,+∞).17.解 (1)依题意,得Δ=a 2-4a=0,所以a=0或a=4.又由a>0得a=4,所以f (x )=x 2-4x+4. 所以S n =n 2-4n+4. 当n=1时,a 1=S 1=1-4+4=1; 当n ≥2时,a n =S n -S n -1=2n-5.所以数列{a n }的通项公式为a n ={1,n =1,2n -5,n ≥2.(2)由题意得c n ={-3,n =1,1-42n -5,n ≥2.由c n =1-42n -5可知,当n ≥5时,恒有c n >0. 又因为c 1=-3,c 2=5,c 3=-3, c 4=-13,c 5=15,即c 1·c 2<0,c 2·c 3<0,c 4·c 5<0, 所以数列{c n }的变号数为3.。
高一数列的概念及简单表示方法知识点+例题+练习 含答案
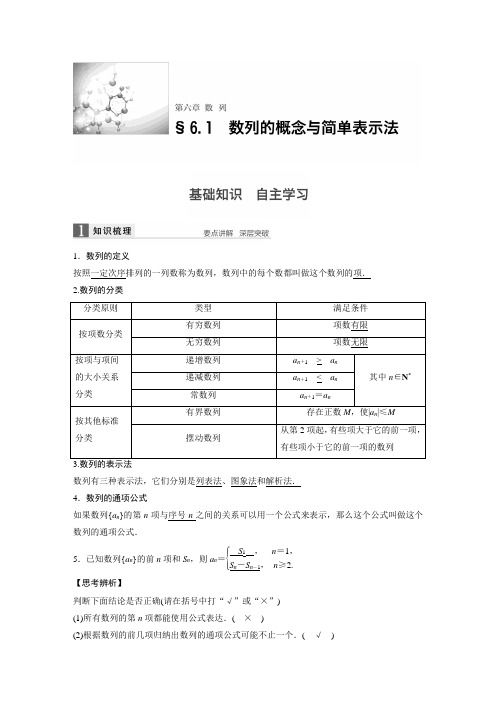
1.数列的定义按照一定次序排列的一列数称为数列,数列中的每个数都叫做这个数列的项. 2.数列的分类 分类原则 类型 满足条件 按项数分类 有穷数列 项数有限 无穷数列 项数无限按项与项间的大小关系分类 递增数列 a n +1__>__a n 其中n ∈N *递减数列 a n +1__<__a n 常数列 a n +1=a n按其他标准分类有界数列 存在正数M ,使|a n |≤M 摆动数列从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列数列有三种表示法,它们分别是列表法、图象法和解析法. 4.数列的通项公式如果数列{a n }的第n 项与序号n 之间的关系可以用一个公式来表示,那么这个公式叫做这个数列的通项公式.5.已知数列{a n }的前n 项和S n ,则a n =⎩⎪⎨⎪⎧S 1 , n =1,S n -S n -1, n ≥2.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)所有数列的第n 项都能使用公式表达.( × )(2)根据数列的前几项归纳出数列的通项公式可能不止一个.( √ )(3)1,1,1,1,…,不能构成一个数列.( × )(4)任何一个数列不是递增数列,就是递减数列.( × )(5)如果数列{a n }的前n 项和为S n ,则对∀n ∈N *,都有a n +1=S n +1-S n .( √ ) (6)在数列{a n }中,对于任意正整数m ,n ,a m +n =a mn +1,若a 1=1,则a 2=2.( √ )1.已知数列{a n }中,a 1=1,1a n +1=1a n +3 (n ∈N *),则a 10=________. 答案128解析 由题意得1a n +1-1a n=3.∴1a 2-1a 1=3,1a 3-1a 2=3,1a 4-1a 3=3,1a 5-1a 4=3,…,1a 10-1a 9=3,对递推式叠加得1a 10-1a 1=27,故a 10=128.2.把1,3,6,10,15,21,…这些数叫做三角形数,这是因为用这些数目的点可以排成一个正三角形(如图).则第7个三角形数是________. 答案 28解析 根据三角形数的增长规律可知第七个三角形数是1+2+3+4+5+6+7=28. 3.数列{a n }的前n 项和记为S n ,a 1=1,a n +1=2S n +1 (n ≥1,n ∈N *),则数列{a n }的通项公式是__________. 答案 a n =3n -1解析 由a n +1=2S n +1可得a n =2S n -1+1 (n ≥2),两式相减得a n +1-a n =2a n ,即a n +1=3a n (n ≥2).又a 2=2S 1+1=3,a 3=3·a 2=32·a 1=32, a 4=3a 3=33… a n =3a n -1=3n -1.4.(教材改编)根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式a n =________.答案 5n -45.已知数列{a n }的前n 项和S n =n 2+1,则a n =________.答案 ⎩⎪⎨⎪⎧2,n =1,2n -1,n ≥2解析 当n =1时,a 1=S 1=2,当n ≥2时, a n =S n -S n -1=n 2+1-[(n -1)2+1]=2n -1,故a n =⎩⎪⎨⎪⎧2,n =1,2n -1,n ≥2.题型一 由数列的前几项求数列的通项公式例1 (1)数列0,23,45,67,…的一个通项公式为________.①a n =n -1n +1(n ∈N *) ②a n =n -12n +1(n ∈N *)③a n =2(n -1)2n -1(n ∈N *) ④a n =2n 2n +1(n ∈N *)(2)数列{a n }的前4项是32,1,710,917,则这个数列的一个通项公式是a n =________.答案 (1)③ (2)2n +1n 2+1解析 (1)注意到分母0,2,4,6都是偶数,对照所给项排除即可.(2)数列{a n }的前4项可变形为2×1+112+1,2×2+122+1,2×3+132+1,2×4+142+1,故a n =2n +1n 2+1.思维升华 根据所给数列的前几项求其通项时,需仔细观察分析,抓住其几方面的特征:分式中分子、分母的各自特征;相邻项的联系特征;拆项后的各部分特征;符号特征.应多进行对比、分析,从整体到局部多角度观察、归纳、联想.根据数列的前几项,写出下列各数列的一个通项公式.(1)-1,7,-13,19,…; (2)0.8,0.88,0.888,…;(3)12,14,-58,1316,-2932,6164,…. 解 (1)数列中各项的符号可通过(-1)n 表示,从第2项起,每一项的绝对值总比它的前一项的绝对值大6,故通项公式为a n =(-1)n (6n -5). (2)数列变为89⎝⎛⎭⎫1-110,89⎝⎛⎭⎫1-1102,89⎝⎛⎭⎫1-1103,…, 故a n =89⎝⎛⎭⎫1-110n . (3)各项的分母分别为21,22,23,24,…,易看出第2,3,4项的分子分别比分母小3. 因此把第1项变为-2-32,原数列化为-21-321,22-322,-23-323,24-324,…,故a n =(-1)n 2n -32n .题型二 由数列的前n 项和求数列的通项公式例2 设数列{a n }的前n 项和为S n ,数列{S n }的前n 项和为T n ,满足T n =2S n -n 2,n ∈N *. (1)求a 1的值;(2)求数列{a n }的通项公式. 解 (1)令n =1时,T 1=2S 1-1,因为T 1=S 1=a 1,所以a 1=2a 1-1,所以a 1=1. (2)n ≥2时,T n -1=2S n -1-(n -1)2, 则S n =T n -T n -1=2S n -n 2-[2S n -1-(n -1)2] =2(S n -S n -1)-2n +1=2a n -2n +1. 因为当n =1时,a 1=S 1=1也满足上式, 所以S n =2a n -2n +1(n ≥1),当n ≥2时,S n -1=2a n -1-2(n -1)+1, 两式相减得a n =2a n -2a n -1-2,所以a n =2a n -1+2(n ≥2),所以a n +2=2(a n -1+2), 因为a 1+2=3≠0,所以数列{a n +2}是以3为首项,公比为2的等比数列. 所以a n +2=3×2n -1,所以a n =3×2n -1-2, 当n =1时也成立, 所以a n =3×2n -1-2.思维升华 数列的通项a n 与前n 项和S n 的关系是a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2.当n =1时,a 1若适合S n -S n -1,则n =1的情况可并入n ≥2时的通项a n ;当n =1时,a 1若不适合S n -S n -1,则用分段函数的形式表示.(1)已知数列{a n }的前n 项和S n =n +1n +2,则a 4=________.(2)已知数列{a n }的前n 项和S n =3n 2-2n +1,则其通项公式为________________.答案 (1)130 (2)a n =⎩⎪⎨⎪⎧2,n =1,6n -5,n ≥2解析 (1)a 4=S 4-S 3 =56-45=130. (2)当n =1时,a 1=S 1=3×12-2×1+1=2; 当n ≥2时,a n =S n -S n -1=3n 2-2n +1-[3(n -1)2-2(n -1)+1] =6n -5,显然当n =1时,不满足上式.故数列的通项公式为a n =⎩⎪⎨⎪⎧2,n =1,6n -5,n ≥2.题型三 由数列的递推关系求通项公式例3 (1)设数列{a n }中,a 1=2,a n +1=a n +n +1,则通项a n =________. (2)数列{a n }中,a 1=1,a n +1=3a n +2,则它的一个通项公式为a n =________. 答案 (1)n (n +1)2+1 (2)2×3n -1-1解析 (1)由题意得,当n ≥2时, a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =2+(2+3+…+n )=2+(n -1)(2+n )2=n (n +1)2+1.又a 1=2=1×(1+1)2+1,符合上式,因此a n =n (n +1)2+1.(2)方法一 (累乘法)a n +1=3a n +2,即a n +1+1=3(a n +1), 即a n +1+1a n +1=3, 所以a 2+1a 1+1=3,a 3+1a 2+1=3,a 4+1a 3+1=3,…,a n +1+1a n +1=3.将这些等式两边分别相乘得a n +1+1a 1+1=3n .因为a 1=1,所以a n +1+11+1=3n ,即a n +1=2×3n -1(n ≥1), 所以a n =2×3n -1-1(n ≥2), 又a 1=1也满足上式,故数列{a n }的一个通项公式为a n =2×3n -1-1. 方法二 (迭代法) a n +1=3a n +2,即a n +1+1=3(a n +1)=32(a n -1+1)=33(a n -2+1) =…=3n (a 1+1)=2×3n (n ≥1), 所以a n =2×3n -1-1(n ≥2), 又a 1=1也满足上式,故数列{a n }的一个通项公式为a n =2×3n -1-1.思维升华 已知数列的递推关系,求数列的通项时,通常用累加、累乘、构造法求解. 当出现a n =a n -1+m 时,构造等差数列;当出现a n =xa n -1+y 时,构造等比数列;当出现a n =a n -1+f (n )时,用累加法求解;当出现a na n -1=f (n )时,用累乘法求解.(1)已知数列{a n }满足a 1=1,a n =n -1n·a n -1(n ≥2),则a n =________.(2)已知数列{a n }的前n 项和为S n ,且S n =2a n -1(n ∈N *),则a 5=________. 答案 (1)1n(2)16解析 (1)∵a n =n -1n a n -1 (n ≥2),∴a n -1=n -2n -1a n -2,…,a 2=12a 1.以上(n -1)个式子相乘得 a n =a 1·12·23·…·n -1n =a 1n =1n .当n =1时也满足此等式,∴a n =1n .(2)当n =1时,S 1=2a 1-1,∴a 1=1. 当n ≥2时,S n -1=2a n -1-1, ∴a n =2a n -2a n -1,∴a n =2a n -1. ∴{a n }是等比数列且a 1=1,q =2, 故a 5=a 1×q 4=24=16.题型四 数列的性质命题点1 数列的单调性例4 已知数列{a n }的前n 项和S n =n 2+1,数列{b n }满足b n =2a n +1,且前n 项和为T n ,设c n =T 2n +1-T n .(1)求数列{b n }的通项公式; (2)判断数列{c n }的增减性.解 (1)a 1=2,a n =S n -S n -1=2n -1(n ≥2).∵b n =2a n +1,∴b n =⎩⎨⎧23,n =1,1n , n ≥2,n ∈N *.(2)∵c n =b n +1+b n +2+…+b 2n +1 =1n +1+1n +2+…+12n +1, ∴c n +1-c n =12n +2+12n +3-1n +1=12n +3-12n +2=-1(2n +3)(2n +2)<0, ∴c n +1<c n .∴数列{c n }为递减数列. 命题点2 数列的周期性例5 数列{a n }满足a n +1=11-a n ,a 8=2,则a 1=_____________________________________.答案 12解析 ∵a n +1=11-a n,∴a n +1=11-a n =11-11-a n -1=1-a n -11-a n -1-1=1-a n -1-a n -1=1-1a n -1=1-111-a n -2=1-(1-a n -2)=a n -2, ∴周期T =(n +1)-(n -2)=3. ∴a 8=a 3×2+2=a 2=2. 而a 2=11-a 1,∴a 1=12.命题点3 数列的最值例6 数列{a n }的通项a n =nn 2+90,则数列{a n }中的最大项的值是________.答案119解析 令f (x )=x +90x (x >0),运用基本不等式得,f (x )≥290当且仅当x =310时等号成立.因为a n =1n +90n ,所以1n +90n ≤1290,由于n ∈N *,不难发现当n =9或10时,a n =119最大.思维升华 1.解决数列的单调性问题可用以下三种方法(1)用作差比较法,根据a n +1-a n 的符号判断数列{a n }是递增数列、递减数列或是常数列. (2)用作商比较法,根据a n +1a n (a n >0或a n <0)与1的大小关系进行判断.(3)结合相应函数的图象直观判断. 2.解决数列周期性问题的方法先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值. 3.数列的最值可以利用数列的单调性或求函数最值的思想求解.(1)数列{a n }满足a n +1=⎩⎨⎧2a n ,0≤a n ≤12,2a n-1,12<a n<1,a 1=35,则数列的第2 015项为________.(2)设a n =-3n 2+15n -18,则数列{a n }中的最大项的值是________. 答案 (1)25(2)0解析 (1)由已知可得,a 2=2×35-1=15,a 3=2×15=25,a 4=2×25=45,a 5=2×45-1=35,∴{a n }为周期数列且T =4, ∴a 2 015=a 3=25.(2)∵a n =-3⎝⎛⎭⎫n -522+34,由二次函数性质,得当n =2或3时,a n 最大,最大值为0.5.数列中的新定义问题典例 (1)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 014项与5的差,即a 2 014-5=__________.(用式子表示)(2)对于数列{x n },若对任意n ∈N *,都有x n +x n +22<x n +1成立,则称数列{x n }为“减差数列”.设b n =2t -tn -12n -1,若数列b 3,b 4,b 5,…是“减差数列”,则实数t 的取值范围是____________.思维点拨 (1)观察图形,易得a n -a n -1=n +2(n ≥2)可利用累加法求解.(2)由“减差数列”的定义,可得关于b n 的不等式,把b n 的通项公式代入,化归为不等式恒成立问题求解.解析 (1)因为a n -a n -1=n +2(n ≥2),a 1=5,所以a 2 014=(a 2 014-a 2 013)+(a 2 013-a 2 012)+…+(a 2-a 1)+a 1=2 016+2 015+…+4+5 =(2 016+4)×2 0132+5=1 010×2 013+5,所以a 2 014-5=1 010×2 013.(2)由数列b 3,b 4,b 5,…是“减差数列”, 得b n +b n +22<b n +1(n ≥3), 即t -tn -12n +t -t (n +2)-12n +2<2t -t (n +1)-12n ,即tn -12n +t (n +2)-12n +2>t (n +1)-12n ,化简得t (n -2)>1. 当n ≥3时,若t (n -2)>1恒成立,则t >1n -2恒成立,又当n ≥3时,1n -2的最大值为1,则t 的取值范围是(1,+∞).答案 (1)1 010×2 013 (2)(1,+∞)温馨提醒 解决数列的新定义问题要做到:(1)准确转化:解决数列新定义问题时,一定要读懂新定义的本质含义,将题目所给定义转化成题目要求的形式,切忌同已有概念或定义相混淆.(2)方法选取:对于数列新定义问题,搞清定义是关键,仔细认真地从前几项(特殊处、简单处)体会题意,从而找到恰当的解决方法.[方法与技巧]1.求数列通项或指定项.通常用观察法(对于交错数列一般用(-1)n 或(-1)n +1来区分奇偶项的符号);已知数列中的递推关系,一般只要求写出数列的前几项,若求通项可用归纳、猜想和转化的方法.2.强调a n 与S n 的关系:a n =⎩⎪⎨⎪⎧S 1, n =1,S n -S n -1, n ≥2. 3.已知递推关系求通项:对这类问题的要求不高,但试题难度较难把握.一般有两种常见思路:(1)算出前几项,再归纳、猜想;(2)利用累加法或累乘法可求数列的通项公式.4.数列的性质可利用函数思想进行研究.[失误与防范]1.数列a n =f (n )和函数y =f (x )定义域不同,其单调性也有区别:y =f (x )是增函数是a n =f (n )是递增数列的充分不必要条件.2.数列的通项公式可能不存在,也可能有多个.3.由a n =S n -S n -1求得的a n 是从n =2开始的,要对n =1时的情况进行验证.A 组 专项基础训练(时间:40分钟)1.数列23,-45,67,-89,…的第10项是________. 答案 -2021解析 所给数列呈现分数形式,且正负相间,求通项公式时,我们可以把每一部分进行分解:符号、分母、分子.很容易归纳出数列{a n }的通项公式a n =(-1)n +1·2n 2n +1,故a 10=-2021. 2.数列{a n }的前n 项积为n 2,那么当n ≥2时,a n =__________.答案 n 2(n -1)2解析 设数列{a n }的前n 项积为T n ,则T n =n 2,当n ≥2时,a n =T n T n -1=n 2(n -1)2. 3.若S n 为数列{a n }的前n 项和,且S n =n n +1,则1a 5=________. 答案 30解析 当n ≥2时,a n =S n -S n -1=n n +1-n -1n =1n (n +1),所以1a 5=5×6=30. 4.若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为________.答案 7解析 ∵a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列,∴a n =19+(n -1)×(-3)=22-3n .∵a 7=22-21=1>0,a 8=22-24=-2<0,∴n =7时,数列{a n }的前n 项和最大.5.已知数列{a n }的通项公式为a n =n 2-2λn (n ∈N *),则“λ<1”是“数列{a n }为递增数列”的______________条件.答案 充分不必要解析 若数列{a n }为递增数列,则有a n +1-a n >0,即2n +1>2λ对任意的n ∈N *都成立,于是有3>2λ,λ<32.由λ<1可推得λ<32,但反过来,由λ<32不能得到λ<1,因此“λ<1”是“数列{a n }为递增数列”的充分不必要条件.6.(2015·大连双基测试)已知数列{a n }的前n 项和S n =n 2+2n +1(n ∈N *),则a n =________.答案 ⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥2 解析 当n ≥2时,a n =S n -S n -1=2n +1,当n =1时,a 1=S 1=4≠2×1+1,因此a n =⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥2. 7.数列{a n }中,已知a 1=1,a 2=2,a n +1=a n +a n +2(n ∈N *),则a 7=________. 答案 1解析 由已知a n +1=a n +a n +2,a 1=1,a 2=2,能够计算出a 3=1,a 4=-1,a 5=-2,a 6=-1,a 7=1.8.已知数列{a n }的前n 项和为S n ,S n =2a n -n ,则a n =________. 答案 2n -1解析 当n =1时,S 1=a 1=2a 1-1,得a 1=1,当n ≥2时,a n =S n -S n -1=2a n -n -2a n -1+(n -1),即a n =2a n -1+1,∴a n +1=2(a n -1+1),∴数列{a n +1}是首项为a 1+1=2,公比为2的等比数列,∴a n +1=2·2n -1=2n ,∴a n =2n -1.9.数列{a n }的通项公式是a n =n 2-7n +6.(1)这个数列的第4项是多少?(2)150是不是这个数列的项?若是这个数列的项,它是第几项?(3)该数列从第几项开始各项都是正数?解 (1)当n =4时,a 4=42-4×7+6=-6.(2)令a n =150,即n 2-7n +6=150,解得n =16或n =-9(舍去),即150是这个数列的第16项.(3)令a n =n 2-7n +6>0,解得n >6或n <1(舍去).所以从第7项起各项都是正数.10.已知数列{a n }中,a 1=1,前n 项和S n =n +23a n. (1)求a 2,a 3;(2)求{a n }的通项公式.解 (1)由S 2=43a 2得3(a 1+a 2)=4a 2, 解得a 2=3a 1=3.由S 3=53a 3得3(a 1+a 2+a 3)=5a 3, 解得a 3=32(a 1+a 2)=6. (2)由题设知a 1=1.当n ≥2时,有a n =S n -S n -1=n +23a n -n +13a n -1, 整理得a n =n +1n -1a n -1. 于是a 1=1,a 2=31a 1, a 3=42a 2, ……a n -1=n n -2a n -2, a n =n +1n -1a n -1. 将以上n 个等式两端分别相乘,整理得a n =n (n +1)2. 显然,当n =1时也满足上式.综上可知,{a n }的通项公式a n =n (n +1)2. B 组 专项能力提升(时间:20分钟)11.已知数列{a n }满足a 1=33,a n +1-a n n =2,则a n n的最小值为________. 答案 10.5解析 由题意可知a n +1=a n +2n ,由迭代法可得a n =a 1+2[1+2+3+4+…+(n -1)]=n 2-n+33,从而a n n =n +33n -1.当n =6时,a n n取得最小值10.5. 12.数列{a n }满足a n +a n +1=12(n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 21=________. 答案 72解析 ∵a n +a n +1=12,a 2=2, ∴a n =⎩⎪⎨⎪⎧-32,n 为奇数,2,n 为偶数.∴S 21=11×⎝⎛⎭⎫-32+10×2=72. 13.定义:称n P 1+P 2+…+P n为n 个正数P 1,P 2,…,P n 的“均倒数”.若数列{a n }的前n 项的“均倒数”为12n -1,则数列{a n }的通项公式为____________. 答案 a n =4n -3解析 ∵n a 1+a 2+…+a n =12n -1, ∴a 1+a 2+…+a n n =2n -1, ∴a 1+a 2+…+a n =(2n -1)n ,a 1+a 2+…+a n -1=(2n -3)(n -1)(n ≥2),当n ≥2时,a n =(2n -1)n -(2n -3)(n -1)=4n -3;a 1=1也适合此等式,∴a n =4n -3.14.若数列{n (n +4)(23)n }中的最大项是第k 项,则k =________. 答案 4解析 由题意得⎩⎨⎧ k (k +4)(23)k ≥(k +1)(k +5)(23)k +1,k (k +4)(23)k ≥(k -1)(k +3)(23)k -1,所以⎩⎪⎨⎪⎧k 2≥10,k 2-2k -9≤0,由k ∈N *可得k =4. 15.(2015·开封模拟)已知数列{a n }中,a n =1+1a +2(n -1)(n ∈N *,a ∈R 且a ≠0). (1)若a =-7,求数列{a n }中的最大项和最小项的值;(2)若对任意的n ∈N *,都有a n ≤a 6成立,求a 的取值范围.解 (1)∵a n =1+1a +2(n -1)(n ∈N *,a ∈R ,且a ≠0), 又a =-7,∴a n =1+12n -9(n ∈N *).结合函数f (x )=1+12x -9的单调性,可知1>a 1>a 2>a 3>a 4,a 5>a 6>a 7>…>a n >1(n ∈N *).∴数列{a n }中的最大项为a 5=2,最小项为a 4=0.(2)a n =1+1a +2(n -1)=1+12n -2-a 2, 已知对任意的n ∈N *,都有a n ≤a 6成立,结合函数f (x )=1+12x -2-a 2的单调性, 可知5<2-a 2<6,即-10<a <-8.。
数列的概念与简单的表示法基础训练题(有详解)

绝密★启用前数列的概念与简单的表示法基础训练题(有详解)一、单选题1.数列0.3,0.33,0.333,0.3333,…的通项公式是a n =( ) A .1(101)9n- B .111310n⎛⎫-⎪⎝⎭C .2(101)9n- D .3(101)10n - 2.已知数列{}n a 中,21n a n n =++,则3(a = )A .4B .9C .12D .133.数列1-,3,5-,7,9-,,的一个通项公式为( )A .21n a n =-B .(1)(12)nn a n =-- C .(1)(21)nn a n =--D .1(1)(21)n n a n +=--4.数列1,,,,,…的一个通项公式是( ) A . B .C .D .5.若(n∈N *),则当n =2时,f(n)是( ).A .1+B .C .1+D .非以上答案 6.已知数列的首项,且,则( )A .B .C .D . 7.数列的通项公式为,则的第5项是( )A .13B .C .D .158.数列的一个通项公式是 ( ) A .B .C .D .9.数列{}n a 的前n 项和()2*23N n S n n n =-∈,则4a 等于( ) A .11 B .15 C .17 D .2010.若数列{}n a 满足11a =, 131n n a a +=+,则4a =( ) A .7 B .13 C .40 D .121A .20B .21C .22D .23 12.已知数列的前四项为1,,1,,则该数列的通项公式可能是( ) A .B .C .D .13.已知数列{a n }中,a 1=2,a n =1﹣(n≥2),则a 2017等于( )A .﹣B .C .﹣1D .2 14.数列3,5,7,9,,23n + 的项数为( )A .23n +B .1n +C .nD .2n +15.设n a =211111123n n n n n ++++++++(n ∈N *),则3a =( ) A .13 B .11113456+++ C .19 D .111349+++16.数列1,3,6,10,x,21,…中的x 等于 A .17 B .16 C .15 D .1417.数列{a n }中,如果n a =3n(n =1,2,3,…) ,那么这个数列是( ). A .公差为2的等差数列 B .公差为3的等差数列 C .首项为3的等比数列 D .首项为1的等比数列18.数列{a n }的通项公式为a n =3n 2﹣28n ,则数列{a n }各项中最小项是( ) A .第4项 B .第5项C .第6项D .第7项二、填空题19.在数列{}n a 中,11a =,112n n a a -=+,则2a =______. 20.在数列11310,,,,,,4382n n -中,37是它的第_____项. 21.已知数列{}n a 满足:12a =,()()()*1122,n n n a n a n N ++-+=∈,则3a =__________.22.已知数列{}n a 的首项11a =,且1(1)12nn na a n a +=+…,则5a =____.23.已知数列的前n 项和,求数列的通项公式 .24.已知数列{a n }的前n 项和S n =n 2+3n +1, 则a n = .参考答案1.B 【解析】 【分析】利用观察法求数列通项即可 【详解】111=0.910-,211=0.9910-,311=0.99910-,411=0.999910-,…;明显地 1111=0.3310⎛⎫- ⎪⎝⎭,2111=0.33310⎛⎫- ⎪⎝⎭,3111=0.333310⎛⎫- ⎪⎝⎭,4111=0.3333310⎛⎫- ⎪⎝⎭,…;显然数列0.3,0.33,0.333,0.3333,…的通项公式是111310n n a ⎛⎫=-⎪⎝⎭, 答案选B 【点睛】本题考查利用观察法求数列通项问题,属于基础题 2.D 【解析】 【分析】将n=3直接代入通项中即可求得结果. 【详解】∵21n a n n =++,∴393113a =++=. 故选:D . 【点睛】本题考查了由通项公式求特定项的方法,只需代入n 值即可,属于简单题. 3.C 【解析】 【分析】首先注意到数列的奇数项为负,偶数项为正,其次数列各项绝对值构成一个以1为首项,以2为公差的等差数列,从而易求出其通项公式.【详解】∵数列{a n}各项值为1-,3,5-,7,9-,,∴各项绝对值构成一个以1为首项,以2为公差的等差数列,∴|a n|=2n﹣1又∵数列的奇数项为负,偶数项为正,∴a n=(﹣1)n(2n﹣1).故选:C.【点睛】本题给出数列的前几项,猜想数列的通项,挖掘其规律是关键.解题时应注意数列的奇数项为负,偶数项为正,否则会错.4.D【解析】【分析】通过观察数列的分子和分母,猜想出数列的通项公式.【详解】由于数列的分母是奇数列,分子是自然数列,故通项公式为.故选D.【点睛】本小题考查观察数列给定的项,猜想数列的通项公式.根据分子和分母的规律,易得出正确的选项.属于基础题.5.C【解析】【分析】把n=2代入=,即可解决。
高考数学复习专题九考点23《数列的概念与简单表示法》练习题(含答案)

高考数学复习专题九考点23《数列的概念与简单表示法》练习题(含答案)1.已知数列{}n a 的通项公式为2n a n kn =-,且{}n a 单调递增,则实数k 的取值范围是( ) A.(,2]-∞B.(,2)-∞C.(,3]-∞D.(,3)-∞2.22,24,…,则162( ) A.第8项B.第9项C.第10项D.第11项3.已知在数列{}n a 中,11a =,123n n a a +=+,则n a 等于( ) A.123n -+B.123n ++C.123n --D.123n +-4.数列{}n a 中,12a =,m n m n a a a +=.若155121022k k k a a a ++++++=-,则k =( )A.2B.3C.4D.55.已知数列{}n a 满足32111232n n a a a a n ++++=-,则n a =( ) A.112n-B.312n - C.12nD.2nn 6.已知数列{}n a 的前n 项和为()*n S n ∈N ,且2n S n λ=+.若数列{}n a 为递增数列,则实数λ的取值范围为( ) A.(,1)-∞B.(,2)-∞C.(,3)-∞D.(,4)-∞7.《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,…,生数皆终,万物复苏,天以更远作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90~100),其余19人的年龄依次相差一岁,则年龄最小者的年龄为( ) A.65B.66C.67D.688.已知数列{}n a 的前n 项和为112321 ,,0,3,2,1(3)22n n n n n n a aS a a a a n a a +--∈===⋅=++N .若100m a =,则m =( )A.50B.51C.100D.1019.若数列{}n a 满足12211,1,n n n a a a a a ++===+,则称数列{}n a 为斐波那契数列.1680年卡西尼发现了斐波那契数列的一个重要性质:211(1)(2)n n n na a a n -+-=-≥.在斐波那契数列{}n a 中,若k 满足22111(21)(21)999kki i i i i i a a i a ++==--≤-∑∑,给出下列结论:①k 可以是任意奇数;②k 可以是任意正偶数:③若k 是奇数,则k 的最大值是999;④若k 是偶数,则k 的最大值是500.其中正确结论的序号是( )A.①④B.②③C.①②D.③④10.已知集合{}{}1*21*3,,1333,n n A x x n B x x n --==∈==++++∈N N ∣∣.将A B ⋃的所有元素从小到大排列构成数列{}n c ,其前n 项和为n T ,则下列命题中真命题的个数为( ) ①202320222021c c c =+; ②{}2212n n c c --是等比数列;③使503n T >成立的n 的最小值为100; ④112ni ic =<∑恒成立. A.4B.3C.2D.111.在斐波那契数列{}n a 中,11a =,21a =,()122n n n a a a n --=+>.已知n S 为该数列的前n 项和,若2020S m =,则2022a =_____________.12.已知数列{}n a 中,11a =,()*12n n a a n +=∈N ,则数列{}n a 的通项公式为n a =___________.13.数列{}n a 满足2(1)31n n n a a n ++-=-,前16项和为540,则1=a ___________. 14.已知数列{}n a 满足12a =,且31122(2)234n n a a a a a n n-++++=-≥,则{}n a 的通项公式为_______________.15.已知正项数列{}n a 的前n 项和为n S ,11a =,2211n n n S a S λ++=-,其中λ为常数.(1)证明:12n n S S λ+=+.(2)是否存在实数λ,使得数列{}n a 为等比数列?若存在,求出λ;若不存在,请说明理由.参考答案1.答案:D解析:∵数列{}n a 中()2*n a n kn n =-∈N ,且{}n a 单调递增,10n n a a +∴->对于*n ∈N 恒成立,即()22(1)(1)210n k n n kn n k +-+--=+->对于*n ∈N 恒成立. 21k n ∴<+对于*n ∈N 恒成立,即3k <.故选D.2.答案:B22(2),3(2),4(2),…,由此可归纳该数列的通项公式为()*(2)n n ∈N .又9162(2),所以1629项.故选B.3.答案:D解析:由123n n a a +=+,得()1323n n a a ++=+,且134a +=,则{}3n a +是以4为首项,2为公比的等比数列,则1342n n a -+=⨯,所以123n n a +=-. 4.答案:C解析:因为数列{}n a 中,m n m n a a a +=,令1m =,则112n n n a a a a +==,所以数列{}n a 是首项为2,公比为2的等比数列,则11122k k k a a ++=⋅=.所以()()1011101111210122212212k k k k k k k a a a a +++++++-+++==-=--,则1111552222k k ++-=-,所以4k =,故选C. 5.答案:D 解析:32111232n n a a a a n ++++=-①,当2n 时,31211112312n n a a a a n --++++=--②,则①-②得,1111222n n n n a n -=-=,故(2)2n n n a n =.当1n =时,112a =,也符合2n n na =,故选D. 6.答案:B解析:当1n =时,111a S λ==+;当2n 时,221(1)21n n n a S S n n n λλ-==+---=--.则120n n a a --=>,所以当2n 时,数列{}n a 为递增数列.若数列{}n a 为递增数列,只需21a a >,即31λ>+,所以2λ<.故选B.7.答案:B解析:设年龄最小者的年龄为n ,年龄最大者的年龄为([90,100])m m ∈,所以(1)(18)1520n n n m ++++++=,所以191349n m +=,所以134919m n =-,所以90134919100n -,所以14565661919n ,因为年龄为正整数,所以66n =,故选B.8.答案:D 解析:因为3412122a a a a ⋅=++,所以45a =,同理可得564,7a a ==.令2(3)2nn n a b n a -=+,则11n n b b +=,因为31b =,所以3452 1,2n n n b b b b a a -======+,则有21202(1)2 2 , 32(1)21k k a k k a k k -=+-=-=+-=+,故(1)n n a n =+-.若(1)100m m a m =+-=,则101m =.故选D. 9.答案:B解析:由211(1)(2)n n n na a a n -+-=-≥可得212111(21)(21)1357(1)(21)kkk i i i i i i a ai a k +++==-⋅--=-+-++--∑∑.若k 为偶数,则22111(21)(21)1357(21)kki i i i i i a a i a k k ++==---=-+-+--=-∑∑,此时22111(21)(21)999kki i i i i i a a i a ++==--≤-∑∑,即999k -≤,k 无最大值,所以②正确,④错误;若k 为奇数,则22111(21)(21)1357(21)kki i i i i i a a i a k k ++==---=-+-++-=∑∑,此时22111(21)(21)999k ki i i i i i a a i a ++==--≤-∑∑,即999k ≤,此时k 的最大值为999,所以①错误,③正确.故选B. 10.答案:B解析:设1*3,n n a n -=∈N ,则数列{}n a 是首项为1、公比为3的等比数列,其前n 项和213113332n n n B --=++++=.因为111a B ==,且当2n ≥时,131332n n n --<<, 所以把A B ⋃的所有元素从小到大排列为122334455,,,,,,,,,B a B a B a B a B ,所以212131,32n n n n n n c B c a -+-====.对于①,1221213131322n n nn n n c c c +-+--+=+==,取1011n =,有202320222021c c c =+,故①正确.对于②,因为2213123212n nn n c c ---=-⨯=是常数,所以{}2212n n c c -- 是以1为首项、1为公比的等比数列,故②正确.对于③,易知49503a =,则数列{}n c 的前98项和()()98235012349T a a a B B B B =++++++++()234912350234950B B B B a a a B B B B =++++++++=++++()5123505014931073333224-=⨯+++-=<,前99项和515050509998999850310731531093424T T c T B --⨯-=+=+=+=>,故使得503n T >成立的n 的最小值为99,故③错误.对于④,因为当2n ≥时,0n n B a >>,所以11113n n n B a -<=, 所以2121122311111111111112122333333nn nn i i n n c B B B a a a -=+⎛⎫⎫⎛⎛⎫⎛⎫=+++++++<+++++++=-< ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎝⎭⎭∑,又因为21211112n n i i i i c c -==<<∑∑,所以112ni ic =<∑恒成立,故④正确.11.答案:1m +解析:由已知,得123a a a +=,234a a a +=,…,202020212022a a a +=,以上各式相加,得1234202020222a a a a a a +++++=,即220202022a S a +=.又21a =,2020S m =,所以20221a m =+.12.答案:12n -解析:易知0n a ≠,由()*12n n a a n +=∈N ,可得12n na a +=, 所以当2n ≥时,12nn a a -=, 所以()113211221122222n n n n n n n a a a a a a a a a a -----=⨯⨯⨯⨯=⨯⨯⨯⨯=个, 所以()122n n a n -=≥. 因为当1n =时也满足上式,所以数列{}n a 的通项公式为()1*2n n a n -=∈N . 13.答案:7解析:令()2n k k *=∈N ,则有()22261k k a a k k *++=-∈N , 2468101214165,171,942=,a a a a a a a a ∴+=+=+=+,∴前16项的所有偶数项和 517294192S =+++=偶,∴前16项的所有奇数项和 54092448S =-=奇,令()21n k k *=-∈N ,则有()212164k k a a k k *+--=-∈N .()()()211315375k a a a a a a a a +∴-=-+-+-+ ()2121281464k k a a k +-+-=++++-=()(264)(31)2k k k k k *+-=-∈N ,()211(31)k a k k a k *+∴=-+∈N ,31517192,10,24,44a a a a a a a ∴=+=+=+=+ 1111131151,70,102,140a a a a a a a =+=+=+,∴前16项的所有奇数项和13 S a a =+++奇151182102444701021408a a a =+++++++=+392448=. 17a ∴=.14.答案:1n a n =+解析:依题意数列{}n a 满足12a =,且31122234n n a a a a a n-++++=-①. 当2n =时,1222a a =-,23a =, 3112122341n n n a a aa a a n n -++++++=-+②, ②-①得11n n n a a a n +=-+,121n n a n a ++=+ 则()112n n a n n a n-+=≥, 所以13211221132112n n n n n a a a a n n a a n a a a a n n ---+=⋅⋅⋅⋅⋅=⋅⋅⋅⋅=+-, 1a ,2a 都符合上式.所以{}n a 的通项公式为1n a n =+. 故答案为:1n a n =+. 15.答案:(1)见解析 (2)存在,1λ=.解析:(1)11n n n a S S ++=-,2211n n n S a S λ++=-,()2211n n n n S S S S λ++∴=--,()1120n n n S S S λ++∴--=.0n a >,10n S +∴>,120n n S S λ+∴--=,12n n S S λ+∴=+.(2)12n n S S λ+=+, 122n n S S n λ-∴=+≥(), 两式相减,得1(22)n n a a n +≥=. 212S S λ=+,即2112a a a λ+=+, 21a λ∴=+,由20a >,得1λ>-.若{}n a 是等比数列,则2132a a a =,即22(1)(1)λλ+=+,得1λ=. 经检验,1λ=符合题意.故存在1λ=,使得数列{}n a 为等比数列.。
高中数学选择性必修二 4 1 数列的概念与简单表示法(含答案)

课时同步练4.1 数列的概念与简单表示法(1)一、单选题1.已知数列{}n a 中,2n+5,则3a =( ) A .13 B .12 C .11 D .10【答案】C【解析】由已知得2×3+5=11. 故选C .2.有下面四个结论:①数列的通项公式是唯一的;②每个数列都有通项公式;③数列可以看作一个定义在正整数集上的函数;④数列的图象是坐标平面上有限或无限个离散的点.其中真命题的个数为( ) A .0个B .1个C .2个D .3个 【答案】B【解析】对①,数列1,1,1,1,--其通项公式1(1)n n a +=-,也可以是3(1)n n a +=-,故①错误; 对②,数列的项与n 具备一定的规律性,才可求出数列的通项公式,所以有的数列是无通项公式的,故②错误;对③,数列可以看作一个定义在正整数集上或正整数集的子集上的函数,故③错误; 对④,由数列的定义知命题正确.故选B.3.已知数列-1,0,19,18,…,22n n -,…中,则572是其( ) A .第14项 B .第12项 C .第10项 D .第8项【答案】B 【解析】令22n n-=572,化为:5n 2﹣72n +144=0, 解得n =12,或n =125(舍去). 故选B .4.数列{}n a 的通项公式()*2n a n n =∈N不满足下列递推公式的是( ) A .()122n n a a n -=+ B .()1223n n n a a a n --=-C .()()()11222n n n n a a a a n ---=-D .()122n n a a n -= 【答案】D【解析】将2n a n =代入四个选项得:A. 22(1)2n n =-+ 成立;B. 222(1)2(2)n n n =⨯--- 成立;C. ()2222(1)2(1)][2n n n n -=--- 成立;D. 222n n =⨯ 不恒成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、数列的概念选择题1.数列1,3,6,10,…的一个通项公式是( )A .()21n a n n =-- B .21n a n =-C .()12n n n a +=D .()12n n n a -=2.已知数列{}n a 满足: 12a =,111n na a +=-,设数列{}n a 的前n 项和为n S ,则2017S =( ) A .1007B .1008C .1009.5D .10103.已知数列{}n a 满足11a =),2n N n *=∈≥,且()2cos3n n n a b n N π*=∈,则数列{}n b 的前18项和为( ) A .120B .174C .204-D .37324.设数列{}n a 的前n 项和为n S 已知()*123n n a a n n N++=+∈且1300nS=,若23a <,则n 的最大值为( )A .49B .50C .51D .525.已知数列{}n a 满足1n n n a a +-=,则20201a a -=( ) A .20201010⨯B .20191010⨯C .20202020⨯D .20192019⨯6.已知数列{}ij a 按如下规律分布(其中i 表示行数,j 表示列数),若2021ij a =,则下列结果正确的是( )A .13i =,33j =B .19i =,32j =C .32i =,14j =D .33i =,14j =7.已知数列{}n a 前n 项和为n S ,且满足*112(N 3)33n n n n S S S S n n --+≤+∈≥+,,则( )A .63243a a a ≤-B .2736+a a a a ≤+C .7662)4(a a a a ≥--D .2367a a a a +≥+8.已知数列{}n a 的前n 项和为n S ,且21n S n n =++,则{}n a 的通项公式是( )A .2n a n =B .3,12,2n n a n n =⎧=⎨≥⎩C .21n a n =+D .3n a n =9.在数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,则下列结论正确的是( )A .存在正整数0N ,当0n N >时,都有n a n ≤.B .存在正整数0N ,当0n N >时,都有n a n ≥.C .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≤.D .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≥. 10.在数列{}n a 中,()1111,1(2)nn n a a n a --==+≥,则5a 等于A .32B .53 C .85D .2311.公元13世纪意大利数学家斐波那契在自己的著作《算盘书》中记载着这样一个数列:1,1,2,3,5,8,13,21,34,…满足21(1),n n n a a a n ++=+≥那么24620201a a a a +++++=( )A .2021aB .2022aC .2023aD .2024a12.删去正整数1,2,3,4,5,…中的所有完全平方数与立方数(如4,8),得到一个新数列,则这个数列的第2020项是( ) A .2072B .2073C .2074D .207513.已知等差数列{}n a 中,13920a a a ++=,则574a a -=( ) A .30B .20C .40D .5014.数列{}n a 的前n 项和记为n S ,()*11N ,2n n n a a a n n ++=-∈≥,12018a =,22017a =,则100S =( )A .2016B .2017C .2018D .201915.已知数列{}n b 满足12122n n b n λ-⎛⎫=-- ⎪⎝⎭,若数列{}n b 是单调递减数列,则实数λ的取值范围是( ) A .101,3B .110,23⎛⎫- ⎪⎝⎭C .(-1,1)D .1,12⎛⎫-⎪⎝⎭16.已知lg3≈0.477,[x ]表示不大于x 的最大整数.设S n 为数列{a n }的前n 项和,a 1=2且S n +1=3S n -2n +2,则[lg(a 100-1)]=( ) A .45B .46C .47D .4817.已知数列{}n a 满足2122111,16,2n n n a a a a a ++===则数列{}n a 的最大项为( ) A .92B .102C .8182D .11218.设数列{}n a 的通项公式为2n n a n+=,要使它的前n 项的乘积大于36,则n 的最小值为( ) A .6B .7C .8D .919.在数列{}n a 中,11(1)1,2(2)nn n a a n a --==+≥,则3a =( ) A .0B .53C .73D .320.数列{}n a 满足111n na a +=-,12a =,则2a 的值为( ) A .1B .-1C .13D .13-二、多选题21.已知数列{}n a 中,11a =,1111n n a a n n +⎛⎫-=+ ⎪⎝⎭,*n N ∈.若对于任意的[]1,2t ∈,不等式()22212na t a t a a n<--++-+恒成立,则实数a 可能为( ) A .-4B .-2C .0D .222.已知等差数列{}n a 的公差0d ≠,前n 项和为n S ,若612S S =,则下列结论中正确的有( ) A .1:17:2a d =-B .180S =C .当0d >时,6140a a +>D .当0d <时,614a a >23.等差数列{}n a 的前n 项和为n S ,1385a a S +=,则下列结论一定正确的是( ) A .100a = B .911a a = C .当9n =或10时,n S 取得最大值D .613S S =24.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,则( ) A .若59S >S ,则150S > B .若59S =S ,则7S 是n S 中最大的项 C .若67S S >, 则78S S >D .若67S S >则56S S >.25.已知数列{}2nna n +是首项为1,公差为d 的等差数列,则下列判断正确的是( ) A .a 1=3 B .若d =1,则a n =n 2+2n C .a 2可能为6D .a 1,a 2,a 3可能成等差数列26.朱世杰是元代著名数学家,他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔,小明模仿“堆垛”问题,将它们全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从最下面一层开始,每一层比上一层多1根,则该“等腰梯形垛”应堆放的层数可以是( ) A .4B .5C .7D .827.无穷等差数列{}n a 的前n 项和为S n ,若a 1>0,d <0,则下列结论正确的是( ) A .数列{}n a 单调递减 B .数列{}n a 有最大值 C .数列{}n S 单调递减D .数列{}n S 有最大值28.记n S 为等差数列{}n a 的前n 项和.已知450,5S a ==,则( ) A .25n a n =-B .310na nC .228n S n n =- D .24n S n n =-29.等差数列{}n a 的前n 项和记为n S ,若10a >,717S S =,则( ) A .0d < B .120a > C .13n S S ≤D .当且仅当0nS <时,26n ≥30.设{}n a 是等差数列,n S 是其前n 项和,且56678,S S S S S <=>,则下列结论正确的是( ) A .0d < B .70a =C .95S S >D .67n S S S 与均为的最大值31.记n S 为等差数列{}n a 的前n 项和.已知535S =,411a =,则( ) A .45n a n =-B .23n a n =+C .223n S n n =-D .24n S n n =+32.设等差数列{}n a 的前n 项和为n S ,公差为d .已知312a =,120S >,70a <则( ) A .60a > B .数列1n a ⎧⎫⎨⎬⎩⎭是递增数列C .0nS <时,n 的最小值为13D .数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项 33.设等差数列{a n }的前n 项和为S n ,公差为d .已知a 3=12,S 12>0,a 7<0,则( ) A .a 6>0B .2437d -<<- C .S n <0时,n 的最小值为13D .数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项34.公差为d 的等差数列{}n a ,其前n 项和为n S ,110S >,120S <,下列说法正确的有( ) A .0d <B .70a >C .{}n S 中5S 最大D .49a a <35.已知{}n a 为等差数列,其前n 项和为n S ,且13623a a S +=,则以下结论正确的是( ). A .10a =0B .10S 最小C .712S S =D .190S =【参考答案】***试卷处理标记,请不要删除一、数列的概念选择题 1.C 解析:C 【分析】首先根据已知条件得到410a =,再依次判断选项即可得到答案. 【详解】由题知:410a =,对选项A ,()2444113a =--=,故A 错误;对选项B ,244115a =-=,故B 错误;对选项C ,()4441102a ⨯+==,C 正确; 对选项D ,()444162a ⨯-==,故D 错误. 故选:C 【点睛】本题主要考查数列的通项公式,属于简单题.2.D解析:D 【分析】根据题设条件,可得数列{}n a 是以3为周期的数列,且3132122S =+-=,从而求得2017S 的值,得到答案. 【详解】由题意,数列{}n a 满足: 12a =,111n na a +=-, 可得234111,121,1(1)2,22a a a =-==-=-=--=,可得数列{}n a 是以3为周期的数列,且3132122S =+-= 所以20173672210102S =⨯+=. 故选:D. 【点睛】本题主要考查了数列的递推公式的应用,其中解答中得出数列{}n a 是以3为周期的数列,是解答的关键,着重考查了推理与运算能力,属于中档试题.3.B解析:B 【分析】将题干中的等式化简变形得211n n a n a n --⎛⎫= ⎪⎝⎭,利用累乘法可求得数列{}n a 的通项公式,由此计算出()32313k k k b b b k N *--++∈,进而可得出数列{}nb 的前18项和.【详解】)1,2n a n N n *--=∈≥,将此等式变形得211n n a n a n --⎛⎫= ⎪⎝⎭,由累乘法得22232121211211123n n n aa a n a a a a a n n--⎛⎫⎛⎫⎛⎫=⋅⋅=⨯⨯⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ()2cos3n n n a b n N π*=∈,22cos 3n n b n π∴=, ()()222323134232cos 231cos 29cos 233k k k b b b k k k k k k πππππ--⎛⎫⎛⎫∴++=--+--+ ⎪ ⎪⎝⎭⎝⎭592k =-,因此,数列{}n b 的前18项和为()591234566921151742⨯+++++-⨯=⨯-=. 故选:B. 【点睛】本题考查并项求和法,同时也涉及了利用累乘法求数列的通项,求出32313k k k b b b --++是解答的关键,考查计算能力,属于中等题.4.A解析:A 【分析】对n 分奇偶性分别讨论,当n 为偶数时,可得2+32n n nS =,发现不存在这样的偶数能满足此式,当n 为奇数时,可得21+342n n n S a -=+,再结合23a <可讨论出n 的最大值.【详解】当n 为偶数时,12341()()()n n n S a a a a a a -=++++⋅⋅⋅++(213)(233)[2(1)3]n =⨯++⨯++⋅⋅⋅+-+ 2[13(1)]32n n =⨯++⋅⋅⋅+-+⨯2+32n n=,因为22485048+348503501224,132522S S ⨯+⨯====,所以n 不可能为偶数;当n 为奇数时,123451()()()n n n S a a a a a a a -=+++++⋅⋅⋅++1(223)(243)[2(1)3]a n =+⨯++⨯++⋅⋅⋅+-+21342n n a +-=+因为2491149349412722S a a +⨯-=+=+,2511151351413752S a a +⨯-=+=+,又因为23a <,125a a +=,所以 12a > 所以当1300n S =时,n 的最大值为49 故选:A 【点睛】此题考查的是数列求和问题,利用了并项求和的方法,考查了分类讨论思想,属于较难题.5.B解析:B 【分析】由题意可得211a a -=,322a a -=,433a a -=,……202020192019a a -=,再将这2019个式子相加得到结论. 【详解】由题意可知211a a -=,322a a -=,433a a -=,……202020192019a a -=, 这2019个式子相加可得()20201201912019123 (2019201910102)a a +-=++++==⨯.故选:B. 【点睛】本题考查累加法,重点考查计算能力,属于基础题型.6.C解析:C 【分析】可以看出所排都是奇数从小到大排起.规律是先第一列和第一行,再第二列和第二行,再第三列第三行,并且完整排完n 次后,排出的数呈正方形.可先算2021是第几个奇数,这个奇数在哪两个完全平方数之间,再去考虑具体的位置. 【详解】每排完n 次后,数字呈现边长是n 的正方形,所以排n 次结束后共排了2n 个数.20211110112-+=,说明2021是1011个奇数. 而22961311011321024=<<=,故2021一定是32行,而从第1024个数算起,第1011个数是倒数第14个,根据规律第1024个数排在第32行第1列,所以第1011个数是第32行第14列,即2021在第32行第14列. 故32,14i j ==. 故选:C. 【点睛】本题考查数列的基础知识,但是考查却很灵活,属于较难题.7.C解析:C 【分析】由条件可得出11n n n n a a a a -+-≤-,然后可得3243546576a a a a a a a a a a -≤-≤-≤-≤-,即可推出选项C 正确.【详解】因为*112(N 3)33n n n n S S S S n n --+≤+∈≥+,,所以12133n n n n S S S S -+-≤--,所以113n n n n a a a a +-≤++ 所以11n n n n a a a a -+-≤-,所以3243546576a a a a a a a a a a -≤-≤-≤-≤-所以()6232435465764a a a a a a a a a a a a -=-+-+-+-≤- 故选:C 【点睛】本题主要考查的是数列的前n 项和n S 与n a 的关系,解答的关键是由条件得到11n n n n a a a a -+-≤-,属于中档题.8.B解析:B 【分析】根据11,1,2n nS n a S S n -=⎧=⎨-≥⎩计算可得;【详解】解:因为21n S n n =++①,当1n =时,211113S =++=,即13a =当2n ≥时,()()21111n S n n -=-+-+②,①减②得,()()2211112n n n n n n a ⎡⎤++--+-+=⎦=⎣所以3,12,2n n a n n =⎧=⎨≥⎩故选:B 【点睛】本题考查利用定义法求数列的通项公式,属于基础题.9.A解析:A 【分析】运用数列的单调性和不等式的知识可解决此问题. 【详解】数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,121n n n n a a a a +++∴≥--,设1n n n d a a +=-,则1n n d d +≥,∴数列{}n d 是递减数列.对于A ,由11a =,20192019a =, 则201911220182019a a d d d =+++=,所以1220182018d d d +++=,又1232018d d d d ≥≥≥≥,所以1122018201820182018d d d d d ≥+++≥,故120181d d ≥≥,2018n ∴≥时,1n d ≤,02019N ∃=,2019n >时, 20192019202012019111n n a a d d d n -=+++≤++++=即存在正整数0N ,当0n N >时,都有n a n ≤,故A 正确; 结合A ,故B 不正确;对于C ,当n →+∞,且0n d >时,数列{}n a 为递增数列, 则n a 无最大值,故C 不正确;对于D ,由数列{}n d 是递减数列,当存在0n d <时,则n a 无最小值,故D 不正确; 故选:A 【点睛】本题考查了数列的单调性以及不等式,属于基础题.10.D解析:D 【解析】分析:已知1a 逐一求解2345122323a a a a ====,,,. 详解:已知1a 逐一求解2345122323a a a a ====,,,.故选D 点睛:对于含有()1n-的数列,我们看作摆动数列,往往逐一列举出来观察前面有限项的规律.11.A解析:A 【分析】根据数列的递推关系式即可求解. 【详解】由21(1),n n n a a a n ++=+≥ 则2462020246210201a a a a a a a a a +++++++++=+3462020562020201920202021a a a a a a a a a a =+++=+++=+=.故选:A12.C解析:C 【分析】由于数列22221,2,3,2,5,6,7,8,3,45⋯共有2025项,其中有45个平方数,12个立方数,有3个既是平方数,又是立方数的数,所以还剩余20254512+31971--=项,所以去掉平方数和立方数后,第2020项是在2025后的第()20201971=49-个数,从而求得结果. 【详解】∵2452025=,2462116=,20202025<,所以从数列22221,2,3,2,5,6,7,8,3,45⋯中去掉45个平方数,因为331217282025132197=<<=,所以从数列22221,2,3,2,5,6,7,8,3,45⋯中去掉12个立方数,又66320254<<,所以在从数列22221,2,3,2,5,6,7,8,3,45⋯中有3个数即是平方数, 又是立方数的数,重复去掉了3个即是平方数,又是立方数的数, 所以从数列22221,2,3,2,5,6,7,8,3,45⋯中去掉平方数和立方数后还有20254512+31971--=项,此时距2020项还差2020197149-=项, 所以这个数列的第2020项是2025492074+=, 故选:C. 【点睛】本题考查学生的实践创新能力,解决该题的关键是找出第2020项的大概位置,所以只要弄明白在数列22221,2,3,2,5,6,7,8,3,45⋯去掉哪些项,去掉多少项,问题便迎刃而解,属于中档题.13.B解析:B 【分析】利用等差数列{}n a 的通项公式代入可得574a a -的值. 【详解】由13920a a a ++=,得131020a d +=,则有5711144(4)631020a a a d a d a d -=+--=+=. 故选:B. 【点睛】考查等差数列通项公式的运用,知识点较为简单.14.A解析:A 【分析】根据题意,由数列的递推公式求出数列的前8项,分析可得数列{}n a 是周期为6的数列,且1234560a a a a a a +++++=,进而可得1001234S a a a a =+++,计算即可得答案. 【详解】解:因为12018a =,22017a =,()*11N ,2n n n a a a n n +-=-∈≥,则321201720181a a a =-=-=-, 432(1)20172018a a a =-=--=-,543(2018)(1)2017a a a =-=---=-, 654(2017)(2018)1a a a =-=---=, 76511(2017)2018a a a a =-=--==, 8762201812017a a a a =-=-==,…,所以数列{}n a 是周期数列,周期为6, 因为12560a a a a ++⋅⋅⋅++=,所以()100125697989910016S a a a a a a a a =++⋅⋅⋅++++++12342016a a a a =+++=.故选:A . 【点睛】本题考查数列的递推公式的应用,关键是分析数列各项变化的规律,属于基础题.15.A解析:A 【分析】由题1n n b b +>在n *∈N 恒成立,即16212nn λ⎛⎫-<+ ⎪⎝⎭,讨论n 为奇数和偶数时,再利用数列单调性即可求出. 【详解】数列{}n b 是单调递减数列,1n n b b +∴>在n *∈N 恒成立,即()122112+1222nn n n λλ-⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭恒成立,即16212nn λ⎛⎫-<+ ⎪⎝⎭, 当n 为奇数时,则()6212nn λ>-+⋅恒成立,()212n n -+⋅单调递减,1n ∴=时,()212n n -+⋅取得最大值为6-,66λ∴>-,解得1λ>-;当n 为偶数时,则()6212nn λ<+⋅恒成立,()212n n +⋅单调递增,2n ∴=时,()212n n +⋅取得最小值为20,620λ∴<,解得103λ<, 综上,1013λ-<<. 故选:A. 【点睛】关键点睛:本题考查已知数列单调性求参数,解题的关键由数列单调性得出16212nn λ⎛⎫-<+ ⎪⎝⎭恒成立,需要讨论n 为奇数和偶数时的情况,这也是容易出错的地方. 16.C解析:C【分析】利用数列的递推式,得到a n +1=3a n -2,进而得到a n =3n -1+1,然后代入[lg(a 100-1)]可求解 【详解】当n ≥2时,S n =3S n -1-2n +4,则a n +1=3a n -2,于是a n +1-1=3(a n -1),当n =1时,S 2=3S 1-2+2=6,所以a 2=S 2-S 1=4.此时a 2-1=3(a 1-1),则数列{a n -1}是首项为1,公比为3的等比数列.所以a n -1=3n -1,即a n =3n -1+1,则a 100=399+1,则lg(a 100-1)=99lg3≈99×0.477=47.223,故[lg(a 100-1)]=47. 故选C17.B解析:B 【分析】本题先根据递推公式进行转化得到21112n n n n a a a a +++=.然后令1n n na b a +=,可得出数列{}n b 是等比数列.即11322nn n a a +⎛⎫= ⎪⎝⎭.然后用累乘法可求出数列{}n a 的通项公式,根据通项公式及二次函数的知识可得数列{}n a 的最大项. 【详解】解:由题意,可知: 21112n n n na a a a +++=. 令1n n n ab a +=,则112n n b b +=. 21116a b a ==, ∴数列{}n b 是以16为首项,12为公比的等比数列. 111163222n nn b -⎛⎫⎛⎫∴== ⎪⎪⎝⎭⎝⎭.∴11322nn n a a +⎛⎫= ⎪⎝⎭. ∴1211322aa ⎛⎫= ⎪⎝⎭, 2321322a a ⎛⎫= ⎪⎝⎭,111322n n n a a --⎛⎫= ⎪⎝⎭.各项相乘,可得: 12111111(32)222n n na a --⎛⎫⎛⎫⎛⎫=⋯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)2511()22n n n --⎛⎫= ⎪⎝⎭ 2115(1)221122n n n ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭211552212n n n --+⎛⎫= ⎪⎝⎭21(1110)212n n -+⎛⎫= ⎪⎝⎭.令2()1110f n n n =-+,则,根据二次函数的知识,可知:当5n =或6n =时,()f n 取得最小值. ()2551151020f =-⨯+=-,()2661161020f =-⨯+=-,()f n ∴的最小值为20-. ∴211(1110)(20)1022101112222n n -+⨯--⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.∴数列{}n a 的最大项为102.故选:B . 【点睛】本题主要考查根据递推公式得出通项公式,构造新数列的方法,累乘法通项公式的应用,以及利用二次函数思想求最值;18.C解析:C 【分析】先求出数列{}n a 的前n 项的乘积为n D ,令0n D >解不等式,结合*n N ∈,即可求解. 【详解】记数列{}n a 的前n 项的乘积为n D ,则()()12112451232312n n n n n n n D a a a a n n -++++=⋅⋅=⨯⨯⨯⨯⨯=- 依题意有()()12362n n ++>整理得()()23707100n n n n +-=-+>解得:7n >,因为*n N ∈,所以min 8n =, 故选:C19.B解析:B 【分析】由数列的递推关系式以及11a =求出2a ,进而得出3a . 【详解】11a =,21123a a ∴=+=,321523a a -=+= 故选:B20.B解析:B 【分析】根据数列的递推公式,代入计算可得选项. 【详解】 因为111n n a a +=-,12a =,所以21111112a a ===---, 故选:B. 【点睛】本题考查由数列递推式求数列中的项,属于基础题.二、多选题 21.AB 【分析】由题意可得,利用裂项相相消法求和求出,只需对于任意的恒成立,转化为对于任意的恒成立,然后将选项逐一验证即可求解. 【详解】 ,, 则,,,,上述式子累加可得:,, 对于任意的恒成立解析:AB 【分析】由题意可得11111n n a a n n n n +-=-++,利用裂项相相消法求和求出122n a n n=-<,只需()222122t a t a a --++-+≥对于任意的[]1,2t ∈恒成立,转化为()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,然后将选项逐一验证即可求解.【详解】111n n n a a n n++-=,11111(1)1n n a a n n n n n n +∴-==-+++,则11111n n a a n n n n --=---,12111221n n a a n n n n ---=-----,,2111122a a -=-, 上述式子累加可得:111n a a n n -=-,122n a n n∴=-<,()222122t a t a a ∴--++-+≥对于任意的[]1,2t ∈恒成立,整理得()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,对A ,当4a =-时,不等式()()2540t t +-≤,解集5,42⎡⎤-⎢⎥⎣⎦,包含[]1,2,故A 正确;对B ,当2a =-时,不等式()()2320t t +-≤,解集3,22⎡⎤-⎢⎥⎣⎦,包含[]1,2,故B 正确;对C ,当0a =时,不等式()210t t +≤,解集1,02⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故C 错误;对D ,当2a =时,不等式()()2120t t -+≤,解集12,2⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故D 错误, 故选:AB. 【点睛】本题考查了裂项相消法、由递推关系式求通项公式、一元二次不等式在某区间上恒成立,考查了转化与划归的思想,属于中档题.22.ABC 【分析】因为是等差数列,由可得,利用通项转化为和即可判断选项A ;利用前项和公式以及等差数列的性质即可判断选项B ;利用等差数列的性质即可判断选项C ;由可得且,即可判断选项D ,进而得出正确选项解析:ABC 【分析】因为{}n a 是等差数列,由612S S =可得9100a a +=,利用通项转化为1a 和d 即可判断选项A ;利用前n 项和公式以及等差数列的性质即可判断选项B ;利用等差数列的性质961014a d a a d a =++=+即可判断选项C ;由0d <可得6140a a d +=<且60a >,140a <即可判断选项D ,进而得出正确选项.【详解】因为{}n a 是等差数列,前n 项和为n S ,由612S S =得:1267891011120S S a a a a a a -=+++++=,即()91030a a +=,即9100a a +=,对于选项A :由9100a a +=得12170a d +=,可得1:17:2a d =-,故选项A 正确; 对于选项B :()()118910181818022a a a a S ++===,故选项B 正确;对于选项C :911691014a a a a a a d d =+=++=+,若0d >,则6140a a d +=>,故选项C 正确;对于选项D :当0d <时,6140a a d +=<,则614a a <-,因为0d <,所以60a >,140a <,所以614a a <,故选项D 不正确, 故选:ABC 【点睛】关键点点睛:本题的关键点是由612S S =得出9100a a +=,熟记等差数列的前n 项和公式和通项公式,灵活运用等差数列的性质即可.23.ABD 【分析】由题意利用等差数列的通项公式、求和公式可得,结合等差数列的性质,逐一判断即可得出结论. 【详解】∵等差数列的前项和为,, ∴,解得, 故,故A 正确; ∵,,故有,故B 正确; 该数解析:ABD 【分析】由题意利用等差数列的通项公式、求和公式可得19a d =-,结合等差数列的性质,逐一判断即可得出结论. 【详解】∵等差数列{}n a 的前n 项和为n S ,1385a a S +=, ∴()111875282a a d a d ⨯++=+,解得19a d =-, 故10190a a d =+=,故A 正确;∵918a a d d d =+=-=,11110a a d d =+=,故有911a a =,故B 正确; 该数列的前n 项和()21119222n n n n S na d d d n -=+=-⋅ ,它的最值,还跟d 的值有关,故C 错误; 由于61656392S a d d ⨯=+=-,131131213392S a d d ⨯=+=-,故613S S =,故D 正确, 故选:ABD. 【点睛】思路点睛:利用等差数列的通项公式以及前n 项和公式进行化简,直接根据性质判断结果.24.BC 【分析】根据等差数列的前项和性质判断. 【详解】A 错:;B 对:对称轴为7;C 对:,又,;D 错:,但不能得出是否为负,因此不一定有. 故选:BC . 【点睛】关键点点睛:本题考查等差数列解析:BC 【分析】根据等差数列的前n 项和性质判断. 【详解】A 错:67895911415000S a a a a a S a S ⇒+++<>⇒+<⇒<;B 对:n S 对称轴为n =7;C 对:6770S S a >⇒<,又10a >,887700a S a d S ⇒⇒<<⇒<>;D 错:6770S S a >⇒<,但不能得出6a 是否为负,因此不一定有56S S >. 故选:BC . 【点睛】关键点点睛:本题考查等差数列的前n 项和性质,(1)n S 是关于n 的二次函数,可以利用二次函数性质得最值;(2)1n n n S S a -=+,可由n a 的正负确定n S 与1n S -的大小;(3)1()2n n n a a S +=,因此可由1n a a +的正负确定n S 的正负. 25.ACD 【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解 【详解】因为,,所以a1=3,an =[1+(n-1)d](n+2n).若d =1,则an =n(n+2n);若d=0,则a2=解析:ACD 【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解 【详解】 因为1112a =+,1(1)2n n a n d n =+-+,所以a 1=3,a n =[1+(n -1)d ](n +2n ).若d =1,则a n =n (n +2n );若d =0,则a 2=6.因为a 2=6+6d ,a 3=11+22d ,所以若a 1,a 2,a 3成等差数列,则a 1+a 3=a 2,即14+22d =12+12d ,解得15d =-. 故选ACD26.BD 【分析】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为,公差即每一层比上一层多的根数为,设一共放层,利用等差数列求和公式,分析即可得解. 【详解】依据题意,根数从上至下构成等差解析:BD 【分析】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为1a ,公差即每一层比上一层多的根数为1d =,设一共放()2n n ≥层,利用等差数列求和公式,分析即可得解. 【详解】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为1a ,公差为1d =,设一共放()2n n ≥层,则总得根数为:()()111110022n n n d n n S na na --=+=+= 整理得120021a n n=+-, 因为1a *∈N ,所以n 为200的因数,()20012n n+-≥且为偶数, 验证可知5,8n =满足题意. 故选:BD. 【点睛】关键点睛:本题考查等差数列的求和公式,解题的关键是分析题意,把题目信息转化为等差数列,考查学生的逻辑推理能力与运算求解能力,属于基础题.27.ABD【分析】由可判断AB ,再由a1>0,d <0,可知等差数列数列先正后负,可判断CD. 【详解】根据等差数列定义可得,所以数列单调递减,A 正确; 由数列单调递减,可知数列有最大值a1,故B 正解析:ABD 【分析】由10n n a a d +-=<可判断AB ,再由a 1>0,d <0,可知等差数列数列{}n a 先正后负,可判断CD. 【详解】根据等差数列定义可得10n n a a d +-=<,所以数列{}n a 单调递减,A 正确; 由数列{}n a 单调递减,可知数列{}n a 有最大值a 1,故B 正确;由a 1>0,d <0,可知等差数列数列{}n a 先正后负,所以数列{}n S 先增再减,有最大值,C 不正确,D 正确. 故选:ABD.28.AD 【分析】设等差数列的公差为,根据已知得,进而得,故,. 【详解】解:设等差数列的公差为,因为所以根据等差数列前项和公式和通项公式得:, 解方程组得:, 所以,. 故选:AD.解析:AD 【分析】设等差数列{}n a 的公差为d ,根据已知得1145460a d a d +=⎧⎨+=⎩,进而得13,2a d =-=,故25n a n =-,24n S n n =-.【详解】解:设等差数列{}n a 的公差为d ,因为450,5S a == 所以根据等差数列前n 项和公式和通项公式得:1145460a d a d +=⎧⎨+=⎩,解方程组得:13,2a d =-=,所以()31225n a n n =-+-⨯=-,24n S n n =-.故选:AD.29.AB【分析】根据等差数列的性质及可分析出结果.【详解】因为等差数列中,所以,又,所以,所以,,故AB 正确,C 错误;因为,故D 错误,故选:AB【点睛】关键点睛:本题突破口在于由解析:AB【分析】根据等差数列的性质及717S S =可分析出结果.【详解】因为等差数列中717S S =,所以89161712135()0a a a a a a ++++=+=, 又10a >,所以12130,0a a ><,所以0d <,12n S S ≤,故AB 正确,C 错误; 因为125251325()2502a a S a +==<,故D 错误, 故选:AB【点睛】关键点睛:本题突破口在于由717S S =得到12130a a +=,结合10a >,进而得到12130,0a a ><,考查学生逻辑推理能力.30.ABD【分析】由,判断,再依次判断选项.【详解】因为,,,所以数列是递减数列,故,AB 正确;,所以,故C 不正确;由以上可知数列是单调递减数列,因为可知,的最大值,故D 正确.故选:AB解析:ABD【分析】由1n n n S S a --=()2n ≥,判断6780,0,0a a a >=<,再依次判断选项.【详解】因为5665600S S S S a <⇒->⇒>,677670S S S S a =⇒-==,788780S S S S a >⇒-=<,所以数列{}n a 是递减数列,故0d <,AB 正确; ()9567897820S S a a a a a a -=+++=+<,所以95S S <,故C 不正确;由以上可知数列{}n a 是单调递减数列,因为6780,0,0a a a >=<可知,67n S S S 与均为的最大值,故D 正确.故选:ABD【点睛】本题考查等差数列的前n 项和的最值,重点考查等差数列的性质,属于基础题型.31.AC【分析】由求出,再由可得公差为,从而可求得其通项公式和前项和公式【详解】由题可知,,即,所以等差数列的公差,所以,.故选:AC.【点睛】本题考查等差数列,考查运算求解能力.解析:AC【分析】由535S =求出37a =,再由411a =可得公差为434d a a =-=,从而可求得其通项公式和前n 项和公式【详解】由题可知,53535S a ==,即37a =,所以等差数列{}n a 的公差434d a a =-=, 所以()4445n a a n d n =+-=-,()2451232n n n S n n --==-. 故选:AC.【点睛】本题考查等差数列,考查运算求解能力.32.ACD【分析】由已知得,又,所以,可判断A ;由已知得出,且,得出时,,时,,又,可得出在上单调递增,在上单调递增,可判断B ;由,可判断C ;判断 ,的符号, 的单调性可判断D ;【详解】由已知解析:ACD【分析】由已知得()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,可判断A ;由已知得出2437d -<<-,且()12+3n a n d =-,得出[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d =-,可得出1na 在1,6n n N 上单调递增,1n a 在7n n N ,上单调递增,可判断B ;由()313117713+12203213a a a S a ⨯==<=,可判断C ;判断 n a ,n S 的符号, n a 的单调性可判断D ;【详解】由已知得311+212,122d a a a d ===-,()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,故A 正确;由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩,解得2437d -<<-,又()()3+312+3n a n d n d a =-=-,当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d=-,所以[]1,6n ∈时,1>0na ,7n ≥时,10n a <, 所以1na 在1,6n n N 上单调递增,1n a 在7n n N ,上单调递增,所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列,故B 不正确;由于()313117713+12203213a a a S a ⨯==<=,而120S >,所以0n S <时,n 的最小值为13,故C 选项正确 ;当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,当[]1,12n ∈时,>0n S ,13n ≥时,0n S <,所以当[]7,12n ∈时,0n a <,>0n S ,0n nS a <,[]712n ∈,时,n a 为递增数列,n S 为正数且为递减数列,所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项,故D 正确; 【点睛】本题考查等差数列的公差,项的符号,数列的单调性,数列的最值项,属于较难题.33.ABCD【分析】S12>0,a7<0,利用等差数列的求和公式及其性质可得:a6+a7>0,a6>0.再利用a3=a1+2d =12,可得<d <﹣3.a1>0.利用S13=13a7<0.可得Sn <0 解析:ABCD【分析】S 12>0,a 7<0,利用等差数列的求和公式及其性质可得:a 6+a 7>0,a 6>0.再利用a 3=a 1+2d =12,可得247-<d <﹣3.a 1>0.利用S 13=13a 7<0.可得S n <0时,n 的最小值为13.数列n n S a ⎧⎫⎨⎬⎩⎭中,n ≤6时,n n S a >0.7≤n ≤12时,n n S a <0.n ≥13时,n n S a >0.进而判断出D 是否正确.【详解】∵S 12>0,a 7<0,∴()67122a a +>0,a 1+6d <0.∴a 6+a 7>0,a 6>0.∴2a 1+11d >0,a 1+5d >0,又∵a 3=a 1+2d =12,∴247-<d <﹣3.a 1>0. S 13=()113132a a +=13a 7<0.∴S n <0时,n 的最小值为13. 数列n n S a ⎧⎫⎨⎬⎩⎭中,n ≤6时,n n S a >0,7≤n ≤12时,n n S a <0,n ≥13时,n n S a >0. 对于:7≤n ≤12时,n n S a <0.S n >0,但是随着n 的增大而减小;a n <0, 但是随着n 的增大而减小,可得:n nS a <0,但是随着n 的增大而增大.∴n =7时,n nS a 取得最小值. 综上可得:ABCD 都正确.故选:ABCD .【点评】本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于难题.34.AD【分析】先根据题意得,,再结合等差数列的性质得,,,中最大,,即:.进而得答案.【详解】解:根据等差数列前项和公式得:,所以,,由于,,所以,,所以,中最大,由于,所以,即:解析:AD【分析】先根据题意得1110a a +>,1120a a +<,再结合等差数列的性质得60a >,70a <,0d <,{}n S 中6S 最大,49a a <-,即:49a a <.进而得答案.【详解】解:根据等差数列前n 项和公式得:()111111102a a S +=>,()112121202a a S +=< 所以1110a a +>,1120a a +<,由于11162a a a +=,11267a a a a +=+,所以60a >,760a a <-<,所以0d <,{}n S 中6S 最大,由于11267490a a a a a a +=+=+<,所以49a a <-,即:49a a <.故AD 正确,BC 错误.故选:AD.【点睛】本题考查等差数列的前n 项和公式与等差数列的性质,是中档题.35.ACD【分析】由得,故正确;当时,根据二次函数知识可知无最小值,故错误;根据等差数列的性质计算可知,故正确;根据等差数列前项和公式以及等差数列的性质可得,故正确.【详解】因为,所以,所以,即解析:ACD【分析】由13623a a S +=得100a =,故A 正确;当0d <时,根据二次函数知识可知n S 无最小值,故B 错误;根据等差数列的性质计算可知127S S =,故C 正确;根据等差数列前n 项和公式以及等差数列的性质可得190S =,故D 正确.【详解】因为13623a a S +=,所以111236615a a d a d ++=+,所以190a d +=,即100a =,故A 正确;当0d <时,1(1)(1)922n n n n n S na d dn d --=+=-+2(19)2d n n =-无最小值,故B 错误;因为127891*********S S a a a a a a -=++++==,所以127S S =,故C 正确; 因为()1191910191902a a S a +⨯===,故D 正确.故选:ACD.【点睛】本题考查了等差数列的通项公式、前n 项和公式,考查了等差数列的性质,属于中档题.。
