计算机网络原理实验八、Link States Algorithm的实现
计算机网络中的路由算法

计算机网络中的路由算法路由算法在计算机网络中起着关键的作用,它用于确定数据包在网络中的传输路径。
根据不同的网络拓扑和需求,有多种不同的路由算法被应用。
本文将介绍几种常见的路由算法。
1. 距离矢量算法(Distance Vector Algorithm)距离矢量算法是一种分布式的路由算法,每个节点在路由表中记录到达目的节点的距离向量。
节点之间通过交换距离向量信息来更新路由表,并且通过Bellman-Ford算法来计算最短路径。
该算法简单易实现,但是在大型网络中容易产生计数到无穷大的问题,即由于链路故障等原因产生的无限循环。
2. 链路状态算法(Link State Algorithm)链路状态算法是一种集中式的路由算法,每个节点都会收集与自身相连的链路状态信息,并通过最短路径算法(如Dijkstra算法)计算出到达其他节点的最短路径。
然后,每个节点都将自己的链路状态信息广播给所有其他节点,使得每个节点都有完整的网络拓扑和链路状态信息。
该算法需要节点之间频繁的广播和计算,但是能够保证收敛,即要么找到最短路径,要么不进行路由。
3. 路径向量算法(Path Vector Algorithm)路径向量算法可以看作是距离矢量算法和链路状态算法的结合,它通过回退进行路径检测和避免计数到无穷大的问题。
每个节点在路由表中记录到达目的节点的路径和向量信息,通过交换路径向量信息来更新路由表。
在计算最短路径时,路径向量算法使用类似链路状态算法的Dijkstra算法,但是在寻找路径时,会检查前面的节点是否已经在路径中出现,以避免产生环路。
4. 队列距离矢量算法(Queue Distance Vector Algorithm)队列距离矢量算法是距离矢量算法的一种改进算法,主要解决计数到无穷大问题。
该算法引入了队列和计数器,通过计数器和链路状态信息来确定数据包是否进入队列。
每个节点在路由表中记录到达目的节点的距离向量和队列的长度。
计算机网络实验八

计算机⽹络实验⼋计算机⽹络实验指导书昆明理⼯⼤学信⾃学院实验⼋:计算机⽹络协议分析实验⼀、实验⽬的:了解各种协议的格式与⼯作机制,学习使⽤Wireshaek协议分析⼯具。
通过eNSP抓包⼯具,分析所获取报⽂的内容。
⼆、实验原理:1.TCP协议通讯的双⽅由IP地址和端⼝号标识。
32位序号、32位确认序号、窗⼝⼤⼩。
4位⾸部长度和IP协议头类似,表⽰TCP协议头的长度,以4字节为单位,因此TCP协议头最长可以是4x15=60字节,如果没有选项字段,TCP协议头最短20字节。
URG、ACK、PSH、RST、SYN、FIN是六个控制位。
16位检验和将TCP协议头和数据都计算在内。
2.UDP协议3.IP协议IP数据报的⾸部长度和数据长度都是可变长的,但总是4字节的整数倍。
对于IPv4,4位版本字段是4。
4位⾸部长度的数值是以4字节为单位的,最⼩值为5,也就是说⾸部长度最⼩是4x5=20字节,也就是不带任何选项的IP⾸部,4位能表⽰的最⼤值是15,就是说⾸部长度最⼤是60字节。
8位TOS字段有3个位⽤来指定IP数据报的优先级(⽬前已经废弃不⽤),还有4个位表⽰可选的服务类型(最⼩延迟、最⼤呑吐量、最⼤可靠性、最⼩成本),还有⼀个位总是0。
总长度是整个数据报的字节数。
每传⼀个IP数据报,16位的标识加1,可⽤于分⽚和重新组装数据报。
3位标志和13位⽚偏移⽤于分⽚。
TTL(Time to live)是这样⽤的:源主机为数据包设定⼀个⽣存时间,⽐如64,每过⼀个路由器就把该值减1,如果减到0就表⽰路由已经太长了仍然找不到⽬的主机的⽹络,就丢弃该包,因此这个⽣存时间的单位不是秒,⽽是跳(hop)。
协议字段指⽰上层协议是TCP、UDP、ICMP还是IGMP。
然后是校验和,只校验IP⾸部,数据的校验由更⾼层协议负责。
IPv4的IP地址长度为32位。
4.ICMP报⽂类型ICMP全称Internet Control Message Protocol(⽹际控制信息协议)。
简述link-state路由算法的工作过程及其特点。

Direct Layout Illustrate View ECAD
• 功能
– 铅笔、笔刷、虚幻、加粗等多种处 理功能
– 修正 – 创建布局和曲线 – 层的控制 – 支持TIF, BMP, JPG, PNG等
• 益处
– 数字化“头脑风暴”,开发构思 – 允许非CAD专家参与讨论 – 共享输入的草绘数据
第一章
Creo软件 参数式设计特性
一、 Creo软件概述
• Pro/Engineer:美国参数技术公司(Parametric Technology Corporation,PTC)开发的机械产品设计软件
• PTC成立于1985年,1988年发布 Pro/E 1.0,1988年上 市,三维设计进入参数化时代
维护工程师
二、 Creo参数式设计特性
1. 3 D 实体模型(Solid model)
实体模型:将设计者的设计概念以 最真实的模型在计算机上展现出来
因为系统预设参数(System parameters),使用 者可随时计算出产品的体积、面积、质心、重量、 惯性矩等。用以了解产品的真实性;并补足传统 面架构、线构架(Wireframe)的不足。使用者 在产品设计过程中,可以随时掌握以上设计物理 参数,并减少许多人为计算时间。
View ECAD
• 功能
Sketch
– 查看和分析ECAD数据
– 分类对象、检查PCB数据、跟踪 信号
– 交叉检查原理图和布置图
– 测量位置、网络和器件
– 采用电子方式沟通
– ECAD ↔ MCAD协同
• 益处
– 快速检查
– 离散团队间沟通
– 尽早发现问题
• 使用
– 详细设计,结构、电器设计协作
2-链路状态路由算法的实现
设ቤተ መጻሕፍቲ ባይዱ题目
链路状态路由算法的实现★★
已知技术参数和设计要求
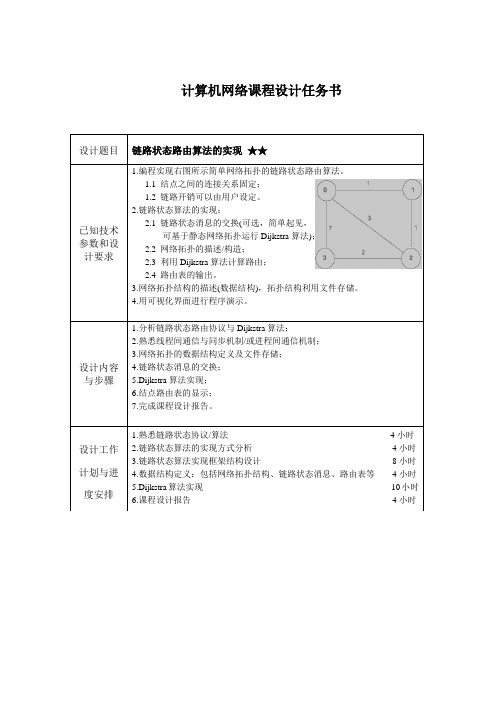
1.编程实现右图所示简单网络拓扑的链路状态路由算法。
1.1结点之间的连接关系固定;
1.2链路开销可以由用户设定。
2.链路状态算法的实现:
2.1链路状态消息的交换(可选,简单起见,
可基于静态网络拓扑运行Dijkstra算法);
6.课程设计报告4小时
4.链路状态消息的交换;
5.Dijkstra算法实现;
6.结点路由表的显示;
7.完成课程设计报告。
设计工作计划与进度安排
1.熟悉链路状态协议/算法4小时
2.链路状态算法的实现方式分析4小时
3.链路状态算法实现框架结构设计8小时
4.数据结构定义:包括网络拓扑结构、链路状态消息、路由表等4小时
5.Dijkstra算法实现10小时
2.2网络拓扑的描述/构造;
2.3利用Dijkstra算法计算路由;
2.4路由表的输出。
3.网络拓扑结构的描述(数据结构),拓扑结构利用文件存储。
4.用可视化界面进行程序演示。
设计内容与步骤
1.分析链路状态路由协议与Dijkstra算法;
2.熟悉线程间通信与同步机制/或进程间通信机制;
3.网络拓扑的数据结构定义及文件存储;
链路状态路由算法原理实验教案

5
小组建立
当成员到达预定数量后, 当成员到达预定数量后,可选择确定完成小 组建立
6
本地信息
建立小组后回到主界面,本节点ID和本地直 建立小组后回到主界面,本节点ID和本地直 连信息已经建立, 连信息已经建立,选择实验的路由算法
7
选择链路状态算法
在发送路由信息窗口出现链路状态算法下的路由信 息的一般格式
实验前的准备
填写实验报告中实验原理部分 分组
2
实 验 软 件 主 界 面
3
建立小组
4~10人一组,互相配合,多多益善。 4~10人一组,互相配合,多多益善。 人一组 建立小组过程: 建立小组过程:设置组名和小组人数
4
建立小组: 建立小组:设置组名和成员数
同一小组成员设置的成员数量应一致 设置完成后选择加入, 设置完成后选择加入,可观察到其他成员加 入的情况
11
测试路由
选择Routed 选择Routed
向各目的发送一份数据报文,报文内容自理 向各目的发送一份数据报文,
路由表中可 以到达目的 的下一站
12
中继节点
数据报文送到中继节 点时, 点时,自动弹出数据 报文接收窗口
实验者根据路由表选 择是转发还是报文已经 到达目的 转发的数据, 转发的数据,须填写 下一站结点的ID 下一站结点的ID13Fra bibliotek目的节点
数据到达目的节点后
实验者可选择查看内 容 同时可观察到该报文 经过的路由器, 经过的路由器,通过 这个信息可以测试路 由是否正确, 由是否正确,是否为 最短路由
14
注意
实验各步骤都需要进行记录
请翔实、忠实地记录实验数据 翔实、忠实地记录实验数据 如果路由发生错误,将小组的记录数据汇总后, 如果路由发生错误,将小组的记录数据汇总后, 分析并发现错误产生的原因。 分析并发现错误产生的原因。
路由算法之链路状态路由算法LS

路由算法之链路状态路由算法LS 把我与谁连接告诉所有的路由器,那么所有的路由器就都具有了⼀幅⽹络图由这副图计算每条具体的路径所以实现的关键在于链路状态信息的可靠分发根据链路状态信息计算路由步骤1. 发现邻接点, 获得邻居的⽹络地址.每⼀个点对点链路发送 HELLO 分组邻居返回响应多个路由器通过LAN连接,路有器的⼀个端⼝有多个邻居,如何抽象?把 LAN 当做⼀个节点 LAN上指定的⼀个路由器来运⾏路由协议2. 测量到每⼀个邻居的代价发送⼀个 ECHO 分组,邻居迅速返回响应测量往返时间, / 2即是到邻居的延迟多测⼏次取平均值3. 构造链路状态分组(邻居信息)LSP (Link-State Packet,链路状态分组)和路由计算相关的项产⽣ LSP节点的ID直接相连的邻居列表到每个邻居的代价和可靠性相关的项序号( sequence number),区分新旧消息年龄( age)更新计时器超时通常⼏⼗分钟⽹络变化时直接连接的链路断开可以⽤链路层协议检测直接连接的邻居下线通过定期发送 “hello” 检测4. 分发链路状态包(发送给所有其它路由器).⽬的:保证所有参加路由的节点得到其它所有节点的链路状态信息的⼀个拷贝⽅法:可靠泛洪(Reliable Flooding)将 LSP发送到所有直接相连的链路收到 LSP 的节点将它转发到所有其它链路存储每个节点的最新 LSP向所有相邻节点转发每个LSP,但不发送给发来该LSP的节点相邻路由器之间有确认和重传的机制控制泛洪规模Packet: 包含⼀个序号保证拥有最新 copy序号存在的问题问题1:序号回转解决:使⽤⼤的序号空间,如32bit问题2:⼀个路由器崩溃了, 将丢失所有序号记录,恢复后从0开始,将会拒绝正常分组问题3:序号本⾝被破坏解决增加 age域 (TTL) 每经过⼀个路由器,age递减 Age=0,抛弃Router: 记录见过的分组 ( router, sequence number )如果 LSP 是 duplicate , 就丢弃Duplicate: LSP序号 is lower当⼀个 LSP 到来时, it wait a short while, ⽽不是⽴即转发当⼀个 LSP 到来, 先放到⼀个保留区等⼀会有新 LSP 到来, ⽐较序号相等,是重复分组,不再转发不同,⽐较年龄,丢弃旧的分组5. 计算到每个节点的最短路径优缺点优点没有慢收敛问题,对坏消息响应迅速代价存储空间开销存储所有的链路状态分组CPU 开销任何拓扑变化都要重新计算最⼩代价树⽐较和 DV对⽐,都要交流信息DV(距离向量)Who: 邻居What:距离向量,可能有不确定(道听途说)的消息使⽤最短路径优先算法,算法复杂度为O(n^2) n个结点(不包括源结点),需要n*(n+1)/2 次⽐较使⽤更有效的实现⽅法,算法复杂度可以达到O(nlogn) 可能存在路由振荡(oscillations)结点会⼴播错误的链路开销每个结点只计算⾃⼰的路由表LS(链路状态)Who: 所有路由器What :LSP,仅通告确定的消息收敛时间不定可能会出现路由循环结点会⼴播错误的路径开销每个结点的路由表被别的结点使⽤,错误会传播到全⽹。
计算机组成原理实验八简单模型计算机实验

计算机组成原理实验八简单模型计算机实验关键信息项:1、实验目的2、实验设备3、实验原理4、实验步骤5、数据记录与分析6、注意事项7、故障处理8、实验结果评估标准11 实验目的本实验旨在通过构建和操作简单模型计算机,深入理解计算机组成原理中的核心概念,包括数据存储、运算处理、指令执行等,培养学生的实际动手能力和对计算机系统的综合理解能力。
111 具体目标1111 掌握简单模型计算机的基本结构和工作原理。
1112 熟悉各种指令的编码和执行过程。
1113 能够运用所学知识设计和实现简单的计算任务。
12 实验设备121 硬件设备计算机主机、实验箱、连接线等。
122 软件工具特定的模拟软件、编程环境等。
13 实验原理131 模型计算机结构包括运算器、控制器、存储器、输入设备和输出设备等主要部件,以及它们之间的连接和协同工作方式。
132 指令系统定义了各种操作指令的格式、功能和编码方式。
133 数据存储与传输说明数据在存储器中的存储方式和在各部件之间的传输机制。
14 实验步骤141 连接实验设备按照正确的方式将计算机主机与实验箱等设备进行连接,并确保连接稳定可靠。
142 启动软件工具打开相应的模拟软件和编程环境,进行初始化设置。
143 设计指令序列根据实验要求,设计一系列的指令来完成特定的计算任务。
144 输入指令到模型计算机通过编程环境将指令输入到模型计算机的存储器中。
145 启动模型计算机运行设置相关参数,启动模型计算机执行指令序列。
146 观察运行过程和结果密切观察模型计算机在执行指令过程中的各种状态变化,以及最终的输出结果。
15 数据记录与分析151 记录实验过程中的关键数据包括指令的执行时间、存储器的状态变化、运算结果等。
152 对数据进行分析对比预期结果,分析实验数据的准确性和合理性,找出可能存在的偏差和错误原因。
16 注意事项161 设备操作规范严格按照设备的操作说明进行连接和使用,避免因不当操作造成设备损坏。
链梯法和b-f法

链梯法和b-f法链梯法(Link State Algorithm)和B-F法(Bellman-Ford Algorithm)是两种常用的网络路由算法,用于在计算机网络中寻找最短路径或最佳路径。
虽然两者在算法基本原理上有所不同,但都是为了解决相同的问题,即在网络中找到最佳的路径。
链梯法是一种逐步迭代的算法,其基本思想是将整个网络划分为多个子网,并通过交换路由信息来构建网络图。
每个路由器根据收集到的链路状态信息,计算出到达目标节点的最佳路径,并将该路径信息广播到整个网络中。
最后,每个节点记录下到达目标节点的最佳路径,并根据该路径来进行数据包转发。
链梯法的优点是收敛速度快、计算复杂度低,但同时也存在着一些问题,如计算延迟大、存储开销大等。
B-F法是一种迭代更新的算法,其基本思想是通过多次迭代更新网络中每个节点的最短路径信息,直到收敛为止。
B-F法通过比较每个节点的当前最短路径和新发现的路径,选择其中较短的路径作为节点的最短路径,并逐渐将最短路径信息从源节点向目标节点进行传播。
B-F法的优点是适用于不同类型的网络,计算复杂度相对较低,但也存在着一些问题,如慢收敛、计算开销大等。
在实际应用中,选择使用链梯法还是B-F法需要根据具体的网络场景和需求来确定。
一般来说,链梯法适用于网络规模较大、带宽充足且稳定的网络,它能够快速进行路径计算,并具有较好的收敛性能。
而B-F法适用于网络规模较小、带宽较为有限或不稳定的网络,它能够适应网络拓扑结构的动态变化,但收敛速度相对较慢。
总结来说,链梯法和B-F法是两种常用的网络路由算法,它们都能够找到最短路径或最佳路径。
在选择具体算法时,需要考虑网络规模、带宽情况、网络拓扑结构的动态变化等因素,根据具体需求和场景来确定最合适的算法。
通过深入理解和研究这两种算法,可以更好地理解和应用网络路由技术,提高计算机网络性能和效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 6 7 8 9 10 11 12 13 14 15
then D(j) = c(u,j) else D(j) = ∞ Loop find i not in N' such that D(i) is a minimum add i to N' update D(j) for all j adjacent to i and not in N' : D(j) = min( D(j), D(i) + c(i,j) ) /* new cost to j is either old cost to j or known shortest path cost to i plus cost from i to j */ until all nodes in N'
printf("\n\n请选择出发节点的编号:"); scanf("%d",&i); printf("请选择目的节点的编号:"); scanf("%d",&j); for(int k=0;k<g.vexnum;k++)/*g.vexnum表示网中的顶点 个数*/ if(i==g.vexs[k].num) i=k;/*在网中找到其编号与输入的 出发景点的编号相同的顶点*/ for(int l=0;l<g.vexnum;l++) if(j==g.vexs[l].num) j=l;/*在网中找到其编号与输入的 目地景点的编号相同的顶点*/ Dijkstra(g,i,j);/*调用Dijkstra函数,用来输出两个景点 间的最短路径*/ } void main() {int i=0,j=0; int b[5]={1,2,3,4,5};/*整型数组,用来给每个顶点的编号进 行赋值*/ char *c[5]={"A","B","C","D","E"};/*字符串指针数组,用来 给每个顶点的名称进行赋值*/ MGraph g;/*定义一个MGraph类型的变量g,用来创建一个无向 网*/ /*建立一个无向网,并用无向网表示节点的平面图*/ int A[5][5]={ /*用INF表示对应顶点间没有直达的路径,用其它整型变量表 示对应顶点间有直达的路径,且路径的长度就是该整型变量的值*/ {0,7,INF,INF,1}, {7,0,1,INF,8}, {INF,1,0,2,INF}, {INF,INF,2,0,2}, {1,8,INF,2,0} }; g.vexnum=5;/*网中顶点的个数为*/ g.arcnum=6;/*网中边的个数为*/ for(i=0;i<g.vexnum;i++)
4.实验分析,回答下列问题 (1)给出LSA算法的主要思想。 答: LSA算法的主要思想为:该算法用迭代算法,其性质是经算法 的第K次迭代后, 可知道K个目的节点的最低费用路径。 A:邻居节点发现与测试:各节点主动测试所有与之相邻的节点的 状态。方法是 周期性的向邻,居节点广播简短的查询报文, 通过接收邻居节点的响应报文,来获取与邻居的状态信息。 B:链路状态信息发布:根据收集到的状态信息,构造一个包含所 有邻居列表在 内的分组LS,并通过洪泛法通告给算法作用区 域内的所有节点。 C:路由选择算法:收到LS分组的节点,采用Dijkstra算法,为每 个节点选择 最短的路径。 (2)通过图表算出任何两个节点之间的最短路径,并给出每个节 点上的转发表。 代码: #include<stdio.h> #include<string.h> #define MAXV 20 #define MAXSIZE 20 #define MAXLEN 500 #define INF 10000/*用表示∞*/ int a=0; typedef struct {int num;
char name[MAXSIZE]; char content[MAXLEN]; }VertexType; typedef struct { int edges[MAXV][MAXV]; int vexnum,arcnum; VertexType vexs[MAXV]; }MGraph; int visited[MAXV]; int p[MAXV]; void Path(MGraph g,int i,int j,int k) /*确定路径上第k+1个节点的编号*/ {int s; if(p[k]==j)/*找到一条路径*/ { a++;/*路径的条数值加*/ printf("第%d条:\n",a); for(s=0;s<=k-1;s++)/*输出一条路径*/ printf("%s->",g.vexs[p[s]].name); printf("\n"); } s=0; while(s<g.vexnum) {if(s!=i)/*保证找到的是简单路径*/ {if(g.edges[p[k]][s]!=INF&&visited[s]==0) /*当vk与vs之间有边存在且vs未被访问过*/ {visited[s]=1;/*置访问标志位为,即已访问的*/ p[k+1]=s;/*将顶点s加入到p数组中*/ Path(g,i,j,k+1); visited[s]=0;/*重置访问标志位为,以便该顶点能被重新 使用*/ }} s++; } }
A B E C D 7 1 8 1 2 2
通过链路状态算法计算A点到其它各点的cost,最终输出A的路由 表。 算法提示: Initialization: 2 N' = {u} /*u is source node*/ 3 for all nodes j /* j is dest node*/ 4 if j adjacent to u
{ int dist[MAXV],path1[MAXV]; int s[MAXV]; int mindis,i,j,u,n=g.vexnum; for(i=0;i<n;i++) {dist[i]=g.edges[v0][i];/*距离初始化*/ s[i]=0;/*s[]置空*/ if(g.edges[v0][i]<INF)/*路径初始化*/ path1[i]=v0; else path1[i]=-1; } s[v0]=1;path1[v0]=0;/*源点编号v0放入s中*/ for(i=0;i<n;i++) {mindis=INF; u=-1; for(j=0;j<n;j++)/*选取不在s中具有最小距离的节点u*/ if(s[j]==0&&dist[j]<mindis) {u=j; mindis=dist[j]; } s[u]=1;/*顶点u加入s中*/ for(j=0;j<n;j++)/*修改不在s中的节点的距离*/ if(s[j]==0) if(g.edges[u][j]<INF&&dist[u]+g.edges[u][j]<dist[j]) /*修正dist[i],path1[i]*/ {dist[j]=dist[u]+g.edges[u][j]; path1[j]=u; } } Dispath(g,dist,path1,s,n,v0,p);/*输出最短路径*/ } void Search(MGraph g) {printf("节点:\n1.A\n2.B\n3.C\n4.D\n5.E"); int i=0,j=0; char s=0;
实验八、Link States Algorithm的实现 序号: 姓名: 学号: 成绩
1.实验目的: 通过编程模拟实现LSA. 2.实验环境: 软件开发平台,可以使用任何编程语言。 3.实验要求 (1)求网络中任何两个结点之间的最短路径(网络中至少有4个节 点)。 (2)得到任何一个节点上的转发表。 4.实验内容、拓扑结构
for(j=0;j<g.vexnum;j++) g.edges[i][j]=A[i][j];/*建立无向网的邻接矩阵*/ for(i=0;i<g.vexnum;i++) {g.vexs[i].num=b[i];/*给每个节点一个编号*/ strcpy(g.vexs[i].name,c[i]);/*通过字符串复制函数给每 个节点一个名称*/ } int select;/*定义一个整型变量,用来输入不同的选择*/ do/*可提供循环输入选择,当输入的选择为时,退出循环*/ {printf("\n1.求节点间的最短路径0.退出"); printf("\n请选择操作:"); scanf("%d",&select); switch(select) /*判断select的值,根据其值跳转到相应的子模块继续执 行*/ { case 1: Search(g);/*节点间的最短路径*/ break; case 0:/*退出程序*/ break;} }while(select!=0);/*当select的值不为时,继续循环*/ } 截图:
void Display(MGraph g,int i,int j) {int k; p[0]=i; for(k=0;k<g.vexnum;k++) visited[i]=0;/*初始化各节点的访问标志位*/ a=0;/*初始化路径的条数*/ Path(g,i,j,0);/*通过调用path函数,找到从vi到vj的所有 路径并输出*/ } void Path2(MGraph g,int path1[],int i,int v0) {int k; k=path1[i]; if(k==v0)/*找到最短路径,则返回*/ return; Path2(g,path1,k,v0);/*否则,递归调用之*/ printf("%s->",g.vexs[k].name);/*依次输出路径中的节点 */ } void Dispath(MGraph g,int dist[],int path1[],int s[],int n,int v0,int i) { if(s[i]==1&&i!=v0) /*当v0不等于i,且i∈s*/ {printf("\n从%s到%s的最短路径 是:\n",g.vexs[v0].name,g.vexs[i].name); printf("%s->",g.vexs[v0].name); Path2(g,path1,i,v0);/*调用ppath函数,输出路径中的节 点*/ printf("%s ",g.vexs[i].name); printf("路径长度:%d\n",dist[i]); } } void Dijkstra(MGraph g,int v0,int p)
