机器人导论-英文版
《机器人学导论》课程教学大纲

《机器人学导论》课程教学大纲课程名称:机器人学导论课程编号:BF(英文):Introduction to Robotics先修课程:线性代数、机构学、自动控制适用专业:机械电子、机械工程及自动化开课系(所):机械与动力工程学院机器人研究所教材和教学参考书:1.1.教材:机器人学、蔡自兴、清华大学出版社、20002.教学参考书: 机器人学导论,约翰J.克雷格、西北工业大学出版社、1987 注:上述教材和参考书将根据教材课购买情况可互换一、一、本课程的性质、地位、作用和任务面对21世纪知识经济时代的机遇与挑战,人类(地球人)正在以非凡的智慧构思新世纪的蓝图。
世界的明天将更加美好。
但是,地球人在发展中也面临着环境、人口、资源、战争和贫困等普遍问题,同时还要学会与机器人共处,这是21世纪地球人必须正视和处理的紧要问题,是影响地球人生存和发展的休戚与共的重大事件。
机器人学是一门高度交叉的前沿学科,机器人技术是集力学、机械学、生物学、人类学、计算机科学与工程、控制论与控制工程学、电子工程学、人工智能、社会学等多学科知识之大成,是一项综合性很强的新技术。
自第一台电子编程工业机器人问世以来,机器人学已取得令人瞩目的成就。
正如宋健教授1999年7月5日在国际自动控制联合会第14届大会报告中所指出的:“机器人学的进步和应用是本世纪自动控制最有说服力的成就,是当代最高意义上的自动化。
”机器人技术的出现与发展,不但使传统的工业生产面貌发生根本性的变化,而且将对人类的社会生活产生深远的影响。
二、二、本课程的教学内容和基本要求1.1.绪言简述机器人学的起源与发展,讨论机器人学的定义,分析机器人的特点、结构与分类。
2.2.机器人学的数学基础空间任意点的位置和姿态变换、坐标变换、齐次坐标变换、物体的变换和逆变换,以及通用旋转变换等。
3.3.机器人运动方程的表示与求解机械手运动姿态、方向角、运动位置和坐标的运动方程以及连杆变换矩阵的表示,欧拉变换、滚-仰-偏变换和球面变换等求解方法,机器人微分运动及其雅可比矩阵等4.4.机器人动力学机器人动力学方程、动态特性和静态特性;着重分析机械手动力学方程的两种求法,即拉格朗日功能平衡法和牛顿-欧拉动态平衡法;然后总结出建立拉格朗日方程的步骤5.5.机器人的控制机器人控制与规划6.6.机器人学的现状、未来包括国内外机器人技术和市场的发展现状和预测、21世纪机器人技术的发展趋势、我国新世纪机器人学的发展战略等。
机器人学导论(双语)

天津大学本科课程描述(表格内容:题头为加黑小四号宋体,内容为普通小四号宋体,1.5倍行距)学院:电气与自动化工程专业名称:自动化本科课程信息课程名称:机器人学导论(双语) 课程编号:2030373学分: 2 学时:32课程描述:本课程为双语教学课程,是针对自动化专业本科生开设的专业选修课。
本课程主要学习有关机器人的基础知识、机器人运动与齐次变换、机器人正/逆运动学、机器人速度运动学、机器人动力学等内容。
通过本课程的学习,使学生对机器人学的基础知识有一个全面的理解和应用,同时能够掌握基本的机器人学英语术语。
课程名称:机器人学导论(双语) 课程编号:2030373 学分: 2 学时:32课程描述:本课程为双语教学课程,是针对自动化专业本科生开设的专业选修课。
本课程主要学习有关机器人的基础知识、机器人运动与齐次变换、机器人正/逆运动学、机器人速度运动学、机器人动力学等内容。
通过本课程的学习,使学生对机器人学的基础知识有一个全面的理解和应用,同时能够掌握基本的机器人学英语术语。
Course Description(表格内容:题头为加黑小四号Times New Roman,内容为普通小四号Times New Roman,1.5倍行距)School:School of ElectricalEngineering andAutomationMajor:Automation EngineeringInformation of undergraduate courses:Title:Introduction of Robotics Code:2030373 Credit points:32 Hours: 2Course Description: Spatial description of rigid body, homogeneous transformation; link description of robot manipulator, the derivation of D-H table; the solvability of inverse kinematics problem, examples of PUMA 560 robots' inverse kinmeatics; linear and angular velocity of rigid bodies, derivation of Jacobian matrix; using Larange and Netwon-Euler methods to calculate dynamic equations for a rigid bodyTitle:Introduction of Robotics Code:2030373 Credit points:32 Hours: 2Course Description: Spatial description of rigid body, homogeneous transformation; link description of robot manipulator, the derivation of D-H table; the solvability of inverse kinematics problem, examples of PUMA 560 robots' inverse kinmeatics; linear and angular velocity of rigid bodies, derivation of Jacobian matrix; using Larange and Netwon-Euler methods to calculate dynamic equations for a rigid body。
机器人导论英语资料考试

1. A robot may not injure a human being or, through inaction, allow a human being to come toharm.2. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.3. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.4. A robot may not injure a human being or, through inaction, allow a human being to come toharm.5. A robot must obey the orders given to it by human beings, except where such orders would Arobot may not injure a human being or, through inaction, allow a human being to come to harm.6. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.7. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.8. A robot may not injure a human being or, through inaction, allow a human being to come toharm.9. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.10. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.11. conflict with the First Law.12. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.13. A robot may not injure a human being or, through inaction, allow a human being to come toharm.14. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.15. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.16. A robot may not injure a human being or, through inaction, allow a human being to come toharm.17. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.18. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.19. A robot may not injure a human being or, through inaction, allow a human being to come toharm.20. A robot must obey the orders given to it by human beings, except where such orders wouldconflict with the First Law.21. A robot must protect its own existence as long as such protection does not conflict with the Firstor Second Law.22.。
第一学期第六讲机器人导论
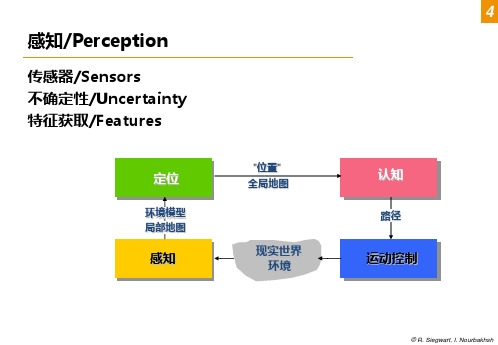
交叉敏感度/Cross-sensitivity
对与目标参数正交的环境参数的敏感度
误差与准确度/Error & Accuracy
传感器输出值与真实值之间的差
error
4.1.2
m =测量值 ,v = 真实值
移动机器人需要感知、分析和解释周围的状态 真实环境中的测量是动态变化并产生误差的. 例如:
变化的光照条件/changing illuminations 镜面产生的反射/specular reflections 吸收声光的表面/Light or sound absorbing surfaces 机器人传感器对机器人姿态和机器人环境动力学的交叉敏感度
光学陀螺仪/Optical Gyroscopes
商用开始于80年代初期在飞机上安装使用. 观学陀螺仪/Optical gyroscopes
利用同一光源发射的两个单色束角或激光光束获得 速度(导向)传感器. 一束顺时针行进通过光纤, 另一束绕圆柱体逆时针行进 激光光束沿着旋转方向行进 行进路径偏短-> 表现出较高的频率 两束光频率之差Df 正比于圆柱体的角速度 W 新的固体光学陀螺仪也是基于同样原理采用微加工工艺制作.
© R. Siegwart, I. Nourbakhsh
一般分类/General Classification (1)
/触觉 /轮置电机传感器
/朝向
4.1.1
© R. Siegwart, I. Nourbakhsh
一般分类/General Classification (2)
/地面信标 /主动测距
机器人学导论 chapter2

DONG QiuhuangCollege of Mechanical and Electronic Engineering, FAFU.Mathematical BasisManipulator-Mechanism Design 2Mathematical basisIntroduction4and tools will be some sort of mechanism.How to define the manipulate mathematical quantities (数学量)that represent location of the body?IntroductionRigid Body Motion (刚体运动)Position andOrientation Mathematical Quantities (Coordinates)Velocities, Forces (速度和力)must define coordinate systems representation.Mathematical basisDescription (描述)83×1 position vector.DescriptionCatesian coordinate system (笛卡尔坐标系):9Description10Description of Orientations (姿态描述)position , but also need to describe its orientation in the space.DescriptionHow to describe the orientation of a body ?Description of Orientationsreference system.Description12Description of OrientationsDescription1314Description of OrientationsDescriptionDescription of OrientationsDescriptionObtain the projection of that vector onto the unit directions of its reference coordinate.Example:Compute the Rotation MatrixRotation about axisExample:Rotation about axis:Rotation about axis:Description of OrientationsDescription19Description20manipulator hand is a position DescriptionWe define such a entity which contain the pair of position and Mathematical basiscoordinate system .工具坐标系目标坐标系固定坐标系基座坐标系Mapping23Mathematics of changing descriptions of the same quantity from frame to frame.1. Translation(平移)已知S 点在坐标系{B}中的表达,那么在坐标系{A}中如何表达?242. Rotation (旋转)求矢量在坐标系{A}三个主轴上的投影。
机器人学导论chapter6

机器人学导论chapter6Manipulator DynamicsOutlineIntroduction运动学控制Why do we need to study the dynamics 4Given a set of force or torques applied the manipulator, try to calculate how the manipulator Given a desired trajectory, try to find out the desired torque inputs to cause this motion. E.g.: ControlContents of Dynamics:5RobotTwo methods for formulating dynamics model :OutlineAcceleration of a Rigid Bodycalled linear acceleration /angular acceleration :Vectors of linear acceleration / angular acceleration can be described in different reference frame1.Linear acceleration of rigid body:9frame {A} and frame {B} have coincident origins, the velocity This form of the equation will be useful when deriving the corresponding acceleration equation.1.Linear acceleration of rigid body:10By differentiating1.Linear acceleration of rigid body:11origins are not coincident, we add one term which gives the origin of {B}:The above equation will be utilized to calculate thelinear acceleration of a manipulator (both revolute joint and prismatic joint). 2.Angular acceleration of rigid body: Consider that frame {B} rotate with respect to frame {A} with and frame {C} rotate with respect to frame {B} with , we can obtain:By differentiating:Applying equation (6.6):This equation will be utilized to calculate the angularacceleration of the links of a manipulator.Outline Mass DistributionMass Distributionexpressed in the following matrix form:whereMass moments of inertia Mass products of inertia Mass Distribution16As note, the inertia tensor is a functionof the location and orientation of thereference frame.{C}Where {C} is located at the center ofmass of the body.Mass Distributionwhereparallel-axis theorem:If the reference frame {C}(body frame) are selected such that theproducts of inertia being set to zero, the axes of this reference frameare called “principal axes(主轴)”, and the mass moment arenoted as “principal moments of inertia(主惯性矩)”.Outline1. Newton-Euler Dynamic Formulation 19rate of change of the linearmomentum is equal to theapplied forceLinear Momentum (动量) 1. Newton-Euler Dynamic Formulation 20Angular Momentum (角动量)Inertia Tensor1. Newton-Euler Dynamic Formulation where m is the mass of a rigid body, represent inertia tensor , F C is the external force on the center of gravity, N is the torque on the rigid body, v C represent the translational velocity , while ω is the angular velocity .2. Iterative (递推)Newton-Euler Dynamic Formulation 2.1 Compute velocities and accelerations Angular velocity from link to link:By differentiating:When joint i +1 is prismatic:2. Iterative (递推)Newton-Euler Dynamic Formulation The linear velocity of each link-frame origin:By differentiating: When joint i +1 is prismatic:The linear acceleration of the center of mass of each link:2. Iterative (递推)Newton-Euler Dynamic Formulation2. Iterative (递推)Newton-Euler Dynamic Formulation The torque-balance relationship for link i :2. Iterative (递推)Newton-Euler Dynamic Formulation 26Rearrange the force and torque equations:These equations are evaluated link by link, starting from linkn and working inward toward the base of the robot (inward force iterations ).2. Iterative (递推)Newton-Euler Dynamic Formulation As in the static case, the required joint torque are Found by taking the component of the torque Applied by one link on its neighbor: prismatic:2. Iterative (递推)Newton-Euler Dynamic Formulation 28Outward iterations: i: 0→n292. Iterative (递推)Newton-Euler Dynamic Formulation 2. Iterative (递推)Newton-Euler Dynamic Formulation Inward iterations: i: n →1移动关节转动关节2. Iterative (递推)Newton-Euler Dynamic Formulation32Newton-Euler Formulation of Manipulator Dynamics All mass exists as a point mass : The vectors that locate the Center of mass for each link:The inertia tensor for each link:33Newton-Euler Formulation of Manipulator Dynamics : There are no force acting on the end-effector:The base of the robot is not rotating:To include gravity force, we will use:34Newton-Euler Formulation of Manipulator Dynamics : The rotation between successive 35Newton-Euler Formulation of Manipulator Dynamics iteration for link 1:36Newton-Euler Formulation of Manipulator Dynamics iteration for37Newton-Euler Formulation of Manipulator Dynamics iteration for 38Newton-Euler Formulation of Manipulator Dynamics : The outward iteration for 39Newton-Euler Formulation of Manipulator Dynamics Example:Step 4: The outward iteration for link 2:40Newton-Euler Formulation of Manipulator Dynamics : The outward iteration for link 2:41Newton-Euler Formulation of Manipulator Dynamics : The inward iteration for 42Newton-Euler Formulation of Manipulator DynamicsNewton-Euler Formulation of Manipulator Dynamics 44Newton-Euler Formulation of Manipulator Dynamics torque: Written in Matrices Form:Newton-Euler Formulation of Manipulator Dynamics Example:有效惯量(effective inertial):关节i 的加速度在关节i 上产生的惯性力Newton-Euler Formulation of Manipulator Dynamics 耦合惯量(coupled inertial):关节i,j 的加速度在关节j ,i 上产生的惯性力Newton-Euler Formulation of Manipulator Dynamics 向心加速度(acceleration centripetal)系数关节i,j 的速度在关节j ,i 上产生的向心力Newton-Euler Formulation of Manipulator Dynamics 哥氏加速度(Coriolis accelaration)系数:关节j,k 的速度引起的在关节i 上产生的哥氏力(Coriolis force)Newton-Euler Formulation of Manipulator Dynamics 重力项(gravity):关节i,j 处的重力OutlineLagrangian Formulation of Manipulator Dynamics 51Lagrangian Formulation of Manipulator Dynamics522-links manipulatorand Potential Energy Lagrangian Formulation of Manipulator Dynamics 53Example:2-links manipulatorKinetic Energy K 2 and Potential Energy P 2 of link 2:where Lagrangian Formulation of Manipulator Dynamics542-links manipulatorLagrangian Formulation of Manipulator Dynamics55OutlineFormulation Manipulator Dynamics in Cartesian Space The above dynamic equations is developed interms of the manipulator joint angles (jointspace).We could use the serial-link nature ofmechanism to advantage in deriving theequations.Sometimes, it might be desirable to express thedynamics with respect to Cartesian variablesform.57Formulation Manipulator Dynamics in Cartesian Space58 whereSummarySummarize steps to form Lagrangian Equation of n-link。
学年第二学期第四讲机器人导论
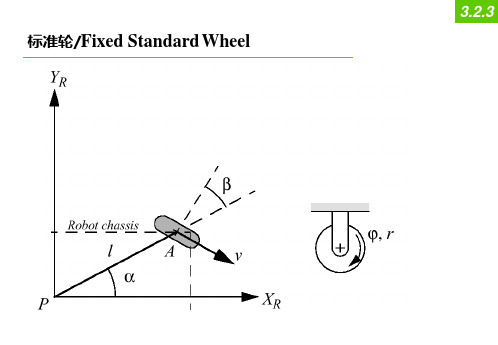
机器人的底盘运动学由一组独立的约束组成
rankC1(s )
C,1(s ) 秩越大, 移动受到的约束越多
从数学上来讲
m dimNC1(s ) 3 rankC1(s )
无所标有准方轮向情都形受到约ra束nkCr1a(nksC)1(0s ) 3
0 rankC1(s ) 3
例如
单轮: 仅有一个固定的标准轮
N f Ns 1
C1(
s
)
C1 f
C1s (
s
)
N f Ns 3
3.2.5
差动机器人案例/Example: Differential Drive Robot
• 详见黑板上的推导过程/Presented on blackboard
YI
YR
YI
XR
XR
YR
P
XI
XI
差动机器人案例/Example: Omnidirectional Robot
DDOF m DOF
•完整性机器人 完整性运动学约束可以显式的表示成仅是位置变量的函数 非完整约束需要 微分关系, 例如位置变量的导数 固定和转向标准轮形成的是非完性整约束 完整性的机器人,当且仅当
DOF= DDOF
全向机器人:DOF= DDOF=3
3.4.2
完整性机器人实例:锁定转向的自行车
3.4.3
路径 / 轨迹 : 双转向/Two-Steer
自行车:
DDOF = 1; DOF=3
全向小车:
DDOF=3; DOF=3
M m s 11
M m s 11
移动机器人工作空间: 自由度和完整性 Degrees of Freedom, Holonomy
移动自由度/DOF degrees of freedom: 机器人姿态可达的能力
(麻省理工)机器人学导论-类人机器人与生物感应机器人

Photo removed for copyright reasons.
Amputee with force feedback. MIT Leg Lab/Media Lab, Hugh Herr
Hami Kazerooni’s Robotic Exoskeleton
UC Berkeley, Human Engineering and Robotics Lab
Snake Robots by Shigeo Hirose
(Courtesy of Prof. Shigeo Hirose. Used with permission.)
Biologically-Inspired Robots
(Courtesy of MIT. Used with permission.)
Shape Memory Alloy Actuators
H N N H H N N H H N
Electroactive Polymer Actuators
Carbon Nanotube Actuator
Courtesy of NASA JPL.
Strain
Photos removed for copyright reasons.
Figures removed for copyright reasons.
Stanford Cockroach Robot
Mark Cutkosky
Biomimetic Design and Fabrication of a Hexapedal Running Robot
Stanford University, Center for Design Research
Torso
Inertial Force Acceleration Gravity Reaction Force from the Floor
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Outline
Introduction Robot Components Kinematics Dynamics Control Motion Planning Simulation
Outline
Introduction Robot Components Kinematics Dynamics Control Motion Planning Simulation
History
The idea of robot goes back to ancient time of china.
The Spring and Autumn Period, our country had a renowned carpenter Lu Ban(鲁班). He was also an inventor in the mechanical aspect, according to “Mo Jing”(《墨经》) records. Once he had made a wooden bird that could in the aerial flight “on three days”, which manifest working people's intelligent wisdom in our country.
张 衡
计里鼓车
History
The idea of robot goes back to ancient time of china.
诸葛亮
Eastern Han Dynasty Three Kingdom era, Shu Prime Minister Zhuge Liang created a ancient transport vehicle called “wooden cattle and walking horse” successfully, and shipped the military provisions to the warfront with it.
木牛流马
History
The idea of robot goes back to ancient time in the world.
The 2nd century B.C., the ancient Greece person in Alexander time‘s has invented the most primitive robot “ automaton”. By the power of the water, the air and the steam pressure, the statue(雕像) can move and even open the door as well as sing.
Introduction
History Definition Robotics Types of Robots
History
HistoryΒιβλιοθήκη The idea of robot goes back to ancient time of over 3000 years ago in the world.
History
The idea of robot goes back to ancient time of china.
The 1800 year‘s ago, Han Dynasty, great scientist Zhang Heng has not only invented the seismograph(地动仪) but also the count drum vehicle(计里鼓车). On the vehicle, the wooden figurine beats a drum each mile and strikes a clock every ten miles.
The Western Zhou Dynasty, our country‘s skilled craftsman Yan (偃师)developed the actor who could sing and dance well, this was the robot which our country recorded most early.
History
The idea of robot goes back to ancient time in the world.
Leonardo da Vinci created many human-inspired, robot-like sketches, designs, and models in the 1500’s.
The 1738 year, French talent technician Jake ·Wore ·Wack has invented a machine duck. It can quack calls, swim and drink water, even eat food and drains. The original intention of Wack is to perform the biological function with the mechanization to carry on the medicine analysis.
Introduction to robotics
Huashan Feng
School of Mechanical Engineering, NPU. Shaanxi Engineering & Technology Research Center of Special Digital Manufacturing Equipment.
References
S. K. SAHA. Introduction to Robotics. China Machine Press
References
John J. Craig 贠超 等译 Introduction to Robotics
Mechanics and Control.
