高一三角同步练习5(同角三角函数的基本关系式)
高一数学同角三角函数的基本关系式和诱导公式试题答案及解析

高一数学同角三角函数的基本关系式和诱导公式试题答案及解析1.已知,,则角的终边在第()象限A.一B.二C.三D.四【答案】B【解析】由题意,确定的象限,然后取得结果 .由,得在第二、四象限,由,得在第二、三象限,所以在第二象限.,故选B【考点】任意角的三角函数的定义.2.已知,则= ;【答案】【解析】分子分母同除,便会出现,【考点】三角函数的计算3.已知,且为第三象限角,(1)求的值;(2)求的值。
【答案】(1)(2)【解析】(1)由,再结合第三象限,余弦值为负,算出结果(2)先化简上式,根据,再结合(1)算出结果。
试题解析:(1)且(2分)为第三象限角(4分)(2)==(7分)=(8分)【考点】同角三角函数基本关系的运用以及三角函数的化简.4.已知,那么角是()A.第一或第二象限角B.第二或第三象限角C.第三或第四象限角D.第一或第四象限角【答案】B【解析】要,即,因此角是第二或第三象限角,故选择B.【考点】同角三角函数基本关系及三角函数值的符号确定.5.已知.【答案】.【解析】对式子两边平方,得,从而.【考点】同角三角函数基本关系(平方关系),注意通过平方可与联系.6.已知是第三象限角,且.(1)求的值;(2)求的值【答案】(1);(2).【解析】解题思路:(1)先求,再求,进而求;(2)联立方程组,解得,进而求所求值.规律总结:涉及“”的“知一求二”问题,要利用以下关系式:;.注意点:由的值,求的值,要注意结合角的范围确定符号.试题解析:,是第三象限角,由得.【考点】同角三角函数基本关系式.7.设函数(1)求;(2)若,且,求的值.(3)画出函数在区间上的图像(完成列表并作图)。
(1)列表(2)描点,连线【答案】(1)2;(2);(3)见解析【解析】(1)由正弦函数周期公式得,=,即可求得;(2)将代入的解析式,得到关于的方程,结合诱导公式即可求出,再利用平方关系结合的范围,求出,再利用商关系求出;(3)先由为0和算出分别等于,,在(,)分别令取,0,,求出相应的值和值,在给定的坐标系中描出点,再用平滑的曲线连起来,就得到所要作的图像.试题解析:(1),2分(2)由(1)知由得:, 4分∵∴ 6分∴. 8分(其他写法参照给分)(3)由(1)知,于是有(1)列表11分(2)描点,连线函数 14分【考点】正弦函数周期公式;诱导公式;同角三角函数基本关系式;五点法作图8.已知且是第四象限角,则A.B.C.D.【答案】A【解析】∵=,∴,又∵是第四象限角,∴==,故选A.由诱导公式知,=,∴,由是第四象限角知,,结合同角三角函数基本关系中的平方关系得==.【考点】诱导公式;同角三角函数基本关系式;三角函数在各象限的符号9.已知,.(1)求;(2)求的值.【答案】(1);(2).【解析】(1)由同角三角函数的基本关系:,,结合条件,可得,再由可知,从而;(2)由(1)可知,可将欲求值的表达式化为与只有关的,根据齐次的数学思想,可分子分母同时除以,从而可得:.试题解析:(1)∵,,∴, 2分又∵,∴, 4分∴; 6分(2) 9分12分.【考点】同角三角函数基本关系.10.已知为锐角,则 .【答案】.【解析】∵为锐角,,∴,,∴.【考点】1.同角三角函数基本关系;2.两角和的正切公式.11.已知x,y均为正数,,且满足,,则的值为.【答案】【解析】因为,所以而所以由得,因此或∵x、y为正数,∴【考点】同角三角函数关系,消参数12.已知的值为()A.-2B.2C.D.-【答案】D【解析】由原式可得,解得.【考点】同角三角函数间的基本关系.13.已知,则的值为 .【答案】【解析】,即,又,故.【考点】诱导公式,同角三角函数的基本关系式.14.已知:,其中,则=【答案】【解析】因为,所以,又因,所以,.【考点】诱导公式.15.已知角的终边过点.(1)求的值;(2)若为第三象限角,且,求的值.【答案】;【解析】(1)由角的终边过点求出,利用诱导公式化简即可;(2)由为第三象限角,,可求出,结合(1)求出,利用展开式即可(1)因为的终边过点,所以,而;(2)因为为第三象限角,且,,故【考点】三角函数的定义,诱导公式,同角三角函数基本关系式,两角和与差的三角函数16.已知是第四象限的角,则= .【答案】【解析】是第四象限的角,则,而.【考点】二倍角公式、同角三角函数的基本关系.17.已知()A.B.C.D.【答案】A【解析】由即①由即②所以①+②可得即即,选A.【考点】1.同角三角函数的基本关系式;2.两角差的余弦公式.18.已知(1)化简;(2)若是第三象限角,且,求的值.【答案】(1) ;(2) .【解析】(1)根据诱导公式进行化简;(2)首先化简,根据第三象限角,同角基本关系式求,确定的值.试题解析:解:(1);. (6)(2),又是第三象限角,,.. (6)【考点】1.诱导公式;2同角基本关系式.19.比较大小:(用“”,“”或“”连接).【答案】>.【解析】在单位圆中,做出锐角1的正切线、正弦线、余弦线,观察他们的长度,发现正切线最长,余弦线最短,故有 tan1>sin1>cos1>0.【考点】三角函数线.20.函数在区间上的最大值为,则实数的值为( )A.或B.C.D.或【答案】A【解析】因为,令,故,当时,在单调递减所以,此时,符合要求;当时,在单调递增,在单调递减故,解得舍去当时,在单调递增所以,解得,符合要求;综上可知或,故选A.【考点】1.同角三角函数的基本关系式;2.二次函数的最值问题;3.分类讨论的思想.21.已知函数(1)求函数的最小正周期及在区间上的最大值和最小值;(2)若,求的值.【答案】(1)(2)【解析】(1)先利用诱导公式,二倍角公式,化一公式将此函数化简为的形式,利用周期公式,求周期,用x的范围求出整体角的范围,结合三角函数图像求其最值。
高中数学-同角三角函数的基本关系式练习

高中数学-同角三角函数的基本关系式练习34,选D. 答案:D5.已知θ∈(0,2π),且sin θ,cos θ是方程x 2-kx +k +1=0的两个实根,求k ,θ的值.解析:依题意有sin θ+cos θ=k ,① sin θcos θ=k +1,②又(sin θ+cos θ)2=1+2sin θcos θ, 所以k 2-2k -3=0,解得k =3或k =-1, 显然|sin θcos θ|=|k +1|≤1,因此k =-1,代入①②得⎩⎪⎨⎪⎧sin θ+cos θ=-1,sin θcos θ=0,从而⎩⎪⎨⎪⎧sin θ=0,cos θ=-1或⎩⎪⎨⎪⎧sin θ=-1,cos θ=0.又θ∈(0,2π),所以θ=π或3π2.(限时:30分钟)1.已知α是第四象限角,cos α=1213,则sin α等于( )A.513 B .-513 C.512 D .-512解析:∵α是第四象限角, ∴sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫12132=-513.答案:B2.已知tan α=-12,则2sin αcos αsin 2α-cos 2α的值是( ) A.43 B .3 C .-43D .-3解析:2sin αcos αsin 2α-cos 2α=2tan αtan 2α-1,将tan α=-12代入得: 2sin αcos αsin 2α-cos 2α=2×⎝ ⎛⎭⎪⎫-1214-1=43,故选A. 答案:A 3.化简⎝⎛⎭⎪⎫1sin α+1tan α(1-cos α)的结果是( )A .sin αB .cos αC .1+sin αD .1+cos α解析:原式=⎝ ⎛⎭⎪⎫1sin α+cos αsin α(1-cos α)=1+cos α1-cos αsin α=sin 2αsin α=sin α. 答案:A4.已知sin αcos α=18,且π<α<5π4,则cos α-sin α的值为( )A.32 B .-32C.34 D .-34解析:∵(cos α-sin α)2=1-2sin αcos α=1-2×18=34,且π<α<5π4,∴cos α<sin α,∴cos α-sin α<0,∴cos α-sin α=-34=-32. 答案:B5.已知sin α-cos α=-52,则tan α+1tan α的值为( ) A .-4 B .4 C .-8 D .8解析:tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=1sin αcos α.∵sin α-cos α=-52,∴1-2sin αcos α=54, ∴sin αcos α=-18,∴1sin αcos α=-8.答案:C6.已知1+sin x cos x =-13,则cos xsin x -1的值等于( )。
人教版数学高一B版必修4同步训练1.2.3同角三角函数的基本关系式

1.2.3 同角三角函数的基本关系式知识点一:平方关系1.若α是第四象限角,cosα=1213,则sinα等于 A.513 B .-513 C.512 D .-5122.化简1-2sin4cos4的结果为A .sin4+cos4B .sin4-cos4C .cos4-sin4D .-sin4-cos43.已知cosα=15,且tanα<0,则sinα的值为 A .±265 B.612 C .- 265 D .±6124.化简sin 2α+cos 2αsin 2α+cos 4α=__________.5.化简1-2sin10°·cos10°sin10°-1-sin 210°的值为__________. 知识点二:商数关系6.已知sinα=35,α∈(0,π),则tanα的值为 A.43 B.34 C .±34 D .±437.已知cosθ=35且3π2<θ<2π,那么tanθ的值为 A.43 B .-43 C.35 D .-34 8.若tanα=32,则4sinα+cosα5sinα-2cosα的值等于 A.1411 B .2 C .-109 D.1411或10199.下列四个命题可能成立的是A .sinα=12且cosα=12B .sinα=0且cosα=-1C .tanα=1且cosα=-1D .tanα=-1且sinα=3210.已知α是第四象限角,tanα=-512,求sinα.能力点一:利用基本关系式求值11.若角α的终边落在直线y =-x 上,则sinα1-sin 2α+1-cos 2αcosα的值等于 A .0 B .2 C .-2 D .2tanα12.已知tanα=-12,则2sinαcosαsin 2α-cos 2α的值是 A.43 B .3 C .-43D .-3 13.若sinx +sin 2x =1,则cos 2x +cos 4x =__________.14.(2010全国高考Ⅱ,文13)已知α是第二象限的角,tanα=12,则cosα=__________. 15.已知sinα+cosαsinα-cosα=2,求下列各式的值: (1)3sinα-cosα2sinα+3cosα; (2)sin 2α-2sinαcosα+1.16.已知sinα=45,求tanα的值.能力点二:利用基本关系式化简17.使1-cosα1+cosα=cosα-1sinα成立的α的范围是A .{α|2kπ-π<α<2kπ,k ∈Z }B .{α|2kπ-π≤α≤2kπ,k ∈Z }C .{α|2kπ+π<α<2kπ+3π2,k ∈Z } D .只能是第三或第四象限的角18.已知sinθ+cosθ=-1,则sin 2 009θ+cos 2 009θ的值为__________.19.化简下列各式. (1)1-2sin20°cos20°sin20°-1-sin 220°; (2)(1+sinα1-sinα-1-sinα1+sinα)·(1-cosα1+cosα-1+cosα1-cosα).能力点三:利用基本关系式证明20.求证:(1)tanα-1tanα=1-2cos 2αsin αcosα; (2)(1+tanα)2+(1-tanα)2=2cos 2α.21.求证:3-sin 4α-cos 4α2cos 2α=1+tan 2α+sin 2α. 22.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1.23.已知在△ABC 中,sinA +cosA =15. (1)求sinAcosA ;(2)判断△ABC 是锐角三角形还是钝角三角形;(3)求tanA 的值.答案与解析基础巩固1.B2.C 原式=|sin4-cos4|,而4>5π4,由单位圆中的三角函数线得:sin4<cos4<0,∴原式=cos4-sin4.3.C ∵cosα=15>0且tanα<0, ∴角α为第四象限角.∴sinα=-1-cos 2α=-265. 4.1 原式=sin 2α+cos 2α(sin 2α+cos 2α)=sin 2α+cos 2α=1.5.-1 原式= (sin10°-cos10°)2sin10°-cos 210°=|sin10°-cos10°|sin10°-cos10°=cos10°-sin10°sin10°-cos10°=-1.6.C 由sin 2α+cos 2α=1,α∈(0,π),∴cosα=±45. ∴tanα=sinαcosα=±34. 7.B8.A ∵tanα=32,∴cosα≠0. ∴原式=4sinαcosα+15sinαcosα-2 =4tanα+15tanα-2=4×32+15×32-2=1411. 9.B10.解法一:由⎩⎪⎨⎪⎧sin 2α+cos 2α=1,s inαcosα=-512, 解得sinα=±513. 又∵α为第四象限角,∴sinα<0.∴sinα=-513. 解法二:∵α是第四象限角,∴sinα<0.又∵tanα=-512, ∴可设α终边上一点坐标为(12,-5),∴sinα=-513. 能力提升11.A 原式=sinα|cosα|+|sinα|cosα,当角α终边在y =-x(x ≥0)上时,cosα>0,sinα<0; 当角α终边在y =-x(x<0)上时,cosα<0,sinα>0.综上知,原式=0.12.C 原式=2tanαtan 2α-1=2×(-12)(-12)2-1=-43. 13.1 由sinx +sin 2x =1得sinx =1-sin 2x =cos 2x ,∴cos 2x +cos 4x =sinx +sin 2x =1.14.-255 由1cos 2α=1+tan 2α得 1cos 2α=1+14=54. ∴cos 2α=45. ∵α是第二象限的角,∴cosα<0.∴cosα=-255. 15.解:由sinα+cosαsinα-cosα=2,得sinα=3cosα. ∴tanα=3.(1)解法一:原式=3×3cosα-cosα2×3cosα+3cosα=8cosα9cosα=89. 解法二:原式=3·sinαcosα-cosαcosα2·sinαcosα+3·cosαcosα=3tanα-12tanα+3=3×3-12×3+3=89. (2)原式=sin 2α-2sinαcosαsin 2α+cos 2α+1=tan 2α-2tanαtan 2α+1+1 =32-2×332+1+1=1310. 16.解:∵sinα=45>0, ∴α是第一象限或第二象限的角.若α是第一象限角,则cosα>0,tanα>0.∴cosα=1-sin 2α =1-(45)2=35, tanα=sinαcosα=4535=43. 若α是第二象限角,则cosα<0,tanα<0,∴cosα=-1-sin 2α=-35, tanα=sinαcosα=45-35=-43. 17.A ∵1-cosα1+cosα=(1-cosα)21-cos 2α=1-cosα|sinα|, ∴sinα<0.故{α|2kπ-π<α<2kπ,k ∈Z }.18.-1 由sinθ+cosθ=-1,平方得:sin 2θ+cos 2θ+2sinθcosθ=1, 又∵sin 2θ+cos 2θ=1,∴sinθcosθ=0,sinθ=0或cosθ=0.又∵sinθ+cosθ=-1,∴θ的终边在x 轴非正半轴或y 轴非正半轴上.当θ的终边在x 轴非正半轴上时,sin 2 009θ+cos 2 009θ=-1; 当θ的终边在y 轴非正半轴上时,sin 2 009θ+cos 2 009θ=-1. 综上所述:sin 2 009θ+cos 2 009θ=-1.19.解:(1)∵1-2sin20°cos20°=sin 220°+cos 220°-2sin20°·cos20° =(sin20°-cos20°)2,∴原式=|sin20°-cos20°|sin20°-|cos20°|=cos20°-sin20°sin20°-cos20°=-1. (2)原式=[(1+sinα)2cos 2α-(1-sinα)2cos 2α]·[(1-cosα)2sin 2α-(1+cosα)2sin 2α] =|1+sinα|-|1-sinα||cosα|·|1-cosα|-|1+cosα||sinα|=2sinα·(-2cosα)|cosα|·|sinα|=-4sinαcosα|sinαcosα|=⎩⎨⎧ -4,α∈(kπ,kπ+π2),k ∈Z ,4,α∈(π2+kπ,kπ+π),k ∈Z .20.证明:(1)左边=sinαcosα-cosαsinα=sin 2α-cos 2αsinαcosα=1-cos 2α-cos 2αsinαcosα=1-2cos 2αsinαcosα=右边, ∴原题得证.(2)左边=(1+sinαcosα)2+(1-sinαcosα)2 =(sinα+cosα)2cos 2α+(cosα-sinα)2cos 2α =1+2sinαcosα+1-2s inαcosαcos 2α=2cos 2α=右边, ∴原题得证.21.证法一:作差:因为3-sin 4α-cos 4α2cos 2α-(1+tan 2α+sin 2α) =3-sin 4α-cos 4α2cos 2α-(1+sin 2αcos 2α+sin 2α) =3-sin 4α-cos 4α-2cos 2α-2sin 2α-2sin 2αcos 2α2cos 2α=3-(sin 2α+cos 2α)2-2(sin 2α+cos 2α)2cos 2α=2-22cos 2α=0. 所以3-sin 4α-cos 4α2cos 2α=1+tan 2α+sin 2α.证法二:左边=3-[(sin 2α+cos 2α)2-2sin 2αcos 2α]2cos 2α=2+2sin 2αcos 2α2cos 2α=1cos 2α+sin 2α =sin 2α+cos 2αcos 2α+sin 2α =1+tan 2α+sin 2α=右边,所以原等式成立.22.证明:∵tan 2α=2tan 2β+1,∴sin 2αcos 2α=2sin 2βcos 2β+1=2sin 2β+cos 2βcos 2β=1+sin 2βcos 2β, ∴sin 2α1-sin 2α=1+sin 2β1-sin 2β, ∴sin 2α(1-sin 2β)=(1-sin 2α)(1+sin 2β)∴sin 2β=2sin 2α-1.拓展探究23.解:(1)由sinA +cosA =15, 可得(sinA +cosA)2=125, ∴sinAcosA =-1225. (2)∵A ∈(0,π)且sinAcosA<0,∴A ∈(π2,π). ∴△ABC 是钝角三角形.(3)∵A ∈(π2,π), ∴sinA -cosA>0.∴sinA -cosA =(sinA -cosA )2 =1-2sinAcosA =1-2×(-1225)=75. 由⎩⎨⎧ sinA -cosA =75,sinA +cosA =15, 解得sinA =45,cosA =-35. ∴tanA =sinA cosA =-43.。
2024年新高一数学初升高衔接《同角三角函数的基本关系》含答案解析
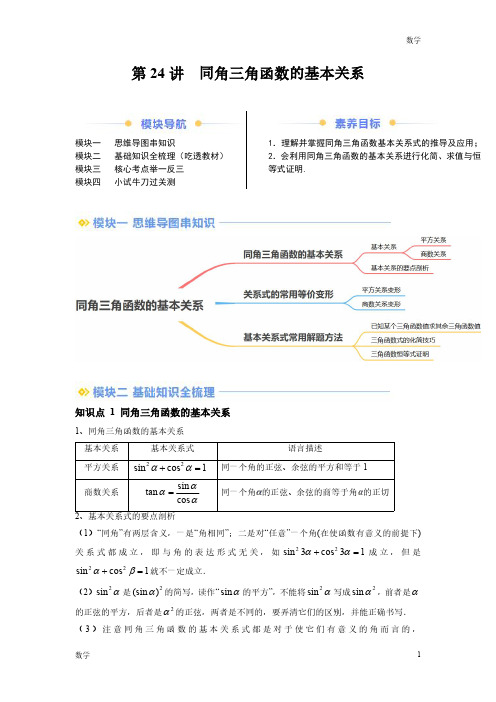
第24讲同角三角函数的基本关系模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解并掌握同角三角函数基本关系式的推导及应用;2.会利用同角三角函数的基本关系进行化简、求值与恒等式证明.知识点1同角三角函数的基本关系1、同角三角函数的基本关系基本关系基本关系式语言描述平方关系22sin cos 1αα+=同一个角的正弦、余弦的平方和等于1商数关系sin tan cos ααα=同一个角的正弦、余弦的商等于角的正切2、基本关系式的要点剖析(1)“同角”有两层含义,一是“角相同”;二是对“任意”一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如22sin 3cos 31αα+=成立,但是22sin cos 1αβ+=就不一定成立.(2)2sin α是2(sin )α的简写,读作“sin α的平方”,不能将2sin α写成2sin α,前者是α的正弦的平方,后者是2α的正弦,两者是不同的,要弄清它们的区别,并能正确书写.(3)注意同角三角函数的基本关系式都是对于使它们有意义的角而言的,22sin cos 1αα+=对一切R α∈恒成立,而sin tan cos ααα=仅对()2k k Z παπ≠+∈成立.知识点2关系式的常用等价变形1、2222222sin 1cos cos 1sin sin cos 1sin cos (sin cos )12sin cos αααααααααααα⎧=-⎪=-⎪⎪+=⇒=⎨⎪=⎪⎪+=±⎩2、sin tan cos sin tan sin cos cos tan ααααααααα=⎧⎪=⇒⎨=⎪⎩【注意】使用变形公式sin α=,cos α=时,“±”由α的终边所在的象限来确定,而对于其他形式的变形公式则不必考虑符号问题.知识点3基本关系式常用解题方法1、已知某个三角函数值求其余三角函数值的步骤第一步:由已知三角函数的符号,确定其角终边所在的象限;第二步:依据角的终边所在象限分类讨论;第三步:利用同角三角函数关系及其变形公式,求出其余三角函数值。
高中数学同角三角函数之间的关系总结练习含答案解析X

3.2.2 同角三角函数之间的关系1.同角三角函数之间的关系式(1)平方关系:① .该关系体现了正弦与余弦的互化.(2)商数关系:② .该关系体现了切、弦的互化.2.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形:sin 2α=③ ;cos 2α=④ ;(sin α+ cos α)2=⑤ ;(sin α-cos α)2=⑥ ;(sin α+cos α)2+(sin α- cos α)2=⑦ .(2)tan α=sinαcosα的变形:sin α=⑧ ;cos α=⑨ .一、填空题1.化简sin 2α+cos 4α+sin 2αcos 2α的结果是 .2.已知α是第四象限角,tan α=-512,则sin α= .3.若sin α+sin 2α=1,则cos 2α+cos 4α= .4.若sin α=45,且α是第二象限角,则tan α的值等于 .5.已知tan α=-12,则1+2sinαcosαsin 2α-cos 2α的值为 .6.已知sin α-cos α=-√52,则tan α+1tanα的值为 .7.已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ= .8.已知sin αcos α=18且π4<α<π2,则cos α-sin α= .二、解答题9.求证:1-2sin2xcos2x cos 2x -sin 2x =1-tan2x 1+tan2x .10.已知sin θ、cos θ是关于x的方程x2-ax+a=0的两个根(a∈R).(1)求sin3θ+cos3θ的值;的值.(2)求tan θ+1tanθ知识清单①sin 2α+cos 2α=1 ②tan α=sinαcosα ③1-cos 2α ④1-sin 2α ⑤1+2sin αcos α ⑥1-2sin αcos α ⑦2 ⑧tan α·cos α ⑨sinαtanα基础过关一、填空题1.答案 1解析 sin 2α+cos 4α+sin 2αcos 2α=sin 2α+cos 2α(cos 2α+sin 2α)=sin 2α+cos 2α=1.2.答案 -513 解析 由1cos 2α=sin 2α+cos 2αcos 2α=tan 2α+1=169144得cos 2α=144169,因为α是第四象限角,所以cos α>0,所以cos α=1213,∴sin α=tan α·cos α=-512×1213=-513.3.答案 1解析 ∵sin α+sin 2α=1,∴sin α=1-sin 2α=cos 2α,∴cos 2α+cos 4α=sin α+sin 2α=1.4.答案 -43解析 ∵sin α=45,且α是第二象限角,∴cos α=-35,∴tan α=-43.5.答案 -13解析 1+2sinαcosαsin 2α-cos 2α=sin 2α+2cosαsinα+cos 2α(sinα+cosα)(sinα-cosα)=sinα+cosαsinα-cosα=tanα+1tanα-1,将tan α=-12代入,得原式=-12+1-12-1=-13. 6.答案 -8解析 tan α+1tanα=sinαcosα+cosαsinα=1sinαcosα.∵sin αcos α=1-(sinα-cosα)22=-18,∴tan α+1tanα=-8.7.答案 45解析 sin 2θ+sin θcos θ-2cos 2θ=sin 2θ+sinθcosθ-2cos 2θsin θ+cos θ=tan 2θ+tanθ-2tan θ+1,又tan θ=2,故原式=4+2-24+1=45.8.答案 -√32解析 (cos α-sin α)2=1-2sin αcos α=34,∵π4<α<π2,∴cos α<sin α.∴cos α-sin α=-√32.二、解答题9.证明 左边=cos 22x+sin 22x -2sin2xcos2xcos 2x -sin 2x=(cos2x -sin2x )2(cos2x -sin2x )(cos2x+sin2x )=cos2x -sin2x cos2x+sin2x =1-tan2x1+tan2x =右边,∴原等式成立.10.解析 由韦达定理知sin θ+cos θ=a,sin θ·cos θ=a.∵(sin θ+cos θ)2=1+2sin θcos θ,∴a 2=1+2a,解得a=1-√2或a=1+√2.∵sin θ≤1,cos θ≤1,∴sin θcos θ≤1,即a≤1,∴a=1-√2.(1)sin3θ+cos3θ=(sin θ+cos θ)(sin2θ-sin θ·cos θ+cos2θ) =(sin θ+cos θ)(1-sin θcos θ)=a(1-a)=√2-2.(2)tan θ+1tanθ=sinθcosθ+cosθsinθ=sin2θ+cos2θsinθcosθ=1sinθcosθ=1a,将a=1-√2代入得,原式=1-√2=-1-√2.。
高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析1.已知,则.【答案】3【解析】===3.【考点】同角三角函数基本关系式2.若tan α=3,则 sin2α-2 sin αcos α+3 cos2α=______.【答案】【解析】sin2α-2 sin αcos α+3 cos2α====.3.已知f(α)=,则f的值为________.【答案】-【解析】∵f(α)==-cos α,∴f=-cos=-cos=-cos=-.4.化简+=________.【解析】原式=+=-sin α+sin α=0.5.已知α∈(,π),tanα=-,则sin(α+π)=()A.B.-C.D.-【答案】B【解析】由题意可知,由此解得sin2α=,又α∈(,π),因此有sinα=,sin(α+π)=-sinα=-,故选B.6.记cos(-80°)=k,那么tan100°=()A.B.-C.D.-【答案】B【解析】解法一:因为cos(-80°)=cos80°=k,sin80°==,所以tan100°=-tan80°=-=-.解法二:因为cos(-80°)=k,所以cos80°=k,所以tan100°=-tan80°==-.7.已知sinαcosα=,且π<α<,则cosα-sinα的值为()A.-B.C.-D.【答案】B【解析】∵π<α<,∴cosα>sinα,∴cosα-sinα>0,又∵(cosα-sinα)2=1-2cosαsinα=,∴cosα-sinα=.8.若3cos(-θ)+cos(π+θ)=0,则cos2θ+sin2θ的值是________.【答案】【解析】∵3cos(-θ)+cos(π+θ)=0,即3sinθ-cosθ=0,即tanθ=.∴cos2θ+sin2θ======.9.(5分)(2011•福建)若α∈(0,),且sin2α+cos2α=,则tanα的值等于()A.B.C.D.【答案】D【解析】把已知的等式中的cos2α,利用同角三角函数间的基本关系化简后,得到关于sinα的方程,根据α的度数,求出方程的解即可得到sinα的值,然后利用特殊角的三角函数值,由α的范围即可得到α的度数,利用α的度数求出tanα即可.解:由cos2α=1﹣2sin2α,得到sin2α+cos2α=1﹣sin2α=,则sin2α=,又α∈(0,),所以sinα=,则α=,所以tanα=tan=.故选D点评:此题考查学生灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,是一道基础题.学生做题时应注意角度的范围.10.已知sin α=+cos α,且α∈,则的值为________.【答案】-【解析】将sin α-cos α=两边平方,得2sin α·cos α=,(sin α+cos α)2=,sin α+cos α=,==-(sin α+cos α)=-.11.在△ABC中,若sinA,cosA是关于x的方程3x2-2x+m=0的两个根,则△ABC是 ( )A.钝角三角形B.直角三角形C.锐角三角形D.不能确定【答案】A【解析】∵sinA,cosA是关于x的方程3x2-2x+m=0的两个根∴sinA+cosA=∴(sinA+cosA)2=1+2sinAcosA=即sinAcosA=-∵0o<A<180o,∴sinA>0,所以cosA<0,即90o<A<180o故知△ABC是钝角三角形12.已知,则()A.B.C.D.【答案】A【解析】∵,∴,∴,∴,∴,∴,∴.【考点】三角函数求值.13.在中,角A,B,C的对边a,b,c成等差数列,且,则 .【答案】【解析】∵成等差数列,∴,∴,∵,∴,∴,∴,(1)∵且,∴代入(1)式中,,∴,∴,∴,∴.【考点】1.等差中项;2.倍角公式;3.诱导公式.14.已知,,则.【答案】【解析】由题意,,.【考点】同角间的三角函数关系.15.若则【答案】【解析】,得,∴.【考点】求三角函数值.16.α是第二象限角,tanα=-,则sinα=________.【答案】【解析】由解得sinα=±.∵α为第二象限角,∴sinα>0,∴sinα=.17. cos=________.【答案】-【解析】cos=cos=cos(17π+)=-cos=-.18.已知其中若.(1)求的值;(2)求的值.【答案】(1);(2).【解析】(1)先由已知条件求得的值,再由平方关系可得的值,把拆为,最后利用两角和的余弦公式即可求得的值;(2)考查了三角函数中知一求三的思想,即这几个量“知一求三”.可先利用差角余弦公式将展开,求得的值,两边平方即可求得的值,再由平方关系即可求得的值,最后由商关系即可求得的值.试题解析:(1)由已知得:,(2)由,得,两边平方得:,即,∵,且,从而. 12分【考点】1.平面向量的数量积运算;2.应用三角恒等变换求三角函数的值.19.已知x∈(0,),则函数f(x)=的最大值为()A.0B.C.D.1【答案】C【解析】由已知得,f(x)==tanx-tan2x=-(tanx-)2+,∵x∈(0,),∴tanx∈(0,1),=.故当tanx=时,f(x)max20.已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.(1)求cos3(-θ)+sin3(-θ)的值.(2)求tan(π-θ)-的值.【答案】(1) -2 (2) 1+【解析】【思路点拨】先由方程根的判别式Δ≥0,求a的取值范围,而后应用根与系数的关系及诱导公式求解.解:由已知,原方程的判别式Δ≥0,即(-a)2-4a≥0,∴a≥4或a≤0.又(sinθ+cosθ)2=1+2sinθcosθ,则a2-2a-1=0,从而a=1-或a=1+(舍去),因此sinθ+cosθ=sinθcosθ=1-.(1)cos3(-θ)+sin3(-θ)=sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθ·cosθ+cos2θ)=(1-)[1-(1-)]=-2.(2)tan(π-θ)-=-tanθ-=-(+)=-=-=1+.21.若sinθcosθ>0,则θ在()A.第一、二象限B.第一、三象限C.第一、四象限D.第二、四象限【答案】B【解析】∵sinθcosθ>0,∴sinθ,cosθ同号.当sinθ>0,cosθ>0时,θ在第一象限,当sinθ<0,cosθ<0时,θ在第三象限,因此,选B.22.=()A.-B.-C.D.【解析】====sin 30°=.23.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=________.【答案】-【解析】f(x)=sin x-2cos x==sin(x-φ),其中sin φ=,cos φ=,当x-φ=2kπ+ (k∈Z)时,函数f(x)取得最大值,即θ=2kπ++φ时,函数f(x)取到最大值,所以cos θ=-sin φ=-.24. 4cos 50°-tan 40°=________.【答案】【解析】4cos 50°-tan 40°======.25.已知α∈,且cos α=-,则tan α=________.【答案】2【解析】利用同角三角函数的基本关系求解.由条件可得sin α=-,所以tan α===2.26.若α,β∈,cos =,sin =-,则cos (α+β)=________.【答案】【解析】∵α,β∈,∴-<α-<,-<-β<,由cos =和sin =-得α-=±,-β=-,当α-=-,-β=-时,α+β=0,与α,β∈矛盾;当α-=,-β=-时,α=β=,此时cos (α+β)=-.27.若cos =,则cos =().A.-B.-C.D.【答案】D【解析】∵cos =,∴cos =2cos 2-1=-,即sin 2x=,∴cos =sin 2x=.28.已知sin θ+cos θ=,则sin θ-cos θ的值为________.【答案】-【解析】∵sin θ+cos θ=,∴(sin θ+cos θ)2=1+2cos θsin θ=,∴2cos θsin θ=,∴(sin θ-cos θ)2=1-=,又θ∈,∴sin θ<cos θ,∴sin θ-cos θ=-.29.已知,则=____________.【答案】【解析】,根据,可知:,故答案为.【考点】同角三角函数的基本关系式的运算30.已知,且,则.【答案】【解析】因为,所以。
高一数学同角三角函数的基本关系式和诱导公式试题答案及解析

高一数学同角三角函数的基本关系式和诱导公式试题答案及解析1.已知,并且是第二象限的角,那么的值等于()A.B.C.D.【答案】A【解析】由,又为第二象限角,,则.故选A.【考点】三角函数的平方公式.2.己知a为锐角,且,,则sina的值是( ). A.B.C.D.【答案】C.【解析】根据诱导公式,已知条件的两个式子可化为如下关系:,解得,又本题要求的是,因此由前述可知有,解得(a为锐角).【考点】诱导公式,同角三角函数的基本关系.3.已知,则的值为.【答案】-11【解析】【考点】弦化切4.求的值域.【解析】可利用同角三角函数的基本关系式将函数化为利用换元法令原函数变为一元二次函数,可用一元二次函数求值域的方法解,注意的取值范围.解:原函数可化为令可得则【考点】同角三角函数的基本关系式,一元二次函数求值域.5.已知(1)化简;(2)若是第三象限角,且,求的值.【答案】(1);(2).【解析】(1)根据诱导公式,将中的三角函数都转化为的三角函数,即可得到;(2)由,可得,又由条件是第三象限角及(1)中得到的的表达式,即可得到.(1);(2)由得,,因为是第三象限角,所以,∴.【考点】1.诱导公式;2.同角三角函数基本关系.6.已知 .【答案】【解析】∵,∴,∴原式=.【考点】1.诱导公式;2.同角三角函数基本关系.7.已知,则tanα的值是()A.±B.C.D.无法确定【答案】B【解析】∵,∴,即.【考点】同角三角函数的基本关系.8.( )A.B.C.D.【答案】D【解析】.【考点】同角三角函数基本关系.9.已知,则 ( )A.B.C.D.【答案】A【解析】由【考点】同角三角函数基本关系10. sin的值是()A.B.-C.D.-【答案】B【解析】.【考点】诱导公式,特殊角的三角函数值.11.已知,则的值为()A.B.C.D.【答案】A【解析】由条件,得,整理得:,即①,代入中,得,整理得:,即,解得(舍)或,把,代入①,得,所以,故选A.【考点】同角三角函数基本关系.12.若,的化简结果为()A.B.C.D.【答案】D【解析】,=.【考点】同角的基本关系.13.已知(1)求的值;(2)求的值.【答案】(1);(2).【解析】(1)因为,可得=−2,α为钝角且cosα<0.再由sin2α+cos2α=1,求得cosα的值.(2)原式=,把tanα=-2代入运算求得结果.试题解析:解:(1)因为,所以cosa=(2)原式=【考点】1.同角三角函数间的基本关系;2.三角函数的化简求值.14.若,则计算所得的结果为()A.B.C.D.【答案】A【解析】先根据诱导公式化简,原式=,再将代入即得答案为A.【考点】诱导公式.15.已知=,则的值等于( )A.B.-C.D.±【答案】A【解析】诱导公式,注意,,所以选A【考点】诱导公式16.已知,则的值是( )A.B.C.D.【答案】C【解析】由与可得,而,选C.【考点】同角三角函数的基本关系式.17.已知为第三象限角,.(1)化简;(2)若,求的值.【答案】(1);(2).【解析】(1)应用三角诱导公式进行化简即可得出答案;(2)根据同角三角函数的基本关系式求出,由求出,最后由正切的二倍角公式可计算得结果.试题解析:(1) 6分(结果为酌情给3分)(2)由,得. 又已知为第三象限角所以,所以 8分所以 10分故 12分.【考点】1.诱导公式;2.同角三角函数的基本关系式;3.二倍角公式.18.已知tanα,是关于x的方程x2-kx+k2-3=0的两实根,且3π<α<π,求cos(3π+α)-sin(π+α)的值.【解析】关于方程两根的问题可用韦达定理解决,,从而求出k =±2,再根据角的范围可知为正,从而求得。
(新教材)高中数学人教A必修第一册同步练习:5.2.2同角三角函数的基本关系

∴sin
α=-
2 √5
.∴cos
5
α=-
√5
-2sin
α=-
√5
.
5
∴
tan
α=
sin??
cos??=
2.
(方法二 )∵cos α+ 2sin α=- √5 , ∴cos2α+ 4sin αcos α+ 4sin 2α= 5.
5.2.2 同角三角函数的基本关系 课后篇 巩固提升
1.已知
cos
θ=
ቤተ መጻሕፍቲ ባይዱ
4
5,
且
3π
2<
θ<
2π,则
ta1n??的值为
(
)
基础达标练
3
3
4
4
A. 4
B. -4
C. 3
D. - 3
解析
因为
cos
θ=
4 5
,且
3π
2<
θ<
2π,
所以
sin
θ=-
√1-cos2
??=-
3
5.
所以
tan
θ=-
3
4,故
1
tan??=-
√11+-ccooss????.
解 ∵32π< α< 2π,∴sin α< 0. ∴原式
= √ (1 -cos??)2
+ √ (1+cos??)2
(1+cos??)(1 -cos??)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一三角同步练习5(同角三角函数的基本关系式)
一、选择题
1、),0(,5
4
cos παα∈=
,则αcot 的值等于 ( )
A .
3
4 B .4
3 C .3
4±
D . 4
3±
2、已知A 是三角形的一个内角,sin A +cos A = 2
3
,则这个三角形是 ( )
A .锐角三角形
B .钝角三角形
C .不等腰直角三角形
D .等腰直角三角
形
3、已知sin αcos α = 1
8
,则cos α-sin α的值等于 ( )
A .±34
B .±23
C .23
D .-2
3
4、已知θ是第三象限角,且9
5
cos sin 44=
+θθ,则=θθcos sin ( ) A .
32 B . 32- C . 3
1 D . 31- 5、如果角θ满足2cos sin =+θθ,那么θθcot tan +的值是 ( )
A .1-
B .2-
C .1
D .2
6、若
2cos sin 2cos sin =-+α
αα
α,则=αtan
( )
A .1
B . - 1
C .
4
3 D .3
4-
7、已知
21cos sin 1-=+x x ,则
1
sin cos -x x
的值是 A .
21 B . 2
1
- C .2 D .-2 8、若θθcos ,sin 是方程0242=++m mx x 的两根,则m 的值为
A .51+
B .51-
C .51±
D .51--
二、填空题
1、若15tan =α,则=αcos
;=αsin
.
2、若3tan =α,则α
αα
α3333cos 2sin cos 2sin -+的值为________________.
3、已知
2cos sin cos sin =-+α
αα
α,则ααcos sin 的值为
.
4、已知5
24cos ,53sin +-=
+-=
m m
m m θθ,则m=_________;=αtan . 三、解答题
1、:已知5
1
sin =
α,求ααtan ,cos 的值.
2、已知22cos sin =
+αα,求α
α22cos 1sin 1+的值.
3、已知5
1
cos sin =
+ββ,且πβ<<0. (1)求ββcos sin 、ββcos sin -的值;
(2)求βsin 、βcos 、βtan 的值.
*4、已知:m =αcot ,()0≠m ,求αsin ,αcos 的值.
参考答案
一、选择题
ABBA DAAB
二、填空题
1、4
1±
;415±(α在一象限时取正号,在三象限时取负号).
2、
2529. 3、103. 4、0=m 或8=m ;43tan -=α或12
5tan -=α.
三、解答题
1、562cos ±
=α;12
6
tan ±=α(α在一象限时取正号,在二象限时取负号). 2、由2
2
cos sin =
+αα可得:
2
1cos sin 21cos cos sin 2sin 22=
+=++αααααα; 于是:4
1
cos sin -=αα,∴16cos sin cos sin cos 1sin 12
22222=+=+αααααα.
3、
(1)由5
1
cos sin =
+ββ可得: 25
1cos sin 21cos cos sin 2sin 22=
+=++ββββββ; 于是:2512cos sin -
=ββ,()25
49cos sin 21cos sin 2
=-=-ββββ; ∵0cos sin <ββ且πβ<<0,∴0sin >β,0cos <β.
于是:5
7cos sin =
-ββ. (2)54sin =
β;53cos -=β;3
4tan -=β. 4、
∵ m ==
α
α
αsin cos cot ,∴ ααsin cos m =, 代入:1cos sin 22=+αα可得: ()
1sin 122=+αm ∴ 2
211
sin m +=
α;
当α在第一、第二象限时,2
11sin m
+=
α, 2
1cot sin cos m
m +=
=ααα;
当α在第三、第四象限时,2
11sin m
+-
=α,2
1cot sin cos m
m +-
==ααα.。
