珠海北大附属实验学校八年级下数学第三次月考试卷
初二数学下册第三次月考试卷(带答案)

初二数学下册第三次月考试卷(带答案)学校:___________班级:___________姓名:___________考号:___________【不等关系、不等式的基本性质与不等式的解集(100分)】1.(5分)用不等号填空:(1)-π__________-3;(2)x2__________0;(3)|x|+|y|__________|x+y|;(4)(-5)÷(-1)__________(-6)÷(-7);(5)当a__________0时,|a|=-a.2.(3分)若a>b,则下列不等式变形正确..的是()A.ac2>bc2B.ab>1 C.-ca>-cb D.3a-c>3b-c3.(3分)下列不等式变形中,一定正确....的是()A.若ac>bc,则a>bB.若a>b,则am2>bm2C.若ac2>bc2,则a>bD.若m>n,则-m2>-n24.(3分)若关于x的不等式mx+1>0的解集为x<15,则关于x的不等式(m-1)x>-1-m的解集为_______________.5.(8分)若|x-4|+(5x-y-m)2=0,求当y≥0时,m的取值范围.6.(6分)已知x=3是不等式mx+2<1-4m的一个解,如果m是整数,求m的最大值.7.(7分)若不等式2x<4的解都能使不等式x-a<5成立,求a的取值范围.8.(3分)实数a,b,c满足a<b<0<c,则下列式子中正确..的是()A.ac>bcB.|a-b|=a-bC.-a<-b<cD.-a-c>-b-c9.(3分)在△ABC中,若AB=8,BC=6,则第三边AC的长度m的取值范围是__________;若m的值为偶数,则m=______________________________. 10.(3分)若实数a是不等式2x-1>5的解,但实数b不是不等式2x-1>5的解,则下列选项中,正确..的是()A.a<bB.a>bC.a≤bD.a≥b11.(6分)若不等式a(x-1)>x+1-2a的解集为x<-1,求a的取值范围.12.(7分)已知不等式3x-a≤0的正整数解有3个:1,2,3,求a的取值范围.13.(7分)题目:2x+13-x+52≥______已知这道题的正确答案是x≥7,且“______”是一个常数项,请求出“______”中的数.14.(4分)若关于x的不等式|x-2|+|x+3|≥a对于x取任何值都成立,请直接写出a的取值范围.15.(7分)(1)比较a2+b2与2ab的大小关系:①当a=3,b=5时,a2+b2__________2ab;②当a=-3,b=5时,a2+b2__________2ab;③当a=b=1时,a2+b2__________2ab.(2)根据上述结果请你猜想a2+b2与2ab的大小关系:__________ 并进行验证.16.(7分)已知关于x的不等式ax+2x<2a+4.(1)当a=1时,求该不等式的解集;(2)a取何值时,该不等式有解?并求出解集.17.(每题3分,共18分)解下列不等式:(1)2(x-3)<3(x-1);(2)2y3-1<y4+4;(3)5(x-2)+8<6(x-1)+7;(4)2x-13-3x-12<1;(5)x-x-12≤2-x+23;(6)x-3(x-3)<3[x-2(x-2)].【一元一次方程、不等式的应用(20分)】18.[一元一次不等式](8分)矿山爆破时,为了确保安全,点燃引火线后,人要在爆破前转移到300m以外的安全地区.引火线燃烧的速度是0.8cm/s,人离开的速度是5m/s,问:引火线的长度至少应为多少cm?19.[一元一次方程](8分)上海浦东机场(PVG)到新加坡樟宜机场(SIN)的直线距离约为5000km,一架波音式飞机的速度约为800km/h;一架普通飞机的速度约为500km/h.两架飞机都从上海飞往新加坡.普通飞机航班先出发,3h后,波音式飞机航班出发,问:波音式飞机什么时候追上普通飞机,这时离新加坡樟宜机场还有多远?20.(4分)现有若干本连环画册分给小朋友,如果每人分8本,那么不够分,现在如果每人分7本,还多10本,则小朋友人数最少有()A.7人B.8人C.10人D.11人参考答案阅卷提示:提供的答案除选择题和填空题外,不一定都是唯一正确的,对于那些与此答案不同的答案正确的同样给分.评分标准只是根据一种思路与方法给出的,在阅卷时会出现各种不同情况,可根据本评分标准的精神制定出具体的方案,但不要与评分标准有太大的偏离.【不等关系、不等式的基本性质与不等式的解集(100分)】1.(1)<;(2)≥;(3)≥;(4)>;(5)≤.(每空1分,共5分)2.D(3分)3.C(3分).(3分)4.x<-235.m≤20.(8分)6.-1.(6分)7.a≥-3.(7分)8.D(3分)9.2<m<14;(2分) 4或6或8或10或12. (1分)10.B(3分)11.a<1.(6分)12.9≤a<12.(7分)13.“______”中的数为-1.(7分)14.a≤5.(4分)15.(1)①>;②>;③=.(每空1分,共3分)(2)a2+b2≥2ab,(1分)证明过程略.(3分)16.(1)x<2;(2分)(2)当x≠-2时有解;(1分)解集:x<2或x>2(每个解集2分,共4分)17.(1)x>3;(2)y≤12;(3)x>3;(4)x>-1;(5)x≤1;(6)x<3. (每题3分,共18分)【一元一次方程、不等式的应用(20分)】18.48cm.(8分)19.5h后追上(5分),距新加坡还有1000km.(3分)20.D(4分)。
2021年(北师大版)八年级下学期第三次月考数学试题卷及答案
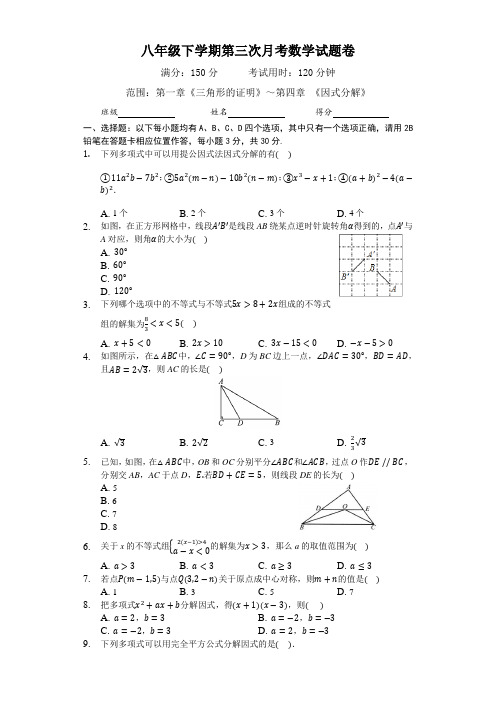
八年级下学期第三次月考数学试题卷满分:150分考试用时:120分钟范围:第一章《三角形的证明》~第四章《因式分解》班级姓名得分一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B 铅笔在答题卡相应位置作答,每小题3分,共30分.1.下列多项式中可以用提公因式法因式分解的有()①11a2b−7b2;②5a2(m−n)−10b2(n−m);③x3−x+1;④(a+b)2−4(a−b)2.A. 1个B. 2个C. 3个D. 4个2.如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A. 30°B. 60°C. 90°D. 120°3.下列哪个选项中的不等式与不等式5x>8+2x组成的不等式<x<5()组的解集为83A. x+5<0B. 2x>10C. 3x−15<0D. −x−5>04.如图所示,在△ABC中,∠C=90°,D为BC边上一点,∠DAC=30°,BD=AD,且AB=2√3,则AC的长是()A. √3B. 2√2C. 3D. 2√335.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE//BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为()A. 5B. 6C. 7D. 82(x−1)>4的解集为x>3,那么a的取值范围为()6.关于x的不等式组{a−x<0A. a>3B. a<3C. a≥3D. a≤37.若点P(m−1,5)与点Q(3,2−n)关于原点成中心对称,则m+n的值是()A. 1B. 3C. 5D. 78.把多项式x2+ax+b分解因式,得(x+1)(x−3),则()A. a=2,b=3B. a=−2,b=−3C. a=−2,b=3D. a=2,b=−39.下列多项式可以用完全平方公式分解因式的是().A. 9p2−4q2B. a2+2ab−b2C. 9m2−24m+16D. −x2−4xy+4y210.如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是()A. 6B. 3C. 2D. 1.5二、填空题(本大题共5小题,共20.0分)11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=时,△POQ是等腰三角形.12.不等式组{x+1>0a−13x<0的解集是x>−1,则a的取值范围是______.13.已知点A(1,−2),B(−1,2),E(2,a),F(b,3),若将线段AB平移至EF,点A,E为对应点,则a+b的值为________.14.边长为a,b的长方形的周长为12,面积为10,则a2b+ab2的值为.15.为迎接建国70周年,某商店购进A,B,C三种纪念品共若干件,且A,B,C三种纪念品的数量之比为8:7:9.一段时间后,根据销售情况,补充三种纪念品后,库存总数量比第一次多200件,且A,B,C三种纪念品的比例为9:10:10.又一段时间后,根据销售情况,再次补充三种纪念品,库存总数量比第二次多170件,且A,B,C三种纪念品的比例为7:6:6.已知第一次三种纪念品总数量不超过1000件,则第一次购进A种纪念品______件.三、解答题(本大题共10小题,共100.0分)16.(8分)解不等式:x6−1>x−23,并把它的解集在数轴上表示出来.17.(10分)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC(1)求证:AE=AD;(2)若∠ACB=65°,求∠BDC的度数.18.(10分)在ABC中,CA=CB,∠ACB=90°.点P是平面内不与点A、C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转90°得到线段DP,连接AD,BD,CP.(1)如图1,求BDCP的值及直线BD与直线CP相交所成的较小角的度数;(2)如图2,若点E、F分别是CA、CB的中点,点P在直线EF上,当点C,P,D在同一直线上时,求ADCP的值.19.(10分)(1)解不等式组:{x−3(x−1)>5x−35−1≤x+12(2)因式分解3x3−12x2y+12xy220.(8分)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“和谐数”.如4=22−02,12=42−22,20=62−42,因此,4,12,20都是“和谐数”.36和2020这两个数是“和谐数”吗?为什么?21.(10分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.(1)平移△ABC,使得点A与点O重合,画出平移后的△A′B′C′;(2)画出△ABC关于点O成中心对称的△DEF;(3)判断△A′B′C′与△DEF是否成中心对称.22.(10分)我国沪深股市交易中,如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股,若他期望获利不低于1000元,问他至少要等到该股票涨到每股多少元时才能卖出?(精确到0.01元)23.(10分)如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.24.(12分)阅读理解应用待定系数法:设某一多项式的全部或部分系数为未知数、利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求的值.待定系数法可以应用到因式分解中,例如问题:因式分解:x3−1.因为x3−1为三次多项式,若能因式分解,则可以分解成一个一次多项式和一个二次多项式的乘积.所以我们可以猜想x3−1可以分解成(x−1)(x2+ax+b),展开等式右边得:x3+ (a−1)x2+(b−a)x−b,根据待定系数法原理,等式两边多项式的同类项的对应系数相等:a−1=0,b−a=0,−b=−1,从而可以求出a=1,b=1.所以x3−1=(x−1)(x2+x+1).(1)若x取任意值,等式x2+5x+3=x2+(2−a)x+3恒成立,则a=____;(2)已知多项式x3+2x+12有因式x+2,请用待定系数法求出该多项式的另一因式;(3)请判断多项式x4+x2+1是否能分解成两个整系数二次多项式的乘积,如果能分解,请求出分解结果;如果不能分解,请说明理由.25.(12分)如图,在四边形ABCD中,AD//BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.已知AD=2cm,BC=5cm.(1)求证:FC=AD;(2)求AB的长.答案1.B2.C3.C4.A5.A6.D7.C8.B9.C10.B11.103或1012.a≤−1313.−114.6015.32016.解:x<−2.解集在数轴上表示略.17.证明:(1)∵∠BAC=∠EAD∴∠BAC−∠EAC=∠EAD−∠EAC即:∠BAE=∠CAD在△ABE和△ACD中{∠ABE=∠ACD AB=AC∠BAE=∠CAD,∴△ABE≌△ACD(ASA),∴AE=AD;(2)解:∵∠ACB=65°,AB=AC,∴∠ABC=∠ACB=65°,∴∠BAC=180°−∠ABC−∠ACB=180°−65°−65°=50°,∵∠ABD=∠ACD,∠AOB=∠COD,∴∠BDC=∠BAC=50°.18.解:(1)如图1中,设BD交AC于点O,BD交PC于点E.∵∠PAD=∠CAB=45°,∴∠PAC=∠DAB,∵ABAC =ADAP=√2,∴△DAB∽△PAC,∴∠PCA=∠DBA,BDPC =ABAC=√2,∵∠EOC=∠AOB,∴∠CEO=∠OAB=45°,∴直线BD与直线CP相交所成的较小角的度数为45°.(2)如图2中,当点D在线段PC上时,延长AD交BC的延长线于H.∵CE=EA,CF=FB,∴EF//AB,∴∠EFC=∠ABC=45°,∵∠PAO=45°,∴∠PAO=∠OFH,∵∠POA=∠FOH,∴∠H=∠APO,∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA,∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°,∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC,设AD=a,则DC=AD=a,PD=√22a,∴ADCP =aa+√22a=2−√2.如图3中,当点P在线段CD上时,同法可证:DA=DC,设AD=a,则CD=AD=a,PD=√22a,∴PC=a−√22a,∴ADPC =a−√22a=2+√2.19.解:(1)解:{x−3(x−1)>5①x−35−1≤x+12②解①得x<−1,解②得x≥−7,则该不等式组的解集为:−7≤x<1.(2)3x3−12x2y+12xy2=3x(x2−4xy+4y2)=3x(x−2y)220.解:36和2020都是和谐数.理由如下:设a=(n+2)2−n2=(n+2−n)(n+2+n)=2(2n+2)=4(n+1),令36=4(n+1),解得n=8.∴36=102−82.同理:令2020=4(n+1),解得n=504.∴2020=5062−5042.21.解:(1)如图,△A′B′C′即为所求作.(2)如图,△DEF即为所求作.(3)△A′B′C′与△DEF成中心对称,对称中心是线段A′D与线段FC′的交点.22.解:设涨到每股x元时卖出,根据题意得1000x−(5000+1000x)×0.5%≥5000+1000,解这个不等式得x≥1205,199即x≥6.06.答:至少涨到每股6.06元时才能卖出.23.解:∠E=30°.24.解:(1)−3;(2)设另一个因式为(x2+ax+b),(x+2)(x2+ax+b)=x3+(a+2)x2+(2a+b)x+2b=x3+2x+12∴a+2=0,2b=12,∴a=−2,b=6,∴多项式的另一因式为x2−2x+6;(3)多项式x4+x2+1能分解成两个整系数二次多项式的乘积.设多项式x4+x2+1能分解成①(x2+1)(x2+ax+b)或②(x2+x+1)(x2+ax+1),①(x2+1)(x2+ax+b)=x4+ax3+bx2+x2+ax+b=x4+ax3+(b+1)x2+ax+b∴a=0,b+1=1由b+1=1得b=0≠1∴舍去②(x2+x+1)(x2+ax+1)=x4+(a+1)x3+(a+2)x2+(a+1)x+1∴a+1=0,a+2=1,解得a=−1.即x4+x2+1=(x2+x+1)(x2−x+1);∴x4+x2+1能分解成两个整系数二次三项式的乘积.25.证明:(1)∵AD//BC(已知),∴∠ADC=∠ECF(两直线平行,内错角相等),∵E是CD的中点(已知),∴DE=EC(中点的定义).∵在△ADE与△FCE中,{∠ADC=∠ECFDE=EC∠AED=∠CEF,∴△ADE≌△FCE(ASA),∴FC=AD;(2)∵△ADE≌△FCE,∴AE=EF,AD=CF,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF,∵AD=CF,AD=2cm,BC=5cm.∴AB=BC+AD=2+5=7(cm).。
八年级下学期第三次月考数学试卷及答案

八年级下学期第三次月考数学试卷满分:150分考试用时:120分钟范围:第十六章《二次根式》~第十九章《一次函数》班级姓名得分一、选择题(本大题共12小题,每小题4分,共48.0分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请用2B铅笔把答题卡上对应题目答案标号涂黑、涂满)1.如果式子√2x+6有意义,那么x的取值范围在数轴上表示出来正确的是()A.B.C.D.2.△ABC中,AB=10,BC=16,BC边上的中线AD=6,则AC的长是().A. 6B. 8C. 10D. 163.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是()A. AO=COB. AO=CO=BO=DOC. AO=CO,BO=DO,AC⊥BDD. AO=BO=CO=DO,AC⊥BD4.如图所示,在矩形AOBC中,A(−2,0),B(0,1).若正比例函数y=kx(k≠0)的图象经过点C,则k的值为()A. −12B. 12C. −2D. 25.下列函数中,y随x的增大而增大的是()A. y=−2x+1B. y=−x−2C. y=x+1D. y=−2x−16.如图,△ABC中,∠A+∠B=90∘,AD=DB,CD=3,则AB的长度为()A. 3B. 4C. 5D. 67.下列说法正确的是()A. 若a,b,c是△ABC的三边长,则a2+b2=c2B. 若a,b,c是Rt△ABC的三边长,则a2+b2=c2C. 若a ,b ,c 是Rt △ABC 的三边长,∠A =90∘,则a 2+b 2=c 2D. 若a ,b ,c 是Rt △ABC 的三边长,∠C =90∘,则a 2+b 2=c 28. 下列各式中,最简二次根式是( ).A. √15B. √0.5C. √5D. √50 9. 实数a 、b 在数轴上的对应点的位置如图所示,化简√(a −b)2−|a +b +1|的结果是 ( )A. −2b −1B. 2b −1C. 2a −1D. −2a −110. 如图,在▵ABC 中,若AB =AC =6,BC =4,D 是BC 的中点,则AD 的长等于( )A. 4√2B. 2√5C. 2√10D. 411. 如下图,四边形OABC 是矩形,A(2,1),B(0,5),点C 在第二象限,则点C 的坐标是( )A. (−1,3)B. (−1,2)C. (−2,3)D. (−2,4)12. 若直线y =3x +6与直线y =2x +4的交点坐标为(a,b),则解为{x =a,y =b 的方程组是( )A. {y −3x =62x +y =4 B. {3x +6+y =02x −4−y =0 C. {3x +6−y =02x +4−y =0D. {3x −y =62x −y =4 二、填空题(本大题共4小题,共16.0分) 13. 已知xy >0,化简二次根式x √−y x2的结果是 (1) . 14. 我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何?”(注:丈,尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,则水池里水的深度是 (1) 尺.15. 如图,在菱形ABCD 中,∠ABC =120∘,AB =10 cm ,,点P是这个菱形内部或边上的一点.若以P ,B ,C 为顶点的三角形是等腰三角形,则P ,A(P,A 两点不重合)两点间的最短距离为 (1) cm .16. 按如图所示的程序计算函数y 的值.若输入的x 值为−3,则输出y 的结果为 (1) .三、解答题(本大题共8小题,共86.0分。
八年级下学期数学第三次月考试题卷及答案

八年级下学期数学第三次月考试题卷满分:150分考试用时:120分钟范围:第十六章《二次根式》~第十九章《一次函数》班级姓名得分一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共30分.1.使得式子有意义的x的取值范围是()√4−xA. x≥4B. x>4C. x≤4D. x<42.如图,数轴上点A表示的数是0,点B表示的数是1,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC长为半径画弧,与数轴交于点D,则点D表示的数为()A. 1.4B. √2C. √3D. 23.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO.添加下列条件,不能判定四边形ABCD是菱形的是()A. AB=ADB. AC=BDC. AC⊥BDD. ∠ABO=∠CBO4.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是()A. k>0,b>0B. k>0,b<0C. k<0,b>0D. k<0,b<05.一本笔记本5元,买x本共付y元,则5和y分别是()A. 常量,常量B. 变量,变量C. 常量,变量D. 变量,常量6.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是()A. 6B. 12C. 18D. 247.下列运算正确的是()A. √50÷√5=10B. √10÷2√5=2√2C. √32+42=3+4=7D. √27÷√3=38.如图,分别以三角形三边为直径向外作三个半圆,若较小两个半圆的面积之和等于较大半圆的面积,则这个三角形为().A. 锐角三角形B. 直角三角形C. 钝角三角形D. 锐角三角形或钝角三角形9.将一个长为10cm、宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(如图①)剪下,将剪下的图形打开,得到的菱形ABCD(如图②)的面积为()A. 10cm2B. 20cm2C. 40cm2D. 80cm210.如图,已知直线l 1:y=−2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(−2,0),则k的取值范围是()A. −2<k<2B. −2<k<0C. 0<k<4D. 0<k<2二、填空题(本大题共5小题,共20.0分)11.已知正比例函数y=3x的图象经过点A(−2,y1),B(−1,y2),则y1y2(填“>”“<”或“=”).12.已知a+b=−8,ab=8,则式子√ba +√ab的值为.13.如图所示,在高3米,斜边长为5米的楼梯的表面铺地毯,地毯的长度至少为米.14.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF.若AB=6cm,BC=8cm,则EF的长是.15.如图,在平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A、C分别在x轴、y轴上,OA=3,OC=4,D为OC边的中点,E是OA边上的一个动点,当△BDE的周长最小时,E点的坐标为.三、解答题(本大题共10小题,共100.0分)16.(10分)一个三角形的三边长分别为5√x5,12√20x,54x√45x.(1)求该三角形的周长(结果化为最简二次根式);(2)请你给出一个适当的x的值,使它的周长为有理数,并求出此时三角形的周长.17.(10分)判断由线段a,b,c组成的三角形是不是直角三角形.(1)a=5,b=13,c=12;(2)a=4,b=5,c=6;(3)a:b:c=3:4:5.18.(10分)如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.求证:∠ABF=∠CBE.19.(10分)在如图所示的平面直角坐标系中,画出函数y=−x的图象.x…−2−1012…y……20.(8分)在如图的平面直角坐标系中,画出函数y=|x|的图象.21.(8分)如图所示,E是□ABCD的边AB的中点,且EC=ED.求证:四边形ABCD是矩形.22.(12分)如图,有一张边长为6√2cm的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为√2cm.求:(1)剪掉四个角后,制作长方体盒子的纸板的面积;(2)长方体盒子的体积.23.(10分)如下图,某市进行老城区道路改造,原来从小明家A地到商场F地需要沿着A→B→C→D→E→F连续多次直角拐弯行进,造成出行困难.行走各段路程数据如下图所示,道路改造后可从小明家A地直达商场F地.求从小明家到商场的路程比原来缩短了多少米.24.(10分)如图所示,顺次延长正方形ABCD的各边AB,BC,CD,DA至E,F,G,H,且使BE=CF=DG=AH.求证:四边形EFGH是正方形.25.(12分)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约20cm时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示.(1)求y与x之间的函数关系式;(2)当这种瓜苗长到大约80cm时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?答案1.D2.B3.B4.C5.C6.B7.D8.B9.A10.D11.<12.2√213.714.2.5cm15.(1,0)16.解:(1)该三角形的周长=5√x5+12√20x+54x√45x=√5x+√5x+√5x=52√5x.(2)答案不唯一,如取x=20时,该三角形的周长=52√5×20=25.17.(1)解:∵a=5,b=13,c=12,∴a2+c2=52+122=169,b2=132=169,∴a2+c2=b2,∴由线段a,b,c组成的三角形是直角三角形;(2)解:∵a=4,b=5,c=6,∴a2+b2=42+52=41,c2=62=36,∴a2+b2≠c2,∴由线段a,b,c组成的三角形不是直角三角形;(3)解:∵a:b:c=3:4:5,∴可设a=3k,b=4k,c=5k,∴∴a2+b2=(3k)2+(4k)2=25k2,c2=(5k)2=25k2,∴a2+b2=c2,∴由线段a,b,c组成的三角形是直角三角形.18.证明:∵四边形ABCD是菱形,∴AB=BC,∠A=∠C,∵在△ABF和△CBE中,{AF=CE ∠A=∠C AB=CB ,∴△ABF≌△CBE(SAS),∴∠ABF=∠CBE.19.解:(1)(2)20.解:如图:21.证明:∵四边形ABCD是平行四边形,∴AB=CD,AB//CD,∴∠A+∠B=180°,∵E是边AB的中点,∴AE=BE,在△ADE和△BCE中{AD=BC AE=BE ED=EC∴△ADE≌△BCE(SSS),∴∠A=∠B=90°,即可得出平行四边形ABCD是矩形.22.解:(1)长方体盒子的纸板的面积:(6√2)2−4×(√2)2=64cm2,答:剪掉四个角后,制作长方体盒子的纸板的面积为64cm2.(2)长方体盒子的体积:(6√2−2√2)(6√2−2√2)×√2=32√2cm3.答:长方体盒子的体积为32√2cm3.23.如图所示,过点A作AH⊥EF于H,则在Rt△AHF中,AH=40+40=80(米),FH =70−20+10=60(米),故改造后小明家与商场的距离AF =√602+802=100米.因为改造前小明家与商场的距离为10+40+20+40+70=180米,所以缩短的距离为180−100=80米.答:从小明家到商场的路程比原来缩短了80米.24.证明:∵四边形ABCD 是正方形,∴AB =BC =CD =DA ,∠EBF =∠HAE =∠GDH =∠FCG ,又∵BE =CF =DG =AH ,∴CG =DH =AE =BF∴△AEH≌△CGF≌△DHG≌△BFE ,∴EF =FG =GH =HE ,∠EFB =∠HEA ,∴四边形EFGH 为菱形,∵∠EFB +∠FEB =90°,∠EFB =∠HEA ,∴∠FEB +∠HEA =90°,∴四边形EFGH 是正方形.25.解:(1)当0≤x ≤15时,设y =kx(k ≠0),则:20=15k ,解得k =43,∴y =43x ; 当15<x ≤60时,设y =k′x +b(k ≠0),则:{20=15k′+b 170=60k′+b, 解得{k′=103b =−30, ∴y =103x −30,∴y ={43x(0≤x ≤15)103x −30(15<x ≤60); (2)当y =80时,80=103x −30,解得x =33,33−15=18(天), ∴这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.。
最新人教版八年级下第三次月考数学试卷(含答案)

_ 第3题图 _ D _ C _ B _ A 八年级下第三次月考数学试卷一、填空题(每小题2分,共20分)1.若分式112++x x 有意义,则x 的取值范围是 . 2.已知反比例函数y =xk 的图象经过点P (-1,2),则这个函数的图象位于第 象限. 3.如图四边形ABCD 中,AD ∥DC ,∠D=90°,若再添加一个条件,就能说明四边形ABCD 是矩形,你添加的条件是 (写出一种情况即可).4.学校校园内有一块如图所示的三角形空地,计划将这块空地建成一个花园,以美化校园环境,若∠A=90°,则BC= ㎝.5.在平行四边形ABCD 中,对角线AC 、DB 相交于点O ,BC=8,则BD 的长度的取值范 围是 .6.如图所示,在矩形ABCD 中,对角线AC 、BD 相交于一点O ,则图中一共有 个等腰直角三角形.7.若三角形的面积是12㎝2,则它的一边长a (㎝)和这条边上的高h (㎝)之间的函数关系式为 .8.如图所示,在矩形ABCD 中,O 为对角线AC 的中点,连接BO ,若BO=2,则AC=.9.菱形的两条对角线分别是24㎝和10㎝,则菱形的周长是 ㎝.10.已知梯形ABCD 的周长为40㎝,上底CD=6㎝,DE ∥BC 交AB 于E ,则△ADE 的周长为 ㎝.二、单项选择题(每小题3分,共18分)11.若分式142+-x x 的值是0,则x 的值是 ( ) A .—2 B.—1 C.2 D.112.在同一直角坐标系中,函数y =3x 与y = x1的图象大致是 ( )_ 8 c m _ 6 c m _ 第4题图 _ C _ B _ A _ O _ 第6题图 _ D _ C _ B _ A 第8题图 ? _ O _ D _ C _ B _ AC.对角形垂直且相等的四边形是菱形D.有两个角相等且有一组对边平行的四边形是矩形14.如图,你听说过亡羊补牢的故事吗?为了防止羊的再次丢失,小明爸爸要在高0.9米,宽1.2米的栅栏门的对角顶点间加一个加固木板,这条木板长需()A.1米B.1.3米C.1.5米D.2米15.如图,在正方形ABCD中CE⊥MN,∠MCE=35°,那么∠ANM等于()A.45°B.50°C.55°D.60°16.如图,在梯形ABCD中,AD∥BC,E、F分别是对角线BD、AC的中点,AD=22㎝BC=38㎝,则EF等于()㎝ C.10㎝ D.12㎝三、解答题(每小题5分,共20分)17.请先化简13112223+-+----xxxxxxx,再取一个使原式有意义而你又喜欢的数代入求值.18.甲、乙两班参加2011年清明节植树活动,已知乙班每小时比甲班多种2棵树,甲班种60棵树所用的时间与乙班种66棵所用的时间相等,求甲、乙两班每小时各种多少棵树?19.如图,平行四边形ABCD中,过对角线的交点O的直线EF与CD和AB的延长线相交于点F、E.求证:AC与EF互相平分.20.如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC,BD=BC.求∠A的度数.四、解答题(每小题6分,共12分)第? 14 题图_ O_ F_ E_ D _ C_ B_ 第19题图?_ A_ D_ C_ B_ 第20题图_ A_ M_ E_ 第15题图_ D_ C_ B_ A_ F_ E_ 第16题图_ D_ C_ B_ A(1)求证:△BCE ≌△FDE ;(2)连结BD 、CF ,判断四边形BCFD 的形状并加以证明.22.在菱形ABCD 中,AB=4,E 为BC 中点,AE ⊥BC ,AF ⊥CD 于点F ,CG ∥AE ,CG 交AF 于点H ,交AD 于点G.(1)求菱形ABCD 的面积;(2)求∠CHA 的度数.五、解答题(每小题7分,共14分)23.如图,四边形ABCD 中,AB=3,BC=4,CD=12,AD=13,∠B=90°.(1)判断△ACD 的形状;(2)求四边形ABCD 的面积.24.如图,双曲线xk y =与直线n mx y +=的图象交于A 、B 两点,AC ⊥x 轴于C ,DB ⊥x 轴于D ,已知AC=3,OC=1,OD=3.(1)求反比例函数的解析式;(2)求一次函数的解析式._ F _ E _ D _ C _ B _ 第21题图 _ A _D _ C _ B 第22题图 ? _D _ C _ B第23题图 ? _ A六、解答题(每小题8分,共16分)25.如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,MN ∥AB ,且分别与AO 、BO 交于点M 、N ,请问:(1)BM=CN 吗?请说明理由;(2)BM ⊥CN 吗?请说明理由.26.如图所示,在矩形ABCD 中,AB=12㎝,BC=6㎝,现有两动点P 、Q ,点P 沿AB 边从点A 开始向点B 以2㎝/s 的速度移动,点Q 沿DA 边从点D 开始向点A 以1㎝/s 的速度移动.如果P 、Q 同时出发,用t (s )表示移动的时间(0≤t≤6).(1)t 为何值时,△QAP 为等腰直角三角形;(2)求四边形QAPC 的面积七、解答题(每小题10分,共20分)27.四边形ABCD 为平行四边形,AD=a ,BE ∥AC ,DE 交AC 的延长线于点F ,交BE 于点E.(1)求证:DF=FE ;(2)若AC=2FC ,∠ADC=60°,AC ⊥DC.求BE 的长(提示:a a 23432 )_ 第25题图 _ O _N _ M _D _ C _ B _ A _ Q _ P 第26题图 ? _D _ C _ B _ A _F _ D _ C _ B _ A28.如图,正方形OABC 的面积为4,点O 为坐标原点,点B 在函数xk y = (k <0,x <0)的图象上,点p (m ,n )是函数xk y =(k <0,x <0)的图象上异于B 的任意一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F.(1) 求k 的值; (2) 设矩形OEPF 的面积为1S ,判断1S 与点P 的位置是否有位置关系(不必说明理由);(3) 从矩形OEPF 的面积中减去其与正方形OABC 重合的面积,剩余面积记为2S ,写出2S 与m 的函数关系式,并标明m 的取值范围。
最新八年级下学期第三次月考数学试题卷(带答案)

八年级下学期第三次月考数学试题卷满分:150分考试用时:120分钟范围:第一章《三角形的证明》~第四章《因式分解》班级姓名得分一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B 铅笔在答题卡相应位置作答,每小题3分,共30分.1.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,−300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是()A. Q(3,240°)B. Q(3,−120°)C. Q(3,600°)D. Q(3,−500°)2.不等式−2x>12的解集是()A. x<−14B. x<−1 C. x>−14D. x>−13.如图所示是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在()A. △ABC的三条中线的交点处B. △ABC的三边的垂直平分线的交点处C. △ABC的三条角平分线的交点处D. △ABC的三条高所在直线的交点处4.下列各式中不能用完全平方公式分解因式的是()A. x2+2x+1B. x2−2xy+y2C. −x2−2x+1D. x2−x+0.255.下列各数中,能整除803−80的是()A. 76B. 78C. 79D. 826.如图,在两个重叠的直角三角形中,将其中的一个直角三角形沿着BC方向平移BE距离得到此图形,其中AB=6,BE=5,DH=3,则四边形DHCF的面积为()A. 35B. 652C. 452D. 317.两个数2−m和−1在数轴上从左到右排列,那么关于x的不等式(2−m)x+2>m的解集是()A. x>−1B. x<−1C. x>1D. x<18.如图,P,Q分别是BC,AC上的点,过点P作PR⊥AB于点R,作PS⊥AC于点S,若AQ=PQ,PR=PS,则下面三个结论:①AS=AR;②QP//AR;③△BRP≌△CSP,正确的是()A. ①③B. ②③C. ①②D. ①②③9.若不等式2x+53−1≤2−x的解集中x的每一个值,都能使关于x的不等式3(x−1)+5>5x+2(m+x)成立,则m的取值范围是()A. m>−35B. m<−15C. m<−35D. m>−1510.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(−1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(−2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2021次跳动至点A2021的坐标是()A. (−1009,1009)B. (−1010,1010)C. (−1011,1011)D. (−1012,1012)二、填空题(本大题共5小题,共20.0分)11.若将点P(m+2,2m+1)向右平移1个单位长度后,点P的对应点正好落在y轴上,则m=.12.若不等式组{−1≤x≤1,2x<a有解,那么a必须满足________.13.如图,△ABC的边AB、AC的垂直平分线相交于点P.连接PB、PC,若∠A=70°,则∠PBC的度数是______ .14.a2+a−1=0,则a2021+a2020−a2019=.15.232−1可以被10和20之间某两个整数整除,则这两个数是______.三、解答题(本大题共10小题,共100.0分)16.(8分)因式分解:(1)4m2−16n2(2)x3y+2x2y2+xy317.(10分)解不等式组{2x+5≤3(x+2)2x−1+3x2<1把它的解集在数轴上表示出来,并写出不等式组的非负整数解.18.(10分)在如图的平面直角坐标系中描出下面各点:A(0,3),B(1,−3),C(3,−5),D(−3,−5),E(3,5),F(5,7),G(5,0).(1)将点C向x轴的负方向平移6个单位,它与点__________重合.(2)连接CE,则直线CE与y轴是什么关系⋅(3)顺次连接点D,E,G,C,D得到四边形DEGC,求四边形DEGC的面积.19.(10分)如图,在△ABC中,AB=AC=24cm,BC=20cm,点D为边AB的中点,如果点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s).(1)若点P与点Q的速度都是3cm/s,则经过多长时间△BPD与△CQP全等?说明理由.(2)若点P的速度比点Q的速度慢2cm/s,则经过多长时间△BPD与△CQP全等.并求出此时点P与点Q的运动速度.20. (10分)如图,在△ABC 中,AB =AC ,D 为BC 边的中点,F 为CA 的延长线上一点,过点F 作FG ⊥BC 于点G ,并交AB 于点E ,求证:(1)AD // FG ;(2)△AEF 是等腰三角形.21. (8分)已知关于x 、y 的二元一次方程组{2x +y =1+2mx +2y =2−m 的解满足不等式组{x −y <8x +y >1,则m 的取值范围是什么?22. (10分)如图,在正方形ABCD 中,E 、F 是对角线BD 上两点,且∠EAF =45∘,将△ADF 绕点A 顺时针旋转90∘后,得到△ABQ ,连接EQ ,求证:(1)EA 是∠QED 的平分线;(2)EF 2=BE 2+DF 2.23.(10分)回答下列问题:(1)利用因式分解进行计算:(a−2)(a+2)−a(a−2),其中a=−1;(2)已知a+b=2,ab=2,求12a3b+a2b2+12ab3的值.24.(12分)若一个三位自然数,十位上的数字恰好等于百位上的数字与个位上的数字之和,则称这个三位数为“三雅数”,例如:在自然数231中,3=2+1,则231是“三雅数”,在自然数583中,8=5+3,则583是“三雅数”.(1)写出最小的三雅数和最大的三雅数;(2)求出所有小于500且能被8整除的“三雅数”.25.(12分)已知△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立?请说明理由.答案1.D2.A3.C4.C5.C6.C7.B8.C9.C10.C11.−312.a>−213.20°14.015.15和1716.解:(1)4m2−16n2 解:原式=4(m2−4n2)=4(m+2n)(m−2n);(2)x3y+2x2y2+xy3解:原式=xy(x2+2xy+y2)=xy(x+y)².17.解:{2x+5≤3(x+2)①2x−1+3x2<1②,由①得:x≥−1,由②得:x<3,∴不等式组的解集为−1≤x<3,在数轴上表示,如图所示,则其非负整数解为0,1,2.18.(1)D(−3,−5);(2)直线CE 与y 轴平行;(3))S 四边形DEGC =S △CDE +S △CEG =12×6×10+12×10×2 =30+10=40.19.解:(1)∵AB =AC =24cm ,∴∠B =∠C .∵点D 为边AB 的中点,∴BD =12cm ,∵点P 与点Q 的速度都是3cm/s ,∴BP =CQ ,∴当BD =CP 时,△BPD 与△CPQ 全等,即12=20−3t ,解得t =83,∴经过83s △BPD 与△CQP 全等.(2)设点P 的速度为xcm/s ,则点Q 的速度为(x +2)cm/s .∵BP ≠CQ ,∠B =∠C ,∴BD =CQ ,BP =CP =10,∴{12=(x +2)t xt =10, 解得:{t =1x =10. ∴当运动时间为1s 时,△BPD 与△CPQ 全等,此时点P 的速度为10cm/s ,点Q 的速度为12cm/s .20.证明:(1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC.∴∠ADC =90°. ∵FG ⊥BC ,∴∠FGC =90°.∴∠ADC =∠FGC .∴AD // FG .(2)∵AB =AC ,D 是BC 的中点,∴∠BAD =∠CAD .∵AD // FG ,∴∠F =∠CAD ,∠AEF =∠BAD .∴∠F =∠AEF ,∴AF =AE .∴△AEF 是等腰三角形.21.解:在方程组{2x +y =1+2m ①x +2y =2−m ②中, ①+②,得:3x +3y =3+m ,即x +y =3+m 3,①−②,得:x −y =−1+3m ,∵{x −y <8x +y >1, ∴{3m −1<83+m 3>1,解得:0<m <3.22. (1)∵将△ADF 绕点A 顺时针旋转90∘后,得到△ABQ ,∴QB =DF ,AQ =AF ,∠BAQ =∠DAF .∵∠EAF =45∘,∴∠DAF +∠BAE =∠BAQ +∠BAE =45∘,∴∠QAE =45∘,∴∠QAE =∠FAE .在△AQE 和△AFE 中,{AQ =AF,∠QAE =∠FAE,AE =AE,∴△AQE ≌△AFE(SAS),∴∠AEQ =∠AEF ,∴EA 是∠QED 的平分线.(2)由(1)得△AQE ≌△AFE ,∴QE =EF ,由旋转知∠ADF =∠ABQ ,又∠ABD +∠ADF =90∘,∴∠ABD +∠ABQ =90∘,即∠QBE =90∘.在Rt △QBE 中,QE 2=BE 2+QB 2,则EF 2=BE 2+DF 2.23.解:(1)(a −2)(a +2)−a(a −2)=(a −2)[(a +2)−a]=2(a −2).当a =−1时,原式=2×(−1−2)=−6.(2)12a 3b +a 2b 2+12ab 3=12ab(a 2+2ab +b 2)=12ab(a +b)2.当a +b =2,ab =2时,原式=12×2×22=4. 24.解:(1)根据题意,用列举法容易得到最小的“三雅数”是110,最大的“三雅数”是990;(2)设这个三位数为ABC −,根据题意得到B =A +C .又∵这个三位数可以表示成ABC −=100A +10B +C .∴ABC −=100A +10(A +C)+C =110A +11C =11(10A +C).可见这个三位数能被11整除,又ABC −<500,且能够被8整除,只有10A +C =8,16,24,32,40.所以得到{A =0C =9(舍去),{A =1C =6,{ A =2C =4,{A =3C =2,{A =4C =0. 这个“三雅数”是176,264,352,440. 25.解:(1)AD =CE .理由:过点D 作DP // BC ,交AB 于点P .∵△ABC 是等边三角形,∴∠APD =∠ABC =∠ACB =∠PDA =60°.∴△APD 也是等边三角形.∴AP =PD =AD .∵DB =DE ,∴∠DBC =∠DEC .∵DP // BC ,∴∠PDB =∠CBD .∴∠PDB =∠DEC .∵∠BPD =180°−∠APD =120°,∠DCE =180°−∠ACB =120°,∴∠BPD =∠DCE .在△BPD 和△DCE 中,{∠PDB =∠CED,∠BPD =∠DCE,DB =ED,∴△BPD≌△DCE(AAS).∴PD =CE .∴AD=CE.(2)AD=CE成立.理由:过点D作DP//BC,交AB的延长线于点P.∵△ABC是等边三角形,∴∠APD=∠ABC=∠ACB=∠PDC=60°.∴△APD也是等边三角形.∴AP=PD=AD.∵DB=DE,∴∠DBC=∠DEC.∵DP//BC,∴∠PDB=∠CBD.∴∠PDB=∠DEC.∵∠DCE=∠ACB=60°,∴∠P=∠DCE.在△BPD和△DCE中,{∠PDB=∠CED,∠P=∠DCE, DB=ED,∴△BPD≌△DCE(AAS).∴PD=CE.∴AD=CE.。
广东省珠海市八年级下学期数学3月月考试卷

广东省珠海市八年级下学期数学3月月考试卷姓名:________ 班级:________ 成绩:________一、选择题(每题5分,共30分)。
(共6题;共30分)1. (5分) (2016八上·鄱阳期中) 如图,在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件是()A . ∠A=∠DB . ∠ACB=∠FC . ∠B=∠DEFD . ∠ACB=∠D2. (5分)无论x取什么值,下列不等式都成立的是()A . x2>0B . x2>xC . x2+1>0D . 2x>x3. (5分) (2018八上·九台期末) 如图,图中的尺规作图是作()A . 线段的垂直平分线B . 一条线段等于已知线段C . 一个角等于已知角D . 角平分线4. (5分) (2018七上·临沭期末) 如图所示,数轴上点A,B对应的有理数分别为,,下列关系式:① ;② ;③ ;④ .正确的有()A . ①②B . ②③C . ①③④D . ①②③5. (5分) (2019八上·江岸期中) 已知△ABC的内角平分线相交于点O,三边的垂直平分线相交于点I,直线OI经过点A.若∠BAC=40°,则∠ABC=()A . 40°B . 50°C . 70°D . 80°6. (5分) (2017七下·德州期末) 若点P(a-2,a)在第二象限,则a的取值范围是()A . 0<a<2B . -2<a<0C . a>2D . a<0二、填空题(每题5分,共20分)。
(共4题;共20分)7. (5分) (2008七下·上饶竞赛) 不等式的正整数解是________.8. (5分) (2019七上·大庆期末) 如图,△ABC和△BDE都是等边三角形,A、B、D三点共线.下列结论:①AE =CD;②BF=BG;③△BFG是等边三角形;④∠AHC=60°.其中正确的有________(只填序号).9. (5分)等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边的长为________ .10. (5分) (2015八下·孟津期中) 如图,已知函数y=2x+b与函数y=kx﹣3的图像交于点P,则不等式kx ﹣3>2x+b的解集是________.三、解答题(第11小题20分,其余每题10分,共50分). (共4题;共50分)11. (20分) (2017七下·西华期末) 解不等式组:并写出它的所有非负整数解.12. (10分) (2015八上·宜昌期中) 如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B 同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s).(1)当t为何值时,△ABQ≌△CBP.(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.13. (10分)甲、乙两车在相距300千米的A、B两地匀速相向而行,两车同时出发,途中甲车配货停留1小时.甲、乙两车离B地的距离y(千米)与出发时间x(小时)之间的关系如图①所示,甲、乙两车间的距离s (千米)与出发时间x(小时)之间的关系如图②所示,(1)求甲、乙两车的速度;(2)求甲车到B地所用的时间,并将图②补充完整;(3)乙出发多少小时时,两车相距20千米?14. (10分)(2017·南岗模拟) 为了相应“足球进校园”的号召,某体育用品商店计划购进一批足球,第一次用6000元购进A品牌足球m个,第二次又用6000元购进B品牌足球,购进的B品牌足球的数量比购进的A品牌足球多30个,并且每个A品牌足球的进价是每个B品牌足球的进价的.(1)求m的值;(2)若这两次购进的A,B两种品牌的足球分别按照a元/个, a元/个两种价格销售,全部销售完毕后,可获得的利润不低于4800元,求出a的最小值.参考答案一、选择题(每题5分,共30分)。
珠海北大附属实验学校八年级下数学第三次月考试卷

珠海北大附属实验学校 2007—2008学年第 二 学期 第三次月 考试 初 二年级 数学 试卷 考试时间: 90 分钟 满分: 100 分 命题人: 肖忠国 审核人; 一、精心选一选(每小题3分,共30分) 1、已知函数y=21--x x 自变量x 的取值范围是 ( ) (A )x ≥1 (B )x ≥2 (C )x ≥1且x ≠2 (D )x ≤1且x ≠2 2、若点(-2,y 1)(-1,y 2)、(1,y 3)都在反比例函数y =-x 1的图象上,则 ( ) A . 321y y y >> B .312y y y >> C .213y y y >> D .123y y y >> 3、将直角三角形三条边的长度都扩大同样的倍数后得到的三角形是( ) A .可能是锐角三角形 B .仍是直角三角形 C .可能是钝角三角形 D .不可能是直角三角 4.如图:有一圆柱,它的高等于cm 8,底面直径等于cm 4(3=π)在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面与A 相对的B 点处的食物,需要爬行的最短路程大约( ) A . cm 10 B .cm 12 C .cm 19 D .cm 20 AE 平分ABCD 中,5.如图,DAB ∠,0100=∠B ,则=∠DAE ( ) A .0100 B .080 C .060 D .040 6.在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 的面积比是( ) A.4:3 B.8:5 C.16:9 D.2:1 7、下列说法正确的是( ) A.真命题的逆命题是真命题 B.每个定理都有逆定理 C .每个命题都有逆命题 D.假命题的逆命题是假命题 8、下列条件中,能判定一个四边形是平行四边形的是( ) A .一组对边相等 B .一组对边平行 C .两条对角线相等 D .两组对角相等 9. 已知四边形ABCD 是平行四边形,则下列结论中哪一个不满足平行四边形的性质( ) A .对角线互相垂直 B.对边分别平行且相等 C.对角分别相等 D.对角线互相平分10、已知ABC ∆的三边边长分别为10,24,26,则最长边上的中线长为( )A. 14B. 13C. 12D. 11二、填空题(每空3分,共30分)1、某种细菌的直径为,用科学记数法表示为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
珠海北大附属实验学校 2007—2008学年第 二 学期 第三次月 考试 初 二年级 数学 试卷 考试时间: 90 分钟 满分: 100 分 命题人: 肖忠国 审核人; 一、精心选一选(每小题3分,共30分) 1、已知函数y=21--x x 自变量x 的取值范围是 ( ) (A )x ≥1 (B )x ≥2 (C )x ≥1且x ≠2 (D )x ≤1且x ≠2 2、若点(-2,y 1)(-1,y 2)、(1,y 3)都在反比例函数y =-x 1的图象上,则 ( ) A . 321y y y >> B .312y y y >> C .213y y y >> D .123y y y >> 3、将直角三角形三条边的长度都扩大同样的倍数后得到的三角形是( ) A .可能是锐角三角形 B .仍是直角三角形 C .可能是钝角三角形 D .不可能是直角三角 4.如图:有一圆柱,它的高等于cm 8,底面直径等于cm 4(3=π)在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面与A 相对的B 点处的食物,需要爬行的最短路程大约( ) A . cm 10 B .cm 12 C .cm 19 D .cm 20
5.如图,ABCD 中,AE 平分DAB ∠,0100=∠B ,则=∠DAE ( ) A .0100 B .080 C .060 D .040 6.在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 的面积比是( ) A.4:3 B.8:5 C.16:9 D.2:1 7、下列说法正确的是( ) A.真命题的逆命题是真命题 B.每个定理都有逆定理
C .每个命题都有逆命题 D.假命题的逆命题是假命题
8、下列条件中,能判定一个四边形是平行四边形的是( )
姓名: 班级: 座位号: 考号: ---------------------------------------------------- 装 -------------------------------- 订 ----------------------------- 线 ------------------------------------- 第4题图 第5题图 第6题图
A .一组对边相等
B .一组对边平行
C .两条对角线相等
D .两组对角相等
9. 已知四边形ABCD 是平行四边形,则下列结论中哪一个不满足平行四边形的性质( )
A .对角线互相垂直 B.对边分别平行且相等
C.对角分别相等
D.对角线互相平分
10、已知ABC ∆的三边边长分别为10,24,26,则最长边上的中线长为( )
A. 14
B. 13
C. 12
D. 11
二、填空题(每空3分,共30分)
1、某种细菌的直径为0.000123,用科学记数法表示为 。
2、 命题“对顶角相等.”的逆命题是 。
3、如图所示,数轴上点A 对应的实数为
4、一组对边 的四边形是平行四边形。
5、在平行四边形ABCD 中,若∠B=100°,则∠A= ,∠C= ,∠D= 。
6、已知,ABC ∆中,5,12,13===BC AC AB ,则ABC ∆的面积为_____.
7、等腰三角形的腰长为5cm,底边长为6cm,则它的高是 .
8、在平行四边形ABCD 中,若∠A :∠B=2:3,则∠C=
9、平行四边形的两邻边的比是2:5,周长为28cm ,则较长的一边是 。
10、。
反比例函数y=k x
的图象当K <0时,图象在第___ __象限. 三、解答下列各题:(共40分)
1、如图,F E ,是ABCD 的对角线AC 上的两点,并且CF AE =,求证:DE=BF (7分)
B C
D A
2. 如图,△ABC 是等边三角形中,cm AB 10 . 求高AD 的长和△ABC 的面积.(结果用根号表示.)(6分)
3、在Rt △ABC 中,∠C=90° ,D 是BC 边上一点,且BD=AD=10, ∠ADC=60°,求△ABC 的面积. (6分)
4﹑已知某开发区有一块四边形的空地ABCD ,如图,现计划在空地上种植草皮,经测量
∠A =90°,AB =3m ,BC =12m ,CD =13m ,DA =4m ,若每平方米草皮需要200元,问需要多少投入?(7分)
C D B
A
5、如图,小明想测量学校旗杆AB 的高度,他采用如下方法:先将旗杆上的绳子垂到地面,还多1米,然后将绳子下端拉直,使它的末端刚好接触地面,测得绳子下端C 离旗杆底部B 点5米,请你计算一下旗杆的高度。
(7分)
6、已知
: ABCD 的对角线AC,BD 交于点O,E,F 分别
在OB,OD 中点上.求证:A E ∥CF (7分)
附加题(5分,计入总分)
已知,如图所示,折叠长方形的一边AD ,使点D 落在BC 边的点F 处,•如果cm BC cm AB 10,8==,求EC 的长.(5分)
C A
B O F E D B
C A。
