度量空间的列紧性与紧性
距离空间的列紧性与紧性选讲全

第10页
第11页
定理5.3 (全有界集的性质) 设X是距离空间,AX是全有界集, 则(1)A一定是有界集;(2)A一定是可分的。
证 (1) AX是全有界集 对=1, A的一个有限的1—网B ={x1,x2,…,xn}A xA, k, 使xS(xk,1), 即(xk,x)<1 A有界。
(2) AX是全有界集 (只要证明A有可数的稠密子集) 对k=1/k, A的有限1/k—网Bk={x1(k) ,x2(k),…,xnk(k)}A
{xn}的每一个子列都不可能是基本列,矛盾。 因此,A是全有界集。
第14页
2 全有界集与列紧集的关系 定理5.5 (豪斯道夫定理—全有界集与列紧集的关系) (1) 设X是距离空间,AX是列紧集A是全有界集 (2) 设X是完备距离空间, 则AX是列紧集A是全有界集
证 (1) 设AX是列紧集 {xn}A,子列{xn(k)}, xn(k)xX (k) {xn(k)}是{xn}的基本子列 A是全有界集。
第9页
定义5.3 (全有界集) 设X是距离空间,AX. 如果>0, A的有 限的—网B={x1,x2,…,xn}, 则称A为全有界集.
例3 闭区间[0,1]使R中的全有界集。 证 >0, 取n>1/, 则有1/n<.
构造有限点集 B={0, 1/n, 2/n, …, (n-1)/n}[0,1] x,yB是相邻两点,有(x,y)=1/n<. B 中各点的开球的全体覆盖了A B是[0,1]区间一个有限的—网 [0,1]区间是全有界集。 注 1) 对全有界集A, 一定能找到它的有限—网BA. 2) 全有界集A的有限的—网的构造方法: 首先,构造一个 有限点集 B={x1,x2,…, xn}A 然后,选取网中 个开球的公共半径,x,yB是相邻两点,有(x,y)<.
列紧性
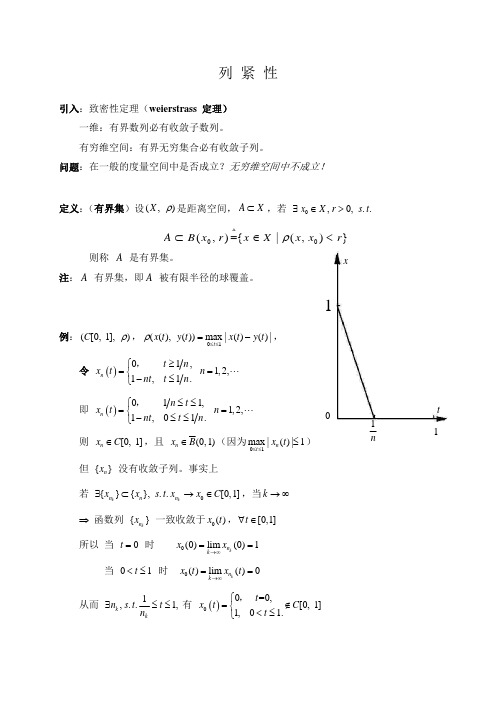
命题 1.3.3 列紧空间的任意(闭)子集都是(自)列紧集。 证:由定义显然。
命题 1.3.4 列紧空间是完备空间。 ( X , ) 列紧 ( X , ) 完备 证: 任取基本列{xn } X
{xnk } {xn }, s. t. xnk x0 X , k ( xn , x0 ) ( xn , xnk ) ( xnk , x0 ) 0
x0 (0) lim xnk (0) 1
k
x0 (t ) lim xnk (t ) 0
k
0, t =0, 1 t 1, 有 x0 t C[0, 1] nk 1, 0 t 1.
定义 1.3.1 (列紧)设 ( X , ) 是距离空间, A X ,若 A 中任意子列在 X 中都有 收敛子列,则称 A 为列紧集;若 A 中任意子列都收敛到 A 中的点,则称 A 为自 列紧集;若 X 是列紧的,则称 X 是列紧空间。 注:1、 A 列紧 {xn } A, {xnk } {xn }, s. t. xnk x0 X
1 1 2 0 n n n
( n p ) (n) ( n p ) (n) 因为 p , ( xn p , xn ) ( xn p , yn ) ( yn , xn )
(k ) 所以 由 ( X , ) 完备,知道 {xk } 在 X 中收敛。
定义 1.3.10 (紧集) 在拓扑空间 X 中,若 X 中每个覆盖 M 的开集族中有有穷个 开集覆盖集合 M ,则称 M 为紧的。若 A 是紧集,则称 A 是相对紧集。 注:1、若 M
G ,
G X , 是开集,则称 {G } 是 M 的开覆盖。
度量空间中关于紧致的几个性质

度量空间中关于紧致的几个性质
赵建红
【期刊名称】《通化师范学院学报》
【年(卷),期】2003(024)004
【摘要】给出了度量空间中关于紧致的两个性质,并进行了证明.
【总页数】2页(P11-12)
【作者】赵建红
【作者单位】通化师范学院数学系,吉林通化,134002
【正文语种】中文
【中图分类】D189
【相关文献】
1.紧致度量空间中一列映射的传递性和混沌性 [J], 吉飞宇;刘磊
2.紧致度量空间及其逆极限空间 [J], 缪克英;邓小琴
3.非紧L-凸度量空间中极大极小不等式的解集性质及其应用 [J], 文开庭;余廷忠;夏仁强
4.局部紧致度量空间的渐进稳定集 [J], 符子晴;霍展福;
5.在两个完备紧致度量空间上满足隐含关系映射的不动点定理[J], A·阿利欧谢;B·费瑟;海治(译);张禄坤(校)
因版权原因,仅展示原文概要,查看原文内容请购买。
度量空间C(Rn)中集合列紧性的判定条件及证明

定义 1.4 [1] 设 ( X , ρ ) 是距离空间, A 是 B 的子集,如果 ∀ε > 0 ,都存在着 A 的一个有限 ε 网,则
称集合 A 是完全有界的。
3. 主要结论
( ) 定理 2.1 C Rn 空间的子集 U 列紧的充要条件是
1) 对任意 k 属于 C ,当 x ≤ k 时,存在 Ck > 0 ,使得 sup u ( x) ≤ Ck ,对 ∀u ∈U 。 x ≤k
有限 ε 网。
定义 1.3 [1] C (M ) 空间:设 M 是一个紧的距离空间,带有距离 ρ ,C (M ) 表示 M → R1 的一切连续
映射的全体。定义
d (= u,v) max u ( x) − v ( x) ,(∀u,v ∈ C (M )). x∈M
通过验证可知 (C (M ), d ) 是完备的距离空间。 定理 1.2 [1] (Arzela-Ascoli)为了 F ⊂ C (M ) 是一个列紧集,当且仅当 F 是一致有界且等度连续的函数
Abstract
Set sequence compactness is an important concept in functional analysis. Using the sequence compactness, one can turn infinite dimensional problems to finite dimensional problems. In this paper, we give a necessary and sufficient condition for set sequence compactness on metric space C(Rn).
− u*
1-3 列紧性 - 2

矛盾。从而,M 列紧。
接下来证明 M 是闭集。 方法一:证明 X\M 是开集,即对于任意给定 的 x X\M,存在 r>0,使得 x 到 M 的距离小于
r,即 B(x,r) X\M
在任意点 y M 处,以 (x,y)/2 为半径作开球。 M B(y, (x,y)/2 )
由于 M 是紧集,可知存在子覆盖,设为 {B(yn, (x,yn)/2) |n k}
由于 M 自列紧,集合 {y1,y2,…}存在子列不 妨仍记作 {y1,y2,…} 收敛到 y0 M。 因而存在 ,y 0 G 。
而 G 是开集,可知存在 >0,B(y0 , ) G 。
由极限的定义: N,n>N 时,yn B(y0 , /2) 从而可以取充分大的 n,使得 B(yn,2/n) B(y0 , ) G 矛盾!因此 M 是紧集。
充分性:和有限覆盖定理的证明相似。 用反证法,设 {G : 且没有有限子覆盖。 } Байду номын сангаас M 的开覆盖,并
由于 M 列紧,从而完全有界。于是, >0,
存在有限 -网。取 =1/n 设 Nn={x1,x2,… xkn} 为有限1/n-网,则 M B(xj,1/n)
再利用有限和无限之间的关系
由于{G :
覆盖都有有限子覆盖,则称 M 为紧集。 紧性和完全有界的区别 完全有界即: >0, M 具有有限的 -网
区别在于完全有界的条件是任意取一个有
限的 -网即可,而紧性则必须在选定的开覆
盖中选择有限子覆盖
紧
完全有界,反之未必成立
定理:设 (X, ) 是度量空间,则 M X 是紧集
当且仅当 M 是自列紧集。 证明:先证必要性,设 M 是紧集。证明目标 有 (1) M 是列紧集,(2) M 是闭集。 (1)回顾:列紧集即任意子集有收敛子列,这等
拓扑学第四章 紧致性

第四章 紧致性紧致性是数学分析中的重要概念。
尽管这个概念出现的较早,但是,从本质上讲,它是一个拓扑概念,也是一个最基本的拓扑性质。
我们先回顾一下度量空间紧性(列紧性)概念(在实直线上,紧性是描述闭区间性质的,而在实分析中,闭区间具有良好的性质)。
§4-1 度量空间(,)X d 中紧性(简单复习)定义1 设A 是(,)X d 的一个子集。
如果A 中任一无穷点列有子列收敛于X 中的一点,则称A 是相对列紧的;如果A 中每个收敛子列的极限点都属于A ,则称A 是列紧的; 如果(,)X d 本身是列紧的,则称为列紧空间。
注释:这里的紧性之所以成为列紧,是因为用序列收敛描述的。
●下面的结论是显然的(由于都是过去的知识,所以不加证明的给出) (1) 有限子集总是列紧的。
(2) 列紧空间是完备的(但,完备空间未必是列紧的)。
(3) 若A 是(,)X d 的列紧子集,则A 是(,)X d 的有界闭集。
(4) 在一般度量空间中,(3)成立,反之未必;如果(,)X d 是列紧空间,则 A 列紧 ⇒ A 是闭集。
(5) 列紧的度量空间必是可分的。
●进一步分析:列紧性能用来刻画闭集,但是,它是利用“序列”形式刻画的。
人们找出了一种非序列刻画的方式。
定义2 设A 是(,)X d 的一个子集。
U 是X 的一族开集,满足U U A ∈⊃U,则称U 为A 在X中的开覆盖;若U 中只有有限个子集,称U 为有限开覆盖;若X 本身的每一开覆盖都有一有限子覆盖,则称X 为紧致空间(有的书成为紧空间) ★ 理论上可以证明:对于度量空间来说,列紧性与紧致性是等价的。
即列紧空间⇔紧致空间(这在泛函分析书中都有介绍)。
§4-2 拓扑空间的紧性在数学分析中,人们很早就注意的,实直线上闭区间[,]a b 具有某些极好的性质,它对于证明极大值定理、一致连续性定理等起着至关重要的作用。
但是,如何在拓扑空间上表述这个特性,长期不得而知。
度量空间中的自列紧集、紧集、连通集与连续映射

由 d x, r r 和 d r, s r s 得 d s, x d r, s d r, x r s r s 。所
以 x N 。同理可得,若 x N ,则 x M 。所以 M N 。
因为集 A 是连通的,所以集合 A \ M N 不空(若空则 M 、 N 分离集 A )。
自列紧集(列紧闭集)与连续映射 1.度量空间的自列紧子集在连续映射下的象是自列紧集。 证明: 设 X、Y 是度量空间, A 是 X 的自列紧子集。
设 f : A Y 是连续映射,象集为 B f X Y 。设yn 是 B 的序列。对任意
正整数 k,设 yk 的某个原象是 xk A X ,这样得到 X 的序列xn 。因为 X 是自
R 的定义是函数值小于 y0 的自变量集合)。同理,对于任意点 s S ,存在邻域
U s, s 使得U s, s A S 。
对任意点 r R ,s S ,设s s 2 ;设 dr inf d r, s s S ,显然 dr 0
(否则,便不存在不包含 S 的点的邻域), d r, s s d r, s s 0 。
紧集与连续映射 1.度量空间的紧子集在连续映射下的象是紧集。 证明:
设 X、Y 是度量空间, A 是 X 的紧子集。设 f : A Y 是连续映射,象集为
B f XY 。
设 B 的一个开覆盖为 G 。任意 S G 是开集,所以对任意 y S ,存在邻域
U y, y S 。对于任意 x f 1 y ( f 1 y 是 y 的原象集),因为 f : A Y 是连
所以,对任意 r R ,s S 都有 d r, s s dr 4 。对任意 r R ,设r dr 4 。
14 度量空间的列紧性与紧性

定理1、4、2设,就是维殴氏空间,那么
(1)就是列紧集当且仅当就是有界集;
(2)就是紧集当且仅当就是有界闭集.
证明(1)必要性显然成立;利用闭球套定理可以证明:如果就是有界得无限集,则具有极限点,从而可证充分性.
(2)由(1)易得.□
注4:由于中得非空紧集就就是有界闭集,定义上得连续函数具有最大与最小值,这一事实在度量(距离)空间中依然成立.首先说明连续映射将紧集映射为紧集.
(2)必要性:设就是得任一点列,取,,因为就是全有界集,故存在有限网,记为.
以有限集得各点为中心,以为半径作开球,那么这有限个开球覆盖了,从而覆盖了,于就是至少有一个开球(记为)中含有得一个子列.
同样以有限集得各点为中心,以为半径作开球,那么这有限个开球覆盖了,于就是至少有一个开球(记为)中含有得一个子列.依次可得一系列点列:
再由为紧集知存在,使得,于就是
令,有,因此就是在上取得得最大值.□
1
刻画列紧性得重要概念之一就是全有界性,通过以下得讨论可知:(1)度量空间中得列紧集必就是全有界集;(2)在完备度量空间中,列紧集与全有界集二者等价.
定义1、4、2网
设就是度量空间,,给定.如果对于中任何点,必存在中点,使得,则称就是得一个网.即
图4、1就是得一个网示意图
例如:全体整数集就是全体有理数得0、6网;平面上坐标为整数得点集就是得0、8网.
图4、2整数集就是全体有理数得0、6网示意图
定义1、4、3全有界集
设就是度量空间,,如果对于任给得,总存在有限得网,则称就是中得全有界集.
注5:根据定义可知就是中得全有界集等价于,,使得,其中表示以中心,以为半径得开邻域.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4度量空间的列紧性与紧性
1.4.1度量空间的紧性Compactness
在微积分中,闭区间上的连续函数具有最大值、最小值、一致连续等,这些性质的成
令{ 集)0x ∈(2)列紧集的子集是列紧集; (3)列紧集必是有界集,反之不真. 证明(1)、(2)易证.下面仅证(3).
假设A X ⊂是列紧集,但A 无界.取1x A ∈固定,则存在2x A ∈,使得12(,)1d x x ≥.对于12,x x ,必存在3x A ∈,使得13(,)1d x x ≥、23(,)1d x x ≥.由于A 是无界集,可依此类推得到X 的点列{}n X 满足:只要i j ≠,就有(,)1i j d x x ≥.显然点列{}n X 无收敛子列,从而A 不是列紧集导致矛盾,故A 是有界集.
反过来,
A 是有界集,A 未必列紧.反例:空间2[,]X L ππ=-上的闭球
B O =有界,而不是列紧集(见例1.1).□
注2:R 中的开区间(0,1)是列紧集,却不是紧集.(由于R 中的有界数列必有收敛子列,所以(0,1)中的数列必有收敛子列,但(0,1)不是闭集,故列紧不紧.)
注3:自然数{1,2,,,}n N =不是列紧集.(N 无界) 推论1.4.1(1)紧空间是有界空间;(2)紧空间是完备空间.
证明(1)若X 为紧空间,那么X 本身为列紧集,而列紧集有界,故X 为有界空间. (2)若X 为紧空间,即它的任何点列有收敛子列,从而知X 中的基本列有收敛子列,根据基本列的性质(若基本列含有收敛子列,则该基本列收敛,且收敛到子列的极限),可得X A 具0()f x E =∈即{点列{}n x (()n n y f x =)存在收敛的子列{}k
n x ,0k
n x x A →∈.从而
00lim lim lim ()()k k n n n n k k y y y f x f x E
→∞
→∞
→∞
====∈,
即E 是闭集.□
定理1.4.3最值定理
设A 是度量空间X 中的紧集,f 是定义在X 上的实值连续函数(泛函),即:f X →R ,那么f 在A 上取得最大值与最小值.
证明设()E f A =,由上述引理知E 是R 中的紧集.所以E 是R 中的有界集,于是上、下确界存在,设
sup{()|}M f x x A =∈,inf{()|}m f x x A =∈.
下证M 是f 在A 上取得的最大值,同理可证m 是f 在A 上取得的最小值.由确界性的定义知,n ∀,n x A ∃∈,使得
1()n f x M n >-
,即可得11
()n M f x M M n n
-<≤<+-. 再由A 为紧集知存在{}{}k
n n x x ⊂,使得*k
n x x A →∈(k →∞),于是 令k →∞,有*()f x M =,因此M 是f 在A 上取得的最大值.□
x',使得d (,)x B
O x ε∈⊂
的一个ε网示意图网;平面上坐标为整数的点集是网.
是全体有理数Q 的0.6如果对于任给的ε,总存在X 中的1
(,)n
i i A O x ε=⊂
,其中,1
n
i i A =⊂
.
证明当A 是全有界集时,0ε∀>,12{,,,}n x x x X ∃⊂,使得1
(,)2n
i i A O x ε
=⊂
.不妨设1i n ∀≤≤有(,)
2
i O x A ε
φ
≠,选取(,)2
i i y O x A ε
∈,显然12{,,,}n y y y Y ⊂以及(,)(,)2
i i O x O y ε
ε⊂,因此
1
1
(,)(,)2n
n i i i i A O x O y ε
ε==⊂
⊂
.□
注6:在n R 中,不难证明全有界集与有界集等价,那么在一般的度量空间中这样的结论成立吗?还是只在完备的度量空间中成立?下面给出有界集和全有界集的关系.
定理1.4.4全有界集的特性
设X 是度量空间,A X ⊂,若A 是全有界集,则(1)A 是有界集;(2)A 是可分集. 证明(1)设A 是全有界集,取1ε=,由定义知,n ∃∈N 及12{,,,}n x x x X ⊂,使得
1
(,1)n
i i A O x =⊂
.
现令121max{(,)}i i n
M d x x ≤≤=+,则易知1(,)A O x M ⊂,可见A 是有界集. (2)设A 是全有界集,下证A 有可列的稠密子集. 由引理1.4.2知对于1
n ε=(1,2,
n =),存在()()()1
2
{,,,}n
n n n n k B x x x A =⊂,使得()1(,)n
k n i A O x n ⊂
,
A ,0δ∀>,存在1
n B ,使
01
(,d x n δ<,从而,中稠密,显然1
n i B ∞
=是可列集,故
:由上述定理知全有界集一定是有界集,然而有界集却不一定是全有界集. 例如全体实数对应的离散度量空间0(,)R d 中的子集{1,23},,是有界集,却不是全有 0网,取
1x ∈A ∈,使1(d x }n x A ⊂,
而{A 存为半径作开球,那么这有限个开球覆盖了盖了{}n x ,于是至少有一个开球(记为1S )中含有{}n x 的一个子列(1)1{}k x S ⊂.
同样以有限集2B 的各点为中心,以2ε为半径作开球,那么这有限个开球覆盖了(1){}k x ,
于是至少有一个开球(记为2S )中含有1{}k x 的一个子列(2)
2{}k x S ⊂.依次可得一系列点列:
(1){}k x :(1)(1)(1)
(1)
123,,,,,k x x x x . (2){}k x :(2)(2)(2)(2)123,,,
,,
k x x x x . ,,,
.
(){}i k x :()()()
()123,,,
,,
i i i i k x x x x .
且每一个点列是前一个点列的子列,取对角线元素作为{}n x 的子列,即
是{}n x 的子列.下证(){}k k x 是基本列.
0ε∀>,取K ,使得12
K K ε
ε=
<,那么当,k p K >时,不妨设p k >,则有()p p k x S ∈,记开球
k S 的中心为*
k
x ,那么有 ()()()**()
(,)(,)+(,)2p k p k p k p k k k k k k d x x d x x d x x εεεε
≤≤+=<,
故(){}k k x 是{}n x 的基本子列.□
推论1.4.2豪斯道夫(Hausdorff)定理设X 是度量空间,A X ⊂. 1.4.5X 完备,
所以X
,,
,1}n
设[,]A C a b ⊂,则A 是列紧集的充要条件为以下两条成立. (1)A 一致有界:0M ∃>,x A ∀∈,对任何[,]t a b ∈有()x t M ≤成立;
(2)A 等度连续:0ε∀>,0δ∃>(δ与t 及x 无关),当12,[,]t t a b ∈及12t t δ-<时,x A ∀∈有
12()()x t x t ε
-<.
注意区别等度连续与映射的一致连续两个概念.
推论1.4.3阿尔采拉(Arzela)引理设{[,],}i i F f f C a b i I =∈∈是[,]C a b 的一致有界且等度连续的函数族,则从F 中必可选出在[,]C a b 上一致连续的子序列{()}n f t .
定理1.4.7设(1)p A l p ⊂≥,则A 是列紧集的充要条件为以下两条成立.
(1)A 一致有界:0M ∃>,12(,,,,)k x x x x A ∀=∈,有11()p
p
k k x M ∞
=<∑;
(2)A 等度连续:0ε∀>,N ∃,12(,,,,)k x x x x A ∀=∈,有11
(
)p
p
k k N x ε
∞
=+<∑
.
例1.4.2设0(,)X d 为离散的度量空间,A X ⊂,证明:A 是紧集的充要条件为A 是有限点集.(2-18)
证明(1)充分性⇐:设A 是有限点集,则A 必为闭集,又无点列,故为紧集. ⇒A ''0(d x 为紧的度量空间,M 是{}n x
是闭子。
