七年级数学上册 4.6 用尺规作线段与角同步导练 (新版)沪科版
七年级数学上册第4章直线与角4.6用尺规作线段与角学案(新版)沪科版

4.6 用尺规作线段与角【学习目标】1.了解尺规作图的概念和意义.2.会用尺规作一条线段等于已知线段,会用尺规作一个角等于已知角,并了解它们在尺规作图中的简单应用.【学习重点】会用尺规作线段与角.【学习难点】作线段与角的和、差、倍数.行为提示:创设情境,引导学生探究新知.行为提示:认真阅读课本,独立完成“自学互研”中的题目.自主的完成有关的练习,并在练习中发现规律,从猜测到探索到理解知识.提示:先作一条直线,在这条直线上连续作出三条线段都等于a即可.方法指导:作图痕迹是尺规作图必不可少的部分,不可擦去.情景导入生成问题旧知回顾:1.什么是角的平分线?答:在角的内部、以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做角的平分线.2.什么样的两个角互补?什么样的两个角互余?答:两个角的和为一个平角,这两个角互为补角,简称互补;两个角的和为一个直角,这两个角互为余角,简称互余.3.补(余)角的性质是什么?答:同角(或等角)的补角相等;同角(或等角)的余角相等.自学互研生成能力知识模块尺规作图阅读教材P153~P154的内容,回答下列问题:问题:什么是尺规作图?答:几何中,通常用没有刻度的直尺和圆规来画图,这种画图方法叫做尺规作图.典例1:已知线段a,如图:.求作:线段AB,使AB=3a.解:作法:(1)作射线AE;(2)在射线AE上顺次截取AC=CD=DB=a,则线段AB即为所求作的线段.典例2:如图,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.解:(1)作射线OA;(2)以射线OA为一边作∠AOC=∠α;(3)以O为顶点,以射线OC为一边,在∠AOC的内部作∠BOC=∠β,则∠AOB就是所求作的角.仿例1:如图,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.解:作法:(1)作射线AF;(2)在射线AF上顺次截取AB=BC=a,CD=b;(3)在线段AD上截取DE=c.所以线段AE即为所求.说明:对于比较复杂的尺规作图,可先画出草图,找到正确作图方法.知识链接:仿例3在直线AB上找一点C,要注意点C在AB之间或AB延长线上两种情况.行为提示:教会学生怎么交流.先对学,再群学.充分在小组内展示自己,分析答案,提出疑惑,共同解决(可按结对子学——帮扶学——组内群学来开展).在群学后期教师可有意安排每组展示问题,并给学生板书题目和组内演练的时间.仿例2:已知:如图,锐角∠AOB,求作:∠β,使得∠β=180°-2∠AOB.解:作法:(1)作∠A′O′B′=∠AOB;(2)以O′B′为始边作∠B′O′C′=∠AOB;(3)反向延长射线O′A′到D′,∠β为图中所示的∠C′O′D′.仿例3:如图,在直线AB上找出一点C,使AC=2CB,则C点应在( D)A.点A、B之间B.点A的左边C.点B的右边D.点A、B之间或点B的右边仿例4:已知线段a,b(a>b),画一条线段,使它等于2a-b.画法:(1)画射线AE;(2)在射线AE上顺次截取AB=BD=a;(3)在线段AD上截取CD=b,线段AC即为所求作的线段.交流展示生成新知1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.知识模块尺规作图课后反思查漏补缺1.收获:________________________________________________________________________2.困惑:________________________________________________________________________。
七年级数学上册 第4章 直线与角 4.6 用尺规作线段与角学案(新版)沪科版

4.6 用尺规作线段和角学习目标:1. 会利用尺规作一个角等于已知角,并能了解尺规作图中的简单应用。
2.能利用尺规作角的和、差、倍数。
学习重点:能按作图语言来完成作图动作,能用尺规作一个角等于已知角。
学习难点:能按作图语言来完成作图动作,能用尺规作一个角等于已知角。
一、探索发现活动1:如图,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB 。
(1) 请过C 点画出与AB 平行的另一边。
(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?思路:要在长方形木板上截一个平行四边形,按上图的方式(平行四边形的一组对边在长方形木板的边缘上),只要保证过点C 作出与AB 平行的另一条线段即可。
而要过点C 作AB 的平行线,可以通过作一个角等于∠BAC 得到。
二 、用尺规作一个角等于已知角1. 已知: ∠AOB求作: ∠A ’O ’B ’ 使∠A ’O ’B ’=∠AOB 。
作法与示范: 作法 示范BO A请用测量工具或者比较等方式验证新作的角是否等于已知角? _________2. 请用没有刻度的直尺和圆规,在活动1 中, 过点C 作AB 的平行线.三 、拓展延伸-角的和1.用尺规作一个角等于已知两角的和例题:如图,已知∠1,∠2,求作一个角,使它等于∠1+∠2作法:(1) 作射线O ’E (2) 以O 为圆心,以任意长为半径分别在∠1,∠2,上画弧,交∠1于A 、B ,交∠2于C 、D 。
(3) 以O ’为圆心,以OA 的长为半径画弧交O ’E 于A ’(4) 以A ’为圆心AB 的长为半径画弧交于B ’,连接O ’、B ’,得到∠A ’O ’B ’=∠1 (1)作射线O ’A ’(2)以点O 为圆心,以任意长为半径画弧,交OA 于点C ,交OB于点D ;D B A C O(3)以点O ’为圆心,以OC 长为半径画弧,交O ’A ’于点C ’;D B A C O A'C'O'(4)以点C ’为圆心,以 CD 长为半径画弧,交前面的弧于点D ’;(5)过点D ’作射线O'B ’。
2022秋七年级数学上册第4章直线与角4.6用尺规作线段与角习题课件新版沪科版20221019239

第4章 直线与角
4.6 用尺规作线段与角
核心必知 1 直尺;圆规 2 (2)已知线段
提示:点击 进入习题
1B 2 见习题 3D 4B 5 见习题
答案显示
6 见习题
1.几何中,通常用没有刻度的___直__尺___和___圆__规___来画 图,这种画图的方法叫做尺规作图.
2.用尺规作一条线段等于已知线段的方法:(1)作一条直 线;(2)在直线上任取一点,并以这一点为圆心,以 __已__知__线__段____的长度为半径画弧,交直线于另一点, 则以这两点为端点的线段即为所求作的线段.
∠AOC=∠α(要求:用直尺和圆规作图,不写作法, 保留作图痕迹).
解:如图所示,∠AOC就是所求作的角.
(2)已知∠AOB=65°,作∠EDF=∠AOB,过点D引射 线DM,使∠EDM=30°,求∠FDM的度数.
解:作图略.分两种情况讨论: ①当DM在∠EDF内部时,∠FDM=65°-30°=35°; ②当DM在∠EDF外部时,∠FDM=65°+30°=95°.
解:如图.
3.如图,点C在∠AOB 的边OB上,用尺规作 出了∠BCN=∠AOC, 作图痕迹中,弧FG是( ) D
A.以点C为圆心,OD长为半径的弧长为半径的弧 D.以点E为圆心,DM长为半径的弧
4.[2021·合肥蜀山区期末]已知:线段a,b,求作:线段AB, 使得AB=2a+b,小明给出了四个步骤(如图):①作一 条射线AE;②则线段AB=2a+b;③在射线AE上作线 段AC=a,再在射线CE上作线段CD=a;④在射线DE 上作线段DB=b.你认为顺序正确的是( B ) A.②①③④ B.①③④② C.①④③② D.④①③②
5.作图题: 已知:线段a,c和∠β(如图),利用直尺和圆规作三角形
七年级数学上册 4.6 用尺规作线段与角同步练习 (新版)沪科版

4.6 用尺规作线段与角知识点 1 尺规作图1.尺规作图是指( )A.用直尺规范作图B.用刻度尺和圆规作图C.用没有刻度的直尺和圆规作图D.直尺和圆规是作图工具知识点 2 作一条线段等于已知线段2.下列画图语言表述正确的是( )A.延长线段AB至点C,使AB=ACB.以点O为圆心作弧C.以点O为圆心,以AC长为半径画弧D.在射线OA上截取OB=a,BC=b,则有OC=a+b3.如图4-6-1,已知线段a,b,c,用直尺和圆规画图(保留画图痕迹,并用字母表示出所画的线段).(1)画一条线段,使它等于a+b;(2)画一条线段,使它等于a-c.图4-6-1知识点 3 作一个角等于已知角4.如图4-6-2,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( )图4-6-2A.以点C为圆心,OD长为半径画的弧B.以点C为圆心,DM长为半径画的弧C.以点E为圆心,OD长为半径画的弧D.以点E为圆心,DM长为半径画的弧5.已知∠1和∠2,如图4-6-3所示,作∠AOB,使∠AOB=∠1+∠2,用尺规作图,保留作图痕迹.图4-6-36.已知:如图4-6-4,有线段m,n,画一条线段AB,使它等于2m+n.图4-6-47.如图4-6-5,已知∠1,∠2,用圆规和直尺画∠3,使∠3=2∠1-∠2(不写作法,保留作图痕迹).图4-6-58.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图4-6-6所示,在打台球时,用白球沿着直线方向击黑球,已知反射角的余角等于入射角的余角(反射角的余角和入射角的余角均指黑球前进方向与台边所夹的锐角).请问黑球经过一次撞击反弹后能否进入F洞?请用尺规作图来判断.(保留作图痕迹,不写作法)图4-6-64.6 用尺规作线段与角1.C2.C .3.解:(1)先画一条直线l,在l上找一点A,以点A为圆心,线段a的长为半径画弧交直线l于点B,再以点B为圆心,以线段b的长为半径画弧,交直线l于点C(点C在线段AB的延长线上),则线段AC即为所求,如图所示.(2)先画一条直线l,在l上找一点A,以点A为圆心,线段a的长为半径画弧交直线l 于点B,再以点B为圆心,以线段c的长为半径画弧,交直线l于点C(点C在线段AB上),则线段AC即为所求,如图所示.4.D5.解:(1)作射线OA;(2)以O为顶点作∠AOC=∠1;(3)以点O为顶点,OC为一边在OC的另一侧作∠COB=∠2,则∠AOB为所求作的角.6.解:画射线AM,并在射线AM上顺次截取AC=CD=m,DB=n.则线段AB就是所求作的线段.如图.7.略8.解:利用尺规作图作出∠2=∠1,即可判断出黑球能进入F洞.如图所示.。
沪科版七年级上册数学4.6用尺规作线段与角同步练习含答案解析
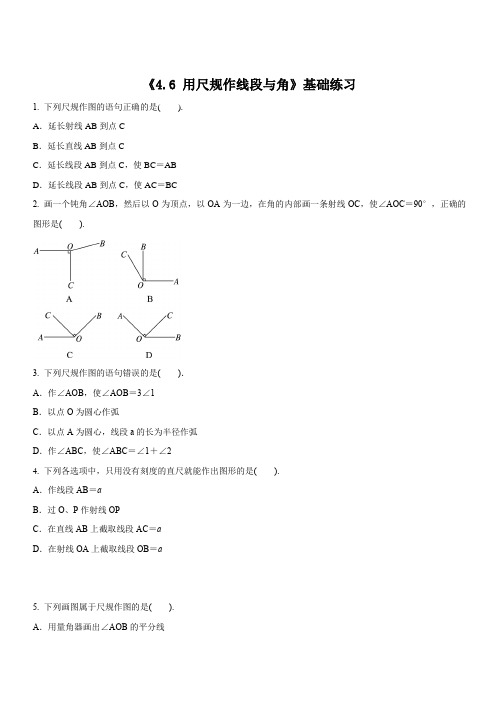
《4.6 用尺规作线段与角》基础练习1. 下列尺规作图的语句正确的是().A.延长射线AB到点CB.延长直线AB到点CC.延长线段AB到点C,使BC=ABD.延长线段AB到点C,使AC=BC2. 画一个钝角∠AOB,然后以O为顶点,以OA为一边,在角的内部画一条射线OC,使∠AOC=90°,正确的图形是().3. 下列尺规作图的语句错误的是().A.作∠AOB,使∠AOB=3∠1B.以点O为圆心作弧C.以点A为圆心,线段a的长为半径作弧D.作∠ABC,使∠ABC=∠1+∠24. 下列各选项中,只用没有刻度的直尺就能作出图形的是().A.作线段AB=aB.过O、P作射线OPC.在直线AB上截取线段AC=aD.在射线OA上截取线段OB=a5. 下列画图属于尺规作图的是().A.用量角器画出∠AOB的平分线B.不用量角器,作∠AOB,使∠AOB=3∠1C.用三角板画∠AOB=90°D.画线段AB=3 cm6. 下列说法正确的有().①利用尺规能作一个角等于已知角;②利用尺规能作一个角等于已知两个角的和;③利用尺规能作一个角等于已知两个角的差;④利用尺规不能作一个角等于已知角的2倍.A.1个B.2个C.3个D.4个7.如图①,已知线段a和线段b,则AE表示的是().图①A.3(a-b) B.3a-b C.2a D.2a+b8.尺规作图是指().A.用直尺规范作图B.用刻度尺和圆规作图C.用没有刻度的直尺和圆规作图D.直尺和圆规是作图工具9. 下列各选项中,只用圆规就能作出图形的是().A.过点O、A作直线OAB.作一个角等于已知角C.在射线OA上截取线段OB=aD.作一条线段等于已知线段10. 如图②,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是().图②A.以点C为圆心,OD长为半径所画的弧B.以点C为圆心,DM长为半径所画的弧C.以点E为圆心,OD长为半径所画的弧D.以点E为圆心,DM长为半径所画的弧11. 如图③,尺规作图:已知线段AB,延长线段AB到C,使BC=2AB.图③12. 如图④,已知线段a和两条互相垂直的直线AB,CD. 求作正方形A′B′C′D′,使其对角线长等于2a.图④13. 如图⑤,已知∠α,∠AOB=90°,求作∠AOC,使其等于∠α的余角.图⑤14. 已知,如图⑥,三条线段a,b,c.请画线段AB,使AB=a+b+c.图⑥15. 已知线段a,如图:.求作:线段AB,使AB=3a.答案和解析【答案】1. C2. D3. B4. B5. B6. C7. B8. C9. C 10. D11. 见答案. 12. 见答案. 13. 见答案.14.见答案. 15. 见答案.【解析】1. 解:射线一旁是无限延伸的,只能反向延长,A错误;直线是无限延伸的,不用延长,B错误;延长线段AB到点C,不可能使得AC=BC,D错误,故选C.解题的关键在于对相关概念的理解.2. 解:由于∠AOC=90°,则B、C错误;因为射线OC在∠AOB的内部,则A错误,D正确,故选D.解题的关键在于对角的相关概念的理解.3. 解:在描述作弧时,要给出圆心和半径,故B错误,故选B.解题的关键在于对尺规作图的相关语句的理解.4. 解:没有刻度的直尺不能作出与已知线段长度相等的线段,故A、C、D错误,但可作出射线,D正确.故选B.只用没有刻度的直尺不能作出与已知线段长度相等的线段,但可直接作出直线或射线.5. 解:A中借助于量角器,C中借助于三角板,D中借助于刻度尺,B不用量角器,用没有刻度的直尺和圆规完成即可,故选B.通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.6. 解:可以用尺规作图的有:①作一个角等于已知角;②作一个角等于已知两个角的和;③作一个角等于已知两个角的差;④作一个角等于已知角的2倍,故正确的有①②③,共3个,故选C.通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.可以用尺规作出已知角的和、差、倍数. 7. 解:已知线段a和线段b,则AE表示的是3a-b.故选B.此题考查的是对尺规作图的认识,解答此题的关键是能灵活运用线段的和、差转化线段之间的数量关系.8. 解:尺规作图是指用没有刻度的直尺和圆规作图,故选C.此题考查的是尺规作图的定义,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.9. 解:只用圆规就能作出图形的是在射线OA上截取线段OB=a,而A、B、D都需要用尺规进行作图,故选C.通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.解题关键是理解只用圆规就能在射线上截取线段.10. 解:由图可知,弧FG是以点E为圆心,DM长为半径所画的弧,故选D.本题主要考查了基本作图,解题关键是理解作图的每一步所代表的意义.11. 解:如图⑦所示,AC即为所求.图⑦利用作线段的方法求解即可.本题主要考查了基本作图,解题的关键是正确使用尺规完成作图.12. 解:作法:(1)利用圆规,在射线OA,OB,OC,OD上作线段OA′,OB′,OC′,OD′,使它们分别与线段a相等.(2)依次连接A′,C′,B′,D′,A′.此题主要考查了基本作图,掌握正方形的性质是解题的关键.13. 解:如图⑧所示,∠AOC就是所求的角.图⑧以OB为一边作∠BOC=∠α,则∠AOC就是所求.本题考查了基本作图,作一个角等于已知角,以及余角的定义,解题时要灵活运用.14. 解:如图⑨所示,AB即为所求.图⑨根据三条线a,b,c,分别在射线上截取,得出AB即可.此题主要考查了基本作图,在解答此类问题时一定要注意各点之间的关系.15. 解:作法:(1)作射线AE;(2)在射线AE上顺次截取AC=CD=DB=a,则线段AB即为所求作的线段.利用作线段的方法求解即可.本题主要考查了基本作图,解题的关键是正确使用尺规完成作图.《4.6 用尺规作线段与角》提高练习1. 如图①,在直线AB上找出一点C,使AC=2CB,则C点应在().图①A. 点A、B之间B.点A的左边C.点B的右边D.点A、B之间或点B的右边2. 如图②,画线段AB;延长线段AB到点C,使BC=2AB;反向延长AB到点D,使AD=AC,则线段CD=()AB.(填CD是AB的倍数)图②A.6B.4C.5D.73. 下列属于尺规作图的是( ).A.用量角器画∠AOB的平分线OPB.利用两块三角板画15°的角C.用刻度尺测量后画线段AB=10 cmD.在射线OP上截取OA=AB=BC=a4.下列关于作图的语句正确的是( ).A.作∠AOB的平分线OE=3 cmB.画直线AB=线段CDC.用直尺作三角形的高是尺规作图D.已知A、B、C三点,过这三点不一定能画出一条直线5. 如图③,已知线段a,b,c(a>b),求作线段AB,使AB=a+c-b.图③6. 已知:如图④,有线段m,n,画一条线段AB,使它等于2m+n.图④7.如图⑤,已知∠1,∠2,且∠1>∠2,用尺规作∠AOB,使得:(1)∠AOB=∠1+∠2;(2)∠AOB=2∠1-∠2.(用圆规、直尺作图,不写作法,但要保留作图痕迹)图⑤8. 已知:如图⑥,锐角∠AOB,求作:∠β,使得∠β=180°-2∠AOB.图⑥9. 如图⑦,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.图⑦10. 如图⑧,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.图⑧答案和解析【答案】1. D2. A3. D4. D5. 见答案.6. 见答案.7. 见答案.8. 见答案.9.见答案. 10. 见答案.【解析】1. 解:在直线AB上找出一点C,使AC=2CB,则C点应在点A、B之间或点B的右边,故选D.点C的存在有两种情况:(1) C点在点A、B之间;(2) C点在点B的右边.2. 解:由图可知,BC=2AB,则AC=AB+BC=AB+2AB=3AB,因为AD=AC,所以CD=AD+AC=2AC=6AB,故选A.此题考查的是对尺规作图的认识,解答此题的关键是能灵活运用线段的和、差转化线段之间的数量关系.3. 解:A中借助于量角器,B中借助于三角板,C中借助于刻度尺,D中用没有刻度的直尺和圆规完成即可,故选D.此题考查的是尺规作图的定义,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.4. 解:射线、直线具有延伸性,不能画出其长度,故A、B错误;尺规作图需用圆规和无刻度的直尺,故C错误;若A、B、C三点不共线,则无法过这三点画出一条直线,故D正确.故选D.解题的关键是掌握尺规作图的定义和射线、直线的相关知识.5. 解:作法:(1)作射线AC;(2)在射线AC上依次截取AD=a,DE=c,得线段AE;(3)在线段AE上,以E为端点,截取EB=b,则线段AB即为所求作的图形.此题主要考查了基本作图,在解答此类问题时一定要注意线段之间的和差关系.6. 解:画射线AM,并在射线AM上顺次截取AC=CD=m,DB=n.则线段AB就是所求作的线段.本题考查了基本作图,掌握作一条线段等于已知线段,以及线段的和、差、倍的意义是解题关键.7. 解:(1)如图①所示,∠AOB即为所求;(2)如图②所示,∠AOB即为所求.本题考查了基本作图,掌握作一个角等于已知角,以及角的和、差、倍的意义是解题关键.8.解:作法:(1)作∠A′O′B′=∠AOB;(2)以O′B′为始边作∠B′O′C′=∠AOB;(3)反向延长射线O′A′到D′,∠β为图中所示的∠C′O′D′.本题考查了基本作图,作一个角等于已知角,以及平角的定义,解题时要灵活运用.9. 解:作法:(1)作射线AF;(2)在射线AF上顺次截取AB=BC=a,CD=b;(3)在线段AD上截取DE=c.所以线段AE即为所求.对于比较复杂的尺规作图,可先画出草图,找到正确作图方法.10. 解:作法:(1)作射线OA;(2)以射线OA为一边作∠AOC=∠α;(3)以O为顶点,以射线OC为一边,在∠AOC的内部作∠BOC=∠β,则∠AOB就是所求作的角.本题考查了基本作图,掌握作一个角等于已知角,以及角的和差的意义是解题关键.《4.6 用尺规作线段与角》培优练习1. 下列画图语言表述正确的是().A.延长线段AB至点C,使AB=ACB.以点O为圆心作弧C.以点O为圆心,以AC长为半径画弧D.在射线OA上截取OB=a,BC=b,则有OC=a+b2. 如图所示,已知线段a,b,c(a>b+c),求作线段AB,使AB=a-b-c.下面利用尺规作图正确的是().3. 如图①,用a,b,c表示线段AF的长应为().图①A. 2a-2b-cB. 2a-b-cC. 2a-b-cD. 2a-2b+c4. 如图②,已知线段a,b(a>b),画一条线段,使它等于2a-b.图②5. 如图③,已知:∠1,∠2,求作:(1)∠3,使得∠3=∠2-∠1;(2)∠4,使得∠4=∠1+5∠2.图③答案和解析【答案】1. C2. D3. A4. 见答案.5. 见答案.【解析】1. 解:延长线段AB至点C,则AC>AB,故A错误;作弧要给出圆心和半径,故B错误,C正确;在射线OA上截取OB=a,BC=b,当点C在点B的右侧时,有OC=a+b,当点C在点B的左侧时,OC≠a+b,故D错误,故选C.此题考查的是尺规作图的相关知识,解题的关键在于对尺规作图的相关语句的理解.2. 解:用尺规先作线段AC=a,再从内部顺次截取CD=b,DB=c,则AB=a-b-c.故选D.此题主要考查了基本作图,在解答此类问题时一定要注意线段之间的和差关系.3. 解:由图可知AF=AB+BC-CD-DE-EF=a+a-b-b-c=2a-2b-c.故选A.此题主要考查了基本作图,在解答此类问题时一定要注意线段之间的和差关系.4. 解:作法:(1)画射线AE;(2)在射线AE上顺次截取AB=BD=a;(3)在线段AD上截取CD=b,线段AC即为所求作的线段.对于比较复杂的尺规作图,可先画出草图,找到正确作图方法.5. 解:(1)作法:①作射线OA;②以OA为边做∠AOB=∠1;③以O为顶点,以射线OA为边,在∠AOB内部作∠AOD=∠2.则∠BOD即为所求的∠3.(2)作法:①作射线OA;②以OA为边做∠AOB=∠1;③以O为顶点,以射线OB为边,在∠AOB外部作∠BOD=∠2.则∠AOD即为所求的∠3.对于比较复杂的尺规作图,可先画出草图,找到正确作图方法.。
数学沪科版七年级(上册)4.6用尺规作线段与角

B1
O
A
O1
A1
量已知角
画射线
描点
对心,对线,读数
对心,对线
所以∠A 1O1 B1 就是我们所要作的角.
如果没有三角尺和量角器,只用尺规作图能画出 一个角等于已知角吗?
例2 作一个角等于已知角 已知: ∠AOB. 求作: ∠A'O'B' 使∠A'O'B' =∠AOB。
作法
(1)作射线O'A';
画一个角等于已知角,可以先用量角器量出已知角的度 数,再画出等于这个度数的角.
几何中,通常用没有刻度的直尺和圆规来画图,这种画 图的方法叫做尺规作图.
例1 作一条线段等于已知线段
已知:线段AB. 求作:线段A'B',使A'B'=AB.
作法与示范:
作
法
(1) 作射线A'C';
(2) 以点A’为圆心, 以AB的长为半径 画弧, 交射线A'C'于点B', A'B'就是所求作的线段。
二 作一条角等于已知角
O 入反 B 射射 角角
A
●红球能被击入右下角的袋中吗? ●你能画出红球在第一次反弹后的运动路线吗?
打台球时,球的反射角总是等于入射角.
用三角板画角
O
30°
A
B
如果入射角是30,你准备怎样画反射角呢? 所以∠AOB就是我们所要画的角. 如果入射角不是一个特殊角呢?
用量角器画角 ●你会利用量角器画一个角等于∠AOB吗?
第4章 直线与角
4.6 用尺规作线段与角
导入新课
讲授新课
当堂练习
课堂小结
2022七年级数学上册 第4章 直线与角4.6用尺规作线段与角习题课件(新版)沪科版
11、人总是珍惜为得到。22.5.816:39:5916:39May-228-May-22 12、人乱于心,不宽余请。16:39:5916:39:5916:39Sunday, May 08, 2022 13、生气是拿别人做错的事来惩罚自 己。22.5.822.5.816:39:5916:39:59May 8, 2022 14、抱最大的希望,作最大的努力。2022年5月8日 星期日 下午4时 39分59秒16:39:5922.5.8 15、一个人炫耀什么,说明他内心缺 少什么 。。2022年5月 下午4时39分22.5.816:39May 8, 2022 16、业余生活要有意义,不要越轨。2022年5月8日 星期日4时39分 59秒16:39:598 May 2022 17、一个人即使已登上顶峰,也仍要 自强不 息。下 午4时39分59秒 下午4时39分16:39:5922.5.8
谢谢பைடு நூலகம்看
9、 人的价值,在招收诱惑的一瞬间被决定 。22.5.822.5.8Sunday, May 08, 2022 10、低头要有勇气,抬头要有低气。16:39:5916:39:5916:395/8/2022 4:39:59 PM
11、人总是珍惜为得到。22.5.816:39:5916:39May-228-May-22 12、人乱于心,不宽余请。16:39:5916:39:5916:39Sunday, May 08, 2022 13、生气是拿别人做错的事来惩罚自 己。22.5.822.5.816:39:5916:39:59May 8, 2022 14、抱最大的希望,作最大的努力。2022年5月8日 星期日 下午4时 39分59秒16:39:5922.5.8 15、一个人炫耀什么,说明他内心缺 少什么 。。2022年5月 下午4时39分22.5.816:39May 8, 2022 16、业余生活要有意义,不要越轨。2022年5月8日 星期日4时39分 59秒16:39:598 May 2022 17、一个人即使已登上顶峰,也仍要 自强不 息。下 午4时39分59秒 下午4时39分16:39:5922.5.8
沪科版七年级数学上册同步练习题-用尺规作线段与角
4.6 用尺规作线段和角一、判断题1.尺规作图是指用刻度尺和圆规作图.( )2.尺规中的尺是指没有刻度的直尺.( )3.用直尺和三角板过直线外一点作已知直线的平行线是尺规作图.( )4.最基本的尺规作图是作线段和角.( ) 二、选择题:1画一个钝角∠AOB ,然后以O 为顶点,以OA 为一边, 在角的内部画一条射线OC , 使∠AOC =90°,正确的图形是( )BCDAO BCAOBC AO BC ACBAO三、填空题1.已知线段AB ,求作:线段A ′B ′,使A ′B ′= A B .作法:(1)作 A ′C ′.(2)以点A ′为圆心,以________ ____交A ′C ′于点B ′, (3)_________就是所作的线段.2.已知:∠A O B .求作:∠A′O′B′,使∠A′O′B′=∠A O B.作法:(1)作O′A′(2)以点O为圆心,以_________长为半径画弧交OA于点C,交OB于点D.(3)以点O′为圆心,以_________长为半径画弧,交O′A′于点C′.(4)以点C′为圆心,以_________长为半径画弧,交前面的弧于点D′.(5)过点D′作射线O′B′,∠A′O′B′就是所求作的角.三、作图用尺规完成下列作图.1.已知线段a ,b (a >b ),利用尺规作线段c ,使c =2a -b . ab2.已知∠α、∠β(∠α>∠β),求作一个角,使它等于2∠α-∠β.3.已知,直线AB 和AB 外一点P ,作一条经过点P 的直线CD ,使C D ∥A B 。
PBA6.已知,如图,∠AOB 及其两边上的点C 、D ,过点C 作CE ∥OB ,过点D 作DF ∥OA ,CE 、DF 交于点P 。
D ABCO。
2022七年级数学上册 第4章 直线与角4.6用尺规作线段与角习题课件(新版)沪科版
谢谢收看
谢谢收看
9、 人的价值,在招收诱惑的一瞬间被决定 。22.2.2822.2.28Monday, February 28, 2022 10、低头要有勇气,抬头要有低气。09:11:3909:11:3909:112/28/2022 9:11:39 AM 11、人总是珍惜为得到。22.2.2809:11: 3909:1 1Feb-2 228-Fe b-22 12、人乱于心,不宽余请。09:11:3909:11:3909:11M onday, February 28, 2022
谢谢收看
9、 人的价值,在招收诱惑的一瞬间被决定 。22.2.2822.2.28Monday, February 28, 2022 10、低头要有勇气,抬头要有低气。09:11:3909:11:3909:112/28/2022 9:11:39 AM 11、人总是珍惜为得到。22.2.2809:11: 3909:1 1Feb-2 228-Fe b-22 12、人乱于心,不宽余请。28, 2022
9、 人的价值,在招收诱惑的一瞬间被决定 。22.2.2822.2.28Monday, February 28, 2022 10、低头要有勇气,抬头要有低气。09:11:3909:11:3909:112/28/2022 9:11:39 AM 11、人总是珍惜为得到。22.2.2809:11: 3909:1 1Feb-2 228-Fe b-22 12、人乱于心,不宽余请。09:11:3909:11:3909:11M onday, February 28, 2022
2021学年七年级数学上册同步备课系列(沪科版)4-6 用尺规作线段与角(作业)
4.6 用尺规作线段与角一、选择题1.下列说法中,正确的有( ) (1)尺规作图就是用刻度尺和圆规作图;(2)用直尺和三角尺作一条线段等于另一条线段是尺规作图;( 3)尺规作图中的直尺是指没有刻度的直尺. A .0个 B .1个 C .2个 D .3个 2.下列画图语言表述正确的是( )A .延长线段AB 至点C ,使AB =AC B .以点O 为圆心作弧 C .以点O 为圆心,AC 长为半径画弧D .在射线OA 上截取OB =a ,BC =b ,则有OC =a +b 3.在直线l 上截取AC =a ,BC =b ,若AB =a +b ,则( ) A .点C 在线段AB 上 B .点C 在线段AB 的延长线上C .点C 在直线AB 外D .点C 可能在直线AB 上,也可能在直线AB 外 4.如图1,用尺规作出∠OBF =∠AOB ,作图痕迹MN ︵是( )图1A .以点B 为圆心,OD 长为半径的弧B.以点B为圆心,DC长为半径的弧C.以点E为圆心,OD长为半径的弧D.以点E为圆心,DC长为半径的弧5.用直尺和圆规作一个角等于已知角,如图2,下列叙述正确的个数为()图2①OA=O′A′;②OB=O′B′;③CD=C′D′;④∠AOB=∠A′O′B′.A.1 B.2 C.3 D.46.如图3所示,已知线段a,b,c(a>b+c),求作线段AB,使AB=a-b-c.下面利用尺规作图正确的是()图3 图47.下列作图属于尺规作图的是(A.画线段MN=3 cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线l的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α二、填空题8.如图5所示,有一个简便的方法能很快作出∠AOB的补角,你的方法是________________________________________________________________________.图5三、解答题9.如图6,已知线段a,b,c(a>b),求作线段AB,使AB=a+c-b.链接听课例1归纳总结图6 10.如图7,已知∠α,∠β,求作:∠AOB,使∠AOB=∠α+∠β.(保留作图痕迹)图711.已知∠α,线段a,b.请按下列步骤完成作图.(不需要写作法,保留作图痕迹)(1)作∠PAQ=∠α;(2)在边AP上截取AB=a,在边AQ上截取AC=b;(3)连接BC.答案解析1.[答案] B2.[答案] C3.[解析] A可以画出草图比较.4.[解析] D根据作一个角等于已知角的方法可得.5.[解析] B由尺规作图知③CD=C′D′正确,④∠AOB=∠A′O′B′正确.故选B.6.[解析] D对比线段的长度会发现,选项A表示a+b+c,错误.选项B表示a+b-c,错误.选项C表示a+c-b,错误.选项D表示a-b-c.故选D.7.[答案] D8.[答案] 反向延长射线OB或反向延长射线OA[解析] 作出的角与∠AOB的和应是180度,因此可以反向延长射线OA或OB.9.解:如图所示.作法:(1)作射线AC;(2)在射线AC上依次截取AD=a,DE=c,得线段AE;(3)在线段AE上,以E为端点,截取EB=b,则线段AB即为所求作的图形.10.解:如图所示:11.解:如图,△ABC即为所求.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用尺规作线段与角
基础导练
1.下列语句错误的是( ).
A.延长线段AB
B.延长射线AB
C.直线m和直线n相交于P点
D.直线AB向两方无限延伸,所以不能延长直线AB
2.平面上有三点A,B,C,如果AB=8,AC=5,BC=3,那么( ).
A.点C在线段AB上
B.点B在直线AC的延长线上
C.点C在直线AB外
D.点C可能在直线AB上,也可能在直线AB外
3. 已知:线段a,b(如图).
求作:线段AB,使AB=3(a-b).
分析:根据题目条件可知,要作线段AB,可以先作出a-b,然后顺次截取3次a-b,就是线段AB;也可以作出3a-3b,这样同样可以得到线段AB.
(1)
能力提升
4.如图,已知∠α,∠β(∠β>∠α).
求作:∠AOB,使得∠AOB=2∠β-∠α.
5.利用一副三角板上的角,能画出多少个小于180°的角,试一一画出来.
6.某班社会实践调查小分队进行社会调查,从学校(A地)出发,沿北偏东60°的方向前进5 km到达B地农村,调查后,再沿东南方向前进到达C地的工厂,而该工厂正好位于学校的正东方向.
(1)按1∶200 000的比例尺画出小分队的路线图;
(2)量得∠ABC,∠BCA各为多少度(精确到1°);
(3)算出A地到C地的实际距离.
7.在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E的距离.
参考答案
基础导练
1.解析:可延长的只有线段和射线,且射线只能反向延长,故延长射线AB为错,故选B. 答案:B
2.解析:因为AC+BC=8,AB=8,所以点C在线段AB上.
答案:A
3.作法:方法一:如图(1).
(1)画射线EF,在EF上截取线段EC=a,EA=b;
(2)在射线EF上顺次截取CD=DB=AC.
线段AB即为所求作的线段.
方法二:如图(2).
(1)画射线AD;
(2)在射线AD上截取AC=3a;
(3)在线段AC上截取CB=3b;
线段AB就是所求作的线段.
(2)
能力提升
4. 作法:如下图.(1)画∠AOC=2∠β;
(2)在∠AOC的内部画∠BOC=∠α.
∠AOB就是所求作的角.
5.解:除了三角板上有现成的角30°,45°,60°,90°外,还可画15°,75°,105°,120°,135°,150°,165°七种度数的角,画法如图所示.
6.分析:本题首先要了解方位角的定义,然后根据题中条件画出相应的图形,进而用相关知识求解.
解:(1)AB=500 000 cm×
1
200000
=2.5 cm,
依题意,小分队行进路线如图所示.
(2)用量角器量得∠ABC=105°,∠BCA=45°.
(3)量出AC=3.4 cm,所以AC的实际距离为3.4×200 000=680 000 cm=6.8 km.
7. 分析:要分情况讨论,因为先截取AB后、再截取AC,没有指明是在AB的延长线上、还是在AB的反向延长线上.
解:(1)若C在线段AB的延长线上,如图①.
因为D是AB的中点,E是AC的中点,
所以AD=11
16
22
AB=⨯=8(cm),
AE=11
40
22
AC=⨯=20(cm).
所以DE=AE-AD=20-8=12(cm).
(2)若C在线段BA的延长线上,如图②.
由题意,得AD=11
16
22
AB=⨯=8(cm),
AE=11
40
22
AC=⨯=20(cm),
所以DE=AE+AD=20+8=28(cm).
所以AB的中点D与AC中点E的距离为12 cm或28 cm.。
