测力轮对状态估计计算方法研究
力量估计实验报告

力量估计实验报告实验目的:估计力量的大小及方向对物体运动的影响。
实验装置:平滑水平面、轮子、细绳、物体(如实验小车)实验步骤:1. 将水平面放在平滑的桌面上,并确保水平面水平。
2. 在物体上固定轮子,使其能够在水平面上滚动。
3. 在物体的一端固定细绳,确保细绳朝向水平面的上方垂直下拉。
4. 将另一端的细绳绕在测力计上,并固定住。
5. 缓慢用手将物体推动,观察并记录物体的运动情况及测力计示数。
6. 重复实验3-5,改变施加力量的大小和方向,并记录相应数据。
实验数据及结果:施加的力大小(N) 施加力的方向物体运动情况测力计示数(N)5 水平向右施加力物体向右匀速运动55 水平向左施加力物体向左匀速运动-510 水平向右施加力物体向右加速运动1010 水平向左施加力物体向左加速运动-105 斜向上向右施加力物体向右上方倾斜一定角度后静止 55 斜向上向左施加力物体向左上方倾斜一定角度后静止-55 斜向下向右施加力物体向右下方倾斜一定角度后静止 55 斜向下向左施加力物体向左下方倾斜一定角度后静止-5实验讨论及分析:从实验结果中可以看出,施加的力量大小和方向对物体运动有着明显的影响。
当水平向右施加5N的力量时,物体向右匀速运动,而当施加同样大小的力量但方向改为水平向左时,物体则向左匀速运动。
这表明物体的运动方向与力量的方向相同。
当施加更大的力量时,物体的运动加速度也增加。
例如,当施加10N的力量时,物体的加速度明显增加。
从测力计示数可以看出,施加力量越大,测力计示数也越大,说明测力计实际上测出的是物体所受力的大小。
除了水平方向外,改变力量的施加方向也会对物体的运动产生影响。
例如,施加斜向上向右的力量时,物体会倾斜一定角度后静止。
这表明斜方向上的力量会使物体产生倾斜而不是直线运动。
施加斜向下的力量时,物体也会倾斜一定角度后静止。
然而,当方向改变为向左时,物体的倾斜方向也随之改变。
这说明力量的方向不仅会影响物体的倾斜程度,还会使物体倾斜的方向相应改变。
地铁车辆连续测力轮对仿真与试验研究

地铁车辆连续测力轮对仿真与试验研究钟旭婕,寇杰,张济民,王承萍(同济大学铁道与城市轨道交通研究院,上海201804)来稿日期:2020-01-21基金项目:国家自然科学基金(51805374)作者简介:钟旭婕,(1996-),女,江西人,硕士研究生,主要研究方向:轨道车辆动力学及噪声;张济民,(1969-),男,四川人,博士研究生,教授,主要研究方向:轨道车辆动力学、噪声及控制1引言轮轨作用力作为轨道车辆运行安全性的重要评价指标一直作为车辆线路安全性测试的重要选项,现有轨道车辆线路测试中有多种轮轨力测量方法。
TB/T 2360-93中列出了辐条式测力轮对、辐板开孔式测力轮对的间断测力轮对原理,辐条式测力轮对、辐板测力轮对的连续测力轮对原理[1]。
通过在车轮几个半径上的合理组桥来尽量消除车轮转动的影响,然后求解多个非线性方程组而得到横向力、垂向力以及轮轨作用点位置[2-5]。
文献[6]研究了根据车轮横向变形测量轮轨横向力的方法。
文献[7]对比分析了1:5车轮上分别采用简易余弦桥和直流桥法的测试精度,分析结果表明简易余璇桥有更高的测试精度,测量结果更接近实际轮轨作用摘要:连续测力轮对作为轨道车辆线路测试中有效的轮轨力测量方法一直是国内外轨道车辆动力学研究的热点。
利用某地铁车辆测力轮对,在有限元仿真和数字分析的基础上,进行了连续测力轮对的贴片、组桥和标定工作,得出以下结论:通过相同半径径向布置的四片应变片组成的全桥,从而消除应变随角度变化函数的偶次及三次谐波值,实现近似余弦变化特性,形成余弦桥。
在标定试验中采用模拟钢轨与三向测力传感器相结合,作为车轮的支撑装置,可以更加真实准确地模拟实际轮轨接触作用力,提高标定测试精度。
全桥输出电压随载荷变化系数均呈余弦特性,且90°布置的两个全桥间的应变系数余弦曲线相位相差90°。
只需要测试出四个全桥的输出电压即可计算出轮轨接触垂向力和横向力,实现连续轮轨力测试。
轮对疲劳寿命预测理论与方法研究

轮对疲劳寿命预测理论与方法研究第一章绪论近年来,随着铁路运输行业的发展,轮对的疲劳寿命成为了人们关注的焦点。
因为轮对的故障不仅对运输效率造成影响,还可能引起严重的事故。
因此,轮对的疲劳寿命预测理论与方法的研究具有重要的实际意义。
第二章轮对疲劳寿命预测理论轮对的疲劳寿命与其寿命分布规律有着密切的关系。
日常使用中,轮对受到的载荷往往是不均匀的,从而导致局部区域的疲劳损伤累积,最终导致整个轮对的损坏。
因此,对轮对的疲劳寿命进行预测需要研究其寿命分布规律。
目前,轮对的疲劳寿命预测理论主要包括基于贝叶斯统计的方法、基于蒙特卡洛模拟的方法、基于计算机仿真的方法、基于有限元分析的方法等。
其中,有限元分析方法是最为常用的方法,其原理是将轮对的材料性质、载荷条件、形状尺寸等因素作为输入,通过数值计算得到轮对的疲劳寿命分布规律。
第三章轮对疲劳寿命预测方法基于有限元分析的方法是目前最为常用的轮对疲劳寿命预测方法,其核心是确定轮对的疲劳损伤分布规律,并据此预测轮对的疲劳寿命。
该方法的具体步骤包括:1. 建立轮对的有限元模型,包括轮辋、车轮胎等部件。
2. 确定轮对的载荷状态,包括轴重、车速等参数。
3. 使用有限元分析软件计算轮对的应力分布和应变分布。
4. 利用疲劳损伤积累理论计算轮对的疲劳寿命分布规律。
5. 对结果进行分析、评估和优化。
需要注意的是,该方法需考虑轮对所处环境的影响,如温度、湿度等因素。
另外,对于实际运营中所受到的不同行车条件,需采用多种载荷组合进行仿真,以确保预测结果的准确性。
第四章影响轮对疲劳寿命的因素轮对疲劳寿命受到多种因素的影响,下面列举部分主要因素:1. 轴重:轮对所受的轴重是影响疲劳寿命的主要因素之一。
2. 转向架结构:不同的转向架结构对轮对的疲劳寿命影响较大。
3. 材料特性:轮对材料的强度、韧性等性质决定了其疲劳寿命的上限。
4. 运营环境:温度、湿度、行车速度等环境因素会影响到轮对的疲劳寿命。
连续测力轮对的数字试验研究
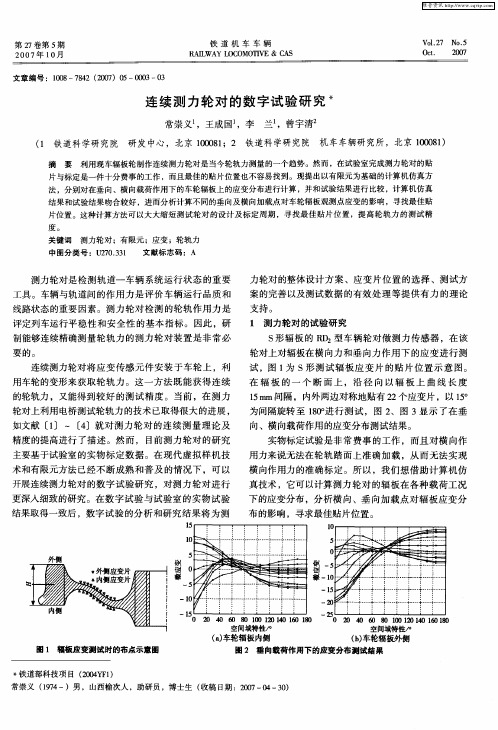
关键词
测 力轮对 ;有 限元 ;应变 ;轮轨力
文 献 标 志 码 :A
中 图分 类 号 :U 7 .3 203 1
测力 轮对 是 检 测轨 道 一 车辆 系 统 运行 状 车 辆运 行 品质 和
力 轮对 的整 体设 计 方 案 、应 变 片 位置 的选 择 、测 试方
片与标 定是 一件 十分费事的工作 ,而且最佳的贴片位置也不容易找到 。现提 出以有 限元为基础 的计算机仿真方 法 ,分别对 在垂 向 、横向载荷 作用下的车轮辐板上的应变分布进行计算 ,并和试验结果进行 比较 ,计算机仿 真 结 果和试 验结果 吻合 较好 ,进而分析计算不 同的垂向及横 向加载点对车轮辐板观测点应变 的影 响 ,寻找最佳贴 片位置 。这种计算方法可 以大 大缩 短测试 轮对 的设计及标 定周期 ,寻找最佳 贴片位 置 ,提 高轮轨 力 的测试精
+
+
… …
内 0 m} 移3m 垂向
一
+ 一 移lm 横向 _ 内 O m} _
…
滚圆 1 /、 动处 l
外移 1 m J O
…
‰ . … j
罩|
元计算方法可以作 为测力轮对数字试验的分析和研究
工具 。
3 最佳 贴片位 置 的选取 根 据文献 [ ]提 出 的测 力 轮 对 连 续 测 量 的 新 方 1 法 ,该 方法 引人谐 波分 析 建 立 辐 板轮 应 变 的有 效 分 析 方法 ,将 测量 组桥 归 结 于 数 字滤 波 器 设 计 ,路 桥 感 应
用 车轮 的变形来 获 取 轮 轨力 。这一 方 法 既 能 获 得 连续 的轮 轨力 ,又 能得 到较 好 的测 试 精 度 。当前 ,在 测 力 轮对 上利 用 电桥测试 轮 轨力 的技术 已取 得很 大 的进展 ,
机械系统动力学模型的状态观测方法研究

机械系统动力学模型的状态观测方法研究在现代工程领域中,机械系统的性能和可靠性至关重要。
为了实现对机械系统的有效控制和优化设计,准确了解系统的状态是必不可少的。
机械系统动力学模型的状态观测方法就是解决这一问题的关键手段之一。
机械系统动力学模型通常用于描述系统的运动和力的关系。
然而,在实际应用中,直接测量系统的所有状态变量往往是困难甚至不可能的。
这就需要我们通过间接的方法来估计系统的状态,即状态观测。
状态观测的基本思想是利用系统的可测量输出和已知的系统模型来推算系统的内部状态。
常见的状态观测方法包括卡尔曼滤波、龙伯格观测器等。
卡尔曼滤波是一种基于概率论和线性系统理论的最优估计方法。
它通过不断地预测和修正,来估计系统的状态。
在机械系统中,卡尔曼滤波可以用于处理噪声干扰下的状态估计问题。
例如,在车辆的悬挂系统中,通过测量车身的加速度和车轮的位移,利用卡尔曼滤波可以估计出悬挂系统的阻尼和刚度等参数。
龙伯格观测器则是一种基于系统模型的确定性观测方法。
它通过构造与系统模型相似的观测器,并利用系统的输出误差来修正观测器的状态,从而实现对系统状态的估计。
与卡尔曼滤波相比,龙伯格观测器的计算量相对较小,在一些实时性要求较高的系统中具有优势。
在实际应用中,选择合适的状态观测方法需要考虑多种因素。
首先是系统的复杂性和非线性程度。
如果系统具有较强的非线性特性,传统的线性观测方法可能不再适用,需要采用非线性观测方法,如扩展卡尔曼滤波、无迹卡尔曼滤波等。
其次,测量噪声的特性也会影响观测方法的选择。
如果噪声具有较大的方差或非高斯分布,可能需要采用更鲁棒的观测方法来应对。
另外,计算资源和实时性要求也是重要的考虑因素。
一些复杂的观测方法可能需要较高的计算能力和较长的计算时间,在资源受限或对实时性要求极高的系统中可能无法应用。
为了提高状态观测的精度和可靠性,还可以采用多种方法相结合的策略。
例如,将卡尔曼滤波与龙伯格观测器结合使用,或者将基于模型的观测方法与基于数据驱动的方法相结合。
机械系统动力学模型的状态估计方法研究

机械系统动力学模型的状态估计方法研究在现代工程领域中,机械系统的性能和可靠性对于各种应用至关重要。
为了确保机械系统的稳定运行、优化设计以及故障诊断等,对其动力学模型的状态进行准确估计是一项关键任务。
机械系统动力学模型的状态估计方法旨在通过对系统的观测数据和已知信息进行处理和分析,来推断系统内部状态的变化情况。
机械系统通常具有复杂的动态特性,受到多种因素的影响,如摩擦力、惯性、弹性力等。
这些因素使得精确描述和预测机械系统的行为变得具有挑战性。
而状态估计方法则为解决这一问题提供了有力的工具。
常见的机械系统动力学模型包括集中参数模型和分布参数模型。
集中参数模型将系统的质量、刚度和阻尼等特性集中在几个特定的点上,便于分析和计算;分布参数模型则更能准确地反映系统的连续特性,但计算复杂度相对较高。
在实际应用中,需要根据具体问题的特点选择合适的模型。
状态估计方法可以大致分为两类:基于模型的方法和基于数据的方法。
基于模型的方法依赖于对机械系统的先验物理知识,建立精确的数学模型,并结合观测数据进行状态估计。
卡尔曼滤波及其扩展算法是这类方法中的典型代表。
卡尔曼滤波通过预测和更新两个步骤,不断修正对系统状态的估计值。
然而,在实际应用中,由于模型的不确定性和噪声的复杂性,卡尔曼滤波可能会出现性能下降的情况。
为了应对这些挑战,扩展卡尔曼滤波和无迹卡尔曼滤波等改进算法被提出。
扩展卡尔曼滤波适用于非线性系统,但在强非线性情况下估计精度可能受到影响。
无迹卡尔曼滤波通过选择一组特定的采样点来近似状态的概率分布,从而提高了对非线性系统的估计性能。
基于数据的方法则不需要对系统建立精确的物理模型,而是直接从观测数据中挖掘有用信息。
人工神经网络、支持向量机等机器学习方法在机械系统状态估计中得到了广泛应用。
这些方法能够自动学习数据中的特征和模式,但需要大量的训练数据来保证估计的准确性和泛化能力。
在实际应用中,常常将基于模型和基于数据的方法相结合,以充分发挥各自的优势。
一种测力轮对的连续测量方法及装置[发明专利]
![一种测力轮对的连续测量方法及装置[发明专利]](https://img.taocdn.com/s3/m/73f94d085ef7ba0d4b733b54.png)
专利名称:一种测力轮对的连续测量方法及装置
专利类型:发明专利
发明人:李谷,祖宏林,储高峰,胡爱全,焦文,孙浩清,俞展猷,王希玲,赵永智,章润鸿
申请号:CN200910244626.6
申请日:20091231
公开号:CN102116691A
公开日:
20110706
专利内容由知识产权出版社提供
摘要:本发明涉及铁道机车车辆轮轨力测量领域,为了解决现有技术中测力轮对测量方法繁杂,测量精度不够高等问题,提供了一种新型的测力轮对的连续测量方法及装置,其中方法包括采用在同周期内一个测量电桥的灵敏度为正弦形,另一个测量电桥的灵敏度为余弦形的第一组双桥路对轮轨垂向力进行测量;采用在同周期内一个测量电桥的灵敏度为正弦形,另一个测量电桥的灵敏度为余弦形的第二组双桥路对轮轨横向力进行测量。
本发明实施例的有益效果在于,由于对垂向力、横向力使用了同样周期的双桥路的测量手段,并经过迭加合成处理,就可以使得在车轮旋转的整个轮周范围内测量灵敏度保持恒定,并且与测力轮对的转动角度无关,测量更加准确。
申请人:中国铁道科学研究院机车车辆研究所
地址:100081 北京市海淀区大柳树路2号
国籍:CN
代理机构:北京三友知识产权代理有限公司
代理人:任默闻
更多信息请下载全文后查看。
静态状态估计及其算法

在x0附近泰勒展开,忽略二次以上的项:
f (x) x
|x0
x
f
(x0 ) 0
f (x) (H TW (Z h(x)) H TWH
x
x
牛顿法状态估计迭代格式:
(H h(x)) x
xk
f xk
1
f
(xk )
(H TWH )1 H TW (Z
h(xk ))
xk1 xk xk
信息矩阵 1 HTWH
d ( A) d A dA
da
da
da
状态估计数学基础准备-矩阵的微分运算
(3) d ( AT ) ( dA)T
da da
(4)A、B分别为m*n和n*l阶函数矩阵
d(AB) dA B A dB
da da
da
(5) d ( A1) A1 dA A1
da
da
证明:
AA1
d ( AA1) I,
dA A1
dA1 A
dI
0
da da
da da
dA1 A1 dA A1
da
da
状态估计数学基础准备-矩阵的微分运算
(7)h为实变量a的n维矢量函数: h [h1, h2,..., hn ]T
d (hT h) 2hT dh
da
da
证明:
hT h h12 h22 ... hn2
d (hT h)
=HTR-1RR-1H
一般来说,测点越多, 越小,估计精度越高
量测Jacobi矩阵H(x)
H
(x)
h(x) xT
m * n维,为竖条结构
根据不同的量测类型,分别写出量测函 数h(x),然后求导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测力轮对状态估计计算方法研究任愈;陈建政【摘要】Accurate measurement of wheel/rail force is the premise and basis of monitoring the train operation status.The discontinuous and continuous measurement methods of instrumented wheelset were analysed,the variable characteristics of wheel /rail contact state were studied,the space model for wheel /rail contact force state estimation was established and the wheel /rail force calculation method based on state estimation was proposed.The algorithm was verified by simulation calculations.Moreover,a continuous measurement was achieved in actual track test by using a simple discontinuous instrumented wheelset.%对轮轨间相互作用力的准确测量是监测列车运行安全状况的前提和基础。
分析了测力轮对间断测量和连续测量方法,通过研究轮轨接触状态的变化特征,建立了轮轨接触力估计状态空间模型,提出基于状态估计的测力轮对轮轨力计算方法;在此基础上进行了仿真计算验证了算法的有效性,并在线路试验中以简单的间断测量测力轮对实现了轮轨力的连续测量。
【期刊名称】《振动与冲击》【年(卷),期】2015(000)009【总页数】5页(P111-115)【关键词】测力轮对;状态估计;间断测量;连续测量【作者】任愈;陈建政【作者单位】西南交通大学牵引动力国家重点实验室,成都 600031;西南交通大学牵引动力国家重点实验室,成都 600031【正文语种】中文【中图分类】U270.7;U216.3;TH721脱轨是列车运行中最危险的安全事故,也是列车提速中需要研究的关键问题之一。
由于轮轨系统的实际运行行为复杂,影响脱轨的因素众多,至今对脱轨机理尚未完全掌握。
但可以肯定的是,轮轨力变化是引起脱轨的直接原因。
高精度的轮轨力检测,可以为脱轨机理研究、车辆动力学研究和列车安全检测提供重要的基础信息,对轮轨间相互作用力的准确测量是监测列车运行安全状况的前提和基础。
目前,最直接、最准确的轮轨力测量技术就是测力轮对方法,它以车轮作为轮轨力的检测传感器,在车轮辐板有限点处位置贴片组桥,通过测量应变信号实现轮轨接触力的检测。
列车运行过程中,由于车轮和轨道间时变、非平稳的轮轨作用力和轮对转动对辐板应变信号的调制作用,使得辐板应变信号较为复杂。
不同的组桥方式对应的计算方法也有所不同,从测量方式来看,主要分为间断式测量和连续式测量两种。
间断测量实现方式和计算方法都相对简单,并且可以最大程度的避免横向力、垂向力和轮轨接触点位置三者之间耦合对应变信号的影响。
目前在国内测力轮对实测试验中使用较多的是间断式的测力轮对。
间断式测量通过特殊的轮对制作方法,使特定电桥输出只受横向力或垂向力影响。
其中,垂向桥输出如图1所示。
垂向桥输出波形中波峰和波谷交替出现,每个波峰和波谷之间轮对相位差为180°;同一辐板上两组垂向桥之间相位差为90°。
通过搜索轮对旋转过程中数据的峰值,可以得到间隔角度为90°间断测量的间断点时间坐标,从间断点时间坐标取得间断点的横向桥和垂向桥输出,代入参数方程进行计算,得到间断点的轮轨横向力和垂向力。
间断测量方法实际上是一种近似的空间采样方法,采样频率为车轮转速的1/4,决定了其采样频率较低,其主要作用是用于评估列车运行中的一些关键参数(脱轨系数、轮重减载率等),对于轮轨间的高频冲击很难进行有效测量;另外,如果频率较高的冲击发生在靠近实际间断点位置,很容易导致间断点位置判断不准确,从而影响间断测量计算结果精度。
连续测量方法可以有效克服间断测量的弊端,是测力轮对技术的发展趋势。
早期连续测力轮对方法是通过仿真和试验选择合适的组桥半径,分别建立横向桥、垂向桥和作用点位置桥,近似的认为轮轨接触力对车轮辐板应变的影响不耦合,其存在的问题是针对不同的轮对,需要设计不同的组桥方案,并且很难找到特别合适的贴片半径。
目前常用的方法是建立特定的应变桥,使电桥输出波形近似正余弦波形或三角波,通过特定方程进行计算[1-2]。
如果不能得到良好的输出波形,一般利用三角函数关系式的性质将复杂的非线性方程组简化为线性方程组,通过计算得到轮轨作用力[3-4]。
这种方法的问题是应变组桥方法繁琐,并且计算过程相对复杂,对检测精度和可靠性存在一定影响。
一般情况下,采用解方程组方式的测力轮对轮轨接触状态计算方法都是假设采集得到的应变桥输出信号即为应变信号真值。
但是实际上,采集到的信号都叠加了相对高频的测试噪声,而噪声的来源包括多个因素,很难通过改进某一具体环节对其进行消除。
常规消除噪声干扰的方法是对测试信号进行选频滤波,以滤波后的数据进行计算。
实际上,对于测力轮对这一特殊的应用环境,辐板电桥信号不仅受到轮轨力影响,也被轮对转动所调制,见图2。
假定车轮辐板应变信号经过组桥后输出载波信号为较简单形式,即仅含有一次谐波z(t)=acos(ω0t),同时将轮轨力描述为傅里叶级数形式:根据式(1),任意一个轮轨力信号分量在经过轮对转动调制后都变为含有θn+ω0和θn-ω0这两个频率分量的信号。
可以看出,无论滤波频率选择在什么范围,都会导致有更高频率的轮轨力与车轮转动载波信号的|θn-ω0|分量混合在其中,而更高频率信号中的分量已经被滤波消除了,则滤波后的信号输出为:从信号测试的角度分析,轮轨接触力的变化是由车辆在行驶过程中受到随机激励引起的,而随机激励在任意不同时刻的取值之间都是无关的。
而从微观的角度分析,在车辆行驶阶段的任意间隔较短时间内,轮轨接触状态在时间上存在一定的延续性。
也就是说,在正常行驶状态下,只要保证采样频率相对于需要检测的轮轨力的频率足够高,则可以认为当前状态是在前一时刻状态基础上有一些规律性的变化。
状态空间法(State-space Techniques)是现代控制理论中建立在状态变量描述基础上对控制系统分析和综合的方法[5-9]。
状态变量是能完全描述系统运动的一组变量。
如果系统的外输入为已知,那么由这组变量的现时值就能完全确定系统在未来各时刻的运动状态。
状态空间模型是动态时域模型,以隐含着的时间为自变量。
状态空间模型包括两个模型:一是状态转移模型,反映动态系统在输入变量作用下在某时刻所转移到的状态,如式(3);二是量测模型,描述输出变量与状态变量和输入变量间的变换关系,如式(4)。
两者构成了状态空间模型。
通过分析辐板应变输出与轮轨接触状态的关系,可以认为导致轮对应变桥输出改变的作用因素包括横向力Q、垂向力P、作用点位置X和轮对旋转角度θ,即可设轮轨接触状态向量为x=[Q,P,X,θ]T。
设uk为状态的激励变化量,wk为状态转移噪声。
在常规条件下,可以近似地假设轮轨接触状态变化为:确定状态向量后,需确定各成员变量的递推规律进行统计和推导。
图3为在西南交通大学滚振试验台上进行的测力轮对滚动试验中的轮轨力输出,从图中可以看出在极短的时间内(一个采样周期),每个采样点得到的轮轨力值相对于其前一个采样点有微小变化。
由于轮轨力受未知轨道激励等各方面不确定因素的影响,其变化情况呈现出一定的随机性,一般考虑其服从高斯分布。
同样的,认为在较短的采样周期内,轮轨接触作用点在原作用点基础上发生一个随机变化。
根据经验,在车辆正常运行时,作用点位置在名义滚动圆附近20 mm以内摆动,一般认为其变化服从高斯分布。
在较短的时间(轮对转动一周)内车速不会发生明显变化,即短时间内轮对转动角速度不会发生明显变化。
可以将应变片组成间断测量的方式来取得轮对转动零角度时刻Ts和终止角度时刻Te,推导出在这段时间内轮对角速度ωθ,从而得到轮对转动角速度的估计ωθ=2π/(Te-Ts)。
实际运行工程中车辆在运行过程中车速的变化(加速、减速过程及速度随机变化量)导致轮对转动角速度存在一个随机变化,设其模型如下:辐板应变电桥的组桥输出是由上述四个状态因素的改变引起的,表示为:式(7)和式(8)构成了测力轮对轮轨力检测的状态空间计算模型,测力轮对非线性方程组的计算问题转化为对于轮轨接触状态向量的估计问题。
一般采用卡尔曼滤波类方法或粒子滤波类方法,卡尔曼滤波类方法一般处理线性或弱非线性估计问题,因此考虑采用粒子滤波类方法处理。
对于测力轮对轮轨力估计,观测方程对于最终估计结果精度有较大影响,而观测方程与组桥方式是对应的。
另外,组桥方式的复杂程度也关系着测力轮对测试系统的复杂程度和可靠性;不同的观测方程意味着不同的测力轮对制作的复杂程度、可靠性和测试精度。
通过仿真试验对比,在车轮辐板上的应变组桥方案中,最简单的组桥方式是对称片桥,但其输出的谐波成分较为复杂,估计轮轨接触状态结果精度最低;而谐波成分较为简单的信号估计结果精度较高,但其往往则对应着复杂组桥方式。
本文采用文献[3]中提到的保留一次和七次谐波的组桥方案对某动车组轮对进行有限元仿真,并通过标准粒子滤波(PF)、卡尔曼粒子滤波(EKPF)、无迹粒子滤波(UPF)三种方法对仿真应变桥输出进行状态估计计算,其结果如图4所示。
上述计算结果对应的均方根误差见表1。
通过多次仿真计算,证明粒子滤波类方法能有效处理测力轮对轮轨力计算问题,其计算精度受设定参数和计算模型影响。
在相同设定情况下,采用扩展卡尔曼粒子滤波方法和无迹卡尔曼粒子滤波方法优于标准粒子滤波算法,但计算复杂程度更大。
在车辆实际运行过程中,受到轨道不平顺激励及其它因素的影响(轨缝的冲击、经过道岔等),轮轨力在受激的短时间内会产生剧烈变化,从而导致轮轨力状态转移过程不满足状态转移方程式中对力信号变化参数的假设,对含有垂向冲击信号的仿真数据计算结果误差见表2。
可以看出,标准粒子滤波算法完全没有突变状态跟踪能力,垂向力计算产生了较大误差,而EKPF和UPF的估计结果明显优于标准粒子滤波算法,但估计结果的均方根误差值也有所增加。
在测力轮对轮轨力测试系统实际应用时,除了上面提到系统状态发生剧烈变化的问题,还存在着其它一些导致系统模型与实际情况产生误差的因素,如轮对不均匀、实际应用参数与标定数据产生误差、检测设备性能发生变化等。
