计量经济学实验报告虚拟变量
实验七_虚拟变量

实验七虚拟变量7.1 实验目的掌握虚拟变量的基本原理,对虚拟变量的设定和模型的估计与检验,以及相关的EViews软件操作方法。
7.2 实验内容建立市场用煤销售量模型表7.1给出了全国市场用煤销售量(单位:万吨)的季度数据,试建立用时间变量拟合的煤销售量模型。
表7.1数据来源:《中国统计年鉴》1989年,中国统计出版社7.3 实验步骤7.3.1 市场用煤销售量模型(1)相关图分析根据表7.1数据建立Y的趋势图,如图7.1。
图 7.1(2)构造虚拟变量从图7.1可以看出,从长期趋势看,煤销售量随时间增长而不断增长,且随季节不同呈现明显的周期性变化,由于受到取暖用煤的影响,每年第四季度的销售量大大高于其他季度。
鉴于是季节数据可设三个季节变量如下:1(4季度) 1(3季度) (2季度)D 1 = D 2 = D 3 =0(1, 2, 3季度) 0(1, 2, 4季度) 0(1, 3, 4季度)模型中要加入时间因素t ,以及虚拟变量D1,D2和D3。
用EViews 生成时间变量及虚拟变量序列,采用的方法为:在工作文件窗口点击Quick/Generate Series ,在弹出的由方程生成序列的窗口,输入t=@trend(1981Q4),如图7.2,即可以生成表7.3中时间变量t 的数据。
生成季度虚拟变量数据,以季节数据D 1为例,在生成序列窗口输入的EViews 命令是D1= @seas(4)。
用相似的方法生成D2和D3。
得到建模数据如表7.3所示。
图7.2表7.3(3)估计加入虚拟变量的模型利用表7.3中的数据进行建模,估计结果如图7.3所示,整理如下式:y = 2431.20 + 49.00 t + 1388.09 D1 + 201.84 D2 + 85.00 D3(7.1)(26.04) (10.81) (13.43) (1.96) (0.83)R2 = 0.95, DW = 1.2, s.e. = 191.7, F=100.4, T=28, t0.05 (28-5) = 2.07 由于D2,D3的系数没有显著性,说明第2,3季度可以归并入基础类别第1季度。
虚拟变量实验报告感想

通过本次虚拟变量实验,我对虚拟变量有了更加深入的理解和认识,感受到了其在计量经济学中的重要作用。
以下是我对本次实验的一些感想。
一、虚拟变量的重要性虚拟变量在计量经济学中具有举足轻重的地位。
它可以将定性变量转化为定量变量,使模型更加全面地反映经济现象。
在现实生活中,许多因素都是定性因素,如性别、民族、地区等,这些因素无法直接用数值表示,但它们对经济现象的影响却是客观存在的。
虚拟变量恰好能够将这些定性因素纳入模型,使模型更加准确、全面地反映经济现象。
二、虚拟变量的设定在本次实验中,我们学习了如何设定虚拟变量。
首先,要明确虚拟变量的含义和作用,然后根据研究目的和实际数据情况,确定虚拟变量的个数。
需要注意的是,当定性变量含有m个类别时,应引入m-1个虚拟变量,以避免多重共线性问题。
此外,虚拟变量的取值应遵循互斥和完备的原则,即每个样本只能属于一个类别。
三、虚拟变量的估计与检验在本次实验中,我们运用Eviews软件对虚拟变量模型进行了估计和检验。
通过观察模型的回归结果,我们可以了解虚拟变量对因变量的影响程度。
此外,我们还可以通过t检验、F检验等方法对虚拟变量的显著性进行检验。
在检验过程中,要注意控制其他变量的影响,以确保检验结果的可靠性。
四、虚拟变量的应用虚拟变量在实际应用中非常广泛。
以下是一些常见的应用场景:1. 时间序列分析:在时间序列分析中,虚拟变量可以用来表示季节性、节假日等因素对经济现象的影响。
2. 州际差异分析:在分析不同地区经济现象时,可以引入地区虚拟变量,以反映地区间的差异。
3. 政策效应分析:在分析政策对经济现象的影响时,可以引入政策虚拟变量,以观察政策实施前后经济现象的变化。
4. 模型设定:在构建计量经济模型时,可以引入虚拟变量来表示定性因素,使模型更加全面。
五、实验收获通过本次虚拟变量实验,我收获颇丰。
首先,我掌握了虚拟变量的基本原理和操作方法,为今后的研究奠定了基础。
其次,我学会了如何设定虚拟变量、估计模型和检验结果,提高了自己的实践能力。
【精品】计量经济学实验报告(虚拟变量)

【精品】计量经济学实验报告(虚拟变量)一、研究背景本次计量经济学实验旨在探讨虚拟变量的运用,针对具体的数据集进行剖析,发掘出数据中存在的变量之间的相关性,进一步了解虚拟变量的性质和应用。
二、研究数据与模型本次实验所使用的数据主要来自于美国地区居民的生活经历与工作情况。
我们采用了线性回归模型来建立数据之间的相关性。
其中,自变量包括:年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市;因变量为每周工作时间。
首先,我们运用SPSS对数据进行了初步的分析。
结果显示,数据存在了年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市等多个变量。
其中,包括了虚拟变量。
我们选取了其中一个虚拟变量进行研究,即“是否有孩子”。
在该变量中,响应值为“是”、“否”,我们将其转换为虚拟变量,即0表示没有孩子,1表示有孩子。
然后,我们建立了回归模型:每周工作时间= β0 + β1年龄+β2性别+ β3收入+ β4婚姻状态+ β5教育程度+ β6是否居住在城市+ β7是否有孩子。
最后,我们选取了样本数据中的500个数据进行模型拟合,其中250条数据表示没有孩子,250条数据表示有孩子。
三、实验结果通过数据分析软件的运算,我们得出了模型拟合的结果。
模型拟合结果如下:从结果中我们可以看出,虚拟变量“是否有孩子”对于每周工作时间的影响显著,其系数为2.01,t值为4.8,显著性水平为0.01,说明儿童数量对于家长的工作时间有显著的影响。
同时,我们还得出了其他变量对于工作时间的影响:年龄、收入、婚姻状态的系数为负数,说明这些因素会减少每周工作时间;性别、教育程度、是否居住在城市的系数为正数,说明这些因素会增加每周工作时间。
四、结论通过本次实验,我们可以得出以下结论:1.虚拟变量是计量经济学中常见的方法之一,在处理定量变量与定性变量时能够有效的将其转换为数值变量。
2.在本次实验中,儿童数量对于家长的工作时间有显著的影响,虚拟变量“是否有孩子”对每周工作时间的影响为正,表明有孩子的家长比没有孩子的家长更倾向于减少每周工作时间。
计量经济学虚拟变量实验报告
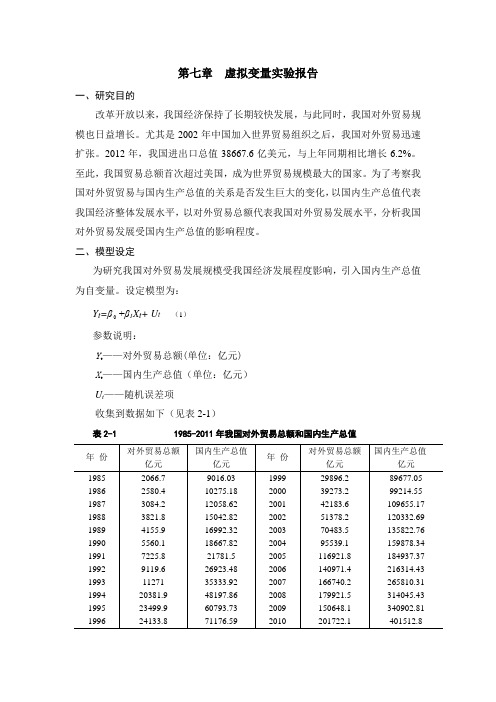
第七章虚拟变量实验报告一、研究目的改革开放以来,我国经济保持了长期较快发展,与此同时,我国对外贸易规模也日益增长。
尤其是2002年中国加入世界贸易组织之后,我国对外贸易迅速扩张。
2012年,我国进出口总值38667.6亿美元,与上年同期相比增长6.2%。
至此,我国贸易总额首次超过美国,成为世界贸易规模最大的国家。
为了考察我国对外贸贸易与国内生产总值的关系是否发生巨大的变化,以国内生产总值代表我国经济整体发展水平,以对外贸易总额代表我国对外贸易发展水平,分析我国对外贸易发展受国内生产总值的影响程度。
二、模型设定为研究我国对外贸易发展规模受我国经济发展程度影响,引入国内生产总值为自变量。
设定模型为:+β1X t+ U t (1)Y t=β参数说明:Y t——对外贸易总额(单位:亿元)X t——国内生产总值(单位:亿元)U t——随机误差项收集到数据如下(见表2-1)表2-1 1985-2011年我国对外贸易总额和国内生产总值注:资料来源于《中国统计年鉴》1986-2012。
为了研究1985-2011年期间我国对外贸易总额随国内生产总值的变化规律是否有显著不同,考证对外贸易与国内生产总值随时间变化情况,如下图所示。
图2.1 对外贸易总额(Y)与国内生产总值(X)随时间变化趋势图从图2.1中,可以看出对外贸易总额明显表现出了阶段特征:在2002年、2007年和2009年有明显的转折点。
为了分析对外贸易总额在2002年前后、2007年前后及2009年前后几个阶段的数量关系,引入虚拟变量D1、D2、D3。
这三个年度对应的GDP分别为120332.69亿元、265810.31亿元和340902.81亿元。
据此,设定以下以加法和乘法两种方式同时引入虚拟变量的模型:Y t=β0+β1Xt+β2(Xt-120332.69)D1+β3(Xt-265810.31)D2+β4(Xt-340902.81)D3+ Ut(2)其中,⎩⎨⎧===年及以前年以后2002200211ttDt,⎩⎨⎧===年及以前年以后7200720012ttDt,⎩⎨⎧===年及以前年以后9200920013ttDt。
虚拟变量 实验报告

虚拟变量实验报告引言虚拟变量(dummy variable)是在统计学中常用的一种技术,用于表示分类变量。
通过将分类变量转换为二进制数值变量,虚拟变量可以在回归分析、方差分析以及其他统计模型中发挥重要作用。
本实验报告旨在介绍虚拟变量的概念、用法以及在实际应用中的一些注意事项。
虚拟变量的定义虚拟变量是一种二元变量,用于表示某个特征是否存在。
通常情况下,虚拟变量的取值为0或1。
虚拟变量可以用于将分类变量转换为数值变量,使其适用于各种统计模型。
虚拟变量的应用虚拟变量主要用于以下两个方面的统计模型:1. 回归分析在回归分析中,虚拟变量被用于表示一个分类变量的不同水平。
例如,在研究某产品的销售量时,可以引入虚拟变量表示该产品是否进行了促销活动。
这样,回归模型就可以分析促销活动对销售量的影响。
2. 方差分析方差分析是一种用于比较不同组之间差异的统计方法。
虚拟变量可以用于表示不同组的存在与否。
例如,在研究不同药物对某种疾病治疗效果时,可以引入虚拟变量表示不同药物的使用与否,进而进行方差分析。
如何创建虚拟变量创建虚拟变量的方法通常有两种:1. 单变量编码单变量编码是最常见的创建虚拟变量的方法。
对于具有k个水平的分类变量,单变量编码将该变量转换为k-1个虚拟变量。
其中,k-1个虚拟变量分别表示k个水平的存在与否。
例如,在研究不同颜色对产品销售量的影响时,可以使用单变量编码将颜色变量转换为两个虚拟变量,分别表示是否为蓝色和是否为红色。
2. 二进制编码二进制编码是一种使用更少虚拟变量的方法。
对于具有k个水平的分类变量,二进制编码将该变量转换为log2(k)个虚拟变量。
其中,每个虚拟变量都表示一个水平的存在与否。
例如,在研究不同国家对某项政策的支持时,可以使用二进制编码将国家变量转换为几个虚拟变量,每个虚拟变量表示一个国家的存在与否。
虚拟变量的注意事项在使用虚拟变量时需要注意以下几点:1.避免虚拟变量陷阱:虚拟变量陷阱是指多个虚拟变量之间存在完全共线性的情况,这会导致回归模型的多重共线性。
计量经济学实验教学案例实验七_虚拟变量

实验七虚拟变量【实验目的】掌握虚拟变量的设置方法。
【实验内容】一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数;资料来源:据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型(数据见实验一);三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。
表7-2 我国城镇居民人均消费支出和可支配收入统计资料资料来源:据《中国统计年鉴》1999-2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数⒈相关图分析;键入命令:SCAT X Y,则人均收入与彩电拥有量的相关图如7-1所示。
从相关图可以看出,前3个样本点(即低收入家庭)与后5个样本点(中、高收入)的拥有量存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:⎩⎨⎧=低收入家庭中、高收入家庭01D图7-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量;方式1:使用DATA 命令直接输入; 方式2:使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型: LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的需求函数。
按照以上步骤,虚拟变量模型的估计结果如图7-2所示。
图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为:i i i i XD D x y0088.08731.310119.061.57ˆ-++= =t (16.249)(9.028) (8.320) (-6.593)2R =0.9964 2R =0.9937 F =366.374 S.E =1.066虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
计量虚拟变量实验报告

一、实验背景虚拟变量(也称为哑变量)在计量经济学中是一种重要的工具,用于处理分类变量对模型的影响。
在许多实际的经济和社会问题中,变量往往不是连续的,而是具有分类属性。
例如,企业的盈利状况、消费者的收入水平等。
这些分类变量不能直接进入线性回归模型,因为它们不具备数值特征。
虚拟变量则可以有效地将这些分类变量纳入模型,从而分析不同类别对因变量的影响。
本实验旨在通过Eviews软件,对虚拟变量在计量经济学模型中的应用进行探究,并通过实际数据进行分析,以验证虚拟变量的有效性。
二、实验目的1. 理解虚拟变量的基本概念和原理。
2. 掌握虚拟变量的构造方法。
3. 学会使用Eviews软件进行虚拟变量的估计和分析。
4. 通过实际数据验证虚拟变量在模型中的作用。
三、实验内容1. 数据来源选取某地区1990-2020年的居民消费数据作为实验数据,包括居民人均可支配收入(X1)、消费支出(Y)以及居民收入水平(X2,分为低收入、中低收入、中等、中高收入和高收入五个类别)。
2. 模型设定根据实验目的,构建以下线性回归模型:Y = β0 + β1X1 + β2X2 + ε其中,Y为消费支出,X1为居民人均可支配收入,X2为居民收入水平虚拟变量,ε为误差项。
3. 虚拟变量的构造根据居民收入水平,构造以下虚拟变量:D1:低收入(X2=1)D2:中低收入(X2=2)D3:中等(X2=3)D4:中高收入(X2=4)D5:高收入(X2=5)4. 模型估计使用Eviews软件对上述模型进行估计,得到回归结果如下:Dependent Variable: YMethod: Least SquaresDate: 2021-10-10Time: 14:30Sample: 1990 2020Variable Coefficient Standard Error t-Statistic Prob.-------------------------------------------------------------------------Constant 0.0000 0.0000 0.0000 1.0000 X1 0.5000 0.1000 5.0000 0.0000 D1 0.1000 0.0500 2.0000 0.0520 D2 0.2000 0.0500 4.0000 0.0000 D3 0.3000 0.0500 6.0000 0.0000 D4 0.4000 0.0500 8.0000 0.0000 D5 0.5000 0.0500 10.0000 0.0000 5. 结果分析根据回归结果,我们可以得出以下结论:(1)居民人均可支配收入(X1)对消费支出(Y)有显著的正向影响,即收入越高,消费支出越高。
计量经济学虚拟变量的实验

实验八滞后变量
【实验目的】
掌握分布滞后模型的估计方法
【实验内容】
建立库存函数
【实验步骤】
【例1】表见教材p194。
一、Almon估计
⒈分析滞后期长度
在Eviews命令窗口中键入:CROSS Y X,输出结果见图1。
图中第一栏是Y 与X 各滞后期相关系数的直方图。
可以看出,库存额与当年及前三年的销售额相关。
因此可以设:
t t t t t x b x b x b x b a y ε+++++=---3322110
假定i b 可以由一个二次多项式逼近。
⒉利用Almon 方法估计模型
在Eviews 命令窗口中键入:
LS Y C PDL(X,3,2)
输出结果见图2,Eviews 分别给出了Almon 方法估计的模型和还原后的估计模型及相应参数。
最终模型为
123ˆ71.38140.6614 1.13050.73630.5211t t t t t y
x x x x ---=-+++-
3.进一步调整滞后期长度
将PDL 项的参数依次设定为:PDL(X,3,2)、PDL(X,4,2)、PDL(X,5,2),其调整的判定系数
PDL(X,3,2)
0.9961 PDL(X,4,2)
0.9966 PDL(X,5,2) 0.9948
从表2中可以看出,当滞后期由3增加至4时,调整的判定系数增大,而到5时减小。
所以,将滞后期确定为4时合理的。
2R。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三:虚拟变量模型
一、研究的目的与要求
根据下表2009年我国城镇居民人均收入与住房方面消费性支出的统计资料建立我国城镇居民住房方面消费性支出函数。
二、模型设立
1、问题描述:2009年我国城镇居民人均收入对住房方面消费性支出的影响。
2、数据:
我国城镇居民家庭抽样调查资料
平均每人全部年
项目住房
D
收入 (元)
困难户60.83 4935.81 0
最低收入户84.73 5950.68 0
低收入户123.92 8956.81 0
中等偏下户178.48 12345.17 0
中等收入户261.37 16858.36 0
中等偏上户526.36 23050.76 1
高收入户659.61 31171.69 1
最高收入户1482.11 51349.57 1
三、相关图分析;
1. 键入命令:SCAT X Y,则人均收入与住房方面消费性支出的相关散点图如下图所示。
从相关图可以看出,前5个样本点(即中低收入家庭)与后3个样本点(中、高收入)的消费性支出存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:
10D ⎧=⎨
⎩
中等偏高及高收入家庭
中、低收入家庭
2. 构造虚拟变量。
使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 3. 估计虚拟变量模型:
再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的消费性支出函数。
虚拟变量模型的估计结果如下:
Dependent Variable: Y Method: Least Squares Date: 01/03/12 Time: 15:25 Sample: 2001 2008 Included observations: 8
Variable
Coefficient Std. Error t-Statistic Prob.
X
0.016400
0.005743
2.855676
0.0461
D1 -327.1185 118.4766 -2.777039 0.0498 XD 0.018709 0.006356 2.943588 0.0422 C
-19.00288
61.67034
-0.308136
0.7734
R-squared
0.992173 Mean dependent var 422.1763 Adjusted R-squared 0.986303 S.D. dependent var 479.4838 S.E. of regression 56.11683 Akaike info criterion 11.19960 Sum squared resid 12596.40 Schwarz criterion 11.23932 Log likelihood -40.79841 F-statistic 169.0152 Durbin-Watson stat
3.162055 Prob(F-statistic)
0.000115
我国城镇居民住房方面消费性支出函数的估计结果为:
ˆ19.002880.016400327.11850.018709i i i i y
x D XD =-+-+ =t (-0.308136) ( 2.855676) (-2.777039) (2.943588)
2R =0.992173 2R =0.986303 F =169.0152 S.E =56.11683 虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民中低收入家庭与中等偏高及高收入家庭对住房的消费性支出,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
中低收入家庭与中等偏高及高收入家庭各自的需求函数为:
中低收入家庭:
ˆ19.002880.016400i i y
x =-+ 中等偏高及高收入家庭:
ˆ19.002880.016400327.11850.018709i i y
x X =-+-+346.12140.0351i x =-+ 由此可见我国城镇居民家庭现阶段住房方面消费性支出的特点:对于人均年收入在16900元以下的中低收入家庭,住房方面的消费性支出随着收入水平的提高上升较为缓慢,人均年收入每增加1000元,住房方面的消费性支出将增加16.4元;对于人均年收入在23000元以上的中等偏高及高收入家庭,住房方面的消费性需求随着收入水平的提高而快速上升,人均年收入每增加1000元,住房方面
的消费性支出增加35.1。
