数据统计学第四章测试答案
统计学第四章课后题及答案解析

第四章一、单项选择题1。
由反映总体单位某一数量特征的标志值汇总得到的指标是()A。
总体单位总量 B.质量指标C。
总体标志总量 D。
相对指标2。
各部分所占比重之和等于1或100%的相对数( )A.比例相对数 B.比较相对数C.结构相对数D.动态相对数3。
某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为( )A.104。
76%B.95.45%C.200%D.4。
76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度( )A。
14。
5%B。
95% C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A。
只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D。
可以存在多个单位总量和多个标志总量6。
计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A。
大量的B.同质的 C。
有差异的 D。
不同总体的7。
几何平均数的计算适用于求()A。
平均速度和平均比率 B.平均增长水平C。
平均发展水平D。
序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是( )A.3 B.13 C。
7。
1 D。
79。
某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是( )A。
方差 B。
极差 C.标准差 D。
变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等 B。
两个总体的平均数应相等C。
两个总体的单位数应相等 D。
两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用( )A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12。
统计学第四章课后习题答案

第四章一.思考题1、一组数据的分布特征可以从哪几个方面进行测度?答:可以从三个方面进行测度和描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布的偏态和峰态。
2、怎样理解平均数在统计学中的地位?答:平均数在统计学中具有重要的地位,它是进行统计分析和统计推断的基础。
从统计学思想上看,平均数是一组数据的重心所在,是数据误差相互抵消后的必然结果。
3、简述四分位数的计算方法。
答:四分位数是一组数据排序后处于25%和75%位子上的值。
四分位数是通过3个点将全部数据等分成4分,其中每部分包含25%的数据。
中间的四分位数就是中位数,因此通常所说的四分位数是指处在25%位置上的数值和处在75%位置上的数值。
它是根据为分组数据计算四分位数时,首先对数据进行排序,然后确定四分位数所在的位置,该位置上的数据就是四分位数。
4、对于比率数据的平均数为什么采用几何平均?答:几何平均数是适用于特殊数据的一种平均数,主要适用于计算平均比率。
当所掌握的变量值本身是比率的形式时,采用几何平均法计算平均比率更为合理。
5、简述众数、中位数、平均数的特点和应用场合。
答:众数是数据中出现次数次数最多的变量值。
主要应用于分类数据。
中位数是一组数据排序后处于中间位置的变量值,其适用于顺序数据。
平均数也称均值,它是一组数据相加后除以数据个数的结果,是集中去世的主要测量值,它适用于数值型数据。
6、简述异众比率、四分位差、方差、标准差的使用场合。
答:异众比率主要适合测度分类数据的离散程度,对于顺序数据以及数值型数据也可以计算异众比率。
四分位差主要用于测度顺序数据的离散程度。
方差和标准差适用于测度数值型数据的离散程度。
7、标准分数有哪些用途?答:首先是比较不同单位和不同质数据的位置。
其次是和正态分布结合起来,求得概率和标准分值之间的对应关系。
还有就是在假设检验和估计中应用。
统计学第四章习题答案-贾俊平
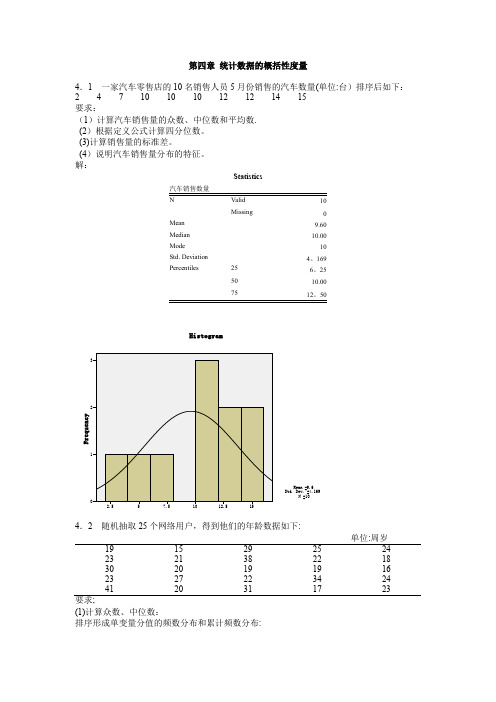
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数.(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing0Mean9.60Median10.00Mode10Std. Deviation4。
169Percentiles256。
255010.0075单位:周岁19152925242321382218302019191623272234244120311723要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18。
75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0。
75×2=26.5。
(3)计算平均数和标准差;Mean=24。
00;Std。
Deviation=6。
652(4)计算偏态系数和峰态系数:Skewness=1。
080;Kurtosis=0。
773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 — 最小值)÷ 组数=(41-15)÷6=4。
3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图::一种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客.得到第一种排队方式的平均等待时间为7.2分钟,标准差为1.97分钟。
统计学课后习题答案_(第四版)4.5.7.8章

《统计学》第四版 第四章练习题答案4.1 (1)众数:M 0=10; 中位数:中位数位置=n+1/2=5.5,M e =10;平均数:6.91096===∑nxx i(2)Q L 位置=n/4=2.5, Q L =4+7/2=5.5;Q U 位置=3n/4=7.5,Q U =12 (3)2.494.1561)(2==-=∑-n i s x x (4)由于平均数小于中位数和众数,所以汽车销售量为左偏分布。
4.2 (1)从表中数据可以看出,年龄出现频数最多的是19和23,故有个众数,即M 0=19和M 0=23。
将原始数据排序后,计算中位数的位置为:中位数位置= n+1/2=13,第13个位置上的数值为23,所以中位数为M e =23(2)Q L 位置=n/4=6.25, Q L ==19;Q U 位置=3n/4=18.75,Q U =26.5(3)平均数==∑nx x i600/25=24,标准差65.612510621)(2=-=-=∑-n i s x x(4)偏态系数SK=1.08,峰态系数K=0.77(5)分析:从众数、中位数和平均数来看,网民年龄在23-24岁的人数占多数。
由于标准差较大,说明网民年龄之间有较大差异。
从偏态系数来看,年龄分布为右偏,由于偏态系数大于1,所以,偏斜程度很大。
由于峰态系数为正值,所以为尖峰分布。
4.3 (1(2)==∑nx x i63/9=7,714.0808.41)(2==-=∑-n i s x x (3)由于两种排队方式的平均数不同,所以用离散系数进行比较。
第一种排队方式:v 1=1.97/7.2=0.274;v 2=0.714/7=0.102.由于v 1>v 2,表明第一种排队方式的离散程度大于第二种排队方式。
(4)选方法二,因为第二种排队方式的平均等待时间较短,且离散程度小于第一种排队方式。
4.4 (1)==∑nx x i8223/30=274.1中位数位置=n+1/2=15.5,M e =272+273/2=272.5(2)Q L 位置=n/4=7.5, Q L ==(258+261)/2=259.5;Q U 位置=3n/4=22.5,Q U =(284+291)/2=287.5(3) 17.211307.130021)(2=-=-=∑-n i s x x4.5 (1)甲企业的平均成本=总成本/总产量=41.193406600301500203000152100150030002100==++++乙企业的平均成本=总成本/总产量=29.183426255301500201500153255150015003255==++++原因:尽管两个企业的单位成本相同,但单位成本较低的产品在乙企业的产量中所占比重较大,因此拉低了总平均成本。
统计学第四章习题答案-贾俊平
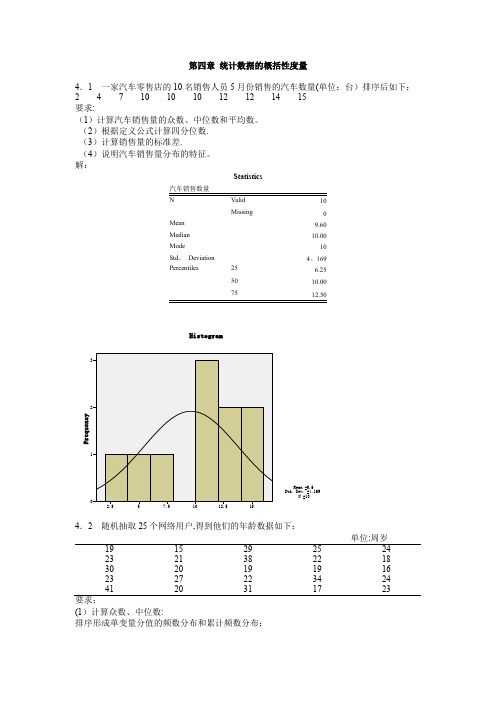
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数.(3)计算销售量的标准差.(4)说明汽车销售量分布的特征。
解:Statistics10Missing0Mean9.60Median10.00Mode10Std。
Deviation4。
169Percentiles25 6.255010.0075单位:周岁19152925242321382218302019191623272234244120311723要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数.Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18。
75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0。
75×2=26。
5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1。
080;Kurtosis=0。
773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 — 最小值)÷ 组数=(41—15)÷6=4。
3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图::一种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待.为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客.得到第一种排队方式的平均等待时间为7.2分钟,标准差为1.97分钟.第二种排队方式的等待时间(单位:分钟)如下:5.5 6.6 6.7 6.8 7.1 7.3 7.4 7.8 7.8要求:(1)画出第二种排队方式等待时间的茎叶图。
统计学4章练习题+答案

第4章练习题1、一组数据中出现频数最多的变量值称为(A)A.众数B.中位数C.四分位数D.平均数2、下列关于众数的叙述,不正确的是(C)A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3、一组数据排序后处于中间位置上的变量值称为(B)A.众数B.中位数C.四分位数D.平均数4、一组数据排序后处于25%和75%位置上的值称为(C)A.众数B.中位数C.四分位数D.平均数5、非众数组的频数占总频数的比例称为(A)A.异众比率B.离散系数C.平均差D.标准差6、四分位差是(A)A.上四分位数减下四分位数的结果B.下四分位数减上四分位数的结果C.下四分位数加上四分位数D.下四分位数与上四分位数的中间值7、一组数据的最大值与最小值之差称为(C)A.平均差B.标准差C.极差D.四分位差8、各变量值与其平均数离差平方的平均数称为(C)A.极差B.平均差C.方差D.标准差9、变量值与其平均数的离差除以标准差后的值称为(A)A.标准分数B.离散系数C.方差D.标准差10、如果一个数据的标准分数-2,表明该数据(B)A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差11、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围之内大约有(B)A.68%的数据B.95%的数据C.99%的数据D.100%的数据12、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=4,其意义是(C)A.至少有75%的数据落在平均数加减4个标准差的范围之内B. 至少有89%的数据落在平均数加减4个标准差的范围之内C. 至少有94%的数据落在平均数加减4个标准差的范围之内D. 至少有99%的数据落在平均数加减4个标准差的范围之内13、离散系数的主要用途是(C)A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平14、比较两组数据离散程度最适合的统计量是(D)A.极差B.平均差C.标准差D.离散系数15、偏态系数测度了数据分布的非对称性程度。
统计学第五版第四章课后习题答案ppt课件

.
23
4.13、
答:
(1)、我认为应用标准差或者离散系数来反 应投资的风险。
(2)、如图所示,高科技类股票的离散系数 较大,所以风险较大;而商业类股票的离散系 数较小,所以风险相对较小。如果选择风险小 的股票进行投资,应选择商业类股票。
(3)、如果进行股票投资,我希望能够获取 高收益,所以我会选择高科技类股票。
.
3
4.2 (1)(2)(3)(4):
.
4
(4):网民年龄的分布特征:
如图所示:
大多网络用户的年龄为19岁,网络用户年 龄的中间值为23岁,上四分位数为27岁, 下四分位数为19岁,说明年龄在19-23岁和 23-27岁的网络用户数量差不多,网络用户 的平均年龄是24岁,证明有个别网络用户 的年龄较大,把整体平均数给拉高了,使整 体分布表现为右偏分布。
以女生体重的差异较大。 (2)、
男生体重的平均数:x =60*2.21=132.6b
男生体重的标准差:s=5*2.21=11.05b
女生体重的平均数: x =50*2.21=110.5b
女生体重的标准差:s=5*2.21=110.5b
.
16
(3)&(4)讲该抽样近似看做正态分布进行估计:
.
12
4.6
.
13
这20家企业利润
额的平均数为
426.67万元,标
准差为116.48,
说明这120家企业
盈利不等且相差较
大,SK为正值,
所以这120家企业
利润的正离差值较
大,属于右偏分布
倾斜程度不是很大,
且为扁平分布,数
据的分布较分散。
.
14
4.7
统计学第四章习题答案
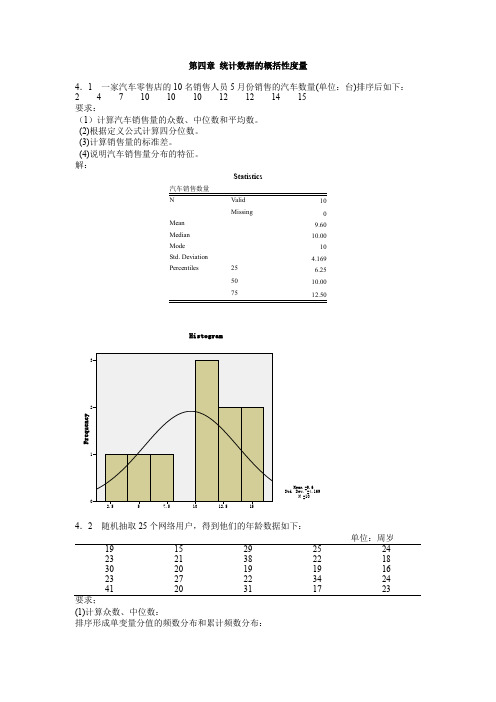
第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics10Missing0Mean9.60Median10.00Mode10Std. Deviation 4.169Percentiles25 6.255010.0075单位:周岁19152925242321382218302019191623272234244120311723要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数: ()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:种是所有颐客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
为比较哪种排队方式使顾客等待的时间更短.两种排队方式各随机抽取9名顾客。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
25,某小区准备采取新的物业管理措施,随机抽取了 100 户居民进行调查,其中赞成的有 69
户,中立的有 22 户,反对的有 9 户,描述该组数据的集中趋势宜采用( )
A.众数
B.中位数
C.四分位数
D.平均数
26-30AABAC
26. 某小区准备采取新的物业管理措施,随机抽取了 100 户居民进行调查,其中赞成的有 69
16-20BCCDA
16、如果一组数据不是对称分布的,根据切比雪夫不等式,对于 k=3,其意义是 ()
A.至少有 75%的数据落在平均数加减 2 个标准差的范围之内 B.至少有 89%的数据落在平均数加减 2 个标准差的范围之内 C.至少有 94%的数据落在平均数加减 2 个标准差的范围之内 D.至少有 99%的数据落在平均数加减 2 个标准差的范围之内 17、如果一组数据不是对称分布的,根据切比雪夫不等式,对于 k=3,其意义是 () A.至少有 75%的数据落在平均数加减 2 个标准差的范围之内 B.至少有 89%的数据落在平均数加减 2 个标准差的范围之内 C.至少有 94%的数据落在平均数加减 2 个标准差的范围之内 D.至少有 99%的数据落在平均数加减 2 个标准差的范围之内 18、离散系数的主要用途是( ) A.反映一组数据的离散水平 B.反映一组数据的平均水平 C.比较多组数据的离散程度 D.比较多组数据的平均水平 19、比较两组数据的离散程度最适合的统计量是( ) A.极差 B.平均差 C.标准差 D.离散系数 20、偏态系数测度了数据分布的非对称性程度。如果一组数据的分布是对称的, 则偏态系数( ) A.等于 0 B.等于 1 C.大于 0 D.大于 1
户,中立的有 22 户,反对的有 9 户,该组数据的中位数是( )
A.赞成
B.69
C。中立
D.22
27.某班有 25 名学生,期末统计学课程的考试分数分别为:68,73,66,76,86,74,61,
89,65,90,69,67,76,62,81,63,68,81,70,73,60,87,75,64,56,该班
C.下四分位数加上四分位数
D.下四分位数与上四分位数的中间值
7、一组数据的最大值与最小值之差称为( )
A.平均差 B.标准差 C.极差 D.四分位差
8、各变量值与其平均数离差平方的平均数称为( )
A.极差
B.平均差 C.方差 D.标准差
9、变量值与其平均数的离差除以标准差后的值称为( )
A.标准分数 B.离散系数 C.方差 D.标准差
23、如果峰态系数 k>0,表明该组数据是( )
A.尖峰分布 B.扁平分布 C.左偏分布 D.右偏分布
24,某大学经济管理学院有 1200 名学生,法学院有 800 名学生,医学院有 320 名学生,理
学院有 200 学生。在上面的描述中,众数是( )
A.1200
B.经济管理学院
C.200
D.理学院
A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 15、如果一组数据不是对称分布的,根据切比雪夫不等式,对于 k=2,其意义是 ()
A.至少有 75%的数据落在平均数加减 2 个标准差的范围之内
B.至少有 89%的数据落在平均数加减 2 个标准差的范围之内
C. 至少有 94%的数据落在平均数加减 2 个标准差的范围之内 D. 至少有 99%的数据落在平均数加减 2 个标准差的范围之内
考试分数的下四分位数和上四分位数分别为(
)
A.64.5 和 78.5
B.67.5 和 71.5
C.64.5 和 71.5
D.64.5 和 67.5
28.假定一个样本由 5 个数据组成:3,7,8,9,13,该样本的方差为( )
A.8
B.13
C.9.7
D.ห้องสมุดไป่ตู้0.4
29.对于右偏分布,平均数、中位数和众数之间的关系是(
B.中位数 C. 四分位数 D.平均数
4、一组数据排序后处于 25%和 75%位置上的值称为( )
A.众数
B.中位数 C. 四分位数 D.平均数
5、非众数组的频数占总频数的比例称为( )
A.异众比率 B.离散系数 C.平均差 D.标准差
6、四分位差是( )
A.上四分位数减下四分位数的结果
B.下四分位数减下四分位数的结果
12、经验法则表明,当一组数据对称分布时,在平均数加减 1 个标准差的范围内 大约有( )
A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 13、经验法则表明,当一组数据对称分布时,在平均数加减 2 个标准差的范围内 大约有( )
A.68%的数据 B.95%的数据 C.99%的数据 D.100%的数据 14、经验法则表明,当一组数据对称分布时,在平均数加减 3 个标准差的范围内 大约有( )
10、如果一个数据的标准分数是-2,表明该数据( )
A.比平均数高出 2 个平均差 B.比平均数低 2 个标准差
C.等于 2 倍的平均数 D.等于 2 倍的标准差
11-15AABCA
11、如果一个数据的标准分数是 3,表明该数据( ) A.比平均数高出 3 个标准差 B. 比平均数低 3 个标准差 C.等于 3 倍的平均数 D.等于 3 倍的标准差
第四章
1、一组数据中出现频数最多的变量值称为( )
A.众数
B.中位数 C.四分位数 D.平均数
2、下列关于众数的叙述,不正确的是( )
A.一组数据可能存在多个众数 B.众数主要适用于分类数据
C.一组数据的众数是唯一的 D.众数不受极端值的影响
3、一组数据排序后处于中间位置上的变量值称为( )
A.众数
21-25 BAABB
21、如果一组数据分布的偏态系数在 0.5~1 或-1~-0.5 之间,则表明该组数据属
于( )
A.对称分布 B.中等偏态分布 C.高度偏态分布 D.轻微偏态分布
22、峰态通常是与标准正态分布相比较而言的。如果一组数据服从标准正态分布,
则峰态系数的值( )
A. 等于 0 B.等于 1 C.大于 0 D.大于 1
)
A.平均数>中位数>众数
B.中位数>平均数>众数
C. 众数>中位数>平均数
D.众数>平均数>中位数
30.在某行业中随机抽取 10 家企业,第一季度的利润额(万元)分别为:72,63.1,54.7,
