概率论第四章课后习题解答
概率论第四章习题解答

1第四章随机变量的数字特征I 教学基本要求1、理解随机变量的数学期望与方差的概念,掌握它们的性质与计算,会求随机变量函数的数学期望;2、掌握两点分布、二项分布、泊松分布、均匀分布、指数分布、正态分布的数学期望与方差;3、了解切比雪夫不等式及应用;4、掌握协方差、相关系数的概念与性质,了解矩和协方差矩阵的概念;5、了解伯努利大数定理、切比雪夫大数定律、辛钦大数定理;6、了解林德伯格-列维中心极限定理、棣莫弗―拉普拉斯中心极限定理,掌握它们在实际问题中的应用.II 习题解答A 组1、离散型随机变量X 的概率分布为X -2 0 2 p0.400.300.30求()E X 、(35)E X +、2()E X ?解:()(2)0.4000.3020.300.2E X =-⨯+⨯+⨯=-;(35)3()5 4.4E X E X +=+=;2222()(2)0.4000.3020.30 1.8E X =-⨯+⨯+⨯=.2、某产品表面瑕疵点数服从参数0.8λ=的泊松分布,规定若瑕疵点数不超过1个为一等品,每个价值10元,多于4个为废品,不值钱,其它情况为二等品,每个价值8元求产品的平均价值?解:设X 为产品价格,则0X =、8、10.通过查泊松分布表可知其相应概率分布为X 0 8 10 p0.00140.80880.1898则()80.1898100.80889.61E X =⨯+⨯≈(元).3、设随机变量X 的分布函数为00()/40414x F x x x x ≤⎧⎪=<≤⎨⎪>⎩.求()E X ?解:由分布函数知X 的密度函数为1/404()0x f x <≤⎧=⎨⎩其它则4()()24x E X xf x dx dx +∞-∞===⎰⎰.4、设随机变量X 服从几何分布,即1()(1)k p X k p p -==-(1,2,)k = ,其中01p <<是常数.求()E X ?解:1111()(1)(1)k k k k E X kp p pk p +∞+∞--===-=-∑∑由级数2121123(1)k x x kx x -=+++++- (||1)x <,知 211()[1(1)]E X p p p =⨯=--.5、若随机变量X 服从参数为λ的泊松分布,即的泊松分布,即()!kp X k e k λλ-== (0,1,2,)k =求()E X 、2()E X ?解:1()!(1)!kk k k E X k ee ee k k λλλλλλλλλ-+∞+∞---======-∑∑;12201(1)()[]!(1)!!kk kk k k k k E X keee k k k λλλλλλλλ-+∞+∞+∞---===+===-∑∑∑1210[]()(1)!!k kk k e e e e k k λλλλλλλλλλλλ-+∞+∞--===+=+=+-∑∑. 6、某工程队完成某项工程的时间X (单位:月)服从下述分布X 10 11 12 13 p0.40.30.20.1(1) 求该工程队完成此项工程的平均时间;(2) 设该工程队获利50(13)Y X =-(万元).求平均利润? 解:(1)()100.4110.3120.2130.111E X =⨯+⨯+⨯+⨯=(月);(2) ()[50(13)]65050()100E Y E X E X =-=-⨯=(万元). 7、若随机变量X 服从区间[,]a b 上的均匀分布,即1()a x b f x b a ⎧≤≤⎪=-⎨⎪⎩其它求()E X 、2()E X ?解:()()2bax a b E X xf x dx dx b a +∞-∞+===-⎰⎰;22222()()3baxa ab b E X x f x dx dx b a +∞-∞++===-⎰⎰. 8、若随机变量X 服从参数为λ的指数分布,即的指数分布,即0()0x ex f x x λλ-⎧>=⎨≤⎩0求()E X 、2()E X ?解:0()()xxE X xf x dx x edxxdeλλλ+∞+∞+∞---∞===-⎰⎰⎰1xxxeedxλλλ+∞+∞--=-+=⎰;2222202()()2xxxE X x f x dxx edxx exedxλλλλλ+∞+∞+∞+∞----∞-∞===-+=⎰⎰⎰.9、离散型随机变量X 的概率分布为X 0 2 6 p3/12 4/12 5/12求()E X 、[ln(2)]E X +?解:34519()0261212126E X =⨯+⨯+⨯=;34513[ln(2)]ln(02)ln(22)ln(62)ln 21212126E X +=+⨯++⨯++⨯=.10、设2~(,)X N μσ,求(||)E X μ-?解:22()21(||)||2x E X x e dx μσμμπσ--+∞-∞-=-⎰令x t μσ-=,由偶函数性质有222022(||)()2t t E X e d μσσππ+∞--==⎰.11、设某商品需求量(10,30)X U ,销售商进货量n 在(10,30)之间,是一个整数.每销售一件商品获利500(元),若供小于求,每件产品亏损100(元).若供大于求,则从外地调运,每件商品可获利300(元).为使利润期望值不少于9280(元),进货量最少应为多少?解:按题意利润Y 与X 、n 的关系为500300()1030500100()1030n X n n X Y X n X X n +-≤<≤⎧=⎨--≤<≤⎩则利润平均值为10101()[[500100()][500300()]20n n E Y X n X dx n X n dx =--++-⎰⎰ 27.53505250n n =-++由题意知27.535052509280n n -++≥解得62263n ≤≤,则最少进货量为21.12、某保险公司规定,如果一年内顾客投保事件A 发生,则赔偿顾客a 元.以往资料表明事件A 发生的概率为p .为使公司收益期望值为0.1a ,则应向顾客收取都少保费?解:设应向顾客收取x 元保费,公司的收益为Y 元则Yx x a - p1p -p按题意()(1)()0.1E Y x p x a p a =-+-= 解得0.1x ap a =+.13、设随机变量X 的密度函数为1cos0()220x x f x π⎧≤≤⎪=⎨⎪⎩其它.对X 进行独立重复观测4次,Y 表示观测值大于/3π的次数,求2Y 的数学期望?解:显然~(4,)Y b p ,其中p 是(/3)X π>的概率,故31()cos 0.5322xp p Xdx πππ=>==⎰所以44()0.50.5kkkp Y k C -==⨯ (0,1,2,3,4)k =则有42244()0.50.55k kkk E Y k C -==⨯=∑.14、设随机变量X 、Y 相互独立,且都服从标准正态分布求22Z X Y =+的数学期望?解:由题意知X 、Y 的联合密度函数为2221(,)2x y f x y eπ+-=于是22222221()(,)2x y E Z x y f x y dxdy x y edxdy π++∞+∞+∞+∞--∞-∞-∞-∞=+=+⎰⎰⎰⎰令cos x r θ=、sin y r θ=得222222201()22r r E Z r e drd r e drππθπ+∞+∞--===⎰⎰⎰.15、已知(,)X Y 的分布如下,令max{,}Z X Y =,求()E Z ?YX0 5 10 15 0 0.02 0.06 0.02 0.10 5 0.04 0.15 0.20 0.10 100.010.150.140.01解:由题设可得Z 的分布为Z 0 510 15 p 0.020.25 0.52 0.21()00.0250.25100.52150.219.6E Z =⨯+⨯+⨯+⨯=.16、设(,)X Y 的联合密度函数为21201(,)0yy x f x y ⎧≤≤≤=⎨⎩其它求()E X 、()E Y 、()E XY 、22()E X Y +?解:12004()(,)125xE X xf x y dxdydx xy dy+∞+∞-∞-∞-∞===⎰⎰⎰⎰; 1303()(,)125x E Y yf x y dxdy dx y dy +∞+∞-∞-∞===⎰⎰⎰⎰;;131()(,)122xE XY xyf x y dxdy dx xy dy +∞+∞-∞-∞-∞===⎰⎰⎰⎰; 122222220016()()(,)()15xE XY xy f x y dxdydx xy y dy+∞+∞-∞-∞-∞+=+=+=⎰⎰⎰⎰. 17、设随机变量(,)X Y 的密度函数为1()02,02(,)8x y x y f x y ⎧+≤≤≤≤⎪=⎨⎪⎩其它求()E X ?解:22007()(,)()88xE X xf x y dxdyxy dxdy+∞+∞-∞-∞==+=⎰⎰⎰⎰. 18、甲乙二人相约在12:00~13:00之间会面,设X 、Y 分别表示甲乙到达时间,且相互独立已知X 、Y 的密度函数为2301()0x x f x ⎧<<=⎨⎩其它、201()0y y f y <<⎧=⎨⎩其它求先到达者需要等待时间的数学期望?解:等待时间可以表示为||X Y -,由于X 、Y 的联合密度函数为2601,01(,)0x y x y f x y ⎧<<<<=⎨⎩其它11200(||)||6E X Y x y x ydxdy ⇒-=-⎰⎰112200001()6()|64xyx y x ydydx y xx ydxdy =-+-=⎰⎰⎰⎰.19、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求数学期望()E X 、()E Y ?解:设(,)X Y 的联合密度函数为(,)(,)0(,)c x y G f x y x y G∈⎧=⎨∉⎩,由密度函数性质解出9/2c =下面分别求出边沿密度函数当12x -≤≤时,有22222()(2)99x X xf x dy x x +==+-⎰,故此 22(2)12()90X x x x f x ⎧+--≤≤⎪=⎨⎪⎩其它 当01y ≤≤时,有24()99y Y y f y dx y--==⎰当14y <≤时,有222()(2)99y Y y f y dx y y --==+-⎰,所以 40192()(2)1490Y y y f y y y y ⎧≤≤⎪⎪⎪=+-<≤⎨⎪⎪⎪⎩其它从而22121()()(2)92XE X xfx dx x x x dx +∞-∞--==+-=⎰⎰; 1401428()()(2)995Y E Y yf y dy y yd y y y dy +∞-∞-∞==++-=⎰⎰⎰. 20、离散型随机变量X 的概率分布为X -2 0 2 p0.40 0.30 0.30求()D X ?解:由题意易知()0.2E X =-、2() 1.8E X =,所以22()()[()] 1.80.04 1.76D X E X E X =-=-=.21、设随机变量X 的分布函数为00()/40414x F x x x x ≤⎧⎪=<≤⎨⎪>⎩.求()D X解:由题意易知X 的密度函数为1/404()0x f x <≤⎧=⎨⎩其它,且()2E X=,则242(2)4()(())()43x D X x E X f x dx dx +∞-∞-=-==⎰⎰. 22、若随机变量X 服从参数为λ的泊松分布,求()D X ? 解:由题意易知()E X λ=、22()E X λλ=+,故22()()[()]D X E X E X λ=-=.23、设随机变量(,)X Y 的密度函数为1()02,02(,)80x y x y f x y ⎧+≤≤≤≤⎪=⎨⎪⎩其它求()D X ?解:由题意易知7()8E X =,故2222001711()[()](,)()()8636D X x E X f x y dxdy x x y dxdy +∞+∞-∞-∞-∞=-=-+=⎰⎰⎰⎰. 24、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求方差()D X 、()D Y ?解:由题意易知22(2)12()90X x x x f x ⎧+--≤≤⎪=⎨⎪⎩其它、40192()(2)1490Y yy f y y y y ⎧≤≤⎪⎪=+-<≤⎨⎪⎪⎪⎩其它1()2E X =、8()5E Y =22222127()()(2)910X E X x f x dx x x x dx+∞-∞--==+-=⎰⎰14222214247()()(2)9914Y E Yy f y dyy ydyy y dy +∞-∞-∞==++-=⎰⎰⎰229()()[()]20D X E X E X =-=;22279()()[()]350D YE Y E Y =-=.25、设10只同种元件中由2只是坏的,装配仪器时,从中任取1只,如果是不合格品,则扔掉后重取1只,求取出合格品前取出次品数的方差?只,求取出合格品前取出次品数的方差?解:设X 表示取出合格品前已取出次品的数目,则X0 1 2 p8/10 16/90 2/90故2()9E X =、24()15E X =所以2288()()[()]405D XE X E X =-=.26、设随机变量X 的密度函数为||1()2x f x e -=.求()E X 、()D X ?解:||1()()02x E X xf x dx x e dx+∞+∞--∞-∞===⎰⎰; 222||2011()(())()222x xD XE X E X x f x dx x e dx x e dx +∞+∞+∞---∞-∞=-====⎰⎰⎰.27、设X 为随机变量,证明:对任意常数C ,有2()()D X E X C ≤-,当()C E X =时等号成立.证明:22222()(2)()2()E X C E X CX C E X CE X C -=-+=-+22222()[()]{[()]2())}()[()]E X E X E X CE X C D X E X C =-+-+=+-由于2[()]E X C -非负,从而有2()()D X E X C ≤-,且当()C E X =时2()()D X E X C =-.28、设U 服从(-2,2)上的均匀分布,定义X 、Y 如下1111U X U -<-⎧=⎨>-⎩、1111U Y U -<⎧=⎨>⎩求()D X Y +?解:先求X Y +的分布(2)(1,1)(1,1)(1)1/4p X Y p X Y p U U p U +=-==-=-=<-<=<-= (2)(1,1)(1,1)(1)1/4p X Y p X Y p U U p U +=====≥-≥=≥= (0)1(2)(2)1/2p X Y p X Y p X Y +==-+=-+=-=所以()0E X Y +=,从而2()()2D X Y E X Y +=+=.29、已知()750E X =、2()15D X =.请估计概率(700800)p X <<? 解:由切比雪夫不等式有2215(700800)(|750|50)10.9150p X p X <<=-<≥-≈.30、设()2E X =-、()1D X =、()2E Y =、()4D Y =、0.5XY ρ=-,利用由切比雪夫不等式估计概率(||6)p X Y +≥的上限?解:因为()0E X Y +=、()()()2(,)3D X Y D X D Y Cov X Y +=++=,所以,所以2()1(||6)(|()()|6)612D X Y p X Y p X YE X Y ++≥=+-+≥≤=. 31、设()4D X =、()9D Y =、0.5XY ρ=,求(23)D X Y -? 解:(,)()()3XY Cov X Y D X D Y ρ==(23)4()9()2(2,3)16813661D X Y D X D Y Cov X Y -=++-=+-=.32、设(,)X Y 的联合密度函数为21201(,)0yy x f x y ⎧≤≤≤=⎨⎩其它求(,)Cov X Y ?解:由题意易知4()5E X =、3()5E Y =、1()2E XY =,故 1431(,)()()()25550Cov X Y E XY E X E Y ⨯=-=-=⨯. 33、设二维随机变量(,)X Y 在曲线2y x =、2y x =+所围区域G 内服从均匀分布,内服从均匀分布,求求协方差(,)Cov X Y 与相关系数XY ρ?解:由题意易知1()2E X =、8()5E Y =、9()20D X =、279()350D Y =2221225()994x x G E XY xy dxdy xdx ydy +-===⎰⎰⎰⎰所以9(,)()()()20Cov X Y E XY E X E Y =-=; (,)0.751()()XYCov X Y D X D Y ρ=≈.34、设二维随机变量(,)X Y 的联合分布为YX-1 0 1 00.07 0.18 0.15 100.080.320.20求22(,)Cov X Y解:先求2X 、2Y 、22X Y 的分布2(0)0.4p X ==、2(1)0.6p X == 2(0)0.5p Y ==、2(1)0.5p Y == 22(0)0.72p X Y ==、22(1)0.28p X Y ==所以2()0.6E X =、2()0.5E Y =、22()0.28E X Y =,由此得222222(,)()()()0.02Cov X Y E X Y E X E Y =-=-.35、随机变量(,)X Y 的密度函数为201,11(,)0x x y f x y ≤≤-≤≤⎧=⎨⎩其它求()D X Y +?解:当01x <<时,有11()22X x f x d y x -==⎰;当01y <<时,有11()22Y y f y d x y -==⎰,故2()()3E X E Y ==、1()()18D X D Y == 由于(,)()()X Y f x y f x f y ≠,即X 与Y 不独立.所以11015()212xE XY xydxdy -==⎰⎰541(,)()()()12936Cov X Y E XY E X E Y =-=-=- 1()()()2ov(,)18D X Y D X D Y C X Y +=++=.36、将1枚硬币抛n 次,以X 、Y 分别表示正面向上与反面向上的次数,求(,)Cov X Y 、XY ρ解:由于X Y n+=,即Y n X=-,于是1XYρ=-;又因~(,0.5)X b n 、~(,,0.5)Y b n ,所以()()/4D X D Y n ==,故(,)(,)(,)()/4Cov X Y Cov X n X Cov X X D X n =-=-==.37、设X 与Y 独立,且都服从参数为λ的泊松分布,令2U X Y =+、2V X Y =-求U 与V 的相关系数?解:由于()(2)4()()5D U D X Y D X D Y λ=+=+= ()(2)4()()5D V D X Y D X D Y λ=-=+=所以(,)(2,2)Cov U V Cov X Y X Y =+-4()(,2)(2,)()3D X Cov Y X Cov X Y D Y λ=+--=由此得(,)35(),()XYCov X Y D X D Y ρ==. 38、设二维随机变量(,)X Y 的联合密度函数为1||0,01(,)0y x f x y <<<⎧=⎨⎩其它判断X 与Y 之间的相关性与独立性.解:由于12()3x xE X xdydx -==⎰⎰、、10()0x xE Y ydydx -==⎰⎰、10()0xxE XY xydydx -==⎰⎰,则(,)()()()0Cov X Y E X E Y E XY =-=故X 与Y 之间不相关;又因当01x <<时,有()2xXxf x dy x-==⎰,即201()0X x x f x <<⎧=⎨⎩其它同理可以求出110()1010X y y f x y y +-<<⎧⎪=-<<⎨⎪⎩其它由于(,)()()X Y f x y f x f y ≠,故X 与Y 之间不独立.39、设a 为区间(0,1)上一定点,随机变量(0,1)X U ,Y 是X 到a 的距离.问a 为何值时X 与Y 是不相关?解:由题设知()0.5E X =、||Y X a =-,所以11201()||()()2aaE Y x a dx a x dx x a dx a a =-=-+-=-+⎰⎰⎰3101()()()323a a a a E XY x a x dx x x a dx =-+-=-+⎰⎰31(,)3212a aCov X Y =-+令31(,)03212a a Cov X Y =-+=,可得方程2(21)(221)0a a a ---=在(0,1)内解得0.5a =,即0.5a =时,X 与Y 不相关. 40、设计算器进行加法计算时,所有舍入误差相互独立且在(0.5,0.5)-上服从均匀分布.(1) 将1500个数相加,问误差总和的绝对值超过15的概率是多少;(2) 最多可以有几个数相加,其误差总和的绝对值小于10的概率不小于0.90? 解:设第i 个数的舍入误差为i X (1,,)i n = ,故()0i E X =、()1/12i D X = (1,,)i n =记1ni i X X ==∑(1) 由林德伯格-列维中心极限定理有15001150001515000(||15)(||)15001/1215001/12i i x p X p =-⨯-⨯>=>∑151[2()1]0.180215001/12≈-Φ-=;(2) 由林德伯格-列维中心极限定理有1100100.90(||10)(||)2()11/121/121/12ni i x n n p X p n n n =-⨯-⨯≤<=≤≈Φ-∑即10()0.951/12n Φ≥,由于(1.645)0.95Φ=,则101.6451/12n ≥因此443.45n £,再由n 为整数得满足题意的个数为443.41、一批木材中有80%的长度不小于3m ,从中任取100根,求其中至少有30根长度短于3m 的概率?解:以X 表示100根木材中长度短于3m 的数目,则~(100,0.2)X b ,于是()20E X =,()16D X =.由于100n =较大,则由中心极限定理,近似有2~(20,4)X N ,由此有20302010(30)1(30)1()1()0.0062444X p X p X p --≥=-<=-<≈-Φ-=. 42、某商店出售价格分别为1(元)、1.2(元)、1.5(元)的3种蛋糕,种蛋糕,每种蛋糕被购买的概每种蛋糕被购买的概率分别为0.3、0.2、0.5.若某天售出300只蛋糕,(1) 求这天收入为400(元)的概率;(2) 求这天售出价格为1.2(元)蛋糕多于60只的概率?解:(1) 设第i 只蛋糕价格为iX (1,,300)i = .则i X的分布为i X1 1.2 1.5 p0.30.20.5于是可得() 1.29i E X =、2() 1.713iE X =、()0.0489i D X =令3001i i X X ==∑表示总收入,则由林德伯格-列维中心极限定理有300 1.29400300 1.29(400)()1(3.39)0.00033000.04893000.0489X p X p -⨯-⨯≥=>≈-Φ=⨯⨯;(2) 记Y 为300只蛋糕中售价为1.2(元)的蛋糕数目,则~(300,0.2)Y b ,于是()60E Y =、()48D Y =,由中心极限定理,近似有~(60,48)X N ,由此有606060(60)1()1(0)0.54848Y p Y p --≥=-<≈-Φ=.43、进行独立重复试验,每次试验中事件A 发生的概率为0.25.问能以95%的把握保证1000次试验中事件A 发生的频率与概率相差多少?此时A 发生的次数在什么范围内?解:设X 为1000次试验中事件A 发生的次数,则~(1000,0.25)X b ,由二项分布的性质知()250E X =、()187.5D X =,而事件A 发生的频率为/1000X .根据题意,可得如下不等式(|0.25|)0.951000X p ε-≤≥即(|250|1000)0.95p X ε-≤≥,由棣莫弗―拉普拉斯定理有25010001000(||)2()10.95187.5187.5187.5X p εε-≤≈Φ-≥即1000()0.975(1.96)187.5εΦ≥=Φ解得0.026ε³,这表明1000次试验中事件A 发生的频率与概率相差不超过0.026,相应的有1000次试验中事件A 发生的次数在224到276之间.44、某车间有同型号车床150台,在1小时内每台车床约有60%的时间在工作.假定各车床工作相互独立,工作时每台车床要消耗电能15kw.问至少要多少电能,才可以有99.5%的可能性保证此车间正常工作?解:以X 表示同时工作的车床数,则~(150,0.6)X b ,于是()90E X =、()36D X =,由题意知x 应使得下式成立(0)0.995p X x ≤≤≥由中心极限定理,近似有~(90,36)X N ,故有090909090(0)()()(15)0.9956666X x x p X x p ----≤≤=<<≈Φ-Φ-≥ 查标准正态分布表得90 2.586x -≥,即105.28x ≥,取整得106x =.故要保证车间有99.5%的可能性正常工作,需供电能151061590⨯=()kw .B 组1、将n 只球(1n 号)随机的装入n 只盒子(1n 号),一只盒子装一只球.若一只球装入的盒子与球同号,称为一个配对.记X 为配对数,求()D X ?解:引入随机变量i X (1,)i n = ,1i X =表示第i 号配对,0i X =表示第i 号不配对,则1n X X X =++ ,且1(1)i p X n ==(1,)i n = 即1()i E X n = (1,)i n =于是1()()1n E X E X X =++=因为i X 之间不独立,所以11111()()2(,)nn ni i i i j ii ij D X D X Cov X X -=====+∑∑∑∑下面考虑i j X X 的分布,由于i j X X 的取值只能是0、1,且1(1)(1,1)(1)i j i j p X X p X X n n =====- 所以1()(1)i j E X X n n =-,因此 21()()()()(1)i j i j i j Cov X X E X X E X E X n n =-=- 2211()21(1)nn D X Cnn n -⇒=+=-.2、设随机变量X 的分布函数为()F x ,其数学期望存在,证明()[1()]()E X F x dx F x dx +∞-∞=--⎰⎰.证明:00()()()()E X xf x dxxf x dxxf x dx +∞+∞-∞-∞==-⎰⎰⎰由于00()()()xxf x dxxdy f x dx +∞-∞=-⎰⎰⎰改变积分次序有00()(())()yxf x dxf x dx dyF y dy +∞-∞-∞-∞=-=-⎰⎰⎰⎰同理有()[1()]xf x dx F y dy +∞+∞=-⎰⎰ 0()[1()]()E X F x dxF x dx +∞-∞⇒=--⎰⎰.3、设随机变量X 的分布函数为0111()arcsin 11211x F x x x x π⎧<-⎪⎪=+-≤<⎨≥⎪⎩求()E X ?解:由上一题结论有()[1()]()E X F x dxF x dx +∞-∞=--⎰⎰111111[1arcsin ](arcsin )022x dx x dx ππ--=---+=⎰⎰.4、设连续随机变量X 的密度函数为()f x 若对任意常数c 有()()f c x f c x +=- (0)x >且()E X 存在.证明()E X c =.证明:令x t c =-则有()()()()()()E X xf x dxc t f c t dtcf c t dttf c t dt +∞+∞+∞+∞-∞-∞-∞-∞==++=+++⎰⎰⎰⎰由密度函数性质有()()cf c t dt cf c t dt c +∞+∞-∞-∞+=+=⎰⎰令u t =-,有()()()()tf c t dttf c t dtuf c u duuf c u du +∞+∞-∞-∞+=-=+=-+⎰⎰⎰⎰故()0tf c t dt +∞-∞+=⎰所以()E X c =.5、证明事件A 在一次试验中发生次数的方差不超过0.25.证明:设X 表示事件A 在一次试验中发生的次数,则(1,)X b p ,其中p 是事件A 发生的概率,则()(1)0D X p p =-≥由均值不等式得,当0.5p =时,()D X 有最大值0.25. 6、设随机变量X 服从几何分布,即1()(1)k p X k p p -==-(1,2,)k = ,其中01p <<是常数.求()D X解:1111()(1)(1)k k k k E X kp p p k p +∞+∞--===-=-∑∑由级数2121123(1)k x x kx x -=+++++- (||1)x <,知211()[1(1)]E X p p p =⨯=--又111[(1)](1)()(1)(1)k k k E X Xk k p Xk pk k p +∞+∞-==+=+==+-∑∑将21(1)x -的展开式两端求导得 1321223(1)(1)k x k kx x -=⋅+⋅++-+- 3222[(1)][1(1)]E X X pp p ⇒+==--222()()[()][(1)][()]D X E X E X E X X X E X ⇒=-=+-- 221[(1)]()[()]p E X X E X E X p-=+--=. 7、一只昆虫所生虫卵X 服从参数为λ的泊松分布,而每个虫卵发育成幼虫的概率为p ,且每个虫卵是否发育成幼虫相互独立,求一只昆虫所生幼虫数Y 的期望与方差?解:由题意知()!np X n en λλ-==(0,1,2,)λ= ,而n 个虫卵发育成k ()k n ≤个幼虫的概率为(|)(1)k kn knp Y k X n C p p -===- (0,1,,)k n =由全概率公式,对任意0,1,,k n = 有()()(|)(1)!nkkn kn n k n k p Y k p X n p Y k X n e C p p n λλ+∞+∞--========-∑∑(1)()[(1)]()()!()!!!k n kk kp pn k p p p p e e e e k n k k k λλλλλλλλ-+∞----=-===-∑即Y服从参数为pλ的泊松分布所以()()E Y D Y p λ==.8、设随机变量X 的密度函数()f x 是偶函数,且2(||)E X <+∞,证明X 与2X 不相关,但不独立.证明:因()f x 是偶函数,所以()xf x 、3()x f x 是奇函数,故此3()()0E X E X ==222(,)()()()0Cov X X E X X E X E X ⇒=⋅-=因而,X 与2X 不相关;选取0a >使得()1p X a ≤<,考察如下特定事件概率22(,)()()()p X a X a p a X a p X a p a X a ≤≤=-≤≤>≤-≤≤ 22()()p X a p X a =≤≤即2222(,)()()p X a X a p X a p X a ≤≤≠≤≤ 故X 与2X 不独立.9、设1X 、…、n X 中任意两个的相关系数都是ρ,试证:11n ρ≥--. 证明:因为111110()()2(,)nnni iiiji i i j D X D X Cov X X-====≤=+∑∑∑∑1111()2()()nni i i j i ij D X D X D X ρ-====+∑∑∑11111()[()()]()[1(1)]n ni ni i j i i i j i D X D X D X D X n ρρ-====≤++=+-∑∑∑∑11n ρ⇒≥--.。
概率论习题及解答-第四章特征函数

ξ = a min{Y, x} − bx.
从而平均利润
∫∞ E(ξ) = aE(min{Y, x}) − bx = a min{y, x}λe−λydy − bx
(∫ x
∫∞ 0
)
=a
yλe−λydy +
xλe−λydy − bx
(0
∫x x
)
= a − xe−λx + e−λydy + xe−λx − bx
∑ ∞
∑ ∞ ∑i
E(η) = iP(η = i) =
P(η = i)
i=1
i=1 k=1
∑ ∞ ∑ ∞
∑ ∞
=
P(η = i) = P(η k).
注意到
P(min{ξ1, ξ2, · · · , ξn}
k=1 i=k
k) = P(ξ1 k, ξ2
k=1
k, · · · , ξn
( ∑ )n
k) =
记 µk = p0 + p1 + · · · + pk−1, νk = 1 − µk, 试证明
∑ ∞ E(min{ξ1, ξ2, · · · , ξn}) = νkn,
k=1
∑ ∞ E(max(ξ1, ξ2, · · · , ξn)) = (1 − µnk ).
k=1
4
证明: 若 η 为取非负整值随机变量, 则
得
∑ ∞
∑ ∞
E(max{ξ1, ξ2, · · · , ξn}) = P(max{ξ1, ξ2, · · · , ξn} k) = (1 − µnk ).
k=1
k=1
练习4.1.11 设随机变量 ξ, η 独立同分布, ξ ∼ N (a, σ2), 试证明
概率论第四章 习题答案

1 ⎛2⎞ 1 DX = EX − ( EX ) = − ⎜ ⎟ = . 2 ⎝ 3 ⎠ 18 1 2 DZ = 4 DX = 4 × = . 18 9
【解毕】
9.在一次拍卖中,两人竞买一幅名画,拍卖以暗标的形式进行,并以最高价成交.设两人 的出价相互独立且均服从(1,2)上的均匀分布,求这幅画的期望成交价. 解:设两人的出价分别为随机变量 X , Y ,则这幅画的期望成交价为 Z = max { X , Y } 由题意知, X 与Y 独立,且 X ∼ U (1, 2); Y ∼ U (1, 2) 先求 Z 的分布函数 当 1 < z < 2 时, F ( z ) = P ( Z £ z ) = P (max { X , Y } £ z ) = P ( X £ z ,Y £ z )
= P( X £ z ) P (Y £ z ) = ( z -1)2
当 z £ 1 时, F ( z ) = 0 ;当 z ³ 2 时, F ( z ) = 1 于是 Z 的密度函数为 f ( z ) = ï í
ì2( z -1),1 < z < 2 ï ï 0, 其它 ï î 5 3
EZ = ò
+¥
3 X .求: ( 1)常数 a, b, c; (2) Ee . 4
【解】 (1)由概率密度的性质知,有
+∞ 2 4
1=
又因为
−∞
∫
f ( x )dx = ∫ axdx + ∫ ( cx + b )dx = 2a + 6c + 2b.
0 2
+∞
2
4
2 = EX =
−∞
∫ xf ( x )dx = ∫ xiaxdx + ∫ x ( cx + b )dx
《概率论与数理统计》第04章习题解答

第四章 正态分布1、解:(0,1)ZN(1){ 1.24}(1.24)0.8925P Z ∴≤=Φ={1.24 2.37}(2.37)(1.24)0.99110.89250.0986P Z <≤=Φ-Φ==-= {2.37 1.24}( 1.24)( 2.37)(1.24)(2.37)0.89250.99110.0986P Z -<≤-=Φ--Φ-=-Φ+Φ=-+=(2){}0.9147()0.9147 1.37{}0.05261()0.0526()0.9474 1.62P Z a a a P Z b b b b ≤=∴Φ==≥=-Φ=Φ==,,得,,,得2、解:(3,16)XN8343{48}()()(1.25)(0.25)0.89440.59870.295744P X --∴<≤=Φ-Φ=Φ-Φ=-= 5303{05}()()(0.5)(0.75)44(0.5)1(0.75)0.691510.77340.4649P X --<≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 31(25,36){25}0.95442(3,4){}0.95X N C P X C X N C P X C -≤=>≥、()设,试确定,使;()设,试确定,使解:(1)(25,36){25}0.9544X N P X C -≤=,{2525}0.9544P C X C ∴-≤≤+=25252525()()0.954466()()2()10.9544666()0.9772,21266C C C C CC CC +---Φ-Φ=-Φ-Φ=Φ-=Φ=∴==即, (2)(3,4){}0.95XN P X C >≥,331()0.95()0.952231.6450.292C CCC ---Φ≥Φ≥-≥≤-即,,4、解:(1)2(3315,575)XN4390.2533152584.753315{2584.754390.25}()()575575(1.87)( 1.27)(1.87)1(1.27)0.969310.89800.8673P X --∴≤≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= (2)27193315{2719}()( 1.04)1(1.04)10.85080.1492575P X -≤=Φ=Φ-=-Φ=-=(25,0.1492)YB ∴4440{4}(0.1492)(10.1492)0.6664ii i i P Y C -=∴≤=-=∑5、解:(6.4,2.3)X N{}{}1()81(1.055)10.85540.14462.3(85}0.17615 6.451(0.923)(0.923)0.82121()2.3P X P X X P X -Φ>-Φ-∴>>======->-Φ-Φ-Φ6、解:(1)2(11.9,(0.2))XN12.311.911.711.9{11.712.3}()()(2)(1)(2)1(1)0.20.20.977210.84130.8185P X --∴<<=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 设A ={两只电阻器的电阻值都在欧和欧之间} 则2()(0.8185)0.6699P A ==(2)设X , Y 分别是两只电阻器的电阻值,则22(11.9,(0.2))(11.9,(0.2))X N Y N ,,且X , Y 相互独立[]22212.411.9{(12.4)(12.4)}1{12.4}{12.4)}1()0.21(2.5)1(0.9938)0.0124P X Y P X P Y -⎡⎤∴>>=-≤⋅≤=-Φ⎢⎥⎣⎦=-Φ=-=7、一工厂生产的某种元件的寿命X (以小时计)服从均值160μ=,均方差为的正态分布,若要求{120200}0.80P X <<≥,允许最大为多少解:因为2(160,)XN σ由2001601201600.80{120200}()()P X σσ--≤<<=Φ-Φ从而 40402()10.80()0.9σσΦ-≥Φ≥,即,查表得401.282σ≥,故σ≤8、解:(1)2(90,(0.5))XN8990{89}()(2)1(2)10.97720.02280.5P X -∴<=Φ=Φ-=-Φ=-= (2)设2(,(0.5))X N d由808080{80}0.991()0.99()0.99 2.330.50.50.5d d d P X ---≥≥∴-Φ≥Φ≥≥,,,即 从而d ≥ 9、解:22~(150,3),~(100,4)X Y X N Y N 与相互独立,且则(1)2221~(150(100,3)4)(250,5)W X Y N N =+++=()222222~2150100,(2)314(200,52)W X Y N N =+-⨯+-⨯+⨯=-22325~(125,)(125,(2.5))22X Y W N N +== (2)242.6250{242.6}()( 1.48)1(1.48)10.93060.06945P X Y -+<=Φ=Φ-=-Φ=-= 12551255125522212551251255125()1()(2)1(2)2.5 2.522(2)220.97720.0456X Y X Y X Y P P P ⎧+⎫++⎧⎫⎧⎫->=<-+>+⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭--+-=Φ+-Φ=Φ-+-Φ=-Φ=-⨯=10、解:(1)22~(10,(0.2)),~(10.5,(0.2))X N Y N X Y ,且与相互独立22~(0.5,2(0.2))(0.5,(0.282))X Y N N ∴--⨯=-0(0.5){0}()(1.77)0.96160.282P X Y ---<=Φ=Φ=(2)22~(10,(0.2)),~(10.5,)X N Y N X Y σ设,且与相互独立222~(0.5,2(0.2))(0.5,(0.2))X Y N N σ∴--⨯=-+0.90{0}P X Y ≤-<=Φ=Φ由1.28≥,故σ≤11、设某地区女子的身高(以m 计)2(1.63,(0.025))WN ,男子身高(以m 计)2(1.73,(0.05))MN ,设各人身高相互独立。
概率论第四、五章课后习题答案

第四章 随机变量的数字特征2.某产品的次品率为0.1,检验员每天检验4次,每次随机地取10件产品进行检验,如发现其中的次品数多于1,就去调整设备。
以X 表示一天中调整设备的次数,试求E (X )。
(设诸产品是否为次品是相互独立的。
)解:先求检验一次,决定需要调整设备的概率。
设抽检出次品件数为Y ,则Y ~b (10,0.1).记需调整设备一次的概率为p ,则2639.01.09.01109.01}1{}0{1)1(910=⨯⨯⎪⎪⎭⎫ ⎝⎛--==-=-=>=Y P Y P Y P p 又因各次检验结果相互独立,故)2639.0,4(~b X X 的分布律为于是0556.12639.0444)1(43)1(62)1(41)(43223=⨯==⨯+-⨯+-⨯+-⨯=p pp p p p p p X E以后将会知道若X ~b (n ,p ),则np X E =)(.6.(1)设随机变量X 的分布律为求)53(),(),(22+XE X E X E(2)设)(~λπX ,求)11(+X E解:(1)E (X )=(-2)⨯0.4+0⨯0.3+2⨯0.3=-0.2 由关于随机变量函数的数学期望的定理,知E (X 2)=(-2)2⨯0.4+02⨯0.3+22⨯0.3=2.8E (3X 2+5)=[3⨯ (-2)2+5]⨯0.4+[3⨯ 02+5]⨯0.3+[3⨯22+5]⨯0.3=13.4如利用数学期望的性质,则有E (3X 2+5)=3E (X 2)+5=3⨯2.8+5=13.4(2)因)(~λπX ,故!}{k ek X P k λλ-==)1(1)1()1!(!)!1()!1(}{11)11(1100λλλλλλλλλλλλλλλλ--∞=-∞=-∞=+-∞=-∞=-=-=-==+=+==+=+∑∑∑∑∑eeej ej ek ek ek X P k X E j jj jk k k k k7. (1)设随机变量X 的概率密度为⎩⎨⎧≤>=-0,00,)(x x e x f x求(I)Y =2X ;(II) Y =e -2X 的数学期望(2)设随机变量n X X X ,,2,1 相互独立,且都服从(0,1)上的均匀分布,(I)求},,max{2,1n X X X U =的数学期望;(II)求},,min{2,1n X X X V =的数学期望。
概率论与数理统计(第三版)第四章课后答案

第四章数字待征4・1 解:£(X) = Vx p ;=iE (门=2>少产09I•.甲机床生产的零件茨品数多于乙机床生产蹒件次融,又•.•两硼床的^的产量相同 ••.乙机床生产的豹的质量较好.4・2解;X 的所有可能取值为:3, 4, 5E(X) = Vxp. =3x0・l + 4x0.3 + 5x0.6 =4.5P{X= 5}=fl0.6尸心3}=P{X = 4} =00$T =0001*OOS-粹(000—畔1-了 +呻i =ooor z OOH护(x)/J =(y)jL l = £Oxt = ^ = CY)y (LO £)&-/!«审伽里必坊叱也範銮黔砲OK申站尋卄d .[(d_DT】= 二Y = — = ^-i)^Z= d^Z = Cr)j……£ = [ = “¥«_【対={—汕4.10裁见课本后面231页参考答秦心腿抿題1泊: 4.11解:设i酒为“,方差为(J:,则X~N( UP(A F>96)=1-P(X<96)= 1-P( )所以酸在60到84的抚率为P(60 S X S 84) = P(竺丄 < 丄上12 a4151)=20(1)-1-2x0.8413 ・1=0.68264.!2E(X 2) = OxO4+l :xO.3 + 22xO2+3:xO 1 = 2£(5X 2 + 4) = 4x0.4+(5xl 2 + 4)x0.3 + (5x22 + 4)x0 2+(5x3:+ 4)x0.1 = 14EQ ・)=£(2X) = F 2xe^dx =£( V) = H V |: + 不呦4.13 H :=2(-厂)|; = 24 15聲看课本后面231页答案E(T) = E(<?4) = {「Q-3x4.14 H: r = —3设球的肓径为x 则:/(x) = ^-a■a<x<b其它4^Xi够胡_子)胡尹兄◎挣牛在 夕卜吕(》如4.16 解:仁(x)=匸/(〔>)4 = f. 12yd> = 4xf (v)=匸fg)e=j l lydx=12y -12y3£W =匸/「(X)•曲叮 4.X逐 WE(T)=匸/ (x) ydy = [ 12y -12y*d> = |E(AT)= [f f(x,y)xydxdy = [f 12xy dxdy = ' 12xtic =0<><xS 03 0 2E(X、心(环讼諒4.&=|£(丫)=匚/())y0 = fl2y°-12ydy =;4"解•.X与Y相互独立,■• •EQT) = E(X)E(D = f 疋还f〉/迪.二(扌斗:)J; "(4)°JO= jx(一“i|;+J;/•⑥)=亍[5 + (r 灯)卩彳x(5+l) = 44.18, 4.19, 4・20势看课本后面231, 232页答秦• 9•4上设X表示10颗骰子皈的点数之和,X (心1丄…10)表示第:颗般子出现的点«,则X^X:,且X\,X“・X*是*1独立同分布的,又E(A;)=1X1+2X1+...+6X1=A1o o 6 610 10 九^£(A^ = £(yXJ = X£W = 1Ox^ = 35MI Z64.22爹看课本后面232页答案4.23 E(X\ = OxO4 + l2xO.3 + 22xO2+35xO 1 = 2D(X)= £(X:)-[£(X)]2 =2-l2=l£(F2)=O X O.3+12X O5+22X O.2+32X O=1.3z)(y)=£(r2)-[£(r)j2=1.3-0.^ =0.49 4.24E(X:)叮斗皿+胆毎存*卜护+护|;十¥ = ¥DW = E(X:) - [E(X)f =y-4 = |Var(X) = E(X:)-[E(X)f =[我[[加r],0 其它-1 < > < 1 其它4.25Zr(x) = {呼—0 其它二扌-1<X<10其它w •计 m 吏支ue >n ¥x =p > “轻H£5>^V 3«20)P A#・0Z —X GUNbl -%十»・x )4+・:+(E 4.+c r )4MKs s(T )Q +(电Q «(W+...+W +WQ »§(小)2•士小 N+示)3 Hf …咅麗&。
概率论与数理统计》课后习题答案第四章

习题4.11.设10个零件中有3个不合格. 现任取一个使用,若取到不合格品,则丢弃重新抽取一个,试求取到合格品之前取出的不合格品数X 的数学期望.解 可得X 的概率分布为0123~77711030120120X ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为7771()012310301201204531208E X =⨯+⨯+⨯+⨯==2..某人有n 把外形相似的钥匙,其中只有1把能打开房门,但他不知道是哪一把,只好逐把试开.求此人直至将门打开所需的试开次数X 的数学期望.解 可得X 的概率分布为12~111n X nn n ⎡⎤⎢⎥⎢⎥⎣⎦于是X 的数学期望为111()121(1)122E X n n n nn n n n =⨯+⨯++⨯++==3.设5次重复独立试验中每次试验的成功率为0.9,若记失败次数为X ,求X 的数学期望。
解 由题意~(5,0.1)X B ,则X 的数学期望为 ()50.10.E X =⨯= 4.设某地每年因交通事故死亡的人数服从泊松分布.据统计,在一年中因交通事故死亡一人的概率是死亡两人的概率的21,求该地每年因交通事故死亡的平均人数。
解 设该地每年因交通事故死亡的人数为X ,由题意X 服从泊松分布() (0)P λλ>.因1{1}{2}2P X P X === 即121 41!22!ee λλλλλ--=⇒= 于是X 的数学期望为()4E X λ== 所以地每年因交通事故死亡的平均人数为4人。
5.设随机变量X 在区间(1,7)上服从均匀分布,求2{()}P X E X <. 解 因X 在区间(1,7)上服从均匀分布,故X 的数学期望为17()42E X +== 于是22{()}{4}1 {22}6P X E X P X P X <=<=<-<<=6.设连续型随机变量X 的概率密度为01() (,0)0 b ax x p x a b ⎧<<=>⎨⎩其它又知()0.75E X =,求,a b 的值解 由密度函数的性质可得()1p x dx +∞-∞=⎰即1111b aax dx b =⇒=+⎰又由()0.75E X =,可得1()0.75b xp x dx x ax dx +∞-∞=⋅=⎰⎰即0.752ab =+ 求解110.752ab a b ⎧=⎪⎪+⎨⎪=⎪+⎩可得 3,2a b ==.7.设随机变量X 的概率密度为0<1()2 120 x x p x x x <⎧⎪=-≤<⎨⎪⎩其它求数学期望()E X解1201331221()() (2) ()133E X xp x dxx xdx x x dx x x x +∞-∞==⋅+⋅-=+-=⎰⎰⎰8.设随机变量X 的概率分布为X -2 -1 0 1 P 0.2 0.3 0.1 0.4 求 (1)(21)E X -;(2)2()E X .解 (1) (21)2()1E X E X -=- 其中()20.210.3010.40.3E X =-⨯-⨯++⨯=-则(21)2()12(0.3)1 1.6E X E X -=-=⨯--=-(2)22222()0.2(2)0.3(1)0.100.41 1.5E X =⨯-+⨯-+⨯+⨯=9.假设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作。
概率论第四章习题解答
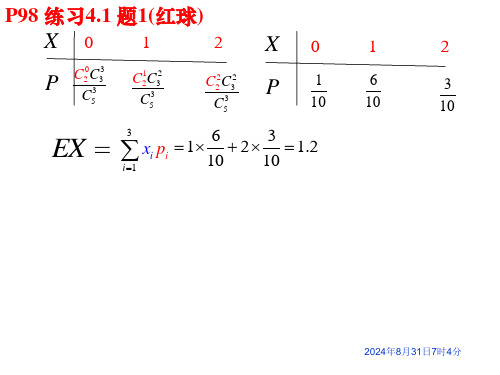
X9
EX 9
9
9
8 9
20
2024年8月31日7时4分
P104 练习4.2 题1 SD 1
1,1
f XY
x,
y
1 0
0 x 1, x y x 其它
yx
DZ D2X 1 4DX
EX xf x, ydxdy
0D
y x 1
1 0
x x
xdy
dx
1 2x2dx 2
P113 习题四 一 填空题 7 X与Y相互独立
f
X
x
2x
0
0
x 其它
1,fY
y
x y t
FT t PT t P X Y t fXY x, y dxdy
x yt
1当t 0时:FT t 0dxdy 0
0
x yt
2 当0 t时:FT
t
t
dx
tx 25e5x5 ydy
0
0
1 e5t 5te5t
t,0
x
FT
t
1
e5t
0
5te5t
t0 t0
33
2 EX 2
xi2 pij
i1 j1
20.1 30.3 30.1 2
33
3 EY 2
yi2 pij
12 0.212 0.112 0.1 22 0.1
22 0.132 0.332 0.1 4.8
i1 j1
12 0.2 12 0.1 12 0.1
12 0.1 12 0.1 0.6
2024年8月31日7时4分
P100 练习4.1 题12
2
f XY
x,
y
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论第四章习题解答1(1)在下列句子中随机地取一个单词,以X 表示取到的单词所饮食的字母个数,写出X 的分布律并求数学期望()E X 。
“THE GIRL PUT ON HER BEAUTIFUL RED HAT ” (2)在上述句子的30个字母中随机地取一个字母,以Y 表示取到的字母所在单词所包含的字母数,写出Y 的分布律并求()E Y(3)一人掷骰子,如得6点则掷第二次,此时得分为6加第二次得到的点数;否则得分为第一次得到的点数,且不能再掷,求得分X 的分布律。
解 (1)在所给的句子中任取一个单词,则其所包含的字母数,即随机变量X 的取值为:2,3,4,9,其分布律为所以 151115()234988884E X =⨯+⨯+⨯+⨯=。
(2)因为Y 的取值为2,3,4,9当2Y =时,包含的字母为“O ”,“N ”,故121{2}3015C P Y ===; 当3Y =时,包含的3个字母的单词共有5个,故135151{3}30302C P Y ==== 当4Y =时,包含的4个字母的单词只有1个,故1442{4}303015C P Y ==== 当9Y =时,包含的9个字母的单词只有1个,故 993{9}303010P Y ====112314673()234915215103015E Y =⨯+⨯+⨯+⨯==。
(3)若第一次得到6点,则可以掷第二次,那么他的得分为:X =7,8,9,10,11,12;若第一次得到的不是6点,则他的得分为1,2,3,4,5。
由此得X 的取值为: 1,2,3,4,5,7,8,9,10,11,12。
1(1)(2)(3)(4)(5)6P X P X P X P X P X ==========(7)(8)(9)(10)P X P X P X P X =======(11)(12)P X P X ==== 111=⨯= 6121711215759()63663612i i E X i i ===+=+=∑∑2 某产品的次品率为0.1,检验员每天检验4次,每次随机地取10件产品进行检验,如果发现其中的次品多于1,就去调整设备。
以X 表示一天中调整设备的次数,试求()E X 。
(设诸产品是否为次品是相互独立的。
)解 (1)求每次检验时产品出现次品的概率因为每次抽取0件产品进行检验,且产品是否为次品是相互独立的,因而可以看作是进行10次独立的贝努利试验,而该产品的次品率为0.1,设出现次品的件数为Y ,则(10,0.1)Y B :,于是有 1010{}(0.1)(0.9)kk k P Y k C -== (2)一次检验中不需要调整设备的概率{1}{0}{1}P Y P Y P Y ≤==+=101191010(0.1)(0.9)(0.1)(0.9)k k k C C -=+ 109(0.9)(0.9)34860.38740.7361=+=+=则需要调整设备的概率 {1}1{}10.73610.2639P Y P Y >=-≤=-= (3)求一天中调整设备的次数X 的分布律由于X 取值为0,1,2,3,4。
0.2369p =,则(4,0.2369)X B :于是 0044{0}(0.2639)(0.7361)0.2936P X C ===134{1}(0.2639)(0.7361)40.26390.39890.4211P X C ===⨯⨯= 2224{2}(0.2639)(0.7361)60.06960.54180.2263P X C ===⨯⨯=334{3}(0.2639)(0.7361)40.01840.73610.0542P X C ===⨯⨯= 444{4}(0.2639)0.0049P X C ===(4)求数学期望()00.293610.421120.226330.054240.0049E X =⨯+⨯+⨯+⨯+⨯1.0556=。
3 有3只球4个盒子的编号为1,2,3,4。
将球逐个独立地随机地放入4个盒子中去,以X 表示其中至少有一只球的盒子的最小号码(例如X =3,表示第1号、第2号盒子是空的,第3个盒子至少有一只球。
)试求()E X 。
解 (1)求X 的分布律由于每只球都有4种方法,由乘法定理共有3464= 种放法。
其中3只球都放到第4号盒子中的放法仅有1种,从而 1{4}64P X ==; 又{3}X = “3X=”表示事件:“第1号、第2号盒子是空的,第3号盒子不空”,从而3只球只能放在第3、4号两个盒子中,共有328=种放法,但其中有一种是3只坏都放在第4号盒子中,即3号盒子是空的,这不符合3X=这一要求,需要除去,故有3217{3}6464P X -===“2X=”表示事件:“第1号是空的,第2号盒子不空”,从而3只球只能放在第2、3、4号三个盒子中,共有3327=种放法,但其中有一种是3只球都放在第3、或4号盒子中,共有328=种放法,即2号盒子是空的,这不符合2X=这一要求,需要除去,故有333219{2}6464P X -===171937{1}1{1}164646464P X P X ==-≠=---= 即(2)求()E X37197110025()1234 1.5625646464646416E X =⨯+⨯+⨯+⨯===。
4(1)设随机变量X 的分布律为132{(1)}3j j j P X j +=-=,(1,2,3,j =L ),说明X 的数学期望不存在。
(2)一个盒中装有1只黑球,一只白球,作摸球游戏,规则如下:一次随机地从盒中摸出一只球,若摸到白球,则游戏结束;若摸到黑球,放回再放入一只黑球,然后再从盒中随机地摸取一只球。
试说明要游戏结束的摸球次数X 的数学期望不存在。
解 (1)因为级数111113332(1){(1)}(1)3j j j j j j j j j P j j j ∞∞+++==--=-⋅∑∑11(1)2j j j +∞=-=∑, 这是一个莱布尼茨交错级数,收敛而非绝对收敛。
所以其数学期望不存在。
(2)以k A 记事件“第k 次摸到黑球”,以k A 记事件“第k 次摸到白球”,以k C 表示事件“游戏在k 次摸球时结束”,1,2,3,k =L 。
按题意,121k k k C A A A A -=L ,由乘法公式得1211122211()(|)(|)(|)()k k k k k P C P A A A A P A A A A P A A P A ---=L L L 而 11{1}()2P X P A ===2211111{2}()(|)()32P X P A A P A A P A ====⨯ 21221112111(|)(|)()43243P A A A P A A P A =⨯⨯=⨯,一般地,若当X k =时,盒中共有1k +只球,其中只有一只白球,故1211211122211()()(|)(|)(|)()k k k k k k P X k P A A A A P A A A A P A A A A P A A P A ----===L L L L1121211111432k k k k k k k--=⨯⨯⨯⨯=⨯+-+L 若()E X 存在,则根据数学期望的定义,就有111111()()11k k k E X kP X k k k k k ∞∞∞======⨯=++∑∑∑,而调和级数111k k ∞=+∑却是发散的,此即表明数学期望()E X 不存在。
5设在某一规定的时间间隔里,某电气设备用于最大负荷的时间X (以min 计)是一个随机变量,其概率密度为221,01500,15001()(3000),15003000,15000,x x f x x x ⎧≤≤⎪⎪-⎪=-<≤⎨⎪⎪⎪⎩其它 求()E X解 按连续型随机变量的数学期望的定义有01500()()()()E X xf x dx xf x dx xf x dx ∞-∞-∞==+⎰⎰⎰300015003000()()xf x dx xf x dx ∞++⎰⎰201500201500x dx dx -∞=⋅+⎰⎰300022150030001(3000)01500x x dx dx ∞-+-+⋅⎰⎰ 315000231500x =⨯323000150021(1500)15003x x -+-6 设随机变量X 的分布律为求()E X ,2()E X ,2(35)E X + (2)设()X πλ:,求11E X ⎛⎫⎪+⎝⎭解 ()20.400.320.302E X =-⨯+⨯+⨯=-; 2222()(2)0.4(0)0.3(2)0.3 2.8E X =-⨯+⨯+⨯= 或 所以 2()00.340.7 2.8E X =⨯+⨯=。
222(31)(3)(5)3()53 2.8113.4E X E X E E X +=+=+=⨯+=(2)因为 !k k e p k λλ-=,0,1,2,k =L所以 001111!(1)!k k k k e E e X k k k λλλλ-∞∞-==⎛⎫=⋅= ⎪+++⎝⎭∑∑ 1011(1)(1)!!k kk k ee e k k λλλλλλλ+∞∞--=====-+∑∑11(1)(1)e e e λλλλλ-=-=-(注 在公式0()k k k E X x p ∞==∑中现在的11k x k =+,!k k e p k λλ-=,0!k k e k λλ∞==∑) 7 (1)设随机变量X 的概率密度为,0()0,0x e x f x x -⎧>=⎨≤⎩求(ⅰ)2Y X =,(ⅱ)2XY e-=的数学期望;(2)设随机变量1X ,2X ,…,n X 相互独立,且都服从(0,1)上的均匀分布(ⅰ)求12max{,,,}n U X X X =L 的数学期望, (ⅱ)求12min{,,,}n V X X X =L 的数学期望。
解 (1)0()(2)2()2x E Y E X xf x dx xe dx ∞∞--∞===⎰⎰02()x x xee dx ∞-∞-=-+⎰022xe -∞=-=2220()()()Xx x x E Y E e e f x dx e e dx ∞∞-----∞===⎰⎰3301133x xe dx e ∞--∞==-=⎰。
(2)因为(ⅰ)因为随机变量1X ,2X ,…,n X 相互独立,且都服从(0,1)上的均匀分布,其概率密度为1,01()0,i X x f x <⎧=⎨⎩<其它其分布函数为0,0(),011,1i X x F x x x x <⎧⎪=≤<⎨⎪≥⎩1,2,,i n =L而 12max{,,,}n U X X X =L 的分布函数为即max 0,0(),011,0nz F z z z z <⎧⎪=≤<⎨⎪>⎩,于是1max ,01()0,n nz z f z -⎧≤<=⎨⎩其它111max 00()()11n n n nE Z zf z dz nz dz z n n ∞+-∞====++⎰⎰。
