abaqus四面体单元类型
abaqus中单元的选取

ABAQUS中单元的选取总结实体单元的选择1. 如果不需要模拟非常大的应变或进行复杂的需改变接触条件的问题,则应采用二次减缩积分单元(CAX8R、CPE8R、CPS8R、C3D20R等);2. 如果存在应力集中,则在局部应采用二次完全积分单元(CAX8、CPE8、CPS8、C3D20等)。
它们可用最低费用提供应力梯度最好的解答。
3. 涉及到非常大的网格扭曲问题(大变形分析),建议采用细网格剖分的线性减缩积分单元(CAX4R、CPE4R、CPS4R、C3D8R等);4. 对接触问题采用线性减缩积分单元或细分的非协同单元(CAX4I、CPE4I、CPS4I、C3D8I等);5. 尽可能的减少网格变形的扭歪,形状扭歪的粗网格线性单元会导致非常差的结果。
壳单元的选择1.当要求解十分精确时,可使用线性、有限薄膜应变、完全积分的四边形壳单元(S4),这个壳单元十分适合于要考虑膜作用或有弯曲模式沙漏的问题,也适合于有平面弯曲的问题;2.线性、有限薄膜应变、减缩积分、四边形壳单元(S4R)较流行,适合于各类问题的应用;3.线性、有限薄膜应变、三角形壳单元(S3/S3R)可作为一般的壳单元来使用。
因为在单元内部是常应变应力场,求解弯曲变形和高应变梯度时需要精细的网格剖分;4.考虑到在复合材料层合壳模型中剪切柔度的影响,可应用厚壳单元(S4、S4R、S3、S3R、S8R)来模拟它,此时需检验平面假定是否满足;5.四边形或三角形的二次壳单元,对于一般的小变形薄壳来说是很有效的,它们对于剪力锁闭和薄膜锁闭不敏感;6.如果在接触问题中一定要用二阶单元,不要选用二阶三角形壳单元(STRI65),而要采用9节点的四边形壳单元(S9R5);7.对于几何线性的,但规模又非常大的模型,线性薄壳单元(S4R5)通常将比一般壳单元效率更高。
梁单元的选择1. 对任何涉及到接触的分析,应使用一阶的、有剪切变形的梁单元(B21、B31);2. 对于结构刚度非常大或非常柔软的结构,在几何非线性分析中应当使用杂交梁单元(B21H、B32H等);3. Euler-Benoulli三次梁单元(B23、B33)在模拟承受分布荷载作用的梁,包括动态的振动分析时,会有很高的精度。
abaqus单元属性小结
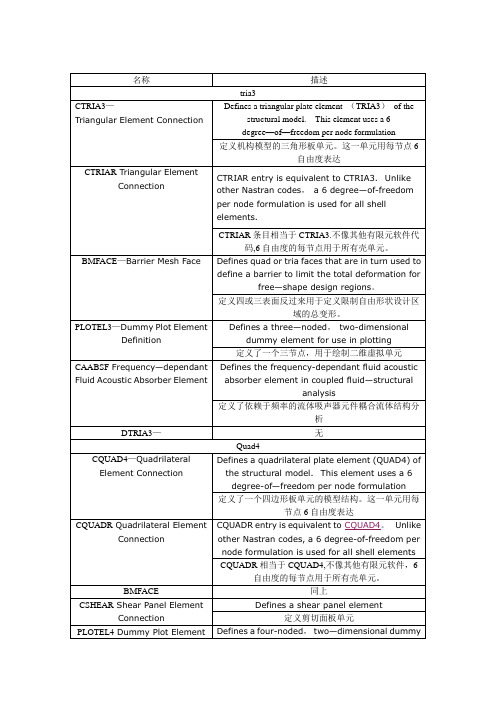
Definition element for use in plotting定义了一个四节点,用于绘制二维虚拟单元CAABSF 同上DQUAD4 无Tetra4CTETRA—Four-sided Solid Element with four or ten gridpoints Defines the connections of the CTETRA element 定义了CTETRA单元的连接DTETRA4 无Pyramid5CPYRA_S3/S3R 单元可以作为通用壳单元使用。
由于单元中的常应变近似,需要划分较细的网格来模拟弯曲变形或高应变梯度。
S4R 单元性能稳定,适用范围很广对于复合材料,为模拟剪切变形的影响,应使用适于厚壳的单元(例如S4、S4R、S3、S3R、S8R),并要注意检查截面是否保持平面。
对于几何非线性分析,在ABAQUS/Standard中的小应变壳单元(S4R5,S8R,S8R5, S8RT,S9R5, STRI3, 和STRI65)使用总体拉格朗日应变算法,应力应变可以相对于参考构型的材料方向改定.垫片单元是小应变小位移单元,默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。
对于有限膜应变单元(所有的膜单元以及S3/S3R,S4,S4R,SAX,和SAXA单元)和在ABAQUS/Explicit 中的小应变单元,其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。
此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。
(更详细地说明可以参考ABAQUS相关手册)。
用户可以决定与*section print和*section file相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转.。
abaqus单元属性大总结(可编辑修改word版)
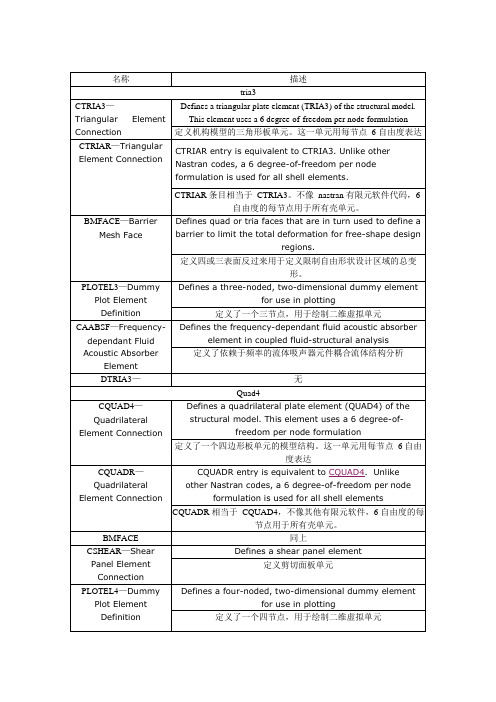
CAABSF 同上DQUAD4 无Tetra4CTETRA—Four-sidedSolid Element withfour or ten gridpointsDefines the connections of the CTETRA element定义了CTETRA 单元的连接DTETRA4 无Pyramid5CPYRA_S3/S3R 单元可以作为通用壳单元使用。
由于单元中的常应变近似,需要划分较细的网格来模拟弯曲变形或高应变梯度。
S4R 单元性能稳定,适用范围很广对于复合材料,为模拟剪切变形的影响,应使用适于厚壳的单元(例如S4、S4R、S3、S3R、S8R),并要注意检查截面是否保持平面。
对于几何非线性分析,在ABAQUS/Standard 中的小应变壳单元(S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65)使用总体拉格朗日应变算法,应力应变可以相对于参考构型的材料方向改定。
垫片单元是小应变小位移单元,默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。
对于有限膜应变单元(所有的膜单元以及S3/S3R, S4, S4R, SAX,和SAXA 单元)和在ABAQUS/Explicit 中的小应变单元,其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。
此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。
(更详细地说明可以参考ABAQUS 相关手册)。
用户可以决定与*section print 和*section file 相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。
ABAQUS中单元的选择宝典

ABAQUS中单元的选择宝典1.完全积分是指当单元具有规则形状时,所用的高斯积分点可以对单元刚度矩阵中的多项式进行精确地积分。
2.剪力自锁将使单元变得“刚硬”,只影响受弯曲荷载的完全积分线性(一阶)单元,这些单元功能在受直接或剪切荷载时没有问题。
二次单元的边界可以弯曲,没有剪力自锁的问题。
3.只有四边形和六面体单元才能采用减缩积分。
所有的楔形、四面体和三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
4.只有四边形和六面体单元才能采用减缩积分。
所有的楔形、四面体和三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
5.非协调单元:只有四边形和六面体单元才能采用减缩积分。
所有的楔形、四面体和三角形实体单元采用完全积分。
减缩积分单元比完全积分单元在每个方向上少用一个积分点。
6.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当的结果,且计算费用明显降低。
对单元扭曲很敏感。
7.ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当的结果,且计算费用明显降低。
对单元扭曲很敏感。
8.杂交单元:ABAQUS对非协调单元采用了增强位移梯度形式。
在弯曲问题中,用非协调单元可得到与二次单元相当的结果,且计算费用明显降低。
对单元扭曲很敏感。
9.一般情况下应采用二次减缩积分单元(CAX8R,CPE8R,CPS8R,C3D20R)。
在应力集中局部采用二次完全积分单元(CAX8,CPE8,CPS8,C3D20)。
对含有非常大的网格扭曲模拟(大应变分析),采用细网格划分的线性减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R)。
对接触问题采用线性减缩积分单元或非协调单元(CAX4I,CPE4I,CPS4II,C3D8I等)的细网格划分。
10.采用非协调单元时应使网格扭曲减至最小。
Abaqus单元类型选择讲课文档

内能
内能
伪应变能
伪应变能
沿厚度方向有两个单元: 伪应变能与内 沿厚度方向有四个单元: 伪应变能与内
能之比为2%。
能之比为0.1%。
第二十四页,共51页。
使用连续体单元模拟弯曲
ABAQUS/analysis_单元选择标 准
• 使用非协调模式单元模拟弯曲 (CPS4I, …) – 对于以弯曲为主的问题中,这种单元可能是效率最高的实体单元。 – 计算费用在一阶和二阶减缩积分单元之间,兼有两种积分方法的优点。 • 可以正确的模拟剪切行为—在纯弯曲问题中没有剪切应变。 • 在厚度方向,仅用一个单元就可以模拟弯曲。 • 没有沙漏模式;在塑性和接触问题中,工作的很好。 – 如果单元严重扭曲,相对一阶减缩积分单元的优势将会减弱;然而, 在严重扭曲的条件下,所有单元的精度都会下降。
第二十五页,共51页。
使用连续体单元模拟弯曲
• 例子:扭曲单元的悬臂梁
ABAQUS/analysis_单元选择 标准
第二十六页,共51页。
平行扭曲
梯形扭曲
使用连续体单元模拟弯曲
• 总结
ABAQUS/analysis_单元选择标准
单元类型 物理行为 二阶插值 一阶插值、全积分 一阶插值、减缩积分
非协调模式
ABAQUS/analysis_单元选择 标准
在厚度方向有四个单元
没有沙漏
第二十二页,共51页。
使用连续体单元模拟弯曲
• 检查并控制沙漏 – 在变形形状的绘图中,可以看到沙漏 现象。
• 例子:带有中心点载荷简支梁的 粗网格和中等网格。
– ABAQUS有内建的沙漏控制方法,用 以限制沙漏产生的问题。
ABAQUS/analysis_单元选择标准
ABAQUS中的网格划分方法

ABAQUS中的网格划分方法应该是所有通用有限元分析软件中最强大的。
本文将对其网格划分做较全面的叙述。
首先介绍一下网格划分技术,包括:结构化网格、扫掠网格、自由网格:1)结构化网格技术(STR UCTUR ED):将一些标准的网格模式应用于一些形状简单的几何区域,采用结构化网格的区域会显示为绿色(不同的网格划分技术会对相应的划分区域显示特有的颜色标示)。
2)扫掠网格技术(S WEEP):对于二维区域,首先在边上生成网格,然后沿着扫掠路径拉伸,得到二维网格;对于三维区域,首先在面上生成网格,然后沿扫掠路径拉伸,得到三维网格。
采用扫掠网格的区域显示为黄色。
3)自由网格划分技术(FREE):自由网格是最为灵活的网格划分技术,几乎可以用于任何几何形状。
采用自由网格的区域显示为粉红色。
自由网格采用三角形单元(二维模型)和四面体单元(三维模型),一般应选择带内部节点的二次单元来保证精度。
4)不能划分网格:如果某个区域显示为橙色,表明无法使用目前赋予它的网格划分技术来生成网格。
这种情况多出现在模型结构非常复杂的时候,这时候需要把复杂区域分割成几个形状简单的区域,然后在划分结构化网格或扫掠网格。
注意:使用结构化网格或扫掠网格划分技术时,如果定义了受完全约束的种子(SE ED),网格划分可能不成功,这时会出现错误信息们,可以忽略错误信息,允许ABAQ US去除对这些种子的约束,从而完成对网格的划分。
使用Quad单元或He x单元划分网格时,有两种可供选择的算法:Media lAxi s(中性轴算法)和A dvanc ing F ront(进阶算法)。
Abaqus单元的选择

Abaqus单元的选择2015-03-06 有限元在线如果想要以合理的费用得到高精度的结果,那么正确的选择单元是非常关键的。
对于ABAQUS经验丰富的使用者,毫无疑问都会自己的单元选择指南来处理各种具体的应用。
但是,在刚开始使用ABAQUS 时,下面的指导是非常有用的。
1、实体单元选择以下单元选择的建议适用于ABAQUS/Standard和ABAQUS/Explicit:(1)尽可能的减小网格的扭曲。
使用扭曲的线性单元的粗糙网格会得到相当差的结果。
(2)对于模拟网格扭曲过分严重的问题,应用网格细划的线性、减缩积分单元(CAX4R,CPE4R,CPS4R,C3D8R等)。
(3)对三维问题应尽可能地采用六面体单元。
它们以最低的成本给出最好的结果。
当几何形状复杂时,采用六面体单元划分网格可能是非常困难的,因此,还需要楔形和四面体单元。
这些单元(C3D4和C3D6)的一阶模式是较差的单元(需要细划网格以取得较好的精确度)。
(4)某些前处理器包含了自由划分网格算法,用四面体单元划分任意几何体的网格。
对于小位移无接触的问题,在ABAQUS/Standard中的二次四面体单元(C3D10)能够给出合理的结果。
这个单元的另一种模式是修正的二次四面体单元(C3D10M),它适用于ABAQUS/Standard和ABAQUS/Explicit,对于大变形和接触问题,这种单元是强健的,展示了很小的剪切和体积自锁。
但是,无论采用何种四面体单元,所用的分析时间都长于采用了等效网格的六面体单元。
(5)对于ABAQUS/Standard求解器,除非需要模拟非常大的应变或者模拟一个复杂的、接触条件不断变化的问题,对于一般的分析工作,应采用二次、减缩积分单元(CAX8R,CPE8R,CPS8R, C3D20R 等)。
(6)对于ABAQUS/Standard求解器,在存在应力集中的局部区域,采用二次、完全积分单元(CAX8, CPE8, CPS8, C3D20等)。
abaqus第二讲:ABAQUS中的实体单元

避免使用
二阶四边形/六面体
一阶全积分四边形/六面 体或二阶四边形/六面 体
一阶全积分四边形/六面 体
一阶
二阶全积分单元
问题分类 完全不可压 (橡胶n = 0.5) 屈曲材料成型(高度网格
扭曲)
复杂的几何模型(线性材 料,没有接触)
复杂的几何模型(非线性 或接触)
自然频率(线性动力学) 非线性动力学(隐式)
• 比较ABAQUS/Standard和ABAQUS/Explicit单元库 两种程序基本上具有相同的单元族:连续体、壳、梁等等。 除了应力分析,ABAQUS/Standard包括许多可以用于其它分析类型 的单元:热传导、土壤固结、声学等等。 • 在ABAQUS/Explicit中也可以使用声学单元。 对于每个单元族,ABAQUS/Standard包含许多变种。 ABAQUS/Explicit包含几乎所有的一阶单元。 • 例外:二阶三角形和四面体单元、二阶梁单元 对于两种程序,许多单元选择的准则是一样的。
“常规的”二阶四面体、二阶楔形和六节点壳和薄膜单元 (C3D10, C3D15, STRI65, M3D6)不能用于模拟接触问题, 除非使用基于罚函数的接触公式。
• 与“经典”的硬接触相比,在单元角点和中点处,一致 压力下面的接触力存在明显的不同。
修正的 二阶三角形/四面体单元(C3D10M, 等等)减轻了其它三角形/ 四面体单元的问题。 • 好的收敛率—与二阶四边形/六面体单元的收敛率相近。 • 最小化剪切锁闭和体积锁闭。 – 利用杂交公式(C3D10MH),可以用于模拟不可压或几乎不 可压材料。 • 在有限变形问题中,这些单元表现强劲。 • 一致的接触压力可以使这些单元精确的模拟接触问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
abaqus四面体单元类型
Abaqus有几种四面体单元类型,其中常用的包括:
1. C3D4:普通四面体单元,具有4个节点和4个积分点。
2. C3D4H:压力四面体单元,具有4个节点和4个积分点,用于模拟固体中的流体流动。
3. C3D10:高阶四面体单元,具有10个节点和4个积分点,比普通四面体具有更高的准确性。
4. C3D10M:由于升级的四面体单元,具有更好的形状函数属性。
它具有10个节点和4个积分点。
5. C3D10H:采用四面体单元H積分法。
它具有10个节点和4个积分点,用于模拟固体中的流体流动。
6. C3D10M:由于升级的高阶四面体单元,具有10个节点和4个积分点。
它通过改进形状函数来提高准确性。
7. C3D10H:采用四面体单元H積分法。
它具有10个节点和4个积分点,用于模拟固体中的流体流动。
这些四面体单元类型具有不同的节点数、积分点数和准确性,可根据具体模拟需求选择合适的单元类型。
