ABAQUS实体单元类型总结

合集下载

ABAQUS单元类型及特点汇总

ABAQUS单元类型及特点汇总1、单元表征单元族：单元名字里开始的字母标志着这种单元属于哪一个单元族。

C3D8I是实体单元；S4R是壳单元；CINPE4是无限元；梁单元；刚体单元；膜单元；特殊目的单元，例如弹簧，粘壶和质量；桁架单元。

自由度dof（和单元族直接相关）：每一节点处的平动和转动1 1方向的平动2 2方向的平动3 3方向的平动4 绕1轴的转动5 绕2轴的转动6 绕3轴的转动7 开口截面梁单元的翘曲8 声压或孔隙压力9 电势11 度（或物质扩散分析中归一化浓度）12＋梁和壳厚度上其它点的温度轴对称单元1 r方向的平动2 z方向的平动6 r-z方向的转动节点数：决定单元插值的阶数数学描述：定义单元行为的数学理论积分：应用数值方法在每一单元的体积上对不同的变量进行积分。

大部分单元采用高斯积分方法计算单元内每一高斯点处的材料响应。

单元末尾用字母“R”识别减缩积分单元，否则是全积分单元。

ABAQUS拥有广泛适用于结构应用的庞大单元库。

单元类型的选择对模拟计算的精度和效率有重大的影响；节点的有效自由度依赖于此节点所在的单元类型；单元的名字完整地标明了单元族、单元的数学描述、节点数及积分类型；所用的单元都必须指定单元性质选项。

单元性质选项不仅用来提供定义单元几何形状的附加数据，而且用来识别相关的材料性质定义；对于实体单元，ABAQUS参考整体笛卡尔坐标系来定义单元的输出变量，如应力和应变。

可以用*ORIENTATION选项将整体坐标系改为局部坐标系；对于三维壳单元，ABAQUS参考建立在壳表面上的一个坐标系来定义单元的输出变量。

可以用*ORIENTATION选项更改这个参考坐标系。

2．实体单元(C)实体单元可在其任何表面与其他单元连接起来。

C3D:三维单元CAX:无扭曲轴对称单元，模拟3600的环，用于分析受轴对称载荷作用，具有轴对称几何形状的结构；CPE:平面应变单元，假定离面应变ε33为零，用力模拟厚结构；CPS:平面应力单元，假定离面应力σ33为零，用力模拟薄结构；广义平面应变单元包括附加的推广：离面应变可以随着模型平面内的位置线性变化。

abaqus单元属性大总结(可编辑修改word版)

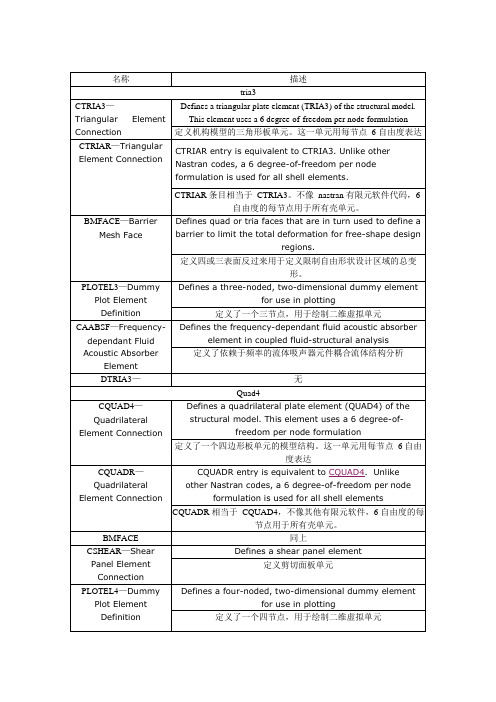
CAABSF 同上DQUAD4 无Tetra4CTETRA—Four-sidedSolid Element withfour or ten gridpointsDefines the connections of the CTETRA element定义了CTETRA 单元的连接DTETRA4 无Pyramid5CPYRA_S3/S3R 单元可以作为通用壳单元使用。

由于单元中的常应变近似，需要划分较细的网格来模拟弯曲变形或高应变梯度。

S4R 单元性能稳定，适用范围很广对于复合材料，为模拟剪切变形的影响，应使用适于厚壳的单元（例如S4、S4R、S3、S3R、S8R），并要注意检查截面是否保持平面。

对于几何非线性分析，在ABAQUS/Standard 中的小应变壳单元（S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65）使用总体拉格朗日应变算法，应力应变可以相对于参考构型的材料方向改定。

垫片单元是小应变小位移单元，默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。

对于有限膜应变单元（所有的膜单元以及S3/S3R, S4, S4R, SAX,和SAXA 单元）和在ABAQUS/Explicit 中的小应变单元，其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。

此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。

（更详细地说明可以参考ABAQUS 相关手册）。

用户可以决定与*section print 和*section file 相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。

(完整版)ABAQUS实体单元类型总结

在ABAQUS中，基于应力/位移的实体单元类型最为丰富：（1）在ABAQUS/Sandard中，实体单元包括二维和三维的线性单元和二次单元，均可以采用完全积分或缩减积分，另外还有修正的二次Tri单元（三角形单元）和Tet单元(四面体单元)，以及非协调模式单元和杂交单元。

（2）ABAQUS/Explicit中，实体单元包括二维和三维的线性缩减积分单元，以及修正的二次二次Tri单元（三角形单元）和Tet单元(四面体单元)，没有二次完全积分实体单元。

------------------------------------------------------------------------------------------------------------按照节点位移插值的阶数，ABAQUS里的实体单元可以分为以下三类：线性单元（即一阶单元）：仅在单元的角点处布置节点，在各个方向都采用线性插值。

二次单元（即二阶单元）：在每条边上有中间节点，采用二次插值。

修正的二次单元（只有Tri 或Tet 才有此类型）：在每条边上有中间节点，并采用修正的二次插值。

******************************************************************************* ***************1、线性完全积分单元：当单元具有规则形状时，所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。

缺点：承受弯曲载荷时，会出现剪切自锁，造成单元过于刚硬，即使划分很细的网格，计算精度仍然很差。

2、二次完全积分单元：优点：（1）应力计算结果很精确，适合模拟应力集中问题；（2）一般情况下，没有剪切自锁问题（shear locking）。

但使用这种单元时要注意：（1）不能用于接触分析；（2）对于弹塑性分析，如果材料不可压缩（例如金属材料），则容易产生体积自锁（volumetric locking）；（3）当单元发生扭曲或弯曲应力有梯度时，有可能出现某种程度的自锁。

abaqus单元属性大总结

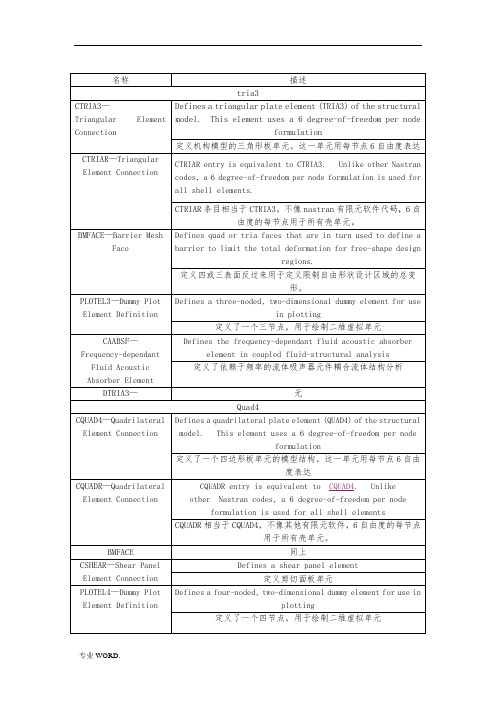
S3/S3R 单元可以作为通用壳单元使用。

由于单元中的常应变近似，需要划分较细的网格来模拟弯曲变形或高应变梯度。

S4R 单元性能稳定，适用围很广对于复合材料，为模拟剪切变形的影响，应使用适于厚壳的单元（例如S4、S4R、S3、S3R、S8R），并要注意检查截面是否保持平面。

对于几何非线性分析，在ABAQUS/Standard中的小应变壳单元（S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65）使用总体拉格朗日应变算法，应力应变可以相对于参考构型的材料方向改定。

垫片单元是小应变小位移单元，默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。

对于有限膜应变单元（所有的膜单元以及S3/S3R, S4, S4R, SAX,和 SAXA单元）和在ABAQUS/Explicit中的小应变单元，其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。

此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。

（更详细地说明可以参考ABAQUS相关手册）。

用户可以决定与*section print和*section file相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。

C3D20RP 20-node brick, triquadratic displacement, trilinear pore pressure, reducedintegration20节点实体，三重二次位移，三线孔隙压力，缩减积分C3D20R PH 20-node brick, triquadratic displacement, trilinear pore pressure, hybrid, linearpressure, reduced integration20节点实体，三重二次位移，三线孔隙压力，混合动力，线压力，缩减积分。

abaqus第二讲：ABAQUS中的实体单元解析

受弯矩M作用下完全积分、二次单元的变形
北京怡格明思工程技术有限公司
Innovating through simulation
只有当确信载荷只会在模型中产生很小的弯曲时，才可以采用完全积分的线性单元。如果对载荷产生的变形类型有所怀疑，则应采用不同类型的单元。在复杂应力状态下，完全积分的二次单元也有可能发生自锁；因此，如果在模型中应用这类单元，应细心地检查计算结果。然而，对于模拟局部应力集中的区域，应用这类单元是非常有用的！
北京怡格明思工程技术有限公司
Innovating through simulation
ABAQUS中的单元
公式（又称数学描述）
• 用于描述单元行为的数学公式是用于单元分类的另一种方法。 • 不同单元公式的例子：平面应变平面应力杂交单元非协调元小应变壳有限应变壳厚壳薄壳
北京怡格明思工程技术有限公司
受弯矩M作用下材料的变形线性单元的边不能弯曲；所以，如果应用单一单元来模拟这一小块材料，其变形后的形状如图所示。
受弯矩M作用下完全积分、线性单元的变形
北京怡格明思工程技术有限公司
Innovating through simulation
为清楚起见，画出了通过积分点的虚线。显然，上部虚线的长度增加，说明1方向的应力是拉伸的。类似地，下部虚线的长度缩短，说明是压缩的。竖直方向虚线的长度没有改变（假设位移是很小的）；所有这些都与受纯弯曲的小块材料应力的预期状态是一致的。但是，在每一个积分点处，竖直线与水平线之间夹角开始时为90度，变形后却改变了，说明这些点上的剪应力不为零。显然，这是不正确的：在纯弯曲时，这一小块材料中的剪应力应该为零。产生这种伪剪应力的原因是因为单元的边不能弯曲，它的出现意味着应变能正在产生剪切变形，而不是产生所希望的弯曲变形，因此总的挠度变小：即单元是过于的刚硬。剪力自锁仅影响受弯曲载荷的完全积分的线性单元的行为。在受轴向或剪切载荷时，这些单元的功能表现很好。而二次单元的边界可以弯曲，故它没有剪力自锁的问题。二次单元预测的自由端位移接近于理论解答。

abaqus实体单元、壳单元、梁单元的定义与用法

abaqus实体单元、壳单元、梁单元的定义与用法文章标题：深度了解abaqus实体单元、壳单元、梁单元的定义与用法一、引言在工程领域中，模拟和分析结构力学行为是非常重要的。

ABAQUS作为有限元分析软件，在工程结构分析和仿真中扮演着重要的角色。

在ABAQUS中，实体单元、壳单元和梁单元是常用的元素类型，它们可以用来模拟各种不同类型的结构和力学行为。

本文将深入探讨这些单元的定义与用法。

二、实体单元的定义与用法1. 实体单元是ABAQUS中最基本的有限元单元之一，通常用于模拟具有三维结构的实体物体。

它能够准确描述物体的体积和构造。

2. 实体单元适用于模拟压力容器、机械零件、汽车车身等实体结构的力学行为。

它能够有效分析结构的应力、应变、变形等力学特性。

3. 在实际工程中，使用实体单元时需要注意单元的类型、材料特性、边界条件和加载方式，以确保分析结果的准确性和可靠性。

三、壳单元的定义与用法1. 壳单元是ABAQUS中常用的二维有限元单元，适用于模拟薄壁结构和板材。

它能够准确描述结构的曲率和变形。

2. 壳单元适用于模拟飞机机翼、船体、薄膜结构等薄壁结构的力学行为。

它能够有效分析结构的弯曲、剪切、挠曲等力学特性。

3. 在实际工程中，使用壳单元时需要注意单元的厚度、材料特性、边界条件和加载方式，以确保分析结果的准确性和可靠性。

四、梁单元的定义与用法1. 梁单元是ABAQUS中用于模拟杆件和梁结构的有限元单元，适用于描述结构的轴向变形和弯曲变形。

2. 梁单元适用于模拟桥梁、支撑结构、梁柱结构等杆件和梁结构的力学行为。

它能够有效分析结构的弯曲、扭转、轴向变形等力学特性。

3. 在实际工程中，使用梁单元时需要注意单元的截面特性、材料特性、边界条件和加载方式，以确保分析结果的准确性和可靠性。

五、个人观点和理解在工程结构分析中，选择合适的有限元单元对于准确模拟和分析结构的力学行为是至关重要的。

实体单元、壳单元和梁单元都有各自的优缺点，工程师需要根据具体的结构特点和分析要求来选取合适的单元类型。

abaqus第二讲：ABAQUS中的实体单元

一阶单元或二阶减缩积分单元
避免使用
二阶四边形/六面体
一阶全积分四边形/六面体或二阶四边形/六面体
一阶全积分四边形/六面体
一阶
二阶全积分单元
问题分类完全不可压 (橡胶n = 0.5) 屈曲材料成型（高度网格
扭曲）
复杂的几何模型（线性材料，没有接触）
复杂的几何模型（非线性或接触）
自然频率（线性动力学）非线性动力学（隐式）
• 比较ABAQUS/Standard和ABAQUS/Explicit单元库两种程序基本上具有相同的单元族：连续体、壳、梁等等。除了应力分析，ABAQUS/Standard包括许多可以用于其它分析类型的单元：热传导、土壤固结、声学等等。 • 在ABAQUS/Explicit中也可以使用声学单元。对于每个单元族，ABAQUS/Standard包含许多变种。 ABAQUS/Explicit包含几乎所有的一阶单元。 • 例外：二阶三角形和四面体单元、二阶梁单元对于两种程序，许多单元选择的准则是一样的。
“常规的”二阶四面体、二阶楔形和六节点壳和薄膜单元 (C3D10, C3D15, STRI65, M3D6)不能用于模拟接触问题，除非使用基于罚函数的接触公式。
• 与“经典”的硬接触相比，在单元角点和中点处，一致压力下面的接触力存在明显的不同。
修正的二阶三角形/四面体单元(C3D10M, 等等)减轻了其它三角形/ 四面体单元的问题。 • 好的收敛率—与二阶四边形/六面体单元的收敛率相近。 • 最小化剪切锁闭和体积锁闭。 – 利用杂交公式(C3D10MH)，可以用于模拟不可压或几乎不可压材料。 • 在有限变形问题中，这些单元表现强劲。 • 一致的接触压力可以使这些单元精确的模拟接触问题。

abaqus系列教程-04应用实体单元

4. 应用实体单元在ABAQUS中，应力/位移单元的实体（continuum）单元族是包含最广泛的。

ABAQUS/Standard和ABAQUS/Explicit的实体单元库多少有所不同。

ABAQUS/Standard实体单元库ABAQUS/Standard的实体单元库包括二维和三维的一阶（线性）插值单元和二阶（二次）插值单元，它们应用或者完全积分或者减缩积分。

二维单元有三角形和四边形；在三维单元中提供了四面体、三角楔形体和六面体（砖型）。

也提供了修正的二阶三角形和四面体单元。

此外，在ABAQUS/Standard中还有杂交和非协调模式单元。

ABAQUS/Explicit实体单元库ABAQUS/Explicit的实体单元库包括二维和三维的减缩积分一阶（线性）插值单元，也有修正的二阶插值三角形和四面体单元。

在ABAQUS/Explicit中没有完全积分或者规则的二阶单元。

关于可选用的实体单元的详细信息，请参阅ABAQUS分析用户手册第14.1.1节“Solid (continumm) elements”。

当做出所有这些各种选项的排列，发现可供使用的实体单元的总数是相当大的，仅就三维模型而言就超过了20种。

模拟的精度将很大程度上依赖于在模型中采用的单元类型。

在这些单元中选择哪一个最适合于你的模型，可能是一件令人苦恼的事情。

特别是在初次使用时。

然而，你会逐渐认识到这种在20多件工具组中的选择，为你提供一种能力，对于一个特殊的模拟能够选择恰当正确的工具或单元。

本章讨论了不同的单元数学描述和积分水平对于一个特定分析的精度的影响，也给出了一些关于选择实体单元的一般性指导意见，这些为你积累ABAQUS的应用经验，并建立自己的知识库提供了的基础。

本章末尾的例子，当你建立和分析一个连接环构件模型时，将允许你应用这些知识。

4.1 单元的数学描述和积分通过考虑一个静态分析的悬臂梁，如图4-1所示，将演示单元阶数（线性或二次）、单元数学描述和积分水平对结构模拟的精度的影响。

abaqus单元形状

abaqus单元形状Abaqus软件是一种用于模拟和分析实体的有限元分析软件，使用者可以选择不同的单元类型来描述物体的形状和行为。

Abaqus提供了多种不同的单元类型，以适应不同类型的问题和目标。

下面我将介绍几种常见的Abaqus单元形状。

1. 线单元（Beam elements）: 线单元用于描述长而细的结构物，如梁和柱。

它们是一维元素，沿着长度方向进行分割，并通过节点连接。

这些单元可以模拟结构物的弯曲和扭转行为。

线单元通常使用于考虑结构物细长性质的工程问题。

2. 平面单元（Plane elements）: 平面单元用于描述平面或轴对称物体。

它们是二维元素，通常用于平面应力和平面应变问题的分析。

平面单元可以分为三角形单元和四边形单元。

三角形单元更适用于不规则形状，而四边形单元更适用于规则形状。

3. 壳单元（Shell elements）: 壳单元用于描述薄壁结构，如板、壳和薄膜等。

它们是二维元素，具有厚度。

壳单元可以包括模拟薄壁结构的平面应力、平面应变和轴对称问题。

壳单元分为四边形壳单元和三角形壳单元。

4. 体单元（Solid elements）: 体单元用于描述实体结构，如块体或立方体。

它们是三维元素，用于分析三维应力和应变问题。

体单元可以分为四面体单元和六面体单元。

四面体单元适用于非规则形状，而六面体单元适用于规则形状。

5. 结合单元（Combined elements）: 结合单元是使用不同类型单元进行组合的元素。

结合单元可以用于描述复杂的几何形状和行为。

例如，可以组合使用线单元、壳单元和体单元来模拟不同部分的结构。

6. 其他单元类型：除了上述常见的单元类型外，Abaqus还提供了许多其他单元类型，如弹簧单元、等效固体单元和连接单元等。

总之，Abaqus提供了丰富的单元形状选择，以满足不同类型的工程和科学问题的分析需求。

根据问题的性质和特点，使用者可以选择适合的单元类型来模拟和分析结构的形状和行为。

(完整版)Abaqus单元类型选择

– 与连续体单元模型相比，结构单元模型需要的单元一般少得多。 • 对于能得到可接受结果的结构单元，壳的厚度和梁截面的尺寸应该小于总体结
构尺寸的1/10，比如： – 支撑或点载荷之间的距离 – 尺寸变化很大的横截面之间的距离 – 最高振动模态的波长
A1.14
结构单元（壳和梁） vs. 连续体单元
• 壳单元 – 使用表面模型构成的壳单元近似模拟三维实体连续体单元。
A1.4
ABAQUS中的单元
族
• 有限元族是一种广泛的分类方法。
• 同族的单元共享许多基本特征。
• 在同一族单元中又有许多变异。
连续体(实体单元)
刚体单元
ABAQUS/analysis_单元选择标准
壳单元
梁单元
薄膜单元
无限单元
特殊单元，如弹簧、阻尼器和质量单元
桁架单元
A1.5
ABAQUS中的单元
ABAQUS/analysis_单元选择标准
Element type
单元类型选择标准
概述
• ABAQUS中的单元 • 结构单元（壳和梁） vs. 连续体单元 • 使用连续体单元模拟弯曲 • 应力集中 • 接触 • 不可压材料 • 网格生成 • 选择实体单元总结
ABAQUS/analysis_单元选择标准
节点个数 (插值) • 节点的单元编号决定了单元域内
节点自由度的插值方式。 • ABAQUS包含一阶和二阶插值方
式的单元。
ABAQUS/analysis_单元选择标准
一次插值
二次插值
A1.6
ABAQUS/analysis_单元选择标准
ABAQUS中的单元
自由度 • 在有限元分析过程中，单元节点的自由度是基本变量。 • 自由度的例子：

ABAQUS实体单元类型总结教学内容

在ABAQUS中，基于应力/位移的实体单元类型最为丰富：(1)在ABAQUS/Sandard中，实体单元包括二维和三维的线性单元和二次单元，均可以采用完全积分或缩减积分，另外还有修正的二次Tri 单元(三角形单元)和Tet 单元(四面体单元)，以及非协调模式单元和杂交单元。

(2)ABAQUS/Explicit 中，实体单元包括二维和三维的线性缩减积分单元，以及修正的二次二次Tri单元(三角形单元)和Tet单元(四面体单元)，没有二次完全积分实体单元。

按照节点位移插值的阶数，ABAQUS里的实体单元可以分为以下三类：线性单元(即一阶单元) ：仅在单元的角点处布置节点，在各个方向都采用线性插值。

二次单元(即二阶单元) ：在每条边上有中间节点，采用二次插值。

修正的二次单元(只有Tri 或Tet 才有此类型) ：在每条边上有中间节点，并采用修正的二次插值。

******************************************************************************* ***************1 、线性完全积分单元：当单元具有规则形状时，所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。

缺点：承受弯曲载荷时，会出现剪切自锁，造成单元过于刚硬，即使划分很细的网格，计算精度仍然很差。

2、二次完全积分单元：优点：(1)应力计算结果很精确，适合模拟应力集中问题；( 2)一般情况下，没有剪切自锁问题( shear locking)。

但使用这种单元时要注意：( 1 )不能用于接触分析；( 2)对于弹塑性分析，如果材料不可压缩 (例如金属材料) ，则容易产生体积自锁 ( volumetric locking)；（3）当单元发生扭曲或弯曲应力有梯度时，有可能出现某种程度的自锁。

3、线性减缩积分单元：减缩积分单元，比普通的完全积分单元在每个方向少用一个积分点；线性缩减积分单元：只在单元的中心有一个积分点，由于存在沙漏数值问题（hourglass）而过于柔软。

abaqus系列教程-04应用实体单元

4. 应用实体单元在ABAQUS中，应力/位移单元的实体（continuum）单元族是包含最广泛的。

ABAQUS/Standard和ABAQUS/Explicit的实体单元库多少有所不同。

二维单元有三角形和四边形；在三维单元中提供了四面体、三角楔形体和六面体（砖型）。

也提供了修正的二阶三角形和四面体单元。

此外，在ABAQUS/Standard中还有杂交和非协调模式单元。

ABAQUS/Explicit实体单元库ABAQUS/Explicit的实体单元库包括二维和三维的减缩积分一阶（线性）插值单元，也有修正的二阶插值三角形和四面体单元。

在ABAQUS/Explicit中没有完全积分或者规则的二阶单元。

关于可选用的实体单元的详细信息，请参阅ABAQUS分析用户手册第14.1.1节“Solid (continumm) elements”。

当做出所有这些各种选项的排列，发现可供使用的实体单元的总数是相当大的，仅就三维模型而言就超过了20种。

模拟的精度将很大程度上依赖于在模型中采用的单元类型。

在这些单元中选择哪一个最适合于你的模型，可能是一件令人苦恼的事情。

特别是在初次使用时。

然而，你会逐渐认识到这种在20多件工具组中的选择，为你提供一种能力，对于一个特殊的模拟能够选择恰当正确的工具或单元。

本章末尾的例子，当你建立和分析一个连接环构件模型时，将允许你应用这些知识。

abaqus瞬态动力学的单元类型

abaqus瞬态动力学的单元类型在进行结构动力学仿真分析时，选择合适的单元类型是非常关键的。

abaqus作为一款常用的有限元分析软件，提供了多种不同类型的单元供用户选择。

其中，用于瞬态动力学分析的单元类型有很多，如C3D8、C3D8R、C3D8I等。

不同的单元类型适用于不同的情况，下面将对abaqus瞬态动力学的几种常用单元类型进行简要介绍。

首先是C3D8单元，它是典型的八节点三维实体单元。

C3D8单元适用于对三维实体结构的动力学分析，具有较好的精度和稳定性。

在模拟结构动态响应时，使用C3D8单元可以较为准确地预测结构的振动特性和动态响应。

其次是C3D8R单元，它是C3D8单元的一种改进类型，具有更好的数值稳定性和收敛性。

C3D8R单元在处理动态加载和振动分析时，可以减少计算误差，提高仿真结果的准确性。

因此，在进行大变形或高速动态加载分析时，选择C3D8R单元可以获得更可靠的仿真结果。

另外，C3D8I单元是一种八节点三维实体单元，具有更高的数值精度和收敛性。

C3D8I单元适用于要求较高精度和准确性的动力学分析，如地震响应分析、碰撞仿真等。

使用C3D8I单元可以有效减小数值误差，提高仿真结果的可靠性。

除了以上介绍的几种单元类型外，abaqus还提供了其他适用于瞬态动力学分析的单元，如C3D10、C3D10M、C3D20等。

用户在选择单元类型时，应根据具体的仿真需求和结构特性进行合理的选择，以获得准确可靠的仿真结果。

总的来说，abaqus提供的各种瞬态动力学单元类型都具有各自的优势和适用范围，用户在进行动力学仿真分析时，应充分了解不同单元类型的特点和适用条件，选择合适的单元类型进行建模和分析。

通过合理选择单元类型，可以提高仿真结果的准确性和可靠性，为工程设计和分析提供有力支持。

(完整版)ABAQUS实体单元类型总结

二次单元（即二阶单元）：在每条边上有中间节点，采用二次插值。

修正的二次单元（只有Tri 或Tet 才有此类型）：在每条边上有中间节点，并采用修正的二次插值。

缺点：承受弯曲载荷时，会出现剪切自锁，造成单元过于刚硬，即使划分很细的网格，计算精度仍然很差。

2、二次完全积分单元：优点：（1）应力计算结果很精确，适合模拟应力集中问题；（2）一般情况下，没有剪切自锁问题（shear locking）。

ABAQUS单元介绍

以C为开头的单元为实体CONTINUUM单元,如:C3D4,CPE4,C3D20R,CPS2E;
以S为开头的单元为壳SHELL单元,如:S4R,S8R5,SAX2,SC8R;
以B为开头的单元为梁BEAM单元,如:B21,B22H,B31,B31H;
以T为开头的单元为桁架TRUSS单元,如:T2D2,T2D2E,T2D3T;
以R为开头的单元为刚性RIGID单元,如:R2D2,R3D3,R3D4,RAX2;
以M为开头的单元为膜MEMBRANE单元,如:M3D3,M3D4R,MAX2;
以F为开头的单元为流体FLUID单元,如:F2D2,F3D4,FAX2;
以AC为开头的单元为声学ACOUSTIC单元,如:AC1D3,AC3D20,ACAX6;
以GK为开头的单元为衬垫GASKET单元,如:GK2D2,GK3D18N,GKAX4;
另外,ABAQUS还提供了点质量单元MASS,管单元PIPE,积分单元IT,连接单元JOINT,线弹性单元LS,无限元CIN,等以适应不同模型的需要.
2D,3D表示二维,三维
PE表示平面应变单元,PS表示平面应力单元
AX表示轴对称单元
2D,3D,PE,PS,AX后面的数字一般指单元所具有的节点个数(梁单元,轴对称膜单元和轴对称壳单元除外,这些单元名称中标明了插值的阶数,如B31表示一阶三维梁单元,B32表示二阶三维梁单元,MAX2表示3节点二次轴对称膜单元,SAX1表示2节点线性轴对称壳单元)
以R结尾的单元为缩减积分单元
以H结尾的单元为杂交单元
以E结尾的单元为考虑压电效应的单元
以T结尾的单元为考虑热效应的耦合单元。

abaqus瞬态动力学的单元类型

abaqus瞬态动力学的单元类型
在ABAQUS中进行瞬态动力学分析时，单元类型的选择非常重要，因为它
直接影响到模拟的精度和计算效率。

以下是一些常用的单元类型：
1. 实体单元：用于模拟三维实体结构，如梁、板和块。

常见的实体单元类型包括六面体（如C3D8R）、四面体（如C3D4）和三棱柱（如C3D6）。

这些单元类型可以模拟复杂的几何形状和结构，适用于大多数瞬态动力学问题。

2. 膜单元：用于模拟薄膜结构，如覆盖层、气瓶和管道。

膜单元通常简化为二维问题，只考虑拉伸和压缩行为。

常见的膜单元类型包括四边形（如S4R）和六面体（如M3D6）。

3. 梁单元：用于模拟细长结构，如桥梁、支柱和悬臂梁。

梁单元可以承受弯曲和轴向力，并且具有较好的计算效率。

常见的梁单元类型包括线性梁（如BE1）和曲梁（如BE3）。

4. 薄壳和厚壳单元：用于模拟薄壁和厚壁圆筒、球壳和其他曲面结构。

这些单元类型可以很好地处理弯曲和剪切行为，适用于需要考虑几何非线性的问题。

5. 点单元：用于模拟节点位移或集中力/力矩。

点单元通常不直接用于瞬态
动力学分析，而是与其他单元类型结合使用，以实现复杂的边界条件或连接方式。

选择合适的单元类型需要根据具体问题来确定。

通常需要根据结构的几何形状、材料属性、边界条件和载荷来确定最合适的单元类型。

同时，还需要考虑计算效率和精度要求，以选择合适的单元大小和网格密度。

ABAQUS中单元特点总结

ABAQUS中单元特点总结ABAQUS中的单元是指用于建模和分析几何结构中的离散要素。

每个单元代表结构中的一个局部区域，可以包含几何形状、材料属性和物理特性等信息。

在ABAQUS中，有多种类型的单元可供选择，每种类型的单元都有其独特的特点和适用范围。

以下是对ABAQUS中单元的几个特点的总结。

1.单元的几何特点：每个单元都可以具有不同的几何形状，如线性、面状或体状。

在ABAQUS中，目前支持的几何形状包括点、线、三角形、四边形和六面体等。

这些几何形状的选择取决于模型的复杂性和所需的准确程度。

2.单元的类型：ABAQUS提供了广泛的单元类型，以适应不同类型的分析。

常用的单元类型包括点单元（节点）、线单元、壳单元和体单元。

每个单元类型都有自己的应用领域和限制。

例如，点单元适用于仅在节点处施加负载或约束的情况，而壳单元适用于描述薄壁结构。

3.单元的连接性：单元的连接性指单元之间的关系，包括节点之间的连接和边界条件的施加。

在ABAQUS中，可以定义节点之间的连接关系，如线节点、面节点或体节点。

通过连接节点，可以构建更大的单元或复杂的结构。

此外，还可以在单元上应用约束和负载，以模拟真实的加载情况。

4.单元的材料特性：每个单元都可以具有不同的材料属性，如弹性模量、泊松比、屈服强度等。

这些材料属性可以用于模拟不同类型的材料行为，如弹性、塑性、粘弹性等。

通过在单元上应用适当的材料属性，可以模拟出材料的真实行为，进而对结构的响应进行分析。

5.单元的计算精度：在进行结构分析时，计算精度对结果的准确性和可靠性至关重要。

在ABAQUS中，不同类型的单元具有不同的计算精度。

例如，线性单元通常用于近似线性材料，而高阶单元可以更好地描述非线性材料。

选择适当的单元类型和计算精度对于获取准确和可靠的分析结果非常重要。

总之，ABAQUS中的单元具有不同的几何特点、类型、材料特性、连接性和计算精度，可以灵活地模拟和分析各种结构的行为。

abaqus单元属性大总结

abaqus单元属性大总结DCAABSF 同上DQUAD4 无Tetra4CTETRA—Four-sided Solid Element with four or ten grid points Defines the connections of the CTETRA element 定义了CTETRA单元的连接DTETRA4 无Pyramid5 CPYRA_S3/S3R 单元可以作为通用壳单元使用。

由于单元中的常应变近似，需要划分较细的网格来模拟弯曲变形或高应变梯度。

对于几何非线性分析，在ABAQUS/Standard中的小应变壳单元（S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65）使用总体拉格朗日应变算法，应力应变可以相对于参考构型的材料方向改定。

垫片单元是小应变小位移单元，默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。

对于有限膜应变单元（所有的膜单元以及S3/S3R, S4, S4R, SAX,和SAXA单元）和在ABAQUS/Explicit 中的小应变单元，其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。

此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。

（更详细地说明可以参考ABAQUS相关手册）。

用户可以决定与*section print和*section file相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。

Tria3S3 3-node triangular general-purpose shell,finite membrane strains (identicaltoelement S3R)三节点三角形通用壳，有限莫应变（相当于S3R特性）DS3 3-node heat transfer triangular shell三节点传热三角形壳STRI 3 3-node triangular facet thin shell 三节点三角形面薄壳S3R 3-node triangular general-purpose shell, finite membrane strains (identical toelement S3)3节点三角形通用壳，有限膜应变（与S3特性相同）M3D 3 3-node triangular membrane 3节点三角形膜S3RT 3-node thermally coupled triangular gen eral-purpose shell, finite membranestrains (identical to element S3T) 3节点热耦合三角通用壳，有限膜应变（与S3T单元相同）SFM3 D3 3-node triangular surface element 三节点三角形面单元F3D3R3D3 3-node 3D rigid triangular facet三节点三维刚性三角切面ACIN 3D3 3-node linear 3D acoustic infinite element三节点的线性三维声无限元Quad4S4 4-node general-purpose shell, finite membrane strains4节点的通用壳，有限膜应变S4R5 4-node thin shell, reduced integration, ho urglass control, using five degrees offreedom per node4节点壳薄，缩减积分，沙漏控制，每个节点使用5个自由度M3D 4 4-node quadrilateral membrane 4节点四边形膜M3D 4R 4-node quadrilateral membrane, reduced integration, hourglasscontrol4节点四边形膜，缩减积分，沙漏控制SFM3 D4 4-node quadrilateral surface element 4节点四边形面单元SFM3 D4R 4-node quadrilateral surface element, reduced integration4节点四边形曲面单元，缩减积分R3D4 4-node 3D bilinear rigid quadrilateral4节点三维双线性刚性四边形DS4 4-node heat transfer quadrilateral shell4节点传热四边形壳F3D4ACIN 3D4 4-node linear 3D acoustic infinite element4节点线性三维声无限元S4R 4-node general-purpose shell, reduced in tegration, hourglass control, finitemembrane strains4节点的通用外壳，缩减积分，沙漏控制，有限膜应变S4RT 4-node thermally coupled general-purpo se shell, reduced integration, hourglasscontrol, finite membrane strains 4节点热耦合通用外壳，缩减积分，沙漏控制，有限膜应变GK3 D4L 4-node three-dimensional line gasket element4节点三维线密封单元GK3 D4LN 4-node three-dimensional line gasket ele ment with thickness-direction behavioronly只有厚度方向反应的4节点三维线密封单元Tetra4C3D4 4-node linear tetrahedron4节点线性四面体C3D4 H 4-node linear tetrahedron, hybrid, linearpressure4节点线性四面体，混合，线压力DC3 D4 4-node linear heat transfer tetrahedron 4节点的线性传热四面体C3D4 E 4-node linear piezoelectric tetrahedron 4节点线性压电四面体DC3 D4E 4-node linear coupled thermal-electricaltetrahedron4节点的线性耦合热—电四面体AC3 D4 4-node linear acoustic tetrahedron 4节点线性声学四面体Pyramid5C3D8 8-node linear brick8节点线性实体C3D8 T 8-node thermally coupled brick, trilineardisplacement andtemperature8节点热耦合实体，三线性位移和温度C3D8 H 8-node linear brick, hybrid, constant pressure8节点线性实体，混合，恒压C3D8 HT 8-node thermally coupled brick, trilinear displacement and temperature, hybrid,constant pressure8节点热耦合实体，三线性位移和温度，混合，恒压C3D8 I 8-node linear brick, incompatible modes 8节点线性实体，非协调模式C3D8 IH 8-node linear brick, hybrid, linear pressu re, incompatible modes8节点线性实体，混合，线压力，非协调模型C3D8 R 8-node linear brick, reduced integration,hourglass control8节点线性实体，缩减积分，沙漏控制C3D8 RH 8-node linear brick, hybrid, constant pre ssure, reduced integration, hourglasscontrol8节点线性实体，混合，恒压，缩减积分，沙漏控制C3D8 E 8-node linear piezoelectric brick 8节点线性压电实体C3D6 6-node linear triangular prism6节点线性三角形棱柱C3D6 H 6-node linear triangular prism, hybrid, constant pressure6节点线性三角形棱柱，混合，恒定压力C3D6 E 6-node linear piezoelectric triangular prism6节点线性压电三角形棱柱C3D8 RT 8-node thermally coupled brick, trilinear displacement and temperature, reducedintegration, hourglass control8节点热耦合实体，三线性位移和温度，缩减积分，沙漏控制C3D8 RHT 8-node thermally coupled brick, trilinear displacement and temperature, reduced integration, hourglass control, hybrid, constant pressure8节点热耦合实体，三线性位移和温度，缩减积分，沙漏控制，混合动力，恒定压力Penta6AC3 D6 6-node linear acoustic triangular prism 6节点线性声学三角形棱柱C3D6 6-node linear triangular prism6节点线性三角形棱柱C3D6 H 6-node linear triangular prism, hybrid, constant pressure6节点线性三角形棱柱，混合动力，恒定压力DC3 D6 6-node linear heat transfer triangular prism6节点线性传热三角形棱柱C3D6 E 6-node linear piezoelectric triangular prism6节点线性压电三角形棱柱DC3 D6E 6-node linear coupled thermal-electricaltriangular prism6节点线性耦合热—电三角形棱柱SC6R 6-node triangular in-plane continuum sh ell wedge, general-purpose continuumshell, finite membrane strains6节点三角形平面内的连续体壳楔，通用的连续体壳，有限膜应变COH 3D6 6-node three-dimensional cohesive element6节点三维粘性单元GK3 D6 6-node three-dimensional gasket element 6节点三维衬垫单元GK3 D6N 6-node three-dimensional gasket element with thickness-direction behavioronly6节点三维衬垫单元只有厚度方向特性SC6R T 6-node linear displacement and temperat ure, triangular in-plane continuum shellwedge, general-purpose continuum shell,finite membranestrains6节点的直线位移和温度，三角形平面内的连续体楔，通用连续体壳，有限膜应变Hex8C3D8 I 8-node linear brick, incompatible modes 8节点线性实体，非协调模型C3D8 8-node linear brick8节点线性实体C3D8 T 8-node thermally coupled brick, trilineardisplacement andtemperature8节点热耦合实体，三线位移和温度C3D8 H 8-node linear brick, hybrid, constant pressure8节点的线性实体，混合动力，恒定压力C3D8 HT 8-node thermally coupled brick, trilinear displacement and temperature, hybrid,constant pressure8节点热耦合实体，三线性位移和温度，混合动力，恒定压力C3D8 IH 8-node linear brick, hybrid, linear pressu re, incompatible modes8节点的线性实体，混合动力，线压力，非协调模型C3D8 R 8-node linear brick, reduced integration,hourglass control8节点的线性实体，缩减积分，沙漏控制C3D8 RH 8-node linear brick, hybrid, constant pre ssure, reduced integration, hourglasscontrol8节点的线性实体，混合动力，恒定压力，缩减积分，沙漏控制C3D8 E 8-node linear piezoelectric brick 8节点线性压电实体DC3 D8 8-node linear heat transfer brick 8节点线性传热实体AC3 D8 8-node linear acoustic brick 8节点线性声学实体DC3 D8E 8-node linear coupled thermal-electricalbrick8节点线性耦合热—电实体DCC8-node convection/diffusion brick3D8 8节点传递/扩散实体DCC 3D8D 8-node convection/diffusion brick, dispersion control8节点传递/扩散实体，扩散性控制SC8R 8-node quadrilateral in-plane general-purpose continuum shell, reduced integration with hourglass control, finitemembrane strains8节点四边形平面内通用连续外壳，具有沙漏控制和缩减积分，有限膜应变COH 3D8 8-node three-dimensional cohesive element8节点三维粘性单元GK3D88-node three-dimensional gasket element8节点三维衬垫单元GK3 D8N 8-node three-dimensional gasket element with thickness-direction behavioronly8节点三维衬垫单元只有厚度方向的特性C3D8 P 8-node brick, trilinear displacement, trilinear pore pressure8节点实体，三线位移，三线孔压C3D8 PH 8-node brick, trilinear displacement, trili near pore pressure, hybrid, constantpressure8节点实体，三线位移，三线孔压，混合动力，恒定压力C3D8 RP 8-node brick, trilinear displacement, trili near pore pressure, reducedintegration8节点实体，三线位移，三线孔隙压力，缩减积分C3D8 RPH 8-node brick, trilinear displacement, trili near pore pressure, reduced integration, hybrid, constant pressure8节点实体，三线位移，三线孔隙压力，缩减积分，混合动力，恒定压力C3D8 RT 8-node thermally coupled brick, trilinear displacement and temperature, reduced integration, hourglass control8节点热耦合实体，三线位移和温度，缩减积分，沙漏控制C3D8 RHT 8-node thermally coupled brick, trilinear displacement and temperature, reduced integration, hourglass control, hybrid, constant pressure8节点热耦合实体，三线位移和温度，缩减积分，沙漏控制，混合动力，恒定压力SC8R T 8-node linear displacement and temperat ure, quadrilateral in-plane general- purpose continuum shell, reduced integr ation with hourglass control, finitemembrane strains8节点的线性位移和温度，四边形平面内通用的连续体外壳，具有沙漏控制和缩减积分，有限膜应变CCL1 2 12-node cylindrical brick 12节点的圆柱形实体Tria6STRI 65 6-node triangular thin shell, using five degrees of freedom pernode6节点三角形薄壳，每个节点有五个自由度DS6 6-node heat transfer triangular shell6节点传热三角形壳M3D 6 6-node triangular membrane 6节点三角形膜SFM3 D6 6-node triangular surface element 6节点三角形面单元Quad8S8R 8-node doubly curved thick shell, reduced integration8节点双重弯曲厚壳，缩减积分S8R5 8-node doubly curved thin shell, reduced integration, using five degrees offreedom per node8节点双重弯曲厚壳，缩减积分，每节点有五个自由度S8RT 8-node thermally coupled quadrilateral general thick shell, biquadraticdisplacement, bilinear temperature in the shell surface8节点热耦合四边形通用厚壳，四次位移，外壳表面的线性位移DS8 8-node heat transfer quadrilateral shell8节点传热四边形壳M3D 8 8-node quadrilateral membrane 8节点四边形膜M3D 8R 8-node quadrilateral membrane, reducedintegration8节点四边形膜，缩减积分SFM3 D8 8-node quadrilateral surface element 8节点四边形面单元SFM3 D8R 8-node quadrilateral surface element, reduced integration8节点四边形曲面单元，缩减积分Tetra10C3D1 0 10-node quadratic tetrahedron 10节点二次四面体C3D1 0H 10-node quadratic tetrahedron, hybrid, constant pressure10节点二次四面体，混合动力，恒定压力C3D1 0M 10-node modified tetrahedron, hourglasscontrol10节点修饰四面体，沙漏控制C3D1 0MH 10-node modified quadratic tetrahedron, hybrid, linear pressure, hourglasscontrol10节点修饰四面体，混合动力，线压力，沙漏控制DC3 D10 10-node quadratic heat transfer tetrahedron10节点二次传热四面体C3D1 0E 10-node quadratic piezoelectric tetrahedron10节点二次压电四面体DC3 D10E 10-node quadratic coupled thermal-electrical tetrahedron10节点二次热—电耦合四面体AC3 D10 10-node quadratic acoustic tetrahedron 10节点二次声学四面体C3D1 0MP 10-node modified displacement and pore pressure tetrahedron, hourglasscontrol10节点修饰位移和孔隙压力四面体，沙漏控制C3D110-node modified displacement and pore0MP Hpressure tetrahedron, hybrid, linear pressure, hourglass control10节点修饰位移和孔隙压力四面体，混合动力，线压力，沙漏控制C3D1 0MT 10-node thermally coupled modified qua dratic tetrahedron, hourglasscontrol10节点热耦合修饰二次四面体，沙漏控制C3D1 0I 10-node general-purpose quadratic tetra hedron, improved surface stressvisualization10节点的通用二次四面体，提高表面应力形象化Pyramid13C3D2 0 20-node quadratic brick 20节点二次实体C3D2 0H 20-node quadratic brick, hybrid, linear pressure20节点二次实体，混合动力，线压力C3D2 0R 20-node quadratic brick, reduced integration20节点二次实体，缩减积分C3D2 0RH 20-node quadratic brick, hybrid, linear pressure, reducedintegration20节点二次实体，混合动力，线压力，缩减积分C3D2 0E 20-node quadratic piezoelectric brick 20节点二次压电实体C3D2 0RE 20-node quadratic piezoelectric brick, reduced integration20节点二次压电实，缩减积分C3D2 0T 20-node thermally coupled brick, triqua dratic displacement, trilineartemperature20节点热耦合实体，三重二次位移，三线性温度C3D2 0HT 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,hybrid, linear pressure20节点热耦合实体，三重二次位移，三线温度，混合动力，线压力C3D2 0RT 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,reduced integration20节点热耦合实体，三重二次位移，三线温度，缩减积分C3D2 0RH T 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,hybrid, linear pressure, reduced integration20节点热耦合实体，三重二次位移，三线温度，混合动力，线压力，缩减积分C3D1 5 15-node quadratic triangular prism 15节点二次三角形棱柱C3D1 5H 15-node quadratic triangular prism, hybrid, linear pressure15节点二次三角形棱柱，混合动力，线压力C3D1 5E 15-node quadratic piezoelectric triangular prism15节点二次压电三角形棱柱Penta15C3D1 5 15-node quadratic triangular prism 15节点二次三角形棱柱C3D1 5H 15-node quadratic triangular prism, hybrid, linear pressure15节点二次三角形棱柱，混合动力，线压力DC3 D15 15-node quadratic heat transfer triangular prism15节点二次传热三角形棱柱C3D1 5E 15-node quadratic piezoelectric triangular prism15节点二次压电三角形棱柱DC3 D15E 15-node quadratic coupled thermal-elect rical triangular prism15节点二次耦合热—电三角形棱柱AC3 D15 15-node quadratic acoustic triangular prism15节点二次声学三角形棱柱Hex20C3D2 0 20-node quadratic brick 20节点二次实体C3D2 0H 20-node quadratic brick, hybrid, linear pressure20节点二次实体，混合动力，线压力C3D2 0R 20-node quadratic brick, reduced integration20节点二次实体，缩减积分C3D2 0RH 20-node quadratic brick, hybrid, linear pressure, reducedintegration20节点二次实体，混合动力，线压力，缩减积分DC3 D20 20-node quadratic heat transfer brick 20节点二次传热实体AC3 D20 20-node quadratic acoustic brick 20节点二次声学实体C3D2 0E 20-node quadratic piezoelectric brick 20节点二次压电实体C3D2 0RE 20-node quadratic piezoelectric brick, reduced integration20节点二次压电实，缩减积分C3D2 0T 20-node thermally coupled brick, triqua dratic displacement, trilineartemperature20节点热耦合实体，三重二次位移，三线性温度C3D2 0HT 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,hybrid, linear pressure20节点热耦合实体，三重二次位移，三线温度，混合动力，线压力C3D2 0RT 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,reduced integration20节点热耦合实体，三重二次位移，三线温度，缩减积分C3D2 0RH T 20-node thermally coupled brick, triqua dratic displacement, trilinear temperature,hybrid, linear pressure, reduced integration20节点热耦合实体，三重二次位移，三线温度，混合动力，线压力，缩减积分DC3 D20E 20-node quadratic coupled thermal-electrical brick20节点二次耦合热—电实体C3D2 0P 20-node brick, triquadratic displacement , trilinear pore pressure20节点实体，三重二次位移，三线孔隙压力C3D2 0PH 20-node brick, triquadratic displacement , trilinear pore pressure, hybrid, linearpressure20节点实体。

ABAQUS中实体单元的应用

ABAQUS中实体单元的应用在ABAQUS的单元库中，应用最广泛的是应力/位移实体单元族。

对三维单元，可以选择六面体、四面体和楔形体；对二维单元则可在三角形与四边形之间进行选择。

这些基本的单元形状，每一种都有线性和二次的两类选择。

对六面体和四边形，还可选择完全积分或减缩积分。

最后，还可选用标准元或杂交元列式。

另外对线性六面体或四边形单元，还有个附加的功能，可选择非协调模式，而对二次的三角形或四面体单元可以应用修正列式。

若列出所有种类的单元，所面临的实体单元的总数目是相当大的，仅三维单元而言就超过20种。

模拟的精度将强烈地依赖于所采用的单元类型。

特别是在初次使用时，在这些单元中选择哪一个最为合适很可能是一件令人苦恼的事情。

然而，用户会逐渐把这个工作看作是从一个20多件的工具组中，有能力选择最恰当的工具或单元来完成的一个有价值的工作。

这一章讨论了不同的单元列式和积分水平对一个特定分析的精度的影响。

同时也讨论了一些选择实体单元的一般性原则。

这些讨论提供了获得更多应用ABAQUS经验和知识的基础。

在本节末的例子将允许用户应用这些知识建立和分析一个连接柄构件的模型。

4.1 单元列式和积分通过图4-1所示的悬臂梁，可阐明单元阶数（线性或二次），单元列式及积分水平等因素对结构模拟精度的影响。

这是评估一个给定单元的性能的经典测试。

因为该构件相对是细长的，我们通常用梁单元来对它建立模型。

但在这里我们用这个测试来帮助评估各种实体单元的效率。

梁长150mm，宽2.5mm，高5mm；一端固定；自由端承受5N的荷载。

材料的杨氏模量E为70GPa，泊松比为0.0。

采用梁的理论，在载荷P作用下，梁自由端的挠度为δtipplEI =3 3其中I bd=312/，l是长度，b是宽度，d是梁的高度。

P = 5N时自由端挠度是3.09mm。

图4-1 自由端受集中载荷的悬臂梁4.1.1 完全积分所谓“完全积分”是指当单元具有规则形状时，所用的Gauss积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。

abaqus单元属性大总结

S3/S3R 单元可以作为通用壳单元使用。

由于单元中的常应变近似，需要划分较细的网格来模拟弯曲变形或高应变梯度。

对于几何非线性分析，在ABAQUS/Standard中的小应变壳单元（S4R5, S8R, S8R5, S8RT, S9R5, STRI3, 和STRI65）使用总体拉格朗日应变算法，应力应变可以相对于参考构型的材料方向改定。

垫片单元是小应变小位移单元，默认情况下其应力应变值也是以初始参考构型定义的行为方向输出。

对于有限膜应变单元（所有的膜单元以及S3/S3R, S4, S4R, SAX,和 SAXA单元）和在ABAQUS/Explicit中的小应变单元，其材料方向是随着曲面的平均刚性旋转运动而变以形成当前构型的材料方向。

此时这些单元的应力应变则是根据当前的参考构型中的材料方向给出的。

（更详细地说明可以参考ABAQUS相关手册）。

用户可以决定与*section print和*section file相关的局部坐标系统是固定不动还是随着曲面的平均刚性运动而旋转。