fftfilt函数的用法matlab
Matlab中的FFT使用说明

FFT是Fast Fourier Transform(快速傅里叶变换)的简称,FFT算法在MATLAB中实现的函数是Y=fft(x,n)。
刚接触频谱分析用到FFT时,几乎都会对MATLAB 的fft函数产生一些疑惑,下面以看一个例子(根据MATLAB帮助修改)。
Fs = 2000; % 设置采样频率T = 1/Fs; % 得到采用时间L = 1000; % 设置信号点数,长度1秒t = (0:L-1)*T; % 计算离散时间,% 两个正弦波叠加f1 = 80;A1 = 0.5; % 第一个正弦波100Hz,幅度0.5f2 = 150;A2 = 1.0 ; % 第2个正弦波150Hz,幅度1.0A3 = 0.5; % 白噪声幅度;x = A1*sin(2*pi*f1*t) + A2*sin(2*pi*f2*t); %产生离散时间信号;y = x + A3*randn(size(t)); % 叠加噪声;% 时域波形图subplot(2,1,1)plot(Fs*t(1:50),x(1:50))title('Sinusoids Signal')xlabel('time (milliseconds)')subplot(2,1,2)plot(Fs*t(1:50),y(1:50))title('Signal Corrupted with Zero-Mean Random Noise')xlabel('time (milliseconds)')NFFT = 2^nextpow2(L); % 设置FFT点数,一般为2的N次方,如1024,512等Y = fft(y,NFFT)/L; % 计算频域信号,f = Fs/2*linspace(0,1,NFFT/2+1);% 频率离散化,fft后对应的频率是-Fs/2到Fs/2,由NFFT个离散频点表示% 这里只画出正频率;% Plot single-sided amplitude spectrum.figure;plot(f,2*abs(Y(1:NFFT/2+1)));% fft后含幅度和相位,一般观察幅度谱,并把负频率加上去,title('Single-Sided Amplitude Spectrum of y(t)')xlabel('Frequency (Hz)')ylabel('|Y(f)|')运行结果时域波形图如图所示:幅度谱如下:由图可见,80Hz的信号幅度为0.4762,频率为80.08,150Hz的信号频率为150.4,幅度0.9348,存在误差。
实验用MATLAB计算傅里叶变换

实验二 用MATLAB 计算傅立叶变换(2课时)一、实验目的1、掌握用MA TLAB 计算DTFT 及系统频率响应的方法。
2、掌握用MA TLAB 计算DFT 和IDFT 的方法。
3、掌握用DFT 计算圆周卷积和线性卷积的方法。
二、实验设备计算机一台,装有MATLAB 软件。
三、实验原理和基本操作1.用MA TLAB 计算DTFT对于序列x (n ),其离散时间傅立叶变换(DTFT )定义为:∑∞-∞=-=n n j e n x j X ωω)()( (1)序列的傅立叶变换(DTFT )在频域是连续的,并且以ω=2π为周期。
因此只需要知道jw X(e )的一个周期,即ω=[0,2π],或[-π,π]。
就可以分析序列的频谱。
用MA TLAB 计算DTFT ,必须在-π≤ω≤π范围内,把ω用很密的、长度很长的向量来近似,该向量中各个值可用下式表示: w=k*dw=k*K π2 (2) 其中:d ω=Kπ2 称为频率分辨率。
它表示把数字频率的范围2π均分成K 份后,每一份的大小,k 是表示频率序数的整数向量,简称为频序向量,它的取值可以有几种方法:通常在DTFT 中,频率取-π≤ω<л的范围,当K 为偶数时,取 k 12,,1,0,1,,12,2--+--=K K K 如果K 为奇数,则取 k 5.02,,1,0,1,,5.02--+-=K K 可以为奇偶两种情况综合出一个共同的确定频序向量k 的公式; k=12K -⎢⎥-⎢⎥⎣⎦ :12K -⎢⎥⎢⎥⎣⎦(3) 上式中⎢⎥⎣⎦表示向下取整。
在MA TLAB 中的向下取整函数为floor ,floor (x )的作用是把x 向下(向-∞方向)取整,所以与(3)式等价的MATLAB 语句为 k ))5.02(:)5.02((-+-=K K floor (4) 给定了输入序列(包括序列x 及其位置向量n ),又设定了频率分辨率d ω及频序向量k ,则DTFT 的计算式(1)可以用一个向量与矩阵相乘的运算来实现。
matlab自带的滤波器函数

matlab自带的滤波器函数
Matlab自带的滤波器函数可以用于对信号进行滤波处理,常用的函数有:
1. fir1函数:设计一阶低通、高通、带通、带阻滤波器的FIR 数字滤波器,可自定义通带和阻带的截止频率。
2. cheby1函数:设计ChebyshevI型低通、高通、带通、带阻数字滤波器,可自定义通带和阻带的截止频率和最大通带波纹。
3. butter函数:设计Butterworth型低通、高通、带通、带阻数字滤波器,可自定义通带和阻带的截止频率和滤波器阶数。
4. filtfilt函数:对信号进行双向滤波处理,可避免滤波后信号的相位畸变和滞后。
这些函数可以在Matlab的Signal Processing Toolbox中找到,可根据需要选择合适的函数进行滤波处理。
- 1 -。
MATLAB中fft函数的正确使用方法

MATLAB中fft函数的正确使⽤⽅法 问题来源:在阅读莱昂斯的《数字信号处理》第三章离散傅⾥叶变换时,试图验证实数偶对称信号的傅⾥叶变换实部为偶对称的且虚部为零。
验证失败。
验证信号为矩形信号,结果显⽰虚部是不为零且最⼤幅值等于信号幅值。
错误原因:MATLAB中的fft函数默认其 N 点输⼊信号的时间序号为从 0 到 N-1 ,默认其输出信号的频率序号为从 0 到 N-1 。
⽽当试图输⼊⼀个时间序号为从 -N/2 到 N/2-1 ( N 为偶数时)或从 -(N-1)/2 到 (N-1)/2 ( N 为奇数)的信号时,输出将会产⽣相移,看到的频谱的实部、虚部和相位都不是原始信号的 fft 的结果。
只有频谱的幅值等于原始信号的 fft 的结果。
解决⽅法:在进⾏ fft 之前须使⽤ ifftshift 函数对原始信号进⾏移位,整个正确的 fft 过程为 fft(ifftshift(signal)) 。
然⽽这样计算得到的 fft 也需要在频域使⽤ fftshift 进⾏移位才能显⽰频率序号为从 -N/2 到 N/2-1 ( N 为偶数时)或从 -(N-1)/2 到 (N-1)/2 ( N 为奇数)的频谱,即fftshift(fft(ifftshift(signal))) 。
在对频率序号为从 -(N+1)/2 到 (N+1)/2 的信号进⾏ ifft 的时候也会有类似的问题,解决⽅式为fftshift(ifft(ifftshift(spectrum))) 。
注意:当 N 为奇数,若要使⽤ ifftshift 构造偶对称信号,须按照时间序号为从 -N/2 到 N/2-1 构造。
即构造 [ 1 2 3 4 5 4 3 2 ] 经过ifftshift 之后变为 [ 5 4 3 2 1 2 3 4 ] ,原信号中位于 0 时间序号的“5”依然在 0 时间序号的位置。
参考资料1. FFT of a real symmtric vector is not real and symmetric2. Correct use of fftshift and ifftshift at input to fft and ifft。
matlab中进行傅里叶变换

matlab中进行傅里叶变换
Matlab中进行傅里叶变换的方法是使用内置函数fft和ifft,它们分别用于实现正反傅里叶变换。
正向傅里叶变换fft(x)是将实际信号x从时域中转换为频域中的复数形式,其中可以通过峰值频率获得信号的特征。
反向傅里叶变换ifft(y)是将频域信号y转换回时域,可以显示该信号在时域中的波形。
Matlab有多种如fft, fft2, fftshift, ifft, ifft2和
ifftshift等内置函数,可用于实现傅里叶变换。
用于实现二维傅里叶变换的函数fft2及ifft2,用于实现一维傅里叶变换的函数fft及ifft,都可以在Matlab中使用。
在Matlab中使用正反傅里叶变换的步骤如下:
1. 生成原始信号。
2. 使用fft函数对原始信号进行正向傅里叶变换,从而将其转换到频谱中。
3. 检查和分析转换后的频谱数据。
4. 使用ifft函数对原始信号进行反向傅里叶变换,从而将其转换回时域中。
5. 分析和检查反变换后的时域数据。
6. 进行模糊处理,以消除低频干扰 (如果需要的话)。
7. 如果需要的话,对频谱中的关键峰值进行分析,以检查非线性特性或其他特殊特征。
最后,在Matlab中使用傅里叶变换之前,应该先审查要处理的信号,以确定是否需要进行任何预处理,如移除低频带或其他可能影响数据质量的干扰因素。
[FFT] matlab中关于FFT的使用(理解频率分辨率、补零问题)
![[FFT] matlab中关于FFT的使用(理解频率分辨率、补零问题)](https://img.taocdn.com/s3/m/a70abc3d0912a21614792974.png)
[FFT] matlab中关于FFT的使用(理解频率分辨率、补零问题)一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
matlab中fft的用法及注意事项
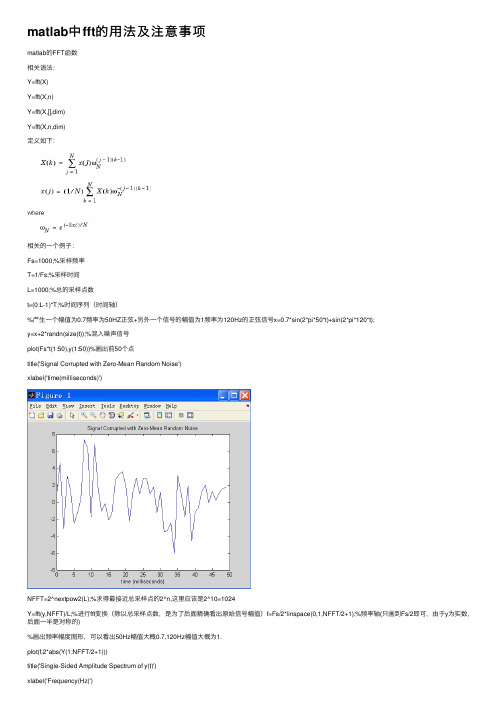
matlab中fft的⽤法及注意事项matlab的FFT函数相关语法:Y=fft(X)Y=fft(X,n)Y=fft(X,[],dim)Y=fft(X,n,dim)定义如下:相关的⼀个例⼦:Fs=1000;%采样频率T=1/Fs;%采样时间L=1000;%总的采样点数t=(0:L-1)*T;%时间序列(时间轴)%产⽣⼀个幅值为0.7频率为50HZ正弦+另外⼀个信号的幅值为1频率为120Hz的正弦信号x=0.7*sin(2*pi*50*t)+sin(2*pi*120*t);y=x+2*randn(size(t));%混⼊噪声信号plot(Fs*t(1:50),y(1:50))%画出前50个点title('Signal Corrupted with Zero-Mean Random Noise')xlabel('time(milliseconds)')NFFT=2^nextpow2(L);%求得最接近总采样点的2^n,这⾥应该是2^10=1024Y=fft(y,NFFT)/L;%进⾏fft变换(除以总采样点数,是为了后⾯精确看出原始信号幅值)f=Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后⾯⼀半是对称的)%画出频率幅度图形,可以看出50Hz幅值⼤概0.7,120Hz幅值⼤概为1.plot(f,2*abs(Y(1:NFFT/2+1)))title('Single-Sided Amplitude Spectrum of y(t)')xlabel('Frequency(Hz)')ylabel('|Y(f)|')主要有两点注意的地⽅:1、从公式上看,matlab的fft序号是从1到N,但是绝⼤多数教材上是从0到N-1。
2、2、Y=fft(x)之后,这个Y是⼀个复数,它的模值应该除以(length(x)2),才能得到各个频率信号实际幅值。
MATLAB中FFT的运用方法

MATLAB中FFT的使用方法说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MATLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求得Fourier变换后的振幅f=n*fs/N; %频率序列subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N); %对信号进行快速Fourier变换mag=abs(y); %求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fftfilt函数的用法matlab
fftfilt函数是MATLAB中一个用于进行FIR滤波的函数。
它通过使
用快速傅里叶变换(FFT)来实现滤波操作,能够提供高效的信号滤波功能。
该函数可以应用于各种信号处理和通信系统建模任务,例如音频处理、图像处理和信号恢复等。
y = fftfilt(b, x)
其中,b是滤波器的系数向量,x为待滤波的输入信号,y是输出的
滤波结果。
fftfilt函数以时间域的方式进行FIR滤波。
具体来说,它首先将输
入信号x和滤波器系数b分别进行FFT,再将它们的频域表示相乘,最后
进行IFFT以得到最终的滤波结果。
fftfilt函数有效地利用了FFT算法
的高效性质,可以大大加快滤波的速度。
使用fftfilt函数的一般步骤如下:
1.定义滤波器系数b:滤波器系数决定了滤波过程中的频率响应。
可
以通过各种设计方法,如窗函数法、频率采样法或优化法来获得。
滤波器
系数向量b的长度决定了滤波器的阶数。
通常,滤波器的阶数越高,滤波
器的性能越好,但计算成本也会增加。
2.准备待滤波的输入信号x:输入信号可以是任意时域信号,例如音
频数据、图像数据或电子信号等。
3. 调用fftfilt函数进行滤波:使用fftfilt函数对输入信号x进
行滤波,得到滤波结果y。
滤波器系数b会被用于对输入信号进行滤波。
4.分析和处理滤波结果:根据具体的应用需求,对滤波结果进行分析和处理。
可以使用MATLAB提供的各种工具来进行进一步的信号处理和分析,例如绘图、频谱分析或特征提取等。
1. 滤波器系数b的选择非常重要,它决定了滤波器的特性和性能。
根据应用需求,需要选择适当的滤波器类型和参数。
MATLAB提供了一些滤波器设计函数,如fir1和fir2等,可以用于生成合适的滤波器系数。
2. 输入信号x和滤波器系数b的长度应该相等或有关系,否则会引发尺寸不匹配的错误。
可以使用MATLAB的函数padarray或resample来调整信号的长度。
3. fftfilt函数支持多通道信号滤波。
如果输入信号x是一个多通道矩阵,则会对每个通道分别进行滤波。
4. 对于长时间序列的滤波,fftfilt函数的速度比直接使用filter 函数要快。
所以在对长时间序列进行滤波时,推荐使用fftfilt函数。
5. 虽然fftfilt使用FFT和IFFT进行滤波,但得到的结果与使用filter函数基于直接卷积的滤波结果是一致的,只是速度更快。
因此,fftfilt是一个高效的替代filter函数的工具。
综上所述,fftfilt函数是MATLAB中一个强大的FIR滤波工具,可以通过FFT加速滤波过程,提供高效、快速的滤波功能。
它广泛应用于各种信号处理任务,帮助工程师和科学家在音频处理、图像处理和通信系统建模等领域取得出色的成果。
