对坐标曲线积分例题与习题
空间曲线中对坐标的曲线积分的一题多解

空间曲线中对坐标的曲线积分的一题多
解
摘要:计算空间曲线中对坐标的曲线积分的计算较复杂,本文针对此类曲线积分提供了三种新的解法,为空间曲线中对坐标的曲线积分提供了新思路。
关键词:空间曲线;曲线积分;一题多解
一、预备知识
设空间曲线的参数方程为
法一
法二
法三
二、简单应用
应用1 计算曲线积分,其中是曲面
和曲面的交线,从轴正向看去为逆时针方向.
解法一:由题可知,作出曲线的图,见图1
图1
曲线的参数方程为
则
解法二:取为边界的曲面,取上侧在面上的投影区域为
的单位法向量为
且
则
解法三:
应用2 计算,其中是圆柱面和平面的交线,从轴正向看去为逆时针方向.
解法一由题可知,作出曲面的图,见图2
图2
曲线的参数方程为
则
解法二:取为边界的曲面,取上侧在面上的投影区域为
的单位法向量为
且
则
解法三:
四、结语
综上可知,本文给出了求空间曲线中对坐标的曲线积分的三种求解方法,针对两个典型应用题,并给出了相应的解法。
参考文献:
[1]同济大学数学系编,高等数学[M],-7版,北京:高等教育出版社,2014,07.
[2]齐小军.关于对坐标的曲面积分若干问题研究[J].华东纸业.2022,02.
[3]银俊成、蔡智辉.一题多解探讨曲线积分的计算[J].高等数学研
究.2023,02.。
练习112(对坐标的曲线积分及两类曲线积分之间的关系) - 答案

练习册 112 对坐标的曲线积分及两类曲线积分之间的关系(答案)1、设L 是xoy 平面内直线a x =上的一段,求()⎰=Ldx y x P I ,。
解:a x = ,0=dx , ()0,==∴⎰Ldx y x P I 。
2、设L 是xoy 平面内直线a y =上的一段,求()⎰=Ldy y x Q I ,。
解:a y = ,0=dy , ()0,==∴⎰Ldy y x Q I 。
3、设L 是xoy 平面内x 轴上从点()0,a 到点()0,b 的一直线段,求()⎰=Ldx y x P I ,。
解:因为L :0=y ,x 从a 变化到b ,所以()()⎰⎰==ba L dx x f dx y x P I 0,,。
4、计算⎰=Lxydx I ,其中L 为圆周()()0222>=+-a a y a x 及x 轴所围成的在第一象限内的区域的按照逆时针方向的整个边界。
解:令从点O 到点A 的有向直线段为1L ,从点A 到点O 的有向半圆弧(第一象限内)为2L (如右图所示),有21L L L +=,又因为1L :0=y ,x 从0变化到a 2,2L :θcos a a x =-,θsin a y =,θ从0变化到π, 所以,()()⎰⎰⎰⎰⎰-++⋅=+==πθθθθ020sin sin cos 021d a a a a dx x xydx xydx xydx I a L L L ()πππππθθθθθθθθθθθ 0 32022022022022sin 31sin 2sin cos sin sin cos 1⎥⎦⎤⎢⎣⎡--=--=+-=⎰⎰⎰⎰d a d a d a d a 2222212a a ππ-=⨯⨯-=。
5、计算⎰Γ+-=ydz dy dx I ,其中Γ为有向折线ABCA ,这里A ,B ,C 的坐标分别为()0,0,1,()0,1,0,()1,0,0。
解:Γ可以分成光滑有向线段AB ,BC 和CA 。
高等数学D10习题课

Pdx Qdy Rdz
dydz dzdx dxdy
PdydzQdzdx Rdxdy
x
y
z
PQ R
(Px
Q y
R)dv z
(三)场论初步
梯度 gra duiu u juk x y z
通量 散度
Pdy Q dzd zR dxdxdy
diA vPQR x y z
环流量 PdQ x d R y dz
计
f(x, y,z)ds
R(x,y,z)dxdy
算
f[x,y,z(x,y)]1zx 2z2 ydxdyR[x,y,z(x,y)d] xdy
D xy
Dxy
一代,二换,三投(与侧无关) 一代,二投,三定向 (与侧有关)
(二)各种积分之间的联系
曲线积分
计算
定积分
Stokes公式
计算 曲面积分
Guass公式
格林公式
3.三重积分与曲面积分的联系
( P x Q y R z)d v P d Q yd d R zzd dx xd
高斯公式
4.曲面积分与曲线积分的联系
R Q
P R
Q P
(yz)dyd(zzx)dzdx (xy)dxd
PdxQdyRdz
斯托克斯公式
Green公式,Guass公式,Stokes公式 之间的关系
旋度 rA o ( R t Q ) i ( P R ) j ( Q P ) k y z z x x y
二、典型例题
例 1 计 算 I (x22x)ydx (x2y4)d, y L
其 中 L为 由 点 O(0,0)到 点 A(1,1)的 曲 线 ysi nx. 2
(PcosQcos Rcos)ds
D8.1_曲线积分_习题课
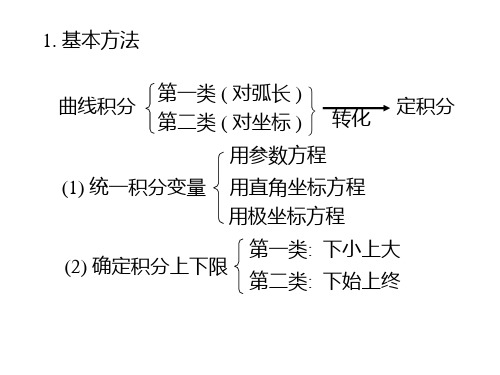
其中L 是沿逆
时针方向以原点为中心, a 为半径的上半圆周.
y
C
这说明积分与路径无关, 故
L
2
I
AB a 2 x dx a
( x y ) d x ( y x ) dy
2
B
o
Ax
解法2 添加辅助线段 BA , 它与L所围区域为D, 则
I
L BA
( x y ) d x ( y x) d y ( xz
B
利用对称性
3
AB AB
y d x z d y xdz xd z
3
A x
o
C y
3 (1 z )d z
0
1
考研真题
1. (数学一 2010)
已知曲线 L 的方程为 y 1 x (x [1,1]) 起点是 (1, 0), 终点是 (1, 0), 则曲线积分 xydx x 2dy =
I 2 ( x y y ) d x ( y 2 x) d y
2
2
L
练习题:
1. 计算
其中L为上半圆周
沿逆时针方向.
x
提示:
I e sin y d x (e cos y 2)d y 2 y d x
x L L
L AB
AB
2 yd x
L
y
2 为从点 A(3, ) 到 B(1,2) 的直线段。 3 13 2 1 4 2 解: ∴原式= 3 [1 f ( x)]dx 2 2 [y2f (y) 1]dy 2 9 3 3 y
2 3 2 2 1 [ f ( x)]dx 2 [ f ( y) 2 ]dy 3 2 3 3 y 3 1
高数--对坐标的曲线积分

• B(1,1) y2 = x
x = y 2 dx = 2 ydy , y从− 1到1 到
∫L
xy d x = ∫ y 2 ⋅ y ⋅ 2 ydy
−1
1
O
x
• A(1,−1)
= 2 ∫ y4 dy −
1
1
4 = 5
15
对坐标的曲线积分
例 计算 ∫ xdx + ydy + ( x + y − 1)dz
17
对坐标的曲线积分
计算 ∫ x 2dx + ( y − x )dy , 其中
L
(2) L是x轴上由点 A(a ,0) 到点B( − a ,0) 的线段 的线段. 是 轴上由点 (2) L的方程为 y = 0, x从a到− a. 的方程为 原式= 原式
∫a
−a
x dx
2
y
2 3 =− a 3
B(−a,0) O
Γ
其中Γ是由点 到点B(2,3,4)的直线段 的直线段. 其中 是由点A(1,1,1)到点 是由点 到点 的直线段
x −1 y −1 z −1 = = 直线AB的方程为 解 直线 的方程为 1 2 3
化成参数式方程为 x = 1+ t, y = 1 + 2t, z = 1+ 3t + A点对应 t = 0, B点对应 t = 1, 于是 点对应 点对应
i =1
n
取极限 W = lim [ P (ξ i ,η i ) ⋅ ∆xi + Q(ξ i ,η i ) ⋅ ∆yi ] ∑
λ→0i =1
精确值
3
对坐标的曲线积分
二、对坐标的曲线积分的概念
1. 定义 面内从点A到点 的一条有向 设L为xOy面内从点 到点 的一条有向光滑 为 面内从点 到点B的一条有向光滑 曲线弧, 曲线弧 函数P ( x , y ), Q ( x , y )在L上有界 用L上的点 上的点: 上的点 上有界. 上有界 M 1 ( x1 , y1 ), M2 ( x2 , y2 ), LM n −1 ( x n −1 , y n−1 ) 分成n个有向小弧段 把L分成 个有向小弧段 Mi −1 Mi (i = 1,2,L, n; 分成
对坐标的曲线积分习题解析

(以下各题解析仅供参考,大家还可想想其他方法.)1、计算下列对坐标的曲线积分 (1)d Lx y x ⎰,其中L 为圆周222()(0)x a y a a -+=>及x 轴所围成的区域在第一象限内的整个边界(取逆时针方向); 答案: 312a π-解析: 方法一本题考查课本第131页知识点——本题中的有向曲线段L (图1)由逆时针方向弧段2221:()(0)L x a y a y -+=≥和x 轴上直线段2:0(:02)L y x a =→两个部分构成. 分别求出两条积分弧段上的曲线积分,再求和.先看2221:()(0)L x a y a y -+=≥,其方程可化为 参数方程cos sin x a a ty a t =+⎧⎨=⎩,由于L 的方向取作逆时针方向,可知起点(2,0)a 对应的0t =,终点(0,0)对应的t π=.本题只要求对坐标x 的曲线积分,根据上述知识点中的计算公式,有1d L x y x ⋅⎰20(1a π=+⎰30(1a π=-⎰3(cos d )a t t π=-⋅⋅⎰图1利用倍角公式降次凑微分32001cos 2[d sin d(sin )]2ta t t t ππ-=-⋅+⎰⎰330011sin (d cos 2d )223ta t t t πππ=-⋅-+⎰⎰3011[cos 2d()0]22122a t t ππ⋅=-⋅⋅-⋅+⎰33301(sin 2)(0)2422a t a a ππππ=-⋅-⋅=-⋅-=-. 再看x 轴上直线段2:0(:02)L y x a =→0y =⎩. 根据对坐标的曲线积分计算公式,有2d L x y x ⋅⎰2000d ax x =⋅=⎰.综上所述,所求积分d Lx y x ⎰1233d d 022L L x y x x y x a a ππ=⋅+⋅=-+=-⎰⎰.方法二 利用格林公式——本题只要求对坐标x 的曲线积分d Lx y x ⎰,我们可以记(,)P x y xy =,(,)0Q x y =,求得P x y ∂=∂,0Q x ∂=∂,这里P Qy x∂∂≠∂∂. 本题中的{(,)|02,0D x y x a y =≤≤≤≤,如图1 (1) 所示,化为极坐标{(,)|0,02cos }2D a πρθθρθ=≤≤≤≤(方程222x y ax +=可化为22cos a ρρθ=),容易验证本题满足格林公式的条件,根据格林公式来计算积分值(本题中是把曲线积分化为二重积分计算)——d 0d Lx y x y +⎰()d DQ P x yσ∂∂=-∂∂⎰⎰ (0)d Dx σ=-⎰⎰2cos 20d (cos )d a πθθρθρρ=-⋅⎰⎰凑微分图1 (1)==3383134222a a ππ=-⋅⋅⋅=-.(大家可以对比方法一和方法二的运算量,选取简便的方法或自己熟悉的方法计算.) (2)2d d d x x z y y z Γ+-⎰,其中Γ为曲线x θ=,cos y θ=,sin z θ=上对应θ从0到π的一段弧;答案:313ππ-解析: 本题中的积分弧段Γ(图2)是一条有向空间 曲线,根据已知条件中Γ的参数方程及指定的方向,可 2d d()cos sin s d(o in c )s πππθθθθθθ=+-⎰⎰⎰20d ()sin c si o d n c s d os πππθθθθθθθθ-=+⋅-⋅⎰⎰⎰2220d (sin cos )d ππθθθθθ=-+⎰⎰31d 3ππθθ=-⎰33ππ=-.(本题中的积分弧段是空间曲线,而格林公式是讨论平面上的情况,因此不适用格林公式.)图2为了计算简便, 可以根据积分的性质, 把这两个积分合并在一起.1331(242213421(253n n n n n n π----为偶数为奇数(3)(2)d d Ly x x y -+⎰,其中L 为摆线sin 1cos x t ty t=-⎧⎨=-⎩对应10t =到22t π=的一段弧; 答案: 2π-解析: 本题中的积分弧段L (图3)是一条有向平面曲线, 根据已知条件中L 的参数方程及指定的方向,可得(2)d d Lx y x y -+⎰220si [2()]d()1cos 1cos ()d()n sin t t t t t t ππ-+-=---⎰⎰2201c cos s (1)()d os sin )d in (t t t t t t t ππ-+-=+⋅⋅⎰⎰22220(1cos )d (sin sin )d t t t t t t ππ=-+⋅-⎰⎰22222201d cos d sin d sin d t t t t t t t t ππππ=-+⋅-⎰⎰⎰⎰2222201d (cos sin )d sin d t t t t t t t πππ=-++⋅⎰⎰⎰22201d 1d d(cos )t t t t πππ=-+-⎰⎰⎰2200(cos )(cos )d t t t t ππ=⋅---⎰220(cos )cos d t t t t ππ=-⋅+⎰20(210)sin 202tππππ=-⋅-+=-+=-.(本题中的积分弧段是摆线,用参数方程表示比较简便,要转化成直角坐标情形比较麻烦,所以,不方便利用格林公式转化成二重积分计算.) (4)22(2)d (2)d Lx xy x y xy y -+-⎰,其中L 为抛物线2y x =上从点(1,1)A -到点(1,1)B 的一段弧;答案: 1415-解析: 方法一本题中的积分弧段L (图4)是一条有向平面曲线, 根据已知条件中L 的方程及指定的方向(:11x -→),可得为了计算简便, 可以根据积分的性质, 把这两个积分合并在一起.分部积分法“反、对、幂、指、三”图3图422(2)d (2)d Ly y y y x x x x -+-⎰1122121222(2)d [()2)]d()x x x x x x x x --=-⋅+-⋅⎰⎰11234311(2)d (2)(2)d x x x x x x x --=-+-⋅⎰⎰111123541111d 2d 2d 4d x x x x x x x x ----=-+-⎰⎰⎰⎰351111435x x --=-⋅221443515=-⋅=-.方法二 利用格林公式——本题中的积分弧段L 并不是封闭的,所以 , 不能直接用格林公式计算,要通过做辅助线, 围出一个闭区域,再利用格林公式计算 .做辅助线1:1(:11)L y x =→-,与2:(:11)L y x x =-→共同围出了闭区域2{(,)|11,1}D x y x x y =-≤≤≤≤,如图4(1)所示,L 和L 1 是D 的正向边界(观察者沿边界走的时候,D 位于其左手边).本题中2(,)2P x y x xy =-,2(,)2Q x y y xy =-,可求得2P x y ∂=-∂,2Qy x∂=-∂,这里P Qy x∂∂≠∂∂. 容易验证在闭区域D 满足格林公式的条件,根据格林公式,有 12222(2)d (2)d (2)d (2)d LL x xy x y xy y x xy x y xy y-+-+-+-⎰⎰()d (22)d DDQ P y x x y σσ∂∂=-=-+∂∂⎰⎰⎰⎰,也即 12222(2)d (2)d (22)d (2)d (2)d LL Dxxy x y xy y y x x xy x y xy y σ-+-=-+--+-⎰⎰⎰⎰211122112d ()d (21)d (121)d(1)xx x y y x x x x --=---⋅+-⋅⎰⎰⎰22211121112()d (2)d 02x x y x yx x x x --=--++⎰⎰奇函数在对称区间 的定积分为0图4 (1)奇函数在对称区间 的定积分为0431311112()d 0223x x x x x --=--++-⎰51111222140002535315x x--=--++-=-++=-. (5)d Lx y ⎰,其中L 为指数曲线e x y =上从点(0,1)A 到点(ln 2,2)B 的一段弧;答案: 2ln2-1解析: 方法一本题只要求对坐标y 的曲线积分,本题中的积分弧段L (图5)是一条有向平面曲线,根据已知条件中L 的 方程及指定的方向(:0ln 2x →),可得d Lx y ⎰ln 2d()e x x =⎰ln 2ln 2(e )e d x x x x =⋅-⎰ln 20(ln 220)e x=⋅--2ln 2(21)2ln 21=--=-.方法二 利用格林公式—— 本题只要求对坐标y 的曲线积分d Lx y ⎰,我们可以记(,)0P x y =,(,)Q x y x =,求得0P y ∂=∂,1Q x ∂=∂,这里P Qy x∂∂≠∂∂. 本题中的积分弧段L 并不是封闭的,所以 ,不能直接用格林公式计算,要 做辅助线,围出一个闭区域,如图5(1) 所示,再利用格林公式计算 .顺着L 的方向做辅助线1:ln 2(:20)L x y =→,2:0(:ln 20)L y x =→,3:0(:01)L x y =→,它们与L 共同围出了闭区域图5分部积分法“反、对、幂、指、三”图5 (1)奇函数在对称区间 的定积分为0{(,)|0ln 2,0e }x D x y x y =≤≤≤≤,但是,L 和L 1、L 2、L 3并不是D 的正向边界,而是123d )(0d d )(0d d )(0d d )L L L y x x y x x y x x y ++++++⎰⎰⎰)d (10)d DDP y σσ-∂-=-∂⎰⎰,也即 123d 1d (d d d )LL L L Dx y x y x y x y σ=-++-⎰⎰⎰⎰⎰⎰,(请大家自己试着完成后续计算,再对比两种方法的运算量. 从本题可以看出,格林公式并不是“万能”的,有些情况下,用格林公式并不能简化计算. ) (6)d Lx y ⎰,其中L 为由两坐标轴及直线123x y+=所围成的三角形区域整个边界并取逆时针方向;答案: 3解析: 方法一本题只要求对坐标y 的曲线积分,本题中的积分 弧段L (图6)由三条有向直线段构成,要分别求出三条 线段上的曲线积分再求和.先看1:1(:20)23x y L x +=→,即1(:203(1)):2xL x y ⋅-→=,有 1d L x y ⎰02332d()x x -=⎰ 023()d 2x x =⋅-⎰203()d 2x x =⋅--⎰23d 2x x =⎰ 2203()22x =⋅3(40)34=⋅-=. 再看20:(:30)x L y y y=⎧→⎨=⎩,有2d L x y ⎰030d 0y ==⎰.最后看3:(:02)0x xL x y =⎧→⎨=⎩,有3d L x y ⎰20d00x ==⎰.综上所述,d Lx y ⎰123d d d 3003L L L x y x y x y =++=++=⎰⎰⎰.(说明:从本题可以看出,在坐标轴上求曲线积分比在其他积分弧段上求曲线积分简便.)图6方法二 利用格林公式—— 本题只要求对坐标y 的曲线积分d Lx y ⎰,我们可以记(,)0P x y =,(,)Q x y x =,求得0P y ∂=∂,1Q x ∂=∂,这里P Qy x∂∂≠∂∂. 本题中的积分弧段L 是封闭的,围出了闭区域3{(,)|02,03}2xD x y x y =≤≤≤≤-,如图6(1) 所示,L 是D 的正向边界,容易验证在闭区域D 满足格林公式的条件,根据格林公式,有0d d Lx x y +⎰1()d (10)d 2332DDQ P x y σσσ∂∂=-=-==⋅⋅=∂∂⎰⎰⎰⎰. (从本题来看,用格林公式更简便.)(7)2(2)d L x xy y +⎰,其中L 为上半椭圆22221(0)x y y a b+=≥并取逆时针方向,这里a ,b 为常数且0a >,0b >;答案:243ab解析: 方法一本题只要求对坐标y 的曲线积分,本题中的有向 弧段L 如图7所示.先把上半椭圆22221(0)x y y a b +=≥方程化为参数方程cos sin x a t y b t=⎧⎨=⎩,L 的方向取作逆时针方向,将起点(,0)a 代入参数方程可得对应的0t =,将终点(,0)a -代入参数方程可得对应的π=⎰0π=⎰0π=⎰2a = 图71331(242213421(253n n n n n n π----为偶数为奇数图6 (1)222200cos cos d 2cos sin d a b t t t abt t t ππ=⋅+⋅⎰⎰22220(1sin )d(sin )2cos d(cos )a b t t abt t ππ=--⎰⎰3222200cos 1d(sin )sin d(sin )23ta b t a b t t abπππ=--⎰⎰322200sin (11)(sin )()233t a b t a b ab ππ--=⋅-⋅- 222(2)0023a b a b ab -=⋅-⋅- 240+3ab =.方法二 利用格林公式——本题中的积分弧段L 并不是封闭的,所以 , 不能直接用格林公式计算,要通过做辅助线, 围出一个闭区域,再利用格林公式计算 .做辅助线1:0(:)L y x a a =-→,与2222:1(0,:)x y L y x a a a b +=≥→-共同围出了闭区域{(,)|,0D x y a x a y =-≤≤≤≤,如图7(1)所示,L 和L 1 是D的正向边界(观察者沿边界走的时候,D 位于其左手边).本题只要求对坐标y 的曲线积分2(2)d Lx xy y +⎰,我们可以记(,)0P x y =,2(,)2Q x y x xy =+,求得0P y ∂=∂,22Q x y x ∂=+∂,这里P Qy x∂∂≠∂∂. 容易验证在闭区域D 满足格林公式的条件,根据格林公式,有1220d (2)d 0d (2)d LL x xxy y x x xy y +++++⎰⎰()dDDQ Px y σ∂∂=-=∂∂⎰⎰⎰⎰2(2)d 2LDx xy y +=⎰⎰⎰202(0d d )(20)d(0)aaaax y y x x --=+-+⋅⎰⎰⎰凑微分图7 (1)22(02aay x -=-⎰22222()d 2aab x b a x --=⎰2222d d aaaab b x x x a--=⋅-⎰⎰2、计算d ()d Lx y x y x y +-⎰,其中L 为:(1)抛物线2x y =上从点(0,0)O 到点(1,1)A 的一段弧; (2)从点(0,0)O 到点(1,1)A 的直线段;(3)先沿x 轴从点(0,0)O 到点(1,0)B ,再沿平行于y 轴的直线到点(1,1)A 的折线.答案: (1)1730(2)13 (3)12-解析: (1)本题中的有向弧段2:(:01)L x y y =→ 如图8所示,此时,d ()d Ly y x x y x +-⎰1122020()d()()d y y y y y y =⋅+-⎰⎰112022()()d ()d y y y y y y y =⋅⋅+-⎰⎰1114202d d d y y y y y y =+-⎰⎰⎰52311102523y y y =⋅+-2111752330=+-=.(2)本题中的有向弧段:(:01)L x y y =→ 如图9所示,此时,d ()d Ly y x x y x +-⎰11()d ()d y y y y y y =⋅+-⎰⎰11200d 0d y y y =+⎰⎰31133y ==.图8图923222222422333a ab x ab ab b a ab a -=⋅-⋅=-=.先看:(:01)0OB x xL x y =⎧→⎨=⎩,此时,d ()d OBL x x x y y y +-⎰11()d ()0d 000x x x =⋅+-=⎰⎰.再看1:(:01)BA x L y y y =⎧→⎨=⎩,此时, d ()d Ly y x x y x +-⎰11()d()()111d y y y =⋅+-⎰⎰11000d 1d y y y =+-⎰⎰211111222y y=-=-=-. 综上所述,11d ()d 0()22Lx y x y x y +-=+-=-⎰.说明:上述三个小题中,被积函数都是相同的,起点和终点也是相同的,但是积分弧段不同,在不同积分弧段上求出的曲线积分也不同.从下一节的内容中,我们将会看到,被积函数、起点和终点都相同,但是积分弧段不同时,只要满足特定的条件,在不同积分弧段上求出的曲线积分也会相同.3、单位质点在力F y i x j =+的作用下,由原点(0,0)O 沿抛物线2y x =移动到点(1,1)A ,求变力F 所作的功.答案: 1解析: 本题考查以下知识点——图10(3)本题中的有向曲线L (见图10)由:(:01)0OB x x L x y =⎧→⎨=⎩和1:(:01)BA x L y y y =⎧→⎨=⎩两个部分构成. 先分别求出两条积分弧段上的曲线积分,再求和.沿抛物线2y x =移动到点(1,1)A ,此变力F 所作的功d d LW y x x y =+⎰.本题中的有向弧段2:(:01)L y x x =→如图11所示,此时,d d Lx x y y +⎰1111222d d()d )2(d x x x x x x x x x =+=+⋅⎰⎰⎰⎰123103d 1x x x ===⎰.图114、设力F 的方向沿纵轴负方向,其大小等于作用点的横坐标的平方,求该力作用下质点沿抛物线21x y =-从点(1,0)A 到点(0,1)B 所作的功. 答案: 815-解析: 根据已知条件“力F 的方向沿纵轴负方向,其大小等于作用点的横坐标的平方”,可知F F 的作用下,沿抛物线21x y =-从点(1,0)A 到点(0,1)B y .本题中的有向弧段2:1(:01)L x y y =-→ 如图12所示. 此时,20d d Lx x y -⎰2102(1)d y y =--⎰1240(12)d y y y =--+⎰1112401d 2d d y y y y y =-+-⎰⎰⎰351110235y y y =-+⋅-21813515=-+-=-.图12附录证明:(1)20sin d 2sin d nnx x x x ππ=⎰⎰;(2)20cos d 2cos d nnx x x x ππ≡⎰⎰. 证:(1)根据积分区间的可加性,有22sin d sin d sin d nnn x x x x x x ππππ=+⎰⎰⎰,要证明“20sin d 2sin d nnx x x x ππ=⎰⎰”,只需证明“202sin d sin d nnx x x x πππ=⎰⎰”. 下面就来证明202sind sin d nn x x x x πππ=⎰⎰——左边x t ==令=x 令2202sin d sin d sin d 2sin d nnnn x x x x x x x x πππππ=+=⎰⎰⎰⎰.(2)根据积分区间的可加性,有202cos d cos d cos d nnn x x x x x x ππππ=+⎰⎰⎰,下面就来分析2cos d nx x ππ⎰和20cos d n x x π⎰的关系——x t ==令==x 令综上所述,20cos d 2cos d nn x x x x ππ≡⎰⎰,而是——200202cos d ,cos d 2cos d ,n nn x x n x x x x n πππ⎧=⎪⎪⎨⎪≠⎪⎩⎰⎰⎰当为偶数时当为奇数时.。
对坐标曲线积分例题与习题
y
B ( 1, 1 )
2 2
x y
yx
4
1 0 1 3 x dx 0
A(1, 0 ) x
解: (1) 原式
( 2 y 2 y 2 y y 4 )d y (2) 原式
(3) 原式
0 dy
0
目录 上页 下页 返回 结束
1
例4. 设在力场 沿 移动到
作用下, 质点由 z 其中 为
称为对 y 的曲线积分.
若记 d s (d x , d y ), 对坐标的曲线积分也可写作
L F d s L P( x, y)dx Q( x, y)d y
类似地, 若 为空间曲线弧 , 记 d s (d x , d y , d z )
F ( x, y, z ) ( P( x, y, z ) , Q( x, y, z ) , R( x, y, z ))
称为被积函数 , L 称为积分弧段 或 积分曲线 .
目录 上页 下页 返回 结束
L P( x, y)d x lim0 k1 P( k , k )xk ,
n k 1
n
称为对 x 的曲线积分;
L Q( x, y)d y lim0 Q( k , k ) yk ,
4. 两类曲线积分的联系
L P d x Q d y P d x Q d y R d z
目录 上页 下页 返回 结束
2. 已知 为折线 ABCOA(如图), 计算
提示:
AB
0 1
dxd y
0 1
BC
d y y d z 0 OA d x
1
2dx (1 y )d y dx
11-2 对坐标的曲线积分
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
对坐标的曲线积分
一、 对坐标的曲线积分的概念 二 、对坐标的曲线积分的性质 三 、对坐标的曲线积分的计算 四 、对坐标的曲线积分的应用 五 、两类曲线积分之间的联系
P
[
x,j
(
x)]
+
Q
[
x,j
(
x)]j
¢(
x
)}
dx
(2) L:x =y ( y) (y=c 对应L的起点,y=d 对应L的终点)
òL
P(
x,
y
)dx
+
Q(
x,
y)dy
=
d
òc
{P
[y
(
y),
y
]y
¢(
y)
+
Q
[y
(
y
),
y]}
dy
Ø推广
空间曲线弧Γ: x = j(t), y =y (t), z = w(t)
一、 对坐标的曲线积分的概念
(一)引例 (二)对坐标的曲线积分的定义
一、 对坐标的曲线积分的概念
(一)引例 (二)对坐标的曲线积分的定义
变力沿曲线作功
y
B
设一质点在xoy面内从点A沿曲线
L移动到点B
Dyi
力F! ( x,
y)
=
P( x,
! y)i
+
Q( x,
y)
! j
变力所作的功 ?
A o
L
辽宁工业大学高数习题课(10)
(这里 L 为区域 D 的正向边界曲线) 3.利用积分与路径无关的条件计算法.
c . Pdx Qdy 与路径无关 Pdx Qdy 0 ,为区域内任意闭曲线
L
c
P Q , ( x, y ) G ─单连域. y x
du Pdx Qdy, ( x, y ) G —单连域.
所以
AB
dx dy ydz [1 (1 x )]dx 2;
1
0
BC
dx dy ydz [(1 z ) (1 z )z ]dz ( 2 z )dz
0
0
1
1
3 2
CA
dx dy ydz 1 dx 1
采用框图中线路2→21的方法计算;此时应注意首先要利
用积分曲线方程将被积函数中的分母化简,去掉奇点,使 其满足格林公式的条件。
解法1:化为定积分计算。
x a cos t L 的参数方程为: , t 从 0 变到 2 . 则 y a sint
( x y )dx ( x y )dy I L x2 y2 1 2 2 [(a cos t a sint )(a cos t ) (a cos t a sint )(a sint )]dt a 0 1 2 2 [( a 2 )dt 2 a 0
0
1
从而
I
dx dy ydz (
3 1 1 2 2
AB
BC
) dx dy ydz
CA
2
解法2:利用斯托克斯公式计算. 设 为平面 x y z 1 上 L AB BC CA 所围成部分的上侧,
第二节 对坐标的曲线积分
一 问题的提出
二 对坐标的曲线积分的概念
三 对坐标的曲线积分的计算
四 小结与思考判断题
2013-9-10
1
一
问题的提出
常力所作的功
y
yi M i 1 x i
B
M i M n 1
例 常力沿直线所作的功
L
A
W F AB.
M2 M1
考察 变力沿曲线所作的功 (微元素法)
解 (1) 化为对 x 的积分.
B(1,1)
L : y x , x从0变到1,
2
y x2
原式 ( 2 x x 2 x 2 2 x )dx
1 0
4 x 3 dx 1.
1 0
A(1,0)
2013-9-10
17
( 2) 化为对 y 的积分.
x y2
B(1,1)
L : x y 2 , y从 0 变到 1 ,
L L
2)存在条件
当P ( x, y ), Q( x, y )在光滑曲线弧 上连续时 第二类 L , 曲线积分存在
3)变力F沿曲线L 所做的功可表示为 W F ds. L 其中 F Pi Qj , ds dxi dyj .
2013-9-10 6
4)推广
空间有向曲线弧
Pdx Qdy Rdz. P ( x, y, z )dx lim P ( , , )x .
n
0 i 1 n i i i i
Q( x, y, z )dy lim Q(i , i , i )yi . 0 i 1 R( x, y, z )dz lim R(i , i , i )zi . 0 i 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
lim
0
k 1
P(k , k
记作
)xk
Q(k
, k
)yk
L P(x, y)dx Q(x, y)dy
都存在, 则称此极限为函数
在有向曲线弧 L 上
对坐标的曲线积分, 或第二类曲线积分. 其中,
称为被积函数 , L 称为积分弧段 或 积分曲线 .
4
目录 上页 下页 返回 结束
n
L
P(x,
y)dx
• 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
目录 上页 下页 返回 结束
例2. 计算
其中 L 为
y
(1) 半径为 a 圆心在原点的
B
A
上半圆周, 方向为逆时针方向;
a
ax
(2) 从点 A ( a , 0 )沿 x 轴到点 B (– a , 0 ).
lim
0
k
1
P(
k
, k
)xk ,
称为对
x
的曲线积分;
n
L
Q(x,
y)dy
lim
0
Q( k
k 1
,
k
)yk ,
称为对
y
的曲线积分.
若记 d s (d x , dy), 对坐标的曲线积分也可写作
L F d s L P(x, y)dx Q(x, y)dy
类似地, 若 为空间曲线弧 , 记 d s (d x , dy , dz)
y x
OB : y x, x : 0 1
O y xx
xydx xydx xydx
L
AO
OB
解法2 取 y 为参数, 则
A(1,1)
2
1
3
x2
dx
4
0
5
xydx 1 y2 y( y2 )dy
L
1
8
目录 上页 下页 返回 结束
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
(t)d
t
• 对有向光滑弧 L : y (x) , x : a b
ab P[x, (x)] Q[x, (x)] (x)dx
13
目录 上页 下页 返回 结束
• 对空间有向光滑弧 :
x (t) y (t), t : z (t)
P
[
(t
),
(t
)
,
(t
)]
(t
)
Q[ (t), (t), (t)] (t)
O
xA
y
2π (R2 k 2t ) d t 0
(2) 的参数方程为
2πk
y d x x d y z d z t d t
AB
0
12
目录 上页 下页 返回 结束
3. 计算
•
对有向光滑弧
L
:
x y
(t) (t)
,
t :
P[
(t ),
(t )] (t )
Q[
(t ),
(t)]
F (x, y, z) (P(x, y, z), Q(x, y, z), R(x, y, z))
5
目录 上页 下页 返回 结束
3. 性质 (1) 若 L 可分成 k 条有向光滑曲线弧
则 P(x, y)dx Q(x, y)dy L
k
P(x, y)dx Q(x, y)dy
i1 L i
(2) 用L- 表示 L 的反向弧 , 则
W F AB cos
B F AB
“常代变” “近似和” “取极限”
1
目录 上页 下页 返回 结束
1) “大化小”. 把L分成 n 个小弧段, F 沿
所做的功为
则
n
W Wk
k 1
2) “常代变”
有向小弧段
用有向线段
近似代替, 在
上任取一点
y F (k , k )
L
M ykk B
Mxk k1
A
x
则有
Wk F (k , k ) M k 1M k P(k , k )Δ xk Q(k , k )Δ yk
2
目录 上页 下页 返回 结束
3) “近似和”
n
W P(k , k )xk Q(ξk , k )yk
k 1
4) “取极限”
n
W
lim
0 k 1
P (ξk , ηk
)Δ xk
Q(ξk , ηk
)Δ yk
(其中 为 n 个小弧段的
最大长度)
y F (k , k )
L
M ykk B
Mxkk1
A
x
3
目录 上页 下页 返回 结束
2. 定义. 设 L 为xOy 平面内从 A 到B 的一条有向光滑 弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点, 极限
(2) 抛物线
y x2
(3) 有向折线 L : OA AB.
A(1, 0) x
解: (1) 原式
4 1 x3 dx 0
(2) 原式
1
(
2y2
y
2y
y
4
)d y
0
(3) 原式
1
0 dy 0
11
目录 上页 下页 返回 结束
例4. 设在力场
沿 移动到
作用下, 质点由
其中 为
z
B
试求力场对质点所作的功. 解: (1)
存在, 且有
P
[
(t),
(t
)]
(t)
Q[
(t),
(t
)]
(t
)d
t
7
目录 上页 下页 返回 结束
例1. 计算
xyd x , 其中L 为沿抛物线
L
y2 x 从点
A(1, 1)到B(1, 1)的一段.
y B(1,1)
解法1 取 x 为参数, 则 L : AO OB AO : y x, x :1 0
说明:
P(x, y)dx Q(x, y)dy L
• 对坐标的曲线积分必须注意积分弧段的方向 !
• 定积分是第二类曲线积分的特例.
6
目录 上页 下页 返回 结束
二、对坐标的曲线积分的计算法
定理:
在有向光滑弧 L 上有定义且
连续, L 的参数方程为
x (t)
y
(t)
t : , 则曲线积分
一、 对坐标的曲线积分的概念与性质
1. 引例: 变力沿曲线所作的功. 设一质点受如下变力作用
F (x, y) (P(x, y), Q(x, y))
y L
B
A x
在 xOy 平面内从点 A 沿光滑曲线弧 L 移动到点 B, 求移
动过程中变力所作的功W. 变力沿直线所作的功
解决办法: “大化小”
F A
R[ (t), (t), (t)](t)d t
4. 两类曲线积分的联系
L P d x Q d y
Pd x Qd y Rd z
14
目录 上页 下页 返回 结束
2. 已知 为折线 ABCOA(如图), 计算
提示:
Байду номын сангаас
AB d x d y BC d y y d z 0 OA d x
0
1
2dx
0
1
(1
y)dy
1
0 dx
z C(0,0,1)
2 (1 1) 1 2
y z 1 B(0,1,0)
O y
A(1,0,0) x y 1 x
15
目录 上页 下页 返回 结束
作业
P200 3 (2), (4), (6), (7) ; 4; 5; 7; 8
16
第三节 目录 上页 下页 返回 结束
解: (1) 取L的参数方程为
则
y2 dx π a2 sin 2 t (a sin t )d t
L
0
2a3 2 1 4 a3 33
(2) 取 L 的方程为 y 0, x : a a,则
10
目录 上页 下页 返回 结束
例3. 计算
其中L为 y
B(1,1)
(1) 抛物线 L : y x2, x : 0 1; x y 2
