小升初六年级奥数几何知识专题
六年级奥数小升初数学能力培训教材之几何问题培优

六年级奥数小升初数学能力培训教材第五章:几何问题例题1:如图所示,△ABC是等腰直角三角形,求阴影部分的面积(单位:厘米)。
练习1:求下图形中阴影部分的面积(单位:厘米)。
例题2:在正方形ABCD中,对角线AC=BD=8厘米。
求阴影部分的面积。
练习2:如图所示,半圆的面积是62.8平方厘米,求阴影部分的面积。
例题3:、如图,已知AB=BC=6厘米,且AB⊥BC,三角形BCE的面积比三角形ADE的面积大3平方厘米,则AD长是多少厘米?练习3:如图,平行四边形ABCD的面积是20平方厘米,E是CD边延长线上的一点,EB和AD相交于F,三角形ABF比三角形EDF的面积大4平方厘米,CD长4厘米,求ED的长?例题4:如图所示,BE长5厘米,长方形AEFD面积是33平方厘米。
求CD的长度。
练习4:如图所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO 1O 的面积。
例题5:如图所示,三角形ABC 的面积是31.2平方厘米,圆的直径AC =6厘米,BD :DC =3:1。
求阴影部分的面积。
练习5:如图所示,AE ED =,CD=3BD ,30ABC S ∆=(cm 2)。
求阴影部分的面积。
例题6:如图,两个半径相等的圆A 和圆B 相交,三角形DBC 是等腰直角三角形,面积是100cm 2,四边形ABDC 是平行四边形.图中阴影部分的面积是多少cm 2?O DC A 练习6:如图,梯形ABCD 中,上底6厘米,下底是10厘米,BE DE 32,其中 三角形ABD 的面积是45平方厘米,求阴影部分的面积.例题7:.如图,四边形ABCD 中,AC 与BD 相交于O ,三角形AOD 的面积比三角形COD 的面积大4平方厘米,三角形AOB 的面积为三角形AOD 的面积的2倍,三角形BOC 与三角形COD 的面积和与三角形AOD 的面积相等.则四边形ABCD 的面积为多少平方厘米?练习7:如图两线段把三角形ABC 分成四块,已知其中3块的面积为5、9、9, 那么阴影部分的面积是多少?例题8:点E 、F 分别在正方形ABCD 上,AB BE 31=,BC BF 21=, 正方形ABCD 的面积为8400,则四边形BFHG 的面积为多少?练习8:如图,已知AB 是圆O 的直径,点M 是小圆的圆心,且图中正方形的面积是72,则图中阴影部分的周长是多少?(π取3.14)。
小升初六年级奥数几何知识专题

第一讲:几何综合之圆与扇形解析第四讲:几何综合之几何之比解析第六讲:几何综合之差不变原理解析第七讲:几何综合之等积变化解析第九讲:几何综合之等积变化解析第十讲:几何综合之图形综合训练题第十一讲:几何综合之等积变化练习几何综合之图形综合训练题(六年级奥数)1.明和爷爷分别沿小圆(A →B →C →D →E →A)和大圆两条路线散步.(如图)如果速度相同,两人同时出发,谁先回到出发地点?为什么?4用胶带捆住两根直径1分米的毛竹,捆一周(接头不计)胶带至少要多少分米?5、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知:AB =BC =10cm,那么阴影部分的面积是多少?(圆周率14.3=π)6、计算图中阴影部分的面积。
(单位:厘米)7.上右图是一个矩形,长为10厘米,宽为5厘米,则阴影部分面积为______平方厘米.8.图中,每个小正方形的面积均为1个面积单位,共9个面积单位,则图中阴影部分面积为多少个面积单位?9.图中△AOB 的面积为152cm ,线段OB 的长度为OD 的3倍,则梯形ABCD 的面积为______.10.在下左图中ABCD 是梯形,AECD 是平行四边形,则阴影部分的面积是______平方厘米(图中单位:厘米).图形的计数。
例1、数出下列各图中长方形的个数分别是多少?A BC D C D例2 下图中共有多少个正方形?例3下图中有多少个角?练习1、有( )个角。
2、下图中共有多少个正方形?3.如图,O 为△A1A6A12的边A1A12上的一点,分别连结OA2,OA3,…,OA11,图中共有______个三角形.4、数一数(1)、下图中一共有多少个长方形。
E FDAB CO5、将ABC 的每一边4等分,过各分点作边的平行线,在所得下图中有多少个三角形?6. 图中,圆的面积与长方形的面积相等。
长方形的长是12厘米,圆的半径是( )厘米。
7. 三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米.8.图中三个圆的半径都是5厘米,三个圆两两相交于圆心,求阴影部分面积。
小升初六年级数学专项练习《(33)一半模型》知识点总结复习训练

小升初小学六年级数学复习总结·知识点专项练习题+答案(33)一半模型知识要点:1、一半模型是小学奥数中的重要模型,常用于平行四边形这种特殊的四边形中。
2、常见的一半模型有以下几种:(1)平行四边形的对角线把整个四边形的面积平分。
(2)平行四边形中选取三角形,其中三角形的底边落在四边形的某条边上,另外一个顶点在对边上。
(3)平行四边形内部取一点,连结该点与四个顶点的连线,将四边形分成上下左右四块,其中上下两块的面积和=左右两块的面积和=四边形面积的一半。
习题精选:1. 如图,ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是()平方厘米。
A.3B.4C.5D.62. 如图所示,在长方形内画出一些直线,已知边上有三块面积分别是13,35,49,那么图中阴影部分的面积是()。
A.97B.84C.62D.以上答案均不对3. 如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为()厘米。
A.3.2B.5C.6.4D.以上答案均不对4. 如图,长方形ABCD的面积是56,点E、F、G分别是长方形ABCD边上的中点,H为AD边上的任意一点,阴影部分的面积是()。
A.56B.28C.42D.以上答案均不对5. 如图,平行四边形的面积为50,P是其中任意一点,三角形P AB的面积是13,三角形PCD的面积是()。
A.10B.12C.15D.206. 如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是()平方厘米。
A.10B.12C.15D.207. 一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是21平方厘米,长方形的面积是()平方厘米。
A.30B.40C.50D.608. 长方形ABCD中,阴影部分甲和乙都是长方形,且阴影部分甲的面积为36,阴影部分乙的面积是()。
六年级奥数秋季班-(第10讲)小升初几何重点考查内容-(五大模型-蝴蝶模型与燕尾模型)
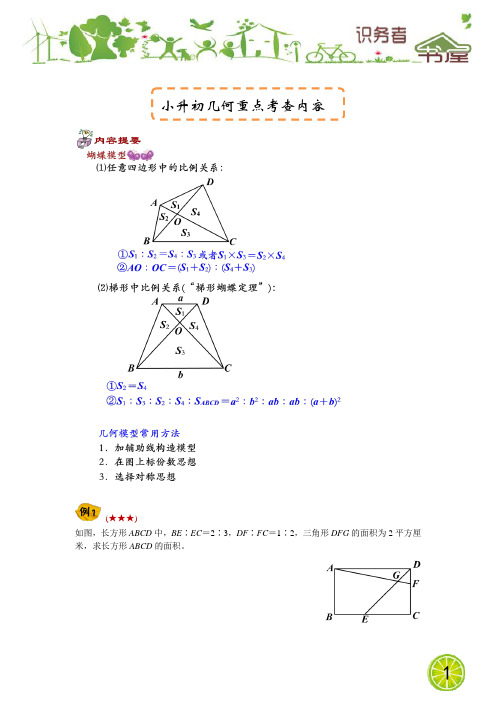
(★★★)
如图,长方形ABCD中,BE∶EC=2∶3,DF∶FC=1∶2,三角形DFG的面积为2平方厘米,求长方形ABCD的面积。
小升初几何重点考查内容
(★★★)
在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是多少平方厘米。
(★★★)
如图,在梯形ABCD中,AD∶BE=4∶3,BE∶EC=2∶3,且△BOE的面积比△AOD的面积小10平方厘米。
梯形ABCD的面积是多少平方厘米?
(★★★)
在三角形ABC中,三角形AEO的面积是1,三角形ABO的面积是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?
(★★★★)
如图,E在AC上,D在BC上,且AE∶EC=2∶3,BD∶DC=1∶2,AD与BE交于点F。
四边形DFEC的面积等于22cm2,则三角形ABC的面积是______。
小学奥数 六年级奥数 小升初几何重点考查内容—(立体几何表面积与体积常考题型

1小升初几何重点考查内容(★★)(2010年第8届走美6年级第9题)21个棱长为1厘米的小正方形组成一个立体如下图,它的表面积是______平方厘米。
(★★☆)(第四届希望杯2试试题)如图,底面积为50平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为5厘米的正方体木块,木块浮出水面的高度是2厘米,若将木块从容器中取出,水面将下降______厘米。
(★★★)一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深8厘米,现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后,现在水深多少厘米?(★★★☆)(2008年仁华考试题)如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径是20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是多少平方米?(★★★★)(2006年第十一届华杯赛决赛试题)如图,ABCD是矩形,BC=6厘米,AB=10厘米,对角线AC、BD相交于点O。
图中的阴影部分以CD为轴旋转一周,则阴影部分扫出的立体图形的体积是多少立方厘米?在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节!1.图中的立体图形是由14个棱长为5CM的立方体组成的,求这个立体图形的表面积?A.1000B.950C.1050D.11002.在一只长为40厘米宽为25厘米水深为20厘米的玻璃鱼缸中放入一个棱长为10厘米的正方体铁块,水可上升到多少厘米?A.20B.1C.21D.193.一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?A.15厘米B.14厘米C.12厘米D.12.4厘米4.厚度为1毫米的纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是6厘米,内直径是4厘米。
这卷纸的总长是多少米?A.15.7米B.1.57米C.157米D.0.157米5.如图,ABCD是矩形,6cmAB=,对角线AC、BD相交O。
六年级奥数--几何问题
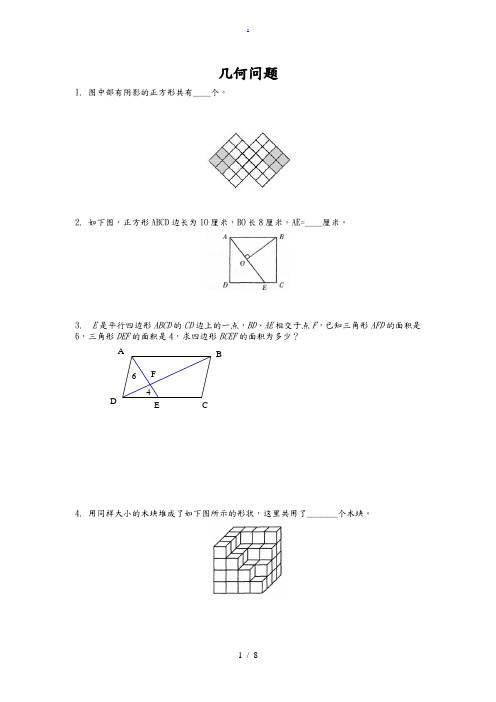
几何问题1. 图中部有阴影的正方形共有____个。
2. 如下图,正方形ABCD边长为lO厘米,BO长8厘米。
AE=____厘米。
3. E是平行四边形ABCD的CD边上的一点,BD、AE相交于点F,已知三角形AFD的面积是6,三角形DEF的面积是4,求四边形BCEF的面积为多少?46FED CBA4. 用同样大小的木块堆成了如下图所示的形状,这里共用了_______个木块。
面积问题1. 一个长方体的表面积是400平方厘米,其中有一个顶点处两条棱长分别是5cm和10cm,求此处的另一条棱长。
2. 如下图,有一个边长是6cm的立方体,如果它的左上方截去一个边分别是6,4,2cm的长方体,那么它的表面积现在是多少?3. 用棱长是1厘米的立方块拼成如下图所示的立体图形,问该图形的表面积是多少平方厘米?4. 把19个棱长为1厘米的正方体重叠在一起,按下图中的方式拼成一个立体图形.,求这个立体图形的表面积.5. 有三个大小一样的正方体,将接触的面用胶粘接在一起成图示的形状,表面积比原来减少了16平方厘米.求所成形体的表面积。
6. 在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?7. 一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?8. 21个棱长为1厘米的小正方体组成一个立体如右图.它的表面积是平方厘米.9. 如下图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?10. 一个长方体的宽和高相等,并且都等于长的一半(如图).将这个长方体切成12个小长方体,这些小长方体的表面之和为600平方分米.求这个大长方体原来的表面积.11. 如右图,以OA为斜边的直角三角形的面积是24 平方厘米,斜边长10 厘米,将它以O点为中心旋转90°,问:三角形扫过的面积是________?( π取3)A. 90B. 93C. 96D. 99答案:1. 面积为1 的正方形有8 个,面积为4 的正方形有8 个,面积为9 的正方形有8 个,面积为16 的正方形有2 个,共计26 个.2. 解:△AOB与△EDA相似,对应边成比例。
小升初几何奥数竞赛题

小升初几何奥数竞赛题小升初几何奥数竞赛题一:1. 在平面直角坐标系中,有三个点A(-3,4),B(5,-2)和C(1,3)。
求三角形ABC的面积。
解:首先,我们需要计算三角形ABC的底长和高。
根据平面坐标系中两点之间的距离公式,我们可以得到线段AB的长度为√((-3-5)²+(4-(-2))²)=√(8²+6²)=√(64+36)=√100=10,线段BC的长度为√((5-1)²+(-2-3)²)=√(4²+(-5)²)=√(16+25)=√41。
因此,三角形ABC的底边长度为10,而高的长度为√41。
根据三角形的面积公式,三角形ABC的面积为1/2 * 10 * √41 = 5√41。
小升初几何奥数竞赛题二:2. 在平面直角坐标系中,点A(3,-2)和B(7,4)分别是线段AB的两个端点。
点C为线段AB上一点,满足阳平分线AC的斜率为1/2。
求点C的坐标。
解:由题意可知,线段AB的斜率为(4-(-2))/(7-3)=6/4=3/2。
由于阳平分线AC的斜率为1/2,所以线段AC的斜率为-2。
通过斜率和一点得直线方程,我们可以得到直线AC的方程为y-(-2)=-2(x-3),即y=-2x+4。
另一方面,点C在线段AB上,所以它的横坐标x必定介于3和7之间。
将直线AC的方程代入点C的坐标(x,y)中,我们可以得到y=-2x+4。
将此方程与直线AB的方程联立,我们可以解得点C的横坐标x。
将解得的横坐标x代入直线AC的方程,我们可以得到点C的纵坐标y。
解方程得x=5/2,将其代入直线AC的方程得y=-2(5/2)+4=3。
因此,点C的坐标为(5/2,3)。
小升初几何奥数竞赛题三:3. 在平面直角坐标系中,有一个直线y=2x-1和一个圆心在原点半径为2的圆。
求直线与圆的交点坐标。
解:首先,我们需要将直线y=2x-1和圆的方程x²+y²=4带入联立解方程。
小学六年级奥数几何初步认识知识点

小学六年级的数学中,几何初步认识是非常重要的一部分。
在几何学中,学生将学习各种形状、图形的属性和关系。
这方面的知识能够帮助他们理解空间和形状,并发展他们的空间思维能力。
以下是小学六年级奥数几何初步认识的一些重要知识点。
1.点、线和面:学生需要了解点、线和面的概念。
点是没有大小和形状的,线是由无限多个点组成的,面是由无限多个线段组成的,可以看作是没有厚度的平面。
2.二维和三维:学生需要区分二维和三维的概念。
二维是指平面上的图形,只有长度和宽度,而三维是指有高度的图形,具有长度、宽度和高度。
3.直线和曲线:学生需要能够辨别直线和曲线。
直线是由无限多个连续的点组成的,在两个点之间是最短的路径。
曲线则是有弯曲的,没有最短路径的。
4.线段和射线:学生需要理解线段和射线的概念。
线段是由两个端点及其之间的点组成的,有确定的长度。
射线则是由一个起点和其上的任意点组成的,没有终点,但有一个方向。
5.角:学生需要学习角的概念。
角是由两条射线共享一个起点形成的,起点叫做角的顶点,两条射线叫做角的边。
6.直角、锐角和钝角:学生需要学习直角、锐角和钝角的概念。
直角是90度的角,锐角是小于90度的角,钝角是大于90度小于180度的角。
7.平行和垂直:学生需要学会判断两条线段或者两条线是否平行或者垂直。
平行的线段在同一平面上,永远不会相交。
垂直的线段或线相交,并且形成90度的角。
8.三角形:学生需要学习三角形的属性和分类。
三角形是由三条线段组成的图形。
根据边的长度和角的大小,三角形可以分为等边三角形、等腰三角形和普通三角形。
9.正方形、长方形和平行四边形:学生需要学习正方形、长方形和平行四边形的属性和特点。
正方形的四条边都相等,四个角都是直角。
长方形的相对边相等,四个角都是直角。
平行四边形的对边平行,相对边相等。
10.圆和圆心:学生需要学习圆和圆心的概念。
圆是平面上到一个固定点距离相等的所有点的集合。
这个固定点叫做圆心,到圆心的距离叫做半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初六年级奥数几何
知识专题
WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】
第一讲:几何综合之圆与扇形解析
第三讲:几何综合之立体涂色解析
第四讲:几何综合之几何之比解析
第五讲:几何综合之差不变原理解析
第六讲:几何综合之差不变原理解析
第七讲:几何综合之等积变化解析
第八讲:几何综合之等积变化解析
第九讲:几何综合之等积变化解析
第十讲:几何综合之图形综合训练题
第十一讲:几何综合之等积变化练习
几何综合之图形综合训练题(六年级奥数)
1.明和爷爷分别沿小圆(A→B→C→D→E→A)和大圆两条路线散步.(如图)如果速度相同,两人同时出发,谁先回到出发地点?为什么?
4用胶带捆住两根直径1分米的毛竹,捆一周(接头不计)胶带至少要多少分米?5、ABC是等腰直角三角形. D是半圆周的中点, BC:AB=BC=10cm,
π)
那么阴影部分的面积是多少?(圆周率14
.3
=
6、计算图中阴影部分的面积。
(单位:厘米)
7.上右图是一个矩形,长为10厘米,宽为5厘米,则阴影部分面积为______平方厘米.
8.图中,每个小正方形的面积均为1个面积单位,共9个面积单位,则图中阴影部分面积为多少个面积单位?
9.图中△AOB 的面积为152cm ,线段OB 的长度为OD 的3倍,则梯形ABCD 的面积为______.
10.在下左图中ABCD 是梯形,AECD 是平行四边形,则阴影部
分的面积是______平方厘米(图中单位:厘米).
图形的计数。
例1、数出下列各图中长方形的个数分别是多少? 例2 下图中共有多少个正方形?
例3下图中有多少个角? 练习 1、有( )个角。
2、下图中共有多少个正方形?
3.如图,O 为△A1A6A12的边A1A12上的一点,分别连结OA2,OA3,…,OA11,图中共有______个三角形.
4、数一数 (1)、下图中一共有多少个长方形。
5、将ABC 的每一边4等分,过各分点作边的平行线,在所得下图中有多少个三角形?
A
B C D A B C
D 图1图2
E F D A B C O
6. 图中,圆的面积与长方形的面积相等。
长方形的长是12厘米,圆的半径是
( )厘米。
7. 三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米. 8.图中三个圆的半径都是5厘米,三个圆两两相交于圆心,求阴影部分面积。
A
B C
12。
