2017年北京市西城区初三一模试卷及答案数学

合集下载

北京市西城区2017届九年级上期末数学试卷含答案解析

A．5 B． C．3 D． 8．制造弯形管道时，经常要先按中心线计算“展直长度”，再下料．右图是一段弯形管道，其中∠O=∠O’=90°，中心线的两条弧的半径都是 1000mm，这段变形管道的展直长度约为（取 π3.14）（）
A．9280mmB．6280mmC．6140mmD．457mm 9．当太阳光线与地面成 40°角时，在地面上的一棵树的影长为 10m，树高 h （单位：m）的范围是（） A．3＜h＜5B．5＜h＜10 C．10＜h＜15 D．15＜h＜20 10．在平面直角坐标系 xOy 中，开口向下的抛物线 y=ax2+bx+c 的一部分图象如
第 1 页（共 41 页）
A．（2，5） B．（，5） C．（3，5） D．（3，6） 6．如图，AB 是⊙O 的直径，C，D 是圆上两点，连接 AC，BC，AD，CD．若∠ CAB=55°，则∠ADB 的度数为（）
A．55° B．45° C．35° D．2 D，连接 OA．若 AB=4，CD=1，则⊙O 的半径为（）
21．一张长为 30cm，宽 20cm 的矩形纸片，如图 1 所示，将这张纸片的四个角
各剪去一个边长相同的正方形后，把剩余部分折成一个无盖的长方体纸盒，如
图 1 所示，如果折成的长方体纸盒的底面积为 264cm2
边长．
，求剪掉的正方形纸片的
第 5 页（共 41 页）
2016-2017 学年北京市西城区九年级（上）期末数学试卷
一、选择题（本题共 30 分，每小题 3 分）下面各题均有四个选项，其中只有一个是符合题意的． 1．抛物线 y=（x﹣12）+2 的对称轴为（） A．直线 x=1 B．直线 x=﹣1 C．直线 x=2D．直线 x=﹣2 2．我国民间，流传着许多含有吉祥意义的文字图案，表示对幸福生活的向往，良辰佳节的祝贺．比如下列图案分别表示“福”、“禄”、“寿”、“喜”，其中是轴对称图形，但不是中心对称图形的是（）

年西城区初三一模数学试卷及答案副本

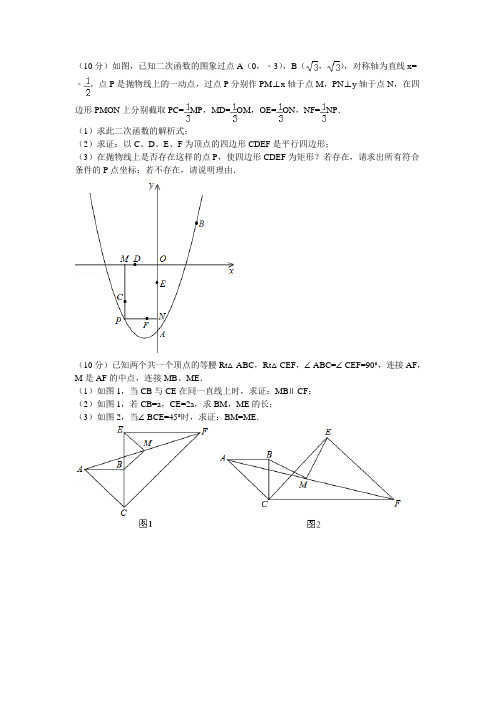
（10分）如图，已知二次函数的图象过点A（0，﹣3），B（，），对称轴为直线x=﹣，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC=MP，MD=OM，OE=ON，NF=NP．（1）求此二次函数的解析式；（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．（10分）已知两个共一个顶点的等腰Rt△ABC，Rt△CEF，∠ABC=∠CEF=90°，连接AF，M是AF的中点，连接MB、ME．（1）如图1，当CB与CE在同一直线上时，求证：MB∥CF；（2）如图1，若CB=a，CE=2a，求BM，ME的长；（3）如图2，当∠BCE=45°时，求证：BM=ME．平面直角坐标系xOy中，抛物线244=-++与x轴交于点A、点B，与yy ax ax a c轴的正半轴交于点C，点A的坐标为(1, 0)，OB=OC，抛物线的顶点为D．(1) 求此抛物线的解析式；(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB，求点P的坐标；(3) Q为线段BD上一点，点A关于∠AQB的平分线的对称点为A'，若2-QBQA，求点Q的坐标和此时△QAA'的面积．=（1）解：设抛物线的解析式为：y=a（x+）2+k，∵点A（0，﹣3），B（，）在抛物线上，∴，解得：a=1，k=．∴抛物线的解析式为：y=（x+）2=x2+x﹣3．（2）证明：如右图，连接CD、DE、EF、FC．∵PM⊥x轴于点M，PN⊥y轴于点N，∴四边形PMON为矩形，∴PM=ON，PN=OM．∵PC=MP，OE=ON，∴PC=OE；∵MD=OM，NF=NP，∴MD=NF，∴PF=OD．在△PCF与△OED中，∴△PCF≌△OED（SAS），∴CF=DE．同理可证：△CDM≌△FEN，∴CD=EF．∵CF=DE，CD=EF，∴四边形CDEF是平行四边形．（3）解：假设存在这样的点P，使四边形CD EF为矩形．设矩形PMON的边长PM=ON=m，PN=OM=n，则PC=m，MC=m，MD=n，PF=n．若四边形CDEF为矩形，则∠DCF=90°，易证△PCF∽△MDC，∴，即，化简得：m2=n2，∴m=n，即矩形PMON为正方形．∴点P为抛物线y=x2+x﹣3与坐标象限角平分线y=x或y=﹣x的交点．联立，解得，，∴P1（，），P2（﹣，﹣）；联立，解得，，∴P3（﹣3，3），P4（﹣1，1）．∴抛物线上存在点P，使四边形CDEF为矩形．这样的点有四个，在四个坐标象限内各一个，其坐标分别为：P1（，），P2（﹣，﹣），P3（﹣3，3），P4（﹣1，1）．如答图1a，延长AB交CF于点D，则易知△ABC与△BCD均为等腰直角三角形，∴AB=BC=BD，∴点B为线段AD的中点，又∵点M为线段AF的中点，∴BM为△ADF的中位线，∴BM∥CF．证法二：如答图1b，延长BM交EF于D，∵∠ABC=∠CEF=90°，∴AB⊥CE，EF⊥CE，∴AB∥EF，∴∠BAM=∠DFM，∵M是AF的中点，∴AM=MF，∵在△ABM和△FDM中，，∴△ABM≌△FDM（ASA），∴AB=DF，∵BE=CE﹣BC，DE=EF﹣DF，∴BE=DE，∴△BDE是等腰直角三角形，∴∠EBM=45°，∵在等腰直角△CEF中，∠EC F=45°，∴∠EBM=∠ECF，∴MB∥CF；如答图2a所示，延长AB交CF于点D，则易知△BCD与△ABC为等腰直角三角形，∴AB=BC=BD=a，AC=AD=a，∴点B为AD中点，又点M为AF中点，∴BM=DF．分别延长FE与CA交于点G，则易知△CEF与△CEG均为等腰直角三角形，∴CE=EF=GE=2a，CG=CF=a，∴点E为FG中点，又点M为AF中点，∴ME=AG．∵CG=CF=a，CA=CD=a，∴AG=DF=a，∴BM=ME=×a=a．解法二：∵CB=a，CE=2a，∴BE=CE﹣CB=2a﹣a=a，∵△ABM≌△FDM，∴BM=DM，又∵△BED是等腰直角三角形，∴△BEM是等腰直角三角形，∴BM=ME=BE=a；（3）证法一：如答图3a，延长AB交CE于点D，连接DF，则易知△ABC与△BCD均为等腰直角三角形，∴AB=BC=BD，AC=CD，∴点B为AD中点，又点M为AF中点，∴BM=DF．延长FE与CB交于点G，连接AG，则易知△CEF与△CEG均为等腰直角三角形，∴CE=EF=EG，CF=CG，∴点E为FG中点，又点M为AF中点，∴ME=AG．在△ACG与△DCF中，，∴△ACG≌△DCF（SAS），∴DF=AG，∴BM=ME．证法二：如答图3b，延长BM交CF于D，连接BE、DE，∵∠BCE=45°，∴∠ACD=45°×2+45°=135°∴∠BAC+∠ACF=45°+135°=180°，∴AB∥CF，∴∠BAM=∠DFM，∴M是AF的中点，∴AM=FM，在△ABM和△FDM中，，∴△ABM≌△FDM（ASA），∴AB=DF，BM=DM，∴AB=BC=DF ，∵在△BCE 和△DFE 中，，∴△BCE ≌△DFE （SAS ）， ∴BE=DE ，∠BEC=∠DEF ，∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°， ∴△BDE 是等腰直角三角形，又∵BM=DM ， ∴BM=ME=BD ，故BM=ME ．25．解：（1）∵ 2244(2)y ax ax a c a x c =-++=-+，∴ 抛物线的对称轴为直线2x =．∵ 抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，点A 的坐标为(1,0)，∴ 点B 的坐标为(3,0)，OB ＝3．…………… 1分可得该抛物线的解析式为(1)(3)y a x x =--． ∵ OB =OC ，抛物线与y 轴的正半轴交于点C ， ∴ OC =3，点C 的坐标为(0,3)．将点C 的坐标代入该解析式，解得a =1．……2分∴ 此抛物线的解析式为243y x x =-+．（如图9）…………………… 3分（2）作△ABC 的外接圆☉E ，设抛物线的对称轴与x 轴的交点为点F ，设☉E 与抛物线的对称轴位于x 轴上方的部分的交点为点1P ，点1P 关于x 轴的对称点为点2P ，点1P 、点2P 均为所求点.（如图10）可知圆心E 必在AB 边的垂直平分线即抛物线的对称轴直线2x =上．∵ 1APB ∠、ACB ∠都是弧AB 所对的圆周角， ∴ ACB B AP ∠=∠1，且射线FE 上的其它点P 都不满足ACB APB ∠=∠．由（1）可知 ∠OBC=45°，AB=2，OF=2．可得圆心E 也在BC 边的垂直平分线即直线y x =上．∴ 点E 的坐标为(2,2)E ．………………………………………………… 4分∴ 由勾股定理得 5EA =．∴ 15EP EA ==． ∴ 点1P 的坐标为1(2,25)P+．…………………………………………… 5分由对称性得点2P 的坐标为2(2,25)P -． ……………………………… 6分∴符合题意的点P 的坐标为1(2,25)P +、2(2,25)P -. （3）∵ 点B 、D 的坐标分别为(3,0)B 、(2,1)D -，图9xyO 1DCBA可得直线BD 的解析式为3y x =-，直线BD 与x 轴所夹的锐角为45°． ∵ 点A 关于∠AQB 的平分线的对称点为A '，（如图11）若设AA '与∠AQB 的平分线的交点为M ，则有 QA QA '=，AM A M '=，AA QM '⊥，Q ，B ，A '三点在一条直线上． ∵ 2QA QB -=，∴ .2''=-=-=QB QA QB QA BA作A N '⊥x 轴于点N ．∵ 点Q 在线段BD 上， Q ，B ，A '三点在一条直线上， ∴ sin451A N BA ''=⋅︒=，cos451BN BA '=⋅︒=． ∴ 点A '的坐标为(4,1)A '． ∵ 点Q 在线段BD 上，∴ 设点Q 的坐标为(,3)Q x x -，其中23x <<． ∵ QA QA '=，∴ 由勾股定理得 2222(1)(3)(4)(31)x x x x -+-=-+--．解得114x =．经检验，114x =在23x <<的范围内．∴ 点Q 的坐标为111(,)44Q -． …………………………………………… 7分此时1115()2(1)2244QAA A AB QAB A Q S S S AB y y '''∆∆∆=+=⋅⋅+=⨯⨯+=．… 8分图10xy O 1FP 2EP 1DCBA图11xyO QMA'DB AN。

西城区初三数学试卷及答案

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √9B. √-1C. √4/3D. π2. 下列各式中，正确的是（）A. 2x + 3 = 5x + 1B. 2x - 3 = 5x - 1C. 2x + 3 = 5x - 1D. 2x - 3 = 5x + 13. 若a > b，则下列不等式中成立的是（）A. a - 2 > b - 2B. a + 2 > b + 2C. a - 2 < b - 2D. a + 2 < b + 24. 在直角坐标系中，点P（-2，3）关于原点对称的点的坐标是（）A.（2，-3）B.（-2，-3）C.（-2，3）D.（2，3）5. 若等腰三角形底边长为6，腰长为8，则该三角形的周长是（）A. 14B. 18C. 22D. 266. 下列函数中，是奇函数的是（）A. y = x^2B. y = 2xC. y = -x^2D. y = x^37. 下列各式中，正确的是（）A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^28. 下列各式中，正确的是（）A. a^3 ÷ a^2 = aB. a^3 ÷ a = a^2C. a^3 ÷ a^2 = a^2D. a^3 ÷ a = a9. 下列各式中，正确的是（）A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab + b^210. 下列各式中，正确的是（）A. a^3 ÷ a^2 = aB. a^3 ÷ a = a^2C. a^3 ÷ a^2 = a^2D. a^3 ÷ a = a二、填空题（每题5分，共20分）11. 若a = -2，b = 3，则a^2 - b^2 = ________。

西城区2017初三上学期期末考试数学试题答案

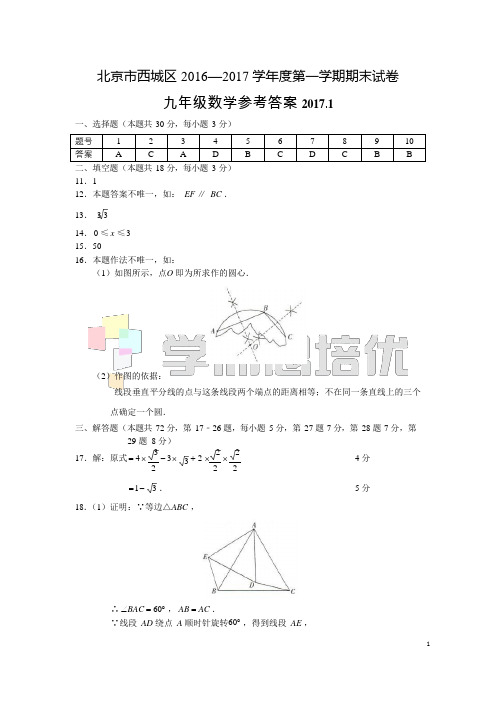
33北京市西城区2016—2017 学年度第一学期期末试卷九年级数学参考答案2017.1一、选择题（本题共30 分，每小题3 分）题号 1 2 3 4 5 6 7 8 9 10 答案 A C A D B C D C B B 二、填空题（本题共18 分，每小题3 分）11．112．本题答案不唯一，如：EF ∥ BC ．13．3 314．0 ≤x ≤315．5016．本题作法不唯一，如：（1）如图所示，点O 即为所求作的圆心．（2）作图的依据：线段垂直平分线的点与这条线段两个端点的距离相等；不在同一条直线上的三个点确定一个圆．三、解答题（本题共72 分，第17﹣26 题，每小题5 分，第27 题7 分，第28 题7 分，第29 题8 分）17．解：原式= 4 ⨯3- 3⨯+ 2 ⨯2⨯24 分2 2 2=1 -． 5 分18．（1）证明：∵等边△ABC ，∴∠BAC = 60︒，AB =AC ．∵线段AD 绕点A 顺时针旋转60︒，得到线段AE ，∴ ∠DAE = 60︒ ， AE = AD ．∴ ∠BAD + ∠EAB = ∠BAD + ∠DAC ． ∴ ∠EAB = ∠DAC ． ∴ △EAB ≌△DAC ． ∴ ∠AEB = ∠ADC ． 3 分（2）解：∵ ∠DAE = 60︒ ， AE = AD ，∴ △EAD 为等边三角形． ∴ ∠AED = 60︒ ，又∵ ∠AEB = ∠ADC = 105︒ ． ∴ ∠BED = 45︒ ． 5 分 19．解：（1） y = x 2 + 4x + 3= x 2 + 4x + 22 - 22 + 3= (x + 2)2-12 分（2）列表：x … -4 -3 -2 -1 0 … y (3)0 -1 03…（3）本题答案不唯一，如：当 x < -2 时， y 随 x 的增大而减小，当 x > -2 时， y 随 x 的增大而增大．5 分20．（1）证明：∵ CE = CD ，∴ ∠CDE = ∠CED ．∴ ∠ADB = ∠CEA ． ∵ ∠DAC = ∠B ，∴ △ABD ∽△CAE ．3 分（2）解：由（1） △ABD ∽△CAE ，∴ AB = BD ． AC AE∵ AB = 6 ， AC = 9， BD = 2 ，2∴ AE =3． 5 分221．解：设剪掉的正方形纸片的边工为x cm ． 1 分由题意，得(30 - 2x)(20 - 2x)= 264 ． 3 分整理，得x2- 25x + 84 = 0 ．解方程，得x1=4，x2= 21（不符合题意，舍去）． 4 分答：剪掉的正方形纸片的边长为4 cm ． 5 分22．解：本题答案不唯一，如：（1）以AB 所在直线为x 轴，以抛物线的对称轴为y 轴建立如图所示的平面直角坐标系xOy ，则A(-4，0)， B (4，0)， C (0，6)．设这条抛物线的表达式为y =a (x - 4)(x + 4)．∵抛物线经过点C ，∴-16a = 6 ．∴a =-3 ．8∴这条抛物线表示的二次函数表达式为y =-3x2 + 6 ． 4 分8（2）当x = 1时，y =45．8∵4.4 + 0.5 = 4.9 <45，8∴这辆货车能安全通过这条隧道． 5 分23．（1）证明：连接OC．∴AB 是O 的直径，∴ ∠ACB = 90︒，即∠1 +∠3 = 90︒．∵O A =OC ，∴ ∠1 = ∠2 ．∴ ∠BCD = ∠CAB = ∠1． ∴ ∠BCD + ∠3 = 90︒ ． ∴ OC ⊥ DC 于点C ． ∴ DC 是 O 的切线．3 分（2）解：在Rt △OCD 中， OC = 3 ， sin D = 3，5∴ OD = 5 ， AD = 8 ，∵ CE = CB ， ∴ ∠2 = ∠4 ． ∴ ∠1 = ∠4 ． ∴ OC ∥ AF ． ∴ △DOC ∽△DAF ．∴ OC = OD ． AF AD∴ AF = 24． 5 分524．本题答案不唯一，如：（1）测量工具有：简单测角仪，测量尺等； 1 分（2）设CD 表示祈年殿的高度，测量过程的几何图形如图所示．需要测量的几何量如下：①在点 A ，点 B 处用测角仪分别测出仰角α ， β ；②测出 A ， B 两点之间的距离 s m ． 3 分（3）求解思路：a ．设CD 为 x m ．在Rt △DBC 中，由∠DBC = β ，可得 BC = x；tan β同理，在Rt △DAC 中，可得 AC =x．tan α b ．由 AB = AC - BC 得 s = x tan α- xtan β ，x 可求．5 分25．（1）证明：∵直径 DE ⊥ AB 于点 F ，∴ AF = BF ． ∴ AM = BM ． 2 分（2）解：连接 AO ， BO ，如图．3 6 2∵ DE ⊥ AB ，AO = BO ， ∴ ∠AOF = ∠BOF = 1∠AOB ．2由（1）可得 AM = BM ， ∵ AM ⊥ BM ，∴ ∠MAF = ∠MBF = 45︒ ． ∴ ∠CMN = ∠BMF = 45︒ ． ∵ ∠N = 15︒ ，∴ ∠ACM = ∠CMN + ∠N = 60︒ ，即∠ACB = 60︒ ．∵ ∠ACB = 1∠AOB ，2∴ ∠AOF = ∠ACB = 60︒ ． ∵ D E = 8 ， ∴ AO = 4 ．在Rt △AOF 中，由sin ∠AOF = AF，得 AF = 2 ．AO在Rt △AMF 中， AM = BM = 2AF = 2 ．在Rt △ACM 中，由tan ∠ACM = AM ，得CM = 2 2 ．CM∴ BC = CM + BM = 2 + 2 26．解：（1）补全表格如下：． 5 分方程两根的情况对应的二次函数的大致图象 a ， b ， c 满足的条件方程有一个负实根和一个正实根⎧a > 0 ⎪∆ = b 2 - 4ac > 0 ⎪ ⎨- b> 0⎪ 2a ⎪ ⎪⎩c > 06⎪⎩ 3 分（2）解：设一元二次方程x2-(2m + 3)x - 4m = 0 对应的二次函数为：y =x2-(2m + 3)x - 4m ，∴一元二次方程x2-(2m +3)x-4m = 0 有一个负实根和一个正实根，且负实根大于-1，⎧⎪-4m < 0∴⎨(-1)2 -(2m + 3)⋅(-1)- 4m > 0．。

2017北京市西城区初三数学一模试题及答案

北京市西城区2017年九年级统一测试数学试卷一、选择题（本题共30分，每小题3分）1．春节假期，北京市推出了庙会休闲娱乐、传统文化展演、游园赏景赏花、冰雪项目体验等精品文化活动，共接待旅游总人数9608000人次，将9608000用科学记数法表示为（）．A ．3960810´B ．4960.810´C ．596.0810´D ．69.60810´2．在数轴上，实数a ，b 对应的点的位置如图所示，且这两个点关于原点对称，下列结论中，正确的是（）．b1aA ．0a b +=B ．0a b -=C ．||||a b <D ．0ab >3．如图，AB CD ∥，DA CE ^于点A ．若55EAB Ð=°，则D Ð的度数为（）．A ．25°B ．35°C ．45°D ．55°4．右图是某几何体的三视图，该几何体是（）．A ．三棱柱B ．长方体C ．圆锥D ．圆柱5．若正多边形的一个外角是40°，则这个正多边形是（）．A ．正七边形B ．正八边形C ．正九边形D ．正十边形6．用配方法解一元二次方程2650x x --=，此方程可化为（）．A ．2(3)4x -=B ．2(3)14x -=C ．2(9)4x -=D ．2(9)14x -=7．如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2m ，旗杆底部与平面镜的水平距离为16m ．若小明的眼睛与地面的距离为1.5m ，则旗杆的高度为（单位：m ）（）．A ．163B ．9C ．12D ．6438．某商店举行促销活动，其促销的方式是“消费超过100元时，所购买的商品按原价打8折后，再减少20元”．若某商品的原价为x 元（100x >），则购买该商品实际付款式的金额（单位：元）是（）．A ．80%20x -B ．80%(20)x --C ．20%20x -D ．20%(20)x -9．某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：年龄（单位：岁）13141516频数（单位：名）515x10x-对于不同的x ，下列关于年龄的统计量不会发生改变的是（）．A ．平均数、中位数B ．平均数、方差C ．众数、中位数D ．众数、方差DBC AE10．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数．“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多；“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少．右下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况，下列说法中，正确的是（下的燃油效率情况，下列说法中，正确的是（））．A ．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多B ．以低于80km/h 的速度行驶时，行驶相同路程，三辆车中，乙车消耗汽油最少C ．以高于80km/h 的速度行驶时，行驶相同路程，丙车比乙车省油D ．以80km/h 的速度行驶时，行驶100公里，甲车消耗的汽油量约为10升二．填空题（本题共18分，每小题3分）11．分解因式：22ax ax a -+=__________．12．若函数的图象经过点(1,2)A ，点(2,1)B ，写出一个符合条件的函数表达式__________． 13．下表记录了一名球员在罚球线上罚篮的结果：．下表记录了一名球员在罚球线上罚篮的结果：投篮次数n100 150 300 500 800 1000 投中次数m 5896174302484601投中频率m n0.580 0.640 0.580 0.604 0605 0.601 这名球员投篮一次，投中的概率约是__________．14．如图，四边形ABCD 是⊙O 内接四边形，若30BAC Ð=°，80CBD Ð=°，则BCD Ð的度数为_______°．ODACB15．在平面直角坐标系xOy 中，以原点O 为旋转中心，将AOB △顺时针旋转90°得到A OB ¢¢△，其中点A ¢与点A 对应，点B ¢与点B 对应．若点(3,0)A -，(1,2)B -，则点A ¢的坐标为__________，点B ¢的坐标为__________．1510504080燃油效率（km/L ）速度（km/h ）甲车乙车丙车4321-1-2-3-4xAB O1234y16．下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程．已知：如图1，直线l 和直线l 外一点P ．PlmC DA OBlP求作：直线l 的平行直线，使它经过点P ．作法：如图2．（1）过点P 作直线m 与直线l 交于点O ；（2）在直线m 上取一点()A OA OP <，以点O 为圆心，OA 长为半径画弧，与直线l 交于点B ；（3）以点P 为圆心，OA 长为半径画弧，交直线m 于点C ，以点C 为圆心，AB 长为半径画弧，两弧交于点D ；（4）作直线PD ．所以直线PD 就是所求作的平行线．请回答：该作图的依据是______________．三、解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明，演算步骤或证明过程．17．计算：()101232sin 60322-æö---°+-ç÷èø．18．解不等式组：5234722x x x x <≥-+ìïí+ïî．19．已知2x y =，求代数式222112x xy y y x x y æö-+-¸ç÷èø的值．20．如图，在ABC △中，BC 的垂直平分线交BC 于点D ，交AB 延长线于点E ，连接CE ．求证：BCE A ACB Ð=Ð+Ð．AB EDC21．某科研小组计划对某一品种的西瓜采用两种种植技术种植．在选择种植技术时，该科研小组主要关心的问题是：西瓜的产量和产量的稳定性，以及西瓜的优等品率．为了解这两种种植技术种出的西瓜的质量情况，科研小组在两块自然条件相同的试验田进行对比试验，并从这两块实验田中各随机抽取20个西瓜，分别称重后，将称重的结果记录如下：表1甲种种植技术种出的西瓜质量统计表编号 12345678910编号西瓜质量（单位：kg） 3.5 4.8 5.4 4.9 4.2 5.0 4.9 4.8 5.8 4.8编号11121314151617181920西瓜质量（单位：kg） 5.0 4.8 5.2 4.9 5.1 5.0 4.8 6.0 5.7 5.0表2乙种种植技术种出的西瓜质量统计表编号12345678910西瓜质量（单位：kg） 4.4 4.9 4.8 4.1 5.2 5.1 5.0 4.5 4.7 4.9编号11121314151617181920西瓜质量（单位：kg） 5.4 5.5 4.0 5.3 4.8 5.6 5.2 5.7 5.0 5.3回答下列问题：回答下列问题：（1）若将质量为4.5 5.5（单位：kg）的西瓜记为优等品，完成下表：优等品西瓜个数平均数方差甲种种植技术种出的西瓜质量 4.980.27乙种种植技术种出的西瓜质量 15 4.970.21乙种种植技术种出的西瓜质量（2）根据以上数据，你认为该科研小组应选择哪种种植技术，并请说明理由．22．在平面直角坐标系xOy 中，直线1y x =-与y 轴交于A ，与双曲线ky x-交于点(),2B m ．（1）求点B 的坐标及k 的值；的值；（2）将直线AB 平移，使它与x 轴交于点C ，与y 轴交于点D ，若ABC 的面积为6，求直线CD 的表达式．的表达式．23．如图，在平行四边形ABCD 中，对角线BD 平分ABC Ð，过点A 作AE BD ∥，交CD 的延长线于点E ，过点E 作EF BC ^，交BC 延长线于点F ．（1）求证：四边形ABCD 是菱形；（2）若45ABC Ð=°，2BC =，求EF 的长．x-5-4-3-2-154321O-1-2-3-4-512345y B C FD EA24．汽车保有量是指一个地区拥有车辆的数量，一般是指在当地登记的车辆．进入21世纪以来，我国汽车保有量逐年增长．下图是根据中国产业信息网上的有关数据整理的统计图．长．下图是根据中国产业信息网上的有关数据整理的统计图．20072015年全国汽车保有量及增速统计图根据以上信息，回答下列问题：根据以上信息，回答下列问题：（1）2016年汽车保有量净增2200万辆，为历史最高水平，2016年汽车的保有量为_______________万辆，与2015年相比，2016年的增长率约为______________%；（2）从2008年到2015年，_______________年全国汽车保有量增速最快；（3）预估2020年我国汽车保有量将达到_____________万辆，预估理由是_________________．25．如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点C 作⊙O 的切线，交BA 的延长线交于点D ，过点B 作BE BA ^，交DC 延长线于点E ，连接OE ，交⊙O 于点F ，交BC 于点H ，连接AC ．（1）求证：ECB EBC Ð=Ð；（2）连接BF ，CF ，若6CF =，3sin 5FCB Ð=，求AC 的长．O HE FC D AB26．阅读下列材料：某种型号的温控水箱的工作过程是：接通电源后，在初始温度20℃下加热水箱中的水；当水温达到设定温度80℃时，加热停止；此后水箱中的水温开始逐渐下降，当下降到20℃时，再次自动加热水箱中的水至80℃时，加热停止；当水箱中的水温下降到20℃时，再次自动加热，……，按照以上方式不断循环．小明根据学习函数的经验，对该型号温控水箱中的水温随时间变化的规律进行了探究，发现水温y 是时间x 的函数，其中y （单位：℃）表示水箱中水的温度，x （单位：min ）表示接通电源后的时间．下面是小明的探究过程，请补充完整：（1）下表记录了32min 内14个时间点的温控水箱中水有温度y 随时间x 的变化情况接通电源事的时间x （单位：min ）0 1 23 4 58 10 16 18 20 21 24 32 ×××水箱中水的温度y （单位：℃）20 35 50 65 80 64 40 32 20 m 80 64 40 20 ××× m 的值为_____________；（2）①当04x ≤≤时，写出一个符合表中数据的函数解析式______________；当416x <≤时，写出一个符合表中数据的函数解析式_________________；②如图，在平面直角坐标系xOy 中，描出了上表中部分数据对应的点，根据描出的点，画出当032x ≤≤时，温度y 随时间x 变化的函数图象；20406080100Oxy 343230282624222018161412108642（3）如果水温y 随时间x 的变化规律不变，预测水温第8次达到40℃时，距离接通电源___________min ．27．在平面直角坐标系xOy 中，二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点．（1）求m 的取值范围；（2）若m 取满足条件的最小的整数，①写出这个二次函数的解析式；②当1n x ≤≤时，函数值y 的取值范围是64y n --≤≤，求n 的值；③将此二次函数图象平移，使平移后的图象经过原点O ．设平移后的图象对应的函数表达式为2()y a x h k =-+，当2x <时，y 随x 的增大而减小，求k 的取值范围．28．在ABC △中，AB BC =，BD AC ^于点D ．（1）如图1，当90ABC Ð=°时，若CE 平分ACB Ð，交AB 于点E ，交BD 于点F ．①求证：BEF △是等腰三角形； ②求证：1()2BD BC BF =+；（2）点E 在AB 边上，连接CE ．若1()2BD BC BE =+，在图2中补全图形，判断ACE Ð与ABC Ð之间的数量关系，写出你的结论，并写出求解ACE Ð与ABC Ð关系的思路．图1图2D CABFEAD CB29．在平面直角坐标系xOy 中，若点P 和点1P 关于y 轴对称，点1P 和点2P 关于直线l 对称，则称点2P 是点P 关于y 轴，直线l 的二次对称点．（1）如图1，点(1,0)A -．①若点B 是点A 关于y 轴，直线1:2l x =的二次对称点，则点B 的坐标为___________________； ②若点(5,0)C -是点A 关于y 轴，直线2:l x a =的二次对称点，则a 的值为___________________； ③若点(2,1)D 是点A 关于y 轴，直线3l 的二次对称点，则直线3l 的表达式为__________________；（2）如图2，⊙O 的半径为1．若⊙O 上存在点M ，使得点'M 是点M 关于y 轴，直线4:l x b =的二次对称点，且点'M在射线3(0)3y x x =≥上，b 的取值范围是_____________________；（3）(,0)E t 是x 轴上的动点，⊙E 的半径为2，若⊙E 上存在点N ，使得点'N 是点N 关于y 轴，直线5:31l y x =+的二次对称点，且点'N 在y 轴上，求t 的取值范围．图2图1yx O4321-1-2-343215-3-2-1-4-5-5-4-1-2-351234-3-2-11234O x y北京市西城区2017年九年级统一测试数学试卷答案及评分参考数学试卷答案及评分参考2017．4 一、选择题（本题共30分，每小题3分）分）题号题号 1 2 3 4 5 6 7 8 9 10 答案答案D A B B C B C A C D 二、填空题（本题共18分，每小题3分）分） 11．2(1)a x -12．答案不唯一，如：2y x= 13．0.60114．7015．(0,3)A ¢，(2,1)B ¢16．三边分别相等的两个三角形全等；全等三角形的对应角相等；同位角相等两直线平行；两点确定一条直线．三．解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分）分）17．解：101(23)2sin60322-æö---°+-ç÷èø3212232=--´+-323=-18．解：解不等式组为5234722x x x x -+ìïí+ïî①②<≥ 解不等式①，得3x <．解不等式②，得73x ≥．∴原不等式组的解集为733x ≤<．19．解：原式22()x y x y xy x y -=×-x x y =-当2x y =时，原式222y y y==-20．证明：∵DE 垂直平分BC 于点D ． ∴BE CE =．∴BCE CBE Ð=．∵CBE ACB A Ð=Ð+Ð． ∴BCE ACB A Ð=Ð+Ð．CDEB A21．解：（1）优等品西瓜个数优等品西瓜个数平均数平均数方差方差甲种种植技术种出的西瓜质量甲种种植技术种出的西瓜质量 15 乙种种植技术种出的西瓜质量乙种种植技术种出的西瓜质量（2）在试验田中，两种种植技术种出的西瓜的优等品率均为75%，平均产量相差不大，乙种种植技术种出的西瓜，质量更稳定，大小更均匀，科研小组应选择乙种种植技术．量更稳定，大小更均匀，科研小组应选择乙种种植技术． 22．解：（1）∵点(,2)B m 在直线1y x =-上，上， ∴12m -=．解得3m =． ∴点(3,2)B ．又∵点(3,2)B 在双曲线ky x=上．上． ∴6k =．（2）设平移后的直线的表达式为y x b =+．则它与y 轴交于点(0,)D b ． ∵AB CD ∥． ∴ABD ABC S S =△△ ∴162ABD B S AD x =×=△． ∴4AD =．∴14b +=或14b --=． ∴3b =或5b =-．∴平移后的直线的表达式为3y x =+或5y x =-．23．（1）证明：在平行四边形ABCD 中，AB CD ∥． ∴ABD BDC Ð=Ð． ∵BD 平分ABC Ð， ∴ABD DBC Ð=Ð． ∴BDC DBC Ð=Ð． ∴BC CD =．∴四边形ABCD 是菱形．是菱形．（2）解：由（1）可得，AB CD ∥，2CD BC AB ===． ∴45ECF ABC Ð=Ð=°． ∵AE BD ∥．∴四边形ABDE 是平行四边形．是平行四边形． ∴2DE AB ==． ∴4CE =．在Rt ECF △中，45ECF Ð=°，4CE =． ∴22EF =．BC FDEA24．（1）19400.13；（2）2010；（3）答案不唯一．如：2020年我国汽车保育量将达到28000万辆，预估理由合理，支撑预估的数据．万辆，预估理由合理，支撑预估的数据． 25．（1）证明：∵BE BA ^于点B ， ∴BE 是⊙O 的切线．的切线． ∵DE 是⊙O 的切线，C 为切点．为切点． ∴BE CE =． ∴ECB EBC Ð=Ð．（2）解：连接AF ． ∵AB 是⊙O 直径，直径，∴90AFB ACB Ð=Ð=°．BE 是⊙O 的切线，切点为B ，CE 是⊙O 的切线，切点为C ． ∴BE CE =，EO 平分BED Ð．∴EO BC ^，CH BH =．∴6BF CF ==，BF CF =，OH AC ∥． ∴FBC BAF FCB Ð=Ð=Ð．在Rt ABF △中，3sin 5BAF Ð=，6BF =．∴10AB =，5OF =．在Rt FCH △中，3sin 5FCB Ð=，6CF =．∴185FH =． ∴75OH OF FH =-=．∴1425AC OH ==．O HEFC D AB26．解：（1）50；（2）①答案不唯一，如：当04x ££时，1520y x =+；当416x <≤时，320y x=； ②246810121416182022242628303234y xO10080604020（3）56．27．解：（1）∵二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点．轴有两个公共点． ∴[]2(21)4(5)0m m m m ¹ìïí-+--ïî> 解得124m ->且0m ¹． ∴m 的取值范围是124m ->且0m ¹．（2）①m 取满足条件的最小的整数，由（1）可知1m =． ∴二次函数的解析式为234y x x =--． ②图象的对称轴为直线32x =．当时312n x ≤≤<，函数值y 随自变量x 的增大而减小．的增大而减小． ∵函数值y 的取值范围是64y n --≤≤， ∴当1x =时，函数值为6-．当x n =时，函数值为4n -．∴2346n n --=-．解得2n =-或4n =（不合题意，舍去）．（不合题意，舍去）． ∴n 的值为2-．③由①可知，1a =，又函数图象经过原点，又函数图象经过原点，∴2k h =-，∵当2x <时，y 随x 的增大而减小，的增大而减小， ∴2h ≥， ∴4k -≤．x=32P O-7-6-5-4-3-2-1-4-3-2-16432112345678y28．证明：在ABC △中，AB BC =，BD AC ^于点D ． ∴ABD CBD Ð=Ð，AD BD =．（1）①∵90ABC Ð=°，FEADCBM∴45ACB Ð=°． ∵CE 平分ACB Ð∴22.5ECB ACE Ð=Ð=°，∴67.5BEF CFD BFE Ð=Ð=Ð=°， ∴BE BF =．∴BEF △是等腰三角形．是等腰三角形．②延长AB 至M ，使得BM AB =，连接CM ．∴BD CM ∥，12BD CM =．∴45BCM DBC ABD BMC Ð=Ð=Ð=Ð=°， BFE MCE Ð=Ð∴BC BM =．由①可得，,BEF BFE BE BF Ð=Ð=． ∴BFE MCE BEF Ð=Ð=Ð． ∴EM MC =．∴1()2BD BC BF =+．（2）14ACE ABC Ð=Ð．FPBACDa ．与（1）②同理可证BD PC ∥，12BD PC =，BP BC =；b ．由1()2BD BC BF =+可知PEC △和BEF △分别是等腰三角形；分别是等腰三角形；c ．由180BEF BFE EBF Ð+Ð+Ð=°，90FCD DFC Ð+Ð=°，可知14ACE ABC Ð=Ð．29．解：（1）①点B 的坐标为(3,0)； ②a 的值为2-．③直线3l 的表达式为2y x =-+．（2）112b -≤≤；（3）将点N 关于y 轴的对称点记为点P ． ∴点P 和点'N 关于直线:31l y x =+对称，对称， ∵直线313y x =+和y 轴关于直线:31l y x =+对称．对称． ∴点P 在直线313y x =+上，上， ∵直线313y x =-+和直线313y x =+关于y轴对称，轴对称，∴点N 在直线313y x =-+上，上， ∴符合题意的点N 是直线313y x =-+与⊙E 的公共点．的公共点．（i ）当直线313y x =-+与⊙E 相离时，则不存在符合题意的点N ．（ii ）当直线313y x =-+与⊙E 相切时，如图所示．相切时，如图所示．则符合题意的点N是直线313y x =-+与⊙E 相切时的切点，相切时的切点，记直线313y x =-+与x 轴交于点(3,0)R ，若点E 在点R 的左侧，的左侧，由112E N =，可得14RE =，143OE =-， ∴143t =-+．若点E 在点R 的右侧，的右侧，由222E N =，可得24RE =，243OE =+． ∴243t =+．（iii ）当直线313y x =-+与⊙E 相交时，相交时，4343t -++<<．综上，t 的取值范围是：4343t -++≤≤．y=-33x +1y=-3x +1y=-33x +1N 1N 2E 2E 1ROxy 5642-2-5。

2016-2017北京西城初三第一学期数学期末试卷(含答案)

2016-2017北京西城初三第一学期数学期末试卷(含答案)北京市西城区2016— 2017学年度第一学期期末试卷九年级数学2017.1一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的．1．抛物线y＝(x-1)2+2的对称轴为（）．A．直线x = 1 B．直线x =﹣1 C．直线x=2 D．直线x=﹣22．我国民间，流传着许多含有吉祥意义的文字图案，表示对幸福生活的向往，良辰佳节的祝贺．比如下列图案分别表示“福”、“禄”、“寿”、“喜”，其中是．轴对称图形，但不是．．中心对称图形的是（）．A B CD1，则3．如图，在Rt△ABC中，∠C=90°，AC=4，tan A=2BC的长度为（）．A．2 B．8 C．34D．54 4．将抛物线y＝-3x2平移，得到抛物线y＝-3 (x-1)2-2，下列平移方式中，正确的是（）．D．52制造弯形管道时，经常要先按中心线计算8．“展直长度”，再下料.右图是一段弯形管道，其中∠O=∠O’=90°，中心线的两条弧的半径都是1000mm，这段变形管道的展直长度约为（取π3.14）（）．A．9280mm B．6280mm C．6140mm D．457mm 9．当太阳光线与地面成40°角时，在地面上的一棵树的影长为10m，树高h（单位：m）的范围是（）．A．3＜h＜5 B．5＜h＜10 C．10＜h＜15 D．15＜h＜2010．在平面直角坐标系xOy中，开口向下的抛物线y= ax2+bx +c的一部分图象如图所示，它与x轴交于A(1，0)，与y轴交于点B(0，3)，则a的取值范围是（）．A．a＜0 B．－3＜a＜0C．a＜3-D．92-＜a＜32-2二、填空题（本题共18分，每小题3分）11．二次函数22y x x m=-+的图象与x轴只有一个公共点，则m的值为．12．如图，在△ABC中，点E，F分别在AB，AC上，若△AEF∽△ABC，则需要增加的一个条件是（写出一个即可）．13．如图，⊙O 的半径为1，PA ，PB 是⊙O两条切线，切点分别为A ，B ．连接OA ，OB ，AB ，PO ∠APB=60°，则△PAB 的周长为．14. 如图，在平面直角坐标系xOy 直线交于点1(0)y kx m k =+≠的抛物线22(0)y ax bx c a =++≠A (0，4)，B (3，1)，当 y 1≤y 2时，x 的取值范围是．15. 如图，在△ABC 中，∠BAC =65°，将△ABC绕点A 逆时针旋转，得到△AB ＇C ＇，连接C C .若C ＇C ∥AB ，则∠BA B ＇= °16．考古学家发现了一块古代圆形残片如图所示，为了修复这块残片，需要找出圆心. （1）请利用尺规作图确定这块残片的圆心O ；（2）写出作图的依据：．三、解答题（本题共72分，第17～26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明，演算步骤或证明过程．17．计算：4cos303tan60+2sin45cos45 o o o o -．18．如图， D 是等边三角形ABC 内一点，将线段AD 绕点A 顺时针旋转60°，得到线段AE ，连接CD ， BE ．（1）求证：∠AEB =∠ADC ；（2）连接DE ，若∠ADC =105°，求∠BED 的度数．19．已知二次函数y =x 2 + 4x + 3．（1）用配方法将二次函数的表达式化为y = a (x -h )2 + k 的形式；（2）在平面直角坐标系xOy 中，画出这个二次函数的图象；（3）根据（2）中的图象，写出一条该二次函数的性质．20．如图，在△ABC 中，点D 在BC 边上，∠DAC =∠B ．点E 在AD 边上， CD =CE ．（1）求证：△ABD ∽△CAE ；（2）若AE 的长.21．一张长为30cm ，宽20cm 的矩形纸片，如图1所示，将这张纸片的四个角各剪去一个边长相同的正方形后，把剩余部分折成一个无盖的长方体纸盒，如图1所示，如果折成的长方体纸盒的底面积．．．为264cm 2，求剪掉的正方形纸片的边长．22．一条单车道的抛物线形隧道如图所示．隧道中公路的宽度AB =8 m , 隧道的最高点C 到公路的距离为6 m ．（1）建立适当的平面直角坐标系，求抛物线的表达式；（2）现有一辆货车的高度是4.4m ，货车的宽度是2 m ，为了保证安全，车顶距离隧道顶部至少0.5m ，通过计算说明这辆货车能否安全通过这条隧道．23．如图，AB 是⊙O 的直径，C 为⊙O 上一点，经过点C的直线与AB 的延长线交于点D ，连接AC ，BC ，∠BCD =∠CAB ．E 是⊙O上一点，弧图1 图2CB=弧CE，连接AE并延长与DC的延长线交于点F．（1）求证：DC是⊙O的切线；（2）若⊙O的半径为3，sin D =35，求线段AF的长．24．测量建筑物的高度在《相似》和《锐角三角函数》的学习中，我们了解了借助太阳光线、利用标杆、平面镜等可以测量建筑物的高度．综合实践活动课上，数学王老师让同学制作了一种简单测角仪：把一根细线固定在量角器的圆心处，细线的另一端系一个重物（如图1）；将量角器拿在眼前，使视线沿着量角器的直径刚好看到需测量物体的顶端，这样可以得出需测量物体的仰角α的度数（如图2，3）．利用这种简单测角仪，也可以帮助我们测量一些建筑物的高度．天坛是世界上最大的祭天建筑群，图1 图2 图31998年被确认为世界文化遗产．它以严谨的建筑分布，奇特的建筑构造和瑰丽的建筑装饰闻名于世．祈年殿是天坛主体建筑，又称祈谷殿（如图4）．采用的是上殿下屋的构造形式，殿为圆形，象征天圆；瓦为蓝色，象征蓝天．祈年殿的殿座是圆形的祈谷坛．请你利用所学习的数学知识，设计一个测量方案，解决“测量天坛祈年殿的高度”的问题．要求：图4（1）写出所使用的测量工具；（2）画出测量过程中的几何图形，并说明需要测量的几何量；（3）写出求天坛祈年殿高度的思路．25．如图，△ABC内接于⊙O，直径DE⊥AB于点F，交BC于点M，DE的延长线与AC的延长线交于点N，连接AM．（1）求证：AM=BM；（2）若AM⊥BM，DE=8，∠N=15°，求BC 的长．26．阅读下列材料：有这样一个问题：关于x 的一元二次方程a x2+ bx + c = 0（a>0）有两个不相等的且非零的实数根．探究a，b，c满足的条件．小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：①设一元二次方程ax2+bx+c = 0（a>0）对应的二次函数为y = ax2+bx +c（a>0）；②借助二次函数图象，可以得到相应的一元二次中a，b，c满足的条件，列表如下：方程根的几何意义：请将（2）补充完整方程两根的情况对应的二次函数的大致图象a，b，c满足的条件方程有两个不相等的负实根20,40,0,20.ab acbac>⎧⎪∆=->⎪⎪⎨-<⎪⎪>⎪⎩0,0.ac>⎧⎨<⎩（1）参考小明的做法，把上述表格补充完整；（2）若一元二次方程()22340mx m x m-+-=有一个负实根，一个正实根，且负实根大于-1，求实数m的取值范围．7.在平面直角坐标系xOy中，抛物线y = -x2+ mx +n与x 轴交于点A，B（A在B的左侧）.（1）抛物线的对称轴为直线x =-3，AB = 4.求抛物线的表达式；（2）平移（1）中的抛物线，使平移后的抛物线经过点O，且与x正半轴交于点C，记平移后的抛物线顶点为P，若△OCP是等腰直角三角形，求点P的坐标；（3）当m =4时，抛物线上有两点M（x1，,y1）和N（x2，,y2），若x1< 2，x2>2，x1+ x2 > 4，试判断y1与y2的大小，并说明理由.28．在Rt△ABC中，∠ACB=90°，AC=BC，C D为AB边上的中线．在Rt△AEF中，∠AEF=90°，AE=EF，AF < AC．连接BF，M，N分别为线段AF，BF的中点，连接MN．（1）如图1，点F在△ABC内，求证：CD = MN；（2）如图2，点F在△ABC外，依题意补全图2，连接CN，EN，判断CN与EN的数量关系与位置关系，并加以证明；（3）将图1中的△AEF绕点A旋转，若AC=a，AF=b （b<a），直接写出EN的最大值与最小值．图 1 图 2 备用图29．在平面直角坐标系xOy中，给出如下定义：对于⊙C及⊙C外一点P，M，N是⊙C上两点，当∠MPN最大，称∠MPN为点．P．关于⊙C的“视角”．直线l与⊙C相离，点Q在直线l上运动，当点Q 关于⊙C的“视角”最大时，则称这个最大的“视角”为直线．．l．关于⊙C的“视角”．（1）如图，⊙O的半径为1，①已知点A（1，1），直接写出点A关于⊙O的“视角”；已知直线y = 2，直接写出直线y = 2关于⊙O 的“视角”；②若点B关于⊙O的“视角”为60°，直接写出一个符合条件的B点坐标；（2）⊙C的半径为1，①点C的坐标为（1，2），直线l: y=kx+b（k > 0）经过点D（231-+，0），若直线l关于⊙C的“视角”为60°，求的值；②圆心C在x轴正半轴上运动，若直线y 33关于⊙C的“视角”大于120°，直接写出圆心C的横坐标x C的取值范围．备用图北京市西城区2016— 2017学年度第一学期期末试卷九年级数学参考答案及评分标准2017.1一、选择题（本题共30分，每小题3分）（2）作图的依据：线段垂直平分线上的点与线段两个端点的距离相等；不在同一直线上的三个点确定一个圆．三、解答题（本题共72分，第17﹣26题，每小题5分，第27题7分，第28题7分，第29题8分）17．解：原式= 4×4分························5分18．（1）证明：∵等边△ABC，∴∠BAC=60°，AB=AC．∵线段AD绕点A顺时针旋转60°，得到线段AE，∴∠DAE=60°，AE=AD．∴∠BAD+∠EAB=∠BAD+∠DAC．∴∠EAB =∠DAC．∴△EAB≌△DAC．∴∠AEB=∠ADC． ·······（2）解：∵∠DAE=60°，AE=AD，∴△EAD为等边三角形．∴∠AED=60°，又∵∠AEB =∠ADC=105°．∴∠BED=45°． ···············5分19．解：（1）y = x 2 + 4x + 3= x 2 + 4x + 22 - 22 + 3= (x +2)2 -1 ··················· 2分（2）列表：··················（3）答案不唯一，如：当x ＜-2时，y 随x 的增大而减小，当x ＞-2时，y 随x 的增大而增大.································· 5分20．（1）证明：∵CE = CD ，∴∠CDE =∠CED .∴∠ADB =∠CEA .∵∠DAC =∠B ，∴△ABD ∽△CAE . ······ 3分（2）解：由（1）△ABD ∽△CAE ，∴AEBD AC AB. ∵AB =6，AC BD =2，∴AE =23． ························ 5分 21．解：设剪掉的正方形纸片的边长为x cm ． 1分由题意，得 (30-2x )(20-2x )=264． 3分整理，得 x 2-25x + 84=0．解方程，得14x =，221x=（不符合题意，舍去）．····················································· 4分答：剪掉的正方形的边长为4cm ． ··· 5分 22．解：（1）本题答案不唯一，如：以AB 所在直线为x 轴，以抛物线的对称轴为y 轴建立平面直角坐标系xOy ，如图所示. ∴A (-4，0), B (4，0), C （0，6）．设这条抛物线的表达式为(4)(4)y a x x =-+ ．∵抛物线经过点C ， ∴－16a =6．∴38a =-． ∴抛物线的表达式为2368y x =-+(-4≤x ≤4)．····················································· 4分（2）当x =1时，458y =．∵4.4+0.5=4.9＜45，8∴这辆货车能安全通过这条隧道. 5分23．（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB =90°．∵OA = OC，∴∠1=∠2．∵∠DCB =∠BAC =∠1．∴∠DCB +∠3=90°．∴OC⊥DF．∴DF是⊙O的切线． ····2分．（2）解：在Rt△OCD中，OC=3，sinD=35∴OD = 5 ，AD =8．∵弧CE=弧CB，∴∠2=∠4．∴∠1=∠4．∴OC∥AF．∴△DOC∽△DAF.∴OC OD=．AF AD∴24AF=．···························5分524．本题答案不唯一，如：（1 1分（2）设CD形如图所示；需要测量的几何量如下：① 在点A ，点B 处用测角仪测出仰角α，β；② 测出A ，B 两点之间的距离s ； 3分（3）求解思路如下：a ．设CD 的高度为x m ．在Rt △DBC 中，由∠DBC =β，可得tan x BC β=；同理，在Rt △DAC 中，由∠DBC =α，可得tan xAC α=； b ．由AB =AC –BC 得tan tan x xs αβ=-，x 可求． ····················································· 5分 25．（1）证明：∵直径DE ⊥AB 于点F ，∴AF =BF ．∴AM =BM ． ················ 2分（2）连接AO ，BO ，如图．由（1）可得 AM =BM ， ∵AM ⊥BM ， ∴∠MAF =∠MBF =45°．∴∠CMN =∠BMF =45°．∵AO =BO ，DE ⊥AB ，∴∠AOF =∠BOF AOB ． ∵∠N =15°，∴∠ACM =∠CMN +∠N = 60°．即∠ACB =60°． ∵∠ACB AOB ． ∴∠AOF =∠ACB =60°． ∵DE =8， ∴AO =4．在Rt △AOF 中，由sin AF AOB AO ∠=，得AF=在Rt △AMF 中，AM = BM=．在Rt △ACM 中，由tan AM ACM CM ∠=，得CM=．∴BC = CM + BM=····· 5分26．解：（1）补全表格如下：20,40,0,20.a b ac ba c >⎧⎪∆=->⎪⎪⎨->⎪⎪>⎪⎩································· 3分（2）解：设一元二次方程()22340mxm x m -+-=对应的二次函数为：()2234y x m x m=-+-，∵一元二次方程()22340mxm x +--=有一个负实根，一个正实根，且负实根大于-1，∴240(1)(23)(1)40m m m -<⎧⎨--+⋅-->⎩解得02m <<．∴m 的取值范围是02m <<．5分27.解：（1）抛物线 y = - x 2 + mx +n 的对称轴为直线x = -3，AB = 4.∴ 点 A （-5，0），点B （-1，0）.∴抛物线的表达式为y = - (x + 5) ( x + 1) ∴ y = - x 2 - 6x -5. ··········· 2分（2）依题意，设平移后的抛物线表达式为：y = - x 2+ bx .∴抛物线的对称轴为直线2b x =，抛物线与x 正半轴交于点C （b ，0）.∴ b > 0.∵△OCP 是等腰直角三角形，∴点P 的坐标（2b ，2b ）. ∴ 2()()222b b bb =-+.解得 b = 2.∴点P 的坐标（1，1）. ···· 5分（3）当m =4时，抛物线表达式为：y = - x 2 + 4x +n .∴抛物线的对称轴为直线 x = 2.∵点M （x 1，,y 1）和N （x 2，,y 2）在抛物线上，且x 1< 2 ， x 2>2，∴点M 在直线x = 2的左侧，点N 在直线x = 2的右侧.∵x 1+ x 2 > 4， ∴2 -x 1< x 2 - 2.∴点P 到直线x = 2的距离比点M 到直线x = 2的距离比点N 到直线x = 2的距离近，如图所示.∴ y 1 > y 2 . ····························· 7分28．解：（1）证明：在Rt△ABC中，∵CD是斜边AB上的中线．∴CD =1AB．2在△ABF中，点M，N分别是边AF，BF的中点，∴MN =1AB，2∴CD = MN． ···········2分（2）答：CN与EN的数量关系CN = EN，CN与EN的位置关系CN⊥EN．3分证明：连接EM，DN，如图．与（1）同理可得CD = MN，EM = DN．在Rt△ABC中，CD是斜边AB边上的中线，∴CD⊥AB．在△ABF中，同理可证EM⊥AF．∴∠EMF=∠CDB= 90 ．∵D，M，N分别为边AB，AF，BF的中点，∴ DN ∥AF ，MN ∥AB ．∴ ∠FMN =∠MND ，∠BDN =∠MND ．∴ ∠FMN = ∠BDN ．∴ ∠EMF +∠FMN =∠CDB +∠BCN ．∴ ∠EMN =∠NDC ． ∴ △EMN ≌△DNC ． ∴ CN = EN ，∠1 =∠2． ∵ ∠1 +∠3 +∠EMN = 10︒， ∴ ∠2 +∠3 +∠FMN = 90︒． ∴ ∠2 +∠3 +∠DNM = 90︒，即∠CNE = 90︒．∴ CN ⊥EN ． ········ 5分（3）EN 的最大值为22b a +，最小值为22ba -. 7分29．解：（1）① 90︒，60︒． ················ 2分② 本题答案不唯一，如：B (0，2) . 3分（2）解：①∵直线l : y =kx + b （k > 0）经过点D （1-，0），∴(1)0k b -+=.∴b k=-.∴直线l :y kx k=+-.对于⊙C 外的点P ，点P 关于⊙C 的“视角”为60°，则点P 在以C 为圆心，2为半径的圆上．又直线l 关于⊙C 的 “视角”为60°，此时，点P 是直线l 上与圆心C 的距离最短的点.∴CP则直线l 作CH ⊥∴点H ∴DH =∴∠CDH =30°，∠PDH =60°，可求得点P 的坐标（1，3）．进而求得 k································· 6分（3）圆心C 的横坐标x C 的取值范围是1133Cx-+<<．································· 8分。

2017.1 西城初三上数学期末答案(1)

12. 【答案】EF //BC （答案不唯一）
13. 【答案】3√3
爱
智
康
14. 【答案】0 ⩽ x ⩽ 3
15. 【答案】50∘
16. 【答案】（1）画图见解析．（2）线段垂直平分线的点与这条线段两个端点的距离相等；不在同一条直线上的三个点确定一个圆．
三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28分7分，第29题8分）
17. 【答案】1 − √3 ．
18. 【答案】（1）证明见解析．（2）∠BED = 45∘ ．
（3）本题答案不唯一，如：当x <
爱
智
−2
Байду номын сангаас
（2）画图见解析．
康
时，y 随x的增大而减小，当x > −2 时，y 随x的增大而增大．
19. 【答案】（1）y = (x + 2)
2
−1
．
20. 【答案】（1）证明见解析．（2）AE =
2016~2017学年北京西城区初三上学期期末数学试卷
一、选择题（本题共30分，每小题3分）
1. 【答案】A
2. 【答案】C
3. 【答案】A
4. 【答案】D
5. 【答案】B
6. 【答案】C
7. 【答案】D
8. 【答案】C
9. 【答案】B
10. 【答案】B
二、填空题（本题共18分，每小题3分）
11. 【答案】1
3 2
．
21. 【答案】剪掉的正方形纸片的边长为4 cm ．
22. 【答案】（1）（答案不唯一）抛物线表示的二次函数表达式为y = − （2）这辆货车能安全通过这条隧道．
3 8

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017年北京市西城区初三一模试卷及答案数学北京市西城区2017年九年级统一测试数学试卷 2017.4一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是．符合题意的．1．春节假期，北京市推出了庙会休闲娱乐、传统文化展演、游园赏景赏花、冰雪项目体验等精品文化活动，共接待旅游总人数9 608 000人次，将9 608 000用科学记数法表示为（A ）3960810⨯（B ）4960.810⨯ （C ）596.0810⨯ （D ）69.60810⨯2．在数轴上，实数a ，b 对应的点的位置如图所示，且这两个点关于原点对称，下列结论中，正确的是（A ）0a b += （B ）0a b -= （C ）a b ＜（D ）0ab ＞ 3．如图，AB ∥CD ，DA ⊥CE 于点A ．若∠EAB = 55°，则∠D 的度数为（A ）25°（B ）35° （C ）45° （D ）55°镜的水平距离为2m ，旗杆底部与平面镜的水平距离为16m ．若小明的眼睛与地面距离为1.5m ，则旗杆的高度为（单位：m ）（A ）163（B ）9 （C ）12 （D ）6438．某商店举行促销活动，其促销的方式是“消费超过100元时，所购买的商品按原价打8折后，再减少20元” ．若某商品的原价为x 元（x ＞100），则购买该商品实际付款的金额（单位：元）是（A ）80%20x - （B ）()80%20x - （C ）20%20x - （D ）()20%20x -9．某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：年龄（单位：岁） 13 14 15 16 频数（单515x10-x位：名）对于不同的x，下列关于年龄的统计量不会发生改变的是（A）平均数、中位数（B）平均数、方差（C）众数、中位数（D）众数、方差10．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数．“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多；“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少．右下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况，下列说法中，正确的是（A）以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多（B）以低于80km/h的速度行驶时，行驶相同路程，三辆车中，乙车消耗汽油最少（C）以高于80km/h的速度行驶时，行驶相同路程，丙车比乙车省油（D）以80km/h的速度行驶时，行驶100公里，甲车消耗的汽油量约为10升二、填空题（本题共18分，每小题3分）11．分解因式：ax2 2ax+a=________．12．若函数的图像经过点A（1，2），点B（2，1），写出一个符合条件的函数表达式_________．13．下表记录了一名球员在罚球线上罚篮的结果：这名球员投篮一次，投中的概率约是．4．如图，四边形ABCD是⊙O内接四边形，若∠BAC=30°，∠CBD=80°，则∠BCD的度数为____________．第14题图第15题15．在平面直角坐标系xOy中，以原点O为旋转中心，将△AOB顺时针旋转90°得到△A'OB'，其中点A'与点A对应，点B'与点B对应．若点A（-3，0），B（-1，2），则点A'的坐标为_______________，点B'的坐标为________________.16．下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程．已知：如图1，直线l和直线l外一点P．求作：直线l的平行直线，使它经过点P．作法：如图2．（1）过点P作直线m与直线l交于点O;（2）在直线m上取一点A（OA＜OP），以点O为圆心，OA长为半径画弧，与直线l交于点B；（3）以点P为圆心，OA长为半径画弧，交直线m 于点C，以点C为圆心，AB长为半径画弧，两弧交于点D；（4）作直线PD．所以直线PD就是所求作的平行线．请回答：该作图的依据是．三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程. 17．计算：(10O1226022sin -⎛⎫-- ⎪⎝⎭18．解不等式组： 52<3+4722x x x x -⎧⎪⎨+≥⎪⎩19．已知x=2y ，求代数式222112x xy y y x x y ⎛⎫-+-÷⎪⎝⎭的值.20．如图，在△ABC中，BC的垂直平分线交BC于点D，交AB延Array长线于点E，连接CE.求证：∠BCE=∠A+∠ACB.21．某科研小组计划对某一品种的西瓜采用两种种植技术种植.在选择种植技术时，该科研小组主要关心的问题是：西瓜的产量和产量的稳定性，以及西瓜的优等品率. 为了解这两种种植技术种出的西瓜的质量情况，科研小组在两块自然条件相同的试验田进行对比试验，并从这两块实验田中各随机抽取20个西瓜，分别称重后，将称重的结果记录如下：表1 甲种种植技术种出的西瓜质量统计表表2 乙种种植技术种出的西瓜质量统计表回答下列问题：（1）若将质量为4.5~5.5（单位：kg）的西瓜记为优等品，完成下表：（2）根据以上数据，你认为该科研小组应选择哪种种植技术，并请说明理由.22．在平面直角坐标系x O y，直线y=x-1与y轴交于点A，与双曲线=k y交于点B（m，2）.x（1）求点B的坐标及k的值;（2）将直线AB平移，使它与x轴交于点C，与y轴交于点D，若△ABC的面积为6，求直线CD的表达式.23．如图，在□ABCD中，对角线BD平分∠ABC，过点A作AE//BD，交CD的延长线于点E，过点E作EF ⊥BC，交BC延长线于点F.（1）求证：四边形ABCD是菱形；（2）若∠ABC=45°，BC=2，求EF的长.B24. 汽车保有量是指一个地区拥有车辆的数量，一般是指在当地登记的车辆．进入21世纪以来，我国汽车保有量逐年增长．下图是根据中国产业信息网上的有关数据整理的统计图．2007—2015年全国汽车保有量及增速统计图根据以上信息，回答下列问题：（1）2016年汽车保有量净增2200万辆，为历史最高水平，2016年汽车的保有量为万辆，与2015年相比，2016年的增长率约为%；（2）从2008年到2015年，年全国汽车保有量增速最快；（3）预估2020年我国汽车保有量将达到万辆，预估理由是25．如图，AB为⊙O的直径，C为⊙O上一点，过点C 作⊙O的切线，交BA的延长线交于点D，过点B作BE ⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC．（1）求证：∠ECB =∠EBC；，求AC （2）连接BF，CF，若CF =6，sin∠FCB =35的长．D26．阅读下列材料：某种型号的温控水箱的工作过程是：接通电源后，在初始温度20℃下加热水箱中的水；当水温达到设定温度80℃时，加热停止；此后水箱中的水温开始逐渐下降，当下降到20℃时，再次自动加热水箱中的水至80℃时，加热停止；当水箱中的水温下降到20℃时，再次自动加热，……，按照以上方式不断循环．小明根据学习函数的经验，对该型号温控水箱中的水温随时间变化的规律进行了探究．发现水温y 是时间x的函数，其中y(单位：℃)表示水箱中水的温度．x(单位：min)表示接通电源后的时间．下面是小明的探究过程，请补充完整：（1）下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况m的值为；（2）①当0 ≤x ≤ 4时，写出一个符合表中数据的函数解析式；当4＜x ≤ 16时，写出一个符合表中数据的函数解析式；②如图，在平面直角坐标系xOy中，描出了上表中部分数据对应的点，根据描出的点，画出当0≤x≤32时，温度y随时间x变化的函数图象：（3）如果水温y随时间x的变化规律不变，预测水温第8次达到40℃时，距离接通电源min．27．在平面直角坐标系xOy中，二次函数y=mx2 -(2m + 1)x + m-5的图象与x轴有两个公共点.（1）求m的取值范围；（2）若m取满足条件的最小的整数，①写出这个二次函数的解析式；②当n ≤ x ≤ 1时，函数值y的取值范围是-6 ≤ y ≤ 4-n，求n的值；③将此二次函数平移，使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 + k，当x < 2时，y随x的增大而减小，求k的取值范围.28．在△ABC中，AB = BC，BD⊥AC于点D.（1）如图1，当∠ABC = 90°时，若CE 平分∠ACB ，交AB 于点E ，交BD 于点F .①求证：△BEF 是等腰三角形； ②求证：BD =12（BC + BF ）；（2）点E 在AB 边上，连接CE .若BD =12（BC + BE ），在图2中补全图形，判断∠ACE 与∠ABC 之间的数量关系，写出你的结论，并写出求解∠ACE 与∠ABC 关系的思路.图2图1D FEDCB AACB29．在平面直角坐标系xOy中，若点P和点P1关于y 轴对称，点P1和点P2关于直线l对称，则称点P2是点P关于y轴，直线l的二次对称点．（1）如图1，点A（-1 , 0）．①若点B是点A关于y轴，直线l1: x=2的二次对称点，则点B的坐标为；②若点C（-5 , 0）是点A关于y轴，直线l2: x = a 的二次对称点，则a的值为；③若点D（2 , 1）是点A关于y轴，直线l3的二次对称点，则直线l3的表达式为；（2）如图2，⊙O的半径为1．若⊙O上存在点M，使得点M＇是点M关于y轴，直线l4: x = b的二次对称点，且点M ＇在射线(0)y x x =≥上，b 的取值范围是；（3）E （t ，0）是x 轴上的动点，⊙E 的半径为2，若⊙E 上存在点N，使得点N ＇是点N 关于y 轴，直线l 5:1y =+的二次对称点，且点N ＇在y 轴上，求t 的取值范围．图1图2。