函数的单调性与导数(公开课)PPT课件
合集下载
函数的单调性与导数 公开课 ppt课件

解:(1)f '(x)=x3+3x= 3(x2+1)>0
所以函数f(x)=x3+3x在R上单调递增。 所以函数f(x)=x3+3x的单调增区间为R。
函数的单调性与导数 公开课
二、讲授新课-----典例精讲
例 3. 判断下列函数的单调性, 并求出单调区间:
(1) f(x)=x2-2x-3,
(2) f(x)=x2-2lnx
函数的单调性与导数 公开课
Байду номын сангаас
1.3.1函数的单调性与导数(第1课时)
函数的单调性与导数 公开课
一、新课导入------复旧知新
1.函数的单调性是怎样定义的?
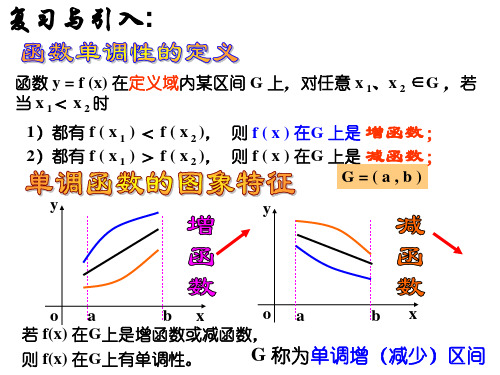
一般地,设函数f(x)的定义域为I: 如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2, 当x1<x2时,都有f(x1)<f (x2),那么就说f(x)在区间D上是增函数; 当x1<x2时,都有f(x1)>f (x2),那么就说f(x)在区间D上是减函数;
致形状如右图所示.
O1
4
x
函数的单调性与导数 公开课
二、讲授新课-----牛刀小试
练习. 设导函数y=f '(x)的图象如图,则其原函数可能为
( C)
(A) y y=f(x) (B) y y=f(x) o 1 2x o 1 2x
y y f '(x)
(C) y
(D) y
o 2x
y=f(x)
y=f(x)
函数的单调性与导数 公开课
四、巩固练习
判断函数f(x)=3x-x3的单调性, 并求出单调区间:
解:
f '(x)=3x-x3=3-3x2=-3(x2-1)=-3(x-1)(x+1) 当f '(x)>0,即-1<x<1时,函数f(x)=3x-x3 单调递增; 当f '(x)<0,即x>1或x<-1时,函数f(x)=3x-x3 单调递减; 所以函数f(x)=3x-x3的单调增区间为 (-1,1),单调
所以函数f(x)=x3+3x在R上单调递增。 所以函数f(x)=x3+3x的单调增区间为R。
函数的单调性与导数 公开课
二、讲授新课-----典例精讲
例 3. 判断下列函数的单调性, 并求出单调区间:
(1) f(x)=x2-2x-3,
(2) f(x)=x2-2lnx
函数的单调性与导数 公开课
Байду номын сангаас
1.3.1函数的单调性与导数(第1课时)
函数的单调性与导数 公开课
一、新课导入------复旧知新
1.函数的单调性是怎样定义的?
一般地,设函数f(x)的定义域为I: 如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2, 当x1<x2时,都有f(x1)<f (x2),那么就说f(x)在区间D上是增函数; 当x1<x2时,都有f(x1)>f (x2),那么就说f(x)在区间D上是减函数;
致形状如右图所示.
O1
4
x
函数的单调性与导数 公开课
二、讲授新课-----牛刀小试
练习. 设导函数y=f '(x)的图象如图,则其原函数可能为
( C)
(A) y y=f(x) (B) y y=f(x) o 1 2x o 1 2x
y y f '(x)
(C) y
(D) y
o 2x
y=f(x)
y=f(x)
函数的单调性与导数 公开课
四、巩固练习
判断函数f(x)=3x-x3的单调性, 并求出单调区间:
解:
f '(x)=3x-x3=3-3x2=-3(x2-1)=-3(x-1)(x+1) 当f '(x)>0,即-1<x<1时,函数f(x)=3x-x3 单调递增; 当f '(x)<0,即x>1或x<-1时,函数f(x)=3x-x3 单调递减; 所以函数f(x)=3x-x3的单调增区间为 (-1,1),单调
高二数学函数的单调性与导数PPT教学课件

第三章 导数及其应用 y
3.3.1 函数的单调性与导数
o
x
观察下列图象的单调区间, 并求单调区间相应的导数.
图象是单调上升的.
y10
在x∈(-∞,0)内 图象是单调下降的.
y2x0
在x∈( 0,+∞)内 图象是单调上升的.
y2x0
图象是单调上升的.
y3x20 (当 x0 时 )
在x∈(-∞,0)内 图象是单调下降的.
当 f(x) >0,
即 x117或 x117 时,
2
2
函数单调递增;
当 f(x) <0,
即 117x1Biblioteka 7时, y22函数单调递减;
图象见右图。
o
x
练习1:确定下列函数的单调区间:
(1) f(x)=x2-2x+4 x<1时,函数单调递减, x>1时,函数单调递增。
(2) f(x)=3x-x3 x<-1或x>1时,函数单调递减, -1<x<1时,函数单调递增。
从而函数f(x)=x3+3x 在x∈R上单调递增, 见右图。
o
x
f (x) x3 3x
(2) f(x)=x2-2x-3 ;
解: f(x)=2x-2=2(x-1)>0
当 f(x)>0,即x>1时,函数单调递增;
当 f(x)<0,即x<1时, 函数单调递减;
y
f (x) x2 2x 3
图象见右图。
当 1<x< 4时,
y
o1
解:由题意可知
yf(x)
当1<x<4时, f(x)为增函数 当x>4,或x<1时,
3.3.1 函数的单调性与导数
o
x
观察下列图象的单调区间, 并求单调区间相应的导数.
图象是单调上升的.
y10
在x∈(-∞,0)内 图象是单调下降的.
y2x0
在x∈( 0,+∞)内 图象是单调上升的.
y2x0
图象是单调上升的.
y3x20 (当 x0 时 )
在x∈(-∞,0)内 图象是单调下降的.
当 f(x) >0,
即 x117或 x117 时,
2
2
函数单调递增;
当 f(x) <0,
即 117x1Biblioteka 7时, y22函数单调递减;
图象见右图。
o
x
练习1:确定下列函数的单调区间:
(1) f(x)=x2-2x+4 x<1时,函数单调递减, x>1时,函数单调递增。
(2) f(x)=3x-x3 x<-1或x>1时,函数单调递减, -1<x<1时,函数单调递增。
从而函数f(x)=x3+3x 在x∈R上单调递增, 见右图。
o
x
f (x) x3 3x
(2) f(x)=x2-2x-3 ;
解: f(x)=2x-2=2(x-1)>0
当 f(x)>0,即x>1时,函数单调递增;
当 f(x)<0,即x<1时, 函数单调递减;
y
f (x) x2 2x 3
图象见右图。
当 1<x< 4时,
y
o1
解:由题意可知
yf(x)
当1<x<4时, f(x)为增函数 当x>4,或x<1时,
2024版《函数的单调性》全市一等奖完整版PPT课件

利用单调性证明不等式
1 2
构造函数 根据不等式的特点,构造一个与不等式相关的函 数。
判断函数单调性 通过求导或差分等方法判断所构造函数的单调性。
3
利用单调性证明不等式 根据函数的单调性,结合不等式的性质,证明不 等式成立。
2024/1/29
18
利用单调性解决实际应用问题
要点一
建立数学模型
要点二
判断函数单调性
2024/1/29
21
导数与微分在函数单调性研究中的应用
导数大于零的区间内函数单调 增加,导数小于零的区间内函 数单调减少。
2024/1/29
导数等于零的点为函数的驻点, 需要进一步判断其左右两侧导 数的符号来确定该点的单调性。
微分的概念可以应用于函数单 调性的研究,通过微分可以分 析函数的局部变化率,进而判 断函数的单调性。
14
指数函数与对数函数
对数函数 $y = log_a x$($a > 0, a neq 1$)的单调 性
当 $0 < a < 1$ 时,函数在 $(0, +infty)$ 上单调递减。
当 $a > 1$ 时,函数在 $(0, +infty)$ 上单调递增。
指数函数与对数函数的图像关于直线 $y = x$ 对称,即 互为反函数。
2024/1/29
19
05
函数单调性与其他知识点关联
2024/1/29
20
函数奇偶性与周期性对单调性影响
奇函数在对称区间上的单调性相 同,偶函数在对称区间上的单调
性相反。
周期函数在一个周期内的单调性 与整体单调性一致,可以通过研 究一个周期内的单调性推断整体
的单调性。
高二数学-函数的单调性与导数公开课优秀课件(经典、值得收藏)

二、题型探究
3.利用导数求参数的取值范围
例.若函数f(x)=2x2+ln x-ax在定义域上单调递增,求实数a的取值范围.
解 ∵f(x)=2x2+ln x-ax的定义域为(0,+∞), 且在(0,+∞)上单调递增,
∴f′(x)=4x+1x-a≥0 在(0,+∞)上恒成立. ∴a≤4x+1x在(0,+∞)上恒成立.
单调性 割线斜率的符号 切线斜率的符号 导数
一、知识讲解:
函数单调性与导函数正负的关系
单调性 割线斜率的符号 切线斜率的符号 导数
观察下面函数的图象,探讨单调性与其导函数正负的关系:
yx
y y x3
y y 1
y
y
x
ya
x o
x o
x o
x o
导数值 >0 <0
切线的斜率 >0 <0
倾斜角 锐角 钝角
曲线的变化趋势 函数的单调性
上升
递增
下降
递减
一般地,设函数y f (x),在区间(a,b)上,思考: 若f x(x) (a0,,b)则, ff(( xx)) 在0该区函间数上f递( x增)在;区间(fa(,xb))为 0增是函f(数x)为增函数 若函f (数x)f(0x,)在则区 f(间x)(a在, b该)为区增间函上递数减。f ( x)的什0恒么成条立件(不?恒等于0)
二、题型探究
2.函数图象与导数图象的关系 (2)如果函数f(x)的图象如图,那么导函数y=f′(x)的图象可能是
解析: 由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,故选A.
二、题型探究
2.函数图象与导数图象的关系
(1)函数的单调性与其导函数的正负的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x) 在(a,b)上单调递增;如果f′(x)<0,则y=f(x)在这个区间上单调递减;若恒有f′(x)=0, 则y=f(x)是常数函数,不具有单调性. (2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
函数的单调性与导数-图课件

单调减函数的性质
03
04
05
函数图像从左至右下降 。
若$f(x)$在区间$I$上单 调递减,且$a, b in I$, 且$a < b$,则有$f(a) geq f(b)$。
若函数$f(x)$在区间$I$ 上单调递减,则其反函 数在相应的区间上单调 递增。
单调性与导数的关系
01
导数与单调性的关系
如果函数在某区间的导数大于0,则该函数在此区间单调递增;如果导
数小于0,则函数在此区间单调递减。
02
导数不存在的点
对于使导数不存在的点,需要单独判断其单调性。
03
高阶导数与单调性的关系
高阶导数的符号可以提供关于函数单调性更精细的信息。例如,二阶导
数大于0表示函数在相应点处有拐点,即由单调递增变为单调递减或反
之。
02 导数在判断函数单调性中 的应用
导数大于0与函数单调性的关系
定义法判断单调性
• 定义法判断单调性是指通过比较函数在某区间内任意两点x1和x2的函数值f(x1)和f(x2),来判断函数在该区间内的单调性。 如果对于任意x1<x2,都有f(x1)<f(x2),则函数在该区间内单调递增;如果对于任意x1<x2,都有f(x1)>f(x2),则函数在该 区间内单调递减。
03 导数在实际问题中的应用
导数在经济学中的应用
边际分析
导数可以用来分析经济函数的边 际变化,例如边际成本、边际收 益等,帮助企业做出更好的经济
决策。
最优化问题
导数可以用来解决最优化问题,例 如最大利润、最小成本等,为企业 提供最优的资源配置方案。
需求弹性
导数可以用来分析需求弹性,例如 价格敏感度、需求变化等,帮助企 业制定更加精准的市场策略。
函数的单调性与导数优秀ppt课件
①当1<x<4时,f’(x)>0; ②当x>4,或x<1时,f’(x)<0; ③当x=4,或x=1时,f’(x) =0. 试画出函数f(x)图象的大致形状。
y y=f(x)
O1
4
x
7/20/2024
例2 求函数 f (x) 2x3 3x2 12x 1 的单调区间
解: f '(x) 6x2 6x 12
7/20/2024
例1
设 f '( x)是函数 f ( x) 的导函数,y f '( x)的图象如
c 右图所示,则 y f ( x) 的图象最有可能的是( )
y
y f (x)
y
y f (x)
y
y f '( x)
o 1 2x o 1 2x
(A)
y y f (x)
(B)
o
2x
y y f (x)
G=(a,b)
y
y
oa
bx
oa
bx
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上有单调性。
G 称为单调增(减少)区间
新授 画出下列函数的图像,并根据图像指出每个函数的单调区间
y x2
y x3
y1 x
y
y
y
ox
ox
o
x
(-∞,0) (0,+∞)
(- ∞ ,+∞) (-∞,0) (0,,+∞)
为增区间; (4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
7/20/2024
课堂练习 求下列函数的单调区间。
(1) f (x) x2 2x 3 (2) f (x) x3 3x
y y=f(x)
O1
4
x
7/20/2024
例2 求函数 f (x) 2x3 3x2 12x 1 的单调区间
解: f '(x) 6x2 6x 12
7/20/2024
例1
设 f '( x)是函数 f ( x) 的导函数,y f '( x)的图象如
c 右图所示,则 y f ( x) 的图象最有可能的是( )
y
y f (x)
y
y f (x)
y
y f '( x)
o 1 2x o 1 2x
(A)
y y f (x)
(B)
o
2x
y y f (x)
G=(a,b)
y
y
oa
bx
oa
bx
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上有单调性。
G 称为单调增(减少)区间
新授 画出下列函数的图像,并根据图像指出每个函数的单调区间
y x2
y x3
y1 x
y
y
y
ox
ox
o
x
(-∞,0) (0,+∞)
(- ∞ ,+∞) (-∞,0) (0,,+∞)
为增区间; (4)解不等式f’(x)<0,解集在定义域内的部分
为减区间.
7/20/2024
课堂练习 求下列函数的单调区间。
(1) f (x) x2 2x 3 (2) f (x) x3 3x
导数与函数的单调性ppt课件

x1x2 x1 - x2
x0x
一般地,设函数y=f(x)在某个区间内可导,则函数在
该区间有下面的结论:
如果在某区间上f/(x)>0,则f(x)为该区间上的增函数;
如果在某区间上f/(x)<0,则f(x)为该区间上的减函数.
引例:讨论函数y=x2-4x+3的单调性.
(方法3:导数法)
解:函数的定义域为R, f/(x)=2x-4 令f /(x)>0,解得x>2, 则f(x)的单增区间为(2,+∞). 再令f /(x)<0,解得x<2, 则f(x)的单减区间(-∞,2).
上是单调递增的,求a的取值范围. a 16
f
(x) 2x
a x2
0对任意x [2, )恒成立.
2x3 a 0对任意x [2, )恒成立.
2x3 a对任意x [2, )恒成立.
变式:(2已x3)知min函数a对f (任x)意xx2[2,a(a)恒 R成)立在.x (, 2] x
课外作业
教材P84页 习题4-1 第1题
步骤:根据导数确定函数的单调性
1.确定函数f(x)的定义域.
. 2.求出函数的导数f/(x)
3.解不等式f/(x)>0,得函数单增区间; 解不等式f/(x)<0,得函数单减区间.
例5:已知函数f (x) x2 a (a R)在x [2, ) x
解:函数的定义域为x>0, f/(x)=lnx+1.
当lnx+1>0时,解得x>1/e.则f(x)的 单增区间是(1/e,+∞). 当lnx+1<0时,解得0<x<1/e.则f(x) 的单减区间是(0,1/e).
函数的单调性与导数PPT教学课件

A1型最密堆积(配位数为12)(例如铜)
2.离子晶体属非等径圆球的密堆积方式:
大球先按一 定的方式做 等径圆球密 堆积
小球再填充 到大球所形 成的空隙中
配位数:一个原子或离子周围所邻接的原子 或离子数目。
NaCl:Cl- 离 子密先堆以积,AN1a型+ 离紧 子再填充到空 隙中。
ZnS: S2-离子 先以A1型紧密 堆积,Zn2+ 离 子再填充到空 隙中。
第一层:密置型排列 第二层:将球对准 1,3,5 位。
1
6
2
5
3
4
12
6
3
54
对准 2,4,6 位,其情形是一样的 吗?
密置双层只有一种
思考
取A、B两个密置层,将B层放 在A层的上面,有几种堆积方式? 最紧密的堆积方式是哪种?它有 何特点?
2
A
B
1
第一种排列
A
B
12
6
3
A
54
B
A
于是每两层形成一个 周期,即 AB AB 堆 积方式。
对于给定区间上的函数f(x): 1.如果对于这个区间上的任意两个自变量x1,x2,当x1<x2时, 都有 f(x1)<f(x2),那么就说f(x)在这个区间上是增函数. 2.如果对于这个区间上的任意两个自变量x1,x2,当x1<x2时, 都有f(x1)>f(x2),那么就说f(x)在这个区间上是减函数 对于函数y=f(x)在某个区间上单调递增或单调递减的性 质,叫做f(x)在这个区间上的单调性,这个区间叫做f(x) 的单调区间。
1. 等径圆球的密堆积
把乒乓球装入盒中,盒中 的乒乓球怎样排列才能使 装入的乒乓球数目最多?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如f(x)=x3,x∈(-1,1)
不一定,应是
结论 若函数f′单(x调)≥递增0.,则
若函数单调递减,则
已知 ,函数
在区间
上是增函数,求实数 的取值范围.
求下列函数的单调区间
(1)f(x)x22x4
(2)f(x)3xx3
(3 )f(x ) six nx,x (0 ,)
(4)f(x)=x+ln x
(5) f (x) lnx x
x
递减
f '(x) 10 f '(x)10
y
f ( x) x2
在 (,0)上 递 减f '(x)2x0
o
x
在 (0,-)上 递 增f '(x)2x03
在 某 个 区 间 (a,b)内 ,
f '(x) 0 f(x ) 在 (a ,b ) 内 单 调 递 增 f '(x) 0 f(x )在 (a ,b ) 内 单 调 递 减
水以匀速注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函 数关系图象.
(1)→B (2)→A (3)→D (4)→C
试从导数的角度解释变化的快慢
在某一范围内|f'(x)|越大,在这个范围内变化 越快,图象就越“陡峭”;反之,就“平缓”.
-
11
问题 若函数f(x)在区间(a,b)内单调递增, 那么f′(x)一定大于零吗?
(D)
类型二 利用导数求函数的单调区间
求函数 y3x2 3x 的单调区间.
解: Qy'6x3
令 y'0 得 x1, 令 y'0 得 x1
2
2
y3x23x的单调递增区间为 ( 1 , )
2
Байду номын сангаас
单调递减区间为 ( , 1 )
2
变1:求函数 y3x33x2 的单调区间.
解: Q y' 9 x 2 6 x 3 x (3 x 2 )
函数的单调性与导数
-
1
yx3 3x?
定义法
你是如何去判断函数 y x 2 的单调性? 图象法
如图:
函数在 ( , 0)上为_减___函数,
y
y x2
在 (0, 上) 为__增__函数.
o
x
-
2
函数及图象
单调性
导数的正负
y
f (x) x 在(,)上
o
x
递增
y
f (x)x 在(,)上
o
a
b
如果在某个区间内恒有 f(x)0,则 f (x)为?
-
4
类型一 利用导数确定函数大致图象
已知导函数的下列信息:
分析:
当2 x3时,f '(x)0; f(x )在 此 区 间 递 减
当x3或x2时,f '(x)0; f(x )在 此 区 间 递 增
当x 3或x 2时,f '(x) 0. f ( x)图象在此两处
令y'0得x2或x0 32
归纳小结
1.“导数法” 求单调区间的步骤:
①求函数定义域
②求 f '( x )
③令f'(x)0 解 不 等 式 f(x)的 递 增 区 间
f'(x)0 解 不 等 式 f(x)的 递 减 区 间
2.如果函数具有相同单调性的单调区间不止一个
,如何表示单调区间?
不能用“∪”连接,应用“,”隔开
-
13
-
14
附近几乎没有升降
画出函数 f ( x ) 图象的大致形状 变化,切线平行x轴
yA
解: f ( x ) 的大致形状如右图: y f (x)
称 A,B两 点 为 “ 临 界 点 ”
B
o 2 3x
跟踪训练
函数y=f(x)的图象如图所示,试画导函数 f′(x)图象的大致形状.
注:图象形状不唯一
试一试 我能行
设 f '( x )是函数 f ( x ) 的导函数,y f '(x)的图象如
右图所示,则 y f (x) 的图象最有可能的是( C )
y
y f (x)
y
y f (x)
y
y f '(x)
o 1 2x o 1 2x
o
2x
(A)
(B)
y y f (x)
y y f (x)
2
o1
x o 12
x
(C)
不一定,应是
结论 若函数f′单(x调)≥递增0.,则
若函数单调递减,则
已知 ,函数
在区间
上是增函数,求实数 的取值范围.
求下列函数的单调区间
(1)f(x)x22x4
(2)f(x)3xx3
(3 )f(x ) six nx,x (0 ,)
(4)f(x)=x+ln x
(5) f (x) lnx x
x
递减
f '(x) 10 f '(x)10
y
f ( x) x2
在 (,0)上 递 减f '(x)2x0
o
x
在 (0,-)上 递 增f '(x)2x03
在 某 个 区 间 (a,b)内 ,
f '(x) 0 f(x ) 在 (a ,b ) 内 单 调 递 增 f '(x) 0 f(x )在 (a ,b ) 内 单 调 递 减
水以匀速注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函 数关系图象.
(1)→B (2)→A (3)→D (4)→C
试从导数的角度解释变化的快慢
在某一范围内|f'(x)|越大,在这个范围内变化 越快,图象就越“陡峭”;反之,就“平缓”.
-
11
问题 若函数f(x)在区间(a,b)内单调递增, 那么f′(x)一定大于零吗?
(D)
类型二 利用导数求函数的单调区间
求函数 y3x2 3x 的单调区间.
解: Qy'6x3
令 y'0 得 x1, 令 y'0 得 x1
2
2
y3x23x的单调递增区间为 ( 1 , )
2
Байду номын сангаас
单调递减区间为 ( , 1 )
2
变1:求函数 y3x33x2 的单调区间.
解: Q y' 9 x 2 6 x 3 x (3 x 2 )
函数的单调性与导数
-
1
yx3 3x?
定义法
你是如何去判断函数 y x 2 的单调性? 图象法
如图:
函数在 ( , 0)上为_减___函数,
y
y x2
在 (0, 上) 为__增__函数.
o
x
-
2
函数及图象
单调性
导数的正负
y
f (x) x 在(,)上
o
x
递增
y
f (x)x 在(,)上
o
a
b
如果在某个区间内恒有 f(x)0,则 f (x)为?
-
4
类型一 利用导数确定函数大致图象
已知导函数的下列信息:
分析:
当2 x3时,f '(x)0; f(x )在 此 区 间 递 减
当x3或x2时,f '(x)0; f(x )在 此 区 间 递 增
当x 3或x 2时,f '(x) 0. f ( x)图象在此两处
令y'0得x2或x0 32
归纳小结
1.“导数法” 求单调区间的步骤:
①求函数定义域
②求 f '( x )
③令f'(x)0 解 不 等 式 f(x)的 递 增 区 间
f'(x)0 解 不 等 式 f(x)的 递 减 区 间
2.如果函数具有相同单调性的单调区间不止一个
,如何表示单调区间?
不能用“∪”连接,应用“,”隔开
-
13
-
14
附近几乎没有升降
画出函数 f ( x ) 图象的大致形状 变化,切线平行x轴
yA
解: f ( x ) 的大致形状如右图: y f (x)
称 A,B两 点 为 “ 临 界 点 ”
B
o 2 3x
跟踪训练
函数y=f(x)的图象如图所示,试画导函数 f′(x)图象的大致形状.
注:图象形状不唯一
试一试 我能行
设 f '( x )是函数 f ( x ) 的导函数,y f '(x)的图象如
右图所示,则 y f (x) 的图象最有可能的是( C )
y
y f (x)
y
y f (x)
y
y f '(x)
o 1 2x o 1 2x
o
2x
(A)
(B)
y y f (x)
y y f (x)
2
o1
x o 12
x
(C)
