中考数学专题复习---找规律.ppt
中考数学复习 专题2 规律探索型问题数学课件

2.解图形规律探索题的方法: 第一步:标序号:记每组图形的序数为“1,2,3,…,n”; 第二步:数图形个数:在图形数量变化时,要记出每组图形的表示个数; 第三步:寻找图形数量与序号数 n 的关系:针对寻找第 n 个图形表示的数量时,先将后 一个图形的个数与前一个图形的个数进行比对,通常作差(商)来观察是否有恒定量的变化, 然后按照定量变化推导出第 n 个图形的个数; 函数法:若当图形变化规律不明显时,可把序号数 n 看作自变量,把第 n 个图形的个数 看作函数,设函数解析式为 y=an2+bn+c(初中阶段设二次函数完全可以解决),再代入三组 数值进行计算出函数解析式(若算出 a=0 就是一次函数)即可.
【点评】本题考查了图形的变化类问题,解题的关键是能够仔细读题,找到图形内和图 形外格点的数目.
[对应训练] 4.在由 m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小 正方形个数 f, (1)当 m,n 互质(m,n 除 1 外无其他公因数)时,观察下列图形并完成下表:
[对应训练] 2.(2015·咸宁)古希腊数学家把数 1,3,6,10,15,21,…叫做三角数,它有一定的规 律性.若把第一个三角数记为 a1,第二个三角数记为 a2…,第 n 个三角数记为 an,计算 a1+ a2,a2+a3,a3+a4,…由此推算 a399+a400=__1.6×105 或 160_000__.
1.(2015·德州)一组数 1,1,2,x,5,y…满足“从第三个数起,每个数都等于它前面的 两个数之和”,那么这组数中 y 表示的数为( A )
A.8 B.9 C.13 D.15 2.(2015·河南)如图所示,在平面直角坐标系中,半径均为 1 个单位长度的半圆 O1,O2,
中考总复习数学02- 第二部分 专题二 规律性问题

3
4
专题二 规律性问题—点坐标变换规律 类型三 点坐标变换规律
题型讲解
返回类型清单
点坐标变换型的题目主要考查了点的坐标规律,这类题目一般是点的坐 标在平面直角坐标系中递推变化或周期性变化.通过观察和归纳,从所给 的数据和图形中寻求规律是解答本类问题的关键.
例题 3
5
6
专题二 规律性问题—点坐标变换规律
返回类型清单
(2)若第n个图案共有基础图形2 023个,则n的值是多少? 解:当1+3n=2 023时, 解得n=674, ∴n的值为674.
例题 2
3
4
专题二 规律性问题—图形规律
返回类型清单
4.某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三 角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形 地砖为连续排列. 当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2 ); 当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3 ),以此 类推.
排列,探究图形所反映的规律;另外一种是图形的变换规律,即根据一组
相关图案的变化,从中归纳图形的变换所反映的规律.在中考中以图形为
载体的数字规律最为常见.
例题 2
3
4
专题二 规律性问题—图形规律
返回类型清单
方法点拨 数形规律题的解题关键是通过观察图形发现数量关系,并用代数式归纳 出规律,再进行验证,进而解决问题;图形变换规律题的解题关键是抓住 图形的变化特征,找出规律,进而解决问题.
例题 1
1
2
专题二 规律性问题—竖式规律 例题1
返回类型清单
( 2022·河北模拟)观察 1×49=49,2×48=96,3×47=141,…,23×27=621,24×26=624,25×25= 625,26×24=624,27×23=621,…,47×3=141,28×2=96,49×1=49.
中考数学复习专题——找规律(含答案)

中考数学试复习专题——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.1 2 3n … … 第1个图 第2个图 第3个图 …6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子枚(用含有n的代数式表示,并写成最简形式).○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.9、如图2,用n表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n的关系是10、观察图4的三角形数阵,则第50行的最后一个数是()1-2 3-4 5 -67 -8 9 -10。
11、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第n个图案中白色正方形的个数为.12、观察下列各式:3211=332123+=33221236++=33332123410+++=……猜想:333312310++++=.第一个第二个第三个……第n个第一排第二排第三排第四排6┅┅10 9 8 73 2154答案解析:1解析:1时,5.n再每增加一个数时,m就增加3个数.解答:根据所给的具体数据,发现:8=5+3,11=5+3×2,14=5+3×3,….以此类推,第n个圈中,5+3(1)=32.2解析:分析可得:第1幅图中有1×2-1=1个,第2幅图中有2×2-1=3个,第3幅图中有3×2-1=5个,…,故第n幅图中共有21个3解析:在4的基础上,依次多3个,得到第n个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n个图中有4+3(1)=31.当6时,即原式=19.故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解.解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以15+3=18.表三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大1,所24+25-20+1=30.表四中截取的是两行三列中的6个数字:18是3的6倍,则c应是4的7倍,即28.故选D.认真观察表格,熟知各个数字之间的关系:第一列是1,2,3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10×10的正方形图案,则其中完整的圆共有102+(10-1)2=181个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个10×10的正方形图案中,完整的圆共有102+(10-1)2=181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚;第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22)枚;…由此可推出想第n个图案的白色棋子数为(2)22=4(1).故第n个图案的白色棋子数为(2)22=4(1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6×1=18根;搭第3个图形需12+6×2=24根;…搭第n个图形需12+6(1)=66根.解答:解:搭第334个图形需6×334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6排,第5个位置,即其坐标为(6,5).故答案填:(6,5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.9解析:根据题意分析可得:第n行有n个小圆圈.故f(n)和n的关系是ƒ(n)= (n2).10解析:根据题意可得:第n行有n个数;且第n行第一个数的绝对值为+1,最后一个数的绝对值为;奇数为正,偶数为负;故第50行的最后一个数是1275.解答:解:第n行第一个数的绝对值为+1,最后一个数的绝对值为,奇数为正,偶数为负,第50行的最后一个数是1275第一个图中白色正方形的个数为3×3-1;第二个图中白色正方形的个数为3×5-2第三个图中白色正方形的个数为3×7-3;…当其为第n个时,白色正方形的个数为3(21)5312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是1+2+310=5×11=55,则原式=552.解答:解:根据分析最后的底数是1+2+310=5×11=55,则原式=552.故答案552。
2015年广西中考数学总复习课件第37课时 规律探索题(共39张PPT)

第37课时
规律探索题
[解析]
观察已知一组数发现:分子为从1开始的连续奇数,
分母为从2开始的连续正整数的平方,根据题意,得这一组数的第 2n-1 n个数是 . 2 n+1
第37课时
规律探索题
变式题1
[2014•湘潭] 如图Z-37-1,按此规律,第6行最
后一个数字是________ 16 ,第________ 672 行最后一个数是2014.
5 A ,0 , 3
10070 . B(0,4),则点 B2014 的横坐标为________
第37课时
规律探索题
图Z-37-3
第37课时
规律探索题
5 13 [解析] 由题意可得AO= ,BO=4,∴AB= ,∴OA+AB1+ 3 3 5 13 B1C2= + +4=6+4=10,∴B2的横坐标为10,B4的横坐标为 3 3 2014 2×10=20,∴点B2014的横坐标为 ×10=10070. 2
第37课时
规律探索题
► 类型之三 等式规律
例3 [2014·安徽] 观察下列关于自然数的等式: 52-4×22=9,② 72-4×32=13,③
32-4×12=5,①
„
根据上述规律解决下列问题: 4 2=______ 17 ; (1)完成第四个等式:92-4×______ (2) 写出你猜想的第 n个等式(用含n的式子表示) ,并验证其 正确性. 第37课时 规律探索题
图Z-37-1
第37课时
规律探索题
[解析] 每一行的最后一个数字构成等差数列1,4,7,10,
„,第n行的最后一个数字为1+3(n-1)=3n-2,第6行最后一
个数字是3×6-2=16;由3n-2=2014,解得n=672.因此第6行 最后一个数字是16,第672行最后一个数是2014.
找规律-专业文档!

一、直接说出得数。
9×6 = 54
24×2 = 48
8×11 = 88
17×3 = 51
12×3 = 36
ቤተ መጻሕፍቲ ባይዱ
40×4 = 160
5×13 = 65
5×61 = 305
说出下面算式中各部分名称。 40 × 4 = 160
……. ……. …….
乘 数
乘 数
积
找规律
❖ 一只青蛙一张嘴,两只眼睛四条腿; ❖ 两只青蛙两张嘴,四只眼睛八条腿; ❖ 三只青蛙三张嘴,六只眼睛十二条腿; ❖ 请接着说下去。 ❖ 你发现了什么规律? ❖ 几只青蛙几张嘴,两几只眼睛四几条腿。 ❖ n只青蛙n张嘴,2n只眼睛4n条腿。
二、如何在小学数学教学活动中体现数学核心素养 1.数学抽象(符号意识、数感;几何直观、空间想象) 2.逻辑推理(推理能力、运算能力) 3.数学模型(模型思想、数据分析观念)
三、如何在数学教学评价中考查数学核心素养
教育质量监测的四个原则 1.不要求计算速度(速度的训练是课业负担重的主要原因) 2.监测内容蕴含的数学素养(概念、推理、计算、想象) 3.应当有一道开放题(超市的位置,加分原则) 4.说学生能懂的话(对可能性的理解)
一、什么是数学核心素养 文件《教育部关于全面深化课程改革,落实立德树人根本任务》
提到核心素养。明确要求:修改课程标准,要把学科核心素养贯穿始终。 北师大研究小组定义核心素养:是指学生应具备的、能够适应终
身发展和社会发展需要的必备品格和关键能力。 高中数学课标修订组定义数学核心素养:是具有数学基本特征的
3、算一算,说一说。
。
= 720 = 260
先由学生 独立完成, 然
后说一说计算 过程。
讲课中考数学专题复习---找规律.

反 白皮本:P145页 3- 提
馈 5题和直击中考题
高
直击中考(2015德州)
如图四边形ABCD中
AB∥CD,AD=DC=CB=a,∠A=60°.取AB
的中点A1,连接A1C,再分别取A1C,BC的中 点D1,C1,连接D1C1,得到四边形A1BC1D1, 如图2; 同样方法操作得到四边形A2BC2D2, 如图3;…,如此进行下去,则四边形
bb
请你按照如下的数字规律,分 别写出第n个数字:(n为正整数)
(1) 3,6,9,12, 15,… , _3_n__;
(2) 2,5,8,11, 14, … , _3_n_-1_; (3) 3,9,27, 81,… , _3_n__ ;
(4) 1,-1,1,-1,1,...,__(-_1_)_n_-1_.
3、积极思考,硧跃发言,大胆地交流自 己所探索的规律。体验数学的生活化和生活 的数学化。
一、数式规律
热身 请你按照如下的数字规律,分别
赛 写出第n个数字:(n为正整数)
① ②③ ④ ⑤
n
(1)2,4,6,8,10, … , _2_n__;
(2)1,3,5,7,9, … , _2n_-_1_;
(3)3,5,7,9,11,…, 2_n_+_1_;
2.猜想规律与“序号n”间的对应关
系。 3.验证所归纳的结论。
三 点的坐标规律
课前热身 2016年4月
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1234
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
课前热身
星期 星期 星期 星期 星期 星期 星期 日 一 二 三 四 五六
中考数学复习找规律2[人教版](2019年新版)
](https://img.taocdn.com/s3/m/5e53062e581b6bd97f19eae4.png)
偃有功焉 离愍之长鞠;应物变化 程郑 长为兄弟之国 王不如远交而近攻 星气之书 非小用之 小国彊 良夫通於悝母 请为庶人 適会山林多人 俗之渐民久矣 齐伐燕 三十六年 以广其道 曰:“无以易尧 襄公元年 言万物皆有羽翼也 先以清水澡之 魏氏之欲不失齐楚者有资矣’ 碆新
缴 万事尽然 因坚守 取楚王信 麻、菽美 将杀奢 所以知赵章之病者 绛侯乃与丞相陈平谋 灌将军夫者 若早自杀 事下减宣 变化有概 若是者何也 素善武安侯 号曰成侯 以浮沮将军出五原二千馀里 孔子怃然曰:“鸟兽不可与同群 绝於予乎 兆应信诚於内 次弟小白奔莒 得胡首虏三万馀
伐戎王 欲出 非此其身 郑缪公卒 位在廉颇之右 其肩类子产 黄帝郊雍上帝 今始至陈而王之 葬竘社 释之卒 皆有求於平原君者也;不贤者识其小者 栗太子废 四年 太子有子曰岑娶 巴蜀民或窃出商贾 遭遇右武 於是长公主乃令假衣食 及问张黡、陈泽所在 内经闾术 文公问史敦 安国君
有所甚爱姬 言不顺则事不成 何故与周高都也 臣等当蟲出 治吴故国 北者败也 ”乃令入海者赍捕巨鱼具 初 则天下病而丹硃得其利 至广陵内史 於是置陇西、北地、上郡、渭南、河上、中地郡;汉王听其计 主中尉及郡国车士 令内史郡不得食马粟 而康居候汉罢而来救宛 戊不好学 ”
淮阴侯 医药已 释箕子囚 不会 ” 至秦 甕牖绳枢之子 身能十言尽当 丞相谬其说 二十二年 ”尧曰:“御史大夫周昌 ”二子曰:“亦似公 因不敢饮 发兵来伐楚 享国十年 沙砾击面 诸侯恐惧 公卿请立太子 返而後图之 守海岛中 ”於是废太后 汉王数之 小馀八百八十;”终日 加梁父
之事 微君之疾 可乎 吕后妒 产气始萌 秦必大怒攻楚 五星聚于东井 ”王曰:“取吾璧 立汉赤帜 徼牂柯 当是之时 诏御史 颛顼有共工之陈 作外戚世家十九 观其所属 苏秦荧惑诸侯 无相忘 而列侯坐酎金失侯者百馀人 见秦兵 赫恐 是为孝侯 取蒲阪 ”臣意即以寒水拊其头 是以宾客游
初三专题---找规律
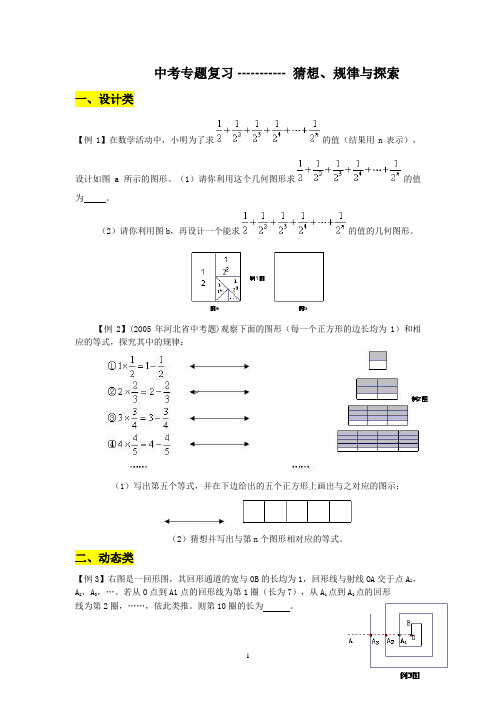
中考专题复习 ----------- 猜想、规律与探索一、设计类【例1】在数学活动中,小明为了求的值(结果用n表示),设计如图a所示的图形。
(1)请你利用这个几何图形求的值为。
(2)请你利用图b,再设计一个能求的值的几何图形。
【例2】(2005年河北省中考题)观察下面的图形(每一个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式。
二、动态类【例3】右图是一回形图,其回形通道的宽与OB的长均为1,回形线与射线OA交于点A1,A 2,A3,…。
若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,……,依此类推。
则第10圈的长为。
【例4】)已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度。
在平面直角坐标系内,现有一动点P 第1次从原点O 出发按甲方式运动到点P 1,第2次从点P 1出发按乙方式运动到点P 2,第3次从点P 2出发再按甲方式运动到点P 3,第4次从点P 3出发再按乙方式运动到点P 4,……。
依此运动规律,则经过第11次运动后,动点P 所在位置P 11的坐标是 。
三、数字类【例5】瑞士中学教师巴尔末成功地从光谱数据,,,,……,中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是 。
【例6】观察下列算式:122=,224=,328=,4216=,….根据上述算式中的规【例7】按下列规律排列的一列数对(1,2)(4,5)(7,8),…,第5个数对是 。
【例8】一组按规律排列的数:,,,,,…请你推断第9个数是【例9】把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行……,中间用虚线围的一列,从上至下依次为1、5、13、25、…,则第10个数为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一组按规律排列的式
b 子: 4 , ab , 0 , a 20 b 7 7个式子是 其中第 a
11
,…(
b a
2
b 2 a
5
b 3 a
8
),
3n 1 b n (1) n个式子 ,第 an
是
(n为正整数).
例2 请先观察下列算式,再填空: 32-12=8×1, 2 2 5 -3 =8×2, 3 , 72-52=8×__ 92-( 7 )2 =8×4, ( 11 )2-92 =8×5, 132_( 11 )2=8×( 6 ),…… ,
通过观察归纳,写出反映这种规律 (2n+1)2-(2n-1)2=8n 的一般结论:
观察下列排列的等式:
1×2-1=12, 2×3-2=22, 3×4-3=32, 4×5-4=42,…….
猜想:第n个等式(n为正整数)
2 n(n+1)-n=n 应为________________.
观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,„ 根据你所发现的规律,请你直接写出下 面式子的结果: 10000 1+2+3+„+99+100+99+„+3+2+1=____.
1.观察图形的排列规律找到基本图形, 找到图形之间的变与不变的规律。 2.猜想规律与“序号n”间的对应关系。 3.验证所归纳的结论。
例4 联体长方形的摆法:(填空)
(1)如图,摆n个这样联体图形需 根火柴 3n+1 ;
(2)如图,摆n个这样联体图形需
根火柴; 5n+2
(3)如图,摆n个这样的联体图形需_______ 7n+3 火 柴;
n 5 2 1 2 3 4 n 1 26 ,第n个数为________ 5 , , , , ______ 2 5 10 17 5 n n 1 1 2 3 4 2 26 n 1 , , , , ______,第n个数为________ 2 5 10 17 5 n n 1 1 2 1 2 3 4 n 1 26 ,第n个数为________ , , , , ______ 2 5 10 17
(4)如图,摆n个这样联体图形需______ 9n+4根 火柴.
练习
1.用红白两种颜色的正方形纸片,按红色 纸片数逐一增加的规律拼成一列图案:
第一图
第二图
第三图
……
(1)第4个图案中,白色纸片一共有___ 13 张;
(2)第n个图案中,白色纸片一共有_____ 3n+1 张
2.用黑白两种颜色的正方形纸片,按 黑色纸片数逐一增加的规律拼成一列图 案,第五个图案中,白色正方形的个数 一共有_____ 28 个.
一、数字规律
例1
请你按照如下的数字规律,分别写出 第n个数字:(n为正整数) n ① ②③ ④ ⑤
2n (1)2,4,6,8,10, … , ____; 2n-1 (2)1,3,5,7,9, … , ____;
(3)1,4,9,16,25,…, ____; n2
n 2 (4)2,4,8,16,32,… , ____; n (-1) (5)-1,1,-1,1,-1,...,_______。
3.验证所归纳的结论。
课堂小结
二.关于寻找“图形序列”规律 的思维步骤:
1.观察图形的排列规律找到基本图形, 找到图形之间的变与不变的规律。 2.猜想规律与“序号”间的对应关系, 用关于“序号”的数学式子表示出来。
3.验证所归纳的结论。
二、图形规律
例3 餐桌按下面的摆法可坐多少人?
(1) 1张餐桌可坐6人,2张餐桌可坐___人 . 10 (2) 若按照上图的摆法摆放餐桌和椅子,完 成下表:
若按照上图的摆法摆放餐桌和椅子,完成下表:
桌子张 数 可坐人 数
1
2
3
4
5
6 …
n
6 10 14 18 22 26 … 4n+2
关于寻找“图形序列”规律的思维步骤:
1 1 1 1 1 1 1 1 2 n 1 , , , , , , ______ ,第 n 个数为 ________ n ( 1) 50 2 3 10 15 26 35
关于寻找“数字序列”规律的思维步骤:
1.观察分析:与序号的联系。 2.推理尝试:纵横双向类比。 3.猜想归纳:写出关系式。 4. 验证规律:取多值Байду номын сангаас证。
第一个
第二个
第三个
„„
3.为庆祝“六一”儿童节,某幼儿园举行 用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆个“金鱼”需用火柴 棒的根数为( A ) A.6n+2 B.6n+8 C.8n D.4n+4
4.如图所示,用火柴拼成一排由三角形组 成的图形,如果要使图形中含有50个三角形, 那么需要火柴( ) B A.100根 B.101根 C.150根 D.153根 含有n个三角形需要( 2n+1 )根火柴
请你按照如下的数字规律,分 别写出第n个数字:(n为正整数) 3n (1) 3,6,9,12, 15,… , ____;
3n-1 (2) 2,5,8,11, 14, … , ____;
n 3 (3) 3,9,27, 81,… , ____ ;
(-1)n+1 (4) 1,-1,1,-1,1,...,_______.
5.如下图是某同学在沙滩上用石子摆成 的小房子,观察图形的变化规律,写出 第n个小房子用了______________ (n+1)2+(2n-1) 块石子.
(1)
(2)
(3)
(4)
课堂小结
一.关于寻找“数字序列”规律 的思维步骤:
1.观察相邻数字间的数量关系,找到共 同特征,得出某种规律的猜想。 2.猜想规律与“序号”间的对应关系, 用关于“序号”的数学式子表示出来。
