单代号搭接网络计划.ppt
合集下载
10-单代号搭接网络计划、双代号时标网络计划计算

3
10 网络图计算 10.1 单代号搭接网络计划计算
搭接网络计划具有如下几个特点: ①直接反映工作之间各种可能出现的顺序关系; ②大大简化了网络计划的图形和计算,尤其适合重复性工作和许多工作同时进行的
情况; ③丰富了网络计划的内容,极大地扩展了应用范围; ④可用多种方法手算,也可以采用计算机计算,方便灵活,适应性强。 因此,它作为一种严格的科学计划方法,借助于计算机手段,得到了广泛的应用和推广
16
10 网络图计算
绘制具体方法
2)间接绘图法 间接绘图法即先算后画。根据先绘制好的无时标网络计划,算出各个节点的最早时间,
确定关键线路,然后,再在时标表上确定节点位置,用箭线标出工作持续时间,某些工作 箭线长度不足以达到该工作的完成节点时,用波形线补足。绘图时一般宜先绘制关键线路 上的工作,再绘制非关键工作。 步骤如下: (1)绘制一般双代号网络计划草图。 (2)计算节点的最早时间,确定关键线路(用双线表示)。 (3)在时标表上,按最早开始时间确定每项工作的起点节点位置(图形尽量与草图一致)。 (4)按各工作的时间长度绘制相应工作的实线部分,使其在时间坐标上的水平投影长度等于 工作时间。虚工作因为不占时间,故只能以垂直虚线表示,其水平段以波形线表示。 (5)用波形线把实线部分与其紧后工作的起点节点连接起来,以表示自由时差。
17
10 网络图计算
(3) 关键线路和时间参数的确定
关键线路——自始至终不出现波形线的线路。 时间参数: (1) 工作最早时间 (2) 工作自由时差 (3) 工作总时差 (4) 工作最迟时间
18
12
10 网络图计算
10.2双代号时间坐标网络参数识别
表示方法 时标网络计划的工作以实箭线表示,虚工作以虚箭线表示,以波形线表示本工作与其紧
10 网络图计算 10.1 单代号搭接网络计划计算
搭接网络计划具有如下几个特点: ①直接反映工作之间各种可能出现的顺序关系; ②大大简化了网络计划的图形和计算,尤其适合重复性工作和许多工作同时进行的
情况; ③丰富了网络计划的内容,极大地扩展了应用范围; ④可用多种方法手算,也可以采用计算机计算,方便灵活,适应性强。 因此,它作为一种严格的科学计划方法,借助于计算机手段,得到了广泛的应用和推广
16
10 网络图计算
绘制具体方法
2)间接绘图法 间接绘图法即先算后画。根据先绘制好的无时标网络计划,算出各个节点的最早时间,
确定关键线路,然后,再在时标表上确定节点位置,用箭线标出工作持续时间,某些工作 箭线长度不足以达到该工作的完成节点时,用波形线补足。绘图时一般宜先绘制关键线路 上的工作,再绘制非关键工作。 步骤如下: (1)绘制一般双代号网络计划草图。 (2)计算节点的最早时间,确定关键线路(用双线表示)。 (3)在时标表上,按最早开始时间确定每项工作的起点节点位置(图形尽量与草图一致)。 (4)按各工作的时间长度绘制相应工作的实线部分,使其在时间坐标上的水平投影长度等于 工作时间。虚工作因为不占时间,故只能以垂直虚线表示,其水平段以波形线表示。 (5)用波形线把实线部分与其紧后工作的起点节点连接起来,以表示自由时差。
17
10 网络图计算
(3) 关键线路和时间参数的确定
关键线路——自始至终不出现波形线的线路。 时间参数: (1) 工作最早时间 (2) 工作自由时差 (3) 工作总时差 (4) 工作最迟时间
18
12
10 网络图计算
10.2双代号时间坐标网络参数识别
表示方法 时标网络计划的工作以实箭线表示,虚工作以虚箭线表示,以波形线表示本工作与其紧
代号网络计划与单代号搭接网络计划教程

强流程性的项目,如生产线、化学反应等。
03
适用于需要优化资源配置的项目
代号网络计划能够清晰地表示工作流程和逻辑关系,有助于项目管理者
更好地安排资源和时间,适用于需要优化资源配置的项目。
Part
02
单代号搭接网络计划概述
定义与特点
定义:单代号搭接网 络计划是一种以单代 号表示的网络图为基 础,通过不同工作之 间的搭接关系来描述 工作流程的网络计划 方法。
案例一
某桥梁工程施工进度管理
THANKS
感谢您的观看
优化项目流程
通过代号网络计划,可以发现项目流 程中的瓶颈和问题,从而优化工作流 程,提高项目执行效率。
代号网络计划的适用范围
01
适用于大型、复杂的工程项目
代号网络计划适用于需要详细规划、复杂逻辑关系的工程项目,能够更
好地满足大型、复杂项目的需求。
02
适用于流程性强的项目
代号网络计划通过节点和箭线表示工作流程和逻辑关系,适用于具有较
适用于大型复杂项目
对于大型复杂项目,单代号搭接网络计划能够更好地描述各项工作之间的逻辑关系,便于项目管理者 更好地掌握和控制项目进度。
适用于需要优化资源配置的场合
通过单代号搭接网络计划,项目管理者可以更好地了解项目的整体流程和关键路径,从而更好地安排 人力、物力和财力等资源,实现资源的优项目的工作流程和组织结构,为后续工作提供组织保障。
确定工作搭接关系
根据项目特点和实际情况,确定各工作单元 之间的搭接关系,确保项目能够顺利进行。
考虑工作单元之间的逻辑关系、先后顺序和 相互依赖性,制定合理的工作搭接计划。
确定工作持续时间
根据历史数据、经验和其他相关信息,估算各工作单元的持续时间,确保项目按计划进 行。
单代号搭界PPT课件

7
7.2.4单代号搭接网络计划概述
1.搭接关系的种类和表达方式
两种关系,四种时距
FTF
i j
STS STF
STF FTF
i j
FTS STS
8
4.2单代号搭接网络计划的计 算
1.结束到开始时距FTS(Finish to Start)
1.
ESj EiFFTi,jS
LF i LSj FTi,jS
14
(三)单代号搭接网络计划时间参数的计算 单代号搭接网络计划与单代号网络计划
和双代号网络计划时间参数的种类相同, 计算原理也基本相同。由于搭接网络具 有几种不同形式的搭接方式,所以其参 数的计算要复杂一些。一般的计算方法 是:依据计算公式,在图上进行计算。
15
l.工作最早时间计算
工作最早时间的计算应从起始节点开始依次 进行。只有紧前工作计算完毕,才能计算本 工作。计算最早时间按以下进行: (1) 因单代号搭接网络计划中的起始节点一 般都代表虚工作,所以,其最早开始时间和 最早完成时间都为零。 (2) 因单代号搭接网络计划中的起始节点一 般都代表虚工作,所以凡与起始节点相连的 工作,其最早开始时间都为零。 (3)其他工作的最早时间根据时距计算。
9
4.2单代号搭接网络计划的计 算
2.开始到开始时距STS(Start to Start )
ESj EiSSTi,jS
LSj LSi STi,Sj
10
4.2单代号搭接网络计划的计 算
3.结束到结束时距FTF(Finish to Finish)
EFj EF i FTi,F j
LFj LF i FTi,F j
5
2.STS(开始到开始)的搭接关系 如道路中铺设路基和浇筑路面,待路基
7.2.4单代号搭接网络计划概述
1.搭接关系的种类和表达方式
两种关系,四种时距
FTF
i j
STS STF
STF FTF
i j
FTS STS
8
4.2单代号搭接网络计划的计 算
1.结束到开始时距FTS(Finish to Start)
1.
ESj EiFFTi,jS
LF i LSj FTi,jS
14
(三)单代号搭接网络计划时间参数的计算 单代号搭接网络计划与单代号网络计划
和双代号网络计划时间参数的种类相同, 计算原理也基本相同。由于搭接网络具 有几种不同形式的搭接方式,所以其参 数的计算要复杂一些。一般的计算方法 是:依据计算公式,在图上进行计算。
15
l.工作最早时间计算
工作最早时间的计算应从起始节点开始依次 进行。只有紧前工作计算完毕,才能计算本 工作。计算最早时间按以下进行: (1) 因单代号搭接网络计划中的起始节点一 般都代表虚工作,所以,其最早开始时间和 最早完成时间都为零。 (2) 因单代号搭接网络计划中的起始节点一 般都代表虚工作,所以凡与起始节点相连的 工作,其最早开始时间都为零。 (3)其他工作的最早时间根据时距计算。
9
4.2单代号搭接网络计划的计 算
2.开始到开始时距STS(Start to Start )
ESj EiSSTi,jS
LSj LSi STi,Sj
10
4.2单代号搭接网络计划的计 算
3.结束到结束时距FTF(Finish to Finish)
EFj EF i FTi,F j
LFj LF i FTi,F j
5
2.STS(开始到开始)的搭接关系 如道路中铺设路基和浇筑路面,待路基
搭接网络图讲解ppt

A、凡与起点节点相连的工作最早开始时间都应为零,即: ESi = 0 B、其他工作j的最早开始时间根据时距应按下列公式计算: 时距为STSi,j时,ESj=ESi+STSi,j 时距为FTFi,j时,ESj=EFi+FTFi,j-Dj 时距为STFi,j时,ESj=ESi+STFi,j-Dj 时距为FTSi,j时,ESj=EFi+FTSi,j ③计算最早开始时间时当最早开始时间出现负值时,应将该 工作与起点节点用虚箭线相连接,并确定时距为: STS=0 ④工作j的最早完成时间EFj应按下式计算: EFj=ESj+Dj
1 4
C 6 0
27
STS=3 LAG=0 28 15 0 6 E 20 35 24 STS=5 LAG=4 1 7 G 10 LAG=1 34 35 0 8 FM 0 0 35
STF=25 LAG=0
0
0
0
0
10
10
0
25
15
0
35
25
1
35
35
35
0 FTF=5 LAG=7 LAG=0 13
13 5 D 22 13
搭 接 网 络
要点: (1)i-代表紧前工序,j-代表紧 后工序。 (2)公式能记更好,主要是搞清楚搭 接关系。 (3)这部分考试必考,不要存在侥幸 心理。
单代号搭接网络计划
前述网络计划,工作之间的逻辑关系是紧前工作完 成之后紧后工作才能开始。但在有些情况下,紧后工作并 不以紧前工作的完成为条件,而是紧后工作可以插入与紧 前工作平行施工,这种关系称之为搭接关系。 时间参数的计算 (1)单代号搭接网络计划时间参数计算,应在确定 各工序持续时间和各项工作之间时距关系之后进行。 (2)单代号搭接网络计划中的时间参数基本内容和 形式应按图所示方式标注。 (3)工作最早开始时间的计算应符合下列规定: ①计算最早开始时间参数必须从起点节点开始依次 进行,只有紧前工作计算完毕,才能计算本工作; ②计算工作最早开始时间应按下列步骤进行:
单代号网络图

单代号网络计划时间参数的计算
ES TF EF
ESi , EFi
i
工作名称
LAGi, j
Di FF
关 键
TFi
FFi
LS
LF
线
路
LSi , LFi
单代号网络计划时间参数的计算步骤如下:
1.计算最早开始时间和最早完成时间
网络计划中各项工作的最早开始时间和最早完成时间的计算 应从网络计划的起点节点开始,顺着箭线方向依次逐项计算。
第五章 单代号网络计划
章节内容
1
单代号网络计划
2
单代号搭接网络计划
第一节 单代号网络图
一 单代号网络图的定义
(一) 单代号网络图是以节点及其编号表示工作,以箭线 表示工作之间逻辑关系的网络图。在单代号网络图中加注工 作的持续时间,以便形成单代号网络计划。 单代号网络图的特点 单代号网络图与双代号网络图相比,具有以下特点: (1)工作之间的逻辑关系容易表达,且不用虚箭线,故绘 图较简单; (2)网络图便于检查和修改; (3)由于工作的持续时间表示在节点之中,没有长度,故 不够形象直观; (4)表示工作之间逻辑关系的箭线可能产生较多的纵横交 叉现象。
单代号网络图中的节点必须编号。编号标注在节点内, 其号码可间断,但严禁重复。箭线的箭尾节点编号应小于 箭头节点的编号。一项工作必须有惟一的一个节点及相应 的一个编号。 2、箭线
三、单代号网络图的绘图规则
(1)单代号网络图必须正确表达已定的逻辑关系。 (2)单代号网络图中,严禁出现循环回路。 (3)单代号网络图中,严禁出现双向箭头或无箭头的连 线。 (4)单代号网络图中,严禁出现没有箭尾节点的箭线和 没有箭头节点的箭线。 (5)绘制网络图时,箭线不宜交叉,当交叉不可避免时, 可采用过桥法或指向法绘制。
单代号搭接网络图实例【PPT】

单代号搭接网络图实例【PPT】
• 2. STS(开始到开始)关系
• 开始到开始关系是通过前项工作开始到后项工作开始之间的时距(STS)
来表达的,表示在i工作开始经过一个规定的时距(STS)后,j工作才能开
始进行。
i j
STS
ESi TFi EFi
i 工作名称
Di
STS LAGi,j
ESj TFj EFj
浇筑砼20d
ESi TFi EFi
i 工作名称
30 LSi FFi LFi
FTF=5 LAGi,j
ESj TFj EFj
j 工作名称
25 LSj FFj LFj
• 4. STF(开始到结束)关系
• 开始到结束关系是通过前项工作开始到后项工作结束之间的时距(STF) 来表达的,它表示i工作开始一段时间(STF)后,j工作才可结束。
其他工作LFi应为:LFi=EFi+TFi • 六、计算工作最迟开始时间
从计划终点节点逆着箭线方向依次逐项计算。 LSi=ESi+TFi=LFi-Di
• 七、关键工作和关键线路的确定 从计划终点节点逆着箭线方向依次逐项计算。 LSi=ESi+TFi=LFi-Di
3 FTS=2 6
B
E
8
10
Fi
ESj TFj EFj
i j
i 工作名称
Di LSi FFi LFi
FTF LAGi,j
j 工作名称
Dj LSj FFj LFj
• FTF搭接关系的时间参数计算式为:ESj=ESi+Di+FTFi,j–Dj; • 如基坑排水工作结束一定时间后,浇注砼工作才能结束。
5d 基坑排水15d
• 2. STS(开始到开始)关系
• 开始到开始关系是通过前项工作开始到后项工作开始之间的时距(STS)
来表达的,表示在i工作开始经过一个规定的时距(STS)后,j工作才能开
始进行。
i j
STS
ESi TFi EFi
i 工作名称
Di
STS LAGi,j
ESj TFj EFj
浇筑砼20d
ESi TFi EFi
i 工作名称
30 LSi FFi LFi
FTF=5 LAGi,j
ESj TFj EFj
j 工作名称
25 LSj FFj LFj
• 4. STF(开始到结束)关系
• 开始到结束关系是通过前项工作开始到后项工作结束之间的时距(STF) 来表达的,它表示i工作开始一段时间(STF)后,j工作才可结束。
其他工作LFi应为:LFi=EFi+TFi • 六、计算工作最迟开始时间
从计划终点节点逆着箭线方向依次逐项计算。 LSi=ESi+TFi=LFi-Di
• 七、关键工作和关键线路的确定 从计划终点节点逆着箭线方向依次逐项计算。 LSi=ESi+TFi=LFi-Di
3 FTS=2 6
B
E
8
10
Fi
ESj TFj EFj
i j
i 工作名称
Di LSi FFi LFi
FTF LAGi,j
j 工作名称
Dj LSj FFj LFj
• FTF搭接关系的时间参数计算式为:ESj=ESi+Di+FTFi,j–Dj; • 如基坑排水工作结束一定时间后,浇注砼工作才能结束。
5d 基坑排水15d
单代号搭接网络图实例讲解
E 按STS关系:
S
j
ESi
STSijຫໍສະໝຸດ LS j LSi STSij
按FTF关系:EFj EFi FTFij
LFj LFi FTFij
如,某修筑道路工程,工作i是修筑路肩,工作j是修筑路面层,在组织这
两项工作时,要求路肩工作至少开始一定时距STS=4以后,才能开始修筑路
面层;而且面层工作不允许在路肩工作完成之前结束,必须延后于路肩完
FTF
ESi TFi EFi
ESj TFj EFj
i j
i 工作名称
Di LSi FFi LFi
FTF LAGi,j
j 工作名称
Dj LSj FFj LFj
• FTF搭接关系的时间参数计算式为:ESj=ESi+Di+FTFi,j–Dj; • 如基坑排水工作结束一定时间后,浇注砼工作才能结束。
5d 基坑排水15d
例如:混凝土沉箱码头工程,沉箱在岸上预制后,要求静置一段养护存放的 时间,然后才可下水沉放。
• 2. STS(开始到开始)关系
• 开始到开始关系是通过前项工作开始到后项工作开始之间的时距(STS)
来表达的,表示在i工作开始经过一个规定的时距(STS)后,j工作才能开
始进行。
i j
STS
ESi TFi EFi
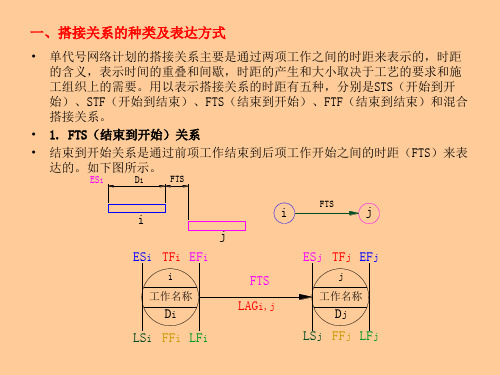
一、搭接关系的种类及表达方式
• 单代号网络计划的搭接关系主要是通过两项工作之间的时距来表示的,时距 的含义,表示时间的重叠和间歇,时距的产生和大小取决于工艺的要求和施 工组织上的需要。用以表示搭接关系的时距有五种,分别是STS(开始到开 始)、STF(开始到结束)、FTS(结束到开始)、FTF(结束到结束)和混合 搭接关系。
第三章 单代号搭接网络汇总

B 15
0
25
ST S= FT 6 F= 2
22 28
24 1 34 35
15 0 35 STF=25 E STS=5 20
G 10
终
0 13 22 FTF=5 D 22
ST
S=
0
10
10
25
15
35
25 35
1
STS=3
13
35
B FTS=2 E
例题2: (4)计算时间间隔LAG
21
1
C 6
27
单代号搭接网络计划
搭接关系图示 STS:start to start ; STF: start to finish FTS: finish to start ; FTF: finish to finish
STFi,j
S F
FTSi,j STSi,j FTFi,j
Di
S
Dj
F
二、单代号搭接网络计划时间参数计算
22 28
15 35 24 34 35
始
A 10
FTS=0
B 15
STF=25
E STS=5 20
G 10
终
0
22
FTF=5
D 22
ST
S=
0
10
10
25
15
35
25 35
1
STS=3
13
35
B FTS=2 E
例题2: (3)计算总时差
21
1
C 6
27
FTS=6
STS=3
0
0
10
10
始
A 10
FTS=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1天
基坑 排水
基坑 或
开挖
STS=1天
A
B
(a)
(b)
图8-5
. STF即开始——结束 TART TO FINISH)关系
紧前活动开始后一段时间,紧后活动 才能结束,这在实际工程中用的较少。
举例说明,工程活动之间存在上述搭接关系。
return
3. FTF,即结束——结束 (FINISH TO FINISH)关系
return
总工期(TD)的确定
取网络的总工期为活动的最早结束时间的 最大值,即: TD=maxEFi=32(周)
return
最迟时间(LS、LF)的计算
最迟时间的计算由结束节点开始, 逆箭头方向由尾节点向首节点逐个推算。
1.令结束节点LFJ=TD=32,即定义项目的最迟结束时 间为总工期。
LS i=LF i-D I ……………(8-2)
1.令首节点 ESA=0,如果用日历表示,则定义 ESA为项目开始期。 活动内存在关系: EF i =ES i十D i ……(8-1) 则: EFA=ESA十DA=0十4=4
return
2. 其他活动的最早时间计算(从前向后传递)
A
B
ESB=EFA十FTSAB
A
B
ESB=ESA十STSAB
A
B
EFB=EFA十FTFAB
return
H有两个紧前活动,则: H:ESH=maxEFF十FTSFH,EFG十 FTSGH
=max18,24=24,则EFH=ESH +DH =30;
I:ESI=maxEFGI十FTSG,EFE十FTFEG-DI =max24+0,8十4-2=24,则 EFI=26;
J:ESJ=maxEFH十FTSHJ,EFI 十 FTSIJ =max30,26 =30,则EFJ=32。
FTS=10天
A
B
=
10天
A
B
5天
FTF=5天
C
D
=
C
D
6天
STS=6天
E
F
=
E
F
STF
I
MA=20天
J
MA=20天
=
I
J
图 8-23
2.单代号搭接网络的基本要求
(l)不能有相同编号的节点。 (2)不能出现违反逻辑的表示。例如:
1.环路(图8-24) 。
2.当搭接时距使用最大值定义时,有时 虽没有环路,但也会造成逻辑上的错误(图8-25)。
则: LSJ=LFJ-DJ=32-3=30。
return
2. 其他活动的最迟时间计算(从后向前传递)
A
B
A
B
A
B
LFA=LSB——FTSAB LSA = LSB——STSAB LFA =LFB——FTFAB
当A有几个紧后活动时,则有几对值,取最小值。
H:LFH=LSJ-FTSHJ=30-0=30, LSH=LFH-DH=30-6=24;
2
时间
10
6
2
2
紧前 活动
搭接 关系
搭接 时距
A
B
C
C
D
F、 G
G
E
H、 I
FTS
FT S
FT S
ST S
FT S
FT S
FT S
FT F
F T S
0
2 0 2 0 0 0 40
作网络图(见图8-31)
B 10
2
F
C
2
6
MA=2
H
6
A
2
4
G
D
10
J
10
2
I 2
E 4
4
图8-31
最早时间计算
最早时间(ES和 EF)计算从首节点开始, 顺着箭头方向向尾节点逐步推算。
return
(三)网络的时间参数
0 项目开始
ES i
LS i
D
最早 安排
TF i
图8-30
EF i
LF i
D
TF i
最迟安排
return
(四)网络分析方法
现以一个单代号搭接网络为例介绍网络 分析过程和计算公式的应用。某工程由下表8-7 所示的活动组成。
过程 A B C D E
F
活动
G
H
I
J
持续 4 10 6 10 4
紧前活动结束后一段时间,紧后活动才能 结束,即紧后活动的结束时间受紧前活动结 束时间的制约。例如基础回填土结束后基坑 排水才能停止,即见图8-6。
0天
基坑 回填土
基坑 或
排水
FTF=0天
A
B
(a)
(b)
图8-6
(二)单代号搭接网络的绘制
1.基本形式
单代号搭接网络以工程活动为节点,以带箭杆表示逻辑 关系。活动之间存在各种形式的搭接 关系(如 FTS、 FTF、STS、STF)。例如图8-23。
网络计划 单代号搭接网络
(一)工程活动的逻辑关系分析 几种形式的逻辑关系
1. FTS,即结束—开始(FINISH TO START) 关系。例如混凝土浇捣成型之后,至少要 养护7天才能拆模,即见图8-3。通常将A称 为B的紧前活动,B称为A的紧后活动。
浇 捣 7天
混凝土
拆模
或
FTS=7天
A
B
(a)
(3)不允许有多个首节点,多个尾节点。
A
MA=3天
C
B
A
C
图8-24
5天
B 8天
图8-25
3.单代号网络的优点
(l)有较强的逻辑表达能力。 (2)其表达与人们的思维方式一致,易于被人们接受。 (3)绘制方法简单,不易出错, (4)在时间参数的算法上双代号网络是单代号搭接网络的
特例,即它仅表示FTS关系,且搭接时距为0的状况。
当B有几个紧前活动时,则有几对值,取最大值.
B:A、B为FTS关系,则 ESB=EFA十FTSAB=4十0=4, EFB=ESB十DB=4十10=14。
同理C:ESc=4,EFc=10, D:ESD=4,EFD=4十10=14, E:ESE=4,EFE=4十4=8。
turn
对于F: F有两个紧前活动,则ESF必有两个 计算结果。
由 B-F关系定义得: ESF1=EFB十FTS BF=14十2=16, EFF1=ES F1十DF=16十2=18 由C-F关系定义得: ESF2=EFc十0=10十0=10 EFF2=ES F2十DF=10十2=12 m这a时x取16最,大10值,=1即6,:同ES时F=得mEaFxFE=1S6F十1,2=E1S8F。2 =
(b)
图8-3
浇捣混凝土
7天
图8-4
拆模最早开始时间, 不得提前但允许推迟
拆模
2. STS,即开始——开始 (START TO START)关系
紧前活动开始后一段时间,紧后活动才能开始, 即紧后活动的开始时间受紧前活动的开始时间 的制约。例如某基础工程采用井点降水,按规 定抽水设备安装完成,开始抽水一天后,即可 开挖基坑,即见图8-5。
return
对于G:同样G有两个紧前活动C和D。 由C-G关系定义:
ESG1=ESC十STSCG=4十2=6, EFG1=ESG1十DG=6十10=16 由D-G关系定义: ESG2=EFD十FTSDG=14十0=14, EFG2=ESG2十DG=14十10=24
取最大值,则ESG=14,EFG=24。
基坑 排水
基坑 或
开挖
STS=1天
A
B
(a)
(b)
图8-5
. STF即开始——结束 TART TO FINISH)关系
紧前活动开始后一段时间,紧后活动 才能结束,这在实际工程中用的较少。
举例说明,工程活动之间存在上述搭接关系。
return
3. FTF,即结束——结束 (FINISH TO FINISH)关系
return
总工期(TD)的确定
取网络的总工期为活动的最早结束时间的 最大值,即: TD=maxEFi=32(周)
return
最迟时间(LS、LF)的计算
最迟时间的计算由结束节点开始, 逆箭头方向由尾节点向首节点逐个推算。
1.令结束节点LFJ=TD=32,即定义项目的最迟结束时 间为总工期。
LS i=LF i-D I ……………(8-2)
1.令首节点 ESA=0,如果用日历表示,则定义 ESA为项目开始期。 活动内存在关系: EF i =ES i十D i ……(8-1) 则: EFA=ESA十DA=0十4=4
return
2. 其他活动的最早时间计算(从前向后传递)
A
B
ESB=EFA十FTSAB
A
B
ESB=ESA十STSAB
A
B
EFB=EFA十FTFAB
return
H有两个紧前活动,则: H:ESH=maxEFF十FTSFH,EFG十 FTSGH
=max18,24=24,则EFH=ESH +DH =30;
I:ESI=maxEFGI十FTSG,EFE十FTFEG-DI =max24+0,8十4-2=24,则 EFI=26;
J:ESJ=maxEFH十FTSHJ,EFI 十 FTSIJ =max30,26 =30,则EFJ=32。
FTS=10天
A
B
=
10天
A
B
5天
FTF=5天
C
D
=
C
D
6天
STS=6天
E
F
=
E
F
STF
I
MA=20天
J
MA=20天
=
I
J
图 8-23
2.单代号搭接网络的基本要求
(l)不能有相同编号的节点。 (2)不能出现违反逻辑的表示。例如:
1.环路(图8-24) 。
2.当搭接时距使用最大值定义时,有时 虽没有环路,但也会造成逻辑上的错误(图8-25)。
则: LSJ=LFJ-DJ=32-3=30。
return
2. 其他活动的最迟时间计算(从后向前传递)
A
B
A
B
A
B
LFA=LSB——FTSAB LSA = LSB——STSAB LFA =LFB——FTFAB
当A有几个紧后活动时,则有几对值,取最小值。
H:LFH=LSJ-FTSHJ=30-0=30, LSH=LFH-DH=30-6=24;
2
时间
10
6
2
2
紧前 活动
搭接 关系
搭接 时距
A
B
C
C
D
F、 G
G
E
H、 I
FTS
FT S
FT S
ST S
FT S
FT S
FT S
FT F
F T S
0
2 0 2 0 0 0 40
作网络图(见图8-31)
B 10
2
F
C
2
6
MA=2
H
6
A
2
4
G
D
10
J
10
2
I 2
E 4
4
图8-31
最早时间计算
最早时间(ES和 EF)计算从首节点开始, 顺着箭头方向向尾节点逐步推算。
return
(三)网络的时间参数
0 项目开始
ES i
LS i
D
最早 安排
TF i
图8-30
EF i
LF i
D
TF i
最迟安排
return
(四)网络分析方法
现以一个单代号搭接网络为例介绍网络 分析过程和计算公式的应用。某工程由下表8-7 所示的活动组成。
过程 A B C D E
F
活动
G
H
I
J
持续 4 10 6 10 4
紧前活动结束后一段时间,紧后活动才能 结束,即紧后活动的结束时间受紧前活动结 束时间的制约。例如基础回填土结束后基坑 排水才能停止,即见图8-6。
0天
基坑 回填土
基坑 或
排水
FTF=0天
A
B
(a)
(b)
图8-6
(二)单代号搭接网络的绘制
1.基本形式
单代号搭接网络以工程活动为节点,以带箭杆表示逻辑 关系。活动之间存在各种形式的搭接 关系(如 FTS、 FTF、STS、STF)。例如图8-23。
网络计划 单代号搭接网络
(一)工程活动的逻辑关系分析 几种形式的逻辑关系
1. FTS,即结束—开始(FINISH TO START) 关系。例如混凝土浇捣成型之后,至少要 养护7天才能拆模,即见图8-3。通常将A称 为B的紧前活动,B称为A的紧后活动。
浇 捣 7天
混凝土
拆模
或
FTS=7天
A
B
(a)
(3)不允许有多个首节点,多个尾节点。
A
MA=3天
C
B
A
C
图8-24
5天
B 8天
图8-25
3.单代号网络的优点
(l)有较强的逻辑表达能力。 (2)其表达与人们的思维方式一致,易于被人们接受。 (3)绘制方法简单,不易出错, (4)在时间参数的算法上双代号网络是单代号搭接网络的
特例,即它仅表示FTS关系,且搭接时距为0的状况。
当B有几个紧前活动时,则有几对值,取最大值.
B:A、B为FTS关系,则 ESB=EFA十FTSAB=4十0=4, EFB=ESB十DB=4十10=14。
同理C:ESc=4,EFc=10, D:ESD=4,EFD=4十10=14, E:ESE=4,EFE=4十4=8。
turn
对于F: F有两个紧前活动,则ESF必有两个 计算结果。
由 B-F关系定义得: ESF1=EFB十FTS BF=14十2=16, EFF1=ES F1十DF=16十2=18 由C-F关系定义得: ESF2=EFc十0=10十0=10 EFF2=ES F2十DF=10十2=12 m这a时x取16最,大10值,=1即6,:同ES时F=得mEaFxFE=1S6F十1,2=E1S8F。2 =
(b)
图8-3
浇捣混凝土
7天
图8-4
拆模最早开始时间, 不得提前但允许推迟
拆模
2. STS,即开始——开始 (START TO START)关系
紧前活动开始后一段时间,紧后活动才能开始, 即紧后活动的开始时间受紧前活动的开始时间 的制约。例如某基础工程采用井点降水,按规 定抽水设备安装完成,开始抽水一天后,即可 开挖基坑,即见图8-5。
return
对于G:同样G有两个紧前活动C和D。 由C-G关系定义:
ESG1=ESC十STSCG=4十2=6, EFG1=ESG1十DG=6十10=16 由D-G关系定义: ESG2=EFD十FTSDG=14十0=14, EFG2=ESG2十DG=14十10=24
取最大值,则ESG=14,EFG=24。
