八年级下册数学期末压轴题专辑(含解析-Word版)

合集下载

【勾股定理期末压轴题训练】2022-2023学年八年级数学下册(人教版)含解析

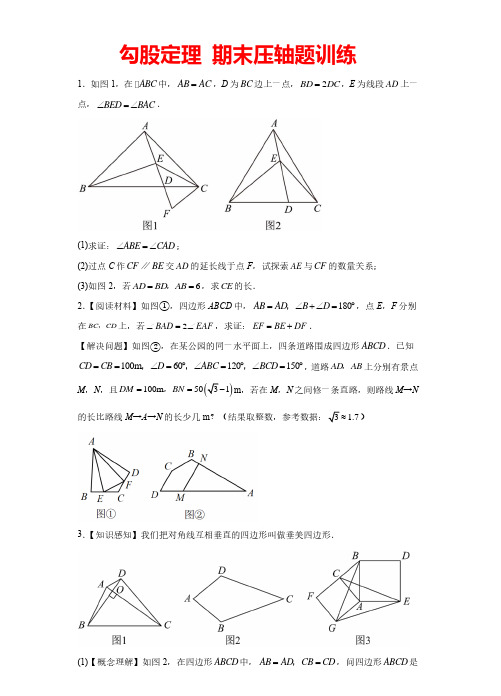
，在ABC 中，BAC ∠(1)求证：ABE CAD ∠=∠；(2)过点C 作CF BE ∥交AD 的延长线于点F ，试探索AE 与CF (3)如图2，若6AD BD AB ==，，求CE 的长．2．【阅读材料】如图①，四边形ABCD 中，AB AD B =∠+∠，3．【知识感知】我们把对角线互相垂直的四边形叫做垂美四边形．Rt ACB的直角边，，，BG GE，在ABC中，在整个运动过程中，当BCP是等腰三角形时，求，在平面直角坐标系中，点AQ CP交于点M，则在P、Q运动的过程中，(1)如图1，连接,（填“会”或“不会”）；(2)如图1，当PBQ是直角三角形时，求点P的坐标；在ABC中，．在等腰直角ABC中，，延长BC∠=∠；(1)求证：MQB PAC(2)若22，，求DQ DH==(3)用等式表示线段MB与CP．在ABC中，(2)如图2，若点D在线段AB上，取．在ABC 中，(1)如图1，当ABC 为锐角三角形时，①依题意补全图形，猜想BAE ∠与BCD ∠之间的数量关系并证明；②用等式表示线段AE ，CE ，DE 的数量关系，并证明．(2)如图2，当ABC ∠为钝角时，直接写出线段问题解决：(1)先考虑特殊情况：①如果点E刚好和点A重合，或者点B刚好和点F重合时，AE “>”，“<”或“=”）；形ABC和△⊥BC AD正方形的三个顶点，可得ABC ，则，在ABC 中，是BC ．如图，ABC 是等腰直角三角形，上一点．时，求DEF 的面．和CDE 中，AC 上，连接(1)如图1，若30EDC ∠=︒，6EF =，求AEF △的面积；(2)如图2，若BD AE =，求AF 、AE 、BC 之间的数量关系；(3)如图3，移动点D ，使得点F 是线段AB 的中点时，3DB =，4AB =别是线段AC ，BC 上的动点，且AP CQ =，连接DP ，FQ ，求DP FQ +(1)如图1，若45CBD ∠=︒①求BCG ∠的度数；②求证：CE DG =；(2)如图2，若60CBD ∠=︒，当6AC DE −=时，求CE 的值(2)如图2，ABC ∆中，2B C ∠=∠，线段AC 的垂直平分线交AC 于点E ，交BC 于点D ．求证：AD 是ABC ∆的一条双腰分割线；(3)如图3，已知ABC ∆中，AD 是三角形ABC 的双腰分割线，且AB AD =．①若64B ∠=︒，求C ∠的度数；②若3AB =，5AC =，求BC 的长．参考答案：1．(1)见解析(2)AE CF =【分析】（1）利用三角形外角的性质以及角的和差定义解决问题即可．（2）如图1中，在AF 上截取AJ ，使得AJ BE =．证明SAS ABE CAJ ≌（），推出AE CJ =，再证明CF CJ =即可解决问题．（3）如图2中，过点B 作BK AD ⊥于K ，作CF BE ∥交AD 的延长线于F ，过点C 作CQ DF⊥于Q ．首先证明BE BD =， CD DF =，再证明EK DK =，DQ FQ =，2DK DQ =，2BK CQ =，AE DE CD CF ===，利用参数构建方程解决问题即可．【解析】（1）证明：∵BED ABE BAE BAC BAE CAD ∠=∠+∠∠=∠+∠，，又∵BED BAC ∠=∠，∴ABE BAE BAE CAD ∠+∠=∠+∠，∴ABE CAD ∠=∠．（2）解：结论：AE CF =．理由：如图1中，在AF 上截取AJ ，使得AJ BE =．∵BA AC ABE CAJ BE AJ =∠=∠=，，，∴SAS ABE CAJ ≌（），∴AE CJ AEB AJC =∠=∠，，∴BED CJF ∠=∠，∵BE CF ∥，∴BEJ F ∠=∠，∴CJF F ∠=∠，∴CJ CF =，∴AE CF =．（3）如图2中，过点B 作BK AD ⊥于K ，作CF BE ∥交AD 的延长线于F ，过点C 作CQ DF ⊥于Q ．设ABE CAD x CBE y ∠=∠=∠=，，∵AB AC DB DA ==，，∴DBA DAB ACB x y ∠=∠=∠=+，∴22BED ABE DAB x y BDE ACB CAD x y ∠=∠+∠=+∠=∠+∠=+，，∴BED BDE ∠=∠，∴BE BD =，∵AB CA ABE CAD =∠=∠，，∴AAS ABE CAD ≌（），∴AE CD BE AD ==，，∵CF BE ∥，∴F BED ∠=∠，∴F CDF ∠=∠，∴CD CF =，∵BE BD BK DE CD CF CQ DF =⊥=⊥，，，，∴EK KD DQ QF ==，，∵CQ BK ∥，∴:::1:2DQ DK CD BD CQ BK ===，∴可以假设2DQ m DK m ==，，∵222BD BE AD CD CF AE =====，∴48AE DE m AD BD m ====，，∴BK ==，∴CQ =，在Rt ABK △中，∵222AB AK BK=+，∴()()22266m =+，∴m， ∴DQ =，CQ ，5EQ m ==，∵90CQE ∠=︒，∴CE =．【点评】本题属于三角形综合题，考查了等腰三角形的判定和性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．2．阅读材料：见解析；解决问题：少370m【分析】阅读材料：延长CB 到点M ，使BM DF =，连接AM ，如图，利用已知条件可得D ABM ∠=∠，进而可证明ABM ADF ≅，可得,AM AF MAB DAF =∠=∠，再证明AEM AEF ≅，可得=ME EF ，进而可得结论；解决问题：如图，作辅助线，构建阅读材料的图形，先根据四边形的内角和定理证明90G ∠=︒ ，分别计算,,,CG DG AD AG 的长，由线段的和与差可得,AM AN 的长，最后由阅读材料的结论可得MN 的长，计算AM AN MN +−可得答案．【解析】阅读材料：证明：延长CB 到点M ，使BM DF =，连接AM ，如图，∵180ABC D ∠+∠=︒，180ABC ABM ∠+∠=︒，∴D ABM ∠=∠，∵,,AB AD ABM D BM DF =∠=∠=，∴ABM ADF ≅，∴,AM AF MAB DAF =∠=∠，∵2BAD EAF ∠∠=，∴BAE DAF BAE BAM EAM EAF ∠+∠=∠+∠=∠=∠，又∵,AM AF AE AE ==，∴AEM AEF ≅，∴=ME EF ，∴EF MB BE BE DF =+=+；解决问题：解：如图，延长DC AB ，交于点G ，连接CN CM ，，∵60120150D ABC BCD ∠=︒∠=︒∠=︒，，，∴3606012015030A ∠=︒−︒−︒−︒=︒，∴90G ∠=︒，∴2AD DG =，在Rt CGB △中，18015030BCG ∠=︒−︒=︒，∴1502BG BC CG ===，∴100DG CD CG =+=+∴2200150AD DG AG ==+==+∵100DM =，∴200100100AM AD DM =−=+=+∵)50501BG BN ==，，∴)150********AN AG BG BN =−−=+−=+GN BG BN =+= ∵60CD DM D =∠=︒，，∴DCM △ 是等边三角形，∴60DCM ∠=︒，∵GC GN ==∴CGN 是等腰直角三角形，∴45GCN ∠=︒，∴453015BCN ∠=︒−︒=︒， ∴11506015752MCN BCD ∠=︒−︒−︒=︒=∠，由【阅读材料】的结论得：)10050150MN DM BN =+=+=+∵()10015050200370AM AN MN +−=++=+≈（m ）． ∴路线M→N 的长比路线M→A→N 的长少370m ．【点评】此题主要考查了含30︒的直角三角形的性质，勾股定理，等腰直角三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定和性质，二次根式的混合运算等知识与方法，解题的关键是作出所需要的辅助线，构造含30︒的直角三角形，再利用线段的和与差进行计算．3．(1)是，见解析(2)2222AD BC AB CD ++＝，见解析【分析】（1）根据垂直平分线的判定定理证明即可；（2）根据垂直的定义和勾股定理解答即可；（3）根据垂美四边形的性质、勾股定理、结合（2）的结论计算．【解析】（1）如图2，四边形ABCD 是垂美四边形．证明：连接AC BD 、交于点E ，∵AB AD =，∴点A 在线段BD 的垂直平分线上，∵CB CD =，∴点C 在线段BD 的垂直平分线上，∴直线AC 是线段BD 的垂直平分线，∴AC BD ⊥，即四边形ABCD 是垂美四边形；（2）猜想结论2222AD BC AB CD ++＝．如图1，已知四边形ABCD 中，∵AC BD ⊥，∴90AOD AOB BOC COD ∠=∠=∠=∠=︒，由勾股定理得，222222AD BC AO DO BO CO +=+++，222222AB CD AO BO DO CO +=+++，∴2222AD BC AB CD ++＝；（3）如图3，连接CG BE 、，∵90CAG BAE ∠=∠=︒，∴CAG BAC BAE BAC ∠+∠=∠+∠，即GAB CAE ∠∠＝，在GA B 和CAE V 中，AG AC GAB CAEAB AE =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS GAB CAE V V ≌， ∴ABG AEC ∠=∠，又90AEC AME ∠+∠=︒，∴90ABG BMN ∠+∠=︒，∴90BNC ∠=︒，即CE BG ⊥，∴四边形CGEB 是垂美四边形，由（2）得，2222CG BE CB GE +=+，∵810AC AB ==，，∴6BC CG ==，BE =∴((22222226292GE CG BE CB =+−=+−=，∴GE ==【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用，正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键．4．(1)4,4t − (2)52t = (3)1或535或9.5或10【分析】（1）利用勾股定理求出AC ，利用CP AC AP =−，求出CP ；（2）过点P 作PD AB ⊥，交AB 于点D ，利用勾股定理列式求解即可；（3）分,,BC CP BP CP BC BP ===，三种情况进行讨论求解即可．【解析】（1）解：∵90,5,3ACB AB BC ∠=︒==，∴4AC =；∵点P 从点A 出发，以每秒1个单位长度的速度沿路线A C B A →→→运动，∴当点P 在AC 上时，AP t =，∴4CP AC AP t =−=−；故答案为：4,4t −；（2）解：点P 作PD AB ⊥，交AB 于点D ，则：90PDA PDB ∠=∠=︒，∵点P 在ABC ∠的角平分线上，90ACB ∠=︒，∴90ACB PDB ∠=∠=︒，PD PC =，又∵BP BP =，∴()HL PBD PBC ≌，∴3BD BC ==，∴2AD AB BD =−=，由（1）知,4AP t CP t ==−，∴4PD PC t ==−，在Rt ADP 中，222AP PD AD =+，即：()22242t t =−+，解得：52t =；（3）解：P 点运动的总时间为：()543112++÷=秒，当BCP 是等腰三角形时： ①当BC CP =，点P 在AC 上时：如图，此时：43t −=，解得：1t =；当BC CP =，点P 在AB 上时：如图，过点C 作CE AB ⊥，交AB 于点E ，则：72BP t AC BC t BE =−−=−=， ∵1122ABC S AC BC AB CE =⋅=⋅，即：435CE ⨯=， ∴125CE =，∴95BE ==， ∴1875BP t =−=， ∴535t =； ②当BP CP =时，如图：由①可知：912,7,55BE BP t CE ==−=， ∴97,75PE t CP t =−−=−，在Rt PEC 中，222CP PE CE =+，即：()2224412755t t ⎛⎫⎛⎫−=−+ ⎪ ⎪⎝⎭⎝⎭，解得：9.5t =；③当BC BP =时，如图：此时：73BP t =−=，解得10t =；综上：当BCP 是等腰三角形时，t 的值为：1或535或9.5或10．【点评】本题考查三角形上的动点问题．熟练掌握勾股定理，以及等腰三角形的定义是解题的关键．注意，分类讨论．5．(1)不会(2)当PBQ 是直角三角形时，点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭(3)(1,P −，120CMQ ∠=︒【分析】(1)先利用SAS 证明ABQ CAP ≌，得BAQ ACP ∠=∠，利用外角的性质并进行等量代换可得60CMQ ACP CAM BAQ CAM BAC ∠=∠+∠=∠+∠=∠=︒(2)分90,90PQB BPQ ︒∠=︒∠=两种情况，利用直角三角形中30度角所对直角边等于斜边的一半列式求解（3）作PM x ⊥轴，先根据30度角的性质和勾股定理求出1MB =cm和MP =cm ，进而求出(1,P −，再根据SAS 证明ACQ CBP ≌，最后根据外角的性质并进行等量代换作答即可【解析】（1）解：在等边三角形ABC 中,60AB AC CBA CAP ︒=∠=∠=且点A 、点Q 同时出发，且它们的速度都为1cm/s AP =BQ ∴(SAS)ABQ CAP ∴≌BAQ ACP ∴∠=∠60CMQ ACP CAM BAQ CAM BAC ∴∠=∠+∠=∠+∠=∠=︒故答案为：不会（2）解：设运动时间为t 秒，则,4AP BQ t PB t ===−①当90PQB ∠=︒时60ABC ∠=︒30BPQ ∠=︒∴12BQ PB ∴=，即1(4)2t t =− 解得43t = 即48433BP =−= 60ABC ∠=︒∴43P ⎛ ⎝⎭ ②当90BPQ ∠=︒时60ABC ∠=︒30PQB ∴∠=︒12PB BQ ∴=，即142t t −= 解得83t = 即84433BP =−=60ABC ∠=︒∴23P ⎛ ⎝⎭ ∴当PBQ 是直角三角形时，点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭ （3）∵12BP BC =∴2BP =cm作PM x ⊥轴∵60ABC ∠=︒∴60PBM ∠=︒∴60PBM ∠=︒∴30MPB ∠=︒∴1MB =cm由勾股定理得MP =cm∴(1,P −在等边三角形ABC 中,60BC AC ABC ACB ︒=∠=∠=∵点A 、点Q 同时出发，且它们的速度都为1cm/sBP CQ ∴=，120PBC ACQ ∠=∠=︒(SAS)ACQ CBP ∴≌CMQ APM PAM APM PAC CAQ AQB PAC CAQ ∴∠=∠+∠=∠+∠+∠=∠+∠+∠180AQB PAC CAQ ABC ∠+∠+∠+∠=︒，60ABC ∠=︒18060120CMQ ∴∠=︒−︒=︒【点评】本题考查了全等三角形的判定和性质，外角的性质，直角三角形30度角的性质，勾股定理，熟练掌握各知识点是解题的关键．6．(1)见解析(2)(1）是，证明见解析；(2）存在，66013CP =.【分析】（1）根据阅读材料给出的定义结合已经学过的三角形的知识点，推到即可得出结论；（2）根据已知条件利用相似三角形即可得出①中的作法是符合条件的；第②小题根据已知条件画出图形，再根据图形得出结论．【解析】（1）解：①∵BD 为△ABC 的角平分线，∠ABC ＝2∠C∴∠=∠DBC C∴BD CD =∴图中相等的线段有BD CD =∵A A ∠=∠，2ADB ABC C ∠=∠=∠∴ADB ABC ∽∴图中相似的三角形有：ADB 和ABC②∵AC 的中垂线交边BC 于点E∴AE EC =∴AEC △是等腰三角形∵2AEB C ∠=∠，2ABC C ∠∠＝∴AB AE =∴ABE 是等腰三角形（2）解：①符合要求，延长EF 交AD 于N ，则四边形ABEN 为矩形∴48AB EN ==，1662AN BE EC BC ====∵33EF =∴483315NF EN EF =−=−=∵PN BC ∥∴PFN CFE ∽ ∴PN NF PF EC EF FC == ∴153366PN = ∴1553311PF FC == ∴663036AP AN PN =−=−=∵90A ∠=︒∴60BP = ∴60513211BP FC == ∴BP PF BC FC = 作FK BP ⊥于K ∴BPF BCF SPF S FC =∴1212FK BP PF FCEF BC ⋅=⋅∴FK EF =∵FK BP ⊥，FE BC ⊥ ∴BF 平分PBC ∠∴1FBE PBC 2∠=∠∵F 在BC 的垂直平分线上∴FB FC =∴FBC FCB ∠=∠∴2PBC PCB ∠=∠∴符合要求②存在， 66013CP =.I.若P 在AD 上时，连接BD ，如图所示，∴PBC DBC ∠>∠，PCB DCB ∠<∠取BD 的中垂线交BC 与G ，作DH BC ⊥于H∴四边形ABHD 为矩形∴48HD AB ==，68BH AD ==，DG GB =，1326864CH BC BH =−=−=，∴80DC =，设GH x =，则68BG DG x ==−∵90DHG ∠=︒∴由勾股定理222GH DH DG +=∴()2226848x x −=+∴22136684811620x =−=⨯ ∴2906417x =<在CH 上取点M ，使29017HM GH ==，连接DM∴DMB DCB PCB ∠>∠>∠∵DG BG =∴DBC GDB ∠=∠∴22DGC GDB DBC DBC PBC ∠=∠+∠=∠<∠∴HM GH =，DH MG ⊥∴DG DM =∴DMB DGC ∠=∠∴2PBC PCB ∠>∠∴在AD 上所有点都满足2PBC PCB ∠>∠∴不存在；II. 若P 在AB 上时，如图所示，∵BP AB BC <<，∴45BCP ∠<︒，∴2PBC BCP ∠≠∠，∴在AB 上不存在其它满足要求的△BCP ；III. 若P 在AB 上时，如图所示，作BC 的垂直平分线交AD 于点L 、交BC 于点R ，作BCD ∠的平分线交RL 于点O ，连结BO 并延长交DC 于点P ，此时有22BCD BCO PBC ∠=∠=∠， ∴△BCP 是以BC 为底边的倍角三角形，作OU DC ⊥于点U ，连结OA 、OD ，∵CO 平分BCD ∠，OR BC ⊥，OU DC ⊥，∴OR OU =，设OR x =，则OU x =，48OL x =−，由AOB BOC COD AOD ABCD S S S S S =+++梯形得11111(68132)4848661328068(48)22222x x x ⨯+⨯=⨯⨯+⨯+⨯+⨯⨯−，解得：22x =在Rt BOR 中，OB =∴OC OB ==∵OCP OCB PBC ∠=∠=∠，2POC PBC OCB PBC PCB ∠=∠+∠=∠=∠，∴PBC PCO ~，∴CP BP BC OP CP OC ==∴OP =，BP =，由BP OP OB −=得= 解得，66013CP =【点评】本题考查了角的倍数关系，角平分线的性质，相似三角形的判定等相关知识，明确题意根据已知条件画出图形是解题的关键．7．(1)45，=(2)(3)【分析】（1）根据等腰直角三角形的三线合一即可得到90,ADC AD CD BD ∠=︒==，由此推出,45BC BA AD D C ⊥∠=︒=∠，证明ADE CDF △△≌，得到,DE DF ADE CDF =∠=∠，求出DEF 是等腰直角三角形，勾股定理得到EF =DE ；（2）证明(SAS)ADE CDF ≌V V ，得到DE DF =，ADE CDF ∠=∠，推出DE DF ⊥，再由勾股定理得到答案；（3）分两种情况，①当H 在线段AC 上时，②当H 在线段AC 的延长线上时，连接MC ，过点M 作MF AC ⊥于F ，由等腰三角形的性质及等腰直角三角形的性质可得出答案．【解析】（1）解：在ABC 中，90BAC ∠=︒，AB AC =，45B BCA ∠=∠=︒，D 是BC 的中点，∴,45BC BA AD D C ⊥∠=︒=∠，∴90,ADC AD CD BD ∠=︒==，∵AE CF =，∴ADE CDF △△≌（SAS ），∴,DE DF ADE CDF =∠=∠，∵90CDF ADF ADC ∠+∠=∠=︒，∴90ADE ADF ∠+∠=︒，∴DEF 是等腰直角三角形，∴EF ==，故答案为：45，=（2）解：∵AB AC =，90BAC ∠=︒，∴45B ACD ∠=∠=︒，∵AB AC =，点D 是BC 的中点，∴AD BC ⊥，45BAD CAD ∠=∠=︒∴AD CD =，90ADC ∠=︒，∴BAD ACD ∠=∠，∴180180BAD ACD ︒−∠=︒−∠，即EAD FCD ∠=∠，∵45ACD CAD ∠=∠=︒，∴AD CD =，在ADE V 和CDF 中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)ADE CDF ≌V V ，∴DE DF =，ADE CDF ∠=∠，∴90EDF CDF EDC ADE EDC ADC ∠=∠+∠=∠+∠=∠=︒，∴DE DF ⊥，在Rt EDF 中，DE DF =，4EF =，∴DE EF ==（3）解：①当H 在线段AC 上时，如图，连接MC ，过点M 作MF AC ⊥于F ，∵,AD BC BD CD ⊥=，∴AM 是线段BC 的中垂线，∴MB MC =，∴MBC MCB ∠=∠，∵AB AC =，∴A ABC CB =∠∠，∴ABM ACM ∠=∠，又∵90BAC BMH ∠=∠=︒，360BAH ABM BMH AHM ∠+∠+∠+∠=︒，∴180ABM AHM ∠+∠=︒，∵180AHM MHC ∠+∠=︒，∴ABM MHC ∠=∠，∴MCH MHC ∠=∠，∴MH MC =，∵2CH =， ∴112HF CF CH ===， ∵6AC =，∴615AF AC CF =−=−=，∵45DAC ∠=︒，∴5AF MF ==，∴AM =∵6AB AC ==，90BAC ∠=︒，D 是BC 的中点，∴12AD BC ==∴DM AM AD =−=②当H 在线段AC 的延长线上时，如图，连接MC ，过点M 作MF AC ⊥于F ，同理可得1CF HF ==，∴617AF AC CF =+=+=，∴AM =∴DM AM AD =−=综上，DM 的长为【点评】此题是三角形的综合题，主要考查了直角三角形的性质，等腰三角形的判定和性质，全等三角形的判定和性质及等腰直角三角形的判定和性质，根据已知得出ADE CDF V V ≌是解题的关键．8．(1)见解析(2)HM =(3)MB ，证明见解析【分析】（1）由直角三角形两个锐角互余即可得出90APC PAC ∠+∠=︒，90MQB APC ∠+∠=︒，从而得出MQB PAC ∠=∠；（2）连接AQ ，DP ．由题意易得出AC 为线段QP 的垂直平分线，即得出2DP DQ ==，QAC PAC ∠=∠，AP AQ =，从而由勾股定理可求出PH DH ．进而易证(AAS)DAH PQH ≌，得出2AH QH DQ DH ==+=，再根据勾股定理可求出2AQ ==．又易证QAM QMA ∠=∠，即得出2QM QA ==，从而由HM QM DH =−求解即可；（3）作ME QB ⊥于点E ，易证(AAS)APC QME ≌，即得出PC ME =．再根据MEB 是等腰直角三角形，即得出MB =，从而得出MB ．【解析】（1）∵90ACB ∠=︒，QH AP ⊥，∴90APC PAC ∠+∠=︒，90MQB APC ∠+∠=︒，∴MQB PAC ∠=∠；（2）如图，连接AQ ，DP ．∵CQ CP =，90ACB ∠=︒，∴AC 为线段QP 的垂直平分线，∴2DP DQ ==，QAC PAC ∠=∠，AP AQ =，∴PH DH =．又∵DAH PQH ∠=∠，90AHD QHP ∠=∠=︒，∴(AAS)DAH PQH ≌，∴2AH QH DQ DH ==+=∴2AQ ==．∵45QAM QAC CAB QAC ∠=∠+∠=∠+︒，45QMA MQB B BQM ∠=∠+∠=∠+︒， ∴QAM QMA ∠=∠，∴2QM QA ==，∴2(2HM QM DH =−=−=（3）MB ．证明如下，如图，作ME QB ⊥于点E ，由（2）可知AP AQ QM ==，又∵90MQE PAC ACP QEM ∠=∠∠=∠=︒，，∴(AAS)APC QME ≌，∴PC ME =．∵MEB 是等腰直角三角形，∴BE ME =．∵222BE ME MB +=，∴MB ，∴MB =．【点评】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理．正确作出辅助线是解题的关键．9．(1)见解析(2)①见解析；②2AE CF =；证明见解析【分析】（1）根据“SAS ”证明≌ACD BCE V V ，得出AD BE =，DAC CBE ∠=∠，证明ABE为直角三角形，根据勾股定理得出222AB BE AE +=，即可得出答案；（2）①根据题意补全图形即可；②延长CF ，截取FG CF =，连接BG ，证明CFD GFB ≌，得出CD BG =，GBF CDF ∠=∠，证明()SAS ACE CBG ≌即可得出结论．【解析】（1）证明：∵90ACB ∠=︒，AC BC =，∴190452CAB CBA ∠=∠=⨯︒=︒，∵90DCE ∠=︒，∴90DCA ACE ACE ECB ∠+∠=∠+∠=︒，∴DCA ECB ∠=∠，∵AC BC =，CE CD =，∴()SAS ACD BCE △≌△，∴AD BE =，DAC CBE ∠=∠，∵180135DAC CAB ∠=︒−∠=︒，∴135CBE ∠=︒，∴90ABE CBE CBA ∠=∠−∠=︒，∴ABE 为直角三角形，∴222AB BE AE +=，∴222AB AD AE +=．（2）解：①依题意补全图2如图所示：②2AE CF =；理由如下：如图，延长CF ，截取FG CF =，连接BG ，∵F 为BD 的中点，∴BF DF =，∵CFD GFB ∠=∠，CF FG =，∴()SAS CFD GFB ≌，∴CD BG =，GBF CDF ∠=∠，∵CD CE =，∴BG CE =，∵45CDF DCA CAD DCA ∠=∠+∠=∠+︒，∴45GBF CDF DCA ∠=∠=∠+︒，∴454590CBG FBG CBA DCA DCA ∠=∠+∠=∠+︒+︒=∠+︒，∵90ACE DCA DCE DCA ∠=∠+∠=∠+︒，∴ACE CBG ∠=∠，∵AC BC =，CE BG =，∴()SAS ACE CBG ≌，∴2AE CG CF FG CF ==+=．【点评】本题主要考查了三角形全等的判定和性质，勾股定理，等腰三角形的性质，三角形外角的性质，余角的性质，解题的关键是作出辅助线，构造全等三角形．10．(1)见解析(2)见解析(3)22AD =，20AB =【分析】（1）由“SAS ”可证AOB ≌COD △，可得OB OD =；（2）由AOB ≌COD △得OAB OCD ∠=∠，AOB COD ∠=∠，从而得出AOC BOD ∠=∠，AOC APC ∠=∠，根据180APC APD ∠+∠=︒和1902APD COB ∠=︒+∠进一步得出结论；（3）作BF OD ⊥于F ，作CG OA ⊥于G ，设2BD OE a ==，根据1122BOD S OD BF BD OE =⋅=⋅，BF =，从而45BF OB ，设4BF k =，5OD OB k ==，则3OF k =，根据B F O C G O ，表示各边，并求出OG 和CG ，根据AB CD =列出方程，从而求得k ，进一步求得结果．【解析】（1）证明：在AOB 和COD △中，OA OC BAO DCOAB CD =⎧⎪∠=∠⎨⎪=⎩，∴AOB ≌COD △，∴OB OD =；（2）证明：由（1）知：AOB ≌COD △，∴OAB OCD ∠=∠，AOB COD ∠=∠，∴AOB BOC COD BOC ∠−∠=∠−∠，即：AOC BOD ∠=∠.∵180A P C O C D C E P ∠=︒−∠−∠，180A O C B A O A E O ∠=︒−∠−∠，∴AOC APC ∠=∠.∵180APC APD ∠+∠=︒，∴180A O C A P D ∠+∠=︒. ∵1902APD COB ∠=︒+∠， ∴1(90)1802AOC COB ∠+︒+∠=︒，∴2180A O C B O C ∠+∠=︒，∴180A O C B O D B O C ∠+∠+∠=︒，∴A ，O ，D 三点共线；（3）解：如图，作BF OD ⊥于F ，作CG OA ⊥于G ，设2BD OE a ==，∵OB OD =，∴BE DE a ==.∵90BEO ∠=︒，∴OD OB ===. ∵1122BOD S OD BF BD OE =⋅=⋅，22BF a a ⋅=⋅，∴BF =，∴45BF OB=， ∴设4BF k =，5OD OB k ==，则3OF k =，∵AOC BOD ∠=∠，90B F O C G O ∠=∠=︒，∴B F O C G O ，∴::::3:4:5O G C G O C O F B F O B ==，设3OG x =，4CG x =，5OC x =，∴57x =，解得75x =， ∴2135OG x ==，2845CG x ==，在Rt CDG △和Rt AFB 中，由勾股定理得，222D C C G D G =+，222AB AF BF =+，且AB CD =， ∴22222821()(5)(37)(4)55k k k ++=++，解得3k =，∴412BF k ==，15OB OD ==，39OF k ==，33716A F =⨯+=，∴71522AD OA OD =+=+=.∵222221216400A B B F A F =+=+=，∴20AB =．【点评】本题主要考查了等腰三角形性质，勾股定理，全等三角形判定和性质等知识，解决问题的关键是作辅助线，根据面积法求得线段间关系．11．(1)①图形见解析；猜想：BAE BCD ∠=∠，理由见解析；②见解析；(2)线段AE ，CE ，DE 的数量关系：CE AE =．【分析】(1)①依题意补全图形，由直角三角形的性质得出90BAE B ∠+∠=︒，90BCD B ∠+∠=︒，即可得出BAE BCD ∠=∠；②在AE 上截取AF CE =，可证出ACD 是等腰直角三角形，得出AD CD =，可证明()ADF CDE SAS ≌△△，得出DF DE =，ADF CDE ∠=∠，可推出90CDE FDC EDF ∠︒+∠=∠=，证出EDF 是等腰直角三角形，即可得出结论CE AE =；(2) 在CE 上截取CF AE =，连接DF ，由CD AD ⊥，AE BC ⊥，可得EAD DCF ∠=∠，由45BAC ∠=︒可得AD CD =，可证()ADE CDF SAS △≌△，可得ED DF =，ADE CDF ∠=∠，可推出90EDF ∠=︒，可得EDF 是等腰直角三角形故EF ，即可得线段AE ，CE ，DE 的数量关系．【解析】（1）解：①依题意，补全图形，如图1所示．猜想：BAE BCD ∠=∠，理由如下：∵CD AB ⊥，AE BC ⊥，∴90BAE B ∠+∠=︒，90BCD B ∠+∠=︒，∴BAE BCD ∠=∠，②证明：如图2，在AE 上截取AF CE =，连接DF∵45BAC ∠=︒，CD AB ⊥，∴ACD 是等腰直角三角形，∴AD CD =，在ADF △和CDE 中，DA CD BAE BCDAF CE =⎧⎪∠=∠⎨⎪=⎩∴()ADF CDE SAS ≌△△，∴DF DE =，ADF CDE ∠=∠，∵AB CD ⊥，∴90ADF FDC ∠+∠=︒，∴90CDE FDC EDF ∠︒+∠=∠=，∴EDF 是等腰直角三角形，∴EF =，∵AF EF AE +=，∴CE AE =．（2）解：依题意补全图形，如图3所示，在CE 上截取CF AE =，连接DF ，∵CD AD ⊥，AE BC ⊥，∴90ADC AEC ∠=∠=︒，∴90EAB ABE ∠+∠=︒，90DBC DCF ∠+∠=︒，ABE CBD ∠=∠，∴EAD DCF ∠=∠，∵45BAC ∠=︒，∴45DCA ∠=︒，∴AD CD =，在ADE V 和CDF 中，AD CD EAD DCFCF AE =⎧⎪∠=∠⎨⎪=⎩∴()ADE CDF SAS △≌△，∴ED DF =，ADE CDF ∠=∠，∵90CDF ADF ∠+∠=︒，∴90ADE ADF ∠+∠=︒，∴90EDF ∠=︒，∴EDF 是等腰直角三角形，∴EF =，∵CE CF EF =+，∴CE AE =，∴线段AE ，CE ，DE 的数量关系：CE AE =．【点评】本题考查了全等三角形的判定与性质等腰直角三角形的判定与性质、直角三角形的性质等知，证明三角形全等是解题的关键．12．(1)①=，②＞(2)＞(3)【分析】（1）①连接BD ，先证明CDB △是等边三角形，即60ACB CBD BDC ∠=︒=∠=∠，当F 点与B 点重合时，即0BF =，根据“三线合一”可得AE EF =，即有AE BF EF +=，同理：如果点E 刚好和点A 重合，同样有AE BF EF +=；问题得解；②先证明DEF 是等边三角形，根据等腰三角形的性质可得AE EF =，再结合含30︒角的直角三角形的性质可以求出BF AC =，即问题得解；（2）将DF 绕D 点逆时针旋转120°至DM ，连接AM ME ，，先证明DEM DEF ≌V V ，再证明ADM BDF ≌△△，问题即可得解；（3）将DF 绕D 点逆时针旋转120︒至DN ，连接AN NE ，，根据（2）中的方法，同理可证明：DEN DEF ≌V V ，ADN BDF ≌V V ，再证明ANE 是直角三角形，90ANE ∠=︒，结合含30︒角的直角三角形的性质即可求解．【解析】（1）①如图，连接BD ，根据题意有90ABC ∠=︒，60ACB ∠=︒，即30CAB ∠=︒，∵点D 为AC 中点， ∴12AD DC BD AC ===，∴CDB △是等边三角形，（此结论也适用于第（2）和（3）问）∴60ACB CBD BDC ∠=︒=∠=∠，∵30CAB ∠=︒，∴在Rt ABC △中，12BC AC =，∴AB AC ，当F 点与B 点重合时，如上图左图，即0BF =，∵60EDF DBC ∠=︒=∠，∴DE BC ∥，∴90AED ABC ∠=∠=︒，∴DE AF ⊥，∵AD BD =，∴AE EF =，∵0BF =，∴AE BF EF +=，同理：如果点E 刚好和点A 重合，同样有AE BF EF +=，故答案为：=；②当30ADE ∠=︒时，如图，∵30ADE ∠=︒，30DAE ∠=︒，∴60DEF ∠=︒，AE DE =，∵60EDF ∠=︒，∴DEF 是等边三角形，90ADF Ð=°，∴DE EF =，∴AE EF =，∵90ADF Ð=°，30DAE ∠=︒，∴在Rt ADF 中，12DF AF =，∴AF AB =，∴AF AC =，∴BF AB AF AC AC AC =−==，∵AE EF =，BF AC ，∴AE BF EF +＞，故答案为：＞；（2）AE BF EF +＞，理由如下：将DF 绕D 点逆时针旋转120︒至DM ，连接AM ME ，，如图，根据旋转的性质有：120MDF ∠=︒，DF DM =，∵60FDE ∠=︒，∴60MDE ∠=︒，∵DE DE =，∴DEM DEF ≌V V ，∴EM EF =，∵60CDB ∠=︒，∴120ADB ∠=︒，即：ADB MDF ∠=∠，∵ADB ADF FDB ∠=∠+∠，MDF ADF ADM ∠=∠+∠，∴BDF ADM ∠=∠，∵AD BD =，MD DF =，∴ADM BDF ≌△△， ∴AM BF =，∴在AME △中，AM AE ME +＞，∴BF AE EF +＞，故答案为：＞；（3）将DF 绕D 点逆时针旋转120︒至DN ，连接AN NE ，，如图，根据（2）中的方法，同理可证明：DEN DEF ≌V V ，ADN BDF ≌V V ，∴AN BF =，NE EF =，DBF DAN ∠=∠，∵222BF EF AE +=，∴222AN NE AE +=，∴ANE 是直角三角形，90ANE ∠=︒，∵在（1）中已证明60CBD ∠=︒，∴30DAN DBF ∠=∠=︒，∴60NAE DAN CAB ∠=∠+∠=︒，∴30AEN ∠=︒， ∴12AN AE =，∴NE AE ，∴EF NE AE AE=．【点评】本题主要考查了全等三角形的判定与性质，含30︒角直角三角形的性质，等腰三角形的判定与性质，勾股定理及其逆定理等知识，合理构筑辅助线，证明三角形全等是解答本题的关键．13．(1)见解析(2) (3)94x =【分析】（1）表示出三个图形的面积进行加减计算可证222+=a b c ；（2）计算出ABC 的面积，再根据三角形的面积公式即可求得AB 边上的高；（3）运用勾股定理在Rt ABD 和Rt ADC 中求出2AD ，列出方程求解即可；【解析】（1）证明：∵2 12ABCD S c =四边形，() 12AEDC S b a b =+梯形，()12BED S a b a =−△， BED ABCD AEDC S S S =+△四边形梯形 ∴()()2111222c b a b a b a =++− ∴2221111122222c b ab a ab =++− ∴222+=a b c（2）111442424226222ABC S =⨯−⨯⨯−⨯⨯−⨯⨯=，AB =11622ABC S AB h =⨯=⨯=， 655h =即AB 边上的高是（3）解：在Rt △ABD 中，由勾股定理得222222416AD AB BD x x =-=-=-∵6BD CD BC +==，∴6CD BC BD x =−=−在Rt ACD △中，由勾股定理得()222222561112AD AC CD x x x =−=−−=−+−∴22161112x x x -=-+-， ∴94x =【点评】此题主要考查了梯形，证明勾股定理，勾股定理的应用，证明勾股定理常用的方法是利用面积证明，是解本题的关键．构造出直角三角形DEF 是解本题的难点．14．(1)见解析(2)(3)【分析】（1）证明ACE BCF △△≌，即可解决问题；（2）先由全等三角形的性质和三角形的外角性质，证出90ACD DFB ∠=∠=︒，再由勾股定理即可解决问题；（3）作FH BC ⊥于H ．先证明BCF △是底角为30°的等腰三角形，再求出CF FB FH ，，的长，然后根据DEF ECD CDF ECF S S S S =+−计算即可．【解析】（1）证明：∵ABC ECF ，都是等腰直角三角形，∴90CA CB CE CF ACB ECF ==∠=∠=︒，，，∴ACE BCF ∠=∠，∴()SAS ACE BCF ≌，∴CAE CBF ∠=∠；（2）解：∵90AC BC ACB ==∠=︒，∴AB ==由（1）得：CAD DBF ∠=∠，∵ADB CAD ACD DBF DFB ∠=∠+∠=∠+∠，∴90DFB ACD ∠=∠=︒，∴AF == （3）解：过点F 作FH BC ⊥于H ，如图3所示：∵ABC 是等腰直角三角形，90ACB AC BC ∠=︒=，，∴45BAC ABC ∠=∠=︒，∵15BAD ∠=︒，∴451530CAE ∠=︒−︒=︒，∴30ACE CAE ∠=∠=︒，∴==AE CE CF ，同（1）得：()SAS ACE BCF ≌，∴30BF AE ACE BCF =∠=∠=︒，，∴CF BF =，∴30BCF CBF ∠=∠=︒，∵FC FB FH BC =⊥，，∴12CH BH BC ===，32FH ==，23CF BF FH ===，∵60903060CED CAE ACE ECD ∠=∠+∠=︒∠=︒−︒=︒，，∴ECD 是等边三角形，∴3EC CF CD ===，∴DEF ECD CDF ECF S S S S =+−21313333222=+⨯⨯−⨯⨯=．【点评】本题属于三角形综合题，考查了等腰直角三角形的性质，等边三角形的判定和性质，含30°角的直角三角形的性质，全等三角形的判定和性质，等腰三角形的性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．15．(1)AEFS =；AC BD =+，证明见解析；(3)DP FQ +【分析】（1）过点F 作FG AC ^于点G ，在Rt EFG △中利用勾股定理求得GF 的长，在等腰直角三角形AFG 中即可求得AG 的长，从而可得答案；（2）过点E 作EH AC ⊥交AB 于点H ，过点H 作HM BC ⊥于点M ，通过证明HEF DBF ≌，利用全等三角形的性质与等腰直角三角形的性质即可得出结论；（3）过点F 作FM AC ⊥于点M ，延长FM 至F '使F M FM '=，则F '与F 关于AC 对称，过点F '作F N BC '⊥，交BC 的延长线于点N ，证明APF CQF ≌，利用轴对称解决路径最短问题即可求得结论．【解析】（1）解：过点F 作FG AC ^于点G ，如图，∵90,ACB AC BC ∠=︒=，∴45A ABC ∠=∠=︒，∵90,30ECD EDC ∠=︒∠=︒，∴60DEG ∠=︒．∵,6FG AC EF ⊥=， ∴132EG EF ==，∴FG ==∵,45FG AC A ⊥∠=︒，∴AG FG ==∴3AE AG EG =−=．∴)11322AEF S AE FG ==⨯=．（2）解：过点E 作EH AC ⊥交AB 于点H ，过点H 作HM BC ⊥于点M ，如图，∵,45EH AC A ⊥∠=︒，∴,AE EH AH ==．∵BD AE =，∴EH BD =．∵,EH AC DC AC ⊥⊥，∴HE CD ∥，∴HEF D ∠=∠．在HEF 和DBF 中，HEF D HFE BFD EH DB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()AAS HEF DBF ≌． ∴12HF BF BH ==．∵90HEC ACB HMC ∠=∠=∠=︒，则90EHM ∠=︒，∴HM AC ∥，而HE CD ∥，∴由平行线间的距离处处相等可得：,CM HE HM CE ==，∵,45HM BC ABC ⊥∠=︒，∴EC HM ==，∴12AF AH HF BH =++． ∴2AE BH =，即：AE AE CE AE AC =++=+． ∴AC BD =+．（3）解：∵AB = F 是线段AB 的中点，90ACB ∠=︒，∴4,45,AF FB FC AC BC A ABC CF AB =====∠=∠=︒⊥．∴45FCQ A ∠=∠=︒．在APF 和CQF △中，AP CQ A FCQ AF FC =⎧⎪∠=∠⎨⎪=⎩，∴APF CQF ≌．∴PF FQ =． ∴DP FQ DP PF +=+．过点F 作FN AC ⊥于点M ，延长FM 至F '使F M FM '=，则F '与F 关于AC 对称，连接DF '交AC 于点P ，如图，则此时DP FP DF '+=，取得最小值，过点F '作F N BC '⊥，交BC 的延长线于点N ，∵90,,45AFC FM AC A ∠=︒⊥∠=︒， ∴112,222AM MC AC FM AC =====． ∴2F M FM '==．。

【常考压轴题】勾股定理常考压轴题汇总—2023-2024学年八年级数学下册(人教版)(解析版)

勾股定理常考压轴题汇总一．选择题（共23小题）1．我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成一个大正方形．如图，直角三角形的直角边长为a、b，斜边长为c．若b﹣a＝2，c＝10，则a+b的值为（）A．12B．14C．16D．18【答案】B【解答】解：由图可得：a2+b2＝c2，∴且a、b均大于0，解得，∴a+b＝6+8＝14，故选：B．2．如图，长方体的长为3，宽为2，高为4，一只蚂蚁从点A出发，沿长方体表面到点B处吃食物，那么它爬行最短路程是（）A．B．C．D．【答案】B【解答】解：第一种情况：把我们所看到的前面和上面组成一个平面，则这个长方形的长和宽分别是6和3，则所走的最短线段是＝3；第二种情况：把我们看到的左面与上面组成一个长方形，则这个长方形的长和宽分别是5和4，所以走的最短线段是＝；第三种情况：把我们所看到的前面和右面组成一个长方形，则这个长方形的长和宽分别是2，所以走的最短线段是＝；三种情况比较而言，第二种情况最短．所以它需要爬行的最短路线的长是，故选：B．3．如图，以Rt△ABC的三条边作三个正三角形，则S1、S2、S3、S4的关系为（）A．S1+S2+S3＝S4B．S1+S2＝S3+S4C．S1+S3＝S2+S4D．不能确定【答案】C【解答】解：如图，设Rt△ABC的三条边AB＝c，AC＝b，BC＝a，∵△ACG，△BCH，△ABF是等边三角形，∴S1＝S△ACG﹣S5＝b2﹣S5，S3＝S△BCH﹣S6＝a2﹣S6，∴S1+S3＝（a2+b2）﹣S5﹣S6，∵S2+S4＝S△ABF﹣S5﹣S6＝c2﹣S5﹣S6，∵c2＝a2+b2，∴S1+S3＝S2+S4，故选：C．4．如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边作三个正方形，点G落在HI 上，若AC+BC＝6，空白部分面积为10.5，则AB的长为（）A．3B．C．2D．【答案】B【解答】解：∵四边形ABGF是正方形，∴∠F AB＝∠AFG＝∠ACB＝90°，∴∠F AC+∠BAC＝∠F AC+∠ABC＝90°，∴∠F AC＝∠ABC，在△F AM与△ABN中，，∴△F AM≌△ABN（ASA），∴S△F AM＝S△ABN，∴S△ABC＝S四边形FNCM，∵在△ABC中，∠ACB＝90°，∴AC2+BC2＝AB2，∵AC+BC＝6，∴（AC+BC）2＝AC2+BC2+2AC•BC＝36，∴AB2+2AC•BC＝36，∵AB2﹣2S△ABC＝10.5，∴AB2﹣AC•BC＝10.5，∴3AB2＝57，解得AB＝或﹣（负值舍去）．故选：B．5．已知，如图长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．3cm2B．4cm2C．6cm2D．12cm2【答案】C【解答】解：将此长方形折叠，使点B与点D重合，∴BE＝ED．∵AD＝9cm＝AE+DE＝AE+BE．∴BE＝9﹣AE，根据勾股定理可知AB2+AE2＝BE2．解得AE＝4．∴△ABE的面积为3×4÷2＝6．故选：C．6．如图，阴影部分表示以Rt△ABC的各边为直径向上作三个半圆所组成的两个新月形，面积分别记作S1和S2．若S1+S2＝7，AC＝3，则BC长是（）A．3.5B．C．4D．5【答案】B【解答】解：以AC为直径的半圆的面积＝×π×＝π，同理：以BC为直径的半圆的面积＝π，以AB为直径的半圆的面积＝π，∴S1+S2＝π+π+△ABC的面积﹣π，∵∠ACB＝90°，∴AC2+BC2＝AB2，∴S1+S2＝△ABC的面积＝AC•BC＝7，∵AC＝3，∴BC＝．故选：B．7．如图，在长方体ABCD﹣EFGH盒子中，已知AB＝4cm，BC＝3cm，CG＝5cm，长为10cm 的细直木棒IJ恰好从小孔G I与底面ABCD接触，当木棒的端点Ⅰ在长方形ABCD内及边界运动时，GJ长度的最小值为（）A．（10﹣5）cm B．3cm C．（10﹣4）cm D．5cm【答案】A【解答】解：当GI最大时，GJ最小，当I运动到点A时，GI最大，此时GI＝cm，而AC2＝AB2+BC2＝42+32＝25，∴GI＝＝＝5（cm），∴GJ长度的最小值为（10﹣5）cm．故选：A．8．勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入长方形内得到的，∠BAC＝90°，AB＝6，BC＝10，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为（）A．420B．440C．430D．410【答案】B【解答】解：如图，延长AB交KL于P，延长AC交LM于Q，由题意得，∠BAC＝∠BPF＝∠FBC＝90°，BC＝BF，∴∠ABC+∠ACB＝90°＝∠PBF+∠ABC，∴∠ACB＝∠PBF，∴△ABC≌△PFB（AAS），同理可证△ABC≌△QCG（AAS），∴PB＝AC＝8，CQ＝AB＝6，∵图2是由图1放入长方形内得到，∴IP＝8+6+8＝22，DQ＝6+8+6＝20，∴长方形KLMJ的面积＝22×20＝440．故选：B．9．国庆假期间，妍妍与同学去玩寻宝游戏，按照藏宝图，她从门口A处出发先往东走9km，又往北走3km，遇到障碍后又往西走7km，再向北走2km，再往东走了4km，发现走错了之后又往北走1km，最后再往西走了1km，就找到了宝藏，则门口A到藏宝点B的直线距离是（）A．3km B．10km C．6km D．km【答案】D【解答】解：过点B作BC⊥AC，垂足为C．观察图形可知AC＝9﹣7+4﹣1＝5（km），BC＝3+2+1＝6（km），在Rt△ACB中，AB＝（km）．答：门口A到藏宝点B的直线距离是km，故选：D．10．如图，Rt△ABC中，∠ACB＝90°，CD⊥AB，AB＝9，BC＝6，则BD的长为（）A．3B．4C．5D．6【答案】B【解答】解：∵∠ACB＝90°，AB＝9，BC＝6，∴，∵，∴AC•BC＝AB•CD，，，∵CD⊥AB，∴∠CDB＝90°，∴，故选：B．11路，居民走新路比走拐角近（）A．2m B．3m C．3.5m D．4m【答案】D【解答】解：根据勾股定理求得：AB＝＝10（m），∴AC+BC﹣AB＝6+8﹣10＝4（m），故选：D．12．如图，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC＝12，BC＝7，将四个直角三角形中边长为12的直角边分别向外延长一倍，得到如图所示的“数学风车”，则这个风车的外围周长是（）A．148B．100C．196D．144【答案】A【解答】解：设将CA延长到点D，连接BD，根据题意，得CD＝12×2＝24，BC＝7，∵∠BCD＝90°，∴BC2+CD2＝BD2，即72+242＝BD2，∴BD＝25，∴AD+BD＝12+25＝37，∴这个风车的外围周长是37×4＝148．故选：A．13．如图，四边形ABCD中，AD⊥CD于点D，BC＝2，AD＝8，CD＝6，点E是AB的中点，连接DE，则DE的最大值是（）A．5B．C．6D．【答案】C【解答】解：如图，连接AC，取AC的中点为M，连接DM、EM，∵AD⊥CD，∴∠ADC＝90°，∵AD＝8，CD＝6，∴AC＝，∵M是AC的中点，∴DM＝AC＝5，∵M是AC的中点，E是AB的中点，∴EM是△ABC的中位线，∵BC＝2，∴EM＝BC＝1，∵DE≤DM+EM（当且仅当点M在线段DE上时，等号成立），∴DE≤6，∴DE的最大值为6．故选：C．14．如图，长为8cm的橡皮筋放置在数轴上，固定两端A和B，然后把中点C垂直向上拉升3cm到D点，则橡皮筋被拉长了（）A．2cm B．3cm C．4cm D．1cm【答案】A【解答】解：∵点C为线段AB的中点，∴AC＝AB＝4cm，在Rt△ACD中，CD＝3cm；根据勾股定理，得：AD＝＝5（cm）；∵CD⊥AB，∴∠DCA＝∠DCB＝90°，在△ADC和△BDC中，，∴△ADC≌△BDC（SAS），∴AD＝BD＝5cm，∴AD+BD﹣AB＝2AD﹣AB＝10﹣8＝2（cm）；∴橡皮筋被拉长了2cm．故选：A．15．如图的数轴上，点A，C对应的实数分别为1，3，线段AB⊥AC于点A，且AB长为1个单位长度，若以点C为圆心，BC长为半径的弧交数轴于0和1之间的点P，则点P表示的实数为（）A．B．C．D．【答案】A【解答】解：由题意可得∠90°，AB＝1，AC＝3﹣1＝2，则CB＝＝，那么点P表示的实数为3﹣，故选：A．16．“四千年来，数学的道理还是相通的”．运用祖冲之的出入相补原理也可证明勾股定理．若图中空白部分的面积是11，整个图形（连同空白部分）的面积是25，则大正方形的边长是（）A．B．C．D．【答案】D【解答】解：如下图，设图中直角三角形的两条直角边长分别为a、b，斜边为c，∵图中空白部分的面积是11，整个图形（连同空白部分）的面积是25，∴可有，解得c2＝18，解得或（不合题意，舍去），∴大正方形的边长是．故选：D．17．如图所示的一段楼梯，高BC是3米，斜边AB长是5米，现打算在楼梯上铺地毯，至少需要地毯的长度为（）A．5米B．6米C．7米D．8米【答案】C【解答】解：∵△ABC是直角三角形，BC＝3m，AB＝5m∴AC＝＝4（m），∴如果在楼梯上铺地毯，那么至少需要地毯为AC+BC＝7米，故选：C．18．勾股定理是人类早期发现并证明的重要数学定理之一，是数形结合的重要细带．数学家欧几里得利用如图验证了勾股定理．以直角三角形ABC的三条边为边长向外作正方形ACKJ，正方形ABFE，正方形BCIH，连接AH．CF，具中正方形BCIH面积为1，正方形ABFE面积为5，则以CF为边长的正方形面积为（）A．4B．5C．6D．10【答案】D【解答】解：过点C作CM⊥EF于点M，交AB于点N，∵正方形ABFE面积为5，正方形BCIH面积为1，∴CN⊥AB，BC＝1，AB＝MN＝，BN＝FN，∵△ABC是直角三角形，∠ACB＝90°，∴AC＝＝＝2，∴，即＝CN，∴CN＝，∴BN＝FM＝＝＝，∴CM＝CN+MN＝＝，∴CF＝10，∴以CF为边长的正方形面积为10．故选：D．19．如图，Rt△ABC中，∠C＝90°．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN．四块阴影部分的面积如图所示分别记为S、S1、S2、S3，若S＝10，则S1+S2+S3等于（）A．10B．15C．20D．30【答案】C【解答】解：如图，过E作BC的垂线交ED于D，连接EM．在△ACB和△BDE中，∠ACB＝∠BDE＝90°，∠CAB＝∠EBD，AB＝BD，∴△ACB≌△BND（AAS），同理，Rt△GDE≌Rt△HCB，∴GE＝HB，∠EGD＝∠BHC，∴FG＝EH，∴DE＝BC＝CM，∵DE∥CM，∴四边形DCME是平行四边形，∵∠DCM＝90°，∴四边形DCME是矩形，∴∠EMC＝90°，∴E、M、N三点共线，∵∠P＝∠EMH＝90°，∠PGF＝∠DGE＝∠BHC＝∠EHM，∴△PGF≌△MHE（AAS），∵图中S1＝S Rt△EMH，S△BHC＝S△EGD，∴S1+S3＝S Rt△ABC．S2＝S△ABC，∴S1+S2+S3＝Rt△ABC的面积×2＝20．故选：C．20．如图，在Rt△ABC中，∠C＝90°，分别以AB、AC、BC为直径向外作半圆，它们的面积分别记作S1、S2、S3，若S1＝25，S3＝16，则S2为（）A．9B．11C．32D．41【答案】A【解答】解：在Rt△ABC中，∠C＝90°，∴AB2＝AC2+BC2．∵S1＝（AB）2π＝AB2＝25，∴AB2＝25×．同理BC2＝16×．∴AC2＝AB2﹣BC2＝25×﹣16×＝9×．∴S1＝（AC）2π＝AC2＝×9×＝9．故选：A．21．如图，在Rt△ABC中，∠ACB＝90°，分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，记四块阴影部分的面积分别为S1、S2、S3、S4．若已知S△ABC＝S，则下列结论：①S4＝S；②S2＝S；③S1+S3＝S2；④S1+S2+S3+S4＝2.5S．其中正确的结论是（）A．①②③B．①②④C．①③④D．②③④【答案】A【解答】解：由题意有Rt△EBD≌Rt△ABC，∴S4＝S；故①正确；过F作AM的垂线交AM于N，由题意，得Rt△ANF≌Rt△ABC，Rt△NFK≌Rt△CAT，所以S2＝S，故②正确；连接FP，FQ，由题意，可得△AQF≌△ACB，则F，P，Q三点共线，由Rt△NFK≌Rt△CAT可得Rt△FPT≌Rt△EMK，∴S3＝S△FPT，可得Rt△AQF≌Rt△ACB，∴S1+S3＝S Rt△AQF＝S，故③正确；S1+S2+S3+S4＝（S1+S3）+S2+S4＝S Rt△ABC+S Rt△ABC+S Rt△ABC＝S Rt△ABC×3＝3S，故④不正确．故选：A．22．如图，有一个水池，水面是一边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面，这根芦苇的长度为（）尺．A．10B．12C．13D．14【答案】C【解答】解：设水深为x尺，则芦苇长为（x+1）尺，根据勾股定理得：x2+（）2＝（x+1）2，解得：x＝12，芦苇的长度＝x+1＝12+1＝13（尺），答：芦苇长13尺．故选：C．23．将四个全等的直角三角形作为叶片按图1摆放成一个风车形状，形成正方形ABCD和正方形EFGH．现将四个直角三角形的较长直角边分别向外延长，且A′E＝ME．B′F ＝NF，C′G＝PG，D′H＝HQ2所示的“新型数学风车”的四个叶片，即△A′EF，△B′FG，△C′CH．△D′HE．若FM平分∠BFE，正方形ABCD和正方形EFGH 的边长比为1：5．若”新型数学风车”的四个叶片面积和是m，则正方形EFCH的面积是（）A．B．C．3m D．【答案】B【解答】解：∵将四个全等的直角三角形作为叶片按图1摆放成一个风车形状，形成正方形ABCD和正方形EFCH．正方形ABCD和正方形EFGH的边长比为1：5．∴设正方形ABCD的边长为a，则正方形EFGH的边长为5a，设AE＝BF＝CG＝DH＝x，在△BEF中，BE2+BF2＝EF2，即（x+a）2+x2＝（5a）2，x2+ax﹣12a2＝0，（x+4a）（x﹣3a）＝0，x＝﹣4a（舍去）或x＝3a，∴BE＝4a，BF＝3a，EF＝5a，∵FM平分∠BFE，∴△EMF边EF上的高为BM，则S△BMF+S△MBF＝S△BEF，即，∴，∴BM＝，∵A'E＝ME＝BE﹣BM＝4a﹣a，若”新型数学风车”的四个叶片面积和是m，∴S△EMF＝S△EF A'＝m，∴，∴a m，∴a＝∴EF＝5a＝，∴S正方形EFCH＝EF＝，故选：B．二．填空题（共14小题）24．如图①，四个全等的直角三角形与一个小正方形，恰好拼成一个大正方形，这个图形是由我国汉代数学家赵爽在为《周髀算经》作注时给出的，人们称它为“赵爽弦图”．如果图①中的直角三角形的长直角边为7cm，短直角边为3cm，连结图②中四条线段得到如图③的新图案，则图③中阴影部分的周长为cm．【答案】32．【解答】解：由题意得：BD＝7cm，AB＝CD＝3cm，∴BC＝7﹣3＝4（cm），由勾股定理得：AC＝＝5（cm），∴阴影的周长＝4（AB+AC）＝4×（3+5）＝32（cm）．故答案为：32．25．如图，在△ABC中，已知：∠ACB＝90°，AB＝10cm，AC＝6cm，动点P从点B出发，沿射线BC以1cm/s的速度运动，设运动的时间为t秒，连接P A，当△ABP为等腰三角形时，t的值为．【答案】16或10或．【解答】解：在△ABC中，∠ACB＝90°，由勾股定理得：BC＝cm，∵△ABP为等腰三角形，当AB＝AP时，则BP＝2BC＝16cm，即t＝16；当BA＝BP＝10cm时，则t＝10；当P A＝PB时，如图：设BP＝P A＝x cm，则PC＝（8﹣x）cm，在Rt△ACP中，由勾股定理得：PC2+AC2＝AP2，∴（8﹣x）2+62＝x2，解得x＝，∴t＝．综上所述：t的值为16或10或．故答案为：16或10或．26．如图，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的“勾股分割点”．已知点M，N是线段AB 的“勾股分割点”，若AM＝4，MN＝5，则斜边BN的长为．【答案】．【解答】解：当BN∵点M，N是线段AB的勾股分割点，∴BN＝＝＝，故答案为：．27．对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示“垂美”四边形ABCD，对角线AC，BD交于点O，若AB＝6，CD＝10，则AD2+BC2＝．【答案】136．【解答】解：∵BD⊥AC，∴∠COB＝∠AOB＝∠AOD＝∠COD＝90°，∴BO2+CO2＝CB2，OB2+OA2＝AB2＝36，OA2+OD2＝AD2，OC2+OD2＝CD2＝100，∴BO2+CO2+OA2+OB2＝36+100，∴AD2+CB2＝BO2+CO2+OA2+OB2＝136；故答案为：136．28．如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（30，0）（0，12），点D是OA的中点，点P在BC上运动，当△ODP是腰长为15的等腰三角形时，点P 的坐标为．【答案】（9，12）或（6，12）或（24，12）．【解答】解：由题意，当△是腰长为15的等腰三角形时，有三种情况：（1）如答图①所示，PD＝OD＝15，点P在点D的左侧．过点P作PE⊥x轴于点E，则PE＝12．在Rt△PDE中，由勾股定理得：DE＝＝＝9，∴OE＝OD﹣DE＝15﹣9＝6，∴此时点P坐标为（6，12）；（2）如答图②所示，OP＝OD＝15．过点P作PE⊥x轴于点E，则PE＝4．在Rt△POE中，由勾股定理得：OE＝＝＝9，∴此时点P坐标为（9，12）；（3）如答图③所示，PD＝OD＝5，点P在点D的右侧．过点P作PE⊥x轴于点E，则PE＝4．在Rt△PDE中，由勾股定理得：DE＝＝＝9，∴OE＝OD+DE＝15+9＝24，∴此时点P坐标为（24，12）．综上所述，点P的坐标为：（9，12）或（6，12）或（24，12）；故答案为：（9，12）或（6，12）或（24，12）．29．《勾股》中记载了这样一个问题：“今有开门去阃（kǔn）一尺不合2寸，问门广几何？”意思是：如图推开两扇门（AD和BC），门边沿D，C两点到门槛AB的距离是1尺（1尺＝10寸），两扇门的间隙CD为2寸，则门槛AB长为寸．【答案】101．【解答】解：设OA＝OB＝AD＝BC＝r寸，如图，过D作DE⊥AB于点E，则DE＝10寸，OE＝CD＝1（寸），AE＝（r﹣1）寸，在Rt△ADE中，由勾股定理得：AE2+DE2＝AD2，即（r﹣1）2+102＝r2，解得：r＝50.5，∴2r＝101，即门槛AB长为101寸，故答案为：101．30．如图，在某次军事演习中，舰艇1号在指挥中心（O处）北偏西30°的A处，舰艇2号在指挥中心南偏东60°的B处，并且OA＝OB．接到行动指令后，舰艇1号向正东方向以60海里/小时的速度前进，舰艇2号沿北偏东60°的方向以m海里/小时的速度前进．1.5小时后，指挥中心观测到两舰艇分别到达点E，F处，若∠EOF＝75°，EF＝210海里，则m的值为．【答案】80．【解答】解：延长AE、BF相交于点C，∵∠AOB＝30°+90°+30°＝150°，∠EOF＝75°，∴∠EOF＝∠AOB，又∵OA＝OB，∠OAC+∠OBC＝（90°﹣30°）+（60°+60°）＝180°，延长FB至D，使BD＝AE，连接OD，∵∠OBD＝∠OBC，∴．∠OBD＝∠A，∴△OBD≌△OAE（SAS），∴OD＝OE，∠BOD＝∠AOE，∵∠EOF＝∠AOB＝∠EOD，∴．∠EOF＝∠DOF，又∵OF＝OF，∴△EOF≌△DOF（SAS），∴EF＝AE+BF，即EF＝1.5×（60+m）＝210．解得m＝80．故答案为：80．31．如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD．连结EG并延长交BC于点M．若AB＝5，EF＝1，则GM的长为．【答案】．【解答】解：由图可知∠AED＝90°，AB＝5，EF＝1，∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，故AE＝BF＝GC＝DH，设DE＝x，则在Rt△AED中，AD＝AB＝5，AE＝1+x，根据勾股定理，得AD2＝DE2+AE2，即52＝x2+（1+x）2，解得：x1＝3，x2＝﹣4（舍去）．过点M作MN⊥FB于点N，如图所示．∵四边形EFGH为正方形，EG为对角线，∴△EFG为等腰直角三角形，∴∠EGF＝∠NGM＝45°，故△GNM为等腰直角三角形．设GN＝NM＝a，则NB＝GB﹣GN＝3﹣a，∵MN∥AF，∴△BMN∽△BAF，∴＝，将MN＝a，AF＝3，BN＝3﹣a，BF＝4代入，得＝，解得a＝，∴MN＝GN＝，在Rt△MGN中，由勾股定理，得GM＝＝＝．故答案为：．32．如图，铁路上A、D两点相距25千米，B，C为两村庄，AB⊥AD于A，CD⊥AD于D，已知AB＝15km，CD＝10km，现在要在铁路AD上建一个土特产品收购站P，使得B、C 两村到P站的距离相等，则P站应建在距点A千米．【答案】10．【解答】解：设AP＝x千米，则DP＝（25﹣x）千米，∵B、C两村到P站的距离相等，∴BP＝PC．在Rt△APB中，由勾股定理得BP2＝AB2+AP2，在Rt△DPC中，由勾股定理得PC2＝CD2+PD2，∴AB2+AP2＝CD2+PD2，又∵AB＝15km，CD＝10km，∴152+x2＝102+（25﹣x）2，∴x＝10．故答案为：10．33．如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为cm（杯壁厚度不计）．【答案】见试题解答内容【解答】解：如图：将杯子侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，A′B＝＝＝20（cm）．故答案为20．34．如图，在△ABC中，AB＝AC＝10，BC＝12，AD＝8，AD⊥BC．若P、Q分别是AD和AC上的动点，则PC+PQ的最小值是．【答案】．【解答】解：如图，连接BP，在△ABC中，AB＝AC＝10，BC＝12，AD＝8，∴BD＝DC，∴BP＝PC，∴PC+PQ＝BP+PQ＝BQ，∴当B，P，Q共线时，PC+PQ的值最小，∴当BQ⊥AC时，BQ令AQ'＝a，则CQ'＝10﹣a，∵BQ'⊥AC，∴AB2﹣AQ'2＝BC2﹣CQ'2，即102﹣a2＝122﹣（10﹣a）2，解得a＝，∴BQ'＝＝，∴PC+PQ的最小值为，故答案为：．35．如图，在△ABC中，∠ABC＝45°，AB＝，AC＝6，BC＞4，点E，F分别在BC，AC边上，且AF＝CE，则AE+BF的最小值为．【答案】2．【解答】解：过A点作AG∥BC，截取AG＝AC，连接FG，BG，过B作BR⊥AG，交AG的反向延长线于R，则∠RBC＝∠BRA＝90°，∴∠GAF＝∠ACE，在△AFG和△CEA中，，∴△AFG≌△CEA（SAS），∴GF＝AE，∴AE+BF的最小值，即为BG的长，∵∠ABC＝45°，∴∠RAB＝∠EBA＝45°，∵AB＝4，∴BR＝AR＝4，∵AC＝6，∴AG＝AC＝6，∴RG＝AR+AG＝4+6＝10，∴BG＝＝＝2，即AE+BF的最小值为2．故答案为：2．36．如图，在△ABC中，AB＝9cm，AC＝12cm，BC＝15cm，M是BC边上的动点，MD⊥AB，ME⊥AC，垂足分别是D、E，线段DE的最小值是cm．【答案】．【解答】解：∵在△ABC中，AB＝9cm，AC＝12cm，BC＝15cm，∴BC2＝AB2+AC2，∴∠A＝90°，∵MD⊥AB，ME⊥AC，∴∠A＝∠ADM＝∠AEM＝90°，∴四边形ADME是矩形，∴DE＝AM，当AM⊥BC时，AM的长最短，根据三角形的面积公式得：AB•AC＝BC•AM，∴9×12＝15AM，AM＝，即DE的最小值是cm．故答案为：．37．如图，Rt△ABC中，．点P为△ABC内一点，P A2+PC2＝AC2．当PB的长度最小时，△ACP的面积是．【答案】．【解答】解：如图所示，取AC中点O，连接PO，BO，∵P A2+PC2＝AC2，∴∠APC＝90°，∴，∵BP+OP≥OB，∴当B、P、O三点共线时BP+OP有最小值，即此时BP有最小值，∵∠ACB＝90°，∴，∴BP＝BO﹣OP＝2，∴BP＝PO，又∠ACB＝90°，∴PC＝BO＝2，∴PC＝PO＝CO，∴△OPC是等边三角形，∴∠PCO＝60°，∠P AC＝30°∴AP＝＝2，∴，故答案为：．三．解答题（共4小题）38．如图，∠AOB＝90°，OA＝9cm，OB＝3cm，一机器人在点B处看见一个小球从点A 出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿BC方向匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？【答案】见试题解答内容【解答】解：∵小球滚动的速度与机器人行走的速度相等，运动时间相等，∴BC＝CA．设AC为x，则OC＝9﹣x，由勾股定理得：OB2+OC2＝BC2，又∵OA＝9，OB＝3，∴32+（9﹣x）2＝x2，解方程得出x＝5．∴机器人行走的路程BC是5cm．39．如图，在Rt△ABC中，∠ACB＝90°，AB＝10cm，AC＝6cm，动点P从B出发沿射线BC以1cm/s的速度运动，设运动时间为t（s）．（1）求BC边的长．（2）当△ABP为等腰三角形时，求t的值．【答案】或10或16．【解答】解：在Rt△ABC中，∠ACB＝90°，AB＝10cm，AC＝6cm，∴BC＝，当AP＝BP时，如图1，则AP＝t，PC＝BC﹣BP＝8﹣t，在Rt△ACP中，AC2+CP2＝AP2，∴62+（8﹣t）2＝t2，解得t＝；当AB＝BP时，如图2，则BP＝t＝10；当AB＝AP时，如图3，则BP＝2BC；∴t＝2×8＝16，综上，t的值为或10或16．40．今年第6号台风“烟花”登陆我国沿海地区，风力强，累计降雨量大，影响范围大，有极强的破坏力．如图，台风“烟花”中心沿东西方向AB由A向B移动，已知点C为一海港，且点C与直线AB上的两点A、B的距离分别为AC＝300km，BC＝400km，又AB ＝500km，经测量，距离台风中心260km及以内的地区会受到影响．（1）海港C受台风影响吗？为什么？（2）若台风中心的移动速度为28千米/时，则台风影响该海港持续的时间有多长？【答案】（1）海港C受台风影响，理由见解答过程；（2）台风影响该海港持续的时间为小时．【解答】解：（1）海港C受台风影响，理由：∵AC＝300km，BC＝400km，AB＝500km，∴AC2+BC2＝AB2，∴△ABC是直角三角形，∠ACB＝90°；过点C作CD⊥AB于D，∵△ABC是直角三角形，∴AC×BC＝CD×AB，∴300×400＝500×CD，∴CD＝240（km），∵以台风中心为圆心周围260km以内为受影响区域，∴海港C受台风影响；（2）当EC＝260km，FC＝260km时，正好影响C港口，∵ED＝（km），∴EF＝2ED＝200km，∵台风的速度为28千米/小时，∴200÷28＝（小时）．答：台风影响该海港持续的时间为小时．41．请阅读下列材料：已知：如图（1）在Rt△ABC中，∠BAC＝90°，AB＝AC，点D、E分别为线段BC上两动点，若∠DAE＝45°．探究线段BD、DE、EC三条线段之间的数量关系．小明的思路是：把△AEC绕点A顺时针旋转90°，得到△ABE′，连接E′D，使问题得到解决．请你参考小明的思路探究并解决下列问题：（1）猜想BD、DE、EC三条线段之间存在的数量关系式，直接写出你的猜想；（2）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图（2），其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明；（3）已知：如图（3），等边三角形ABC中，点D、E在边AB上，且∠DCE＝30°，请你找出一个条件，使线段DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数．【答案】见试题解答内容【解答】解：（1）DE2＝BD2+EC2；（2）关系式DE2＝BD2+EC2仍然成立．证明：将△ADB沿直线AD对折，得△AFD，连FE∴△AFD≌△ABD，∴AF＝AB，FD＝DB，∠F AD＝∠BAD，∠AFD＝∠ABD，又∵AB＝AC，∴AF＝AC，∵∠F AE＝∠F AD+∠DAE＝∠F AD+45°，∠EAC＝∠BAC﹣∠BAE＝90°﹣（∠DAE﹣∠DAB）＝45°+∠DAB，∴∠F AE＝∠EAC，又∵AE＝AE，∴△AFE≌△ACE，∴FE＝EC，∠AFE＝∠ACE＝45°，∠AFD＝∠ABD＝180°﹣∠ABC＝135°∴∠DFE＝∠AFD﹣∠AFE＝135°﹣45°＝90°，∴在Rt△DFE中，DF2+FE2＝DE2，即DE2＝BD2+EC2；解法二：将△EAC绕点A顺时针旋转90°得到△TAB．连接DT．∴∠ABT＝∠C＝45°，AT＝AE，∠TAE＝90°，∵∠ABC＝45°，∴∠TBC＝∠TBD＝90°，∵∠DAE＝45°，∴∠DAT＝∠DAE，∵AD＝AD，∴△DAT≌△DAE（SAS），∴DT＝DE，∵DT2＝DB2+EC2，∴DE2＝BD2+EC2；（3）当AD＝BE时，线段DE、AD、EB能构成一个等腰三角形．如图，与（2）类似，以CE为一边，作∠ECF＝∠ECB，在CF上截取CF＝CB，可得△CFE≌△CBE，△DCF≌△DCA．∴AD＝DF，EF＝BE．∴∠DFE＝∠1+∠2＝∠A+∠B＝120°．若使△DFE为等腰三角形，只需DF＝EF，即AD＝BE，∴当AD＝BE时，线段DE、AD、EB能构成一个等腰三角形，且顶角∠DFE为120°．。

填空题压轴题-2022-2023学年八年级数学下册期末解答压轴题必刷专题训练(华师大版)(解析版)

填空题压轴题【答案】145【详解】解：如图以DAB V 和FAQ △中：DA =∴()SAS DAB FAQ V V ≌，【答案】①②③④⑤⑥【详解】解：如图，过点∵四边形ABCD 是正方形，∴A C D ÐÐÐ==∴AEB EBC ÐÐ=∵FEB EBC ÐÐ=∴AEB BEF ÐÐ=5．如图，已知在△ABC中，AB 作平行四边形MCNB，连接MN【答案】24 5【详解】如图，设MN、BC交于点6．如图，在平面直角坐标系xoyAB AD为边作使2DP AP=，以,【答案】49【详解】解：∵四边形ABCD是平行四边形，∴AD∥BC，AB//CD∴∠E=∠DAE，又∵AE平分∠BAD，【答案】①④⑤【详解】解：∵四边形ABCD ∴AB CD =，AD BC =．设点P 到AB ，BC ，CD ，DA【答案】()453，【详解】解：从正方形的观点考虑，右下角对应的横坐标为1时，共有右下角对应的横坐标为2时，共有右下角对应的横坐标为3时，共有右下角对应的横坐标为4时，共有【答案】10 21【详解】解：设1A，2A，3A【答案】（10112-，10112）【详解】解：∵过点（1，0）作∴1A （1，2），把2y =代入y x =-得2x =-，即把2x =-代入2y x =得4y =-，即同理可得4A （4，4-），5A （32），…直线21y kx k =+-与直线(1)2y k x k =+++那么，COD ABDC S S =V 四边形【答案】22n+【详解】解：对于直线y=x+1∵A0B1∥x轴，∴B1的纵坐标为将y=1代入1122y x=+中得：∴A0B1=1=20，∵A1B1∥y轴，∴A1的横坐标为【答案】404432æöç÷èø【详解】解：∵直线1l ：112y x =-+与直线2l ：332y x =-+与y 轴交于点B ，∴AB 2\=，112BC AB ==，∵BC ⊥AB ，∴()1,3C -，∴四边形PECF 是矩形，∴PC=EF，∴PA=EF，故②正确；∵BD 是正方形ABCD 的对角线，∴∠ABD=∠BDC=∠DBC=45°，∵∠PFC=∠BCD=90°，∴PF∥BC，∴∠DPF=45°，∵∠DFP=90°，∴△FPD 是等腰直角三角形，故①正确；在△PAB 和△PCB 中，AB CB ABP CBP BP BP ìïÐÐíïî＝＝＝ , ∴△PAB≌△PCB，∴∠BAP=∠BCP，在矩形PECF 中，∠PFE=∠FPC=∠BCP，∴∠PFE=∠BAP．故④正确；∵点P 是正方形对角线BD 上任意一点，∴AD 不一定等于PD ，只有∠BAP=22.5°时，AD=PD ，故③错误，故答案为①②④．38．如图，在矩形ABCD 中，5AB =，12BC =，P 是矩形ABCD 内一点，沿PA 、PB 、PC 、PD 把这个矩形剪开，然后把两个阴影三角形拼成一个四边形，则这个四边形的面积为_________；这个四边形周长的最小值为________.【答案】 30 26【详解】如解图①，过点P 作PE AB ^于点E ，延长EP 交CD 于点F ，∵四边形ABCD 是矩形，∴90ABC BCD Ð=Ð=°，5CD AB ==.∴四边形EBCF 是矩形.∴EF BC =.又∵12BC =，故答案为：30，26.39．如图，在△ABC 中，Ð，90BAC Ð=°，点A 为(3P 、A 、C 为顶点的三角形和△全等，则P 点坐标为___________【答案】(6)2-，或(81)，或则90AOB AMP Ð=Ð=°，在AOB V 和V AMP 中，AOB OAB AB ÐìïÐíïî∴(AAS)AOB AMP V V ≌，∴3AM AO ==，2MP OB == ，∴此时点P 的坐标为(6)2-，；②如图，过点C 作CP AC ^，使CP AB =，则(HL)ABC CPA V V ≌．过P 作PF x ^轴于F ，过点C 作CE x ^轴于点E ，作CD y ^轴于点D ．∵90OBA OAB Ð+Ð=°，90EAC OAB Ð+Ð=°，∴OBA EAC Ð=Ð．又∵90BOA AEC Ð=Ð=°，AB AC =，∴(AAS)BOA AEC V V ≌，∴3OD CE OA ===，2AE OB ==，∴5CD OE ==．∵CD x ∥轴，∴DCA FAC Ð=Ð．∵45BCA PAC Ð=Ð=°，∴DCA BCA FAC PAC Ð-Ð=Ð-Ð，即DCB FAP Ð=Ð．又∵90CDB AFP Ð=Ð=°，CB AP =，∴(AAS)CDB AFP V V ≌，∴321PF BD OD OB ==-=-=，5AF CD ==,∴358OF OA AF =+=+=，∴此时点P 的坐标为(81)，；③如图，作CP AC ^，使CP AB =，连接BP ，则(SAS)ABC CPA V V ≌，∵90BAC PCA Ð=Ð=°，且CP AB = ，∴四边形ABPC 是矩形，∴90AB BP ABP =Ð=°，，即90ABO PBM Ð+Ð=°，过点P 作PM y ^轴，则90BPM PBM Ð+Ð=°，∴ABO BPM Ð=Ð，在△AOB 和△BMP 中，AOB BMP ABO BPM AB BP Ð=ÐìïÐ=Ðíï=î，∴()AOB BMP AAS V V ≌，∴3BM OA ==，2PM OB == ，∴此时点P 的坐标为(25)，；④当点P 与点B 重合时，点P 的坐标为(0)2，．综上可知，点P 的坐标为(6)2-，或(81)，或(25)，或(0)2，．。

中学数学八年级下册期末压轴题(含答案)

八年级下册期末压轴题一．填空题（共1小题）1．（2018春•西城区期末）在查阅勾股定理证明方法的过程中，小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法，并尝试按自己的理解将这种方法介绍给同学．（1）根据信息将以下小红的证明思路补充完整：①如图1，在△ABC中，∠ACB＝90°，四边形ADEC，四边形BCFG，四边形ABPQ都是正方形．延长QA交DE于点M，过点C作CN∥AM交DE的延长线于点N，可得四边形AMNC的形状是；②在图1中利用“等积变形”可得S正方形ADEC＝；③如图2，将图1中的四边形AMNC沿直线MQ向下平移MA的长度，得到四边形A′M′N′C′，即四边形QACC′；④设CC′交AB于点T，延长CC′交QP于点H，在图2中再次利用“等积变形”可得S四边形QACC'＝，则有S正方形ADEC＝；⑤同理可证S正方形BCFG＝S四边形HTBP，因此得到S正方形ADEC+S正方形BCFG＝S正方形ABPQ，进而证明了勾股定理．（2）小芳阅读完小红的证明思路后，对其中的第③步提出了疑问，请将以下小红对小芳的说明补充完整：图1中△≌△，则有＝AB＝AQ，由于平行四边形的对边相等，从而四边形AMNC沿直线MQ向下平移MA的长度，得到四边形QACC′．二．解答题（共42小题）2．（2020春•海淀区校级期末）已知△ABC中，∠BAC＝90°，AB＝AC，点M为BC的中点，点P为AB边上一动点，点N为线段BM上一动点，以点P为旋转中心，将△BPN逆时针旋转90°得到△DPE，且点B的对应点为D，点N的对应点为E．（1）当点N与点M重合，且点P不是AB的中点时．①依据题意补全图1；②证明：以A，M，E，D为顶点的四边形是矩形．（2）连接EM，若AB＝4，写出一个BN的值，使得EM＝EA成立，并证明．3．（2020春•海淀区校级期末）∠MON＝45°，点P在射线OM上，点A，B在射线ON上（点B与点O在点A的两侧），且AB＝1，以点P为旋转中心，将线段AB逆时针旋转90°，得到线段CD（点C与点A对应，点D与点B对应）．（1）如图，若OA＝1，OP＝，依题意补全图形；（2）若OP＝，当线段AB在射线ON上运动时，线段CD与射线OM有公共点，求OA的取值范围．（要写过程）4．（2019•都江堰市模拟）定义：若关于x的一元二次方程ax2+bx+c＝0（a≠0）的两个实数根为x1，x2（x1＜x2），分别以x1，x2为横坐标和纵坐标得到点M（x1，x2），则称点M为该一元二次方程的衍生点．（1）若方程为x2﹣2x＝0，写出该方程的衍生点M的坐标．（2）若关于x的一元二次方程x2﹣（2m+1）x+2m＝0（m＜0）的衍生点为M，过点M 向x轴和y轴作垂线，两条垂线与坐标轴恰好围成一个正方形，求m的值．（3）是否存在b，c，使得不论k（k≠0）为何值，关于x的方程x2+bx+c＝0的衍生点M 始终在直线y＝kx﹣2（k﹣2）的图象上，若有请直接写出b，c的值，若没有说明理由．5．（2020春•海淀区校级期末）如图，在正方形ABCD中，AB＝6，M是CD边上一动点（不与D点重合），点D与点E关于AM所在的直线对称，连接AE，ME，延长CB到点F，使得BF＝DM，连接EF，AF．（1）当DM＝2时，依题意补全图1；（2）在（1）的条件下，求线段EF的长；（3）当点M在CD边上运动时，能使△AEF为等腰三角形，请直接写出此时DM与AD 的数量关系．6．（2019春•朝阳区期末）对于平面直角坐标系xOy中的图形M和点P（点P在M内部或M上），给出如下定义：如果图形M上存在点Q，使得0≤PQ≤2，那么称点P为图形M 的和谐点．已知点A（﹣4，3），B（﹣4，﹣3），C（4，﹣3），D（4，3）．（1）在点P₁（﹣2，1），P2（﹣1，0），P3（3，3）中，矩形ABCD的和谐点是；（2）如果直线y＝上存在矩形ABCD的和谐点P，直接写出点P的横坐标t的取值范围；（3）如果直线y＝上存在矩形ABCD的和谐点E，F，使得线段EF上的所有点（含端点）都是矩形ABCD的和谐点，且EF，直接写出b的取值范围．7．（2017春•昌平区期末）（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D．①如果AD＝4，BD＝9，那么CD＝；②如果以CD的长为边长作一个正方形，其面积为S1，以BD，AD的长为邻边长作一个矩形，其面积为S2，则S1S2（填“＞”、“＝”或“＜”）．（2）基于上述思考，小泽进行了如下探究：①如图2，点C在线段AB上，正方形FGBC，ACDE和EDMN，其面积比为1：4：4，连接AF，AM，求证AF⊥AM；②如图3，点C在线段AB上，点D是线段CF的黄金分割点，正方形ACDE和矩形CBGF的面积相等，连接AF交ED于点M，连接BF交ED延长线于点N，当CF＝a时，直接写出线段MN的长为．8．（2018春•浉河区期末）如图1，点A（a，b）在平面直角坐标系xOy中，点A到坐标轴的垂线段AB，AC与坐标轴围成矩形OBAC，当这个矩形的一组邻边长的和与积相等时，点A称作“垂点”，矩形称作“垂点矩形”．（1）在点P（1，2），Q（2，﹣2），N（，﹣1）中，是“垂点”的点为；（2）点M（﹣4，m）是第三象限的“垂点”，直接写出m的值；（3）如果“垂点矩形”的面积是，且“垂点”位于第二象限，写出满足条件的“垂点”的坐标；（4）如图2，平面直角坐标系的原点O是正方形DEFG的对角线的交点，当正方形DEFG 的边上存在“垂点”时，GE的最小值为．9．（2018春•丰台区期末）如图，菱形ABCD中，∠BAD＝60°，过点D作DE⊥AD交对角线AC于点E，连接BE，取BE的中点F，连接DF．（1）请你根据题意补全图形；（2）请用等式表示线段DF、AE、BC之间的数量关系，并证明．10．（2018春•丰台区期末）在平面直角坐标系xOy中，M为直线l：x＝a上一点，N是直线l外一点，且直线MN与x轴不平行，若MN为某个矩形的对角线，且该矩形的边均与某条坐标轴垂直，则称该矩形为直线l的“伴随矩形”．如图为直线l的“伴随矩形”的示意图．（1）已知点A在直线l：x＝2上，点B的坐标为（3，﹣2）①若点A的纵坐标为0，则以AB为对角线的直线l的“伴随矩形”的面积是；②若以AB为对角线的直线l的“伴随矩形”是正方形，求直线AB的表达；（2）点P在直线l：x＝m上，且点P的纵坐标为4，若在以点（2，1），（﹣2，1），（﹣2，﹣1），（2，﹣1）为顶点的四边形上存在一点Q，使得以PQ为对角线的直线l的“伴随矩形”为正方形，直接写出m的取值范围．11．（2019春•海淀区期末）如图，在平面直角坐标系xOy中，直线y＝kx+7与直线y＝x﹣2交于点A（3，m）（1）求k，m的值；（2）已知点P（n，n），过点P作垂直于y轴的直线与直线y＝x﹣2交于点M，过点P 作垂直于x轴的直线与直线y＝kx+7交于点N（P与N不重合）．若PN≤2PM，结合图象，求n的取值范围．12．（2019春•海淀区期末）在Rt△ABC中，∠BAC＝90°，点O是△ABC所在平面内一点，连接OA，延长OA到点E，使得AE＝OA，连按OC，过点B作BD与OC平行，并使∠DBC＝∠OCB，且BD＝OC，连按DE．（1）如图一，当点O在Rt△ABC内部时，①按题意补全图形；②猜想DE与BC的数量关系，并证明．（2）若AB＝AC（如图二），且∠OCB＝30°，∠OBC＝15°，求∠AED的大小．13．（2017春•西城区期末）如图所示，在平面直角坐标系xOy中，B，C两点的坐标分别为B（4，0），C（4，4），CD⊥y轴于点D，直线l经过点D．（1）直接写出点D的坐标；（2）作CE⊥直线l于点E，将直线CE绕点C逆时针旋转45°，交直线l于点F，连接BF．①依题意补全图形；②通过观察、测量，同学们得到了关于直线BF与直线l的位置关系的猜想，请写出你的猜想；③通过思考、讨论，同学们形成了证明该猜想的几种思路：思路1：作CM⊥CF，交直线l于点M，可证△CBF≌△CDM，进而可以得出∠CFB＝45°，从而证明结论．思路2：作BN⊥CE，交直线CE于点N，可证△BCN≌△CDE，进而证明四边形BFEN 为矩形，从而证明结论．…请你参考上面的思路完成证明过程．（一种方法即可）解：（1）点D的坐标为，（2）①补全图形，②直线BF与直线l的位置关系是，③证明：14．（2017春•西城区期末）如图，在由边长都为1个单位长度的小正方形组成的6×6正方形网格中，点A，B，P都在格点上请画出以AB为边的格点四边形（四个顶点都在格点的四边形），要求同时满足以下条件：条件1：点P到四边形的两个顶点的距离相等；条件2：点P在四边形的内部或其边上；条件3：四边形至少一组对边平行．（1）在图①中画出符合条件的一个▱ABCD，使点P在所画四边形的内部；（2）在图②中画出符合条件的一个四边形ABCD，使点P在所画四边形的边上；（3）在图③中画出符合条件的一个四边形ABCD，使∠D＝90°，且∠A≠90°．15．（2017春•西城区期末）如图，在平面直角坐标系xOy中，动点A（a，0）在x轴的正半轴上，定点B（m，n）在第一象限内（m＜2≤a），在△OAB外作正方形ABCD和正方形OBEF，连接FD，点M为线段FD的中点，作BB1⊥x轴于点B1，作FF1⊥x轴于点F1．（1）填空：由≌△，及B（m，n）可得点F的坐标为，同理可得点D的坐标为；（说明：点F，点D的坐标用含m，n，a的式子表示）（2）直接利用（1）的结论解决下列问题：①当点A在x轴的正半轴上指定范围内运动时，点M总落在一个函数图象上，求该函数的解析式（不必写出自变量x的取值范围）；②当点A在x轴的正半轴上运动且满足2≤a≤8时，求点M所经过的路径的长．16．（2019春•西城区期末）四边形ABCD是正方形，AC是对角线，E是平面内一点，且CE＜BC，过点C作FC⊥CE，且CF＝CE．连接AE、AF，M是AF的中点，作射线DM 交AE于点N．（1）如图1，若点E，F分别在BC，CD边上．求证：①∠BAE＝∠DAF；②DN⊥AE；（2）如图2，若点E在四边形ABCD内，点F在直线BC的上方，求∠EAC与∠ADN 的和的度数．17．（2019春•西城区期末）如图1，在菱形ABCD中，对角线AC，BD相交于点O，AC＝4cm，BD＝2cm，E，F分别是AB，BC的中点，点P是对角线AC上的一个动点，设AP ＝xcm，PE＝y1cm，PF＝y2cm．小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：（1）画函数y1的图象①按表中自变量的值进行取点、画图、测量，得到了y1与x的几组对应值：x/cm00.51 1.52 2.53 3.54y1/cm 1.120.50.71 1.12 1.58 2.06 2.55 3.04②在图2所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数y1的图象；（2）画函数y2的图象，在同一坐标系中，画出函数y2的图象；（3）根据画出的函数y1的图象、函数y2的图象，解决问题①函数y1的最小值是；②函数y1的图象与函数y2的图象的交点表示的含义是；③若PE＝PC，AP的长约为cm18．（2019春•西城区期末）平面直角坐标系xOy中，对于点M和图形W，若图形W上存在一点N（点M，N可以重合），使得点M与点N关于一条经过原点的直线l对称，则称点M与图形W是“中心轴对称”．对于图形W1和图形W2，若图形W1和图形W2分别存在点M和点N（点M，N可以重合），使得点M与点N关于一条经过原点的直线l对称，则称图形W1和图形W2是“中心轴对称”的．特别地，对于点M和点N，若存在一条经过原点的直线l，使得点M与点N关于直线l对称，则称点M和点N是“中心轴对称”的．（1）如图1，在正方形ABCD中，点A（1，0），点C（2，1），①下列四个点P1（0，1），P2（2，2），P3（﹣，0），P4（﹣，﹣）中，与点A是“中心轴对称”的是；②点E在射线OB上，若点E与正方形ABCD是“中心轴对称”的，求点E的横坐标x E的取值范围；（2）四边形GHJK的四个顶点的坐标分别为G（﹣2，2），H（2，2），J（2，﹣2），K （﹣2，﹣2），一次函数y＝x+b图象与x轴交于点M，与y轴交于点N，若线段MN 与四边形GHJK是“中心轴对称”的，直接写出b的取值范围．19．（2019春•大兴区期末）有这样一个问题：探究函数y＝+1的图象与性质．小东根据学习函数的经验，对函数y＝+1的图象与性质进行了探究．下面是小东的探究过程，请补充完整：（1）函数y＝+1的自变量x的取值范围是；（2）如表是y与x的几组对应值．x…﹣3﹣2﹣112345…y…393m…求m的值；（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；（4）结合函数的图象，写出该函数的一条性质：．20．（2019春•大兴区期末）如图1，四边形ABCD是平行四边形，A，B是直线l上的两点，点B关于AD的对称点为M，连接CM交AD于F点．（1）若∠ABC＝90°，如图1，①依题意补全图形；②判断MF与FC的数量关系是；（2）如图2，当∠ABC＝135°时，AM，CD的延长线相交于点E，取ME的中点H，连结HF．用等式表示线段CE与AF的数量关系，并证明．21．（2019春•大兴区期末）在平面直角坐标系xOy中，记y与x的函数y＝a（x﹣m）2+n （m≠0，n≠0）的图象为图形G，已知图形G与y轴交于点A，当x＝m时，函数y＝a （x﹣m）2+n有最小（或最大）值n，点B的坐标为（m，n），点A、B关于原点O的对称点分别为C、D，若A、B、C、D中任何三点都不在一直线上，且对角线AC，BD的交点与原点O重合，则称四边形ABCD为图形G的伴随四边形，直线AB为图形G的伴随直线．（1）如图1，若函数y＝（x﹣2）2+1的图象记为图形G，求图形G的伴随直线的表达式；（2）如图2，若图形G的伴随直线的表达式是y＝x﹣3，且伴随四边形的面积为12，求y与x的函数y＝a（x﹣m）2+n（m＞0，n＜0）的表达式；（3）如图3，若图形G的伴随直线是y＝﹣2x+4，且伴随四边形ABCD是矩形，求点B 的坐标．22．（2019春•石景山区期末）正方形ABCD中，点P是直线AC上的一个动点，连接BP，将线段BP绕点B顺时针旋转90°得到线段BE，连接CE．（1）如图1，若点P在线段AC上，①直接写出∠ACE的度数为°；②求证：P A2+PC2＝2PB2；（2）如图2，若点P在CA的延长线上，P A＝1，PB＝，①依题意补全图2；②直接写出线段AC的长度为．23．（2020春•浦东新区期末）在平面直角坐标系xOy中，若P，Q为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．图1为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，2）．（1）如图2，点B的坐标为（b，0）．①若b＝﹣2，则点A，B的“相关矩形”的面积是；②若点A，B的“相关矩形”的面积是8，则b的值为．（2）如图3，点C在直线y＝﹣1上，若点A，C的“相关矩形”是正方形，求直线AC 的表达式；（3）如图4，等边△DEF的边DE在x轴上，顶点F在y轴的正半轴上，点D的坐标为（1，0）．点M的坐标为（m，2），若在△DEF的边上存在一点N，使得点M，N的“相关矩形”为正方形，请直接写出m的取值范围．24．（2016春•无锡期末）已知：如图1，在平面直角坐标中，A（12，0），B（6，6），点C 为线段AB的中点，点D与原点O关于点C对称．（1）利用直尺和圆规在图1中作出点D的位置（保留作图痕迹），判断四边形OBDA的形状，并说明理由；（2）在图1中，动点E从点O出发，以每秒1个单位的速度沿线段OA运动，到达点A 时停止；同时，动点F从点O出发，以每秒a个单位的速度沿OB→BD→DA运动，到达点A时停止．设运动的时间为t（秒）．①当t＝4时，直线EF恰好平分四边形OBDA的面积，求a的值；②当t＝5时，CE＝CF，请直接写出a的值．25．（2019春•东城区期末）有这样一个问题：探究函数y＝﹣3的图象与性质．小亮根据学习函数的经验，对y＝﹣3的图象与性质进行了探究下面是小亮的探究过程，请补充完整：（1）函数y＝3中自变量x的取值范围是（2）下表是y与x的几组对应值．x…﹣3﹣2﹣102345…y…﹣﹣﹣4﹣5﹣7m﹣1﹣2﹣﹣…求m的值；（1）在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；（2）根据画出的函数图象，发现下列特征：该函数的图象与直线x＝1越来越靠近而永不相交，该函数的图象还与直线越来越靠近而永不相交．26．（2019春•东城区期末）在正方形ABCD中，点E是射线AC上一点，点F是正方形ABCD 外角平分线CM上一点，且CF＝AE，连接BE，EF．（1）如图1，当E是线段AC的中点时，直接写出BE与EF的数量关系；（2）当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断（1）中的结论是否成立，并证明你的结论；（3）当点B，E，F在一条直线上时，求∠CBE的度数．（直接写出结果即可）27．（2019春•东城区期末）对于平面直角坐标系xOy中的点P和正方形给出如下定义：若正方形的对角线交于点O，四条边分别和坐标轴平行，我们称该正方形为原点正方形．当原点正方形上存在点Q，满足PQ≤1时，称点P为原点正方形的友好点．（1）当原点正方形边长为4时，①在点P1（0，0），P2（﹣1，1），P3（3，2）中，原点正方形的友好点是；②点P在直线y＝x的图象上，若点P为原点正方形的友好点，求点P横坐标的取值范围；（2）一次函数y＝﹣x+2的图象分别与x轴，y轴交于点A，B，若线段AB上存在原点正方形的友好点，直接写出原点正方形边长a的取值范围．28．（2019春•昌平区期末）如图，△ABC中，AB＝BC＝5cm，AC＝6cm，点P从顶点B出发，沿B→C→A以每秒1cm的速度匀速运动到A点，设运动时间为x秒，BP长度为ycm．某学习小组对函数y随自变量x的变化而变化的规律进行了探究．下面是他们的探究过程，请补充完整：（1）通过取点，画图，测量，得到了x（秒）与y（cm）的几组对应值：x01234567891011y0.0 1.0 2.0 3.0 4.0 4.5 4.14 4.5 5.0要求：补全表格中相关数值（保留一位小数）；（2）在平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当x约为时，BP＝CP．29．（2019春•昌平区期末）在矩形ABCD中，AB＝3，AD＝2，点E是射线DA上一点，连接EB，以点E为圆心EB长为半径画弧，交射线CB于点F，作射线FE与CD延长线交于点G．（1）如图1，若DE＝5，则∠DEG＝°；（2）若∠BEF＝60°，请在图2中补全图形，并求EG的长；（3）若以E，F，B，D为顶点的四边形是平行四边形，此时EG的长为．30．（2019春•昌平区期末）在平面直角坐标系中，过一点分别作x轴，y轴的垂线，如果由这点、原点及两个垂足为顶点的矩形的周长与面积相等，那么称这个点是平面直角坐标系中的“巧点”．例如，图1中过点P（4，4）分別作x轴，y轴的垂线，垂足为A，B，矩形OAPB的周长为16，面积也为16，周长与面积相等，所以点P是巧点．请根据以上材料回答下列问题：（1）已知点C（1，3），D（﹣4，﹣4），E（5，﹣），其中是平面直角坐标系中的巧点的是；（2）已知巧点M（m，10）（m＞0）在双曲线y＝（k为常数）上，求m，k的值；（3）已知点N为巧点，且在直线y＝x+3上，求所有满足条件的N点坐标．31．（2019春•延庆区期末）已知：在正方形ABCD中，点H在对角线BD上运动（不与B，D重合）连接AH，过H点作HP⊥AH于H交直线CD于点P，作HQ⊥BD于H交直线CD于点Q．（1）当点H在对角线BD上运动到图1位置时，则CQ与PD的数量关系是．（2）当H点运动到图2所示位置时①依据题意补全图形．②上述结论还成立吗？若成立，请证明．若不成立，请说明理由．（3）若正方形边长为，∠PHD＝30°，直接写出PC长．32．（2019春•延庆区期末）对于一次函数y＝kx+b（k≠0），我们称函数y[m]＝为它的m分函数（其中m为常数）．例如，y＝3x+2的4分函数为：当x≤4时，y[4]＝3x+2；当x＞4时，y[4]＝﹣3x﹣2．（1）如果y＝x+1的﹣1分函数为y[﹣1]，①当x＝4时，y[﹣1]；当y[﹣1]＝﹣3时，x＝．②求双曲线y＝与y[﹣1]的图象的交点坐标；（2）如果y＝﹣x+2的0分函数为y[0]，正比例函数y＝kx（k≠0）与y＝﹣x+2的0分函数y[0]的图象无交点时，直接写出k的取值范围．33．（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．34．（2017春•西城区校级期末）某学习小组有a个男生，b个女生，其中a和b同时满足以下三个条件：①男生人数不少于女生人数；②a，b是一元二次方程mx2﹣（3m+8）x+24＝0的两个实数根；③男生和女生的总人数不超过10人．请根据以上信息，回答下面两个问题：（1）求整数m的值？（2）若T＝ma+b，求T的所有可能的值？35．（2017春•西城区校级期末）设p，q都是实数，且p＜q．我们规定：如果变量x的取值范围为p≤x≤q，则把实数L＝q﹣p叫做变量x的取值宽度．如果反比例函数y＝在p ≤x≤q的函数值y的取值宽度与自变量x的取值宽度相等，则称此函数在p≤x≤q上具有“等宽性”．例如：函数y＝的函数值y的取值范围为≤y≤2，故而函数y＝具有“等宽性”．（1）下列函数哪些函数具有“等宽性”：（填序号）①y＝（1≤x≤2）；②y＝﹣（﹣2≤x≤﹣1）；③y＝﹣（1≤x≤6）；④y＝﹣（﹣4≤x≤﹣1）；（2）已知函数y＝﹣在a≤x≤﹣1上具有“等宽性”，求a的值；（3）已知直线y＝kx+b与函数y＝﹣交于A（x1，y1）、B（x2，y2）两点，且函数y＝﹣在x1≤x≤x2上具有“等宽性”，则k＝．36．（2018春•海淀区期末）在正方形ABCD中，连接BD，P为射线CB上的一个动点（与点C不重合），连接AP，AP的垂直平分线交线段BD于点E，连接AE，PE．提出问题：当点P运动时，∠APE的度数，DE与CP的数量关系是否发生改变？探究问题：（1）首先考察点P的两个特殊位置：①当点P与点B重合时，如图1﹣1所示，∠APE＝°，用等式表示线段DE与CP之间的数量关系：；②当BP＝BC时，如图1﹣2所示，①中的结论是否发生变化？直接写出你的结论：；（填“变化”或“不变化”）（2）然后考察点P的一般位置：依题意补全图2﹣1，2﹣2，通过观察、测量，发现：（1）中①的结论在一般情况下（填“成立”或“不成立”）（3）证明猜想：若（1）中①的结论在一般情况下成立，请从图2﹣1和图2﹣2中任选一个进行证明；若不成立，请说明理由．37．（2018春•海淀区期末）在平面直角坐标系xOy中，A（O，2），B（4，2），C（4，0）．P 为矩形ABCO内（不包括边界）一点，过点P分别作x轴和y轴的平行线，这两条平行线分矩形ABCO为四个小矩形，若这四个小矩形中有一个矩形的周长等于OA，则称P 为矩形ABCO的矩宽点．例如：下图中的为矩形ABCO的一个矩宽点．（1）在点D（，），E（2，1），F（，）中，矩形ABCO的矩宽点是；（2）若G（m，）为矩形ABCO的矩宽点，求m的值；（3）若一次函数y＝k（x﹣2）﹣1（k≠0）的图象上存在矩形ABCO的矩宽点，则k的取值范围是．38．（2019春•曲阜市期末）如图，在菱形ABCD中，CE⊥AB交AB延长线于点E，点F为点B关于CE的对称点，连接CF，分别延长DC，CF至点G，H，使FH＝CG，连接AG，DH交于点P．（1）依题意补全图1；（2）猜想AG和DH的数量关系并证明；（3）若∠DAB＝70°，是否存在点G，使得△ADP为等边三角形？若存在，求出CG的长；若不存在，说明理由．39．（2018春•朝阳区期末）在平面直角坐标系xOy中，对于与坐标轴不平行的直线l和点P，给出如下定义：过点P作x轴，y轴的垂线，分别交直线l于点M，N，若PM+PN≤4，则称P为直线l的近距点，特别地，直线上l所有的点都是直线l的近距点．已知点A（﹣，0），B（0，2），C（﹣2，2）．（1）当直线l的表达式为y＝x时，①在点A，B，C中，直线l的近距点是；②若以OA为边的矩形OAEF上所有的点都是直线l的近距点，求点E的纵坐标n的取值范围；（2）当直线l的表达式为y＝kx时，若点C是直线l的近距点，直接写出k的取值范围．40．（2018春•昌平区期末）如图，将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动秒时，动点P从点A出发以相同的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．（1）OP＝，OQ＝；（用含t的代数式表示）（2）当t＝1时，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处．①求点D的坐标；②如果直线y＝kx+b与直线AD平行，那么当直线y＝kx+b与四边形P ABD有交点时，求b的取值范围．41．（2018春•昌平区期末）在四边形ABCD中，E、F分别是边BC、CD的中点，连接AE，AF．（1）如图1，若四边形ABCD的面积为5，则四边形AECF的面积为；（2）如图2，延长AE至G，使EG＝AE，延长AF至H，使FH＝AF，连接BG、GH、HD、DB．求证：四边形BGHD是平行四边形；（3）如图3，对角线AC、BD相交于点M，AE与BD交于点P，AF与BD交于点N．直接写出BP、PM、MN、ND的数量关系．42．（2018春•西城区期末）在矩形ABCD中，BE平分∠ABC交CD边于点E．点F在BC 边上，且FE⊥AE．（1）如图1，①∠BEC＝°；②在图1已有的三角形中，找到一对全等的三角形，并证明你的结论；（2）如图2，FH∥CD交AD于点H，交BE于点M．NH∥BE，NB∥HE，连接NE．若AB＝4，AH＝2，求NE的长．43．（2018春•西城区期末）在△ABC中，M是BC边的中点．（1）如图1，BD，CE分别是△ABC的两条高，连接MD，ME，则MD与ME的数量关系是；若∠A＝70°，则∠DME＝°；（2）如图2，点D，E在∠BAC的外部，△ABD和△ACE分别是以AB，AC为斜边的直角三角形，且∠BAD＝∠CAE＝30°，连接MD，ME．①判断（1）中MD与ME的数量关系是否仍然成立，并证明你的结论；②求∠DME的度数；（3）如图3，点D，E在∠BAC的内部，△ABD和△ACE分别是以AB，AC为斜边的直角三角形，且∠BAD＝∠CAE＝α，连接MD，ME．直接写出∠DME的度数（用含α的式子表示）．八年级下册期末压轴题参考答案与试题解析一．填空题（共1小题）1．（2018春•西城区期末）在查阅勾股定理证明方法的过程中，小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法，并尝试按自己的理解将这种方法介绍给同学．（1）根据信息将以下小红的证明思路补充完整：①如图1，在△ABC中，∠ACB＝90°，四边形ADEC，四边形BCFG，四边形ABPQ都是正方形．延长QA交DE于点M，过点C作CN∥AM交DE的延长线于点N，可得四边形AMNC的形状是平行四边形；②在图1中利用“等积变形”可得S正方形ADEC＝S四边形AMNC；③如图2，将图1中的四边形AMNC沿直线MQ向下平移MA的长度，得到四边形A′M′N′C′，即四边形QACC′；④设CC′交AB于点T，延长CC′交QP于点H，在图2中再次利用“等积变形”可得S四边形QACC'＝S四边形QATH，则有S正方形ADEC＝S四边形QATH；⑤同理可证S正方形BCFG＝S四边形HTBP，因此得到S正方形ADEC+S正方形BCFG＝S正方形ABPQ，进而证明了勾股定理．（2）小芳阅读完小红的证明思路后，对其中的第③步提出了疑问，请将以下小红对小芳的说明补充完整：图1中△ADM≌△ABC，则有AM＝AB＝AQ，由于平行四边形的对边相等，从而四边形AMNC沿直线MQ向下平移MA的长度，得到四边形QACC′．【分析】根据平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型即可解决问题；【解答】解：（1）∵四边形ACED是正方形，∴AC∥MN，∵AM∥CN，∴四边形AMNC是平行四边形，∴S正方形ADEC＝S平行四边形AMNC，∵AD＝AC，∠D＝∠ACB，∠DAC＝∠MAB，∴∠DAM＝∠CAB，∴△ADM≌△ACB，∴AM＝AB＝AQ，∴图1中的四边形AMNC沿直线MQ向下平移MA的长度，得到四边形A′M′N′C′，即四边形QACC′，∴S四边形QACC′＝S四边形QATH，则有S正方形ADEC＝S四边形QATH，∴同理可证S正方形BCFG＝S四边形HTBP，因此得到S正方形ADEC+S正方形BCFG＝S正方形ABPQ；故答案为平行四边形，S四边形AMNC，S四边形QATH，S四边形QATH；（2）由（1）可知：△ADM≌△ACB，∴AM＝AB＝AQ，故答案为ADM，ACB，AM；【点评】本题考查平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，属于中考创新题目．二．解答题（共42小题）2．（2020春•海淀区校级期末）已知△ABC中，∠BAC＝90°，AB＝AC，点M为BC的中点，点P为AB边上一动点，点N为线段BM上一动点，以点P为旋转中心，将△BPN 逆时针旋转90°得到△DPE，且点B的对应点为D，点N的对应点为E．（1）当点N与点M重合，且点P不是AB的中点时．①依据题意补全图1；②证明：以A，M，E，D为顶点的四边形是矩形．（2）连接EM，若AB＝4，写出一个BN的值，使得EM＝EA成立，并证。

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1．（三角形翻折问题）如图，在Rt ABC △中，9086ABC AB BC ∠=︒==，，，分别在AB AC ，边上取点E F ，，将AEF △沿直线EF 翻折得到A EF '△，使得点A 的对应点A '恰好落在CB 延长线上，当60EA B '∠=︒时，AE 的长为，当A F AC '⊥时，AF 的长为．【答案】 32− 407【分析】由折叠的性质可得AE A E '=，先求出30A EB '∠=︒，从而可得1122A B A E AE ''==，再由勾股定理可得BE AE =，最后由AE BE AB +=，进行计算即可；令A F '交AB 于G ，连接CG ，由折叠的性质可得：A EA F '∠=∠，AFE A FE '∠=∠，AEF A EF '∠=∠，AF A F '=，由A F AC '⊥得出90A FA A FC ''∠=∠=︒，45AFE A FE '∠=∠=︒，证明()ASA A FC AFG '≌得到CF FG =，设CF FG x ==，则10AF x =−，AG ，根据1122ACG S AC FG AG BC =⋅=⋅建立方程，解方程即可得出CF 的长，即可求解．【详解】解：由折叠的性质可得：AE A E '=，90ABC ∠=︒，18090A BE ABC '∴∠=︒−∠=︒，60EA B '∠=︒，9030A EB EA B ''∴∠=︒−∠=︒，1122A B A E AE ''∴==，BE AE∴==，AE BE AB+=，8AE AE∴=，32AE∴=−如图，令A F'交AB于G，连接CG，A F AC'⊥，90A FA A FC''∴∠=∠=︒，由折叠的性质可得：A EA F'∠=∠，AFE A FE'∠=∠，AEF A EF'∠=∠，AF A F'=，90AFE A FE'∠+∠=︒，45AFE A FE'∴∠=∠=︒，设A EA Fα'∠=∠=，则45FEB AFEα∠=∠=+︒，180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠，()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−，902EA B A EBα''∴∠=︒−∠=，FA C EA B EA F Aα'''∴∠=∠−∠==∠，在A FC'和AFG中，CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩'，()ASAA FC AFG'∴≌，CF FG∴=，在Rt ABC△中，9086ABC AB BC∠=︒==，，，10AC∴，设CF FG x==，则10AF x=−，AG∴==1122ACGS AC FG AG BC=⋅=⋅，106x∴⋅=，整理得：271809000x x+−=，即29014400749x⎛⎫+=⎪⎝⎭，9012077x∴+=±，解得：307x=或30x=−（不符合题意，舍去），307CF∴=，30401077AF AC CF∴=−=−=，故答案为：32−407．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识，熟练掌握以上知识点，添加适当的辅助线是解此题的关键．例2．（坐标系中折叠问题）如图，在平面直角坐标系中，长方形ABCO的边OC OA、分别在x轴、y轴上，6AB=，点E在边BC上，将长方形ABCO沿AE折叠，若点B的对应点F 恰好是边OC的三等分点，则点E的坐标是．【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题，坐标与图形，由折叠的性质可得6AF AB==，BE EF=，90AFE B∠=∠=︒，再分当点F靠近点C时，24CF OF==，，当点F靠近点O 时，则42CF OF==，，两种情况利用勾股定理先求出OA的长，进而得到BC的长，设出CE 的长，进而得到EF的长，在Rt EFC△中，由勾股定理建立方程求解即可．【详解】解：在长方形ABCO 中，6CO AB ==，90BCO B AOC ∠=∠=∠=︒，由折叠的性质可得6AF AB ==，BE EF =，90AFE B ∠=∠=︒，F 恰好是边OC 的三等分点，∴当点F 靠近点C 时，24CF OF ==，，在Rt AFO V中，OA =，∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222EF CF CE =+，∴()2222xx =+，解得x =，∴点E的坐标是⎛− ⎝⎭；当点F 靠近点O 时，则42CF OF ==，，在Rt AFO V中，OA ==∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222CF CE =+，∴()2224x x =+，解得x =∴点E的坐标是(−；综上所述，点E的坐标是⎛− ⎝⎭或(−，故答案为：⎛− ⎝⎭或(−．例3．（四边形折叠问题）如图，已知矩形ABCD ，4AB =，5BC =，点P 是射线BC 上的动点，连接AP ，AQP △是由ABP 沿AP 翻折所得到的图形．(1)当点Q 落在边AD 上时，QC = ；(2)当直线PQ 经过点D 时，求BP 的长；(3)如图2，点M 是DC 的中点，连接MP 、MQ ．①MQ 的最小值为；②当PMQ 是以PM 为腰的等腰三角形时，请直接写出BP 的长．【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】（1）根据折叠的性质和勾股定理进行求解即可；（2）分点P 在线段BC 上，点P 在线段BC 的延长线上，两种情况，进行讨论求解；（3）①连接AM ，勾股定理求出AM 的长，折叠求出AQ 的长，根据MQ AM AQ ≥−，求出最小值即可；②分PM MQ =和PM PQ =两种情况，再分点P 在线段BC 上，点P 在线段BC 的延长线上，进行讨论求解即可．【详解】（1）解：当点Q 落在边AD 上时，如图所示，∵矩形ABCD ，4AB =，5BC =，∴4,5CD AB AD BC ====，90BAD B BCD ADC ∠=∠=∠=∠=︒，∵翻折，∴4,90AQ AB AQP B ==∠=∠=︒，∴1DQ AD AQ =−=，在Rt CDQ △中，CQ ==（2）当直线PQ 经过点D 时，分两种情况：当点P 在线段BC 上时，如图：∵翻折，∴4AQ AB ==，90AQP B ∠=∠=︒，BP PQ =，∴90AQD ∠=︒，∴3DQ ==，设BP PQ x ==，则：5PC BC BP x =−=−，3DP DQ PQ x =+=+，在Rt PCD △中，222DP CP CD=+，即：()()222345x x +=+−，∴2x =；∴2BP =；②当P 在线段BC 的延长线上时：∵翻折，∴4,90AQ AB Q B ==∠=∠=︒，BP PQ =，∴3DQ ==，设BP PQ x ==，则：5PC BP BC x =−=−，3DP PQ DQ x =−=−，在Rt PCD △中，222DP CP CD =+，即：()()222345x x −=+−，∴8x =；∴8BP =；综上：2BP =或8BP =；（3）①连接AM ，∵M 是CD 的中点， ∴122DM CM CD ===，∴AM =∵翻折，∴4AQ AB ==，∵MQ AM AQ ≥−，∴当,,A Q M 三点共线时，MQ 的值最小，即：4MQ AM AQ =−=4；②当PM PQ =时，如图：∵翻折，∴BP PQ PM ==，设BP x =，则：,5PM x CP BC BP x ==−=−，在Rt PCM 中，222PM CM PC =+，即：()22225x x =+−，解得： 2.9x =，即： 2.9BP =；当PM QM =，点P 在线段BC 上时，如图：∵,QM PM DM CM ==，90D C ∠=∠=︒，∴()HL MDQ MCP ≌，∴CP DQ =，点Q 在AD 上，由（1）知：1DQ =，∴1CP DQ ==，∴4BP BC CP =−=；当点P 在BC 的延长线上时：如图：此时点M 在AP 上，连接BM ，∵翻折，∴BM MQ PM ==，∵MC BP ⊥，∴210BP BC ==；综上： 2.9BP =或4BP =或10BP =．质，综合性强，难度大，属于压轴题．利用数形结合和分类讨论的思想进行求解，是解题的关键．【模拟训练】1．如图，在长方形ABCD 中，点E 是AD 的中点，将ABE 沿BE 翻折得到FBE ，EF 交BC 于点H ，延长BF DC 、相交于点G ，若8DG =，10BC =，则DC = ．【答案】258【分析】本题考查了全等三角形的判定与性质，折叠的性质，勾股定理，连接EG ，根据点E 是AD 的中点得DE AE EF ==，根据四边形ABCD 是长方形得90D A ∠=∠=︒，根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒，利用HL 证明Rt Rt EFG EDG △≌△，得8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG V △中，根据勾股定理得，222CG BC BG +=，进行计算即可得．【详解】解：如图所示，连接EG ，∵点E 是AD 的中点，∴DE AE EF ==，∵四边形ABCD 是长方形，∴90D A ∠=∠=︒，∵将ABE 沿BE 翻折得到FBE ，∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中，EF ED EG EG =⎧⎨=⎩，∴()Rt Rt HL EFG EDG V V ≌，∴8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG 中，根据勾股定理得，222CG BC BG +=，∴222(8)10(8)x x −+=+，解得258x =，故答案为：258．2．如图，在Rt ABC △中，90ACB ∠=︒，254AB =，154=AC ，点D 是AB 边上的一个动点，连接CD ，将BCD △沿CD 折叠，得到CDE ，当DE 与ABC 的直角边垂直时，AD 的长是．【答案】154或54【分析】本题考查了勾股定理，平行四边形的判定和性质，折叠的性质，全等三角形的判定和性质，分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案，根据题意，正确画出图形是解题的关键．【详解】解：如图，当DE BC ⊥时，延长ED 交BC 于点F ，CE 与AB 相交于点M ，∵EF BC ⊥，∴90EFC EFB ∠=∠=︒，∴90E ECF ∠+∠=︒，由折叠得，B E ∠=∠，CE CB =，MCD FCD ∠=∠，∴90B ECF ∠+∠=︒，∴90CMB ∠=︒，即C M A B ⊥，∵90ACB ∠=︒，254AB =，154=AC ，∴5BC ==， ∵1122ABC S AC BC AB CM ==△，∴11512552424CM ⨯⨯=⨯⨯，解得3CM =，∴4BM =，∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()AAS CFD CMD ≌，∴3CF CM ==，DF DM =，∴532BF BC CF =−=−=，设DF DM x ==，则4BD x =−，在Rt BFD 中，222DF BF BD +=，∴()22224x x +=−，解得32x =， ∴35422BD =−=， ∴25515424AD AB BD =−=−=；当DE AB ⊥时，如图，设DE 与AC 相交于点M ，由折叠可得，BCD ECD ∠=∠，DE DB =，ED BD =，5EC BC ==，∵DE AB ⊥，90ACB ∠=︒，∴DE BC ∥，∴EDC BCD ∠=∠，∴EDC ECD ∠=∠，∴5ED EC ==，∴5BD ED ==， ∴255544AD AB BD =−=−=；综上，AD 的长是154或54，故答案为：154或54．3．如图，等边三角形ABC 中，16AB BD AC =⊥，于点D ，点E F 、分别是BC DC 、上的动点，沿EF 所在直线折叠CEF △，使点C 落在BD 上的点C '处，当BEC '△是直角三角形时，BE 的值为．【答案】24−或323【分析】本题考查了翻折变换，等边三角形的性质，折叠的性质，熟练运用折叠的性质是本题的关键．由等边三角形的性质可得30DBC ∠=︒，分9090BEC BC E ''∠=︒∠=︒，两种情况讨论，由直角三角形的性质即可求解．【详解】解：ABC 是等边三角形，BD AC ⊥，30,DBC ∴∠=︒ 由折叠的性质可得：,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323．4．如图，在ABC 中，120ACB ∠=︒，8AC =，4BC =，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，使点A 落在CD 的延长线上的点A '处，两条折痕与斜边AB 分别交于点E 、F ，则线段FA '的长为．【答案】【分析】本题考查了折叠的性质，勾股定理，直角三角形的性质，添加恰当辅助线构造直角三角形是本题的关键．过点A 作AH BC ⊥交BC 的延长线于H ，由直角三角形的性质可求142HC AC ==，AH =AB 的长，由面积法可求CE 的长，由折叠的性质可求90BEC DEC ∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，然后再求解即可．【详解】解：如图，过点A 作AH BC ⊥，交BC 的延长线于H ，120ACB ∠=︒，ACB H HAC ∠=∠+∠，30HAC ∴∠=︒，142HC AC ∴==，AH ==，448BH ∴=+=，AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯，4CE ∴=，CE ∴，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，90BEC DEC ∴∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，1602ECF ACB ∴∠=∠=︒，30CFE ∴∠=︒，EF ∴，在Rt BCE中，BE ===，AF AB EF BE ∴=−−==FA AF '∴==故答案为：5．如图，点D 是ABC 的边AB 的中点，将BCD △沿直线CD 翻折能与ECD 重合，若4AB =，2CD =，1AE =，则点C 到直线AB 的距离为．【答案】【分析】连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质及中点性质可得AEB △为直角三角形，且G 为BE 中点，从而CG BE ⊥，由勾股定理可得BE的长，再根据2ABC BDC S S =△△，即11222AB CH CD BG ⋅=⨯⋅，从而可求得CH 的长．【详解】解：连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质可得：BD ED =，CB CE =，∴CG 为BE 的中垂线， ∴12BG BE =，∵点D 是AB 的中点，4AB =，2CD =，1AE =， ∴122BD AD AB ===，CBD CAD S S =，AD DE =，∴DBE DEB ∠=∠，DEA DAE ∠=∠，∵180EDA DEA DAE ∠+∠+∠=︒，即22180DEB DEA ∠+∠=︒，∴90DEB DEA ∠+∠=︒，即90BEA ∠=︒，∴BE∴12BG BE ==， ∵2ABC BDCS S =△△， ∴11222AB CH CD BG ⋅=⨯⋅，∴422CH =⨯，∴CH ，∴点C 到直线AB 的距离为．故答案为：．【点睛】本题考查翻折变换，线段中垂线的判定，等腰三角形的性质，点到直线的距离，直角三角形的判定，勾股定理，利用面积相等求相应线段的长，解题的关键是得出CG 为BE 的中垂线，2ABC BDC S S =△△．6．如图，在ABC 中，90,A AB AC ∠=︒==D 为AC 边上一动点，将C ∠沿过点D 的直线折叠，使点C 的对应点C '落在射线CA 上，连接BC '，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为．【答案】或【分析】由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==时，分别根据勾股定理求出AC '的长，再求出CC '的长即可【详解】解：由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时，90,A AB AC ∠=︒==∴由勾股定理得，222BC AC AB ''−=，即222(2)AC AC ''−=，AC '∴=CC '∴CD ∴；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时，同理得AC 'CC '∴CD ∴；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==由勾股定理得，222AC BC AB ''=−，即22218AC '=−=，AC '∴=CC '∴CD ∴=，0>，CD AB ∴>，此时点D 不在边AC 上，不符合题意，舍去，综上，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为或．故答案为：或．【点睛】本题主要考查图形的翻折变换（折叠问题），勾股定理，等腰直角三角形的性质等知识，灵活运用折叠的性质及勾股定理是解答本题的关键，同时要注意分类思想的运用．7．如图，在ABC 中，90ACB ∠=︒，3AC =，4BC =，P 为斜边AB 上的一动点（不包含A ，B 两端点），以CP 为对称轴将ACP △翻折得到A CP '，连结BA '．当A P AB '⊥时，BA '的长为．【答案】【分析】当A P AB '⊥时，过点C 作CD AB ⊥于D ，可知125CD =，95AD =，得出PDC △为等腰直角三角形，得到PD CD =，求出PA '和BP 的长，利用勾股定理即可求出BA '的长．【详解】过点C 作CD AB ⊥于D ，在Rt ADC 中，90ACB ∠=︒，3AC =，4BC =，∴5AB = ∵1122AC BC AB CD ⨯=⨯，125CD ∴=，在Rt ADC 中，3AC =∴95AD ==，当A P AB '⊥时，如图由折叠性质可知12∠=∠，PA PA '=，又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴，又2390∠+∠=︒，345∴∠=︒，23∴∠=∠，125PD CD ∴==，又PA PD AD =+，12921555PA ∴=+=，又PA PA '=，215PA '∴=，又BP AB PA =−，214555BP ∴=−=，在Rt BPA '△中，90BPA ∠='︒，222BP PA BA ∴='+，2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭，BA '∴=，故答案为：．【点睛】本题考查了勾股定理的应用，折叠问题，熟练掌握勾股定理是解题的关键．8．如图，在ABC 中，90ACB ∠=︒，AC BC =，D 为AB 上一点，连接DC ，将BDC 沿DC 翻折，得到EDC △，连接AE ，若AE CE =，4BC =，则D 到CE 的距离是．【答案】2【分析】本题考查等腰直角三角形中的折叠问题，涉及等边三角形判定与性质，勾股定理应用、面积法等知识．设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，根据将BDC 沿DC 翻折，得到EDC △，AC BC =，AE CE =，可得ACE △是等边三角形，即知60ACE ∠=︒，而90ACB ∠=︒，故150BCE ∠=︒，30ECF ∠=︒，可得75BCD ECD ∠=∠=︒，122EF CE ==，CF =BE =15CBE ∠=︒，可得90BGC ∠=︒，即CG BE ⊥，从而12BG BE GE ===，由勾股定理得CG ，在Rt BDG △中，DG ，即得CD DG CG =+，由面积法可得D 到CE 的距离是2．【详解】解：设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，如图：将BDC 沿DC 翻折，得到EDC △，4BC CE ∴==，BCD ECD ∠=∠，AC BC =，AE CE =，AC BC CE AE ∴===，ACE ∴是等边三角形，60ACE ∴∠=︒，90ACB ∠=︒，150BCE ∴∠=︒，30ECF ∠=︒，75BCD ECD ∴∠=∠=︒，122EF CE ==，CF =在Rt BEF △中，BE ==BCE 中，BC CE =，150BCE ∠=︒，15CBE ∴∠=︒，18090BGC BGC BCD ∴∠=︒−∠−∠=︒，即CG BE ⊥，12BG BE GE ∴==，CG ∴===，45ABC ∠=︒，15CBE ∠=︒，30DBG ∴∠=︒，在Rt BDG△中，DG =，CD DG CG ∴=+=，设D 到CE 的距离是h ，2DCE S CE h DC GE ∆=⋅=⋅，324DC GE h CE ⋅∴===，故答案为：2．9．在生活中、折纸是一种大家喜欢的活动、在数学中，我们可以通过折纸进行探究，探寻数学奥秘．【纸片规格】三角形纸片ABC ，120ACB ∠=︒，CA CB =，点D是底边AB 上一点．【换作探究】(1)如图1，若6AC =，AD =CD ，求CD 的长度；(2)如图2，若6AC =，连接CD ，将ACD 沿CD 所在直线翻折得到ECD ，点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直，求AD 的长；(3)如图3，将ACD 沿CD 所在直线翻折得到ECD ，边CE 与边AB 交于点F ，且DE BC ∥，再将DFE △沿DF 所在直线翻折得到DFG ，点E 的对应点为点G ，DG 与CE 、BC 分别交于H ，K ，若1KH =，请直接写出AC 边的长．【答案】(1)(2)3或(3)3【分析】（1）作CE AB ⊥于E ，求得30A B ==︒∠∠，从而得出132CE AC ==，AE AC =进而得出DE AE AD =−=（2）当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，依次得出45DAE DEA ∠=∠=︒，304575CAE CAD DAE ∠=∠+∠=︒+︒=︒，75CEA CAE ∠=∠=︒，30ACE ∠=︒，15ACD DCE ∠=∠=︒，45CDG CAB DAC ∠=∠+∠=︒，从而DG CG =，进一步得出结果；当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，可推出90AVC ∠=︒，60ACE ∠=︒，从而30ACD DCE ∠=∠=︒，进一步得出结果；当DE BC ⊥时，可推出180ACB BCE ∠+∠=︒，从而90ACD DCE ∠=∠=︒，进一步得出结果；（3）可推出CKH 和CDH △及CHK 是直角三角形，且30HCK ∠=︒，30HDF ∠=︒，45DCH ∠=︒，进一步得出结果．【详解】（1）解：如图1，作CE AB ⊥于E ，90AEC ∴∠=︒，CA CB =，120ACB ∠=︒，30A B ∴∠=∠=︒，132CE AC ∴==，AE =，DE AE AD ∴=−==CD ∴=；（2）解：如图2，当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，由翻折得：AD DE =，CAD CED =∠∠，AC CE =，45DAE DEA ∠∠∴==︒，304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒，75CEA CAE ∴∠=∠=︒，30ACE ∴∠=︒，15ACD DCE ∴∠=∠=︒，45CDG CAB DAC ∴∠=∠+∠=︒，DG CG ∴=，由（1）知：3CG =，AG =3AD AG DG ∴=−=；如图3，当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，90E ACE ∴∠+∠=︒，E A ∠=∠，90A ACE ∴∠+∠=︒，90AVC ∴∠=︒，60ACE∴∠=︒，30ACD DCE∴∠=∠=︒，ACD A∴∠=∠，AD CD∴=，3CV =，CD∴=，AD CD∴==如图4，当DE BC⊥时，30E A∠=∠=︒，60BCE∴∠=︒，180ACB BCE∴∠+∠=︒，90ACD DCE∴∠=∠=︒，AD∴=，综上所述：3AD=或（3）解：如图5，∵DE BC ∥，30B C ∠=∠=︒，30BCF E ∴∠=∠=︒，30EDF B ∠=∠=︒，120ACB ∠=︒，90ACE ∴∠=︒，1452ECD ACD ACE ∴∠=∠=∠=︒，将DFE △沿DF 所在直线翻折得到DFG ，30GDF EDF ∴∠=∠=︒，60EDG ∴∠=︒，90CHK EHD ∴∠=∠=︒，DH CH ∴=1FH ∴==，1CF CH FH ∴=+，3AC ∴==．【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质等知识，解决问题的关键是正确分类，画出图形．10．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 为线段BC 延长线上一点，以AD 为腰作等腰直角DAF △，使90DAF ∠=︒，连接CF ．(1)请判断CF 与BC 的位置关系，并说明理由；(2)若8BC =，4CD BC =，求线段AD 的长；(3)如图2，在（2）的条件下，将DAF △沿线段DF 翻折，使点A 与点E 重合，连接CE ，求线段CE 的长．【答案】(1)CF BC ⊥，理由见解析(2)(3)【分析】（1）证明()SAS ABD ACF △≌△，则ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，可得90FAO DCO ∠=∠=︒，进而可得CF BC ⊥；（2）如图2，过A 作AH BC ⊥于H ，则142BH CH AH BC ====，6DH =，由勾股定理得，AD =（3）由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，证明()AAS ADM DEN ≌，则46DN AM EN DM ====，，6CN =，由勾股定理得，CE =计算求解即可．【详解】（1）解：CF BC ⊥，理由如下：∵等腰直角DAF △，90DAF ∠=︒，∴AD AF =，又∵90BAC ∠=︒，∴BAC CAD DAF CAD ∠+∠=∠+∠，即BAD CAF ∠=∠，∵AB AC =，BAD CAF ∠=∠，AD AF =，∴()SAS ABD ACF △≌△，∴ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，∴90FAO DCO ∠=∠=︒，∴CF BC ⊥；（2）解：∵8BC =，4CD BC =，∴2CD =，如图2，过A 作AH BC ⊥于H ，∵ABC 是等腰直角三角形， ∴142BH CH AH BC ====，∴6DH =，由勾股定理得，AD =∴线段AD 的长为（3）解：由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，∴90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，∴90AMD DNE ∠=︒=∠，同理（2）可知，4AM =，6MD =，∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠，∴ADM DEN ∠=∠，∵90AMD DNE ∠=︒=∠，ADM DEN ∠=∠，AD DE =，∴()AAS ADM DEN ≌，∴46DN AM EN DM ====，，∴6CN =，由勾股定理得，CE =，∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质，三角形内角和定理，勾股定理，折叠的性质，等腰三角形的性质．熟练掌握全等三角形的判定与性质，折叠的性质是解题的关键．11．如图1，在Rt ABC △中，90C ∠=︒，5AC =，12BC =，点D 为BC 边上一动点，将ACD 沿直线AD 折叠，得到AFD △，请解决下列问题．(1)AB =______；当点F 恰好落在斜边AB 上时，CD =______；(2)连接CF ，当CBF V 是以CF 为底边的等腰三角形时，请在图2中画出相应的图形，并求出此时点F 到直线AC 的距离；(3)如图3，E 为边BC 上一点，且4，连接EF ，当DEF 为直角三角形时，CD = ．（请写出所有满足条件的CD 长）【答案】(1)13，103(2)画图见解析，600169(3)52或或5或10【分析】（1）根据勾股定理可得AB 的长，再利用等积法求出CD 即可；（2）过点F 作FG AC ^，交CA 的延长线于G ，首先由等积法求出CH 的长，再根据勾股定理求出AH 的长，再次利用等积法可得FG 的长；（3）分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形，从而解决问题．【详解】（1）解：在Rt ABC △中，由勾股定理得，13AB ，当点F 落在AB 上时，由折叠知，CD DF =， ∴111222AC CD AB DF AC BC ⋅+⋅=⋅，51360CD CD ∴+=，103CD ∴=，故答案为：13，103；（2）过点F 作FG AC ^，交CA 的延长线于G ，BC BF =，AC AF =，AB ∴垂直平分CF ，由等积法得6013AC BC CH AB ⋅==，在Rt ACH 中，由勾股定理得，2513AH ===， 1122ACF S AC FG CF AH =⋅=⋅△，6025260013135169CF AH FG AC ⨯⨯⋅∴===；（3）当90DEF ∠=︒时，当点D 在CE 上时，作FH AC ⊥于H ，则4HF CE ==，5AF AC ==，3AH ∴=，2CH EF AC AH ∴==−=，设CD x =，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)2x x =−+，解得52x =，52CD ∴=，当点D 在EB 上时，同理可得538CH AC AH =+=+=，设CD DF x ==，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)8x x −+=，解得10x =，10CD ∴=，当90DFE ∠=︒时，由勾股定理得AE设CD DF x ==，则520x +=，x ∴，CD ∴=；当90FDE ∠=︒时，则45ADC ADF ∠=∠=︒，5CD AC ∴==，综上：52CD =或或5或10，故答案为：52或或5或10．【点睛】本题是三角形综合题，主要考查了翻折的性质，直角三角形的性质，勾股定理，等腰直角三角形的判定与性质等知识，利用等积法求垂线段的长是解题的关键．。

浙教版初二下册数学期末压轴题及答案

浙教版八下数学期末压轴题1 如图，梯形ABCD 中，AD // BC,/ B=Rt Z, AD=21cm , BC=24cm，动点P 从点A 出发沿AD 边向D以1cm/s的速度运动，另一动点Q同时从点C出发沿CB边向点B以2cm/sP运动时间为t.的速度运动(运动到点B时，P、Q同时停止运动).设点(1)t为何值时，四边形PQCD为平行四边形？(2)t为何值时，四边形PQCD为等腰梯形？2、如图，在直角梯形ABCD 中，AB // CD , / BCD=Rt /, AB=AD=10cm , BC=8cm .点P 从点A 出发，以每秒2cm的速度沿线段AB方向向点B运动，点Q从点D出发，以每秒3cm的速度沿线段DC 方向向点C运动.已知动点P、Q同时发，当点P运动到点B时，P、Q运动停止，设运动时间为t.(1 )求CD的长；(2)当四边形PBQD为平行四边形时，求四边形PBQD的周长；(3)在点P、点Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2?若存在，请求出所有满足条件的t的值；若不存在，请说明理由.3、如图，在梯形ABCD 中，AD // BC，/ B= 90 ° ,AD = 16cm, AB = 12cm, BC = 21cm,动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动，动点Q从点A出发，在线段AD 上以每秒1cm的速度向点D运动，点P, Q分别从点B, A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t(秒).(1 )当t为何值时，四边形PQDC是平行四边形•(2)当t为何值时，以C,D,Q,P为顶点的梯形面积等于60cm2?(3)是否存在点卩，使厶PQD是等腰三角形？若存在，请求出所有满足要求的t的值，若不存在，请说明理由•4、如图，四边形ABCD 中，AD // BC , AD=15 , BC=25, AB=DC=10，动点P从点D 出发，以每秒1个单位长的速度沿线段DA的方向向点A运动，动点Q从点C出发，以每秒2个单位长的速度沿射线CB的方向运动，点P、Q分别从点D、C同时出发，当点P运动到点A时，点Q随之停止运动。

上海(沪)八年级第二学期期末数学压轴题及答案(可转为word)

0 8k b, ∴ „„„„„„„„„„„„„„„„„„„„„„„„„（1 分） 4 5k b,
4 k , 3 „„„„„„„„„„„„„„„„„„„„„„„„„（1 分） ∴ 32 b . 3
4 32 ．„„„„„„„„„„„„（1 分） x 3 3 26．解：（1）BF +AG= AE．„„„„„„„„„„„„„„„„„„„„„„（1 分）证明如下：过点 F 作 FH⊥DA，垂足为 H， ∵在正方形 ABCD 中，∠DAE=∠B=90°，∴四边形 ABFH 是矩形．„（1 分） ∴FH=AB=DA．∵BD⊥FG，∴∠G=90°–∠ADE=∠DEA．又∴∠DAE=∠FHG=90°，∴△FHG≌△DAE． „„„„„„„„„„（1 分） ∴GH=AE，即 HA+AG=AE．∵BF=HA，∴BF+AG=AE．„„„„„„（1 分）
本题满分12分其中第1小题5分第2小题3分第3小题4bcaebcdfdfaeefad四边形aefd是平行四边形efad5aedf?????????????????????????1abcd5rtabertdcfbecfefbccfbecf3在rtabeabaeaebqapaepdcqqcdpabqp当四边形abqp与四边形qcdp的面积相等时3当四边形abqp是平行四边形时pqab当四边形qcdp是平行四边形时可得pqcdcdabpqab此时cqpd11时pqab
FB 3 ，且 AC 10 ，求 FC 的值. BD 5
A
D
F
E
B
C
26．在梯形 ABCD 中， ∠ABC= 90 ， AD∥BC， BC>AD， AB=8cm， BC=18cm， CD=10 cm，点 P 从点 B 开始沿 BC 边向终点 C 以每秒 3cm 的速度移动，点 Q 从点 D 开始沿 DA 边向终点 A 以每秒 2cm 的速度移动，设运动时间为 t 秒. （1）求四边形 ABPQ 为矩形时 t 的值；（2）若题设中的“BC=18cm”改变为“BC= k cm” ，其它条件都不变，要使四边形 PCDQ 是等腰梯形，求 t 与 k 的函数关系式，并写出 k 的取值范围；（3）在移动的过程中，是否存在 t 使 P、Q 两点的距离为 10cm ,若存在求 t 的值. 若不存在请说明理由？

八年级下册数学期末压轴题汇总(含解析)

（近三年）长春市八年级下数学期末压轴题（23.24题）长春市绿园区2020.7八下数学期末试题：24.(10分)如图，在矩形ABCD 中，AB=4，BC=10，E 、F 分别为BC 、AD 的中点，点P 从点A 出发，以每秒2个单位长度的速度沿AD 向终点D 速运动，作PQ ⊥BC 于Q ，当点P 不与点F 重合时，设四边形PQEF 的面积为S ，点P 的运动时间为t(秒)(1)当点P 与点D 重合时，求t 的值(2)用含t 的代数式表示线段PF (3)求S 与t 之间的函数关系式(4)当四边形PQEF 的对角线互相垂直时，直接写出的值24.(12分)如图，在平面直角坐标系中，A(-2，1)，B(1，1).直线y =kx +3与y 轴相交于点C(1)在平面直角坐标系中标记出点C 的位置(2)当直线y =kx +3与直线y =2x 平行时，k 的值为；(3)当直线y =kx +3恰好经过点A 时，求直线y =kx +3的函数关系式；(4)当直线y =kx +3与线段AB 有公共点时，直接写出k 的取值范围。

B A PFDQE C01234-1-2-3-4xyAB -2-3-41234-1答案：23.(1)由题意，得2t =10(1分)t =5(2分)(2)当0≤t <25时，PF =5-2t 当25<t ≤5时，PF =2t -5(5分)(3)当0≤t <25时，S =20-8t当25<t ≤5时，S =8t -20(8分)(4)t =21或t =29(10分)评分说明:第(2)问写成PF =∣5-2t ∣或PF=∣2t -5∣扣1分第(2)间写成当0≤t ≤25一时，PF =5-2t 当25<t ≤5时，PF =2t -5不扣分第(2)、(3)问两个关系式各1分，取值范围共1分24.(1)点C 标记在(0，3)的位置(2分)(2)2(4分)(3)把(-2，1)代入y =kx +3得1=-2k +3(6分)解，得k =1(8分)∴y =x +3(10分)(4)k ≤-2或k ≥1(12分)评分说明:第(1)问只要位置标记正确即可给分长春市朝阳区2020.7数学八下期末试题23.(10分)如图在Rt ∆ABC 中∠C =90º，过点A 作线段AD 平行射线BC ，AB=10，BC=6，AD=15。

八年级下册数学压轴题(含答案)

八年级下压轴题1.如图，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=15，OC=12，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．(1)求CE和OD的长；(2)求直线DE的表达式；(3)直线y=kx+b与AE所在的直线垂直，当它与矩形OABC有公共点时，求出b的取值范围．【答案】解：(1)依题意可知，折痕AD是四边形OAED的对称轴，∴在Rt△ABE中，AE=AO=15，AB=OC=12，BE=√AE2−AB2=√152−122=9，∴CE=15−9=6，在Rt△DCE中，DC2+CE2=DE2，又∵DE=OD，∴(12−OD)2+62=OD2，∴OD=7.5．(2)∵CE=6，∴E(6,12)．∵OD=7.5，∴D(0,7.5)，设直线DE的解析式为y=mx+n，∴{n=7.56m+n=12，解得{m =34n =152， ∴直线DE 的解析式为y =34x +152．(3)∵直线y =kx +b 与AE 所在的直线垂直，DE ⊥AE ，∴直线y =kx +b 与DE 平行，∴直线为y =34x +b ，∴当直线经过A 点时，0=34×15+b ，则b =−454，当直线经过C 点时，则b =12，∴当直线y =kx +b 与矩形OABC 有公共点时，−454≤b ≤12． 2. 如图，在平面直角坐标系中，直线l 1：y =34x 与直线l 2：y =kx +b(k ≠0)相交于点A(a,3)，直线l 2与y 轴交于点B(0,−5)．(1)求直线l 2的函数解析式；(2)将△OAB 沿直线l 2翻折得到△CAB ，使点O 与点C 重合，AC 与x 轴交于点D.求证：四边形AOBC 是菱形；(3)在直线BC 下方是否存在点P ，使△BCP 为等腰直角三角形？若存在，直接写出点P 坐标；若不存在，请说明理由．【答案】解：(1)∵直线l₁：y =34x 与直线l₂：y =kx +b 相交于点A(a,3)，∴A(4,3)，∵直线交l₂交y 轴于点B(0,−5)，∴y =kx −5，把A(4,3)代入得，3=4k −5，∴k =2，∴直线l 2的解析式为y =2x −5；(2)∵OA =√32+42=5，∴OA =OB ，∵将△OAB 沿直线l₂翻折得到△CAB ，∴OB =OC ，OA =AC ，∴OA=OB=BC=AC，∴四边形AOBC是菱形；(3)如图，过C作CM⊥OB于M，则CM=OD=4，∵BC=OB=5，∴BM=3，∴OB=2，∴C(4,−2)，过P1作P1N⊥y轴于N，∵△BCP是等腰直角三角形，∴∠CBP1=90°，∴∠MCB=∠NBP1，∵BC=BP1，∴△BCM≌△P1BN(AAS)，∴BN=CM=4，∴P1(3,−9)；同理可得，P2(7,−6)，P3(72,−112).综上所述，点P的坐标是(3,−9)或(7,−6)或P(72,−112).3.如图，在Rt△ABC中，∠C=90°，∠A=45°，AC=10cm，点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动，同时点E从点B出发沿BA方向以√2cm/s的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D，E运动的时间是t(0<t≤10)s.过点E作EF⊥BC于点F，连接DE，DF．(1)用含t的式子填空；BE=______cm，CD=______cm．(2)试说明，无论t为何值，四边形ADEF都是平行四边形；(3)当t为何值时，△DEF为直角三角形？请说明理由．【答案】√2t t【解析】解：(1)由题意：BE=√2t(cm)，AD=t(cm)，故答案为√2t，t．(2)如图2中，∵CA=CB，∠C=90°，∴∠A=∠B=45°，∵EF⊥BC，∴∠EFB=90°，∴∠FEB=∠B=45°，∴EF=BF，∵BE=√2t，∴EF=BF=t，∴AD=EF，∵∠EFB=∠C=90°，∴AD//EF，∴四边形ADFE是平行四边形．(3)①如图3−1中，当∠DEF=90°时，易证四边形EFCD是正方形，此时AD=DE= CD，t=5．②如图3−2中，当∠EDF=90时，∵DF//AC，∴∠AED=∠EDF=90°，∵∠A=45°，∴AD=√2AE，∴t=√2(10√2−√2t)，，解得t=203③当∠EFD=90°，△DFE不存在．s.综上所述，满足条件的t的值为5s或2034.如图，在矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是(−9,12).矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，且直线BD与OA、x轴分别交于点D、F．(1)求线段BO的长；(2)求△OBD的面积；(3)在x轴上是否存在点M，使得以A、B、F、M为顶点的四边形是平行四边形？若存在，请求出满足条件的M点的坐标；若不存在，请说明理由．【答案】解：(1)∵四边形AB CO是矩形，∴∠BCO=90°．在Rt△BCO中，∵BO2=BC2+OC2，∴BO=√122+92=15．(2)设OD=x，∵四边形ABCO是矩形，∴∠BAD=90°．∵矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，∴△BAD≌△BED，∴BE=BA=9，AD=ED=12−x，∠BED=∠BAD=90°，∴∠OED=90°，EO=BO−BE=15−9=6．在Rt△DEO中，OD2=OE2+DE2，∴x2=62+(12−x)2，解得x=152，即OD=152，∴S△OBD=12OD⋅AB=1354；(3)由(2)知，OD=152得D(0,152)，设直线BD的解析式为y=kx+b，∵B(−9,12)，D(0,152)，∴{−9k+b=12 b=152，解得{k =−12b =152， ∴直线BD 的解析式为y =−12x +152．当y =0时，x =15，∴OF =15．又∵AB =9，∴FM =9， ∴在x 轴上存在点M ，使得以A 、B 、F 、M 为顶点的四边形是平行四边形．满足条件的点M 的坐标为(6,0)或(24,0)．5. 如图，在平面直角坐标系中，O 为坐标原点，矩形OABC 的顶点A(12,0)、C(0,9)，将矩形OABC 的一个角沿直线BD 折叠，使得点A 落在对角线OB 上的点E 处，折痕与x 轴交于点D ．(1)线段OB 的长度为______；(2)求直线BD 所对应的函数表达式；(3)若点Q 在线段BD 上，在线段BC 上是否存在点P ，使以D ，E ，P ，Q 为顶点的四边形是平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】解：(1)15；(2)如图，设AD =x ，则OD =OA −AD =12−x ，根据折叠的性质，DE =AD =x ，BE =AB =9，又OB =15，∴OE =OB −BE =15−9=6，在Rt △OED 中，OE 2+DE 2=OD 2，即62+x 2=(12−x)2，解得 x =92， ∴OD =12−92=152，∴点D(152,0)，设直线BD 所对应的函数表达式为：y =kx +b(k ≠0)，B(12,9)，则{12k +b =9152k +b =0，解得{k =2b =−15， ∴直线BD 所对应的函数表达式为：y =2x −15．(3)过点E 作EP//BD 交BC 于点P ，过点P 作PQ//DE 交BD 于点Q ，则四边形DEPQ 是平行四边形，再过点E 作EF ⊥OD 于点F ，由12⋅OE ⋅DE =12⋅DO ⋅EF ，得EF =6×92152=185，即点E 的纵坐标为185，又点E 在直线OB ：y =34x 上，∴185=34x，解得x=245，∴E(245,185)，由于PE//BD，所以可设直线PE：y=2x+n，∵E(245,185)在直线EP上，∴185=2×245+n，解得n=−6，∴直线EP：y=2x−6，令y=9，则9=2x−6，解得x=152，∴P(152,9)．6.如图，直线y=−12x+3与x轴、y轴分别相交于A，B两点，P是线段AB上的一个动点(不与AB两点重合)，点M的坐标为(4,0)，设P点的横坐标为x，设△OPM 的面积为S．(1)求点A，B的坐标；(2)求S关于x的函数解析式，并写出自变量x的取值范围；(3)当S=12S△AOB时，求点P的坐标；(4)画出函数S的图象．【答案】解：(1)针对于直线y=−12x+3，令x=0，∴y=3，∴B(0,3)，令y=0，∴−12x+3=0，∴x=6，∴A(6,0)；(2)∵点P在直线y=−12x+3上，且P点的横坐标为x，∴P(x,−12x+3)，∵M(4,0)，∴OM=4，∴S=S△OPM=12OM×|y P|=2y P=2(−12x+3)=−x+6(0<x<6)；(3)由(1)知，A(6,0)，B(0,3)，∴S△AOB=12OA×OB=9，由(2)知，S=−x+6(0<x<6)；当S=12S△AOB时，∴−x+6=92，∴x=32，∴y=−12x+3=94，∴P(32,94 )；(4)由(2)知，S=−x+6(0<x<6)，∴函数S的图象如图所示：7.如图，直线l1：y=kx+245与x轴、y轴分别相交于A、B两点，直线l2：y=−2x+b 与x轴、y轴、直线l1分别相交于点C、D、P.已知点A的坐标为(6,0)，点D的坐标为(0,6)，点M 是x 轴上的动点． (1)求k ，b 的值及点P 的坐标；(2)当△POM 为等腰三角形时，求点M 的坐标；(3)是否存在以点M 、O 、D 为顶点的三角形与△AOB 全等？若存在，请求出点M 的坐标；若不存在，请说明理由．【答案】解：(1)∵直线l 1：y =kx +245与x 轴相交于A(6,0)，∴6k +245=0，∴k =−45，∴直线l 1：y =−45x +245①∵直线l 2：y =−2x +b 与y 轴相交于点D(0,6)， ∴b =6，∴直线l 2：y =−2x +6②，联立①②解得，{x =1y =4，∴P(1,4)；(2)∵点M 是x 轴上的动点， ∴设M(m,0)， ∵P(1,4)，∴OP =√17，OM =|m|，MP =√(m −1)2+16， ∵△POM 为等腰三角形， ∴当OM =OP 时， ∴√17=|m|， ∴m =±√17， ∴M(−√17,0)或(√17,0)当OM=MP时，∴|m|=√(m−1)2+16，∴m=172，∴M(172,0)，当OP=MP时，∴√17=√(m−1)2+16，∴m=0(舍)或m=2，∴M(2,0)，即：点M的坐标为(−√17,0)或(√17,0)或(172,0)或(2,0)；(3)∵点A的坐标为(6,0)，点D的坐标为(0,6)，∴OA=OD=6，∵点M在x轴上，∴∠AOB=∠DOM=90°，∵以点M、O、D为顶点的三角形与△AOB全等，∴△AOB≌△DOM，∴OM=OB，∵直线l1：y=−45x+245与y轴相交于B，∴B(0,245)，∴OB=245，∴OM=245，∴M(245,0)或(−245,0)．8.在平面直角坐标系中，一次函数的图象与x轴交于点A，与y轴交于点B，且与正比例函数的图象交于点C(3，4)．(1)求、的值；(2)若D点是线段OC上的动点，过D作DE∥y轴交AC于点E．①设D点的横坐标为，线段DE的长为，则与的函数关系式为_______；②连接AD，若△AOD为等腰三角形，请求出点D的坐标；(3)在平面内是否存在点Q，使以O、A、C、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．【详解】（1）∵正比例函数的图象过点C（3，4），∴，解得：，∴正比例函数为，∵一次函数的图象过点C（3，4），∴，解得：，∴一次函数解析式为：；（2）①∵D在正比例函数上，∴ D点的纵坐标为：，∵E点在一次函数上，∴ E点的纵坐标为：，∴ DE ＝；②∵点A是一次函数与x轴的交点，∴ A（－3，2），即OA＝3，而D的坐标为（，），∵∠AOD是钝角，一定是等腰三角形的顶角，∴OD＝OA，∴OD＝，解得：，则，∴点D的坐标为（，）；（3）根据图象分析：①当OA作为平行四边形的边时，则CQ∥OA，CQ＝OA，此时Q（0，4），（6，4），②当OA作为平行四边形的对角线时，则OQ∥AC，OQ＝AC，此时Q（－6，－4），综上所述，存在，点Q的坐标为（0，4），（6，4），（－6，－4）．9.如图1，在平面直角坐标系xOy中，直线l1:y1=kx+b与l2: y2=kx+3相交于点C(1,2),直线l1与x轴交于点A (-1，0)、直线l2与x轴交于B点.(1) 求直线l1的解析式(表达式) ;(2)判断△ABC的形状并说明理由; (3)在x轴上是否存在点P，使△ACP为等腰三角形?若存在，请直接写出P 点的坐标;若不存在，请说明理由;(4) 如图2，设直线l2与y轴交于点D，点为线段BD上的一个动点，过点M 作ME⊥y轴于点E，作MF⊥x轴于点F，连接EF，问是否存在点M，使EF的值最小?若存在,求出此时EF 的值.10.如图，直线y=kx -3与x 轴、y 轴分别交于B ⎪⎭⎫ ⎝⎛0,23、C 两点，(1)求k 值；(2)若点A(x ，y)是直线y=kx -3上在第一象限内的一个动点，当点A 在运动过程中，试写出△AOB 的面积S 与x 的函数关系式；(不要求写出自变量的取值范围) (3)探究：①当A 点运动到什么位置时，△AOB 的面积为49，并说明理由； ②在①成立的情况下，x 轴上是否存在一点P ，使△AOP 是等腰三角形？若存在，请直接写出满足条件的所有P 点坐标；若不存在，请说明理由．答案解析（1）把B 的坐标代入y=kx -3，得：k -3=0，解得：k=2；（2）OB=，则S=×（2x -3）=x -；（3）①根据题意得：x -=，解得：x=3，则A 的坐标是（3，3）；②OA==3，当O是△AOP的顶角顶点时，P的坐标是（-3，0）或（3，0）；当A是△AOP的顶角顶点时，P与过A的与x轴垂直的直线对称，则P的坐标是（6，0）；当P是△AOP的顶角顶点时，P在OA的中垂线上，OA的中点是（，），与OA垂直的直线的斜率是：-1，设直线的解析式是：y=-x+b，把（，）代入得：=-+b，解得：b=，则直线的解析式是：y=-x+，令y=0，解得：x=，则P的坐标是（，0）．故P的坐标是：（-3，0）或（3，0）或（6，0）或（，0）．。

八年级下册数学期末压轴题(含答案)

八年级数学下册期末压轴题练习（含答案）一、填空题：1.如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ 的最小值为 .2.如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．3.如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AE PQ的周长取最小值时，四边形AEPQ 的面积是．4.如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点(不与点A．点D重合)将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH.现给出以下四个命题（1）∠APB=∠BPH;（2）当点P在边AD上移动时，△PDH的周长不发生变化; （3）∠PBH=450 ; （4）BP=BH.其中正确的命题是．5.如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是．二、综合题：6. (1)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.求证：CE=CF；(2)如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用(1)的结论证明：GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积.7.如图，已知等腰Rt△ABC和△CDE，AC=BC,CD=CE，连接BE、AD，P为BD中点，M为AB中点、N为DE中点，连接PM、PN、MN.（1）试判断△PMN的形状，并证明你的结论；（2）若CD=5，AC=12，求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．（1）①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：．②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：（2）当正方形AEFG旋转任意一个角度时（如图3），（1）中的结论是否仍然成立？若成立请证明，若不成立请说明理由．（3）已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是 cm2．9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．（1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为，周长为；（2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为，周长为；（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．10.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．参考答案1.答案为：3.3.答案为：4.5．2.答案为：7；解法一：如图1所示，过O作OF⊥BC，过A作AM⊥OF，∵四边形ABDE为正方形，∴∠AOB=90°，OA=OB，∴∠AOM+∠BOF=90°，又∠AMO=90°，∴∠AOM+∠OAM=90°，∴∠BOF=∠OAM，在△AOM和△BOF 中，，∴△AOM≌△BOF（AAS），∴AM=OF，OM=FB，又∠ACB=∠AMF=∠CFM=90°，∴四边形ACFM为矩形，∴AM=CF，AC=MF=5，∴OF=CF，∴△OCF为等腰直角三角形，∵OC=6，∴根据勾股定理得：CF2+OF2=OC2，解得：CF=OF=6，∴FB=OM=OF﹣FM=6﹣5=1，则BC=CF+BF=6+1=7．故答案为：7．解法二：如图2所示，过点O作OM⊥CA，交CA的延长线于点M；过点O作ON⊥BC于点N．易证△OMA≌△ONB，∴OM=ON，MA=NB．∴O点在∠ACB的平分线上，∴△OCM为等腰直角三角形．∵OC=6，∴CM=ON=6．∴MA=CM﹣AC=6﹣5=1，∴BC=CN+NB=6+1=7．故答案为：7．4.答案为：（1）（2）（3）．5.答案为：2；解：作D 关于AE 的对称点D′，再过D′作D′P′⊥AD于P′，∵DD′⊥AE，∴∠AFD=∠AFD′，∵AF=AF，∠DAE=∠CAE，∴△DAF≌△D′AF，∴D′是D关于AE的对称点，AD′=AD=4，∴D′P′即为DQ+PQ的最小值，∵四边形ABCD是正方形，∴∠DAD′=45°，∴AP′=P′D′，∴在Rt△AP′D′中，P′D′2+AP′2=AD′2，AD′2=16，∵AP′=P′D'，2P′D′2=AD′2，即2P′D′2=16，∴P′D′=2，即DQ+PQ的最小值为2，6. (1)证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°.∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明：如图2，延长AD至F，使DF=BE，连接CF.由(1)知△CBE≌△CDF，∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°.∵CE=CF，GC=GC，∴△ECG≌△FCG.∴GE=GF，∴GE=GF=DF+GD=BE+GD.(3)解：如图3，过C作CG⊥AD，交AD延长线于G.在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°，根据(1)(2)可知，ED=BE+DG.…∴10=4+DG，即DG=6.设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=(x﹣6)2+(x﹣4)2.解这个方程，得：x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解：（1）①∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E 点旋转到DA的延长线上，∴AE=AG，AB=AD，∠EAB=∠GAD，∴△ABE≌△ADG（SAS），∴△ABE的面积=△ADG的面积；②作GH⊥DA交DA的延长线于H，如图2，∴∠AHG=90°，∵E点旋转到CB的延长线上，∴∠ABE=90°，∠HAB=90°，∴∠GAH=∠EAB，在△AHG和△AEB中，∴△AHG≌△AEB，∴GH=BE，∵△ABE的面积=0.5EB•AB，△ADG的面积=0.5GH•AD，∴△ABE的面积=△ADG的面积；（2）结论仍然成立．理由如下：作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图3，∵∠PAD=90°，∠EAG=90°，∴∠PAE=∠GAH，在△AHG和△AEP中，∴△AHG≌△AEP（AAS），∴GH=BP，∵△ABP的面积=0.5EP•AB，△ADG的面积=0.5GH•AD，∴△ABP的面积=△ADG的面积；（3）∵AB=5cm，BC=3cm，∴AC==4cm，∴△ABC的面积=0.5×3×4=6（cm2）；根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2．故答案为相等；相等；18．8.解：（1）∵AM=MC=AC=a，则∴重叠部分的面积是△ACB的面积的一半为0.25a2，周长为（1+）a．（2）∵重叠部分是正方形∴边长为0.5a，面积为0.25a2，周长为2a．（3）猜想：重叠部分的面积为0.25a2．理由如下：过点M分别作AC、BC的垂线MH、MG，垂足为H、G 设MN与AC的交点为E，MK与BC的交点为F∵M是△ABC斜边AB的中点，AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF，∴∠HME=∠GMF，∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2．9.（1）证明：∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°，∵∠EAF=45°,∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）证明：设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）解：EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2。

八年级数学压轴题期末复习试卷同步检测(Word版含答案)

八年级数学压轴题期末复习试卷同步检测（Word版含答案）一、压轴题1．阅读并填空：如图，ABC是等腰三角形，AB AC=，D是边AC延长线上的一点，E在边AB 上且联接DE交BC于O，如果OE OD，那么CD BE=，为什么？解：过点E作EF AC交BC于F所以ACB EFB∠=∠（两直线平行，同位角相等）D OEF∠=∠（________）在OCD与OFE△中()________COD FOEOD OED OEF⎧∠=∠⎪=⎨⎪∠=∠⎩所以OCD OFE△≌△，（________）所以CD FE=（________）因为AB AC=（已知）所以ACB B=∠∠（________）所以EFB B∠=∠（等量代换）所以BE FE=（________）所以CD BE=2．如图，已知A(3，0)，B(0，-1)，连接AB，过B点作AB的垂线段BC，使BA=BC，连接AC（1）如图1，求C点坐标；（2）如图2，若P点从A点出发沿x轴向左平移，连接BP，作等腰直角BPQ，连接CQ，当点P在线段OA上，求证：PA=CQ；（3）在（2）的条件下若C、P，Q三点共线，直接写出此时∠APB的度数及P点坐标3．如图，在平面直角坐标系中，直线y＝2x＋4与x轴交于点A，与y轴交于点B，过点B 的另一条直线交x轴正半轴于点C，且OC＝3．图1 图2（1）求直线BC的解析式；（2）如图1，若M为线段BC上一点，且满足S△AMB＝S△AOB，请求出点M的坐标；（3）如图2，设点F为线段AB中点，点G为y轴上一动点，连接FG，以FG为边向FG右侧作正方形FGQP，在G点的运动过程中，当顶点Q落在直线BC上时，求点G的坐标；4．在平面直角坐标系中点A（m−3，3m+3），点 B（m，m+4）和 D（0，−5），且点 B 在第二象限．（1）点B 向平移单位，再向下平移（用含m 的式子表达）单位可以与点A 重合；（2）若点B 向下移动 3 个单位，则移动后的点B 和点A 的纵坐标相等，且有点 C（m−2，0）．①则此时点A、B、C 坐标分别为、、．②将线段AB 沿y 轴负方向平移n 个单位，若平移后的线段AB 与线段CD 有公共点，求n 的取值范围．③当m<−1 式，连接AD，若线段AD 沿直线AB 方向平移得到线段BE，连接DE 与直线y=−2 交于点F，则点F 坐标为．（用含m 的式子表达）5．在平面直角坐标系xOy中，若P，Q为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．图1为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，2）．（1）如图2，点B的坐标为（b，0）．①若b＝﹣2，则点A，B的“相关矩形”的面积是；②若点A，B的“相关矩形”的面积是8，则b的值为．（2）如图3，点C在直线y＝﹣1上，若点A，C的“相关矩形”是正方形，求直线AC的表达式；（3）如图4，等边△DEF的边DE在x轴上，顶点F在y轴的正半轴上，点D的坐标为（1，0）．点M的坐标为（m，2），若在△DEF的边上存在一点N，使得点M，N的“相关矩形”为正方形，请直接写出m的取值范围．6．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并说明理由；（4）如图4，△ABC外角∠CBM、∠BCN的平分线交于点Q，∠A=64°，∠CBQ，∠BCQ的平分线交于点P，则∠BPC= ゜，延长BC至点E，∠ECQ的平分线与BP的延长线相交于点R，则∠R= ゜．7．在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、E处，请问：（1）如图1，在爬行过程中，CD和BE始终相等吗，请证明？（2）如果将原题中的“由A向B和由C向A爬行”，改为“沿着AB和CA的延长线爬行”，EB与CD交于点Q，其他条件不变，蜗牛爬行过程中∠CQE的大小保持不变，请利用图2说明：∠CQE=60°；（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，如图3，则爬行过程中，证明：DF=EF∆中，线段AM为BC边上的中线．动点D在直线AM上时，以8．如图，在等边ABC∆，连结BE．CD为一边在CD的下方作等边CDE（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．9．已知ABC 和ADE 都是等腰三角形，AB AC =，AD AE =，DAE BAC ∠=∠．（初步感知）（1）特殊情形：如图①，若点D ，E 分别在边AB ，AC 上，则DB __________EC ．（填＞、＜或=）（2）发现证明：如图②，将图①中的ADE 绕点A 旋转，当点D 在ABC 外部，点E 在ABC 内部时，求证：DB EC =．（深入研究）（3）如图③，ABC 和ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则CDB ∠的度数为__________；线段CE ，BD 之间的数量关系为__________．（4）如图④，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，点C 、D 、E 在同一直线上，AM 为ADE 中DE 边上的高，则CDB ∠的度数为__________；线段AM ，BD ，CD 之间的数量关系为__________．（拓展提升）（5）如图⑤，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，将ADE 绕点A 逆时针旋转，连结BE 、CD ．当5AB =，2AD =时，在旋转过程中，ABE △与ADC 的面积和的最大值为__________．10．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______．（2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系．11．已知，在平面直角坐标系中，(42,0)A ，(0,42)B ，C 为AB 的中点，P 是线段AB 上一动点，D 是线段OA 上一点，且PO PD =，DE AB ⊥于E ．（1）求OAB ∠的度数；（2）当点P 运动时，PE 的值是否变化？若变化，说明理由；若不变，请求PE 的值．（3）若45OPD ∠=︒，求点D 的坐标．12．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ，点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ，点N 从点F 出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ，点,M N 同时开始运动，各自达到相应的终点时停止运动，设运动时间为t 秒，当CMN △为等腰直角三角形时，求t 的值．【参考答案】***试卷处理标记，请不要删除一、压轴题1．见解析【解析】【分析】先根据平行线的性质，得到角的关系，然后证明OCD OFE△≌△，写出证明过程和依据即可．【详解】解：过点E作//EF AC交BC于F，∴ACB EFB∠=∠（两直线平行，同位角相等），∴D OEF∠=∠（两直线平行，内错角相等），在OCD与OFE△中()()()COD FOEOD OED OEF⎧∠=∠⎪=⎨⎪∠=∠⎩对顶角相等已知已证，∴OCD OFE△≌△，（ASA）∴CD FE=（全等三角形对应边相等）∵AB AC=（已知）∴ACB B=∠∠（等边对等角）∴EFB B∠=∠（等量代换）∴BE FE=（等角对等边）∴CD BE=；【点睛】本题考查了全等三角形的判定和性质，平行线的性质，解题的关键是由平行线的性质正确找到证明三角形全等的条件，从而进行证明.2．（1）(1，-4)；（2）证明见解析；（3）()135,1,0APB P︒∠=【解析】【分析】（1）作CH⊥y轴于H，证明△ABO≌△BCH，根据全等三角形的性质得到BH=OA=3，CH=OB=1，求出OH，得到C点坐标；（2）证明△PBA≌△QBC，根据全等三角形的性质得到PA=CQ；（3）根据C、P，Q三点共线，得到∠BQC=135°，根据全等三角形的性质得到∠BPA=∠BQC=135°，根据等腰三角形的性质求出OP ，得到P 点坐标．【详解】解：(1)作CH ⊥y 轴于H ，则∠BCH+∠CBH=90°，因为AB BC ⊥，所以.∠ABO+∠CBH=90°，所以∠ABO=∠BCH ，在△ABO 和△BCH 中，ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3，CH=OB=1，:OH=OB+BH=4，所以C 点的坐标为（1，-4）；(2)因为∠PBQ=∠ABC=90°，,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中，BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ；(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形，:所以∠BQP=45°，当C 、P ，Q 三点共线时，∠BQC=135°，由（2)可知，PBA QBC ∴∆≅∆；所以∠BPA=∠BQC=135°，所以∠OPB=45°，所以.OP=OB=1，所以P 点坐标为（1，0) ．【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质，掌握全等三角形的判定定理和性质定理是解题的关键．3．（1）443y x =-+；（2）612(,)55M ；（3）23(0,)7G 或(0,-1)G【解析】【分析】（1）求出点B，C坐标，再利用待定系数法即可解决问题；（2）结合图形，由S△AMB＝S△AOB 分析出直线OM平行于直线AB，再利用两直线相交建立方程组求得交点M的坐标；（3）分两种情形：①当n＞2时，如图2-1中，点Q落在BC上时，过G作直线平行于x 轴，过点F，Q作该直线的垂线，垂足分别为M，N．求出Q（n-2，n-1）．②当n＜2时，如图2-2中，同法可得Q（2-n，n+1），代入直线BC的解析式解方程即可解决问题．【详解】解：（1）∵直线y=2x+4与x轴交于点A，与y轴交于点B，∴A（-2，0），B（0，4），，又∵OC=3，∴C（3，0），设直线BC的解析式为y=kx+b，将B、C的坐标代入得：304k bb+=⎧⎨=⎩，解得：434kb⎧=-⎪⎨⎪=⎩，∴直线BC的解析式为443y x=-+；（2）连接OM，∵S△AMB＝S△AOB，∴直线OM平行于直线AB，故设直线OM解析式为：2y x=,将直线OM的解析式与直线BC的解析式联立得方程组2443y xy x=⎧⎪⎨=-+⎪⎩，解得：65125xy⎧=⎪⎪⎨⎪=⎪⎩故点612(,)55M；（3）∵FA=FB，A（-2，0），B（0，4），∴F（-1，2），设G（0，n），①当n＞2时，如图2-1中，点Q落在BC上时，过G作直线平行于x轴，过点F，Q作该直线的垂线，垂足分别为M，N．∵四边形FGQP是正方形，易证△FMG≌△GNQ，∴MG=NQ=1，FM=GN=n-2，∴Q（n-2，n-1），∵点Q在直线443y x=-+上，∴41(2)43n n-=--+，∴23=7n,∴23(0,)7G．②当n＜2时，如图2-2中，同法可得Q（2-n，n+1），∵点Q 在直线443y x =-+上， ∴4+1(2)43n n =--+， ∴n=-1，∴(0,-1)G ．综上所述，满足条件的点G 坐标为23(0,)7G 或(0,-1)G 【点睛】本题属于一次函数综合题，考查了待定系数法，三角形的面积，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．4．（1）左；3；(1-2m )；（2）①（-4，0）；（-1，0）（-3，0）； ②当平移后的线段 AB 与线段 CD 有公共点时，1913n ≤≤；③ F 9(,2)12m--．【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后，点B 和点A 的纵坐标相等得到等量关系，可求出m 的值，从而求出A 、B 、C 三点坐标；②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设出K 点坐标，作 KH ⊥BM 与 H 点，表示出H 点坐标，然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离；当 B '在线段 CD 上时，BB '交 x 轴于 M 点，过 B '做 B 'E ⊥OD ，利用S △COD = S △OB'C + S △OB'D ，求出n 的值，从而求出n 的取值范围；③通过坐标平移法用m 表示出E 点的坐标，利用D 、E 两点坐标表示出直线DE 的函数关系式，令y=﹣2，求出x 的值即可求出F 点坐标．【详解】解：（1）根据平移规律可得：B 向左平移；m －（m －1）=3，所以平移3个单位；m+4－（3m+3）=1－2m ，所以再向下平移(1-2m )个单位；故答案为：左；3；(1-2m )（2）①点 B 向下移动 3 个单位得：B （m ，m+1）∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A （-4,0）；B （-1,0）；C （-3,0）；②如图 1，过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设 K 点坐标为（-3，a ）M 点坐标为（-1,0）作 KH ⊥BM 与 H 点，H 点坐标为（-1，a ）AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得：1a =，∴当线段 AB 向下平移 1 个单位时，线段 AB 和 CD 开始有交点，∴ n ≥ 1，当 B'在线段 CD 上时，如图 2BB'交 x 轴于 M 点，过 B'做 B'E ⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S △COD = S △OB'C + S △OB'D∴''222CO OD CO B M OD B E ⨯⨯⨯=+ ∴353(3)51222n ⨯⨯-⨯=+ 解得：193n =，综上所述，当平移后的线段 AB 与线段 CD 有公共点时，1913n ≤≤．③∵A（m−3，3m+3）， B（m，m+4） D（0，−5）且AD 沿直线 AB 方向平移得到线段BE，∴E点横坐标为：3E点纵坐标为：﹣5+m+4－（3m+3）=﹣4－2m∴E（3，﹣4－2m），设DE：y=kx+b，把D（0，﹣5），E（3，﹣4－2m）代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣－﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩，∴y=12mx53－－，把y=﹣2代入解析式得：﹣2=12mx53－－，x=912m－，∴F9(,2) 12m--．【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法，解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用．5．（1）①6；②5或﹣3；（2）直线AC的表达式为：y＝﹣x+3或y＝x+1；（3）m的取值范围为﹣3≤m≤﹣323m≤3．【解析】【分析】（1）①由矩形的性质即可得出结果；②由矩形的性质即可得出结果；（2）过点A（1，2）作直线y＝﹣1的垂线，垂足为点G，则AG＝3求出正方形AGCH的边长为3，分两种情况求出直线AC的表达式即可；（3）由题意得出点M在直线y＝2上，由等边三角形的性质和题意得出OD＝OE＝12DE＝1，EF＝DF＝DE＝2，得出OF3OD3①当点N在边EF上时，若点N与E重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣3，2）或（1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣32）；得出m的取值范围为﹣3≤m≤﹣3或2﹣3≤m≤1；②当点N在边DF上时，若点N与D重合，点M，N的“相关矩形”为正方形，则点M 的坐标为（3，2）或（﹣1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（232）；得出m的取值范围为23≤m≤3或2﹣3≤m≤1；即可得出结论．【详解】解：（1）①∵b＝﹣2，∴点B的坐标为（﹣2，0），如图2﹣1所示：∵点A的坐标为（1，2），∴由矩形的性质可得：点A，B的“相关矩形”的面积＝（1+2）×2＝6，故答案为：6；②如图2﹣2所示：由矩形的性质可得：点A，B的“相关矩形”的面积＝|b﹣1|×2＝8，∴|b﹣1|＝4，∴b＝5或b＝﹣3，故答案为：5或﹣3；（2）过点A（1，2）作直线y＝﹣1的垂线，垂足为点G，则AG＝3，∵点C在直线y＝﹣1上，点A，C的“相关矩形”AGCH是正方形，∴正方形AGCH的边长为3，当点C在直线x＝1右侧时，如图3﹣1所示：CG＝3，则C（4，﹣1），设直线AC的表达式为：y＝kx+a，则214k ak a=+⎧⎨-=+⎩，解得；13ka=-⎧⎨=⎩，∴直线AC的表达式为：y＝﹣x+3；当点C在直线x＝1左侧时，如图3﹣2所示：CG＝3，则C（﹣2，﹣1），设直线AC的表达式为：y＝k′x+b，则212k bk b=+⎧⎨-=-+''⎩，解得：k1 b1=⎧⎨='⎩，∴直线AC的表达式为：y＝x+1，综上所述，直线AC的表达式为：y＝﹣x+3或y＝x+1；（3）∵点M的坐标为（m，2），∴点M在直线y＝2上，∵△DEF是等边三角形，顶点F在y轴的正半轴上，点D的坐标为（1，0），∴OD＝OE＝12DE＝1，EF＝DF＝DE＝2，∴OF OD分两种情况：如图4所示：①当点N在边EF上时，若点N与E重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣3，2）或（1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣2+3，2）或（2﹣3，2）；∴m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤1；②当点N在边DF上时，若点N与D重合，点M，N的“相关矩形”为正方形，则点M的坐标为（3，2）或（﹣1，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（2﹣3，2）或（﹣2+3，2）；∴m的取值范围为2﹣3≤m≤3或﹣1≤m≤﹣2+3；综上所述，m的取值范围为﹣3≤m≤﹣2+3或2﹣3≤m≤3．【点睛】此题主要考查图形与坐标综合，解题的关键是熟知正方形的性质、一次函数的图像与性质及新定义的应用．6．（1） 122°；（2）12BEC α∠=；（3）01902BQC A ；（4）119，29 ；【解析】【分析】（1）根据三角形的内角和角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用A ∠与1∠表示出2∠，再利用E ∠与1∠表示出2∠，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠，然后再根据三角形的内角和定理列式整理即可得解；（4）根据（1），（3）的结论可以得出∠BPC 的度数；根据（2）的结论可以得到∠R 的度数．【详解】解：（1）BP 、CP 分别平分ABC ∠和ACB ∠，12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122，故答案为：122︒；（2）如图2示，CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠，又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠，112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=；（3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠， 180BQC QBC QCB ∠=︒-∠-∠，11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠，结论1902BQC A ∠=︒-∠．（4）由（3）可知，119090645822BQCA ，再根据（1），可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119；由（2）可得：11582922R Q ;故答案为：119，29．【点睛】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．7．（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD≌△CBE，再由全等三角形的性质即可证得CD=BE；（2）先证明△BCD≌△ABE，得到∠BCD=∠ABE，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC，∠CQE=180°-∠DQB，即可解答；（3）如图3，过点D作DG∥BC交AC于点G，根据等边三角形的三边相等，可以证得AD=DG=CE；进而证明△DGF和△ECF全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD和BE始终相等，理由如下：如图1，AB=BC=CA，两只蜗牛速度相同，且同时出发，∴CE=AD，∠A=∠BCE=60°在△ACD与△CBE中，AC=CB，∠A=∠BCE，AD=CE∴△ACD≌△CBE（SAS），∴CD=BE，即CD和BE始终相等；（2）证明：根据题意得：CE=AD，∵AB=AC，∴AE=BD，∴△ABC是等边三角形，∴AB=BC，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC，在△BCD和△ABE中，BC=AB，∠DBC=∠EAB，BD=AE∴△BCD≌△ABE（SAS），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF 始终等于EF 是正确的，理由如下：如图，过点D 作DG ∥BC 交AC 于点G ，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E ，∴△ADG 为等边三角形，∴AD=DG=CE ，在△DGF 和△ECF 中，∠GFD=∠CFE ，∠GDF=∠E ，DG=EC∴△DGF ≌△EDF （AAS ），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．8．（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.9．（1）=；（2）证明见解析；（3）60°，BD=CE ；（4）90°，AM+BD=CM ；（5）7【解析】【分析】（1）由DE ∥BC ，得到DB EC AB AC=，结合AB=AC ，得到DB=EC ；（2）由旋转得到的结论判断出△DAB ≌△EAC ，得到DB=CE ；（3）根据等边三角形的性质和全等三角形的判定定理证明△DAB ≌△EAC ，根据全等三角形的性质求出结论；（4）根据全等三角形的判定和性质和等腰直角三角形的性质即可得到结论；（5）根据旋转的过程中△ADE 的面积始终保持不变，而在旋转的过程中，△ADC 的AC 始终保持不变，即可．【详解】[初步感知]（1）∵DE ∥BC ，∴DB EC AB AC=， ∵AB=AC ，∴DB=EC ，故答案为：=，（2）成立．理由：由旋转性质可知∠DAB=∠EAC，在△DAB和△EAC中AD AEDAB EACAB AC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△DAB≌△EAC（SAS），∴DB=CE；[深入探究]（3）如图③，设AB，CD交于O，∵△ABC和△ADE都是等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，∴∠DAB=∠EAC，在△DAB和△EAC中AD AEDAB EACAB AC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△DAB≌△EAC（SAS），∴DB=CE，∠ABD=∠ACE，∵∠BOD=∠AOC，∴∠BDC=∠BAC=60°；（4）∵△DAE是等腰直角三角形，∴∠AED=45°，∴∠AEC=135°，在△DAB和△EAC中AD AEDAB EACAB AC⎪∠⎪⎩∠⎧⎨＝＝＝，∴△DAB≌△EAC（SAS），∴∠ADB=∠AEC=135°，BD=CE，∵∠ADE=45°，∴∠BDC=∠ADB-∠ADE=90°，∵△ADE都是等腰直角三角形，AM为△ADE中DE边上的高，∴AM=EM=MD ，∴AM+BD=CM ；故答案为：90°，AM+BD=CM ；【拓展提升】（5）如图，由旋转可知，在旋转的过程中△ADE 的面积始终保持不变，△ADE 与△ADC 面积的和达到最大，∴△ADC 面积最大，∵在旋转的过程中，AC 始终保持不变， ∴要△ADC 面积最大，∴点D 到AC 的距离最大，∴DA ⊥AC ，∴△ADE 与△ADC 面积的和达到的最大为2+12×AC×AD=5+2=7，故答案为7．【点睛】此题是几何变换综合题，主要考查了旋转和全等三角形的性质和判定，旋转过程中面积变化分析，解本题的关键是三角形全等的判定．10．90︒，45︒；20︒，30︒；2a γβ+=，2a γβ-=.【解析】【分析】（1）①如图①知1112EMC BMC ∠=∠，1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.（2）①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠，可推出11()BMC EMF EMF C MB ∠-∠-∠=∠，即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠，可推出()112906090A MC ︒︒︒-+∠=，即可求出解.（3）如图⑤-1、⑤-2中分别由折叠可知，a ββγ-=-、a ββγ-=+，即可求得 2a γβ+=、2a γβ-=.【详解】解：（1）①如图①中，1112EMC BMC ∠=∠，1112C MF C MC ∠=∠， ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=，故答案为90︒. ②如图②中，111111,22EBA ABC C BF C BC ∠=∠∠=∠， ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=，故答案为45︒.（2）①如图③中由折叠可知，11,CMF FMC BME EMB ∠=∠∠=∠，1111C MF EMB EMF C MB ∠+∠-∠=∠，11CMF BME EMF C MB ∴∠+∠-∠=∠，11()BMC EMF EMF C MB ∴∠-∠-∠=∠，111808020C MB ︒︒︒∴-=∠=；②如图④中根据折叠可知，11,CMF C MF ABE A BE ∠=∠∠=∠，112290CMF ABE A MC ︒∠+∠+∠=，112()90CMF ABE A MC ︒∴∠+∠+∠=，()1129090EMF AMC ︒︒∴-∠+∠=，()112906090AMC ︒︒︒∴-+∠=， 1130A MC ︒∴∠=；（3）如图⑤-1中，由折叠可知，a ββγ-=-，2a γβ∴+=；如图⑤-2中，由折叠可知，a ββγ-=+，2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换，图形的角度及边长不变及一些角度的计算问题，突出考查学生的观察能力、思维能力以及动手操作能力，本题是代数、几何知识的综合运用典型题目.11．（1）45°；（2）PE 的值不变，PE=4，理由见详解；（3）D(828 ，0)．【解析】【分析】（1）根据(42,0)A ，(0,2)B ，得△AOB 为等腰直角三角形，根据等腰直角三角形的性质，即可求出∠OAB 的度数；（2）根据等腰直角三角形的性质得到∠AOC=∠BOC=45°，OC ⊥AB ，再证明△POC ≌△DPE ，根据全等三角形的性质得到OC=PE ，即可得到答案；（3）证明△POB ≌△DPA ，得到PA=OB=2，DA=PB ，进而得OD 的值，即可求出点D 的坐标．【详解】（1）(42,0)A ，(0,42)B ，∴OA=OB=2∵∠AOB=90°，∴△AOB 为等腰直角三角形，∴∠OAB=45°；（2）PE 的值不变，理由如下：∵△AOB 为等腰直角三角形，C 为AB 的中点，∴∠AOC=∠BOC=45°，OC ⊥AB ，∵PO=PD ，∴∠POD=∠PDO ，∵D 是线段OA 上一点，∴点P 在线段BC 上，∵∠POD=45°+∠POC ，∠PDO=45°+∠DPE ，∴∠POC=∠DPE ，在△POC 和△DPE 中，90OCP PED PO PD ⎪∠=∠=︒⎨⎪=⎩，∴△POC ≅△DPE(AAS)，∴OC=PE ，∵OC=12AB=12××=4， ∴PE=4；（3）∵OP=PD ， ∴∠POD=∠PDO=(180°−45°)÷2=67.5°，∴∠APD=∠PDO−∠A=22.5°，∠BOP=90°−∠POD=22.5°，∴∠APD=∠BOP ，在△POB 和△DPA 中，OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS)，∴PA=OB=DA=PB ，∴DA=PB=-，∴OD=OA−DA=8-，∴点D 的坐标为(8，0)．【点睛】本题主要考查等腰直角三角形的性质，三角形全等的判定与性质定理，图形与坐标，掌握等腰直角三角形的性质，是解题的关键．12．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用AAS 定理证明△ACD ≌△CBE ；（2）分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD 与△CBE 全等．理由如下：∵AD ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，DAC ECB CA CB ⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ）；（2）由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ，点N 在BC 上时，△CMN 为等腰直角三角形，当点N 沿C→B 路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N 沿B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN 为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．。

2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

2021年人教版数学八年级下册期末《压轴题专项》复习卷1.如图，点A的坐标是(－2，0)，点B的坐标是(6，0)，点C在第一象限内且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD，垂足为E，交OC于点F.(1)求直线BD的函数表达式；(2)求线段OF的长；(3)连接BF，OE，试判断线段BF和OE的数量关系，并说明理由．2.阅读下面材料：我们知道一次函数y=kx+b(k≠0，k、b是常数)的图象是一条直线，到高中学习时，直线通常写成Ax+By+C=0(A≠0，A、B、C是常数)的形式，点P(x0，y0)到直线Ax+By+C=0的距离可用公式d=计算．例如：求点P(3，4)到直线y=﹣2x+5的距离．根据以上材料解答下列问题：(1)求点Q(﹣2，2)到直线3x﹣y+7=0的距离；(2)如图，直线y=﹣x沿y轴向上平移2个单位得到另一条直线，求这两条平行直线之间的距离．3.已知正方形ABCD，AB=8，点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t．（1）求证：OE=OF．（2）在点E、F的运动过程中，连结AF．设线段AE、OE、OF、AF所形成的图形面积为S．探究：①S的大小是否会随着运动时间为t的变化而变化？若会变化，试求出S与t的函数关系式；若不会变化，请说明理由．②连结EF，当运动时间为t为何值时，△OEF的面积恰好等于的S．4.如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数的图象交点为C（m，4）．求：（1）一次函数y=kx+b的解析式；（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，则点D的坐标为；（3）在x轴上求一点P使△POC为等腰三角形，请求出所有符合条件的点P的坐标．5.将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0)，MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF.(1)求点G的坐标；(2)求直线EF的解析式；(3)设点P为直线EF上一点，是否存在这样的点P，使以P, F, G的三角形是等腰三角形?若存在，直接写出P点的坐标;若不存在，请说明理由.6.如图,已知直线y=kx+1经过点A(3,-2)、点B(a,2)，交y轴于点M.（1）求a的值及AM的长（2）在x轴的负半轴上确定点P，使得△AMP成等腰三角形，请你直接写出点P的坐标.（3）将直线AB绕点A逆时针旋转45°得到直线AC，点D（-3，b）在AC上，连接BD，设BE是△ABD 的高，过点E的射线EF将△ABD的面积分成2：3两部分，交△ABD的另一边于点F，求点F的坐标.7.阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法．如图1，在等腰△ABC中，AB=AC，AC边上的高为h，点M为底边BC 上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM+S△ACM，可以得出结论：h=h1+h2．类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论．拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y=0.75x+3，l2：y=﹣3x+3，若l2上一点M到l1的距离是1，试运用“阅读理解”和“类比探究”中获得的结论，求出点M 的坐标．8.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x ﹣2与x轴、y轴分别交于点E、F．（1）求：①点D的坐标；②经过点D,且与直线FC平行的直线的函数表达式；（2）直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形？若存在,求出点P 的坐标；若不存在,请说明理由．（3）在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形，请直接写出点M的坐标．9.如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为（4,0）,点B的坐标为（0,1）,点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE．（1）线段OC的长为；（2）求证：△CBD≌△COE；（3）将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1，其中点O,B,D,E的对应点分别为点O1，B1，D1，E1，连接CD,CE,设点E的坐标为（a，0）,其中a≠2,△CD1E1的面积为S．①当1＜a＜2时,请直接写出S与a之间的函数表达式；②在平移过程中,当S=时,请直接写出a的值．10.如图，直线y=2x+m(m>0)与x轴交于点A(-2,0)直线y=-x+n(n>0)与x轴、y轴分别交于B、C 两点，并与直线y=2x+m(m>0)相交于点D，若AB=4．（1）求点D的坐标；（2）求出四边形AOCD的面积；（3）若E为x轴上一点，且△ACE为等腰三角形，直接写出点E的坐标．11.如图，直线l：交x、y轴分别为A、B两点，C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合)，满足∠BPQ=∠BAO.(1)点A坐标是， BC= .(2)当点P在什么位置时，△APQ≌△CBP，说明理由。

八年级数学压轴题期末复习试卷(培优篇)(Word版含解析)

八年级数学压轴题期末复习试卷（培优篇）（Word 版含解析）一、压轴题1．定义：在平面直角坐标系中，对于任意两点(),A a b ，(),B c d ，若点(),T x y 满足3a c x +=，3b d y +=那么称点T 是点A ，B 的融合点．例如：()1,8A -，()4,2B -，当点(),T x y 满足1413x -+==，()8223y +-==时，则点()1,2T 是点A ，B 的融合点．（1）已知点()1,5A -，()7,4B ，()2,3C ，请说明其中一个点是另外两个点的融合点．（2）如图，点()4,0D ，点(),25E t t +是直线l 上任意一点，点(),T x y 是点D ，E 的融合点．①试确定y 与x 的关系式；②在给定的坐标系xOy 中，画出①中的函数图象；③若直线ET 交x 轴于点H ．当DTH 为直角三角形时，直接写出点E 的坐标．2．在平面直角坐标系中，点A 、B 在坐标轴上，其中A(0，a)、B(b ，0)满足：222110a b a b --++-=．（1）直接写出A 、B 两点的坐标；（2）将线段AB 平移到CD ，点A 的对应点为C(-3，m)，如图(1)所示．若S ΔABC =16，求点D 的坐标；（3）平移线段AB 到CD ，若点C 、D 也在坐标轴上，如图(2)所示，P 为线段AB 上一动点(不与A 、B 重合)，连接OP ，PE 平分∠OPB ，交x 轴于点M ，且满足∠BCE=2∠ECD ．求证：∠BCD=3(∠CEP-∠OPE)．3．（1）探索发现：如图1，已知Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，过点A作AD⊥l，过点B作BE⊥l，垂足分别为D、E．求证：AD＝CE，CD＝BE．（2）迁移应用：如图2，将一块等腰直角的三角板MON放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O重合，另两个顶点均落在第一象限内，已知点M的坐标为（1，3），求点N的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线y＝﹣3x+3与y轴交于点P，与x轴交于点Q，将直线PQ绕P点沿逆时针方向旋转45°后，所得的直线交x轴于点R．求点R的坐标．4．如图，已知A(3，0)，B(0，-1)，连接AB，过B点作AB的垂线段BC，使BA=BC，连接AC（1）如图1，求C点坐标；（2）如图2，若P点从A点出发沿x轴向左平移，连接BP，作等腰直角BPQ，连接CQ，当点P在线段OA上，求证：PA=CQ；（3）在（2）的条件下若C、P，Q三点共线，直接写出此时∠APB的度数及P点坐标AB=，5．如图，已知四边形ABCO是矩形，点A，C分别在y轴，x轴上，4BC=．3（1）求直线AC 的解析式；（2）作直线AC 关于x 轴的对称直线，交y 轴于点D ，求直线CD 的解析式．并结合（1）的结论猜想并直接写出直线y kx b =+关于x 轴的对称直线的解析式；（3）若点P 是直线CD 上的一个动点，试探究点P 在运动过程中，||PA PB -是否存在最大值？若不存在，请说明理由；若存在，请求出||PA PB -的最大值及此时点P 的坐标．6．问题背景：（1）如图1，已知△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．求证：DE ＝BD ＋CE ．拓展延伸：（2）如图2，将（1）中的条件改为：在△ABC 中，AB ＝AC ，D 、A 、E 三点都在直线m 上，并且有∠BDA ＝∠AEC ＝∠BAC ．请写出DE 、BD 、CE 三条线段的数量关系．（不需要证明）实际应用：（3）如图，在△ACB 中，∠ACB ＝90°，AC ＝BC ，点C 的坐标为(－2，0)，点A 的坐标为(－6，3)，请直接写出B 点的坐标．7．如图①，在ABC ∆中，12AB =cm ，20BC =cm ，过点C 作射线//CD AB ．点M 从点B 出发，以3 cm/s 的速度沿BC 匀速移动；点N 从点C 出发，以a cm/s 的速度沿CD 匀速移动．点M 、N 同时出发，当点M 到达点C 时，点M 、N 同时停止移动．连接AM 、MN ，设移动时间为t (s)．(1)点M 、N 从移动开始到停止，所用时间为 s ；(2)当ABM ∆与MCN ∆全等时，①若点M 、N 的移动速度相同，求t 的值；②若点M 、N 的移动速度不同，求a 的值；(3)如图②，当点M 、N 开始移动时，点P 同时从点A 出发，以2 cm/s 的速度沿AB 向点B 匀速移动，到达点B 后立刻以原速度沿BA 返回．当点M 到达点C 时，点M 、N 、P 同时停止移动．在移动的过程中，是否存在PBM ∆与MCN ∆全等的情形?若存在，求出t 的值；若不存在，说明理由．8．已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD ．（1）如图1，①求证：点B ，C ，D 在以点A 为圆心，AB 为半径的圆上；②直接写出∠BDC 的度数（用含α的式子表示）为；（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD ；（3）如图3，当α=90°时，记直线l 与CD 的交点为F ，连接BF ．将直线l 绕点A 旋转的过程中，在什么情况下线段BF 的长取得最大值？若AC =22a ，试写出此时BF 的值．9．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______．（2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系．10．已知，在平面直角坐标系中，(42,0)A ，(0,42)B ，C 为AB 的中点，P 是线段AB 上一动点，D 是线段OA 上一点，且PO PD =，DE AB ⊥于E ．（1）求OAB ∠的度数；（2）当点P 运动时，PE 的值是否变化？若变化，说明理由；若不变，请求PE 的值．（3）若45OPD ∠=︒，求点D 的坐标．11．如图，以ABC 的边AB 和AC ，向外作等腰直角三角形ABE △和ACF ，连接 EF ，AD 是ABC 的高，延长DA 交EF 于点G ，过点F 作DG 的垂线交DG 于点H ．（1）求证：FHA ADC ≌△△；（2）求证：点G 是EF 的中点．12．如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，点D 在边AB 上，点E 在边AC 的左侧，连接AE ．（1）求证：AE ＝BD ；（2）试探究线段AD 、BD 与CD 之间的数量关系；（3）过点C 作CF ⊥DE 交AB 于点F ，若BD ：AF ＝1：2，CD 36，求线段AB 的长．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）点C 是点A 、B 的融合点；（2）①2-1y x =；②见详解；③点E 的坐标为：（2，9）或（8，21）【解析】【分析】（1）根据融合点的定义3a c x +=，3b d y +=，即可求解；（2）①由题意得：分别得到x 与t 、y 与t 的关系，即可求解；②利用①的函数关系式解答；③分∠DTH ＝90°、∠TDH ＝90°、∠HTD ＝90°三种情况，分别求解即可．【详解】解：（1）x ＝-17233a c ++==，y ＝54333b d ++==，故点C 是点A 、B 的融合点；（2）①由题意得：x ＝433a c t ++=，y ＝2533b d t ++=，则3-4t x =，则()23-452-13x y x +==； ②令x ＝0，y ＝-1；令y ＝0，x ＝12，图象如下：③当∠THD＝90°时，∵点E（t，2t＋5），点T（t，2t−1），点D（4，0），且点T（x，y）是点D，E的融合点．∴t＝13（t＋4），∴t＝2，∴点E（2，9）；当∠TDH＝90°时，∵点E（t，2t＋5），点T（4，7），点D（4，0），且点T（x，y）是点D，E的融合点．∴4＝13（4＋t）∴t＝8，∴点E（8，21）；当∠HTD＝90°时，由于EH 与x 轴不平行，故∠HTD 不可能为90°；故点E 的坐标为：（2，9）或（8，21）．【点睛】本题是一次函数综合运用题，涉及到直角三角形的运用，此类新定义题目，通常按照题设顺序，逐次求解．2．（1）A （0，3），B （4，0）；（2）D （1，－265）；（3）见解析【解析】【分析】（1）根据非负数的性质求解；（2）如图1中，设直线CD 交y 轴于E ．首先求出点E 的坐标，再求出直线CD 的解析式以及点C 坐标，利用平移的性质得到点D 坐标；（3）如图2中，延长AB 交CE 的延长线于M ．利用平行线的性质以及三角形的外角的性质求证；【详解】（1）∵222110a b a b --++-=，∴220,2110a b a b --=+-=，∴2202110a b a b --=⎧⎨+-=⎩ ， ∴34a b =⎧⎨=⎩， ∴A （0，3），B （4，0）；（2）如图1中，设直线CD 交y 轴于E ．∵CD//AB ，∴S △ACB =S △ABE ，∴12AE×BO=16， ∴12×AE×4=16， ∴AE=8，∴E（0，-5），设直线AB的解析式为y=kx+b，将点A（0，3），（4，0）代入解析式中得：343kb⎧=-⎪⎨⎪=⎩，∴直线AB的解析式为y=334x-+，∵AB//CD，∴直线CD的解析式为y=34x c-+，又∵点E（0，－5）在直线CD上，∴c=5，即直线CD的解析式为y=354x--，又∵点C（-3，m）在直线CD上，∴m=115，∴C（-3，115），∵点A（0，3）平移后的对应点为C（-3，115），∴直线AB向下平移了265个单位，向左平移了3个单位，又∵B（4，0）的对应点为点D，∴点D的坐标为（1，－265）；（3）如图2中，延长AB交CE的延长线于点M．∵AM∥CD，∴∠DCM=∠M，∵∠BCE=2∠ECD，∴∠BCD=3∠DCM=3∠M，∵∠M=∠PEC-∠MPE，∠MPE=∠OPE，∴∠BCD=3（∠CEP-∠OPE）．【点睛】考查了非负数的性质、平行线的性质、三角形的外角的性质、一次函数的应用等知识，解题关键是灵活运用所学知识解决问题，学会添加常用辅助线，利用平行线的性质解决问题．3．（1）见解析（2）（4，2）（3）（6，0）【解析】【分析】（1）先判断出∠ACB=∠ADC，再判断出∠CAD=∠BCE，进而判断出△ACD≌△CBE，即可得出结论；（2）先判断出MF=NG，OF=MG，进而得出MF=1，OF=3，即可求出FG=MF+MG=1+3=4，即可得出结论；（3）先求出OP=3，由y=0得x=1，进而得出Q（1，0），OQ=1，再判断出PQ=SQ，即可判断出OH=4，SH=0Q=1，进而求出直线PR的解析式，即可得出结论.【详解】证明：∵∠ACB＝90°，AD⊥l∴∠ACB＝∠ADC∵∠ACE＝∠ADC+∠CAD，∠ACE＝∠ACB+∠BCE∴∠CAD＝∠BCE，∵∠ADC＝∠CEB＝90°，AC＝BC∴△ACD≌△CBE，∴AD＝CE，CD＝BE，（2）解：如图2，过点M作MF⊥y轴，垂足为F，过点N作NG⊥MF，交FM的延长线于G，由已知得OM＝ON，且∠OMN＝90°∴由（1）得MF＝NG，OF＝MG，∵M（1，3）∴MF＝1，OF＝3∴MG＝3，NG＝1∴FG＝MF+MG＝1+3＝4，∴OF﹣NG＝3﹣1＝2，∴点N的坐标为（4，2），（3）如图3，过点Q 作QS ⊥PQ ，交PR 于S ，过点S 作SH ⊥x 轴于H ，对于直线y ＝﹣3x+3，由x ＝0得y ＝3∴P （0，3），∴OP ＝3由y ＝0得x ＝1，∴Q （1，0），OQ ＝1，∵∠QPR ＝45°∴∠PSQ ＝45°＝∠QPS∴PQ ＝SQ∴由（1）得SH ＝OQ ，QH ＝OP∴OH ＝OQ+QH ＝OQ+OP ＝3+1＝4，SH ＝OQ ＝1∴S （4，1），设直线PR 为y ＝kx+b ，则341b k b =⎧⎨+=⎩ ，解得1k 2b 3⎧=-⎪⎨⎪=⎩ ∴直线PR 为y ＝﹣12x+3 由y ＝0得，x ＝6∴R （6，0）．【点睛】本题是一次函数综合题，主要考查了待定系数法，全等三角形的判定和性质，构造出全等三角形是解本题的关键.4．（1）(1，-4)；（2）证明见解析；（3）()135,1,0APB P ︒∠= 【解析】【分析】（1）作CH ⊥y 轴于H ，证明△ABO ≌△BCH ，根据全等三角形的性质得到BH=OA=3，CH=OB=1，求出OH ，得到C 点坐标；（2）证明△PBA ≌△QBC ，根据全等三角形的性质得到PA=CQ ；（3）根据C 、P ，Q 三点共线，得到∠BQC=135°，根据全等三角形的性质得到∠BPA=∠BQC=135°，根据等腰三角形的性质求出OP ，得到P 点坐标．【详解】解：(1)作CH ⊥y 轴于H ，则∠BCH+∠CBH=90°，因为AB BC ⊥，所以.∠ABO+∠CBH=90°，所以∠ABO=∠BCH ，在△ABO 和△BCH 中，ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3，CH=OB=1，:OH=OB+BH=4，所以C 点的坐标为（1，-4）；(2)因为∠PBQ=∠ABC=90°，,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中，BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ；(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形，:所以∠BQP=45°，当C 、P ，Q 三点共线时，∠BQC=135°，由（2)可知，PBA QBC ∴∆≅∆；所以∠BPA=∠BQC=135°，所以∠OPB=45°，所以.OP=OB=1，所以P 点坐标为（1，0) ．【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质，掌握全等三角形的判定定理和性质定理是解题的关键．5．（1）y =34-x +3；（2）y =34x -3，y =-kx -b ；（3）存在，4，(8，3) 【解析】【分析】（1）利用4AB =，3BC =，找出A 、C 两点的坐标，设直线解析式，利用待定系数法求出AC 的解析式；（2）由直线AC 关于x 轴的对称直线为CD 可知点D 的坐标，设直线解析式，利用待定系数法求出CD 的解析式，对比AC 的解析式进而写出直线y kx b =+关于x 轴的对称直线的解析式；（3）先判断||PA PB -存在最大值，在P 、A 、B 三点不共线时，P 点在运动过程中，与A 、B 两点组成三角形，两边之差小于第三边，得出结论在P 、A 、B 三点共线时，此时||PA PB -最大，y p = y A =3，求出P 点的纵坐标，最后根据点P 在直线CD 上，将P 点的纵坐标代入直线方程可得横坐标，从而求出P 点坐标．【详解】解：（1）在矩形ABCD 中，OC =AB =4，OA =BC =3，故A (0，3)，C (4，0)，设直线AC 的解析式为：y =kx +b (k ≠0，k 、b 为常数)，点A 、C 在直线AC 上，把A 、C 两点的坐标代入解析式可得：340b k b =⎧⎨+=⎩解得：343k b ⎧=-⎪⎨⎪=⎩，所以直线AC 的解析式为：y =34-x +3．（2）由直线AC 关于x 轴的对称直线为CD 可知：点D 的坐标为：(0，-3)，设直线CD 的解析式为：y =mx +n (m ≠0，m 、n 为常数)，点C 、D 在直线CD 上，把C 、D 两点的坐标带入解析式可得：-340n m n =⎧⎨+=⎩解得：343m n ⎧=⎪⎨⎪=-⎩，所以直线CD 的解析式为：y =34x -3，故猜想直线y kx b =+关于x 轴的对称直线的解析式为：y =-kx -b ．（3）点P 在运动过程中，||PA PB -存在最大值，由题意可知：如图，延长AB 与直线CD 交点即为点P ，此时||PA PB -最大，其他位置均有||PA PB -＜AB （P 点在运动过程中，与A 、B 两点组成任意三角形，两边之差小于第三边），此时，||PA PB -= AB =4，y p = y A =3，点P 在直线CD 上，将P 点的纵坐标代入直线方程可得：34x -3=3， x =8，故P 点坐标为(8，3)，||PA PB -的最大值为x p -x B =8-4=4．【点睛】本题主要考查利用待定系数法求解一次函数解析式及类比推理能力，掌握任意三角形两边之差小于第三边是解题的关键．6．（1）证明见解析；（2）DE ＝BD ＋CE ；（3）B(1，4)【解析】【分析】（1）证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（2）根据三角形内角和定理、平角的定义证明∠ABD=∠CAE ，证明△ABD ≌△CAE ，根据全等三角形的性质得到AE=BD ，AD=CE ，结合图形解答即可；（3）根据△AEC ≌△CFB ，得到CF=AE=3，BF=CE=OE-OC=4，根据坐标与图形性质解答．【详解】（1）证明：∵BD ⊥直线m ，CE ⊥直线m ，∴∠ADB ＝∠CEA ＝90°∵∠BAC ＝90°∴∠BAD ＋∠CAE ＝90°∵∠BAD ＋∠ABD ＝90°∴∠CAE ＝∠ABD∵在△ADB 和△CEA 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△CEA （AAS ）∴AE ＝BD ，AD ＝CE∴DE ＝AE ＋AD ＝BD ＋CE即：DE ＝BD ＋CE（2）解：数量关系：DE ＝BD ＋CE理由如下：在△ABD 中，∠ABD=180°-∠ADB-∠BAD ，∵∠CAE=180°-∠BAC-∠BAD ，∠BDA=∠AEC ，∴∠ABD=∠CAE ，在△ABD 和△CAE 中，ABD CAEBDA AECAB CA∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABD≌△CAE（AAS）∴AE=BD，AD=CE，∴DE=AD+AE=BD+CE；（3）解：如图，作AE⊥x轴于E，BF⊥x轴于F，由（1）可知，△AEC≌△CFB，∴CF=AE=3，BF=CE=OE-OC=4，∴OF=CF-OC=1，∴点B的坐标为B（1，4）．【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质，掌握全等三角形的判定定理和性质定理是解题的关键．7．（1）203；（2）①t＝83；②a＝185；（3）t＝6.4或t＝103【解析】【分析】（1）根据时间＝路程÷速度即可求得答案；（2）①由题意得：BM＝CN＝3t，则只可以是△CMN≌△BAM，AB＝CM，由此列出方程求解即可；②由题意得：CN≠BM，则只可以是△CMN≌△BMA，AB＝CN＝12，CM＝BM，进而可得3t＝10，求解即可；（3）分情况讨论，当△CMN≌△BPM时，BP＝CM，若此时P由A向B运动，则12－2t＝20－3t，但t＝8不符合实际，舍去，若此时P由B向A运动，则2t－12＝20－3t，求得t ＝6.4；当△CMN≌△BMP时，则BP＝CN，CM＝BM，可得3t＝10，t＝103，再将t＝103代入分别求得AP，BP的长及a的值验证即可．【详解】解：（1）20÷3＝203，故答案为：203；（2）∵CD∥AB，∴∠B＝∠DCB，∵△CNM与△ABM全等，∴△CMN≌△BAM或△CMN≌△BMA，①由题意得：BM＝CN＝3t，∴△CMN≌△BAM∴AB＝CM，∴12＝20－3t，解得：t＝83；②由题意得：CN≠BM，∴△CMN≌△BMA，∴AB＝CN＝12，CM＝BM，∴CM＝BM＝12 BC，∴3t＝10，解得：t＝10 3∵CN＝at，∴103a＝12解得：a＝185；（3）存在∵CD∥AB，∴∠B＝∠DCB，∵△CNM与△PBM全等，∴△CMN≌△BPM或△CMN≌△BMP，当△CMN≌△BPM时，则BP＝CM，若此时P由A向B运动，则BP＝12－2t，CM＝20－3t，∵BP＝CM，∴12－2t＝20－3t，解得：t＝8 (舍去)若此时P由B向A运动，则BP＝2t－12，CM＝20－3t，∵BP＝CM，∴2t－12＝20－3t，解得：t＝6.4，当△CMN≌△BMP时，则BP＝CN，CM＝BM，∴CM＝BM＝12 BC∴3t＝10，解得：t＝10 3当t＝103时，点P的路程为AP＝2t＝203，此时BP＝AB－AP＝12－203＝163，则CN＝BP＝16 3即at＝163，∵t＝103，∴a＝1.6符合题意综上所述，满足条件的t的值有：t＝6.4或t＝10 3【点睛】本题考查了全等三角形的判定及性质的综合运用，解决本题的关键就是用方程思想及分类讨论思想解决问题，把实际问题转化为方程是常用的手段．8．（1）①详见解析；②12α；（2）详见解析；（3）当B、O、F三点共线时BF最长，a【解析】【分析】（1）①由线段垂直平分线的性质可得AD=AC=AB，即可证点B，C，D在以点A为圆心，AB为半径的圆上；②由等腰三角形的性质可得∠BAC=2∠BDC，可求∠BDC的度数；（2）连接CE ，由题意可证△ABC ，△DCE 是等边三角形，可得AC=BC ，∠DCE=60°=∠ACB ，CD=CE ，根据“SAS”可证△BCD ≌△ACE ，可得AE=BD ；（3）取AC 的中点O ，连接OB ，OF ，BF ，由三角形的三边关系可得，当点O ，点B ，点F 三点共线时，BF 最长，根据等腰直角三角形的性质和勾股定理可求10BO a =，2OF OC a ==，即可求得BF【详解】（1）①连接AD ，如图1．∵点C 与点D 关于直线l 对称，∴AC = AD ．∵AB = AC ，∴AB = AC = AD ．∴点B ，C ，D 在以A 为圆心，AB 为半径的圆上．②∵AD=AB=AC ，∴∠ADB=∠ABD ，∠ADC=∠ACD ，∵∠BAM=∠ADB+∠ABD ，∠MAC=∠ADC+∠ACD ，∴∠BAM=2∠ADB ，∠MAC=2∠ADC ，∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α∴∠BDC=12α 故答案为：12α．（2连接CE ，如图2．∵∠BAC=60°，AB=AC ，∴△ABC 是等边三角形，∴BC=AC ，∠ACB=60°，∵∠BDC=12α， ∴∠BDC=30°，∵BD ⊥DE ，∴∠CDE=60°，∵点C 关于直线l 的对称点为点D ，∴DE=CE ，且∠CDE=60°∴△CDE 是等边三角形，∴CD=CE=DE ，∠DCE=60°=∠ACB ，∴∠BCD=∠ACE ，且AC=BC ，CD=CE ， ∴△BCD ≌△ACE （SAS ） ∴BD=AE ，（3）如图3，取AC 的中点O ，连接OB ，OF ，BF ，，F 是以AC 为直径的圆上一点，设AC 中点为O ， ∵在△BOF 中，BO+OF≥BF ，当B 、O 、F 三点共线时BF 最长；如图，过点O 作OH ⊥BC ，∵∠BAC=90°，2a ，∴24BC AC a ==，∠ACB=45°，且OH ⊥BC ，∴∠COH=∠HCO=45°，∴OH=HC ，∴2OC HC =， ∵点O 是AC 中点，AC 2a ，∴2OC a =， ∴OH HC a ==，∴BH=3a ，∴10BO a =，∵点C 关于直线l 的对称点为点D ，∴∠AFC=90°，∵点O 是AC 中点，∴2OF OC a ==，∴BF a =， ∴当B 、O 、F 三点共线时BF 最长；最大值为)a ．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理，三角形的三边关系，灵活运用相关的性质定理、综合运用知识是解题的关键．9．90︒，45︒；20︒，30︒；2a γβ+=，2a γβ-=.【解析】【分析】（1）①如图①知1112EMC BMC ∠=∠，1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.（2）①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠，可推出11()BMC EMF EMF C MB ∠-∠-∠=∠，即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠，可推出()112906090A MC ︒︒︒-+∠=，即可求出解.（3）如图⑤-1、⑤-2中分别由折叠可知，a ββγ-=-、a ββγ-=+，即可求得 2a γβ+=、2a γβ-=.【详解】解：（1）①如图①中，1112EMC BMC ∠=∠，1112C MF C MC ∠=∠， ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=，故答案为90︒. ②如图②中，111111,22EBA ABC C BF C BC ∠=∠∠=∠， ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=，故答案为45︒.（2）①如图③中由折叠可知，11,CMF FMC BME EMB ∠=∠∠=∠，1111C MF EMB EMF C MB ∠+∠-∠=∠，11CMF BME EMF C MB ∴∠+∠-∠=∠，11()BMC EMF EMF C MB ∴∠-∠-∠=∠，111808020C MB ︒︒︒∴-=∠=；②如图④中根据折叠可知，11,CMF C MF ABE A BE ∠=∠∠=∠，112290CMF ABE A MC ︒∠+∠+∠=，112()90CMF ABE A MC ︒∴∠+∠+∠=，()1129090EMF AMC ︒︒∴-∠+∠=，()112906090AMC ︒︒︒∴-+∠=， 1130A MC ︒∴∠=；（3）如图⑤-1中，由折叠可知，a ββγ-=-，2a γβ∴+=；如图⑤-2中，由折叠可知，a ββγ-=+，2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换，图形的角度及边长不变及一些角度的计算问题，突出考查学生的观察能力、思维能力以及动手操作能力，本题是代数、几何知识的综合运用典型题目.10．（1）45°；（2）PE 的值不变，PE=4，理由见详解；（3）D(828-，0)．【解析】【分析】（1）根据(42,0)A ，(0,2)B ，得△AOB 为等腰直角三角形，根据等腰直角三角形的性质，即可求出∠OAB 的度数；（2）根据等腰直角三角形的性质得到∠AOC=∠BOC=45°，OC ⊥AB ，再证明△POC ≌△DPE ，根据全等三角形的性质得到OC=PE ，即可得到答案；（3）证明△POB ≌△DPA ，得到PA=OB=2，DA=PB ，进而得OD 的值，即可求出点D 的坐标．【详解】（1）(42,0)A ，(0,42)B ，∴OA=OB=∵∠AOB=90°，∴△AOB 为等腰直角三角形，∴∠OAB=45°；（2）PE 的值不变，理由如下：∵△AOB 为等腰直角三角形，C 为AB 的中点，∴∠AOC=∠BOC=45°，OC ⊥AB ，∵PO=PD ，∴∠POD=∠PDO ，∵D 是线段OA 上一点，∴点P 在线段BC 上，∵∠POD=45°+∠POC ，∠PDO=45°+∠DPE ，∴∠POC=∠DPE ，在△POC 和△DPE 中，90POC DPE OCP PED PO PD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴△POC ≅△DPE(AAS)，∴OC=PE ，∵OC=12AB=12××=4， ∴PE=4；（3）∵OP=PD ，∴∠POD=∠PDO=(180°−45°)÷2=67.5°，∴∠APD=∠PDO−∠A=22.5°，∠BOP=90°−∠POD=22.5°，∴∠APD=∠BOP ，在△POB 和△DPA 中，OBP PAD BOP APD OP PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△POB ≌△DPA(AAS)，∴PA=OB=DA=PB ，∴DA=PB=-，∴OD=OA−DA=8-，∴点D 的坐标为(8，0)．【点睛】本题主要考查等腰直角三角形的性质，三角形全等的判定与性质定理，图形与坐标，掌握等腰直角三角形的性质，是解题的关键．11．（1）证明见解析；（2）证明见解析．【解析】【分析】（1）先利用同角的余角相等得到一对角相等，再由一对直角相等，且AF AC =，利用AAS 得到AFH CAD ∆≅∆；（2）由（1）利用全等三角形对应边相等得到FH AD =，再EK AD ⊥，交DG 延长线于点K ，同理可得到AD EK =，等量代换得到FK EH =，再由一对直角相等且对顶角相等，利用AAS 得到FHG EKG ≅△△，利用全等三角形对应边相等即可得证．【详解】证明：（1） ∵FH AG ⊥，90AEH EAH ∴∠+∠=︒，90FAC ∠=︒，90FAH CAD ∴∠+∠=︒，AFH CAD ∴∠=∠，在AFH ∆和CAD ∆中，90AHF ADC AFH CADAF AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()AFH CAD AAS ∴∆≅∆，（2）由（1）得AFH CAD ∆≅∆，FH AD ∴=，作FK AG ⊥，交AG 延长线于点K ，如图；同理得到AEK ABD ∆≅∆，EK AD ∴=，FH EK ∴=，在EKG ∆和FHG ∆中，90EKG FHG EGK FGHEK FH ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()EKG FHG AAS ∴∆≅∆，EG FG ∴=．即点G 是EF 的中点．【点睛】此题考查了全等三角形的判定与性质，熟练掌握K 字形全等进行证明是解本题的关键．12．（1）见解析；（2）BD 2+AD 2＝2CD 2；（3）AB ＝22+4．【解析】【分析】（1）根据等腰直角三角形的性质证明△ACE ≌△BCD 即可得到结论；（2）利用全等三角形的性质及勾股定理即可证得结论；（3）连接EF ，设BD ＝x ，利用（1）、（2）求出EF=3x ，再利用勾股定理求出x ，即可得到答案.【详解】（1）证明：∵△ACB 和△ECD 都是等腰直角三角形∴AC ＝BC ，EC ＝DC ，∠ACB ＝∠ECD ＝90°∴∠ACB ﹣∠ACD ＝∠ECD ﹣∠ACD∴∠ACE ＝∠BCD ，∴△ACE ≌△BCD （SAS ），∴AE ＝BD ．（2）解：由（1）得△ACE ≌△BCD ，∴∠CAE ＝∠CBD ，又∵△ABC 是等腰直角三角形，∴∠CAB ＝∠CBA ＝∠CAE ＝45°，∴∠EAD ＝90°，在Rt △ADE 中，AE 2+AD 2＝ED 2，且AE ＝BD ，∴BD 2+AD 2＝ED 2，∵ED ＝2CD ，∴BD 2+AD 2＝2CD 2，（3）解：连接EF ，设BD ＝x ，∵BD ：AF ＝1：2AF ＝2x ，∵△ECD 都是等腰直角三角形，CF ⊥DE ，∴DF ＝EF ，由（1）、（2）可得，在Rt △FAE 中，EF 3x ，∵AE 2+AD 2＝2CD 2，∴2223)x x ++=，解得x ＝1，∴AB ＝+4．【点睛】此题考查三角形全等的判定及性质，等腰直角三角形的性质，勾股定理.。

八年级下册数学期末压轴题专辑(含解析Word版)

八年级下册数学期末压轴题专辑（含解析）1.如图，ON 为∠AOB 中的一条射线，点P 在边OA 上，PH ⊥OB 于H ，交ON 于点Q ，PM ∥OB 交ON 于点M, MD ⊥OB 于点D ，QR ∥OB 交MD 于点R ，连结PR 交QM 于点S 。

（1）求证：四边形PQRM 为矩形；（2）若OP=12PR ，试探究∠AOB 与∠BON 的数量关系，并说明理由。

（1）证明：∵PH⊥OB，MD⊥OB，∴PH∥MD，∵PM∥OB，QR∥OB，∴PM∥QR，∴四边形PQRM 是平行四边形， ∵PH⊥OB，∴∠PHO=90°，∵PM∥OB，∴∠MPQ=∠PHO=90°，∴四边形PQRM 为矩形；（2）∠AOB=3∠BON．理由如下： ∵四边形PQRM 为矩形，∴PS=SR=SQ=12PR ，∴∠SQR=∠SRQ，又∵OP=12PR ，∴OP=PS，∴∠POS=∠PSO， ∵QR∥OB，∴∠SQR=∠BON，在△SQR 中，∠PSO=∠SQR+∠SRQ=2∠SQR=2∠BON，∴∠POS=2∠BON， ∴∠AOB=∠POS+∠BON=2∠BON+∠BON=3∠BON，即∠AOB=3∠BON． 2.如图，矩形OABC 在平面直角坐标系内（O 为坐标原点），点A 在x 轴上，点C 在y 轴上，点B 的坐标分别为（，点E 是BC 的中点，点H 在OA 上，且AH=12，过点H 且平行于y 轴的HG 与EB 交于点G ，现将矩形折叠，使顶点C 落在HG 上，并与HG 上的点D 重合，折痕为EF ，点F 为折痕与y 轴的交点。

（1）求∠CEF 的度数和点D 的坐标；（2）求折痕EF 所在直线的函数表达式；（3）若点P 在直线EF 上，当△PFD 为等腰三角形时，试问满足条件的点P 有几个？请求出点P 的坐标，并写出解答过程。

（本题部分过程用了三角函数，可以用初二知识点沟通）（备用图）解：（1）∵E 是BC 的中点，∴EC=EB==1．∵cos ∠GED==∵∠DEF=∠CEF ∴∠CEF==60°．在Rt △GED 中，由勾股定理得：DG 2=ED 2-EG 2=1-=∴DG=DH=AB-DG=2-== 故D （-，）（2）∵∠CEF ═60°∴CF=ECtan60°=∴OF=OC-CF=2-= ∴F（0，），E （-1，2）设EF 所在直线的函数表达式为y=kx+b ，由图象，得，解得：故EF 所在直线的函数表达式为：y=-x+；（3）∵DF=CF=点P 在直线EF 上，∴当△PFD 为等腰三角形时，有以下三种情况：（a ）P 1F=DF=，可令P 1（t ，-t+），则：P 1F 2=3 ∴由两点间的距离公式为：（t-0）2+（-t+-）2=3∴t 2+3t 2=3∴t 2=， ∴t 1=-，t 2=∴P 1（-，+）； P 3（，-+）（b ） PD=DF=时，仍令P （t ，-t+），注意D （-，），则：PD 2=3 ∴（t+）2+（-t+-）2=3 ∴t 2+3t++3t 2+3t+=3∴4t 2+6t=0∴t 1=0，t 2=-∵t 1=0对应F 点，此时不构成三角形，故舍去．∴P 4（-，）（c ）当 PD=PF 仍令P （t ，-t+），注意D （-，），F （0，），则：PD 2=PF 2∴（t+）2+（-t+-）2=（t-0）2+（-t+-）2，∴t 2+3t++3t 2+3t+=t ，）．故满足条件的点P 有4个．分别是：（）、（）、（（）．3.如图,在平面直角坐标系xOy 中,已知直线12y =-x+23与x 轴、y 轴分别交于点A 和点B,直线y 2=kx+b （k ≠0）经过点C(1,0)且与线段AB 交于点P,并把△ABO 分成两部分.(1)求△ABO 的面积.(2)若△ABO 被直线CP 分成的两部分的面积相等,求点P 的坐标及直线CP 的函数表达式. 解：(1)在直线中，令，得． ∴B(0，2)．令，得． ∴A(3，0)．备用图、 ∴．(2)．∵点P 在第一象限，∴．解得．而点P 又在直线上，∴．解得．∴P()．将点C(1，0)、P()，代入中，有．∴∴直线CP的函数表达式为．4.如图①,在Rt △ABC 中,已知∠A=90º,AB=AC,G 、F 分别是AB 、AC 上两点，且GF ∥BC ，AF=2，BG=4. (1)求梯形BCFG 的面积.(2)有一梯形DEFG 与梯形BCFG 重合,固定△ABC,将梯形DEFG 向右运动,直到点D 与点C 重合为止, 如图②.①若某时段运动后形成的四边形BDG /G 中,DG ⊥BG /,求运动路程BD 的长,并求此时G /B 2的值. ②设运动中BD 的长度为x,试用含x 的代数式表示出梯形DEFG 与Rt △ABC 重合部分的面积.解：（1）在Rt △ABC 中， ∵AB=AC ，∴∠ABC=∠ACB=45°．又∵GF ∥BC ，∴∠AGF=∠AFG=45°． ∴AG=AF=2，AB=AC=6． ∴S 梯形GBCF =S △ABC -S △AGF =．（2）①∵在运动过程中有DG ′∥BG 且DG ′=BG ，∴BDG ′G 是平行四边形．当DG ⊥BG ′时，BDG ′G 是菱形． ∴BD=BG=4．如图③，当BDG ′G 为菱形时，过点G ′作G ′M ⊥BC 于点M ．在Rt △G ′DM 中，∠G ′DM=45°，DG ′=4， ∴DM=G ′M 且DM 2+G'M 2=DG'2． ∴DM=G ′M=， ∴BM=．连接G ′B ．AG FB(D)C(E)图①AGFB DC EG 'F ' 图②在Rt △G ′BM 中，．②当0≤x ≤时，其重合部分为梯形，如图②．在Rt △AGF与Rt △ABC 中，，．过G 点作GH 垂直BC 于点H ，得GH=．由①，知BD=GG ′=x ，DC=，． ∴S 梯形=．当≤x ≤时，其重合部分为等腰直角三角形，如图③． ∵斜边DC=，斜边上的高为，∴．5.如图,在平面直角坐标系xoy 中,已知直线PA 是一次函数y=x+m(m>0)的图象,直线PB 是一次函数y=-3x ＋n （n ＞m ）的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点。

初中八年级的下数学压轴题与包括答案.docx

---------.八年级下数学压轴题1．已知，正方形ABCD 中，∠MAN=45 °， MAN ∠绕点A顺时针旋转，它的两边分别交 CB 、 DC （或它们的延长线）于点M、N，AH ⊥MN于点H．（ 1）如图①，当∠ MAN绕点A旋转到BM=DN时，请你直接写出AH 与 AB 的数量关系：；（2）如图②，当∠ MAN 绕点 A 旋转到 BM ≠DN 时，（ 1）中发现的 AH 与 AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠ MAN=45 °AH ，⊥ MN 于点 H，且 MH=2 ，NH=3 ，求 AH 的长．（可利用（ 2）得到的结论）专业资料-------------------.2．如图，△ ABC 是等边三角形，点 D 是边 BC 上的一点，以AD 为边作等边△ ADE ，过点 C 作 CF ∥DE 交 AB 于点 F．（ 1）若点 D 是 BC 边的中点（如图①），求证：EF=CD ；（2）在（ 1）的条件下直接写出△ AEF 和△ ABC 的面积比；（3）若点D 是BC 边上的任意一点（除B、C 外如图②），那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．专业资料-------------------.3．（ 1）如图 1，在正方形ABCD 中， E 是 AB 上一点， F 是 AD 延长线上一点，且DF=BE ．求证： CE=CF ；（2）如图 2，在正方形ABCD 中， E 是 AB 上一点， G 是 AD 上一点，如果∠GCE=45 °，请你利用（ 1）的结论证明：GE=BE+GD ．（3）运用（ 1）（ 2）解答中所积累的经验和知识，完成下题：如图 3，在直角梯形ABCD 中， AD ∥BC （BC ＞ AD ），∠B=90 ° AB=BC ，， E 是AB 上一点，且∠DCE=45BE=4 °，， DE=10 ，求直角梯形 ABCD 的面积．专业资料-------------------.专业资料-------------------.4．如图，正方形ABCD 中， E 为 AB 边上一点，过点 D 作 DF ⊥DE ，与 BC 延长线交于点 F．连接 EF ，与 CD 边交于点G，与对角线BD 交于点 H．（1）若 BF=BD=，求BE的长；（2）若∠ ADE=2 ∠ BFE ，求证： FH=HE+HD．专业资料-------------------.5．如图，将一三角板放在边长为 1 的正方形ABCD 上，并使它的直角顶点P 在对角线AC 上滑动，直角的一边始终经过点B，另一边与射线DC 相交于 Q ．探究：设 A 、P 两点间的距离为x．（1）当点 Q 在边 CD 上时，线段 PQ 与 PB 之间有怎样的数量关系？试证明你的猜想；（2）当点 Q 在边 CD 上时，设四边形 PBCQ 的面积为 y，求 y 与 x 之间的函数关系，并写出函数自变量 x 的取值范围；（3）当点 P 在线段 AC 上滑动时，△ PCQ 是否可能成为等腰三角形？如果可能，指出所有能使△ PCQ 成为等腰三角形的点Q 的位置．并求出相应的x 值，如果不可能，试说明理由．专业资料-------------------.6． Rt△ABC 与 Rt△FED 是两块全等的含30 °、60°角的三角板，按如图（一）所示拼在一起， CB 与 DE 重合．（1）求证：四边形ABFC 为平行四边形；（2）取 BC 中点 O，将△ ABC 绕点 O 顺时钟方向旋转到如图（二）中△A′ B′ C′位置，直线 B'C' 与 AB 、CF 分别相交于P、Q 两点，猜想OQ 、OP 长度的大小关系，并证明你的猜想；（3）在（ 2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形？（不要求证明）专业资料-------------------.7．如图，在正方形ABCD 中，点 F 在 CD 边上，射线AF 交 BD 于点 E ，交 BC 的延长专业资料-------------------.线于点 G．（1）求证：△ ADE ≌△ CDE ；（2）过点 C 作 CH ⊥CE ，交 FG 于点 H，求证： FH=GH ；（3）设 AD=1 ，DF=x ，试问是否存在 x 的值，使△ ECG 为等腰三角形？若存在，请求出 x 的值；若不存在，请说明理由．专业资料-------------------.8．在平行四边形ABCD 中，∠ BAD 的平分线交直线BC 于点 E，交直线DC 于点 F．（1）在图 1 中证明 CE=CF ；（2）若∠ ABC=90 °G，是 EF 的中点（如图 2），直接写出∠ BDG 的度数；（3）若∠ABC=120 °FG ，∥ CE ， FG=CE ，分别连接DB 、 DG（如图3），求∠ BDG 的度数．专业资料-------------------.9．如图，已知 ?ABCD 中， DE ⊥ BC 于点 E，DH ⊥ AB 于点 H，AF 平分∠ BAD ，分别交 DC 、DE 、 DH 于点 F、G、M，且 DE=AD ．（1）求证：△ ADG ≌△ FDM ．（2）猜想 AB 与 DG+CE 之间有何数量关系，并证明你的猜想．专业资料-------------------.10 ．如图，在正方形ABCD 中， E 、F 分别为 BC 、 AB 上两点，且BE=BF ，过点 B 作专业资料-------------------.AE 的垂线交 AC 于点 G ，过点 G 作 CF 的垂线交BC 于点 H 延长线段AE 、 GH 交于点 M ．（1）求证：∠ BFC= ∠BEA ；（2）求证： AM=BG+GM ．专业资料-------------------.11 ．如图所示，把矩形纸片OABC 放入直角坐标系xOy 中，使 OA 、OC 分别落在x、y 轴的正半轴上，连接AC ，且 AC=4，（1）求 AC 所在直线的解析式；（2）将纸片 OABC 折叠，使点 A 与点 C 重合（折痕为 EF ），求折叠后纸片重叠部分的面积．（3）求 EF 所在的直线的函数解析式．专业资料-------------------.12 ．已知一次函数的图象与坐标轴交于A、B 点（如图）， AE 平分∠ BAO ，交x 轴于点 E．（1）求点 B 的坐标；（2）求直线 AE 的表达式；（3）过点 B 作 BF ⊥AE ，垂足为 F，连接 OF ，试判断△ OFB 的形状，并求△ OFB 的面积．（4）若将已知条件“ AE 平分∠ BAO ，交 x 轴于点 E”改变为“点 E 是线段 OB 上的一个动点（点 E 不与点 O、 B 重合）”，过点 B 作 BF⊥AE ，垂足为F．设 OE=x ，BF=y ，试求 y 与 x 之间的函数关系式，并写出函数的定义域．专业资料-------------------.13 ．如图，直线l1的解析表达式为：y=﹣3x+3 ，且 l1与 x 轴交于点 D，直线 l2经过点A，B，直线 l1，l2交于点 C．专业资料-------------------.（1）求点 D 的坐标；（2）求直线 l2的解析表达式；（3）求△ ADC 的面积；（4）在直线 l2上存在异于点 C 的另一点 P ，使得△ ADP 与△ ADC 的面积相等，请直接写出点P 的坐标．专业资料-------------------.14 ．如图 1，在平面直角坐标系中，O 是坐标原点，长方形OACB 的顶点A、B 分别在 x 轴与 y 轴上，已知OA=6 ，OB=10 ．点 D 为 y 轴上一点，其坐标为（0， 2），点 P 从点 A 出发以每秒 2 个单位的速度沿线段AC ﹣CB 的方向运动，当点P 与点B 重合时停止运动，运动时间为t 秒．（1）当点 P 经过点 C 时，求直线 DP 的函数解析式；（2）①求△ OPD 的面积 S 关于 t 的函数解析式；②如图②，把长方形沿着OP 折叠，点 B 的对应点B′恰好落在 AC 边上，求点P的坐标．（3）点 P 在运动过程中是否存在使△BDP 为等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．专业资料-------------------.15 ．如图，在平面直角坐标系中，已知O为原点，四边形ABCD 为平行四边形， A、B、C的坐标分别是 A（﹣ 5，1）， B（﹣ 2，4）， C（ 5， 4），点 D 在第一象限．（1）写出 D 点的坐标；（2 ）求经过 B、D 两点的直线的解析式，并求线段BD 的长；（3 ）将平行四边形ABCD 先向右平移 1 个单位长度，再向下平移 1 个单位长度所得的四边形 A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD 与四边A1B1 C1D 1重叠部分的面积．专业资料-------------------.16 ．如图，一次函数的图象与x 轴、 y 轴交于点A、B ，以线段AB 为边在第一象限内作等边△ABC ，（1）求△ ABC 的面积；（2）如果在第二象限内有一点P（a，）；试用含有 a 的代数式表示四边形ABPO 的面积，并求出当△ABP 的面积与△ ABC 的面积相等时 a 的值；专业资料-------------------.（3）在 x 轴上，是否存在点M，使△ MAB 为等腰三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．专业资料-------------------.专业资料-------------------.2018 年06月17日梧桐听雨的初中数学组卷参考答案与试题解析一．解答题（共16 小题）1．已知，正方形ABCD 中，∠MAN=45 °， MAN ∠绕点A顺时针旋转，它的两边分别交 CB 、DC （或它们的延长线）于点M、N， AH ⊥MN于点H．（ 1）如图①，当∠ MAN 绕点 A 旋转到 BM=DN 时，请你直接写出AH 与 AB 的数量关系：AH=AB ；（2）如图②，当∠ MAN 绕点 A 旋转到 BM ≠DN 时，（ 1）中发现的 AH 与 AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠ MAN=45 °， AH ⊥MN 于点 H，且 MH=2 ，NH=3 ，求 AH 的长．（可利用（ 2）得到的结论）【解答】解：（ 1）如图① AH=AB ．（ 2）数量关系成立．如图②，延长CB 至 E，使 BE=DN ．∵ ABCD 是正方形，∴AB=AD ，∠ D= ∠ABE=90 °，在 Rt△AEB 和 Rt△AND 中，，∴Rt△ AEB ≌Rt△ AND ，∴AE=AN ，∠ EAB= ∠ NAD ，∵∠ DAN+ ∠BAN=45 °，专业资料-------------------.∴∠ EAB+ ∠ BAN=45 °，∴∠EAN=45 °，∴∠ EAM= ∠NAM=45 °，在△ AEM 和△ ANM中，，∴△ AEM ≌△ ANM ．∴ S△AEM =S △ANM，EM=MN，∵ AB、AH 是△ AEM 和△ ANM对应边上的高，∴AB=AH ．（ 3）如图③分别沿AM 、AN 翻折△ AMH和△ ANH，得到△ ABM和△ AND，∴BM=2 ，DN=3 ，∠ B= ∠D= ∠BAD=90 °．分别延长BM 和 DN 交于点 C，得正方形ABCD ，由（ 2）可知， AH=AB=BC=CD=AD．设 AH=x ，则 MC=x ﹣2，NC=x ﹣3，在 Rt△ MCN 中，由勾股定理，得MN 2=MC2+NC2∴52=（ x﹣2）2+（x﹣3）2（ 6 分）解得 x1=6 ，x2=﹣ 1．（不符合题意，舍去）∴AH=6 ．专业资料-------------------.2．如图，△ ABC 是等边三角形，点 D 是边 BC 上的一点，以AD 为边作等边△ ADE ，过点 C 作 CF ∥ DE 交 AB 于点 F．（ 1）若点 D 是 BC 边的中点（如图①），求证：EF=CD ；（2）在（ 1）的条件下直接写出△ AEF 和△ ABC 的面积比；（3）若点 D 是 BC 边上的任意一点（除 B、C 外如图②），那么（ 1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．【解答】（ 1）证明：∵△ ABC 是等边三角形， D 是 BC 的中点，∴ AD ⊥BC ，且∠ BAD=∠BAC=30°，∵△ AED 是等边三角形，∴ AD=AE ，∠ADE=60 °，∴∠EDB=90 °﹣∠ADE=90 °﹣60 °=30 °，∵ ED ∥CF ，专业资料----------。

八年级下压轴 50题(含答案及解析)

②当AB＝AE＝2，∠B＝60°时，将四边形ABCE向右平移a（a＞0）个单位后，恰有两个顶点落在反比例函数y＝的图象上，求k的值．
29．如图1，在平面直角坐标系中，直线y＝﹣ x+3与x轴、y轴相交于A、B两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．
（1）求证：∠BFC＝∠BEA；
（2）求证：AM＝BG+GM．
9．如图，正方形ABCD的对角线相交于点O．点E是线段DO上一点，连接CE．点F是∠OCE的平分线上一点，且BF⊥CF与CO相交于点M．点G是线段CE上一点，且CO＝CG．
（1）若OF＝4，求FG的长；
（2）求证：BF＝OG+CF．
10．（1）如图①，两个正方形的边长均为3，求三角形DBF的面积．
①当t＝秒时，以A、P、E、D、为顶点可以构成平行四边形．
②在P点运动过程中，是否存在以B、C、E、D为顶点的四边形是平行四边形？若存在，请求出t的值；若不存在，请说明理由．
23．如图，在平面直角坐标系中，直线y＝x+2与x轴，y轴分别交于A，B两点，点C（2，m）为直线y＝x+2上一点，直线y＝﹣ x+b过点C．
13．如图，菱形ABCD中，点E、M在AD上，且CD＝CM，点F为AB上的点，且∠ECF＝ ∠B．
（1）若菱形ABCD的周长为8，且∠D＝67.5°，求△MCD的面积；
（2）求证：BF＝EF﹣EM．
14．如图1，矩形OABC摆放在平面直角坐标系中，点A在x轴上，点C在y轴上，OA＝3，OC＝2，过点A的直线交矩形OABC的边BC于点P，且点P不与点B、C重合，过点P作∠CPD＝∠APB，PD交x轴于点D，交y轴于点E．

人教版八年级下册数学期末动点压轴题训练(带答案)

人教版八年级下册数学期末动点压轴题训练（带答案）1．如图，平面直角坐标系xOy 中，直线334y x =-+交x 轴于点A ，交y 轴于点B ，点P 是线段OA 上一动点（不与点A 重合），过点P 作PC AB ⊥于点C ．(1)当点P 是OA 中点时，求APC △的面积；(2)连接BP ，若BP 平分ABO ∠，求此时点P 的坐标；(3)BP 平分ABO ∠，在x 轴上有一动点H ，H 横坐标为a ，过点H 作直线l x ⊥轴，l 与线段PC 有交点，求a 的取值范围；(4)BP 平分ABO ∠，M 为x 轴上动点，CPM △为等腰三角形，求M 坐标．2．如图，直线l 1：y ＝kx +b 与y 轴交于点B （0，3），直线l 2：y ＝﹣2x ﹣1交y 轴于点A ，交直线l 1于点P （﹣1，t ）．(1)求k 、b 和t 的值； (2)求△ABP 的面积；(3)过动点D（a，0）作x轴的垂线与直线l1、l2，分别交于M、N两点，且MN＜4．①求a的取值范围；①当△AMP的面积是△AMB的面积的1时，求MN的长度．23．在平面直角坐标系中，坐标轴上的三个点A(a，0)，B(0，b)，C(c，0)(a＜0，b＞0)满足|c﹣1|+(a+b)2＝0，F为射线BC上的一个动点．(1)c的值为，①ABO的度数为．(2)如图（a），若AF①BC，且交OB于点E，求证：OE＝OC．(3)如图（b），若点F运动到BC的延长线上，且①FBO＝2①F AO，O在AF的垂直平分线上，求①ABF的面积．4．已知，长方形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A 的坐标为（10，0），点B的坐标为（10，8）．(1)直接写出点C的坐标为：C（，）；(2)已知Q（5，n）在直线AC；求n的值；(3)若动点P 从A 点出发，沿折线AO →OC 的路径以每秒2个单位长度的速度运动，到达C 处停止．求①OPQ 的面积S 与点P 的运动时间t （秒）的函数关系式．5．在①ABC 中，90ACB ∠=︒，60ABC ∠=︒，点D 是直线AB 上一动点，以CD 为边，在它右侧作等边①CDE ．(1)如图1，当E 在边AC 上时，直接判断线段DE ，EA 的数量关系______； (2)如图2，在点D 运动的同时，过点A 作AF CE ∥，过点C 作CF AE ∥，两线交于点F ，判断四边形AECF 形状，并说明理由；(3)若BC =AECF 为正方形时，直接写出AD 的值．6．已知在平面直角坐标系中，点()0,2A ，动点P 在x 轴正半轴上，作矩形OABP ，点C 为PB 中点，①ABC 沿AC 折叠后得到①ADC ，直线CD 与矩形OABP 一边交于点E ．(1)如图，当点E 与原点O 重合时， ①求证：OCP ADO ≌△△． ①求OP 长．(2)当5EC ED =，求点P 坐标．7．如图（1），在平面直角坐标系中点(),A x y ，()2,0B x 满足0x ，点C 为线段OB 上一个动点，以CA 为腰作等腰直角ACD △，且AC AD =．(1)求点A 、B 的坐标及AOB 的面积；(2)试判断CD 、OC 、BC 间的数量关系，并说明理由；(3)如图（2），若点C 为线段OB 延长线上一个动点，则（2）中的结论是否成立，并说明理由．8．如图，在平面直角坐标系中，直线4y x =+交y 轴于A 点，与直线BC 相交于点B (－2，m )，直线BC 与y 轴交于点C (0，－2)，与x 轴交于点D ；(1)求①ABC 的面积；(2)过点A 作BC 的平行线交x 轴于点E ，求点E 的坐标；(3)在（2）的条件下，点P 是直线AB 上一动点且在x 轴的上方，Q 为直角坐标平面内一点，如果以点D 、E 、P 、Q 为顶点的平行四边形的面积等于①ABC 面积，请求出点P 的坐标，并直接写出点Q 的坐标．9．如图，已知①ABC中，①B = 90°，AB = 8cm，BC = 6cm，P、Q是①ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．(1)出发2秒后，求PQ的长；(2)从出发几秒钟后，①PQB第一次能形成等腰三角形？(3)当点Q运动到CA上时，求能使①BCQ是等腰三角形时点Q的运动时间．10．如图1，四边形形ABCD是一个边长为2的正方形，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B作BF①CE于点G，交AD于点F．(1)求证：①ABF①①BCE；(2)如图2，当点E运动到AB中点时，①求BG的长；①连接DG，求证：DC＝DG．11．如图，在平面直角坐标系中，点O 为坐标原点，点A 、B 、C 的坐标分别为（0，6）、（-8，0）、（-3，0），10AB =，将ABC 沿着射线AC 翻折，点B 落到y 轴上点D 处．(1)求点D 的坐标；(2)动点P 以每秒1个单位长度的速度从点B 出发沿着线段BO 向终点O 运动，运动时间为t 秒，请用含有t 的式子表示PCA 的面积，并直接写出t 的取值范围； (3)在（2）的条件下，动点M 以每秒2个单位长度的速度从点A 出发沿着线段AO 向终点O 运动，动点N 以每秒a 个单位长度的速度从点O 出发沿着x 轴正方向运动，点P 、M 、N 同时出发，点M 停止时，点P 、N 也停止运动，当DOP MON △△≌时，求a 的值．12．如图，在平面直角坐标系中，一次函数21y x =--的图象分别交x 轴、y 轴于点A 和B ，已知点C 的坐标为（－3，0）．若点P 是x 轴上的一个动点．(1)求直线BC 的函数解析式；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的①BPC 为等腰三角形时，请直接写出所有符合条件的P 点坐标．13．如图所示，菱形ABCD 的顶点A B ，在x 轴上，点A 在点B 的左侧，点D 在y 轴的正半轴上．点C 的坐标为(4．动点P 从点A 出发，以每秒1个单位长度的速度，按照A D C B A →→→→的顺序在菱形的边上匀速运动一周，设运动时间为t 秒．(1)①点B 的坐标； ①求菱形ABCD 的面积；(2)当3t =时，问线段AC 上是否存在点E ，使得PE DE +最小，如果存在，求出PE DE +最小值；如果不存在，请说明理由．14．如图，①ABC 中，①C ＝90°，AC ＝8cm ，BC ＝6cm ，若动点P 从点C 开始，按C →A →B →C 的路径运动，且速度为每秒1cm ，设运动的时间为t 秒．(1)当t ＝秒时，CP 把①ABC 的面积分成相等的两部分，此时CP ＝ cm ；(2)当t 为何值时，①ABP 为等腰三角形．(3)若点P 在线段AC 上运动，点Q 是线段AB 上的动点，求PB +PQ 的最小值．15．已知等边①ABC 中，AB ＝8，点D 为边BC 上一动点，以AD 为边作等边①ADE ，且点E 与点D 在直线AC 的两侧，过点E 作EF //BC ，EF 与AB 、AC 分别相交于点F 、G ．(1)求证：四边形BCEF 是平行四边形；(2)设BD ＝x ，FG ＝y ，求y 关于x 的函数解析式，并写出定义域； (3)当AD 的长为7时，求线段FG 的长．16．如图，在平面直角坐标系中，点D 的横坐标为4，直线1l ：2y x =+经过点D ，与x 轴、y 轴分别交于A 、B 两点，直线2l ：y kx b =+经过点()1,0C 、点D 两点．(1)求直线2l 的函数表达式； (2)求ACD △的面积；(3)点P 为线段AD 上一动点，连接CP ． ①求CP 的最小值；①当ACP△为等腰三角形时，直接写出点P的坐标．17．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．(1)如图1，当①DAG＝30°时，求BE的长；(2)如图2，当点E是BC的中点时，求线段GC的长；(3)如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．18．如图1，点A在y轴上，点B，点C在x轴上，点D在第一象限，且△ABC与△ADC均为等边三角形，点B坐标为（﹣3，0），点E为线段BC上一动点，点F为直线DC上一动点，且∠EAF＝60°，连接EF．(1)填空：写出点A、点D的坐标，点A；点D；(2)试判断△AEF的形状，并给予证明；(3)直接写出EF长度的最小值以及此时点F的坐标；(4)将条件改为“点E为CB延长线上一点”，其他条件不变，△AEF的形状是否发生变化？在图2中画全图形（不必证明），直接写出当点E坐标为（﹣5，0）时，EF的长度以及此时点F的坐标．19．如图，在平面直角坐标系中，直线y＝kx过点B（m，6），过点B分别作x轴和y轴的垂线，垂足分别为点A，C，①AOB＝30°．动点P从点O出发，以每秒2个单位C运长度的速度向点B运动，动点Q从点B动．点P，Q同时开始运动，当点P到达点B时，点P，Q同时停止运动，设运动时间为t秒．(1)求m与k的值；(2)设①PQB的面积为S，求S与t的关系式；(3)若以点P，Q，B为顶点的三角形是等腰三角形，请求出t的值．（温擎提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）20．如图，在平面直角坐标系中，OA=OB=6，OD=1，点C为线段AB的中点．(1)直接写出点C的坐标为；(2)点P是x轴上的动点，当PB+PC的值最小时，求此时点P的坐标；(3)在平面内是否存在点F，使得以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．参考答案：1．(1)解：如图，连接BP ，直线334y x =-+交x 轴于点A ，交y 轴于点B ，∴点()4,0A ，点()0,3B ， 4AO ∴=，3OB =，5AB ∴，点P 是OA 中点，2AP OP ∴==，1122ABP S AP OB AB CP =⨯⨯=⨯⨯， 65CP ∴=，85AC ∴==， 124225APC S AC PC ∴=⨯⨯=； (2)如图，连接BP ，BP 平分ABO ∠，OBP CBP ∴∠=∠，又BP BP =，90BOP BCP ∠=∠=︒，BOP ∴①()BCP AAS ，3BO BC ∴==，OP CP =，532AC AB BC ∴=-=-=，222AP PC AC =+，22(4)4OP OP ∴-=+，32OP ∴=， 3,02P ⎛⎫∴ ⎪⎝⎭； (3)过点C 作⊥CH x 轴于点H ．由()2得，OP CP =＝32，2AC =， 4AP ∴=－32＝52， ①65AC CP CH AP ⋅==,AH ∴85， OH OA AH ∴=-＝125， a ∴的取值范围31225a ≤≤； (4)设点(),0M x ，过点C 作⊥CH x 轴于点H ，则22222126()()55MC HM CH x =+=-+，同理可得：2239()24CP ==，223()2MP x =-，当MC CP =时，即221269()()554x -+=，解得3310x =或3(2舍去)；当MC MP =时，同理可得392x =；当CP MP =时，同理可得0x =或3，故点M 的坐标为33,010⎛⎫ ⎪⎝⎭或39,02⎛⎫ ⎪⎝⎭或()0,0或()3,0． 2．解：①点P （﹣1，t ）在直线直线l 2上，①t ＝﹣2×（﹣1）﹣1＝1，即P （﹣1，1），把B 、P 的坐标代入可得13k b b -+=⎧⎨=⎩，解得 23k b =⎧⎨=⎩， ①t ＝1，k ＝2，b ＝3；(2)解：①直线y ＝﹣2x ﹣1交y 轴于点A ，①A （0，﹣1），①P （﹣1，1），B （0，3）， ①1114222PAB SAB =⨯=⨯=； (3)解：①①MN ①y 轴，①M、N的横坐标为a，设M、N的纵坐标分别为ym和yn，由（1）可知直线l1的函数表达式为y＝2x+3，①ym＝2a+3，yn＝﹣2a﹣1，当MN在点P左侧时，此时a＜﹣1，则有MN＝yn﹣ym＝﹣2a﹣1﹣（2a+3）＝﹣4a﹣4，①MN＜4，①﹣4a﹣4＜4，解得a＞﹣2，①此时﹣2＜a＜﹣1；当MN在点P的右侧时，此时a＞﹣1，则有MN＝ym﹣yn＝2a+3﹣（﹣2a﹣1）＝4a+4，①MN＜4，①4a+4＜4，解得a＜0，①此时﹣1＜a＜0；当a＝﹣1时，也符合题意，综上可知当﹣2＜a＜0时，MN＜4；①由（2）可知S△APB＝2，由题意可知点M只能在y轴的左侧，当点M在线段BP上时，过点M作MC①y轴于点C，如图1①S△APM＝12S△AMB，①S△ABM＝23S△APB＝43，①12AB•MC＝43，即2MC＝43，解得MC＝23，①点M的横坐标为﹣23，即a＝﹣23，①MN＝4a+4＝﹣83+4＝43；当点M在线段BP的延长线上时，过点M作MD①y轴于点D，如图2，①S△APM＝12AMB S，①S△ABM＝2S△APB＝4，①12AB•MD＝4，即2MD＝4，解得MD＝2，①点M的横坐标为﹣2，①MN＝﹣4a﹣4＝8﹣4＝4（不合题意舍去），综上可知MN的长度为43．3．解：①|c﹣1|+(a+b)2＝0，①c＝1，a＝﹣b，①OA＝OB，①①ABO＝45°，故答案为：1，45°．(2)证明：①AF ①BC ，①①AOE ＝①BFE ＝90°，①①AEO ＝①BEF ，①①OBC ＝①OAE ，在①AOE 和①BOC 中，===OAE OBC AOE BOC OA OB ∠∠⎧⎪∠∠⎨⎪⎩， ①①AOE ①①BOC (AAS )，①OE ＝OC ；(3)解：连结OF ，过点F 作FG ①x 轴，垂足为点G ，设①F AO ＝x ，则①FBO ＝2①F AO ＝2x ，①O 在AF 的垂直平分线上，①AO ＝OF ，①①OAF ＝①OF A ＝x ，①①GOF ＝①OAF +①OF A ＝2x ，①①FBO ＝2①F AO ＝2x ，OB ＝OA ＝OF ，①①OFC ＝①OBF ＝2x ，①①BCO ＝①COF +①OFB ＝4x ，①①OBC +①OCB ＝90°，①6x ＝90°，解得x ＝15°，①①OBC ＝①GOF ＝2x ＝30°，①C (1，0)，①OC ＝1，①①BOC ＝90°，①OBC ＝30°，①BC ＝2OC ＝2，OB ，①OA ＝OF ＝OB，同理可得：FG = ，①=+AC AO OC ，①S △ABF ＝S △ACB +S △ACF ＝12×AC ×FG +12×AC ×OB ＝12＝94 4．(1)①四边形ABCO 是矩形①AB =OC ，AO =BC①A （10，0），B （10，8）①OC =OB =8①点C 的坐标为（0，8）故答案为：0，8(2)设直线AC 的解析式为y kx b =+把点A （10，0），B （0，8）代入y kx b =+得，1008k b b +=⎧⎨=⎩ 解得，458k b ⎧=-⎪⎨⎪=⎩ ①直线AC 的解析式为485y x =-+ 把点Q （5，n ）代入485y x =-+得， 45845n =-⨯+=； (3)①当05t ≤≤时，102OP OA AP t =-=-过点Q 作QD ①OA 于点D ，如图，①Q （5，4）①QD =4 ①1(102)42042S t t =-⨯=-； ①当59<≤t 时，OP = AP -AO =2t -10过点Q 作QE ①OC 于点E ，如图，①Q （5，4）①QE =5 ①1(210)55252S t t =-⨯=- 综上，204(05)=525(59)t t S t t -≤≤⎧⎨-<≤⎩5(1)①90ACB ∠=︒，60ABC ∠=︒①30A ∠=︒①CDE △为等边三角形①60DEC ∠=︒①DEC ∠是ADE 外角①DEC A ADE ∠=∠+∠①30ADE A ∠=︒=∠①DE EA =故答案为相等．(2)取AB 中点O ，连接OC 、OE①AF CE ∥, CF AE ∥①四边形AECF 是平行四边形①90ACB ∠=︒①OC OB OA ==①60ABC ∠=︒①①BCO 为等边三角形①①CDE 是等边三角形①60DCB OCE DCO ∠=∠=︒-∠①OC BC = CD CE =①BCD OCE ≌△△①60EOC B ∠=∠=︒①60EOA ∠=︒又①OE OE =，OA OC =①()OCE OAE SAS ≌△△①CE EA =①平行四边形AECF 是菱形(3)当点D 在AB 延长线上时，作CH AD ⊥于H ，当四边形AECF 为正方形时，45ACE BCE ∠=∠=︒，90AEC ∠=︒ ①60DCE ∠=︒①15DCB ∠=︒①60ABC ∠=︒①45CDH ∠=︒①BC =①AC ==①12CH AC =①AH ==①CDE △为等边三角形 ①CH DH ==①AD =当点D 在AB 上时作CH AB ⊥于H ，同理可得CDH △是等腰直角三角形，则AD AH DH =-=综上AD =6．解：①矩形OABP 中，()02A ，， AB OP ∴=，2BP OA ==，90AOP OAB ABC OPB ∠=∠=∠=∠=︒ ． ABC 沿AC 折叠后得到ADC ，90ADC ABC ∴∠=∠=︒，AD AB =，AD OP ∴=，当点E 与原点O 重合时，18090ADO ADC ∠=︒-∠=︒，90AOD COP AOP ∠+∠=∠=︒，90AOD OAD ∴∠+∠=︒，COP OAD ∴∠=∠．在OCP △和AOD △中，90OPC ADO COP OAD OP AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()OCP AOD AAS ∴≌；①①点C 为PB 的中点，112CP BC PB ∴===，由①知：OCP AOD ≌，2OC AO ∴==，在Rt COP 中，由勾股定理得OP ，即OP(2)解：当5EC DE =，则4CD DE =．ABC 沿AC 折叠后得到ADC ，1CD BC ∴==，90ADC ABC ∠=∠=︒，AD AB =，1144DE CD ∴==，90ADE ∠=︒，AD OP =， 554CE ED ∴==，设OP p =，则AD AB OP p ===，若点E 在OP 上，连接AE ，如下图，在Rt CPE △中，1CP =，34EP ∴=， 34OE OP PE p ∴=-=-，在Rt AOE 中，22222324AE OA OE p ⎛⎫=+=+- ⎪⎝⎭，在Rt ADE △中， 222221=4AE DE AD p ⎛⎫=++ ⎪⎝⎭， 222213+244p p ⎛⎫⎛⎫∴=+- ⎪ ⎪⎝⎭⎝⎭，即22139+416216p p p =+-+，解得3p =，此时，点P 的坐标为()30，；若点E 在OA 上，点D 在第一象限，过点E 作EF BC ⊥于F 点，如下图，则90EFP EFC ∠=∠=︒，90EOP OPF EFP ∴∠=∠=∠=︒，①四边形EFPO 是矩形，90CEF ECF ∠+∠=︒，EF OP ∴=，90OEF ∠=︒，AD EF ∴=，90CEF AED AEF ∠+∠=∠=︒，AED ECF ∴∠=∠．在AED 和ECF △中，AED ECF ADE EFC AD EF ∠=∠∠=∠=⎧⎪⎨⎪⎩，()AED ECF AAS ∴≌，54AE EC =∴=．在Rt ADE △中，AD ==OP AD ∴== 此时，点P的坐标为0⎫⎪⎪⎝⎭．若点E 在OA 上，点D 在第二象限时，过点C 作CF OA ⊥于F 点，如下图，则90AFC ∠=︒．①①F AB =①B =①AFC =90°，①四边形AFCB 是矩形，①AB =CF ，1AF BC ==ABC 沿AC 折叠后得到ADC ，①90ADC ABC ADE ∠=∠=∠=︒，AD AB OP CF ===，90ADE EFC ∴∠=∠=︒．在AED 和CEF △中，AED CEF ADE EFC AD CF ∠⎪∠⎧=∠∠=⎪⎨⎩=，()AED CEF AAS ∴≌，AE CE ∴=，DE EF =．5EC ED =，1AF AE EF BC =+==，15CE EF CE DE DE DE ∴+==+=+，16DE EF ∴==，556CE DE ==，在Rt EFC 中，CF =即OP ， ∴点P的坐标为⎫⎪⎪⎝⎭．综上所述，点P 坐标()30，或0⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 7．(1)①0x =，①(0x ≥0≥，①x y ==①A ，()B ，132AOB S =⨯=△． (2)结论：222CD OC BC =+．理由：连接，①OA AB ==OB =①222OA OB OB +=，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB ∠=，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90CBD ∠=︒，①222CD BC BD =+．①222CD OC BC =+．(3)（2）中的结论仍然成立理由：连接，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB =，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90OBD DBC ∠=∠=︒，①222CD BC BD =+，①222CD OC BC =+．8．(1)解：将点2()B m -，，代入4y x =+得24m ，解得2m =，①()22B -，，当0x =时，4y =，①()0,4A ， ①12662ABC S ∆=⨯⨯=． (2)解：设直线BC 的解析式为()20y kx k =-≠，将B 点坐标代入得222k --=，解得2k =-，①直线BC 的解析式为22y x =--，故设过点A 且平行于BC 的直线解析式为2y x b =-+，将A 点坐标代入得4b =，①过点A 且平行于BC 的直线解析式为24y x =-+，当0y =时，2x =，①()2,0E ．(3)解：由（2）可得()1,0D -，以点D 、E 、P 、Q 为顶点的平行四边形分两种情况求解： ①当DE 是平行四边形的边长时，则点Q 在x 轴上方，设(),4P m m +，①62DEPQ ABC DEP SS S ===， ①()1432DEP S DE m =⨯+=，解得2m =-，①()2,2P -，①PQ DE ∥，PQ DE =，①()5,2Q -；同理62DEQP ABC DEP S S S ===，①()2,2P -，①()1,2Q ；①当DE 是平行四边形的对角线时，则点Q 在x 轴下方，设(),4P m m +，同理62DQEP ABC DEP S S S ===，①()2,2P -，①D E 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①P Q 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①()3,2Q -；综上所述，P 点坐标为()2,2-，Q 的点坐标为()5,2- 或()1,2 或()3,2-．9．如图所示：BQ=2×2=4cm，BP=AB-AP=8- 2×1=6cm，①①B= 90°①PQ==；(2)当△PQB第一次形成等腰三角形时，BQ =BP，①BQ = 2t，BP= 8-t，①2t= 8-t，解得：t=83；(3)①①B = 90°，AB = 8cm，BC = 6cm，①AC10=cm，①当CQ= BQ时，如图则①C=①CBQ，①①ABC= 90°，①①CBQ +①ABQ = 90°，①①A+①C= 90°，①①A=①ABQ，①BQ= AQ，①CQ=AQ=5cm，①BC+ CQ = 11cm，①t= 11 ÷2= 5.5秒；①当CQ= BC时，如图2，则BC+CQ=12cm，①t= 12÷2= 6秒；①当BC = BQ时，如图3，过B点作BE①AC于点E，则BE=·6824105AB BCAC⨯==cm，①CE185=cm，①CQ= 2CE = 7.2cm，①BC+ CQ = 13.2cm，①t= 13.2÷2= 6.6秒；综上可知，当t为5.5秒或6秒或6.6秒时，△BCQ为等腰三角形．10．(1)证明：①BF ①CE ，①①CGB ＝90°，①①GCB +①CBG ＝90°，①四边形ABCD 是正方形， ①①CBE ＝90°＝①A ，BC ＝AB ， ①①FBA +①CBG ＝90°，①①GCB ＝①FBA ，在①ABF 和①BCE 中，A CBE AB BCABF BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ①①ABF ①①BCE （ASA ）；(2)解:①由题意可知AB ＝CD ＝BC ＝2， ①点E 是AB 的中点，①EA ＝EB ＝12AB ＝1，①CE在Rt①CEB 中，12BG •CE ＝12CB •EB ， ①BG ＝CB EB CE⋅①证明：如图，过点D 作DH ①CE 于H ，由①可得CG = ①①DCE +①BCE ＝90°，①CBF +①BCE ＝90°，①①DCE ＝①CBF ，①CD ＝BC ，①CHD ＝①CGB ＝90°，①①CHD ①①BGC （AAS ），①CH ＝BG①GH ＝CG ﹣CH ＝CH ， ①CH ＝GH ，DH ①CE ，①DC ＝DG ；11．(1)解：①AD 是由AB 折叠得到，①10AD AB ==，①()0,4D -；(2)BP t =，当05t ≤<时，①()8,0B -，()3,0C -，①8OB =，3OC =， ①1163922ACO S OA OC =⋅=⨯⨯=△，8OP OB BP t =-=-， ①()116824322APO S OA OP t t =⋅=⨯-=-△，①2439153PCA APO ACO S S S t t =-=--=-△△△，当58t <≤时，()9243315PCA ACO APO S S S t t =-=--=-△△△，综上所述，PCA 的面积是153S t =-，（05t ≤<），或315S t =-，（58t <≤）．(3)①DOP MON △△≌，①OP ON =，OM OD =，由题意可知：BP t =，2AM t =，ON at =，4OD =①8OP OB BP t =-=-，62OM AO AM t =-=-，①624t -=，解得1t =，8t at -=，解得7a =，①a 的值是7．12．(1)解：①一次函数21y x =--的图象分别交x 轴，y 轴于点A 和B ，①点A （－12，0），点B （0，－1），设直线BC 的解析式y kx b =+代入B （0，－1），C （－3，0）．解得13k =-，1b =- ①直线BC 的函数解析式113y x =--． (2)①设点P （m ，0），则点M （m ，21m --），点N （m ，113m --）依题意可得PM ＝PN ①1210013m m ⎛⎫---=--- ⎪⎝⎭解得：67m =- ①点P （－67，0） (3)设(),0,P x 而0,1,3,0,B C22222223,1,3110,PC x PB x BC 当PC PB =时，2231,x x 解得：4,3x4,0.3P 当,PB BC2110,x解得：3,x =±当3x =-时，不合题意舍去，3,0.P当PC BC =时，2310,x 12310,310,x x 310,0P 或310,0.P综上：点P （3，03，0）或（3，0）或4,03⎛⎫- ⎪⎝⎭． 13．(1)①①(490C AOD ∠=︒，，①4DC AD DO ===，①2OA ==，①四边形ABCD 是菱形，①42AB AD OB AB OA ===-=，，①点B 的坐标(2)0，，故答案为：(2)0，①①在菱形ABCD 中，4DC AB OD ===，①菱形ABCD 的面积•4AB OD ==⨯(2)如图所示：当3t =时，3AP =,在菱形ABCD 中，点P 关于AC 的对称点为3P AP ''=，，连接DP '交AC 于点E ，连接PE ，①PE DE P E ED P D ''+=+=．①2OA OD ==，①1OP '=，在Rt DOP '中，①222DO P O P D ''+=，①P D'①PE DE+14．(1)解：在直角三角形ACB中，由勾股定理得AB10，①CP把△ABC的面积分成相等的两部分，①P为AB的中点，CP＝152AB=．①运动的路径长为AC＋AP＝8＋5＝13．运动的时间为13÷1＝13（秒）所以t＝13；CP＝5．(2)解：①ABP为等腰三角形，点P只能在AC上且P A＝PB，设CP＝t，则AP＝BP＝8﹣t，在Rt①BCP中，BC2＋CP2＝BP2，即62＋t2＝（8﹣t）2，解得，t＝74，①当t＝74时，①ABP为等腰三角形；(3)作点B关于AC的对称点B′，过点B′作AB的垂线段，交AC于点P，交AB于点Q，连接AB′，则垂线段B′Q即为所求的PB＋PQ的最小值，①S△ABB′＝12×BB′×AC＝12×12×8＝48，S△ABB′＝12×AB×B′Q，①B′Q＝485，即PB＋PQ最小值为485．15．(1)①①ABC 是等边三角形① AB ＝AC①60,BAC ABC ACB ∠=∠=∠=︒①①ADE 是等边三角形①AD ＝AE①60,DAE ∠=︒BAC DAC DAE DAC∠-∠=∠-∠ 即BAD CAE∠=∠ ①ABD ACE ∆≅∆ （SAS ）① BD ＝EC①60ACE B ∠=∠=︒①120,BCE ACB ACE ∠=∠+∠=︒①180,B BCE ∠+∠=︒①AB //EC①EF //BC①四边形BCEF 是平行四边形(2)①EF //BC①60CGE ACB ∠=∠=︒①60CGE ACE ∠=∠=︒①GE ＝EC①GE ＝EC ＝BD ＝x①FG FE GE =-①8(08)y x x =-<<(3)作AH ①BC ，垂足为H在Rt AHB ∆中，90,AHD ∠=︒222AH BH AB +=①22248AH +=①AH =在Rt ADH ∆中，90,AHD ∠=︒①222AH DH AD +=即(222(4)7x +-=，解得5x =或3x =； ① 8FG x =-①FG 的长为3或516．(1)将4x =代入2y x =+得：6y =①点D 的坐标为()4,6．将()1,0C ，()4,6D 代入y kx b =+得046k b k b +=⎧⎨+=⎩解得22k b =⎧⎨=-⎩ ①直线2l 的表达式为22y x =-．(2)过点D 作DE x ⊥轴于点E ，①()4,6D ，①6DE =将0y =代入2y x =+得2x =①()2,0A -，①3AC = ①192ACD S AC DE =⋅=△． (3)①由题可知：当CP AB ⊥时，CP 的值最小，由（2）可知6DE =，①点E 坐标为()4,0，①246AE AO OE =+=+=在Rt ADE △中，90AED ∠=︒．①AD ==①192ACD S AD CP =⋅=△①29CP AD ⨯=== ①①点P 在直线y =x +2上，①设点P （x ，x +2）,①A (-2，0)，C (1，0)①22[1(2)]9AC =--=，222(2)PA x =+，222(1)(2)PC x x =-++ （a ）当AP AC =时，即22AP AC =，则：22(2)=9x +解得，x =当x =y =x =时，y =①点P （b ）当AC PC =时，即22AC PC =，则：22(1)(2)9x x -++=解得，x =1或x =-2（舍去）当1x =时，3y =；①点P 的坐标为（13，）（c ）当AP PC =时，即22AP PC =，则：22()2x +22(1)(2)x x =-++ 解得，12x =- ①32y = ①点P 的坐标为（12-，32）综上，点P 的坐标为：13，）或（12-，32） 17(1)解：①四边形ABCD 是矩形，①①BAD ＝90°，①①DAG ＝30°，①①BAG ＝60°由折叠知，①BAE ＝12①BAG ＝30°，在Rt △BAE 中，①BAE ＝30°，AB ＝3，①BE(2)解：如图4，连接GE ，①E 是BC 的中点，①BE ＝EC ，①①ABE 沿AE 折叠后得到△AFE ，①BE ＝EF ，①EF ＝EC ，①在矩形ABCD 中，①①C ＝90°，①①EFG ＝90°，①在Rt △GFE 和Rt △GCE 中，EG EG EF EC =⎧⎨=⎩①Rt △GFE ①Rt △GCE （HL ），①GF ＝GC ；设GC ＝x ，则AG ＝3+x ，DG ＝3﹣x ，在Rt △ADG 中，42+（3﹣x ）2＝（3+x ）2，解得x ＝43． (3)解：如图1，由折叠知，①AFE ＝①B ＝90°，EF ＝BE ， ①EF +CE ＝BE +CE ＝BC ＝AD ＝4，①当CF 最小时，△CEF 的周长最小，①CF≥AC-AF ，①当点A ，F ，C 在同一条直线上时，CF 最小，由折叠知，AF ＝AB ＝3，在Rt △ABC 中，AB ＝3，BC ＝AD ＝4，①AC＝5，①CF＝AC﹣AF＝2，在Rt△CEF中，EF2+CF2＝CE2，①BE2+CF2＝（4﹣BE）2，①BE2+22＝（4﹣BE）2，①BE＝32．18．解：（1）∵△ABC是等边三角形，AO⊥BC，∴OB＝OC，∠BAO＝∠CAO＝30°，∵点B坐标为（﹣3，0），∴OB＝OC＝3，∴AB＝6，∴OA∴A（0，，∵△ABC和△ADC都是等边三角形，∴AD＝AC＝AB＝6，∠ACB＝∠ACD＝∠D＝60°，∴∠D+∠BCD＝180°，∴AD∥BC，∴D（6，，故答案为：（0，，（6，；（2）△AEF是等边三角形．证明：∵△ABC和△ADC都是等边三角形，∴AB＝AC，∠B＝∠ACD＝∠BAC＝60°，∵∠EAF＝60°，∴∠BAE＝∠CAF，∴△ABE≌△ACF（ASA），∴AE＝AF，∴△AEF是等边三角形．（3）由（2）知AE＝EF＝AF，当AE⊥BC时，AE取得最小值，∴AE＝OA＝过点F作FM⊥x轴于点M，∵∠FOM＝30°，OF＝∴FM=∴OM92 =，∴F（92，即EF的最小值为F（92；（4）由（2）可知△ABE≌△ACF（ASA），∵E（﹣5，0），OB＝3，∴BE＝2，∴BE＝CF＝2，CE＝8，∵∠ACD＝∠ACB＝60°，∴∠ECF＝60°，过点F作FN⊥BC于点N，如图3，∴CN 12=CF ＝1，∴NF∴EF∵OC ＝3，∴ON ＝OC ﹣CN ＝3﹣1＝2，∴F （2，．19．(1)解：BA OA ⊥，90BAO ∴∠=︒，30AOB ∠=︒，6(),B m ，OA m ∴=，6AB =，212OB AB ∴==，OA =m ∴=B 6)，直线y kx =过点B 6)，k ∴= (2)如图1，过点P 作PF BC ⊥于点F ，BQ ∴，2OP t =，则122PB t =-，30OBC ∠=︒，∴在Rt PFB ∆中，6PF t =-，()2162S t ∴=⨯-=+； (3)分三种情况：①当BQ BP =122t =-，解得24t =-①当PQ PB =时，如图2，过点P 作PM BQ ⊥于点M ，BM ∴，2)t -，解得4t =；①当OB QP =时，如图3，过点Q 作ON BP ⊥于点N ，则6BN t =-，6t ∴-=，解得125t =；综上所述，当PQB ∆为等腰三角形时，t 的值为24-4或125． 20．(1)解：过点C 作CN OA ⊥于点N ，过点C 作CM OB ⊥于点N ．①CN OA ⊥①//CN OB又①点C 为线段AB 的中点，OA = 6 ①132ON OA == 同理132OM OB == ①C (3,3)(2)作点B关于x轴的对称点B'，连接CB'交x轴于点P，此时PB+PC的值最小，由已知得，点B的坐标为（0，6），①点B关于x轴的对称点B'（0，﹣6），由（1）知，C（3，3），可设直线CB'的解析式为y=kx+b，①633bk b-=⎧⎨=+⎩解得36kb=⎧⎨=-⎩① 直线CB'的解析式为y=3x﹣6，令y=0，则3x﹣6=0，解得：x=2，① P（2，0）；(3)存在点F，使以A、C、D、F为顶点的四边形为平行四边形，设点F的坐标为（m，n）．分三种情况考虑，如图所示：当AC为对角线时，①A（6，0），C（3，3），D（1，0），①1632200322mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：83mn=⎧⎨=⎩，①点F1的坐标为（8，3）；①当AD为对角线时，①A（6，0），C（3，3），D（1，0），①3162230022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：43 mn=⎧⎨=-⎩，①点F2的坐标为（4，-3）；①当CD为对角线时，①A（6，0），C（3，3），D（1，0），①6312203022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：23mn=-⎧⎨=⎩，①点F3的坐标为（-2，3）．综上所述，点F的坐标是（8，3），（4，-3）或（-2，3）．。

八年级数学下册期末动点问题及压轴题带答案

1．（12分）已知：如图，平面直角坐标系中，A（0，4），B（0，2），点C是x轴上一点，点D为OC的中点．（1）求证：BD∥AC；（2）若点C在x轴正半轴上，且BD与AC的距离等于1，求点C的坐标；（3）如果OE⊥AC于点E，当四边形ABDE为平行四边形时，求直线AC的解析式．2．（12分）如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm．一动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB 边向点B以3cm/s的速度运动．P，Q分别从点A和点C同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为t s，则（1）t为何值时，四边形PQCD为平行四边形？（2）t为何值时，四边形PQCD为等腰梯形？（3）AB边的长是否存在一数值，使四边形PQCD为菱形．如果存在，请求出AB 边的长，如果不存在，请说出理由．3．（本题10分）已知：在正方形ABCD 中，AB ＝6，P 为边CD 上一点，过P 点作PE ⊥BD 于点E ，连接BP(1) O 为BP 的中点，连接CO 并延长交BD 于点F① 如图1，连接OE ，求证：OE ⊥OC② 如图2，若53=EF BF ，求DP 的长 (2) CP EP 22+＝___________4．（本题12分）如图1，直线333+-=x y 分别与y 轴、x 轴交于点A 、点B ，点C 的坐标为(－3，0)，D 为直线AB 上一动点，连接CD 交y 轴于点E(1) 点B 的坐标为__________，不等式0333>+-x 的解集为___________(2) 若S △COE ＝S △ADE ，求点D 的坐标(3) 如图2，以CD 为边作菱形CDFG ，且∠CDF ＝60°．当点D 运动时，点G 在一条定直线上运动，请求出这条定直线的解析式.5.（11分）如图1，在平面直角坐标系中，点O 是坐标原点，四边形ABCO 是菱形，点A 的坐标为（﹣3，4），点C 在x 轴的正半轴上，直线AC 交y 轴于点M ，AB 边交y 轴于点H ，连接BM .（1）菱形ABCO的边长是；（2）求直线AC 的解析式；（3）动点P 从点A 出发，沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动，设△PMB 的面积为S （S≠0），点P 的运动时间为t 秒.①求S 与t 之间的函数关系式；②在点P 运动过程中，当S =3，请直接写出t 的值．6.（11分）如图，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，且AD=12cm ，AB=8cm ，DC=10cm ，若动点P 从A 点出发，以每秒2cm 的速度沿线段AD 向点D 运动；动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动，当P 点到达D 点时，动点P 、Q 同时停止运动，设点P 、Q 同时出发，并运动了t 秒，回答下列问题：（1）BC= cm ；（2）当t 为多少时，四边形PQCD 成为平行四边形？（3）当t 为多少时，四边形PQCD 为等腰梯形？（4）是否存在t ，使得△DQC 是等腰三角形？若存在，请求出t 的值；若不存在，说明理由．7、如图①，已知正方形ABCD的边长为1，点P是AD边上的一个动点，点A关于直线BP的对称点是点Q，连接PQ、D Q、CQ、BQ，设AP=x.（1）BQ＋DQ的最小值是_______，此时x的值是_______；（2）如图②，若PQ的延长线交CD边于点E，并且∠CQD=90°.①求证：点E是CD的中点；②求x的值.（3）若点P是射线AD上的一个动点，请直接写出当△CDQ为等腰三角形时x 的值.8、如图1，平面直角坐标系中，直线AB：y=﹣x+b交x轴于点A(8，0)，交y轴正半轴于点B.(1)求点B的坐标；(2)如图2，直线AC交y轴负半轴于点C，AB=BC，P为线段AB上一点，过点P 作y轴的平行线交直线AC于点Q，设点P的横坐标为t，线段PQ的长为d，求d与t之间的函数关系式；(3)在(2)的条件下，M为CA延长线上一点，且AM=CQ，在直线AC上方的直线AB上是否存在点N，使△QMN是以QM为斜边的等腰直角三角形？若存在，请求出点N的坐标及PN的长度；若不存在，请说明理由.1.【解答】解：（1）∵A（0，4），B（0，2），∴OA=4，OB=2，点B为线段OA的中点，又点D为OC的中点，即BD为△AOC的中位线，∴BD∥AC；（2）如图1，作BF⊥AC于点F，取AB的中点G，则G（0，3），∵BD∥AC，BD与AC的距离等于1，∴BF=1，∵在Rt△ABF中，∠AFB=90°，AB=2，点G为AB的中点，∴FG=BG=AB=1，∴△BFG是等边三角形，∠ABF=60°．∴∠BAC=30°，设OC=x，则AC=2x，根据勾股定理得：OA==x，∵OA=4，∴x=∵点C在x轴的正半轴上，∴点C的坐标为（，0）；（3）如图2，当四边形ABDE为平行四边形时，AB∥DE，∴DE⊥OC，∵点D为OC的中点，∴OE=EC，∵OE⊥AC，∴∠OCA=45°，∴OC=OA=4，∵点C在x轴的正半轴上，∴点C的坐标为（4，0），设直线AC的解析式为y=kx+b（k≠0）．将A（0，4），C（4，0）代入AC的解析式得：解得：∴直线AC的解析式为y=﹣x+4．2.【解答】解：（1）由运动知，AP=t，CQ=3t，∴DP=AD﹣AP=24﹣t，∵四边形PQCD为平行四边形，∴DP=CQ，∴24﹣t=3t，∴t=6；（2）如图2，过点D作DE⊥BC于E，过点P作PF⊥BC于F，∴四边形EFPD是矩形，∴DE=PF，[来源:Z|xx|]∵四边形PQCD是等腰梯形，∴∠PQC=∠DCQ，∵∠PFQ=∠DEC=90°，∴△PFQ≌△DEC，∴FQ=CE，∴BE=AD=24，∴CE=BC﹣BE=2，∵四边形PQCD为等腰梯形，∴CQ=DP+2CE，由运动知，AP=t，CQ=3t，∴DP=AD﹣AP=24﹣t，∴24﹣t+2×2=3t，∴t=7，（3）AB边的长是8时，四边形PQCD为菱形，理由：由（1）知，t=6时，四边形PQCD是平行四边形，∴DP=24﹣6=18，∵平行四边形PQCD是菱形，∴CD=DP=18，如图2，过点D作DE⊥BC于E，∴四边形ABED是矩形，∴AB=DE，在Rt△CDE中，CE=2，CD=18，∴DE==8．3.证明：(1) ① ∵∠PEB ＝∠PCB ＝90°，O 为BP 的中点∴OE ＝OB ＝OP ＝OC∴∠POE ＝2∠DBP ，∠POC ＝2∠CBP∴∠COE ＝∠POE ＋∠POC ＝2(∠DBP ＋∠CBP )＝90°∴OE ⊥OC② 连接OE 、CE∵△COE 为等腰直角三角形∴∠ECF ＝45°在等腰Rt △BCD 中，BF 2＋DE 2＝EF 2设BF ＝3x ，EF ＝5x ，则DE ＝4x∴3x ＋4x ＋5x ＝26，解得x ＝22 ∴DP ＝2DE ＝424=x(2) ∵62==-+=+CD C DP CP EP ∴2322=+CP EP4.解：(1) (3，0)、x ＜3(2) ∵S △COE ＝S △ADE∴S △AOB ＝S △CBD 即33321621⨯⨯=⨯⨯D y ，y D ＝233 当y ＝233时，23233333==+-x x ，∴D (23323，) (3) 连接CF∵∠CDF ＝60°∴△CDF 为等边三角形连接AC∵AB ＝AC ＝BC ＝6∴△ABC 为等边三角形∴△CAF ≌△CBD （SAS ）∴∠CAF ＝∠ACB ＝60°∴AF ∥x 轴设D (m ，333+-m )过点D 作DH ⊥x 轴于H∴BH ＝3－m ，DB ＝6－2m ＝AF∴F (2m －6，33)由平移可知：G (m －9，m 3-) 令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6.解：根据题意得：PA=2t ，CQ=3t ，则PD=AD-PA=12-2t ．（1）如图，过D 点作DE ⊥BC 于E ，则四边形ABED 为长方形，DE=AB=8cm ，AD=BE=12cm ，在直角△CDE 中，∵∠CED=90°，DC=10cm ，DE=8cm ，∴22DC DE -，∴BC=BE+EC=18cm ．…………………………………………………………………2分（直接写出最后结果18cm 即可）（2）∵AD ∥BC ，即PD ∥CQ ，∴当PD=CQ 时，四边形PQCD 为平行四边形，即12-2t=3t ，解得t=125秒，故当t=125秒时四边形PQCD 为平行四边形；………………………………………4分（3）如图，过D 点作DE ⊥BC 于E ，则四边形ABED 为长方形，DE=AB=8cm ，AD=BE=12cm ，当PQ=CD 时，四边形PQCD 为等腰梯形．过点P 作PF ⊥BC 于点F ，过点D 作DE ⊥BC 于点E ，则四边形PDEF 是长方形，EF=PD=12-2t ，PF=DE ．在Rt △PQF 和Rt △CDE 中，PQ CD PF DE ==⎧⎨⎩， ∴Rt △PQF ≌Rt △CDE （HL ），∴QF=CE ，∴QC-PD=QC-EF=QF+EC=2CE ，即3t-（12-2t ）=12，解得：t=245，即当t=245时，四边形PQCD 为等腰梯形；……………………………………………8分（4）△DQC 是等腰三角形时，分三种情况讨论：①当QC=DC 时，即3t=10，∴t=103；②当DQ=DC时，36 2t=∴t=4；③当QD=QC时，3t×65 10=∴t=259．故存在t，使得△DQC是等腰三角形，此时t的值为103秒或4秒或259秒．………11分③在Rt△DMQ中，DQ2=DM2+QM2222 (3)8(38) t t=+-36t=100t=25 97.解：（1）；－1；（2）①证明：在正方形ABCD中，AB=BC，∠A=∠BCD=90°∵Q点为A点关于BP的对称点∴AB=QB，∠A=∠PQB=90°∴QB=BC，∠BQE=∠BCE∴∠BQC=∠BCQ∴∠EQC=∠EQB－∠CQB=∠ECB－∠QCB=∠ECQ∴EQ=EC在Rt△ABC中∵∠QDE=90°－∠QCE，∠DQE=90°－∠EQC∴∠QDE=∠DQE∴EQ＋ED∴CE=EQ=ED即E是CD的中点②（3）或或8.解：(1)∵y=﹣x+b交x轴于点A(8，0)，∴0=﹣×8+b，b=6，∴直线AB解析式为y=﹣x+6，令x=0，y=6，B(0，6)；(2)∵A(8，0)，B(0，6)，∴OA=8，OB=6，∵∠AOB=90°，∴AB=10=BC，∴OC=4，∴点C(0，﹣4)，设直线AC解析式为y=kx+b’，∴，∴∴直线AC解析式为y=x﹣4，∵P在直线y=﹣x+6上，∴可设点P(t，﹣t+6)，∵PQ∥y轴，且点Q在y=x﹣4 上，∴Q(t， t﹣4)，∴d=(﹣t+6)﹣(t ﹣4)=﹣t+10；(3)过点M作MG⊥PQ于G，∴∠QGM=90°=∠COA，∵PQ∥y轴，∴∠OCA=∠GQM，∵CQ=AM，∴AC=QM，在△OAC与△GMQ中，，∴△OAC≌△GMQ，∴QG=OC=4，GM=OA=8，过点N作NH⊥PQ于H，过点M作MR⊥NH于点R，∴∠MGH=∠RHG=∠MRH=90°，∴四边形GHRM是矩形，∴HR=GM=8，可设GH=RM=k，∵△MNQ是等腰直角三角形，∴∠QMN=90°，NQ=NM，∴∠HNQ+∠HQN=90°，∴∠HNQ+∠RNM=90°，∴∠RNM=∠HQN，∴△HNQ≌△RMN，∴HN=RM=k，NR=QH=4+k，∵HR=HN+NR，∴k+4+k=8，∴k=2，∴GH=NH=RM=2，∴HQ=6，∵Q(t，t﹣4)，∴N(t+2，t﹣4+6)即 N(t+2，t+2)∵N在直线AB：y=﹣x+6上，∴t+2=﹣(t+2)+6，∴t=2，∴P(2，)，N(4，3)，∴PH=，NH=2，∴PN==.。