2011——2012学年六下学期数学期末试卷
【小升初】2023-2024学年北师大版六年级下学期期末数学毕业模拟测试题2套(含解析)
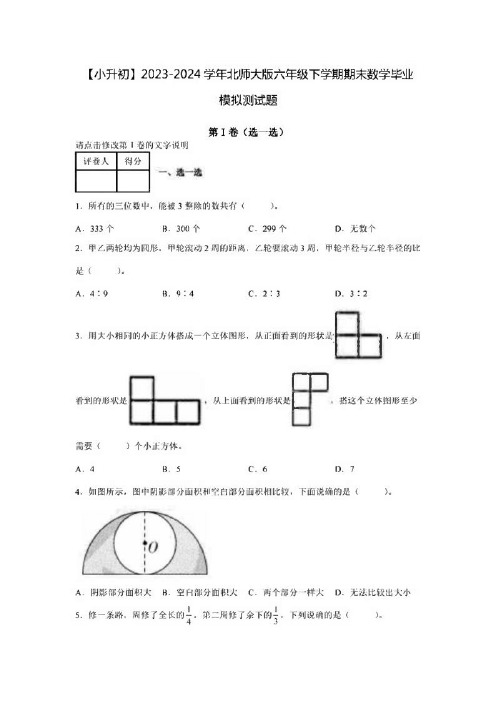
1. 所有的三位数中,能被3整除的数共有( ) 。
A. 333 个B. 300 个C. 299 个D.无数个2. 甲乙两轮均为圆形, 甲轮滚动2周的距离, 乙轮要滚动3周, 甲轮半径与乙轮半径的比是( ) 。
A. 4 :9B. 9 :4C. 2 :3D. 3 :23. 用大小相同的小正方体搭成一个立体图形,从正面看到的形状是I I I,从左面m 看到的形状是 从上面看到的形状是L搭这个立体图形至少需要 ( ) 个小正方体。
【小升初】2023-2024学年北师大版六年级下学期期末数学毕业模拟测试题第I 卷(选一选)请点击修改第I 卷的文字说明 评卷人 得分A. 4B. 5C. 6D. 74.如图所示, 图中阴影部分面积和空白部分面积相比较,下面说确的是( ) 。
A.阴影部分面积大B.空白部分面积大C.两个部分一样大D.无法比较出大小5修.-条路 ,周修了全长的:,第二周修了余下站,下列说确的是 ( ) 。
A.两周修的长度一样B.周修的多C.第二周修的多D.再用两周时间一定可以修完第II 卷(非选一选)56x3 = 720+9 = 5x0.12= 0.21+3 =请点击修改第II 卷的文字说明 评卷人 得分9.17-0.26=二、 口算和估算④ (3.99+1.99) -4.6 ⑥ x —22 33 149⑦ (0.84-0.4+2.9) xo.17 JL --评卷人 得分---------------- 四、解方程或比例6.直接写出得数。
(结果要求最简) 。
236+145 = 487-229= 7.6+4.143 7 5 15-x20 = —X —= —+ —= 4 14 9 12 8评卷人 得分三、脱式计算7.用递等式计算,能简算的要简算。
① 132 + 51+68+49 ③ 146'5 — 8.解方程。
① 40%、= 7.2Q® —x + 3 = 1921 20 5239"20H:21 21—1 F —2= 3 75__5_ 8 1250x-36x = 42④ 6:0.9 = x:2.1评卷人五、填空题9. 20900000 读作( ) ,将这个数改写成“万”作单位的数是(10. 十四亿零七万九千零八写作( ) ,将这个数四舍五入到“亿”位约是( ) 亿。
人教版小学六年级下数学期末试卷及答案

人教版小学六年级下数学期末试卷及答案人教版小学六年级数学下学期期末质量检测题姓名。
班级。
分数:一、填空每个括号0.5分,共18分。
1、40%=8÷(5)=10:(1)=10(小数:0.1)2、1千米20米=(1020)米4.3吨=(4300)千克3时15分=(3:15)时2.07立方米=(2070)立方分米3、四百二十万六千五百写作(xxxxxxx),四舍五入到万位约是(xxxxxxx)万。
4、把单位“1”平均分成7份,表示其中的5份的数是(5/7),这个数的分数单位是(7/5)。
5、4、8、12的最大公约数是(4);最小公倍数是(24),把它分解质因数是(2^3*3)。
6、0.25:4的比值是(1:16),化成最简单整数比是(1:4)。
7、在1、1.83和1.83%中,最大的数是(1.83),最小的数是(1)。
8、在1、2、3……10十个数中,所有的质数比所有的合数少(10%)。
9、晚上8时24时记时法就是(20时24分),从上午7时30分到下午4时30分经过了(9)小时。
10、常用的统计图有(条形)统计图,(折线)统计图和扇形统计图。
11、能被2、3、5整除的最小两位数是(30),最大三位数是(990)。
12、六(1)班期中考试及格的有48人及格,2人不及格,及格率是(96%),优秀率(80分及以上)达到60%,优秀人数有(30)人。
13、学校有图书630本,按2:3:4借出三、四、五三个年级,五年级借到图书(252)本。
14、一个正方体棱长总和是24厘米,这个正方体的一个面的面积是(36)平方厘米,体积是(64)立方厘米。
15、一个圆柱体底面直径是4厘米,高3厘米,底面积是(4π)平方厘米,体积是(3π)立方厘米,与它等底等高的圆锥体体积是(4/3π)立方厘米。
16.2014年是(闰年),全年共有(366)天。
二、火眼金睛辨正误(对的打“√”,错的打“X”,共10分)17.圆的周长和直径成正比例。
陈俊仪——洪武小学2011—2012学年上学期期末试卷(六年级数学)

洪武学校六年级数学上册期末综合测试卷第 1 页 共 2 页 编制:陈俊仪洪武学校六年级数学期末综合测试卷一、认真读题,用心思考,我能正确填写。
(每题2分,共24分)1.一个点在图上的位置可用(4、6)表示,如果这个点向左平移2个单位,其位置应表示为( , )。
2.( )÷8﹦()40﹦12.5%﹦( ):( )﹦( )(填小数)3.把67.8% ,0.67, 0.677, 0.6 7 ,32按从小到大的顺序排列是: ( )。
4.( )比12多31 ;24千克比( )少31。
5.食堂有2吨大米,如果每天吃它的101,那么( )天可以吃完;如果每天吃101吨,那么( )天可以吃完。
6.比54多20%的数是( ),比200千克少12.5%的数是( )。
7.541小时:40分钟,化成最简整数比是( ),比值是( )。
8.李刚家要栽种一批树苗,这种树苗的成活率一般为75%~80%,如果要栽活1200棵树苗,那么至少应栽( )棵。
9.从一张边长10㎝的正方形纸里剪出一个最大的圆,这个圆的周长是( )㎝,面积是( )㎝2。
10.某工人一天生产的次品与合格品的比是1∶49,其产品的合格率是( )。
11.把圆分成若干等份,然后把它剪开,照右图的样子拼成一个近似的长方形。
已知长方形的周长比 原来圆的周长增加了4厘米,这个圆的周长是 ( )厘米,拼成的长方形面积是( )平方厘米。
12.一本故事书,小明第一天看了全书的31,看了24页,小明还要看的页数是从第( )页到第( )页。
二、火眼金睛,我会公正评判。
(6分)1.5米的20%与2米的50%相等。
( ) 2.圆的半径扩大2倍,面积也扩大相同的倍数。
( ) 3.一项工程,甲单独做要10天,以单独做要8天。
甲和乙工作效率的最简 整数比是5∶4。
( )4.5千克铁钉用去51,又用去51千克,两次共用去52千克。
( )5.圆周率是圆的周长与直径的比。
( ) 6.用102粒玉米种子进行发芽试验,结果全部发芽,发芽率是102%。
2011春季小学六年级北师大版版下学期期末试卷、北师大二上数学期末试卷

北师大版六年级数学下册期末诊断题一、填空题:1.一个圆柱的底面积是0.9平方米,高是2米,它的体积是()。
2.一个圆锥的体积是47.1立方米,底面半径是3米,它的高是()。
3.每袋面粉的质量一定,面粉的总质量与袋数成()比例。
4.一幅图上,用4厘米表示实际距离40千米,这幅图的比例尺是()。
5.在比例尺1:3000000的地图上,量得甲、乙两地的距离为2.5厘米,甲、乙两地的实际距离是()千米。
二、选择题:1.一个圆柱,侧面展开图是正方形,它的高是12.56厘米,那么它的底面半径是()。
A.6.28B.4C.22.学校修建一个圆柱形喷水池,容积是37.68立方米,池内直径是4米,那么这个水池深()米。
A.2B.3C.63.汽车的速度一定,汽车所行的路程和时间()。
A.成正比例B.成反比例C.不成比例4.地图上1厘米的线段表示实际距离1千米,这幅地图的比例尺是()。
A.1:10000B.1:100000C.1:1000000三、判断题:1.一个正方体的底面周长与一个圆柱的底面周长相等,它们的高也相等,那么它们的体积也一定相等。
()2.正方形的面积与边长成正比例。
()3.长方形的面积一定,它的长和宽成反比例。
()4.圆锥的体积是圆柱的体积的13。
()5.把一张长62.8厘米,宽31.4厘米的长方形硬纸片,卷成一个圆柱形纸筒(粘贴处宽度不计),它的底面半径是10厘米。
…………()四、看图表填空,根据规律判断比例关系,并填空。
(1)更多免费试卷下载 分站X 与Y( )。
A.成正比例 B.成反比例(2X 与Y( )。
A.成正比例 B.成反比例五、解答题:1.甲市到乙市约200千米,如果在比例尺为1:2000000的地图上画出这两个城市,这两个城市之间的图上距离是多少厘米?2.一个圆柱形油桶直径6分米,高8分米,制作这个油桶至少需要多少平方分米的铁皮?如果每千克油的体积是1.5立方分米,这个油桶可以装多少千克油?3.一个近似圆锥形的沙堆,高3米,底面周长31.4米,又知沙子每立方米重1.5吨,如果用一辆载重5吨的汽车运输,多少次可以运完?(得数保留整数北师大版二年级上册数学期末试卷班级 姓名 成绩送给小朋友:通过一个学期的学习,收获很多吧!运用你所学过的知识来检测一下对知识的掌握情况吧,祝你们取得好成绩! 一、看谁算得又对又快。
2011—2012学年第二学期期中考试六年级数学试卷

ab 2011—2012学年第二学期期中考试六年级数学试卷一、用心思考,正确填空。
(17分)1、( )升( )毫升=4050毫升 6.25小时=( )分2、比45千克多20%是( ) 30吨比( )吨少21吨 3、有一个比例,它的两个外项都是0.5 ,那么它的两个内项乘积的倒数是( )。
4、14 的分子、分母同时加上( )后,约分为54。
5、一幅地图上的比例尺是1:2000000,把它改写成线段比例尺是( ),在这幅地图上量得A 、B 两地的距离是15厘米,A 、B 两地实际距离是( )千米。
6、 5个整数从小到大排列,中位数是7,如果这组数据中唯一的众数是4,则这5个整数的和最小是( )。
7、今年植树节,同学们种植了180棵树,有20棵没有成活,后来大家补种了20棵,全部成活。
今年同学们植树的成活率是( )。
8、 左图是王老师在电脑上下载一份文件的过程示意图。
电脑显示,下载这份文件一共需要25分钟,那么还要等( )分钟才能下载完这份文件。
9、 如图,4个相同的直角三角形围成了一个正方形,已知a ∶b =1∶2,阴影部分的面积占大正方形面积的( )。
10、一个商人,把一件连衣裙标价为680元,经打假人员鉴别,降至100元一 件出售,仍可赚25%,如按原价出售,则每件可赚( )元。
11、把一个圆柱的高减少2厘米,它的表面积就减少25.12平方厘米,这个圆柱的底面积是( )平方厘米,体积减少了( )立方厘米。
12、有240人去春游,想准备一些饮料,商店“优惠告示”写着本店饮料,6只空瓶可换一瓶饮料, 240人至少买( )瓶饮料,就能保证每人都喝一瓶。
13、甲车与乙车速度比是4﹕5,行完同一段路程,乙车所用时间和甲车所用时间的比是( )。
二、仔细推敲,准确判断。
(5分,对的打“√”,错的打“×”)1.一个数增加20%后再减少20%,这个数的大小不变。
( ) 2、计算长方体、正方体和圆柱的体积时,都可以用底面积乘高来计算。
北京市西城区2011—2012学年度第一学期期末试卷(南区)数学word

北京市西城区2011—2012学年度第一学期期末试卷(南区)九年级数学 2012.1一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.抛物线2(1)1y x =-+的顶点坐标为A .(1,1)B .(1,1)-C .(1,1)-D .(1,1)--2.若相交两圆的半径分别为4和7,则它们的圆心距可能是A .2B .3C . 6D .113.在Rt △ABC 中,∠ C =90°,若BC =1,AB tan A 的值为A B C .12D .2 4. 如图,在⊙O 中,直径AB ⊥弦CD 于E ,连接BD ,若∠D =30°,BD =2,则AE 的长为A .2B .3C .4D .55.下列图形中,中心对称图形有A .4个B .3个C .2个D .1个6.抛掷一枚质地均匀的正方体骰子,出现大于3点的概率为A .21 B .31 C .41 D .61 7.如图,抛物线2y ax bx c =++经过点(-1,0),对称轴为x =1,则下列结论中正确的是A .0>aB .当1>x 时,y 随x 的增大而增大C .0<cD .3x =是一元二次方程20ax bx c ++=的一个根8.如图,在平面直角坐标系xOy 中,(2,0)A ,(0,2)B ,⊙C 的圆心为点(1,0)C -,半径为1.若D 是⊙C 上的一个动点,线段DA 与y 轴交于E 点,则△ABE 面积的最大值是A .2B . 83C .2+D . 2二、填空题(本题共16分,每小题4分)9.如图,⊙O 是△ABC 的外接圆,若∠OCB =40°,则∠A= °.10.将抛物线2y x =先向下平移1个单位长度后,再向右平移1个单位长度,所得抛物线的解析式是 .11.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4.以斜边AB 的中点D 为旋转中心,把△ABC 按逆时针方向旋转α角(0120α︒<<︒),当点A 的对应点与点C 重合时,B ,C 两点的对应点分别记为E ,F ,EF 与AB 的交点为G ,此时α等于 °,△DEG 的面积为 . 12.已知二次函数212y x x =-+,(1)它的最大值为 ;(2)若存在实数m , n 使得当自变量x 的取值范围是m ≤x ≤n 时,函数值y 的取值范围恰好是3m ≤y ≤3n ,则m= ,n= .三、解答题(本题共30分,每小题5分)13.计算:2cos302sin 45︒︒-︒.14.如图,网格中每个小正方形的边长均为1,且点A ,B ,C ,P 均为格点.(1) 在网格中作图:以点P 为位似中心,将△ABC 的各边长放大为原来的两倍,A ,B ,C 的对应点分别为A 1 ,B 1 ,C 1;(2) 若点A 的坐标为(1,1),点B 的坐标为(3,2),则(1)中点C 1的坐标为 .15.已知抛物线245y x x =+-.(1)直接写出它与x 轴、y 轴的交点的坐标;(2)用配方法将245y x x =+-化成2()y a x h k =-+的形式.16.如图,三角形纸片ABC 中,∠BCA =90°,∠A =30°,AB =6,在AC 上取一点 E ,沿BE 将该纸片折叠,使AB 的一部分与BC 重合,点A 与BC 延长线上的点D 重合,求DE 的长.17.学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示).设矩形的一边AB 的长为x 米(要求AB <AD ),矩形ABCD 的面积为S 平方米.(1)求S 与x 之间的函数关系式,并直接写出自变量x 的取值范围;(2)要想使花圃的面积最大,AB 边的长应为多少米?18.如图,在Rt △ABC 中,90C ∠=︒,AB 的垂直平分线与BC ,AB 的交点分别为D ,E .(1)若AD =10,4sin5ADC ∠=,求AC 的长和tan B 的值; (2)若AD=1,ADC ∠=α,参考(1)的计算过程直接写出tan2α的值(用sin α和cos α的值表示).四、解答题(本题共20分,每小题5分)19.如图所示,在平面直角坐标系xOy 中,正方形PABC 的边长为1,将其沿x 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形PABC 顺时针旋转90°得到第二个正方形,再以顶点D 为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n 个正方形.设滚动过程中的点P 的坐标为(,)x y .(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P 的坐标;(2)画出点(,)P x y 运动的曲线(0≤x ≤4),并直接写出该曲线与x 轴所围成区域的面积.20.已知函数2y x bx c =++(x ≥ 0),满足当x =1时,1y =-,且当x = 0与x =4时的函数值相等.(1) 求函数2y x bx c =++(x ≥ 0)的解析式并画出它的图象(不要求列表);(2) 若()f x 表示自变量x 相对应的函数值,且2 (0),() 2 (0),x bx c x f x x ⎧++≥=⎨-<⎩又已知关于x 的方程()f x x k =+有三个不相等的实数根,请利用图象直接写出实数k 的取值范围.21.已知:如图,AB 是⊙O 的直径,AC 是弦,∠BAC 的平分线与⊙O 的交点为D ,DE ⊥AC ,与AC 的延长线交于点E .(1)求证:直线DE 是⊙O 的切线;(2)若OE 与AD 交于点F ,4cos 5BAC ∠=,求DF AF的值.22.阅读下列材料:题目:已知实数a ,x 满足a >2且x >2,试判断ax 与a x +的大小关系,并加以说明.思路:可用“求差法”比较两个数的大小,列出ax 与a x +的差()y ax a x =-+再说明y 的符号即可.现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成(1)y a x a =--,要判断y 的符号可借助函数(1)y a x a =--的图象和性质解决. 参考以上解题思路解决以下问题:已知a ,b ,c 都是非负数,a <5,且 2220a a b c ---=,2230a b c +-+=.(1)分别用含a 的代数式表示4b ,4c ;(2)说明a ,b ,c 之间的大小关系.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.已知抛物线2(2)2y kx k x =+--(其中0k >).(1)求该抛物线与x 轴的交点及顶点的坐标(可以用含k 的代数式表示);(2)若记该抛物线顶点的坐标为(,)P m n ,直接写出n 的最小值;(3)将该抛物线先向右平移12个单位长度,再向上平移1k个单位长度,随着k 的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).24.已知:⊙O 是△ABC 的外接圆,点M 为⊙O 上一点.(1)如图,若△ABC 为等边三角形,BM =1,CM =2,求AM 的长;(3) 若△ABC 为等腰直角三角形,∠BAC =90︒,BM a =,CM b =(其中b a >),直接写出AM 的长(用含有a ,b 的代数式表示).25. 已知:在如图1所示的平面直角坐标系xOy 中,A ,C 两点的坐标分别为(2,3)A ,(,3)C n -(其中n >0),点B在x 轴的正半轴上.动点P 从点O 出发,在四边形OABC 的边上依次沿O —A —B —C 的顺序向点C 移动,当点P 与点C 重合时停止运动.设点P 移动的路径的长为l ,△POC 的面积为S ,S 与l 的函数关系的图象如图2所示,其中四边形ODEF 是等腰梯形.(1)结合以上信息及图2填空:图2中的m = ;(2)求B ,C 两点的坐标及图2中OF 的长;(3)在图1中,当动点P 恰为经过O ,B 两点的抛物线W 的顶点时,① 求此抛物线W 的解析式;② 若点Q 在直线1y =-上方的抛物线W 上,坐标平面内另有一点R ,满足以B ,P ,Q ,R 四点为顶点的四边形是菱形,求点Q 的坐标.。
浙江省温州市鹿城区2023-2024学年六年级下学期期末数学试卷 附解析
浙江省温州市鹿城区2023-2024学年六年级下学期期末数学试卷选择(每题只有一个正确答案,共6分)1.第33 届夏季奥运会将于今年7月26日至8月11日在法国巴黎举行,这两个月分别是() A.小月和大月B.大月和小月C.大月和大月D.小月和小月2.小舟在计算如下算式时,算法正确的是()。
A.1.2×0.08=12×8×(0.1×0.1)B.120÷80=12÷8÷10÷10C.1.2×20=12×2×10D.35×68=(3×6)×(15×18)3.因年初一场突如其来的大雪,某地枇杷产量锐减到一成。
那么,今年某地枇杷的产量()。
A.是去年的10%B.比去年减少了10%C.比去年增加了10%D.是去年的90%4.下面各图中的“?”能用2a+4表示的是()。
A.B.C.D.5.下面问题可以用反比例来解决的是()。
A.中国空间站在太空中绕地球运行6周需要大约需要9小时,运行15周大约要多少时间?B.某雨水收集处理站2年可提供5万吨冲厕水。
照这样计算,5年可提供多少吨冲厕水?C.25 元一本的书,小明的钱可以买6本。
用这些钱买30元一本的书,可以买几本?D.某枇杷园每天销售750千克枇杷。
如果每千克售价70元,每天可收入多少元?6.一杯纯果汁,小舟先喝了38。
然后往杯子里加满水,又喝了一半。
她喝的纯果汁和水的比是()。
A.7:3B.11:3C.7:4D.11:4填空(每空1分,共12分)7.“杭温高铁”即将进入开通倒计时,该项目总投资约四百八十四亿九千万元,横线上的数写作 ,改写成用“亿”作单位的数是 亿元。
8.在直线上表示出:−72-2 4.59.()10=4: = ÷20=八折= %10.某地推行中水回用,企业能以0.2元/吨的价格购买中水。
2023-2024学年上海市廊下中学六年级下学期期末考试数学试卷含详解
2023学年第二学期期末诊断评估六年级数学试卷班级_______ 姓名_______一,选择题(每题3分,满分18分)1.在体育课的立定跳远测试中,以2.00m 为标准,若小明跳出了2.35m,可记作0.35m +,则小亮跳出了1.65m,应记作( ) A .0.25m + B .0.25m - C .0.35m - D .0.35m +2.在数轴上,位于3-和3之间的点表示的有理数有( )A .5个B .4个C .3个D .无数个3.观察下列方程其中是二元一次方程是( )A .5x ﹣47y =35B .xy =16C .2x 2﹣1=0D .3z ﹣2(z +1)=6 4.已知m <n ,那么下列各式中,不一定成立的是( )A .2m <2nB .3﹣m >3﹣nC .mc 2<nc 2D .m ﹣3<n ﹣15.如图,在长方体ABCD -EFGH 中,与面ADHE 平行的面是( )A .面ABFEB .面ABCDC .面BCGFD .面EFGH6.下列说法中. (1)联结两点的线段叫做两点之间的距离.(2)用度量法和叠合法都可以比较两个角的大小.(3)铅垂线,三角尺,合页型折纸都可以检验直线和平面垂直.(4)六个面,十二条棱和八个顶点组成的图形都是长方体.你认为正确的个数为( )A .1个B .2个C .3个D .4个二,填空题:(本大题共12题,每题2分,满分24分)7.12-的相反数是 . 8.比较大小:314- ( 1.2)--(填“>”,“<”或“=”). 9.如果1=3x -,则x = .10.现今世界上较先进的计算机显卡每秒可绘制出28000000个三角形,且显示逼真,用科学记数法表示这种显卡每秒绘制出三角形 个.11.将方程210y x -+=变形为用含有y 的式子表示x ,则x = .12.若23x y =-⎧⎨=⎩是方程35kx y -=的一个解,则k = . 13.不等式的342x x -≤+非负整数解共有 个.14.已知3824A '∠=︒,则A ∠的余角的大小是 .15.如图,已知BD =16cm,BD =25AB ,点C 是线段BD 的中点,那么AC = cm .16.已知A ,B 两地的位置如图所示,且150BAC ∠=︒, B 地在A 地的 方向.17.有理数a ,b ,c 在数轴上的位置如图所示,化简:a b a b c b ++++-=18.如图,点A ,O ,B 都在直线MN 上,射线OA 绕点O 按顺时针方向以每秒4°的速度旋转,同时射线OB 绕点O 按逆时针方向以每秒6°的速度旋转(当其中一条射线与直线MN 叠合时,两条射线停止旋转).经过 秒,∠AOB 的大小恰好是60°.三,简答题(本题共6题,每题5分,满分30分)19.计算:()322132|2|2⎛⎫-+---+- ⎪⎝⎭. 20.解方程:2161136x x +--=. 21.解方程组:28325x y x y -=⎧⎨+=⎩①② 22.解不等式组:52(1)16532x x x +->-⎧⎪⎨-≥--⎪⎩,并将其解集在数轴上表示出来.23.解方程组:252130x y z x y z x z -+=⎧⎪+-=⎨⎪-=⎩.24.已知一个锐角的补角比它的余角的3倍大10︒,求这个角的度数.四,解答题(第25,26题7分,第27题6分,第28题8分,满分28分)25.(1)下面四个图分别由六个相同的正方形拼接而成,其中不能折成正方体的是( )A .B .C .D .(2)用斜二侧面法补画下面的图形,使之成为长方体的直观图(虚线表示被遮住的线段,只要在已有图形基础上面出长方体.不必写画法步骤,不必写结论).(3)在这一长方体中,从同一个顶点出发的三个面的面积之比是5:7:2.其中最大的比最小的面积大260cm ,求这个长方体的表面积.26.已知线段a ,b (如图),根据下列要求,依次画图或计算.(1)画出一条线段OA ,使它等于3a ﹣b .(2)画出线段OA 的中点M .(3)如果a =2.5厘米,b =3厘米,求线段OM 的长.(画图时不要求写出画法,但要保留画图痕迹,及写出结论)27.对联是中华传统文化的瑰宝,对联装裱后,如图所示,上,下空白处分别称为天头和地头,左,右空白处统称为边.一般情况下,天头长与地头长的比是6:4,左,右边的宽相等,均为天头长与地头长的和的110.某人要装裱一副对联,对联的长为100cm ,宽为27cm .若要求装裱后的长是装裱后的宽的4倍,求边的宽和天头长.(书法作品选自《启功法书》)28.以直线AB上一点O为端点作射线OC,使∠BOC=40°,将一个直角三角板的直角顶点放在O处,即∠DOE=90°.(1)如图1,若直角三角板DOE的一边OE放在射线OA上,则∠COD=.(2)如图2,将直角三角板DOE绕点O顺时针转动到某个位置,若OE恰好平分∠AOC,则∠COD=.(3)将直角三角板DOE绕点O顺时针转动(OD与OB重合时为停止)的过程中,恰好有∠COD=13∠AOE,求此时∠BOD的度数.1.C【分析】本题主要考查正负数的应用,有理数减法,根据题意得,由1.65m2m-可得结论【详解】解,根据题意得,1.65m2m=0.35m--故选:C2.D【分析】本题主要考查了有理数和数轴的知识,能够掌握有理数所指的数的范围是解题的关键.根据有理数的定义,结合数轴解答即可.【详解】解:∠有理数包括整数和分数.∠在3-和3之间的有理数有无数个,如1-,0,1,32,等等.故选:D.3.A【分析】根据二元一次方程的定义解答即可.【详解】解:A,该方程符合二元一次方程的定义,符合题意.B,该方程是二元二次方程,不符合题意.C,该方程是一元二次方程,不符合题意.D,该方程是一元一次方程,不符合题意.故选:A.【点睛】本题主要考查了二元一次方程的定义,含有两个未知数且每个未知数的次数均为1的方程是二元一次方程.4.C【分析】不等式性质1:在不等式的两边都加上或减去同一个数,不等号的方向不变,性质2:在不等式的两边都乘以或除以同一个正数,不等号的方向不变,性质3:在不等式的两边都乘以或除以同一个负数,不等号的方向改变,根据不等式的性质逐一判断即可.【详解】解:A,由m<n,根据不等式性质2,得2m<2n,本选项成立.B,由m<n,根据不等式性质3,得﹣m>﹣n,再根据不等式性质1,得3﹣m>3﹣n,本选项成立.C,因为c2≥0,当c2>0时,根据不等式性质2,得mc2<nc2,当c2=0时,mc2=nc2,本选项不一定成立.D,由m<n,根据不等式性质1,得m﹣3<n﹣2<n﹣1,本选项成立.故选:C.【点睛】本题考查的是不等式的基本性质,掌握“利用不等式的基本性质判断不等式的变形是否正确”是解本题的关键. 5.C【分析】长方体中相对的两个平面是平行的,找找对面即可.【详解】∠面ADHE的相对面是面BCGF.∠与面ADHE平行的面是面BCGF.故选C.【点睛】本题考查了长方体的相对面的位置关系,准确找到相对面是解题的关键.6.B【分析】根据线段与线段的长度区别可判断(1),根据角的大小比较方法可判断(2),根据检验直线与平面垂直的三种方法是:∠铅垂线法,∠用一副三角尺,∠合页型折纸法可判断C,可判断(3),根据欧拉公式六个面,十二条棱和八个顶点组成的图形多面体不止长方体,还有底面为梯形的四棱柱,可判断(4)即可.【详解】(1)联结两点的线段的长度叫做两点之间的距离,故(1)错误.(2)用度量法和叠合法都可以比较两个角的大小是正确的,故(2)正确.(3)铅垂线,三角尺,合页型折纸可以检验直线与平面垂直是正确的,故(3)正确.(4)由六个面,十二条棱和八个顶点组成的图形可以是底面为梯形的四棱柱,故(4)错误.正确的个数为2.故选:B .【点睛】本题考查线段与线段长度区别,角的大小比较方法,检验直线与平面垂直的方法,长方体与直棱柱的区别,熟悉以上知识是解题关键.7.12【分析】相反数:只有符号不同的两个数互为相反数.【详解】∠12与12-只有符号不同 ∠答案是12. 【点睛】考相反数的概念,掌握即可解题.8.<【分析】本题考查了有理数的大小比较,化简多重符号,进而根据正数的大小比较即可判断大小. 【详解】解: 1.75( 1.2) 1.2314=---=-, ∠( 1.2)314-<-- 故答案为:<.9.4或2-##2-或4【分析】本题主要考查了解绝对值方程,熟练掌握绝对值的性质是解题关键.由绝对值的性质可得13x -=,13x -=-,求解即可获得答案. 【详解】解:因为1=3x -.所以13x -=,13x -=-.解得4x =或2x =-.故答案为:4或2-.10.72.810⨯【分析】本题考查了绝对值大于1的科学记数法的表示,解题的关键在于确定a n ,的值.根据绝对值大于1的数,用科学记数法表示为10n a ⨯,其中110a ≤<,n 的值为整数位数少1.【详解】解:28000000大于1,用科学记数法表示为10n a ⨯,其中 2.8a =,7n =,∠28000000用科学记数法表示为72.810⨯.故答案为:72.810⨯.11.12y + 【分析】本题考查了二元一次方程的解,将y 看作已知数求出x 即可.【详解】解: 210y x -+=∠21x y =+ ∠12y x +=. 故答案为:12y +. 12.−7【分析】本题考查了二元一次方程的解,把方程的解代入方程,得到一个含有未知数k 的一元一次方程,从而可以求出k 的值.【详解】解:∠23x y =-⎧⎨=⎩是方程35kx y -=的一个解. ∠2335k --⨯=解得:7k =-.故答案为:−7.13.4【分析】本题考查了求一元一次不等式的整数解.正确的解一元一次不等式是解题的关键.移项合并,最后系数化为1,可求不等式的解集,进而可得非负整数解的个数.【详解】解:342x x -≤+.26x ≤.解得,3x ≤.∠非负整数解有0,1,2,3共4个.故答案为:4.14.5136'︒【分析】本题考查了余角的定义,根据余角的定义即可求解【详解】解:A ∠的余角的大小是9038245136''︒-︒=︒.故答案为:5136'︒.15.32【分析】先由BD =16cm ,BD =25AB 知AB =52BD =40cm ,再由点C 是线段BD 的中点知BC =12BD =8cm ,根据AC =AB −BC 求解可得答案.【详解】解:∠BD =16cm ,BD =25AB . ∠AB =52BD =52×16=40(cm ). 又∠点C 是线段BD 的中点.∠BC =12BD =8cm . 则AC =AB ﹣BC =40﹣8=32(cm ).故答案为:32.【点睛】本题主要考查两点间的距离,解题的关键是掌握线段的和差计算及线段的中点的性质.16.北偏东60°【分析】本题考查了方向角.熟练掌握方向角的表示是解题的关键.根据方向角的定义作答即可.【详解】解:如图,记D 在A 的正北方向.∠90CAD ∠=︒.∠60DAB BAC CAD ∠=∠-∠=︒.∠ B 地在A 地的北偏东60°方向.故答案为:北偏东60°.17.b c +【分析】先根据数轴可得101a b c -<<<<<,从而可得0,0a b c b +>->,再化简绝对值,然后计算整式的加减即可得.【详解】解:由数轴可知,101a b c -<<<<<.则0,0a b c b +>->. 所以a b a b c b a b a b c b ++++-=-++++-b c =+.故答案为:b c +.【点睛】本题考查了数轴,绝对值的性质,确定有理数加法运算结果的符号,根据数轴确定出绝对值里各个式子的符号是解题关键.18.12或24【分析】设经过x 秒,∠AOB 的大小恰好是60°.分∠AOM +∠AOB +∠BON =180°和∠AOM +∠BON ﹣∠AOB =180°两种情况,可得关于x 的一元一次方程,解之即可求得结论.【详解】设经过x 秒,∠AOB 的大小恰好是60°.由题意可得:当∠AOM +∠AOB +∠BON =180°时,即4606180x x ++=︒︒,解得:12x =当∠AOM +∠BON ﹣∠AOB =180°时,即4660180x x +-=︒︒,解得:24x =.故答案为:12或24.【点睛】本题考查一元一次方程的应用和角的计算,解题的关键是找出等量关系,正确列出一元一次方程.19.1.25【分析】本题主要考查了有理数混合运算,先进行乘方运算,乘除运算和化简绝对值,再进行加减运算即可. 【详解】解:()23213222⎛⎫-+---+- ⎪⎝⎭ 19824=-+++ 1.25=.20.32x =- 【分析】按照解一元一次方程的一般步骤解方程即可. 【详解】2161136x x +--= ()()221616x x +--=42616x x +-+=46621x x -=--23x -=32x =-. 【点睛】本题考查了一元一次方程的解法,解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.21.32x y =⎧⎨=-⎩【详解】分析:利用代入消元法解方程组即可.详解:由∠得y=2x -8 ∠把∠代入∠得3x+2(2x -8)=5解得x=3把x=3代入∠可得y=-2所以方程组的解为:32 xy=⎧⎨=-⎩.点睛:此题主要考查了二元一次方程组的解法,根据题目特点灵活选用加减消元法或代入消元法求解是关键. 22.﹣2<x≤4,数轴见解析【分析】求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.【详解】解:()52116532xxx⎧+->-⎪⎨-≥--⎪⎩①②.由∠得,x>﹣2.由∠得,x≤4.故此不等式组的解集为:﹣2<x≤4.在数轴上表示为:.【点睛】本题考查的是解一元一次不等式组,熟知“同大取大,同小取小,大小小大中间找,大大小小找不到”的原则是解答此题的关键.23.123 xyz=⎧⎪=⎨⎪=⎩【分析】由∠∠相加消去y,与∠组成关于x, z的二元-次方程组, 进一步解二元一次方程组, 求得答案即可.【详解】解:25 2130x y zx y zx z-+=⎧⎪+-=⎨⎪-=⎩①②③∠+∠得,3x+z=6∠∠∠组成二元一次方程组得30 :36x zx z-=⎧⎨+=⎩.解得13 xz=⎧⎨=⎩:.代入∠得,y=2.∠原方程组的解为123xyz=⎧⎪=⎨⎪=⎩.【点睛】本题考查三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解方程组较简单.24.这个角的度数为50︒【分析】本题主要考查了余角和补角的有关计算,一元一次方程的应用,解题的关键是根据这个角的补角比它的余角的3倍大10︒,列出方程,解方程即可.【详解】解:设这个角的度数为x 度,根据题意得:()18039010x x -=-+.解得:50x =.答:这个角的度数为50︒.25.(1)D,(2)见解析,(3)336平方厘米【详解】(1)正方体的展开图1—4—1型,只有D 不是这种情况,所以D 不能折成长方形.故答案为:D .(2)如图所示:(3)设这三个面积分别为25xcm ,27xcm ,22xcm .7260x x -=12x =.()()22512712212336cm ⨯⨯+⨯+⨯=答:这个长方形的表面积是336平方厘米.【点睛】此题考查正方体的展开图和长方体的表面积,重点是理解正方体展开图的种类,求表面积的方法和画图的方法.26.(1)见解析(2)见解析(3)OM =2.25厘米【分析】(1)如图:在射线OP 上依次截取OB =BC =CD =a ,然后在线段DO 上,以D 为圆心,以b 为半径,交OD 于点A .(2)分别以O ,A 为圆心,以大于12AB 画弧,然后连接两弧交点的直线与线段AB 的交点即为所求. (3)将a =2.5厘米,b =3代入3a ﹣b 求出OA 的 长度,然后再根据中点的定义解答即可.【详解】(1)解:如图:OA 即为所求.(2)解:如图,点M 即为所作.(3)解:∠OA =3a ﹣b =3×2.5﹣3=4.5(厘米).而M 点为OA 的中点.∠OM =12OA =2.25厘米. 【点睛】本题主要考查了线段的和差,线段的中点等知识点,正确作出线段OA 是解答本题的关键. 27.边的宽为4cm ,天头长为24cm【分析】设天头长为cm x ,则地头长为2cm 3x ,边的宽为121cm cm 1036x x x ⎛⎫+= ⎪⎝⎭,再分别表示础装裱后的长和宽,根据装裱后的长是装裱后的宽的4倍列方程求解即可.【详解】解:设天头长为cm x .由题意天头长与地头长的比是6:4,可知地头长为2cm 3x . 边的宽为121cm cm 1036x x x ⎛⎫+= ⎪⎝⎭. 装裱后的长为cm cm 2510010033x x x ⎛⎫⎛⎫+++ ⎪⎝⎭⎝⎭=⎪. 装裱后的宽为cm cm 1112727663x x x =⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭. 由题意可得:5110027433x x ⎛⎫+=+⨯ ⎪⎝⎭解得24x =. ∠146x =. 答:边的宽为4cm ,天头长为24cm .【点睛】本题考查了一元一次方程的应用,题中的数量关系较为复杂,需要合理设未知数,找准数量关系. 28.(1)50°,(2)20°,(3)15°或52.5°.【分析】(1)利用余角的定义可求解.(2)由平角的定义及角平分线的定义求解COE ∠的度数,进而可求解.(3)可分两种情况:∠当COD ∠在BOC ∠的内部时,∠当COD ∠在BOC ∠的外部时,根据角的和差可求解.【详解】解:(1)由题意得90BOD ∠=︒.40BOC ︒∠=.904050COD ∴∠=︒-︒=︒.故答案为50︒.(2)180AOC BOC ∠+∠=︒,40BOC ∠=︒.18040140AOC ︒︒︒∴∠=-=. OE 平分AOC ∠.1702COE AOC ∴∠=∠=︒. 90DOE ∠=︒.907020COD ∴∠=︒-︒=︒. 故答案为20︒.(3)∠当COD ∠在BOC ∠的内部时.COD BOC BOD ∠=∠-∠,而40BOC ∠=︒. 40COD BOD ∴∠=︒-∠.180AOE EOD BOD ∠+∠+∠=︒,90EOD ∠=︒. 90AOE BOD ∴∠=︒-∠. 又13COD AOE ∠=∠. ∴140(90)3BOD BOD ︒-∠=︒-∠.15BOD ∴∠=︒.∠当COD ∠在BOC ∠的外部时.COD BOD BOC ∠=∠-∠,而40BOC ∠=︒. 40COD BOD ∴∠=∠-︒.180AOE EOD BOD ∠+∠-∠=︒,90EOD ∠=︒. 90AOE BOD ∴∠=︒-∠. 又13COD AOE ∠=∠. ∴140(90)3BOD BOD ∠-︒=︒-∠. 52.5BOD ∴∠=︒. 综上所述:BOD ∠的度数为15︒或52.5︒.【点睛】本题主要考查余角的定义,角的和差,角平分线的定义等知识的综合运用,分类讨论是解题的关键.。
人教版2012年下学期六年级数学期末考试试卷
六年级数学·第1版(共4 版) 六年级数学·第2版(共 4 版)雨花区2012年下学期期末考试试卷六 年 级 数 学(时量:80分钟 满分:80分) 计分一、填空题。
(每空1分,共 17 分)(1)2.5小时=( )分钟 51米=( )厘米(2)180%读作( ),百分之六十五写作( )。
(3)0.125 :5/8化成最简整数比是( ),比值是( )。
(4)六年级有200人,达到《国家体育锻炼标准》的有182人,达标率为( )%。
(5)一个圆的直径是6厘米,它的周长是( )cm ,面积是( )cm 2。
(6) 20( )=9.1÷13=35∶( )=( )﹪=( )成(7)在π、310、314%、3.144…这些数中,最大的数是( ),最小的数是( )。
(8)笼子里有若干鸡和兔。
从上面数,有20个头,从下面数,有48只脚。
笼中有鸡( )只,兔( )只。
二、判断题。
(对的打“√”,错的打“×” )(5分) (1)打八折就是便宜80%。
( ) (2)分母是100的分数就是百分数。
( ) (3)1和0都没有倒数。
( )(4)圆是轴对称图形,每条直径所在的直线都是圆的对称轴。
( ) (5)如果要清楚地了解各部分数量同总数之间的关系,用扇形统计图最好。
( ) 三、计算题。
(26分) (1)直接写出得数。
(8分)1—25%= 12×43= 20÷54= 20%+37%=4000×20%= 97×75= 31÷43= 23 +34 =(2)计算下列各题,能简算的要简算。
(12分)① 30—1.6 ÷154 ② 3.14 ×(122 —8 2 ) ③ 61÷3+65×31 ④ 512×(65+43)+56(3)解方程。
(6分)①(1+25%)x = 5 ② 4x +2(8—x )=26四、选择题。
六年级下册数学试卷及答案(全套)期中
六年级下学期数学期末测试卷一、填空题1.在一幅条形统计图上,纵轴用1格表示40人,表示120人应画()格;一个直条长3.5格,它表示()人。
2.()统计图可以清楚地表示出各部分与总数之间的关系;()统计图不仅可以表示出各种数量的多少,而且可以清楚地表示出数量的增减变化情况。
3.箱子里有10个球,要使箱子里摸出蓝色球的可能性是710,箱子里应该有()个蓝色球.4.要描述六年级学生参加各课外小组人数占全年级总人数的百分比情况,应选用()统计图;要记录某地区12个月的气温变化情况,应选用()统计图;要直观表示我国几大河流——长江、黄河、黑龙江、珠江的长度,应选用()统计图。
5.下表是对六(3)班同学参加课外活动项目的调查,如果要反映参加各项目的人数与总人数的关系,应制成()统计图,其中打乒乓球的人数占总人数的()%,踢毽子的人数占总人数的()%。
(每人只参加一个活动项目)活动项目打乒乓球打篮球跳绳踢毽子其他人数15141155二、选择题1.护士要用统计图记录一位病人一日内的体温变化情况,应选择()。
A.条形统计图B.折线统计图C.扇形统计图D.以上都不合适2.六(1)班有50人,有48人参加数学考试,2人缺考。
48人的平均分是87分,当缺考的两人补考后,全班平均分变成了86分,其中一人补考得了63分,另一人补考得了()分。
A.61B.65C.70D.713.欢欢班里同学的平均身高是148cm,乐乐班里同学的平均身高是152cm,那么欢欢和乐乐比,()。
A.欢欢高B.乐乐高C.一样高D.无法确定谁高4.一个质地均匀的正方体有1个面是黑色,有2个面是红色,其余3个面是黄色。
掷一下这个正方体,()面朝上的可能性最小。
A.红色B.黑色C.黄色D.无法确定5.同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,下列说法中不可能实现的是()。
A.朝上的面点数之和为12B.朝上的面点数之和小于3C.朝上的面点数之和大于4且小于8D.朝上的面点数之和为13三、判断题1.盒子里有1个白球和100个蓝球,从盒中摸一个球,一定是蓝球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
禄丰县2011—2012学年下学期期末学业水平测试小学六年级
数 学 试 卷
(全卷满分100分,考试时间120分钟)
一、填 空。
(20分)
1.把数轴上的圆点所表示的数填在下面的括号里。
2.15的因数有( )个。
3.4:7=
)
()
(
=( )÷( ) 4. 比例尺=( ): ( )
5.0.1的计数单位是( ),0.12的计数单位是( )。
6.5个点可以连成( )条线段。
7. 1.5小时=( )分 2.5升=( )cm 3
8.
31
、0.3 、100
33 按从小到大的顺序排列是: ( )<( )<( )
二、判 断。
(5分)
1.0既不是正数,也不是负数。
( )
2.7和9都是质数 。
( )
3.圆锥的体积等于与它等底等高的圆柱体积的三分之一。
( )
4.一条直线长18厘米。
( )
5.小数点向右移动一位,所得的数就比原数缩小10倍。
( )
二、选 择。
(5分)
1.下面两组比能组成比例的是( )。
A.5:8和4:6
B. 1.5:3和4:8
C. 12:3和9:4 2.当圆柱的底面积一定时,圆柱的体积与圆柱的高这两个量的关系是( )。
A. 不成比例关系
B. 正比例关系
C. 反比例关系 3. 用数值比例尺表示是( )。
A. 1:5
B. 1:5000
C. 1:500000 4.把10本书放在3个抽屉里,有一个抽屉至少放( )本书。
A. 3本
B. 4本
C. 5本
5.盒子里有同样大小的红、黄、蓝3种颜色的乒乓球各5个,要想摸出的球一定有2个同色的,最少要摸出( )个球。
A. 2
B. 4
C. 5 四、计 算。
(30分) 1.直接写出得数。
(9分)
2.5×4= 125×8= 77÷11= 0.99÷0.1= 1-35%=
21+31= 41×21= 95÷91= 4
3
-0.75= 2.用简便方法计算。
(6分)
0.25+31
+0.75 0.87×99+0.87
54-73-7
2
3.混合运算。
(9分)
64-18×93+
21 (65-8
3)÷(31+81
) 8.5×0.4+6.6÷0.1
4.求未知数χ。
(6分) 8:3=χ:9 127=8 119χ=4
3
五、统 计。
(5分)
1.基本满意、满意、非常满意三个层次的人数占总人数的( )%。
2.不满意和非常不满意的人数占总人数的( )%。
3.从这个统计图中你发现了什么?
六、操 作。
(10分)
1.按2∶1画出下面图形放大后的图形。
(5分)
2.画出将下图向右平移12格后的图。
(5分)
七、解决问题。
(25分)
1.在一幅比例尺是1∶100000的地图上,量得甲地到乙地的距离是8.5cm ,甲地到乙地的实际距离是多少千米?
2.一个底面直径10厘米、高25厘米的有盖子圆柱形茶筒,要给它全身包装上一层彩纸,至少要多少平方厘米的彩纸?
3.建筑工地上有一堆圆锥形的沙子,量得它的底面周长是18.84米,高2.5米,这堆沙子有多少立方米?
4.印刷厂要包装一批书,如果每箱40本,正好有25箱,现在要包装成每箱20本,要包装多少箱?
5.少林寺的练功桶是陀螺形的内空水桶(如下图),从里面量得高3.5分米,桶口直径4分米,这只水桶装满水有31.4立方分米,这只桶圆锥形的部分能装多少水?。
