北师大版九年级数学下册_第二章_二次函数_23_确定二次函数表达式_同步训练(有答案)
北师大版初中数学九年级下册2.3 确定二次函数的表达式

北师大初中数学九年级重点知识精选掌握知识点,多做练习题,基础知识很重要!北师大初中数学和你一起共同进步学业有成!2.3 确定二次函数的表达式类型一:已知顶点和另外一点用顶点式已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数关系式.练习:已知抛物线的顶点是(-1,-2),且过点(1,10),求其解析式类型二:已知图像上任意三点(现一般有一点在y轴上)用一般式已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式.练习:已知抛物线过三点:(-1,2),(0,1),(2,-7).求解析式类型三:已知图像与x轴两个交点坐标和另外一点坐标,用两根式已知二次函数的图象过(-2,0)、(4,0)、(0,3)三点,求这个二次函数的关系式.练习:已知抛物线过三点:(-1,0)、(1,0)、(0,3).(1).求这条抛物线所对应的二次函数的关系式;(2)写出它的开口方向、对称轴和顶点坐标;(3)这个函数有最大值还是最小值?这个值是多少?巩固练习:1.已知二次函数的图象过(3,0)、(2,-3)二点,且对称轴是x=1,求这个二次函数的关系式.2..已知二次函数的图象过(3,-2)、(2,-3)二点,且对称轴是x=1,求这个二次函数的关系式.3.已知二次函数的图象与x轴交于A,B两点,与y轴交于点C。
若AC=20,BC=15,∠ACB=90°,试确定这个二次函数的解析式4.已知一个二次函数当x=8时,函数有最大值9,且图象过点(0,1),求这个二次函数的关系式.小测:1.二次函数y=x2-2x-k的最小值为-5,则解析式为。
x2.若一抛物线与轴两个交点间的距离为8,且顶点坐标为(1, 5),则它们的解析式为。
3.已知一个二次函数的图象经过点(6,0),且抛物线的顶点是(4,-8),求它的解析式。
4.已知二次函数y=ax2+bx+c的图象顶点坐标为(-2,3),且过点(1,0),求此二次函数的解析式.5.已知二次函数y=ax2+bx+c,当x=-1时有最小值-4,且图象在x轴上截得线段长为4,求函数解析式.6.抛物线y=ax2+bx+c经过(0,0),(12,0)两点,其顶点的纵坐标是3,求这个抛物线的解析式.7.已知二次函数y=ax2+bx+c,当x=0时,y=0;x=1时,y=2;x=-1时,y=1.求a、b、c,并写出函数解析式.8.已知抛物线y=ax2经过点A(2,1).(1)求这个函数的解析式;(2)写出抛物线上点A关于y轴的对称点B的坐标;(3)求△OAB的面积;(4)抛物线上是否存在点C,使△ABC的面积等于△OAB面积的一半,若存在,求出C点的坐标;若不存在,请说明理由.相信自己,就能走向成功的第一步教师不光要传授知识,还要告诉学生学会生活。
北师大九年级下《2.3确定二次函数表达式》同步训练含参考答案

北师大九年级数学下册第二章二次函数2.3 确定二次函数表达式同步训练学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(本题共计 10 小题,每题 3 分,共计30分,)1. 抛物线经过点和,且以直线为对称轴,则它的解析式为()A. B.C. D.2. 用配方法将二次函数写成形如的形式,则、的值分别是()A. B.C.,D.,3. 若所求的二次函数图象与抛物线有相同的顶点,并且在对称轴的左侧,随的增大而增大,在对称轴的右侧,随的增大而减小,则所求二次函数的解析式为()A. B.C. D.4. 用配方法将函数写成的形式是()A. B.C. D.5. 二次函数经过配方化成的形式是()A. B.C. D.6. 如图所示,在平面直角坐标系中,二次函数的图象顶点为,且过点,则与的函数关系式为()A. B.C. D.7. 已知抛物线过点,,与轴交于点,且.则这条抛物线的解析式为()A. B.C.或D.或8. 二次函数的图象经过,,三点,则它的解析式为()A. B.C. D.9. 一抛物线的形状、开口方向与相同,顶点在,则此抛物线的解析式为()A. B.C. D.10. 已知二次函数的图象是由的图象经过平移而得到,若图象与轴交于、两点,与轴交于,顶点为,则四边形的面积为()A. B. C. D.二、填空题(本题共计 10 小题,每题 3 分,共计30分,)11. 用配方法把二次函数写成的形式________.12. 如果抛物线的对称轴是,且开口方向,形状与抛物线相同,且过原点,那么________.13. 以直线为对称轴的抛物线过点,,求此抛物线的解析式.________.14. 用配方法将函数化成的形式,则________.15. 已知二次函数的图象经,,三点,那么这个二次函数的解析式是________.16. 已知二次函数的图象经过点,则该函数的关系式为________.17. 二次函数配成的形式是________,其最大值是________.18. 若抛物线的对称轴为轴,则________.19. 已知抛物线的图象顶点为,且过,则抛物线的表达式为________.20. 抛物线用配方法化成的形式是________,抛物线与轴的交点坐标是________,抛物线与轴的交点坐标是________.三、解答题(本题共计 6 小题,每题 10 分,共计60分,)21. 已知函数的图象经过点.求这个函数的解析式;当时,求使的的取值范围.22. 已知二次函数图象上部分点的坐标满足下表:求该二次函数的解析式;23. 已知的图象经过点和.求此函数的解析式;并运用配方法,将此抛物线解析式化为的形式;写出该抛物线顶点的坐标,并求出的面积.24. 抛物线与轴交于点.求抛物线的解析式;求抛物线与坐标轴的交点坐标;①当取什么值时,?②当取什么值时,的值随的增大而减小?25. 已知二次函数.把函数配成的形式;求函数与轴交点坐标;当时,则的取值范围为________.26. 如图,抛物线与轴交于点,对称轴为直线,点为抛物线的顶点.求抛物线解析式和顶点的坐标;求抛物线与轴的两交点、的坐标;你可以直接写出不等式的解集吗?答案1. B2. B3. D4. A5. D6. D7. C8. D9. C10. A11.12.13.14.15.16.17.18.19.20. ,21. 解: ∵函数的图象经过点,∴ ,解得:,则函数解析式为;当时,,根据二次函数性质当时,,则当时,使的的取值范围是.22. 解:把点代入,得.再把点,分别代入中,得,解得:,所以这个二次函数的关系式为:.(2).该二次函数图象的顶点坐标为,对称轴为.23. 解:将点和代入,得:,解得:,∴抛物线的解析式为;;抛物线的顶点坐标为,∴.24. 解:将点代入抛物线,,∴抛物线的解析式;令,,解得,;轴:、;轴:抛物线开口向下,对称轴;所以)①当时,;②当时,的值随的增大而减小.25. 或.当时,取最小值;当时,;当时,.∴当时,的取值范围为.26. 解:根据题意得,,解得,∴抛物线解析式为;∵ ,∴顶点的坐标为;当时,,解得,∴ 、的坐标分别为、;(3)的解集为.。
九年级数学下册第二章二次函数3确定二次函数的表达式练习北师大版

2.3 确定二次函数的表达式类型一:已知顶点和另外一点用顶点式已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数关系式.练习:已知抛物线的顶点是(-1,-2),且过点(1,10),求其解析式类型二:已知图像上任意三点(现一般有一点在y轴上)用一般式已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式.练习:已知抛物线过三点:(-1,2),(0,1),(2,-7).求解析式类型三:已知图像与x轴两个交点坐标和另外一点坐标,用两根式已知二次函数的图象过(-2,0)、(4,0)、(0,3)三点,求这个二次函数的关系式.练习:已知抛物线过三点:(-1,0)、(1,0)、(0,3).(1).求这条抛物线所对应的二次函数的关系式;(2)写出它的开口方向、对称轴和顶点坐标;(3)这个函数有最大值还是最小值?这个值是多少?巩固练习:1.已知二次函数的图象过(3,0)、(2,-3)二点,且对称轴是x=1,求这个二次函数的关系式.2..已知二次函数的图象过(3,-2)、(2,-3)二点,且对称轴是x=1,求这个二次函数的关系式.3.已知二次函数的图象与x轴交于A,B两点,与y轴交于点C。
若AC=20,BC=15,∠ACB=90°,试确定这个二次函数的解析式4.已知一个二次函数当x=8时,函数有最大值9,且图象过点(0,1),求这个二次函数的关系式.小测:1.二次函数y=x2-2x-k的最小值为-5,则解析式为。
2.若一抛物线与轴两个交点间的距离为8,且顶点坐标为(1, 5),则它们的解析式为。
3.已知一个二次函数的图象经过点(6,0),且抛物线的顶点是(4,-8),求它的解析式。
4.已知二次函数y=ax2+bx+c的图象顶点坐标为(-2,3),且过点(1,0),求此二次函数的解析式.5.已知二次函数y=ax2+bx+c,当x=-1时有最小值-4,且图象在x轴上截得线段长为4,求函数解析式.6.抛物线y=ax2+bx+c经过(0,0),(12,0)两点,其顶点的纵坐标是3,求这个抛物线的解析式.7.已知二次函数y=ax2+bx+c,当 x=0时,y=0;x=1时,y=2;x=-1时,y=1.求a、b、c,并写出函数解析式.8.已知抛物线y=ax2经过点A(2,1).(1)求这个函数的解析式;(2)写出抛物线上点A关于y轴的对称点B的坐标;(3)求△OAB的面积;(4)抛物线上是否存在点C,使△ABC的面积等于△OAB面积的一半,若存在,求出C点的坐标;若不存在,请说明理由.。
北师大版九年级数学下册 第二章 二次函数 2.3 确定二次函数的表达式 同步练习题(Word版,无答
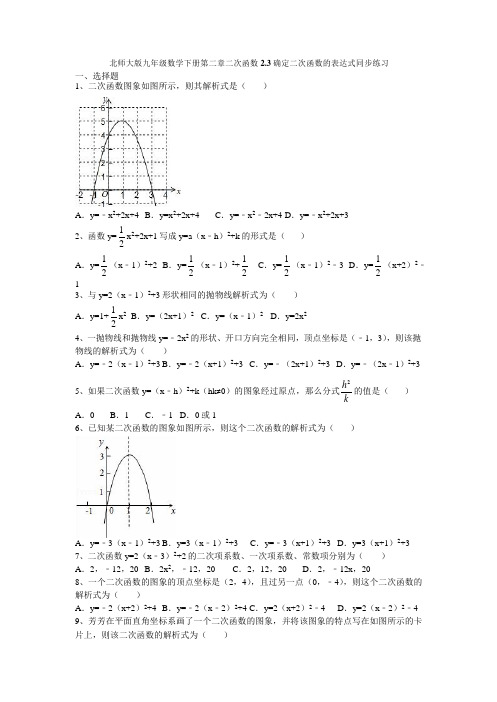
北师大版九年级数学下册第二章二次函数2.3 确定二次函数的表达式同步练习一、选择题1、二次函数图象如图所示,则其解析式是()A.y=﹣x2+2x+4 B.y=x2+2x+4 C.y=﹣x2﹣2x+4 D.y=﹣x2+2x+32、函数y=12x2+2x+1 写成y=a(x﹣h)2+k 的形式是()A.y=12(x﹣1)2+2 B.y=12(x﹣1)2+12C.y=12(x﹣1)2﹣3 D.y=12(x+2)2﹣13、与y=2(x﹣1)2+3 形状相同的抛物线解析式为()A.y=1+12x2 B.y=(2x+1)2 C.y=(x﹣1)2 D.y=2x24、一抛物线和抛物线y=﹣2x2 的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为()A.y=﹣2(x﹣1)2+3 B.y=﹣2(x+1)2+3 C.y=﹣(2x+1)2+3 D.y=﹣(2x﹣1)2+35、如果二次函数y=(x﹣h)2+k(hk≠0)的图象经过原点,那么分式2hk的值是()A.0 B.1 C.﹣1 D.0 或16、已知某二次函数的图象如图所示,则这个二次函数的解析式为()A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3 C.y=﹣3(x+1)2+3 D.y=3(x+1)2+3 7、二次函数y=2(x﹣3)2+2 的二次项系数、一次项系数、常数项分别为()A.2,﹣12,20 B.2x2,﹣12,20 C.2,12,20 D.2,﹣12x,208、一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为()A.y=﹣2(x+2)2+4 B.y=﹣2(x﹣2)2+4 C.y=2(x+2)2﹣4 D.y=2(x﹣2)2﹣4 9、芳芳在平面直角坐标系画了一个二次函数的图象,并将该图象的特点写在如图所示的卡片上,则该二次函数的解析式为()①开口向下;②顶点是原点;③过点(6,﹣6).A .y=﹣216xB .y=216x C .y=﹣6x 2 D .y=6x 2 10、如图,二次函数 y=x 2+bx+c 的图象过点 B (0,﹣2).它与反比例函数 y=﹣8x 的图象交 于点 A (m ,4),则这个二次函数的解析式为()A .y=x 2﹣x ﹣2B .y=x 2﹣x+2C .y=x 2+x ﹣2D .y=x 2+x+2二、填空题11、若抛物线经过(0,1)、(﹣1,0)、(1,0)三点,则此抛物线的解析式为 .12、若 y ﹣4 与 x 2 成正比例,当 x=2 时,y=6,则 y 与 x 的函数关系式是 .13、一个二次函数的图象的顶点坐标为(3,﹣1),与 y 轴的交点(0,﹣4),这个二次函数 的解析式是 .14、如图,抛物线与 x 轴交于点(﹣1,0)和(3,0),与 y 轴交于点(0,﹣3)则此抛物 线对此函数的表达式为 .2之间的函数关系式是.x 轴的正半轴上,C 、D 两点在抛物线 y= ﹣x 2+6x 上.设 OA=m (0<m <3),矩形 ABCD 的周长为 l ,则 l 与 m 的函数解析式为 .三、解答题17、抛物线 y=ax 2+bx+c 与 x 轴的两个交点为(﹣1,0),(3,0),其形状与抛物线 y=﹣2x 2 相同,则 y=ax 2+bx+c 的函数关系式?18、已知二次函数的图象经过(1,0)、(2,0)和(0,2)三点,则该函数的解析式?19、(1)把二次函数y=﹣34x2+32x+94代成y=a(x﹣h)2+k 的形式;(2)写出抛物线y=﹣34x2+32x+94的顶点坐标和对称轴,并说明该抛物线是由哪一条形如y=ax2 的抛物线经过怎样的变换得到的;(3)如果抛物线y=﹣34x2+32x+94中,x 的取值范围是0≤x≤3,请画出图象,并试着给该抛物线编一个具有实际意义的情境.(如喷水、掷物、投篮等)20、已知:二次函数y=﹣x2+2x+3(1)用配方法将函数关系式化为y=a(x﹣h)2+k 的形式,并指出函数图象的对称轴和顶点坐标;(2)画出所给函数的图象;(3)观察图象,指出使函数值y>3 的自变量x 的取值范围.21、某广场中心有高低不同的各种喷泉,其中一支高度为32米的喷水管喷水最大高度为 4 米,此时喷水水平距离为12米,在如图所示的坐标系中,这支喷泉的函数关系式?22、阅读下列材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如,由抛物线y=x2﹣2ax+a2+a﹣3,得到y=(x﹣a)2+a﹣3,抛物线的顶点坐标为(a,a﹣3),即无论a 取任何实数,该抛物线顶点的纵坐标y 和横坐标x 都满足关系式y=x﹣3.请根据以上的方法,确定抛物线y=x2+4bx+b 顶点的纵坐标y 和横坐标x 都满足的关系式?23、如图,在平面直角坐标系xOy 中,抛物线y=x2+bx+c 与x 轴交于A、B 两点,点A 在x 轴负半轴,点B 在x 轴正半轴,与y 轴交于点C,且tan∠ACO=12,CO=BO,AB=3,则这条抛物线的函数解析式?。
2021-2022学年北师大版九年级数学下册第二章二次函数同步训练试题(含答案及详细解析)

北师大版九年级数学下册第二章二次函数同步训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、抛物线y=2(x+1)2不经过的象限是()A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限2、已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=1,则以下结论正确的是()A.ac>0B.c﹣5b<0C.2a﹣b=0D.当a=﹣1时,抛物线的顶点坐标为(1,5)3、抛物线()212=++的顶点坐标是()y xA .(1,2)B .(1,2-)C .(1-,2)D .(1-,2-) 4、对于二次函数()21y x =--的图象的特征,下列描述正确的是( )A .开口向上B .经过原点C .对称轴是y 轴D .顶点在x 轴上5、如图1所示,△DEF 中,∠DEF =90°,∠D =30°,B 是斜边DF 上一动点,过B 作AB ⊥DF 于B ,交边DE (或边EF )于点A ,设BD =x ,△ABD 的面积为y ,图2是y 与x 之间函数的图象,则△ABD 面积的最大值为( )A .B .C .D .6、若抛物线27(4)1y x =-+-平移得到27y x =-,则必须( )A .先向左平移4个单位,再向下平移1个单位B .先向右平移4个单位,再向上平移1个单位C .先向左平移1个单位,再向下平移4个单位D .先向右平移1个单位,再向下平移4个单位7、在同一平面直角坐标系xOy 中,一次函数y =2x 与二次函数2y ax a =-的图象可能是( )A .B .C .D .8、抛物线()20y ax bx c a =++<的图象过点3,0,对称轴为直线1x =,有下列四个结论:①0abc >;②0a b c -+=;③y 的最大值为3;④方程210ax bx c +++=有实数根.其中正确的为( )A .①②B .①③C .②③D .②④9、下列各式中,y 是x 的二次函数的是( )A .21y x =B .211y x x=++C .221y x =-D .y 10、在求解方程20(a 0)++=≠ax bx c 时,先在平面直角坐标系中画出函数2y ax bx c =++的图象,观察图象与x 轴的两个交点,这两个交点的横坐标可以看作是方程的近似解,分析右图中的信息,方程的近似解是( )A .13x =-,22x =B .13x =-,23x =C .12x =-,22x =D .12x =-,23x =第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、小华酷爱足球运动.一次训练时,他将足球从地面向上踢出,足球距地面的高度h (m )与足球被踢出后经过的时间t (s )之间的关系为h =﹣5t 2+12t ,则足球距地面的最大高度是______m .2、二次函数y =2(1)3k k x -+的图象开口向上,则k =___. 3、二次函数21y x x =---的图像有最______点.(填“高”或“低”)4、点()0m ,是抛物线224y x x =--与x 轴的一个交点,则224m m -的值是________. 5、某件商品的销售利润y (元)与商品销售单价x (元)之间满足267y x x =-+-,不考虑其他因素,销售一件该商品的最大利润为______元.三、解答题(5小题,每小题10分,共计50分)1、如图,在平面直角坐标系xOy 中, 抛物线23y ax bx =++与x 轴交于点()1,0A - 和 点()3,0B ,与y 轴交于点C , 顶点为D .(1)求该抛物线的表达式的顶点D 的坐标;(2)将抛物线沿y 轴上下平移, 平移后所得新拋物线顶点为M , 点C 的对应点为E .①如果点M 落在线段BC 上, 求DBE ∠的度数;②设直线ME 与x 轴正半轴交于点P , 与线段BC 交于点Q , 当2PE PQ =时, 求平移后新抛物线的表达式.2、如图,抛物线y =ax 2+bx +6与x 轴交于A (2,0),B (8,0)两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 是抛物线上一动点,当∠PCB 12=∠BCO 时,求点P 的横坐标.3、在平面直角坐标系xOy 中,二次函数225y x mx m =-+的图象经过点()1,2-.(1)求二次函数的表达式;(2)求二次函数图象的对称轴.4、跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为一条抛物线.如图是小涵与小军将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为1 m ,并且相距4 m ,现以两人的站立点所在的直线为x 轴,建立如图所示的平面直角坐标系,其中小涵拿绳子的手的坐标是(0,1).身高1.50 m 的小丽站在绳子的正下方,且距小涵拿绳子的手1 m 时,绳子刚好经过她的头顶.(1)求绳子所对应的抛物线的解析式(不要求写自变量的取值范围);(2)身高1.70m 的小兵,能否站在绳子的正下方,让绳子通过他的头顶?(3)身高1.64m 的小伟,站在绳子的正下方,他距小涵拿绳子的手s m ,为确保绳子通过他的头顶,请直接写出s 的取值范围.5、小明在画一个二次函数的图象时,列出了下面几组y 与x 的对应值.(1)求该二次函数的表达式;(2)该二次函数的图象与直线y n =有两个交点A ,B ,若6AB >,直接写出n 的取值范围.-参考答案-一、单选题1、C【分析】根据顶点式写出顶点坐标,开口向上,进而即可求得的答案【详解】解: y =2(x +1)2,20a =>开口向上,顶点坐标为()1,0-∴该函数不经过第三、四象限如图,故选C【点睛】本题考查了2()y a x h =-图象的性质,根据解析式求得开口方向和顶点坐标是解题的关键.2、B【分析】根据图象可判断a 和c 的符号,即可判断A ;根据图象可知抛物线与x 轴的一个交点为(3,0),即可得出930a b c ++=,再根据抛物线对称轴为直线x =1,即12b a -=,且可判断出0b >,通过整理可得出752b c b -=-,即可判断B ;由12b a-=,即可判断C ;由1a =-,可求出b 、c 的值,即得出抛物线解析式,再变为顶点式,即可判断D .【详解】解:根据图象可知,该二次函数开口向下,∴0a <,该二次函数与y 轴交点在x 轴上方,∴0c >,∴0ac <,故A 选项错误,不符合题意;∵该抛物线与x 轴的一个交点为(3,0),∴930a b c ++=,∵对称轴为直线x =1,即12b a-=, ∴2b a =-, ∴9()302b bc ⨯-++=,即302b c -= ∴752b c b -=-. ∵0a <,∴0b >,∴702b -<, ∴50c b -<,故B 选项正确,符合题意; ∵12b a-=, ∴20a b +=,故C 选项错误,不符合题意;当1a =-时,即12(1)9(1)30b b c ⎧-=⎪⨯-⎨⎪⨯-++=⎩,解得:23b c =⎧⎨=⎩, ∴该二次函数解析式为2y x 2x 3=-++,改为顶点式为2(1)4y x =--+,∴抛物线顶点坐标为(1,4),故D 选项错误,不符合题意;故选B .【点睛】本题考查二次函数的图象和性质,二次函数图象与系数的关系.熟练掌握二次函数的图象和性质是解答本题的关键.3、C【分析】根据顶点式直接写出顶点坐标即可.【详解】解:抛物线()212y x =++的顶点坐标是(1-,2),故选:C .【点睛】本题考查了抛物线的顶点坐标,解题关键是明确二次函数顶点式()2y x h k =-+的顶点坐标为()h k ,. 4、D【分析】根据二次函数2()y a x h =-的性质判断即可.【详解】在二次函数()21y x =--中,∵10a =-<,∴图像开口向下,故A 错误;令0x =,则2(01)10y =--=-≠,∴图像不经过原点,故B 错误;二次函数()21y x =--的对称轴为直线1x =,故C 错误; 二次函数()21y x =--的顶点坐标为(1,0),∴顶点在x 轴上,故D 正确.故选:D .【点睛】本题考查二次函数2()y a x h =-的性质,掌握二次函数相关性质是解题的关键.5、C【分析】由图得点A 到达点E 时,ABD △面积最大,此时12DB =,由三角函数算出AB ,由三角形面积公式即可求解.【详解】由图可得:点A 到达点E 时,ABD △面积最大,此时12DB =,tan 3012AB DB =⋅︒==∴1122ABD S =⨯⨯= 故选:C .【点睛】本题考查二次函数图像问题以及解直角三角形,由题判断点A 运动到哪里能使ABD △面积最大是解题的关键.6、B【分析】根据两抛物线的顶点坐标即可确定平移的方向与距离,从而完成解答.【详解】抛物线27(4)1y x =-+-的顶点为(-4,-1),而抛物线27y x =-的顶点为原点由题意,把抛物线27(4)1y x =-+-的顶点先向右平移4个单位,再向上平移1个单位,即可得到抛物线27y x =-的顶点,从而抛物线27(4)1y x =-+-先向右平移4个单位,再向上平移1个单位即可得到27y x =-.故选:B【点睛】本题考查了二次函数图象的平移,关键是抓住抛物线顶点的平移.7、C【分析】先由一次函数的性质判断,然后结合二次函数中a >0时,a <0时,分别进行判断,即可得到答案.【详解】解:∵一次函数y =2x ,∴一次函数的图像经过原点,且y 随x 的增大而增大,故排除A 、B 选项; 在二次函数2y ax a =-中,当a >0时,开口向上,且抛物线顶点在y 的负半轴上,当a <0时,开口向下,且抛物线顶点在y 的负半轴上,∴D 不符合题意,C 符合题意;故选:C【点睛】此题主要考查了二次函数与一次函数图象,利用二次函数的图象和一次函数的图象的特点求解.8、D【分析】根据抛物线的对称性与过点3,0,可得抛物线与x 轴的另一个交点为()1,0,-可判断②,再依次判断,,a b c 可判断①,由对称轴为直线1x =,可判断③,由函数2y ax bx c =++与1y =-的图象有两个交点,可判断④,从而可得答案.【详解】 解: 抛物线()20y ax bx c a =++<的图象过点3,0,对称轴为直线1x =,∴ 抛物线与x 轴的另一个交点为:()1,0,- 则0,a b c -+= 故②符合题意;∴ 抛物线与y 轴交于正半轴,则0,c >10,2b x a则0,b >0,abc 故①不符合题意;对称轴为直线1x =,∴ 当1x =时,,y a b c 最大值 故③不符合题意;当210ax bx c +++=时,则21,ax bx c而函数2y ax bx c =++与1y =-的图象有两个交点,∴ 方程210ax bx c +++=有实数根.故④符合题意;综上:符合题意的是:②④故选D【点睛】本题考查的是二次函数的图象与性质,掌握“利用二次函数的图象与性质判断,,a b c 的符号以及代数式的符号,函数的最值,方程的根”是解本题的关键.9、C【分析】根据二次函数的定义依次判断.【详解】解:A 、21y x =不是二次函数,不符合题意; B 、211y x x =++,不是二次函数,不符合题意;C 、221y x =-,是二次函数,符合题意;D 、y =故选:C .【点睛】此题考查二次函数的定义:形如2(0)y ax bx c a =++≠的函数是二次函数,解题的关键是正确掌握二次函数的构成特点.10、D【分析】由题意观察2y ax bx c =++的图象,进而根据与x 轴的两个交点的横坐标进行分析即可.【详解】解:因为两个交点的横坐标可以看作是方程的近似解,两个交点的横坐标为:12x =-,23x =, 所以方程的近似解是12x =-,23x =.故选:D.【点睛】本题考查二次函数图象与x 轴的交点问题,熟练掌握并结论方程思想可知与x 轴的两个交点的横坐标可以看作是方程20(a 0)++=≠ax bx c 的近似解进行分析.二、填空题1、365【分析】a =-5开口方向向下,最大值为顶点y 值,由公式可得答案.【详解】解:∵h =-5t 2+12t ,∴a =-5,b =12,c =0,∴足球距地面的最大高度是:24(5)0124(5)⨯-⨯-⨯-=7.2m , 故答案为:7.2.【点睛】本题考察了二次函数的图象和性质,利用二次函数求最值,一是可以通过配方,化为顶点式;二是根据二次函数图象与系数的关系,利用244ac b a - 求出顶点纵坐标.2【分析】由解析式是二次函数可知22k = ,再由图像的开口向上得10k ->,由此求解即可.【详解】解:∵()213k y k x =-+是二次函数,∴22k =,解得k =∵图像的开口向上,∴10k ->即1k >,∴k =.【点睛】本题考查了二次函数的定义与二次函数图像的性质,熟知 图像开口向上时,a >0,图像开口向下时,a <0是解题的关键.3、高【分析】根据二次函数图象的开口即可解答.【详解】解:∵二次函数21y x x =---∴二次函数21y x x =---的图象开口向下∴二次函数21y x x =---的图像有最高点.故答案是高.【点睛】本题主要考查了二次函数的性质,对于y =ax 2+bx +c (a ≠0),当a >0,函数图象开口方向向上,函数图象开口方向向下.4、8【分析】根据抛物线224y x x =--与x 轴的一个交点为(m ,0),代入函数解析式得出,得出224m m -=,代入()222422-=-m m m m 即可求解.【详解】解:∵抛物线224y x x =--轴的一个交点为(m ,0),∴将点(m ,0)代入得,2240m m --=,即224m m -=∴代数式224m m -的值为:()222422248-=-=⨯=m m m m .故答案为:8.【点睛】此题主要考查了抛物线与x 轴的交点,解题的关键是用整体代入法求值.5、2【分析】2267(3)2y x x x =-+-=--+知y 的最大值在3x =时取得,值为2.【详解】解:267y x x =-+-2(3)2y x =--+根据函数图像性质可知在3x =时,y 最大且取值为2故答案为:2.【点睛】本题考查了二次函数实际应用中的最值问题.解题的关键将二次函数化成顶点式.三、解答题1、(1)2y x 2x 3=-++,()1,4D ;(2)①45DBE ∠=︒;②232.2y x x =-+- 【分析】(1)把点()1,0A - 和 点()3,0B 代入抛物线的解析式。
北师大版九年级下册2.2二次函数的图像与性质 同步练习(含答案)

初中数学北师大版九年级下册2.2二次函数的图像与性质同步练习(含答案)一、单选题(共15题;共30分)1.由抛物线y=x2平移得到抛物线y=(x+2)2,下列平移方法可行的是( )A. 向上平移2个单位长度B. 向下平移2个单位长度C. 向左平移2个单位长度D. 向右平移2个单位长度2.已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为()A. 3或6B. 1或6C. 1或3D. 4或63.如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是()A. B.C. D.4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c >0 ⑤9a+3b+c<0,则其中结论正确的个数是()A. 2个B. 3个C. 4个D. 5个5.描点法画函数图象是研究陌生函数的基本方法.对于函数,下列说法:①图象经过 ;②当时,有最小值;③ 随的增大而增大;④该函数图象关于直线对称;正确的是()A. ①②B. ①②④C. ①②③④D. ②③④6.已知抛物线过 、 、 、 四点,则与的大小关系是()A. >B. =C. <D. 不能确定7.把抛物线向下平移个单位长度,再向右平移个单位长度,所得抛物线是()A. B. C. D.8.若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P()A. 有且只有1个B. 有且只有2个C. 至少有3个D. 有无穷多个9.二次函数y=kx2+2x+1(k<0)的图象可能是()A. B. C. D.10.如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是()A. a>0,c>0B. a<0,c>0C. a>0,c<0D. a<0,c<011.函数y=ax2与函数y=ax+a,在同一直角坐标系中的图象大致是图中的()A. B. C. D.12.下列二次函数的图象中,其对称轴是x=1的为()A. B. C. D.13.当时,二次函数有最大值,则实数的值为( )A. B. 或 C. 或 D. 2或或14.对于代数式,下列说法正确的是()①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+cA. ①B. ③C. ②④D. ①③15.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:x -1 0 1 3y -3 1 3 1下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有()A. 1个B. 2个C. 3个D. 4个二、填空题(共6题;共7分)16.二次函数的顶点坐标是________.17.将二次函数的图象先向左平移个单位长度,再向下平移个单位长度,得到函数的图象的表达式是________.18.已知抛物线y=x2+(m-4)x-4m的顶点在y轴上,则m=________;19.已知二次函数有最大值,则,的大小关系为________.20.若二次函数的图象关于轴对称,则的值为:________.此函数图象的顶点和它与轴的两个交点所确定的三角形的面积为:________.21.已知抛物线的对称轴为直线,且经过点 , ,试比较和的大小:________ .(填“ ”,“ ”或“ ”)三、解答题(共8题;共124分)22.若二次函数y=﹣x2图象平移后得到二次函数y=﹣(x﹣2)2+4的图象.(1)平移的规律是:先向________(填“左”或“右”)平移________个单位,再向________平移________个单位.(2)在所给的坐标系内画出二次函数y=﹣(x﹣2)2+4的示意图.23.已知抛物线y=-x2+2x+3.(1)求该抛物线的对称轴和顶点P的坐标.(2)在图中的直角坐标系内用五点法画出该抛物线的图象(3)将该抛物线向下平移2个单位,向左平移3个单位得到抛物线y1,此时点P的对应点为P′,试求直线PP′与y轴的交点坐标24.已知二次函数y=x2+2x﹣3.(1)写出它的顶点坐标;(2)当x取何值时,y随x的增大而增大;(3)求出图象与x轴的交点坐标.(4)当x取何值时y的值大于0.25.二次函数的图象如图所示,根据图象回答:(1)当时,写出自变量的值.(2)当时,写出自变量的取值范围.(3)写出随的增大而减小的自变量的取值范围.(4)若方程有两个不相等的实数根,求的取值范围(用含、、的代数式表示).26.已知一条抛物线的开口方向和大小与抛物线y=3x2都相同,顶点与抛物线y=(x+2)2相同.(1)求这条抛物线的解析式;(2)将上面的抛物线向右平移4个单位会得到怎样的抛物线解析式?(3)若(2)中所求抛物线的顶点不动,将抛物线的开口反向,求符合此条件的抛物线解析式.27.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.28.已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).(1)求证无论k为何值,方程总有两个不相等实数根;(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.29.如图,若抛物线的顶点在抛物线上,抛物线的顶点也在抛物线上(点与点不重合),我们定义:这样的两条抛物,互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.(1)如图,已知抛物线与轴交于点,试求出点关于该抛物线对称轴对称的点的坐标;(2)请求出以点为顶点的的友好抛物线的解析式,并指出与中同时随增大而增大的自变量的取值范围;(3)若抛物线 的任意一条友好抛物线的解析式为 ℎ,请写出与的关系式,并说明理由.答案解析部分一、单选题1.【答案】C2.【答案】B3.【答案】D4.【答案】B5.【答案】B6.【答案】A7.【答案】B8.【答案】B9.【答案】C10.【答案】C11.【答案】B12.【答案】B13.【答案】C14.【答案】B15.【答案】B二、填空题16.【答案】 17.【答案】或18.【答案】4.19.【答案】20.【答案】1;121.【答案】三、解答题22.【答案】(1)右;2;上;4(2)解:抓住顶点(2,4),与y轴(0,0),x轴的交点(4,0)(0,0)等关键点来画.23.【答案】(1)解:∵抛物线y=-x2+2x+3,∴y=-x2+2x+3=-(x-1)2+4,∴对称轴为直线x=1,顶点P(1,4).(2)解:列表得:图像如图:(3)解:依题可得:平移后抛物线为y1=-(x+2)2+2,∴P′(-2,2),设直线PP′的函数解析式为:y=kx+b,依题可得:,解得:,∴直线PP′的函数表达式为y=x+∴直线PP′与y 轴的交点为(0,).24.【答案】(1)解: y=x2+2x﹣3=(x+1)2﹣4,∴顶点坐标为:(﹣1,﹣4)(2)解: ∵y=x2+2x﹣3=(x+1)2﹣4的对称轴为:x=﹣1,开口向上,∴当x>﹣1时,y随x的增大而增大(3)解: 令y=x2+2x﹣3=0,解得:x=﹣3或x=1,∴图象与x轴的交点坐标为(﹣3,0),(1,0).(4)解: 其大致图象如图:由图象可知:当x>1或x<-3时,y的值大于025.【答案】(1)解:当时,或(2)解:当时,;(3)解:∵抛物线的开口向下,对称轴为.∴当时,随的增大而减小(4)解:方程变形为,∴方程有两个不相等的实数根可看作二次函数与直线有两个交点,如图,∴,即26.【答案】(1)解:∵一条抛物线的开口方向和大小与抛物线y=3x2都相同,顶点与抛物线y=(x+2)2相同,∴这条抛物线的解析式为:y=3(x+2)2(2)解:将抛物线向右平移4个单位会得到的抛物线解析式为:y=3(x−2)2(3)解:若(2)中所求抛物线的顶点不动,将抛物线的开口反向,则符合此条件的抛物线解析式为:y=−3(x−2)227.【答案】(1)解:∵抛物线F经过点C(﹣1,﹣2),∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,解得,m=﹣1,∴抛物线F的表达式是:y=x2+2x﹣1(2)解:当x=﹣2时,y p=4+4m+m2﹣2=(m+2)2﹣2,∴当m=﹣2时,y p的最小值﹣2,此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,∴当x≤﹣2时,y随x的增大而减小,∵x1<x2≤﹣2,∴y1>y2(3)解:m的取值范围是﹣2≤m≤0或2≤m≤4,理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),∴或,解得,﹣2≤m≤0或2≤m≤428.【答案】(1)证明:∵△=(k﹣5)2﹣4(1﹣k)=k2﹣6k+21=(k﹣3)2+12>0,∴无论k为何值,方程总有两个不相等实数根(2)解:∵二次函数(﹣)﹣的图象不经过第三象限,∵二次项系数a=1,∴抛物线开口方向向上,∵△=(k﹣3)2+12>0,∴抛物线与x轴有两个交点,设抛物线与x轴的交点的横坐标分别为x1,x2,∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,解得k≤1,即k的取值范围是k≤1(3)解:设方程的两个根分别是x1,x2,根据题意,得(x1﹣3)(x2﹣3)<0,即x1x2﹣3(x1+x2)+9<0,又x1+x2=5﹣k,x1x2=1﹣k,代入得,1﹣k﹣3(5﹣k)+9<0,解得k<.则k的最大整数值为2.29.【答案】(1)解:∵抛物线L3:y=2x2﹣8x+4,∴y=2(x﹣2)2﹣4,∴顶点为(2,-4),对称轴为x=2,设x=0,则y=4,∴C(0,4),∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,4);(2)解:∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,﹣4),∴L4的解析式为y=﹣2(x﹣4)2+4,由图象可知,当2≤x≤4时,抛物线L与L4中y同时随x增大而增大;3(3)解:a1与a2的关系式为a1+a2=0.理由如下:∵抛物线y=a1(x﹣m)2+n的一条“友好”抛物线的解析式为y=a2(x﹣h)2+k,∴y=a2(x﹣h)2+k过点(m,n),且y=a1(x﹣m)2+n过点(h,k),即k=a1(h﹣m)2+n…①n=a2(m﹣h)2+k…②由①+②得:(a1+a2)(h﹣m)2=0.又“友好”抛物线的顶点不重合,∴h≠m,∴a1+a2=0.。
北师大版九年级数学下册2.3确定二次函数的表达式同步测试
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
2.3 确定二次函数的表达式 同步测试答案
一、选择题 1.C 2.D 3.D 4.D 5.D 6.A 7.B 8.C 9.C 10.D 二、填空题 11. y = 3x2 +12x +13 12. y = 1 x2 + 2x +1
8 13.y=18x2-14x+2或y=-18x2+34x+2 14. ①③④ 15. y = −2x2 − 2 16. y = −2x2 + 8x −13 三、综合题 17. y = 3x2 + 6x +1 18. y = − 3 x2 + 3 x + 3
84 19. y = x2 + 2x − 3 20.解:(1)y=-x2+2x+3=-(x-1)2+4,∴顶点M(1,4).
(2)∵A(-1,0),抛物线的对称轴为直线x=1,∴点B(3,0) ,∴EM=1,BN=2,∵EM∥BN,
∴△EMF∽△BNF,∴S△EMF=(EBMN)2=(12)2=14. △ S BNF
18.已知二次函数的图象过(-2,0)、(4,0)、(0,3)三点,求这个二次函 数的关系式.
3/5
知识像烛光,能照亮一个人,也能照亮无数的人。--培根 19.已知二次函数y=ax2+bx+c,当x=-1时有最小值-4,且图象在x轴上截得 线段长为4,求函数解析式.
20.如图,抛物线y=-x2+2x+c与x轴交于A、B两点,它的对称轴与x轴交于点N, 过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(-1,0). (1)求该抛物线的解析式及顶点M的坐标; (2)求△EMF与△BNF的面积之比.
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
北师大版九下数学第2章 二次函数 2.3 确定二次函数的表达式【习题课件】
课堂导练
(2)判断点 P(-2,3)是否在这个二次函数的图象上.如果在,求 出△PAB 的面积;如果不在,说明理由. 解:把 x=-2 代入 y=-x2-2x+3,得 y=3, ∴点 P(-2,3)在二次ห้องสมุดไป่ตู้数的图象上. 令-x2-2x+3=0,得 x1=-3,x2=1. ∴△PAB 的面积为12AB·yP=12×[1-(-3)]×3=6.
课后训练
(3)求 a 和 k 的值. 解:由(2)可知 A 不在抛物线上.结合(1)的结论易知 B,D 一定 在抛物线 y=a(x-1)2+k(a>0)上. ①若点 C(-1,2)在此抛物线上, 则a4+a+k= k=-21,,解得ak= =1-,2.
课后训练
②若点 E(4,2)在此抛物线上, 则a9+a+k= k=-21,,解得ka==-38,181. 综上可知,ak==1-,2或ak= =-38,181.
课堂导练
(3)已知抛物线的顶点为(2,0),且过点(-3,5),求抛物线对应 的函数表达式. 解:设抛物线对应的函数表达式为 y=a(x-2)2,将点(-3,5)的 坐标代入,得 a=15. ∴抛物线对应的函数表达式为 y=15(x-2)2.
课堂导练
5.已知抛物线与 x 轴的交点坐标为(x1,0)和(x2,0),用待定系 数法求函数表达式时,一般设交__点__式__,即 y=a(x-x1)(x-x2).
课后训练
(2)在 y 轴上找一点 P,使 PD+PH 的值最小,则 PD+PH 的最 小值为____1_3___.
课后训练 9.已知 A(1,0),B(0,-1),C(-1,2),D(2,-1),E(4,2)
五个点,抛物线 y=a(x-1)2+k(a>0)经过其中三个点. (1)求证:C,E 两点不可能同时在抛物线 y=a(x-1)2+k(a>0)上. 证明:由题意可知,抛物线的对称轴为直线 x=1. 若 C(-1,2)在此抛物线上, 则 C 点关于直线 x=1 的对称点(3,2)也在此抛物线上. ∴点 E(4,2)不在此抛物线上. ∴C,E 两点不可能同时在抛物线 y=a(x-1)2+k(a>0)上.
北师大版九年级下册数学课件第2章2.3确定二次函数的表达式2
整合方法
12.【2020·宁波】如图,在平面直角坐标系中,二次函数 y=ax2 +4x-3 图象的顶点是 A,与 x 轴交于 B,C 两点,与 y 轴交
于点 D.点 B 的坐标是(1,0).
(1)求 A,C 两点的坐标,并根据图象直接写出当 y>0 时 x 的取值范围.
整合方法
解:把 B(1,0)的坐标代入 y=ax2+4x-3, 得 0=a+4-3,解得 a=-1, ∴y=-x2+4x-3=-(x-2)2+1,∴A(2,1), ∵对称轴为直线 x=2,点 B,C 关于直线 x=2 对称, ∴C(3,0),∴当 y>0 时,1<x<3.
夯实基础
【点拨】由图象知,二次函数图象的对称轴为直线 x=-1,且 函数图象过点(-3,0),(0,3),设二次函数的表达式为 y=a(x + 1)2 + k(a≠0), 将 点 ( - 3 , 0), (0 , 3)的 坐 标 分 别 代 入 ,得 4aa++kk==3,0,解得ak= =- 4. 1,则二次函数的表达式为 y=-(x+1)2 +4=-x2-2x+3.故选 D.
提示:点击 进入习题
3 确定二次函数的表达式
提第示二: 章【点答击二次案函进数】入C习题
夯实基础
10.如图,某抛物线与 x 轴交于点 A(-1,0),B(2,0),与 y 轴 交于点 C(0,1),则这条抛物线的表达式是( C ) A.y=x2-x-2 B.y=-x2+x+2 C.y=-12x2+12x+1 D.y=-12x2-12x+1
-2ba=-3, 的对称轴经过点 A,∴其顶点坐标是(-3,-3)则0-4ab2=-3,
解得a=13,∴该抛物线的表达式为 b=2,
y=13x2+2x.
【答案】A
初中数学北师大版九年级下学期 2.3 确定二次函数的表达式2
北师大版数学九年级下册同步训练:2.3.1 确定二次函数的表达式2一、选择题1.一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为( ) A. y=﹣2(x+2)2+4 B. y=﹣2(x ﹣2)2+4 C. y=2(x+2)2﹣4 D. y=2(x ﹣2)2﹣42.已知一个二次函数,当x=1时,y 有最大值8,其图象的形状、开口方向与抛物线y=﹣2x 2相同,则这个二次函数的表达式是( )A. y=﹣2x 2﹣x+3B. y=﹣2x 2+4C. y=﹣2x 2+4x+8D. y=﹣2x 2+4x+6 3.当k 取任意实数时,抛物线y=﹣9(x ﹣k )2﹣3k 2的顶点所在的曲线的解析式是( ) A. y=3x 2 B. y=9x 2 C. y=﹣3x 2 D. y=﹣9x 24.已知抛物线y=ax 2+bx 经过点A (﹣3,﹣3),且该抛物线的对称轴经过点A ,则该抛物线的解析式为( ) A. y =13x 2+2x B. y =−13x 2+2x C. y =13x 2−2x D. y =−13x 2−2x 5.次函数的图象如图所示,则这个二次函数的解析式为( )A. y 12 (x ﹣2)2+3B. y= 12 (x ﹣2)2﹣3C. y=﹣ 12 (x ﹣2)2+3D. y=﹣ 12 (x ﹣2)2﹣3 6.如果一条抛物线的形状与y=﹣2x 2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是( ) A. y=2(x ﹣4)2﹣2 B. y=﹣2(x ﹣4)2﹣2 C. y=﹣2(x ﹣4)2+2 D. y=﹣2(x+4)2﹣2 7.根据表中的自变量x 与函数y 的对应值,可判断此函数解析式为( )A. y=xB. y=﹣ 1x C. y= 34 (x ﹣1)2+2 D. y=﹣ 34 (x ﹣1)2+2 8.已知抛物线y=x 2﹣8x+c 的顶点在x 轴上,则c 等于( )A. 4B. 8C. ﹣4D. 169.顶点为(6,0),开口向下,开口的大小与函数y=13x 2的图象相同的抛物线所对应的函数是( ) A. y=13(x+6)2 B. y=13(x ﹣6)2 C. y=﹣13(x+6)2 D. y=﹣13(x ﹣6)2 10.已知抛物线y=x 2+bx+c 的顶点坐标为(1,﹣3),则抛物线对应的函数解析式为( ) A. y=x 2﹣2x+2 B. y=x 2﹣2x ﹣2 C. y=﹣x 2﹣2x+1 D. y=x 2﹣2x+1二、填空题11.抛物线y=ax2+12x﹣19顶点横坐标是3,则a=________.12.已知一个二次函数的图象开口向上,顶点坐标为(0,﹣1 ),那么这个二次函数的解析式可以是________.(只需写一个)13.已知某抛物线的顶点坐标为(﹣2,1),且与y轴相交于点(0,4),这个抛物线所表示的二次函数的表达式是________.14.不论m取任何实数,抛物线y=(x﹣m)2+m﹣1(x为自变量)的顶点都在一条直线上,则这条直线的函数解析式是________.15.一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同,顶点坐标是(﹣1,3),则该抛物线的解析式为________.16.一个二次函数,当自变量x=0时,函数值y=﹣1;当x为﹣2与1时,函数值y=0,求这个二次函数解析式.2三、解答题17.已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6).(1)求二次函数的解析式;(2)画出它的图象;(3)写出它的对称轴和顶点坐标.18.已知抛物线y=ax2﹣2x+c的对称轴为直线x=﹣1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.(1)求抛物线的表达式;(2)若点P在x轴上,且PA=PB,求点P的坐标.答案解析部分一、<b >选择题 1.【答案】 B 2.【答案】 D 3.【答案】 C 4.【答案】 A 5.【答案】 C 6.【答案】 B 7.【答案】 D 8.【答案】 D 9.【答案】 D 10.【答案】 B 二、<b >填空题 11.【答案】 -212.【答案】 y=2x 2﹣1 13.【答案】 y= 34 (x+2)2+1 14.【答案】y=x ﹣115.【答案】y=﹣2(x+1)2+316.【答案】 解:根据题意设二次函数解析式为y=a (x+2)(x ﹣12),将(0,﹣1)代入得:﹣a=﹣1,即a=1,则二次函数解析式为y=(x+2)(x ﹣12)=x 2+32x ﹣1. 三、<b >解答题17.【答案】 (1)解:依题意,得: {4a +2b =0a −b =6 ,解得: {a =2b =−4, 所以,二次函数的解析式为:y=2x 2﹣4x(2)解:y=2x 2﹣4x=2(x 2﹣2x+1﹣1)=2(x ﹣1)2﹣2, 由对称性列表如下:(3)解:由y=2(x﹣1)2﹣2可知对称轴为直线x=1,顶点坐标为(1,﹣2)18.【答案】(1)解:∵对称轴为直线x=﹣1,∴﹣−2=﹣1,2a∴a=﹣1,∵△ABO的面积为1,∴1c×1=1,2∴c=2,∴抛物线的表达式为y=﹣x2﹣2x+2(2)解:∵y=﹣x2﹣2x+2=﹣(x+1)2+3,∴A(﹣1,3),设P点的坐标为(x,0).∵PA=PB,B(0,2),∴(x+1)2+32=x2+22,解得x=﹣3.故P点的坐标为(﹣3,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大九年级数学下册第二章二次函数
2.3确定二次函数表达式同步训练
学校:__________班级:__________姓名:__________考号:__________
一、选择题(本题共计10小题,每题3分,共计30分,)1.抛物线y=ax2+bx+c经过点(3, 0)和(2, −3),且以直线x=1为对称轴,则它的解析式为()
A.y=−x2−2x−3B.y=x2−2x−3
C.y=x2−2x+3D.y=−x2+2x−3
2.用配方法将二次函数y=3x2−4x−2写成形如y=a(x+m)2+n的形式,则m、n的值分别是()
A.m=2
3,n=10
3
B.m=−2
3
,n=−10
3
C.m=2,n=6D.m=2,n=−2
3.若所求的二次函数图象与抛物线y=2x2−4x−1有相同的顶点,并且在对称
轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,则所求二次函数的解析式为()
A.y=−x2+2x+4
B.y=−ax2−2ax−3(a>0)
C.y=−2x2−4x−5
D.y=ax2−2ax+a−3(a<0)
4.用配方法将函数y=1
2
x2−2x+1写成y=a(x−ℎ)2+k的形式是()
A.y=1
2(x−2)2−1B.y=1
2
(x−1)2−1
C.y=1
2(x−2)2−3D.y=1
2
(x−1)2−3
5.二次函数y=2x2−12x+13经过配方化成y=a(x−ℎ)2+k的形式是()A.y=2(x+3)2+5B.y=2(x+3)2−5
C.y=2(x−3)2+5D.y=2(x−3)2−5
6.如图所示,在平面直角坐标系中,二次函数y=ax2+bx+c的图象顶点为A(−
2, −2),且过点
B(0, 2),则y与x的函数关系式为()
A.y=x2+2B.y=(x−2)2+2
C.y=(x−2)2−2D.y=(x+2)2−2
7.已知抛物线过点A(2, 0),B(−1, 0),与y轴交于点C,且OC=2.则这条抛物线的解析式为()
A.y=x2−x−2
B.y=−x2+x+2
C.y=x2−x−2或y=−x2+x+2D.y=−x2−x−2或y=x2
+x+2
8.二次函数的图象经过(0, 3),(−2, −5),(1, 4)三点,则它的解析式为()
A.y=x2+6x+3B.y=−3x2−2x+3
C.y=2x2+8x+3D.y=−x2+2x+3
9.一抛物线的形状、开口方向与y=x2−4x+3相同,顶点在(−2, 1),则此抛物线的解析式为()
A.y=1
2(x−2)2+1B.y=1
2
(x+2)2−1
C.y=1
2(x+2)2+1D.y=1
2
(x+2)2+1
10.已知二次函数的y=ax2+bx+c图象是由y=1
2
x2的图象经过平移而得到,若图
象与x轴交于A、C(−1, 0)两点,与y轴交于D(0, 5
2
),顶点为B,则四边形ABCD 的面积为()
A.9B.10C.11D.12
二、填空题(本题共计10小题,每题3分,共计30分,)11.用配方法把二次函数y=2x2+3x+1写成y=a(x+m)2+k的形式________.
12.如果抛物线y=ax2+bx+c的对称轴是x=−2,且开口方向,形状与抛物线y=−3
x2相同,且过原点,那么y=________.
2
13.以直线x=1为对称轴的抛物线过点(3, 0),(0, 3),求此抛物线的解析式.________.
14.用配方法将函数y=2x2+3x+1化成y=a(x+m)2+k的形式,则y=________.
15.已知二次函数的图象经(0, 0),(1, 2),(−1, −4)三点,那么这个二次函数的解析式是________.
16.已知二次函数y=ax2的图象经过点(1, −3),则该函数的关系式为________.
17.二次函数y=−2x2+6x−5配成y=a(x−ℎ)2+k的形式是________,其最大值是________.
18.若抛物线y=x2−(m−3)x+2的对称轴为y轴,则m=________.19.已知抛物线y=ax2+bx+c的图象顶点为(−2, 3),且过(−1, 5),则抛物线的表达式为________.
20.抛物线y=−x2−2x+3用配方法化成y=a(x−ℎ)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.
三、解答题(本题共计6小题,每题10分,共计60分,)21.已知函数y=x2+bx−1的图象经过点(3, 2).
(1)求这个函数的解析式;
(2)当x>0时,求使y≥2的x的取值范围.
22.已知二次函数y=ax2+bx+C图象上部分点的坐标(x, y)满足下表:
(1)求该二次函数的解析式;
23.已知y=−2x2+bx+c的图象经过点A(0, 2)和B(−1, −4).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
24.抛物线y=−x2+(m−1)x+m与y轴交于点(0, 3).
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时,y>0?②当x取什么值时,y的值随x的增大而减小?
25.已知二次函数y=x2+2x−3.
(1)把函数配成y=a(x−ℎ)2+k的形式;
(2)求函数与x轴交点坐标;
(4)y>0
(5)当−3<x<0时,则y的取值范围为________.
26.如图,抛物线y=x2+bx+c与y轴交于点C(0, −3),对称轴为直线x=1,
点D为抛物线的顶点.
(1)求抛物线解析式和顶点D的坐标;
(2)求抛物线与x轴的两交点A、B的坐标;
(3)你可以直接写出不等式x2−2x−3<0的解集吗?
答案
1.B
2.B
3.D
4.A
5.D
6.D
7.C
8.D
9.C
10.A
11.y=2(x+3
4)2−1
8
12.−3
2
x2−6x
13.y=−x2+2x+3
14.2(x+3
4)2−1
8
15.y=−x2+3x 16.y=−3x2
17.y=−2(x−3
2)2−1
2
−1
2
18.3
19.y=2x2+8x+11
20.y=−(x+1)2+4(1, 0),(−3, 0)(0, 3)
21. 解:(1)∵函数y =x 2+bx −1的图象经过点(3, 2), ∴9+3b −1=2, 解得:b =−2,
则函数解析式为y =x 2−2x −1;(2)当x =3时,y =2, 根据二次函数性质当x ≥3时,y ≥2,
则当x >0时,使y ≥2的x 的取值范围是x ≥3.
22. 解:(1)把点(0, −1)代入y =ax 2+bx +c ,得c =−1. 再把点(−1, 2),(1, −6)分别代入y =ax 2+bx −1中,得 {
a −
b −1=2a +b −1=−6
,
解得:{a =−1
b =−4
,
所以这个二次函数的关系式为:y =−x 2−4x −1.(2)y =−x 2−4x −1
=−(x +2)2
−5.
该二次函数图象的顶点坐标为(−2, −5),对称轴为x =−2.
23. 解:(1)将点A (0, 2)和B (−1, −4)代入y =−2x 2+bx +c , 得:{
c =2
−2−b +c =−4
,
解得:{b =4c =2
,
∴抛物线的解析式为y =−2x 2+4x +2;
y =−2x 2+4x +2=−2(x 2−2x +1−1)+2=−2(x −1)2
+4;
(2)抛物线y =−2x 2+4x +2=−2(x −1)2+4的顶点C 坐标为(1, 4), ∴S △CAO =
1
2
×2×1=1. 24. 解:(1)将点(0, 3)代入抛物线y =−x 2+(m −1)x +m , m =3,
∴抛物线的解析式y =−x 2+2x +3;(2)令y =0,−x 2+2x +3=0,
解得x1=3,x2=−1;
X轴:A(3, 0)、B(−1, 0);
Y轴:C(0, 3)(3)抛物线开口向下,对称轴x=1;
所以)①当−1<x<3时,y>0;
②当x≥1时,y的值随x的增大而减小.
25.x<−3或x>1.(5)当x=−1时,y取最小值−4;
当x=−3时,y=0;
当x=0时,y=−3.
∴当−3<x<0时,y的取值范围为−4≤y<0.
26.解:(1)根据题意得x=−b2=1,0+c=−3,解得b=−2,c=−3
∴抛物线解析式为y=x2−2x−3;
∵y=x2−2x−3=(x−1)2−4,
∴顶点D的坐标为(1, −4);(2)当y=0时,x2−2x−3=0,解得x1=3,x2=−1
∴A、B的坐标分别为(−1, 0)、(3, 0);(3)x2−2x−3<0的解集为−1<x<3.。
