机器人的数学基础齐次变换矩阵及其运算ppt课件
合集下载
机器人模型与控制-0前言1齐次变换

三、刚体位姿描述-坐标系的描述
刚体相对于参考坐标系{A}的位姿:可以用与刚体固连 的坐标系{B} 相对于参考坐标系{A}的旋转矩阵和位置矢量 复合在一起来表达
B
YB YA
AP OB
A B
R , POB
A
P1 P1 OB ZB XB
OA ZA
XA
四、手爪位姿的描述
定义一个与手爪固连的手爪坐标系{T},以{T}相对于参 考坐标系{A}位姿来描述手爪位姿
Z轴设在手指接近物体的方向,称为接近矢量 a(approach); Y轴设在两手指的联线方向,称为方位矢量 o(orientation); X轴根据右手法则确定:n= o×a,称为法向矢量 n(normal)。
T
A T
R , POT
A
o(YT) n(XT) OT
,其中
A T
R n o a
* 在每个刚体上定义一个坐标系;
* 刚体内的各点之间的运动学关系固定不变, 在该坐标系内表示;
* 各刚体间及与环境间的位姿关系因关节运动而改变, 以齐次变换表达刚体(坐标系)间的位姿关系。
1.1 刚体位姿描述
• 在刚体上定义坐标系,通过坐标系在参考坐标系中的位置 和姿态表达,来描述刚体位姿。
YB YA
机器人模型与控制
参考教材: 1. 【ROBOT DYNAMICS AND CONTROL】 M W.SPONG, JOHN WILEY & SONS, 2004 2. 【机器人学】 熊有伦等编著 机械工业出版社 1993
内容
• • • • • 前言 相关基础知识:齐次变换 运动学:位置关系和速度关系 静力学 动力学
• • •
A B
工业机器人课件-知识点2.2 机器人坐标系及数学基础

项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.3 机器人坐标系中的各种变换 2、机器人本体的关节运动和连杆变换矩阵
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.3 机器人坐标系中的各种变换 3、机器人工具变换与工具变换数据
基本变换:从机器人世界坐标系变换至机器人基座坐标系的运
动过程,称之为基本变换。
基本变换数据:沿着机器人世界坐标系X、Y、Z轴平移的距离分
别用X、Y、Z表示,绕机器人世界坐标系X、Y、Z轴旋转的角度分别用 A、B、C表示。以上6个数据构成一个一维数组(X,Y,Z,A,B,C), 该数组被称为基本变换数据。
2.2 机器人坐标系的运动变换与数学运算
2.2.4 机器人正运动学与逆运动学
2、逆运动学计算
把根据机器人工具坐标系在 世界坐标系中的直交位置数据计 算出各个关节角度值(J1,J2, J3,J4,J5,J6)的过程称之为
逆运动学计算
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.1 坐标系的运动和变换矩阵 2、坐标系的旋转运动和矩阵表示
例如,将坐标系{F}绕坐标系{U}的X轴正方向旋转30°
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.1 坐标系的运动和变换矩阵 3、复合运动和矩阵表示
例如,将坐标系{F}绕坐标系{U}的X轴正方向旋转30°
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.4 机器人正运动学与逆运动学 (2)构造标志数据FL1 (X,Y,Z,A,B,C,L1,L2)(FL1,FL2)
机器人运动分析中的矩阵变换(PPT52页)

1
▲雅可比矩阵的定义 ▲微分运动与广义速度 ▲雅可比矩阵的构造法 ▲PUMA560机器人的雅可比矩阵 ▲逆雅可比矩阵 ▲力雅可比矩阵
上一章我们讨论了刚体的位姿描述、齐 次变换,机器人各连杆间的位移关系,建立 了机器人的运动学方程,研究了运动学逆解, 建立了操作空间与关节空间的映射关系。
本章将在位移分析的基础上,进行速度分 析,研究操作空间速度与关节空间速度之间 的线性映射关系——雅可比矩阵(简称雅可比)。 雅可比矩阵不仅用来表示操作空间与关节空 间之间的速度线性映射关系,同时也用来表 示两空间之间力的传递关系。
oz
az
0
0
0
ddi
对于移动关节
nz
oz
T
Ji
az
0
0
0
对于转动关节
(P n)z
(
P
0)
z
T
Ji
(
P
a) nz
z
oz
az
例:PUMA560的6个关节都是转动关节,其雅可比 有6列。此处用矢量积法计算J(q)
J ( q) J1 J2
J6
ny oy ay
( (
P P
n) o)
z z
d d
x y
(
P
a) nz
z
d
z
x
oz
y
az z
简写为:
T d RT RT S(P) d
T
0
RT
其中,R是旋转矩阵
nx ox ax
R
ny
oy
a
y
.
nz oz az
S(P)为矢量P的反对称矩阵 S(P)矩阵具有以下性质:
▲雅可比矩阵的定义 ▲微分运动与广义速度 ▲雅可比矩阵的构造法 ▲PUMA560机器人的雅可比矩阵 ▲逆雅可比矩阵 ▲力雅可比矩阵
上一章我们讨论了刚体的位姿描述、齐 次变换,机器人各连杆间的位移关系,建立 了机器人的运动学方程,研究了运动学逆解, 建立了操作空间与关节空间的映射关系。
本章将在位移分析的基础上,进行速度分 析,研究操作空间速度与关节空间速度之间 的线性映射关系——雅可比矩阵(简称雅可比)。 雅可比矩阵不仅用来表示操作空间与关节空 间之间的速度线性映射关系,同时也用来表 示两空间之间力的传递关系。
oz
az
0
0
0
ddi
对于移动关节
nz
oz
T
Ji
az
0
0
0
对于转动关节
(P n)z
(
P
0)
z
T
Ji
(
P
a) nz
z
oz
az
例:PUMA560的6个关节都是转动关节,其雅可比 有6列。此处用矢量积法计算J(q)
J ( q) J1 J2
J6
ny oy ay
( (
P P
n) o)
z z
d d
x y
(
P
a) nz
z
d
z
x
oz
y
az z
简写为:
T d RT RT S(P) d
T
0
RT
其中,R是旋转矩阵
nx ox ax
R
ny
oy
a
y
.
nz oz az
S(P)为矢量P的反对称矩阵 S(P)矩阵具有以下性质:
机器人的数学基础齐次变换矩阵及其运算

表示{C}相对于{A}的描述,是两变换矩阵的乘积。
注意:变换矩阵相乘不满足“交换律”,变换矩阵的左乘 和右乘的运动解释不同。
上海电机学院 机械学院
CAT ABT CBT
A B
R
0
A
pB0 1
B C
R
0
B
pC 1
0
复合变换可解释为: (1)CAT 和 CBT 分别代表同一坐标系{C}相对于{A}和{B}的描述。则
0 0 0 1
上海电机学院 机械学院
CAT ABT CBT
4.变换矩阵相乘
对于给定的坐标系{A}、{B}、{C},已知{B}相对 {A}的描述为 ABT ,{C}相对{B}的描述为 CBT ,则
B pCBT Cp
A p ABT Bp ABT CBT Cp
从而定义复合变换
。
CAT ABT CBT
0 0 1 1
ABT
1 0
0 1
0 0
3 4
0 0 0
1
1 Trans(x, y, z) 0
0 0
0 1 0 0
0 0 1 0
x
y
z
1
cos
Rot(
z,
)
sin 0
0
sin cos
0 0
0 0 1 0
{T}代表工具坐标系; {S}代表工作站坐标系; {G}代表目标坐标系; 它们之间的位姿关系用相应
BST 描述工作站坐标系相对于基座的位姿; GST 描述目标坐标系相对于{S}的位姿; WBT 描述腕部{W}相对于基座{B}的位姿;
[课件](工业机器人)位姿描述与齐次变换PPT
位姿描述与齐次变换PPT](https://img.taocdn.com/s3/m/711ba841caaedd3383c4d3c4.png)
六、齐次表达
根据几何学知识,上面第四小节中给定点的绝对位置为:
Ap b a b a b a c s cs b a
写成三维形式,有:
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同!但后一种方法简单!
问题:是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘,即可以得到齐次变换阵?
0 0 0 0 0 10
O B 在A中位置,记作 A pOB
B在
A 中姿态,记作
A B
R
。
分成两块,不便于记忆!
齐次变换矩阵
若写成如下齐次形式,有:
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置,然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法,得:
aacbs 写成矩阵形式
b as bc
Y A
YB
b
b
XB a
OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成:分为4块。左上角是姿态矩阵,为一单位正交 矩阵;右上角为对象坐标系原点位置值;左下角为 三个0 0 0,简记为0;右下角为1。
根据几何学知识,上面第四小节中给定点的绝对位置为:
Ap b a b a b a c s cs b a
写成三维形式,有:
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同!但后一种方法简单!
问题:是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘,即可以得到齐次变换阵?
0 0 0 0 0 10
O B 在A中位置,记作 A pOB
B在
A 中姿态,记作
A B
R
。
分成两块,不便于记忆!
齐次变换矩阵
若写成如下齐次形式,有:
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置,然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法,得:
aacbs 写成矩阵形式
b as bc
Y A
YB
b
b
XB a
OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成:分为4块。左上角是姿态矩阵,为一单位正交 矩阵;右上角为对象坐标系原点位置值;左下角为 三个0 0 0,简记为0;右下角为1。
工业机器人课件-知识点2.2 机器人坐标系及数学基础

2.2.2 坐标系的齐次坐标变换 3、坐标系旋转运动的齐次坐标变换
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.2 坐标系的齐次坐标变换 3、坐标系旋转运动的齐次坐标变换
当绕固定参考坐标系作纯旋转时为绝对旋转,新坐标系的位置与姿态通过左 乘变换矩阵
当绕运动参考坐标系作纯旋转时为相对旋转,新坐标系的位置与姿态通过右 乘变换矩阵
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.3 机器人坐标系中的各种变换 1、机器人基本变换与基本变换数据
1、基座坐标系与世界坐标系重合; 2、将基座坐标系绕着世界坐标系的X轴旋 转A的角度,单位为°。 3、将基座坐标系绕着世界坐标系的Y轴旋 转B的角度,单位为°。 4、将基座坐标系绕着世界坐标系的Z轴旋 转C的角度,单位为°。 5、将基座坐标系沿着世界坐标系的X、Y、 Z轴分别平移X、Y、Z的距离,单位为mm。
基本变换:从机器人世界坐标系变换至机器人基座坐标系的运
动过程,称之为基本变换。
基本变换数据:沿着机器人世界坐标系X、Y、Z轴平移的距离分
别用X、Y、Z表示,绕机器人世界坐标系X、Y、Z轴旋转的角度分别用 A、B、C表示。以上6个数据构成一个一维数组(X,Y,Z,A,B,C), 该数组被称为基本变换数据。
2.2.4 机器人正运动学与逆运动学 2、逆运动学计算
为了确定关节角度的唯一解,需要约定关节之间的构造标 志和每个关节的旋转圈数。
关节变量解 1
工具的目标位置 与姿态
关节变量解 2
关节变量解 1
关节变量解 2
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.2 坐标系的齐次坐标变换 3、坐标系旋转运动的齐次坐标变换
当绕固定参考坐标系作纯旋转时为绝对旋转,新坐标系的位置与姿态通过左 乘变换矩阵
当绕运动参考坐标系作纯旋转时为相对旋转,新坐标系的位置与姿态通过右 乘变换矩阵
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
2.2.3 机器人坐标系中的各种变换 1、机器人基本变换与基本变换数据
1、基座坐标系与世界坐标系重合; 2、将基座坐标系绕着世界坐标系的X轴旋 转A的角度,单位为°。 3、将基座坐标系绕着世界坐标系的Y轴旋 转B的角度,单位为°。 4、将基座坐标系绕着世界坐标系的Z轴旋 转C的角度,单位为°。 5、将基座坐标系沿着世界坐标系的X、Y、 Z轴分别平移X、Y、Z的距离,单位为mm。
基本变换:从机器人世界坐标系变换至机器人基座坐标系的运
动过程,称之为基本变换。
基本变换数据:沿着机器人世界坐标系X、Y、Z轴平移的距离分
别用X、Y、Z表示,绕机器人世界坐标系X、Y、Z轴旋转的角度分别用 A、B、C表示。以上6个数据构成一个一维数组(X,Y,Z,A,B,C), 该数组被称为基本变换数据。
2.2.4 机器人正运动学与逆运动学 2、逆运动学计算
为了确定关节角度的唯一解,需要约定关节之间的构造标 志和每个关节的旋转圈数。
关节变量解 1
工具的目标位置 与姿态
关节变量解 2
关节变量解 1
关节变量解 2
项目2 工业机器人虚拟工作站的仿真操作
2.2 机器人坐标系的运动变换与数学运算
机器人的数学基础齐次变换矩阵及其运算(共34张PPT)

x' 1 0 0 x x
y'
0
1
0
y
y
z' 0 0 1 z z
1
0
0
0
1
1
a′=Trans(Δx, Δy, Δz)a
平移算子
1 0 0 x
Tran(sx,y,z) 0 1 0 y 0 0 1 z
0 0 0
1
❖ ① 算子左乘: 表示点的平移是相对固定坐标系进行的坐标变换。
❖ ② 算子右乘: 表示点的平移是相对动坐标系进行的坐标变换。
假设手臂绕Z0轴旋转90°,那么手 臂到达G2;假设手臂不动,仅手部 绕手腕Z1轴转90°,那么手部到达 G3.写出手部坐标系G2、G3表达式。
3.复合齐次变换
复合变换是由固定参 考坐标系或当前运动 坐标系的一系列沿轴 平移和绕轴旋转变换 所组成的。任何变换 都可以分解为按一定 顺序的一组平移和旋 转变换。
ny oy
n o k 0 希望得到{A}相对于{B}的描述,这是个齐次变换求逆问题。
从而定义复合变换
z
z
z
nHale Waihona Puke ox ax px0 1kx ky
(2)旋转之前{A’}和 {B’}重合, {A}和{B}也重合。
平移与旋转的结合
令上面两式相等,那么得变换方程
是nx过n原把y点n的上z 单-式位p.矢右量,端求绕三k旋转矩阵相乘,并运用旋转矩阵的正交性质:
zA A
n o k (2)旋转之前{A’}和 {B’}重合, {A}和{B}也重合。
点(1)在空和间分直别角代坐表标同系一中坐的标旋系转{如C}下相z图对。于{A}和z {B}的描z述。
同理,绕x轴、Y轴旋转算子内容为:
第四章齐次变换
耐 心 与 自 学
的 ② R(z, 90°)
热 情 是 成 功 的
关 ③ R(y, 90°)
键
1 0 0 01 1
P' 0 0 -1 02 3 0 1 0 03 2
0 0
0
11
1
(2-14)
0 -1 0 0 1 3
P'' 1 0 0 0 3 1 (2-15) 0 0 1 0 2 2
关 键
(3)平移与旋转相结合的变换。
12
2.5齐次变换矩阵-纯平移
机械工程与汽车学院
• 纯平移的变换:一个坐标系在空间以不变的姿态运动。它
的方向单位向量保持同一方向不变。所有的改变只是坐标
耐 系原点相对于参考坐标系的变化。
心
与• 相对于固定参考坐标系的新的坐标系的位置可以用原来坐
自 标系的原点位置向量加上表示位移的向量求得。若用矩阵
的 学问题
关
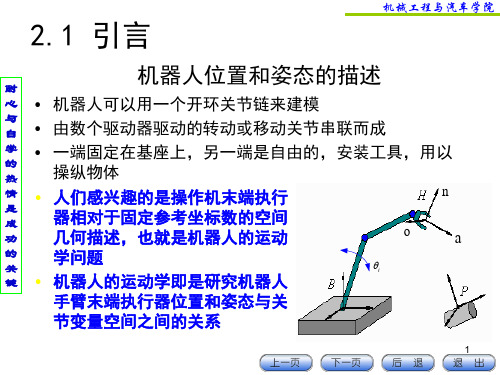
键 • 机器人的运动学即是研究机器人
n
o
a
i
手臂末端执行器位置和姿态与关
节变量空间之间的关系
1
机械工程与汽车学院
• 丹纳维特(Denavit)和哈顿贝格(Hartenberg)
于1955年提出了一种矩阵代数方法解决机器人的
耐 心
运动学问题—D-H方法
与 自
• 具有直观的几何意义
学 的
• 能表达动力学、计算机视觉和比例变换问题
nz 0
oy oz 0
ay az 0
Py
d
y
Pz
1
dz
的
热 情
•
结论:
是 成
1.新坐标系位置可通过在坐标系矩阵前面左乘变换矩阵得到;
的 ② R(z, 90°)
热 情 是 成 功 的
关 ③ R(y, 90°)
键
1 0 0 01 1
P' 0 0 -1 02 3 0 1 0 03 2
0 0
0
11
1
(2-14)
0 -1 0 0 1 3
P'' 1 0 0 0 3 1 (2-15) 0 0 1 0 2 2
关 键
(3)平移与旋转相结合的变换。
12
2.5齐次变换矩阵-纯平移
机械工程与汽车学院
• 纯平移的变换:一个坐标系在空间以不变的姿态运动。它
的方向单位向量保持同一方向不变。所有的改变只是坐标
耐 系原点相对于参考坐标系的变化。
心
与• 相对于固定参考坐标系的新的坐标系的位置可以用原来坐
自 标系的原点位置向量加上表示位移的向量求得。若用矩阵
的 学问题
关
键 • 机器人的运动学即是研究机器人
n
o
a
i
手臂末端执行器位置和姿态与关
节变量空间之间的关系
1
机械工程与汽车学院
• 丹纳维特(Denavit)和哈顿贝格(Hartenberg)
于1955年提出了一种矩阵代数方法解决机器人的
耐 心
运动学问题—D-H方法
与 自
• 具有直观的几何意义
学 的
• 能表达动力学、计算机视觉和比例变换问题
nz 0
oy oz 0
ay az 0
Py
d
y
Pz
1
dz
的
热 情
•
结论:
是 成
1.新坐标系位置可通过在坐标系矩阵前面左乘变换矩阵得到;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16
CAT ABT CBT
A B
R
0
A
pB0 1
B C
R
0
B
pC 1
0
复合变换可解释为: (1)CAT 和 CBT 分别代表同一坐标系{C}相对于{A}和{B}的描述。则
ABT 表示坐标系{C}从 CBT 映射为 CAT 的变换。
(2)坐标系{C}相对于{A}的描述 CAT 是这样得到的:最初{C} 与{A}重合,首先相对于{A}作运动 ABT ,到达{B},然后相 对{B}作运动 CBT ,到达最终位置{C}。
17
5.变换矩阵求逆
如果知道坐标系{B}相对于{A}的描述。希望得到{A}相对 于{B}的描述,这是个齐次变换求逆问题。 求逆问题可以描述为:已知 ABT ,求解 BAT 。
•对4*4矩阵直接求逆; •利用齐次变换矩阵的特点,简化矩阵求逆运算。
ABT
A B
R
0
A
pB 1
0
BAT
B A
R
0
0
0
1 0
0
0
1
1
12
❖ 平移变换和旋转变换可以组合在一个齐次变换中。上例 中点U若还要作4i-3j+7k的平移,则只要左乘上平移变换 算子即可得到最后的列阵表达式。
E Trans(4,3,7)Rot(y,90)Rot(z,90)u
13
14
齐次变换矩阵 ABT 的数学意义: (1)同一点在不同坐标系{B}和{A}中的变换; (2)描述坐标系{B}相对于坐标系{A}的位置和方位; (3)点的运动算子。
0
利用旋转矩阵正交性
A B
R
1
BART
B
pA0 1
利用复合变换公式(2.13) ,求出 A pB0 在{B}中描述。
18
B ( ApB0 ) ABR ApB0 BpA0 0
B pA0 ABR ApB0 BART ApB0
❖ ② 算子右乘: 表示点的平移是相对动坐标系进行的坐标变换。
❖ ③ 该公式亦适用于坐标系的平移变换、 物体的平移变换, 如机 器人手部的平移变换。
5
❖ 例 动坐标系{A}相对于固定坐标系的X0、Y0、Z0轴作
❖ (-1,2,2)平移后到{A’};动坐标系{A}相对于自身坐标系(即动系) 的X、Y、Z轴分别作(-1,2,2)平移后到{A’’}。已知A,写出坐标系 {A’}、 {A’’}
A p ABT Bp
0 0 1 1
ABT
1 0
0 1
0 0
3 4
0 0 0
1
1 Trans(x, y, z) 0
0 0
0 1 0 0
0 0 1 0
x
y
z
1
cos
Rot(
z,
)
sin 0
0
sin cos
0 0
0 0 1 0
0 0 0 1
15
CAT ABT CBT
4.变换矩阵相乘
相对于固定坐标系
算子左乘
相对于动坐标系
算子右乘
11
❖ 已知坐标系中点U的位置矢量 u 7 3 2 1,T 将此点绕Z轴 旋转90°,再绕Y轴旋转90°,如图所示,求旋转变换后 所得的点W。
W Rot(Y,90)Rot(Z,90)U
0 0 1 0 0 1 0 0 7
0
1
0
0
1
0
0
0
3
1 0 0 0 0 0 1 0 2
0
0 0 1
同理,绕x轴、Y轴旋转算子内容为:
Hale Waihona Puke 1 00 0cos 0 sin 0
Rot(x, ) 0
0
c os s in
sin c os
0 0
Rot( y, )
0
sin
1 0
0
c os
0 0
0 0
0 1
0
0 0 1
8
如图所示单操作手臂,并且手腕 也具有一个旋转自由度。已知手 部的起始位姿矩阵为G1.
机器人学基础
——齐次变换矩阵及其运算
LOGO
齐次变换矩阵及其运算
由于各种原因,变换矩 阵应写成方型形式,3*3 或4*4均可.
为保证所表示的矩阵为 方阵,如果在同一矩阵 中既表示姿态又表示位 置,那么可在矩阵中加 入比例因子使之成为4*4 矩阵。
nx ox ax px
F
n
y
oy
ay
p
y
nz 0
oz 0
az 0
pz 1
2
变换可定义为空间的一个运动。 已知一直角坐标系中的某点坐标,那么该点在另一直角坐标系中的 坐标可通过齐次坐标变换来求得。 变换可分为如下形式:
纯平移 纯旋转 平移与旋转的结合
3
❖ 1.平移的齐次变换
❖ 空间某一点在直角坐标系中的平移,由 A(x, y, z)平移至A′(x′, y′, z′), 即
x' x x y' y y z' z z
x' 1 0 0 x x
y'
0
1
0
y
y
z' 0 0 1 z z
1
0 0 0
1
1
a′=Trans(Δx, Δy, Δz)a
4
平移算子
1 0 0 x
Trans(x, y, z) 0 1 0 y 0 0 1 z
0 0 0
1
❖ ① 算子左乘: 表示点的平移是相对固定坐标系进行的坐标变换。
若手臂绕Z0轴旋转90°,则手臂 到达G2;若手臂不动,仅手部绕 手腕Z1轴转90°,则手部到达 G3.写出手部坐标系G2、G3表达 式。
9
10
3.复合齐次变换
复合变换是由固 定参考坐标系或 当前运动坐标系 的一系列沿轴平 移和绕轴旋转变 换所组成的。任 何变换都可以分 解为按一定顺序 的一组平移和旋 转变换。
x' x cos y sin
y'
x
sin
y
c os
z' z
x' cos sin 0 0 x
y'
sin
cos
0
0
y
z' 0
0 1 0 z
1
0
0
0
1
1
记为: a′=Rot(z, θ)a
7
旋转算子
绕Z轴旋转算子内容为:
cos sin 0 0
Rot(z,
)
sin
0
cos
0
0 0 1 0
0 1 0 1
A
1 0
0 0
0 1 1 1
0
0
0 1
0 1 0 0
A' 1 0 0 3 0 0 1 3
0
0
0 1
6
0 1 0 1
A'' 1 0
0
2
0 0 1 1
0
0
0
1
❖ 2.旋转的齐次变换
❖ 点在空间直角坐标系中的旋转如图所示。A(x, y, z)绕Z轴旋 转θ角后至A’(x’, y’, z’),则A与A’之间的关系为 :
对于给定的坐标系{A}、{B}、{C},已知{B}相对 {A}的描述为 ABT ,{C}相对{B}的描述为 CBT ,则
B pCBT Cp
A p ABT Bp ABT CBT Cp
从而定义复合变换
。
CAT ABT CBT
表示{C}相对于{A}的描述,是两变换矩阵的乘积。
注意:变换矩阵相乘不满足“交换律”,变换矩阵的左乘 和右乘的运动解释不同。
