(结构动力学)运动方程的建立
结构动力学第二章 运动方程的建立

h—框架结构的高度 E—弹性模量 Ib和Ic—梁和柱的截面惯性矩
ρ→∞:
k
24EIc h3
ρ→0
:
k
6EIc h3
2.1 基本动力体系
3. 阻尼力(Damping Force)
阻尼:引起结构能量的耗散,使结构振幅逐渐变小的一种作用 阻尼来源(物理机制): (1)固体材料变形时的内摩擦,或材料快速应变引起的热耗散; (2)结构连接部位的摩擦,结构构件与非结构构件之间的摩擦; (3)结构周围外部介质引起的阻尼。例如,空气、流体等。
非保守力做功的变分等于0。
t2 (T V )dt t2 Wncdt 0
t1
t1
Wnc Pncju j
j
其中:
T —— 体系的总动能; V —— 体系的位能,包括应变能及任何保守力的势能; Wnc—— 作用于体系上非保守力(包括阻尼力及任意外荷载)所做的功; δ —— 指(在指定时间段内)所取的变分。
p(t) fI fD fs 0 fI mu fD cu fs ku
mu cu ku p(t)
图2.8 单质点体系的受力分析
2.2 运动方程的建立
3. 虚位移原理
虚位移原理的优点:虚位移原理是建立在对虚功分析的基础之 上,而虚功是一个标量,可以按代数方式运算,因 而比Newton第二定律,或D’Alembert原理中需要采 用的矢量运算更简便。
对如下图所示结构体系,用虚位移原理建立方程更简便一些
2.2 运动方程的建立
4. Hamilton原理
应用变分法来建立结构体系的运动方程。 动力学中广泛应用的变分法是Hamilton原理 体系的平衡位置是体系的稳定位置,在稳定位置,体系的能量取得极值, 一般是极小值。
结构动力学填空简答

一、填空题1、消能减震技术包括:速度相关型消能减震装置,位移相关型消能减震装置,其他相关型消能减震装置2、调频减震技术包括:有调谐质量阻尼器(TMD)和调谐液体阻尼器(TLD)、调谐液柱式阻尼器(TLCD)振动控制系统3、地震动三要素:振幅、频谱、持时4、结构的固有特性:频率、振型,阻尼5、实验测量阻尼比的方法:对数衰减率法、共振放大法、半功率法6、逐步积分法的四个标准:收敛性、计算精度、稳定性、计算效率7、结构离散化方法:集中质量法、广义坐标法、有限元法8、基本力学原理及运动方程的建立:D'Alembert原理、虚功原理、哈密顿原理、拉格朗日方程、牛顿定理9、结构抗震试验方法:伪静力试验方法或低周反复加载、地震模拟振动台试验方法、伪动力试验方法或计算机联机试验10、等效阻尼比用在:等效线性化分析过程中11、常用的阻尼有:粘性阻尼、摩擦阻尼、滞变阻尼、流体阻尼12、测量振动量的仪器:加速度计、位移计、速度计13、单自由度体系对任意荷载的反应分析方法:时域分析法(杜哈梅积分计算)、频域分析法(傅里叶变换法计算)——适用于处理线弹性结构的动力反应问题14、常用的时域逐步积分法有:分段解析法、中心差分法、平均常加速度法、线性加速度法、Newmark-β法、Wilson—θ法15、常用的恢复力模型:当伯格-奥斯左德模型、克拉夫退化双线性模型、武田模型16、振型的归一化方法:特定坐标的归一化方法、最大位移的归一化方法、正交归一法17、恢复力曲线模型三个组成部分:骨架曲线、滞回特性、刚度退化规律18、确定恢复力曲线的方法:试验拟合法、系统识别法、理论计算法二、简答题1。
结构动力学的广义研究内容、目的是什么?内容:结构动力学是研究结构体系的动力特性几起在动力荷载作用下的动力反应分析原理和方法的一门理论和技术学科目的:是确定动力荷载作用下结构的内力和变形,并通过动力分析确定结构的动力特性,为改善工程结构体系在动力环境中的安全性和可靠性提供坚实的理论基础。
结构动力学第二章

∂T ∂V d ∂T ( )− + = Pncj (t ), & dt ∂u j ∂u j ∂u j
其中: T —— 体系的动能;
j = 1,2,L , N
V —— 体系的位能,包括应变能及任何保守力的势能; Pncj ——与 uj 相应的非保守力(包括阻尼力及任意外荷载)。
– 红色部分为引入动力自由度概念的目的,蓝色部分为实 现此目的的手段。 – 概念中的“全部”、“独立”两个条件非常关键。
• 严格来说,所以结构体系质量都是连续分布的,为无限自 由度体系,研究比较困难。但许多情况下,可以作一定的 简化,变为有限自由度体系。 • 简化并确定结构动力自由度最典型的方法:集中质量法
动能
1 & mu 2 转动质量 2
T =
1 &2 Jθ 2
1 2 V = ku 转动弹簧 2
1 &2 V = kθ θ 2
位能
1 1 & & &j T = ∑ ∑ mij u i u j = ∑ m j u 2 2 i j 2 j
V =
1 ∑ ∑ kij ui u j 2 i j
∫
1 体系的动能:T = mu 2 & 2
粘滞(性)阻尼力可表示为:
& f D = -cu
D — 表示阻尼(damping) c — 阻尼系数(Damping coefficient)
k c
u m
f S(t) m f D(t) f I (t)
& u — 质点的运动速度
阻尼系数 c 的确定:
• 不能像结构刚度 k 那样可通过结构几何尺寸、构件尺寸等 来获得,因为 c 是反映了多种耗能因素综合影响的系数, 阻尼系数一般是通过结构原型振动试验的方法得到。 • 粘性(滞)阻尼理论仅是多种阻尼中最为简单的一种。 • 其它常用的阻尼:
结构动力学单

m
罗健
结构动力学
北京建筑工程学院 结构力学教研室
例题
求图示体系的自振频率。
m
l m EI
EI
l/2
2EI
l
l
罗健
结构动力学
北京建筑工程学院 结构力学教研室
例题
求图示体系的自振频率。 m EI1=∞
EI=C EI m
l
EI
刚度系数计算方法
— 利用位移基本体系
l
罗健
l
l
结构动力学
北京建筑工程学院 结构力学教研室
上面方程可写成
(t ) y(t ) 0 y
2
罗健
结构动力学
北京建筑工程学院 结构力学教研室
⑵、柔度法
由达朗伯尔原理,质点m在t时刻的位移y(t)可以看成是t 时刻的惯性力引起的(瞬时)静位移,可将其写成: y(t)
m
FI
1
y(t ) 11 FI (t ) (t )) 11 (m y
2
罗健
结构动力学
北京建筑 (小阻尼)情况:
1,2 i 1 2
令: d 1 2
称为有阻尼自振频率。
y(t ) et (C1 cos d t C2 sin d t )
由初始条件确定任意常数C1和C2: 设 t=0 时,
结构动力学
北京建筑工程学院 结构力学教研室
3.3 有阻尼体系的自由振动 无阻尼自由振动总是以动能和势能交换为特征, 没有考虑结构体系的能量耗散,即结构体系的振动过 程中总能量保持不变。 与能量大小有关的振幅始终保持不变,永不衰减。 但在实际中,任一振动过程随时间的推移,振幅总 是逐渐衰减额,最终消失。质量m静止在静力平衡位置 这种振幅随时间而减少的振动称为阻尼振动。
刘晶波结构动力学课件21w

—最简单的理想化力学模型。
阻尼弹性体系:当线弹性系统中进一步考虑阻尼 影响时
15/45
2.1 基本概念
阻尼系数 c 的确定: 不能像结构刚度k那样可通过结构几何尺寸、构件尺寸和
材料的力学性质等来获得,因为c是反映了多种耗能因 素综合影响的系数,阻尼系数一般是通过结构原型振 动试验的方法得到。 粘性(滞)阻尼理论仅是多种阻尼中最为简单的一种。 其它常用的阻尼: 摩擦阻尼:阻尼力大小与速度大小无关,一般为常数; 滞变阻尼:阻尼力大小与位移成正比(相位与速度相同); 流体阻尼:阻尼力与质点速度的平方成正比。
方向指向体系的平衡位置。
fs ku
fs
k
1
a
d
-u0
O
b
u u0
fs k
1
u
s— 表示弹簧(Spring)
c
(a)
k— 弹簧的刚度(Spring Stiffness)
u— 质点位移
(b)
11/45
2.1 基本概念
2.1.5 惯性力(Inertial Force)
惯性:保持物体运动状态的能力。 惯性力:大小等于物体的质量与加速度的乘积,
动力自由度的定义:结构体系在任意瞬时的一切可能的 变形中,决定全部质量位置所需的独立参数的数目称 为结构的动力自由度(数)。
4/45
2.1.1 广义坐标与动力自由度
静力自由度:确定结构体系在空间中位置所需的独立参 数的数目称为结构的自由度。
动力自由度:决定结构体系质量位置所需的独立参数的 数目称为结构的动力自由度(数)。
结构动力学
教师:刘晶波 助教:王东洋
清华大学土木工程系 2015年秋
【结构动力学】第1章 运动方程 2020

承受动力荷载的任何线性结构体系的主要物理特性是体系的质量、弹 性特性(刚度或柔度)、能量耗散机理或阻尼、以及外部扰力或荷载
单自由度
c
体系模型
k
y (t )
F(t) m
▪ 质量块m,用来表示结构的质量和惯性特性 ▪ 自由度只有一个:水平位移 y(t) ▪ 无重弹簧,刚度为 k,提供结构的弹性恢复力 ▪ 无重阻尼器,阻尼系数c,表示结构的能量耗散,提供结
y P (FI FD )
改写成:
FI
FD
1
y
P
28
位移方程:
FI
FD
1
y
P
其中:
p为动荷载 q(t) 引起的质量沿y方向的位移:
q (t)y(t )
P
5l 4 384 EI
q(t )
惯性力: FI my 阻尼力: FD cy
为自由度方向加单位力所引起的位移,即柔度: 由此得到体系的运动方程:
my cy ky F(t) (2-3)
y(t )
EI l 1
my
cy
12EI
l13
12EI l23
y
FP (t)
12EI 12EI
令: k FS1 FS 2 l13 l23
;k 为(等效)刚度系数。
由此得到体系的运动方程: my cy ky FP (t)
运动方程与(2-3)的形式是一样的!
my cy ky F(t)
(2-3)
14
直接平衡法(达朗贝尔原理)
直接平衡法,又称动静法,将动力学问题转化为任 一时刻的静力学问题:根据达朗贝尔原理,把惯性 力作为附加的虚拟力,并考虑阻尼力、弹性力和作 用在结构上的外荷载,使体系处于动力平衡条件, 按照静力学中建立平衡方程的思路,直接写出运动 方程。
结构动力学-14
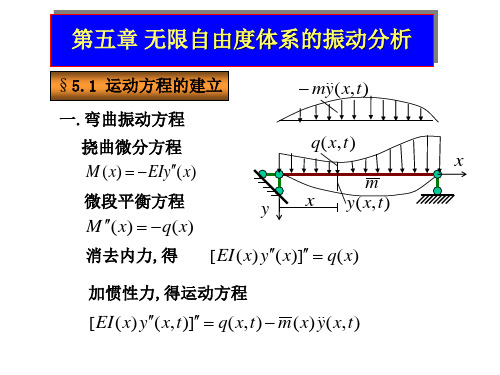
M MD Q 0 EIy(4) cb y (4)I q(x,t) ca y my
EIy(4) cb y (4)I q(x,t) ca y my
2.滞变阻尼 不计阻尼时 计阻尼时
EIy(4) q(x,t) my(x,t)
(1 i )EIy(4) q(x,t) my(x,t)
二.考虑轴力对弯曲的影响时的弯曲振动方程
Fy 0
dQ q(x) dx
M 0
dM Q N dy
dx
dx
y
Q dM N dy dx dx
dQ M (x) Ny(x)
N
dx
M (x) Ny(x) q(x)
q( x, t )
N
m
x
y( x, t )
dx
y
M
dy N
M dM
M (x) EIy(x) [EI (x) y(x)] q(x) Ny
习题:1.求剪切杆的运动方程。 2.求拉压杆的运动方程。
x
x
q( x, t )
ml GA
y
q( x, t )
m EA
l
A
m/A
mI
m
A
I
mr 2
dA A
zdA1
3.运动方程
Fy 0
(x, t)mr 2
M
my(x,t) q( x, t )
dQ q(x,t) my(x,Q
dM Q mr2(x,t)
dx
4.物理方程
M EI Q kGA
5.方程整理 几何方程: dy
dx
物理方程: M EI Q kGA
运动方程: dQ q(x,t) my(x,t) dx dM Q mr2(x,t)
结构动力学-多自由度系统振动

k 2k
y1 y2
0 0
m
M
0
0
k
m, K k
k
2k
解:①由频率方程求固有频率
K 2M 0 k m2
k 0
k 2k m2
展开上式得:(k m2 )(2k m2 ) k 2 0
2 1, 2
3k m
9k 2m2 4k 2m2 2m2
1 0.62
k, m
2 1.62
M20 0
M 21
y2 0
M1y1
M11
列力平衡方程为:M11 M1y1 0 M11 M1 M 21 0, M 31 0
同样的分析可以求得:M12 0, M 22 M 2 , M 23 0; M13 0, M 23 0, M 33 M 3;
所以,得到质量矩阵为: M1 0 0
k2
k3
P
p1 (t) p2 (t)
二、柔度矩阵法 用柔度矩阵法或者刚度矩阵建立方程本质上也是基于力的 动平衡来建立方程,关键在于求柔度系数或刚度系数。
例题 3-2 梁的跨长为 l ,梁上有两个集中质量 M1 和 M 2 ,分别受 到集中力 p1 (t) 和 p2 (t) 的作用。不计梁自身的质量和阻尼,建立 系统的垂向振动方程.
上面的方程为惯性解耦,刚度耦合方程。
kij 的物理意义:j 坐标发生单位位移,其余坐标位移全部为
零时, i 坐标引起的恢复力。
mij 的物理意义:仅在 j 坐标发生单位加速度时,在第 i 坐标所产生 的惯性力.
用柔度矩阵法建立的一般方程:
Y (P MY)
两边同乘以 1
1Y 1(P MY)
例题:针对下图给出的系统,建立振动微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2 (T V )dt t2 Wncdt 0
t1
t1
对上式中的第一项进行分部积分
t2 muudt t1
t2 mu( d u)dt
t1
dt
t2 mu d (u)dt t1 dt
t2 t1
mud(u)
muu
t2 t1
t2 muudt t2 muudt
分析单自由度体系的意义: 第一,单自由度系统包括了结构动力分析中涉及的所有物理量及基本概念。 第二,很多实际的动力问题可以直接按单自由度体系进行分析计算。
图2.1 结构动力分析中常用的单自由度体系力学模型
2.1 基本动力体系
(a)单层框架结构 (b)弹簧―质点体系
两个典型的单自由度体系
物理元件:
集中质量 m 阻尼系数 c 弹簧刚度 k
结构动力学
(2010)
结构动力学
第二章 运动方程的建立
运动方程:描述结构中力与位移关系的数学表达式 (有时称动力方程)
运动方程是进行结构动力分析的基础 运动方程的建立是结构动力学的重点,也是难点
2.1 基本动力体系
单自由度体系:SDOF(Single-Degree-of-Freedom-System) 结构的运动状态仅需要一个几何参数即可以确定
两个力学模型完全等效
两个体系的运动方程相同
2.1 基本动力体系
1. 惯性力(Inertial Force)
惯性:保持物体运动状态的能力 惯性力: 大小等于物体的质量与加速度的乘积,
方向与加速度的方向相反。
fI mu
I — 惯性(Inertial); m— 质量(mass) ; ü — 质点的加速度。
p(t) fI fD fs 0
图2.8 单质点体系的受力分析
fI mu fD cu fs ku
mu cu ku p(t)
2.2 运动方程的建立
3. 虚位移原理
虚位移原理的优点:虚位移原理是建立在对虚功分析的基础之上,而虚功是 一个标量,可以按代数方式运算,因而比Newton第二定 律,或D’Alembert原理中需要采用的矢量运算更简便。
滞变阻尼——时滞阻尼——复阻尼
2.1 基本动力体系 4. 线弹性体系和粘弹性体系 (Linearly Elastic System and Viscous Elastic System)
线弹性体系:由线性弹簧(或线性构件)组成的体系。 —最简单的理想化力学模型。
粘弹性体系:当线弹性系统中进一步考虑阻尼的影响时的体系。 —结构动力分析中的最基本力学模型。
2.1 基本动力体系 5. 非弹性体系 (Inelastic System)
结构构件的力—变形关系为非线性关系,结构刚度不再为常数 构件(或弹簧)的恢复力可表示为
fs fs(u ,u)
fs是位移和速度的非线性函数。
图2.6 非弹性体系中结构构件的力与位移关系
2.2 运动方程的建立
1. 利用牛顿(Newton)第二定律
,
j 1, 2, , N
T —— 体系的动能;
V —— 体系的位能,包括应变能及任何保守力的势能;
Pncj——与uj相应的非保守力(包括阻尼力及任意外荷载)。
用 Hamilton 原理推导 Lagrange 方程
2.2 运动方程的建立
对于有 N 个自由度的结构体系,体系的动能和位能分别为: T T (u1,u2 ,u N ,u1,u2 ,u N )
t2 T t1 u j
d dt
(u
j
)
dt
t2 t1
T u j
d (u
j)
(g)
|
T u j
u j
t2 t1
t2 t1
d dt
(
T u j
)u
j
dt
t2 t1
d dt
(
T u j
)u
j
dt
式(g)代入式(f)得:
N j
t2
(
t1
d dt
F ma
图2.7单质点体系的受力分析
F p(t) fD fs ma fD fs p(t)
a u
fD cu
fs ku
mu cu ku p(t)
单质点体系运动时要满足的控制方程—运动方程
2.2 运动方程的建立 利用牛顿第二定律的优点: 牛顿第二定律是基于物理学中已有知识的直接应用 以人们最容易接受的知识建立体系的运动方程
2.1 基本动力体系
2. 弹簧的恢复力(Resisting Force of Spring)
对弹性体系,弹簧的恢复力也被称为弹性恢复力 弹性恢复力:大小等于弹簧刚度与位移(弹簧变形)的乘积,
方向指向体系的平衡位置。
fs ku
s— 表示弹簧(Spring) k— 弹簧的刚度(Spring Stiffness) u— 质点位移
D’Alembert原理的贡献:建立了动力平衡概念
2.2 运动方程的建立
3. 虚位移原理
虚位移原理:在一组外力作用下的平衡系统发生一个虚位移时,外力在 虚位移上所做的虚功总和恒等于零。
虚位移是指满足体系约束条件的无限小位移。
设体系发生一个虚位移δ u
平衡力系在δ u 上做的总虚功为:
p(t)u fIu fDu fsu 0
t2 t1
N j
( T u j
V u j
Pncj )u j dt
N j
t2 t1
T u j
u j dt
0
(f)
对式(f)的第二项进行分部积分:
t2 t1
T u j
u
j dt
t2 t1
T u j
( du j dt
)dt
2.1 基本动力体系
阻尼系数c 的确定: 不能像结构刚度k那样可通过结构几何尺寸、构件尺寸等来获得, 因为c是反映了多种耗能因素综合影响的系数,阻尼系数一般是
通过结构原型振动试验的方法得到。
粘滞(性)阻尼理论仅是多种阻尼中最为简单的一种。
其它常用的阻尼: 摩擦阻尼:阻尼力大小与速度大小无关,一般为常数 ; 滞变阻尼:阻尼力大小与位移成正比(相位与速度相同); 流体阻尼:阻尼力与质点速度的平方成正比 。
2.2 运动方程的建立
4. Hamilton原理(积分形式的动力问题的变分方法)
Hamilton原理的优点:不明显使用惯性力和弹性力,而分别用 对动能和位能的变分代替。因而对这两项来讲,仅涉及处理 纯的标量,即能量。
而在虚位移中,尽管虚功本身是标量,但用来计算虚功的力和 虚位移则都是矢量。
动能:集中质量 T 1 mu2
2
转动质量
T 1 J2 2
位能:拉伸弹簧
V 1 ku2 2
转动弹簧
V
1 2
k 2
: 动能 位能 多自由度体系
T1 2i
j
mijuiu j
1 2
j
m ju j 2
V1 2i
kijuiu j
j
2.2 运动方程的建立
4. Hamilton原理(用Hamilton原理建立单自由度弹簧-质量体系的运动方程)
非保守力做功的变分等于0。
t2 (T V )dt t1
t2 t1
Wncdt
0
Wnc Pncju j
j
其中:
T —— 体系的总动能;
V —— 体系的位能,包括应变能及任何保守力的势能;
Wnc—— 作用于体系上非保守力(包括阻尼力及任意外荷载)所做的功; δ —— 指(在指定时间段内)所取的变分。
d dt
(
T u j
)
T u j
V u j
Pncj (t)
,
j 1, 2, , N
V
N j
V u j
u
j
(d)
同时,非保守力所做功的变分为:
N
Wnc Pncju j
(e)
j
将式(c)、(d)和(e)代入 Hamilton 原理式(2.11)得:
(1)固体材料变形时的内摩擦,或材料快速应变引起的热耗散; (2)结构连接部位的摩擦,结构构件与非结构构件之间的摩擦; (3)结构周围外部介质引起的阻尼。例如,空气、流体等。
粘滞(性)阻尼力可表示为:
fD cu
D — 阻尼(damping) c — 阻尼系数(Damping coefficient) ù — 质点的运动速度
2.1 基本动力体系
单层框架结构的水平刚度
k
24EI c h3
3 3
1 4
Ib /Ic
h—框架结构的高度 E—弹性模量 Ib和Ic—梁和柱的截面惯性矩
ρ
→∞:
k
24EI c h3
ρ
→0
:
k
6EI c h3
2.1 基本动力体系
3. 阻尼力(Damping Force)
阻尼:引起结构能量的耗散,使结构振幅骤渐变小的一种作用 阻尼来源(物理机制):
5.运动的Lagrange方程
用Lagrange方程方程建立体系的运动方程
体系的动能:T 1 mu2 体系的位能:V p(t)
因此,
d dt
(
T u
)
d dt
(mu)
mu
T 0 u
V ku u
代入Lagrange方程:
d dt
