利用导数求切线方程
求切线方程的三种方法
求切线方程的三种方法宝子们，今天咱们来唠唠求切线方程的那些事儿。
这切线方程啊，就像是给曲线找到一个最亲密接触的直线小伙伴，可有意思啦。
一、利用导数求切线方程。
咱先说说这个用导数的方法。
导数这玩意儿啊，其实就是曲线在某一点的斜率。
比如说有个函数y = f(x)，咱们先求出它的导数f'(x)。
那在某一点x = a处的切线斜率k呢，就等于f'(a)。
这时候啊，我们已经知道了斜率，再知道这个点(a, f(a))在切线上，就可以用点斜式y - y₁ = k(x - x₁)来求出切线方程啦。
就像你知道一个朋友的走路速度（斜率），又知道他从哪个地方（点）出发，就能算出他走的路线（切线方程）啦。
二、设切点法。
再来说说设切点法。
有时候啊，题目没有直接告诉你切点是啥。
这时候咱就可以聪明点，设切点为(x₀, y₀)。
那这个点既在曲线上又在切线上哦。
如果曲线方程是y = f(x)，那y₀ = f(x₀)。
然后呢，求出函数在x₀处的导数f'(x₀)，这就是切线的斜率啦。
再根据点斜式写出切线方程y - y₀ = f'(x₀)(x - x₀)。
这就像是在玩一个猜谜游戏，我们先假设一个神秘的点（切点），然后通过各种线索（曲线方程和导数）来找出这个切线方程这个宝藏呢。
三、利用已知切线方程的形式来求。
还有一种方法呢，就是利用已知切线方程的形式。
比如说对于圆的方程(x - a)²+(y - b)² = r²，在点(x₁, y₁)处的切线方程是(x₁ - a)(x - a)+(y₁ - b)(y - b)= r²。
对于椭圆、双曲线等一些特殊的曲线也有类似的固定形式的切线方程哦。
这就像是有个小秘籍一样，直接套用这个形式就能求出切线方程啦。
就好比你有一把万能钥匙，遇到特定的锁（特殊曲线在某点的切线），直接一插就能打开（求出切线方程）啦。
宝子们，这三种求切线方程的方法是不是很有趣呀？只要多练练，你就能在求切线方程这个小天地里畅游无阻啦。
(完整版)利用导数求曲线的切线和公切线
利用导数求曲线的切线和公切线一.求切线方程【例1】.已知曲线f(x)=x3-2x2+1.(1)求在点P（1,0）处的切线l1的方程；(2)求过点Q（2,1）与已知曲线f(x)相切的直线l2的方程.提醒：注意是在某个点处还是过某个点！二.有关切线的条数【例2】．（2014•北京）已知函数f（x）=2x3﹣3x．（Ⅰ）求f（x）在区间[﹣2，1]上的最大值；（Ⅱ）若过点P（1，t）存在3条直线与曲线y=f（x）相切，求t的取值范围；（Ⅲ）问过点A（﹣1，2），B（2，10），C（0，2）分别存在几条直线与曲线y=f（x）相切？（只需写出结论）【解答】解：（Ⅰ）由f（x）=2x3﹣3x得f′（x）=6x2﹣3，令f′（x）=0得，x=﹣或x=，∵f（﹣2）=﹣10，f（﹣）=，f（）=﹣，f（1）=﹣1，∴f（x）在区间[﹣2，1]上的最大值为．（Ⅱ）设过点P（1，t）的直线与曲线y=f（x）相切于点（x0，y），则y0=2﹣3x，且切线斜率为k=6﹣3，∴切线方程为y﹣y0=（6﹣3）（x﹣x），∴t﹣y0=（6﹣3）（1﹣x），即4﹣6+t+3=0，设g（x）=4x3﹣6x2+t+3，则“过点P（1，t）存在3条直线与曲线y=f（x）相切”，等价于“g（x）有3个不同的零点”．∵g′（x）=12x2﹣12x=12x（x﹣1），∴g（0）=t+3是g（x）的极大值，g（1）=t+1是g（x）的极小值．∴g（0）＞0且g（1）＜0，即﹣3＜t＜﹣1，∴当过点过点P（1，t）存在3条直线与曲线y=f（x）相切时，t的取值范围是（﹣3，﹣1）．（Ⅲ）过点A（﹣1，2）存在3条直线与曲线y=f（x）相切；过点B（2，10）存在2条直线与曲线y=f（x）相切；过点C（0，2）存在1条直线与曲线y=f（x）相切．【例3】．已知函数f（x）=lnax（a≠0，a∈R），．（Ⅰ）当a=3时，解关于x的不等式：1+e f（x）+g（x）＞0；（Ⅱ）若f（x）≥g（x）（x≥1）恒成立，求实数a的取值范围；（Ⅲ）当a=1时，记h（x）=f（x）﹣g（x），过点（1，﹣1）是否存在函数y=h（x）图象的切线？若存在，有多少条？若不存在，说明理由．【解答】解：（I）当a=3时，原不等式可化为：1+e ln3x+＞0；等价于，解得x，故解集为（Ⅱ）∵对x≥1恒成立，所以，令，可得h（x）在区间[1，+∞）上单调递减，故h（x）在x=1处取到最大值，故lna≥h（1）=0，可得a=1，故a的取值范围为：[1，+∞）（Ⅲ）假设存在这样的切线，设切点T（x，），∴切线方程：y+1=，将点T坐标代入得：即，①设g（x）=，则∵x＞0，∴g（x）在区间（0，1），（2，+∞）上是增函数，在区间（1，2）上是减函数，故g（x）极大=g（1）=1＞0，故g（x）极，小=g（2）=ln2+＞0，．又g（）=+12﹣6﹣1=﹣ln4﹣3＜0，由g（x）在其定义域上的单调性知：g（x）=0仅在（，1）内有且仅有一根，方程①有且仅有一解，故符合条件的切线有且仅有一条．【作业1】．（2017•莆田一模）已知函数f （x ）=2x 3﹣3x+1，g （x ）=kx+1﹣lnx ． （1）设函数，当k ＜0时，讨论h （x ）零点的个数；三.切线与切线之间的关系 【例4】．（2018•绵阳模拟）已知a ，b ，c ∈R ，且满足b 2+c 2=1，如果存在两条互相垂直的直线与函数f （x ）=ax+bcosx+csinx 的图象都相切，则a+c的取值范围是 .23a b c ++=则23b c +，∵b 2+c 2=1，∴sin ,cos b a ββ==设，∴235sin()b c βϕ+=+，故a+c ∈[﹣，]，【例5】.已知函数f （x ）=lnx ﹣a （x ﹣1），g （x ）=e x ，其中e 为自然对数的底数． （Ⅰ）设，求函数t （x ）在[m ，m+1]（m ＞0）上的最小值；（Ⅱ）过原点分别作曲线y=f （x ）与y=g （x ）的切线l 1，l 2，已知两切线的斜率互为倒数，求证：a=0或．【解答】（Ⅰ）解：，令t'（x）＞0得x＞1，令t'（x）＜0得x＜1，所以，函数t（x）在（0，1）上是减函数，在（1，+∞）上是增函数，∴当m≥1时，t（x）在[m，m+1]（m＞0）上是增函数，∴当0＜m＜1时，函数t（x）在[m，1]上是减函数，在[1，m+1]上是增函数，∴t（x）min=t（1）=e．（Ⅱ）设l2的方程为y=k2x，切点为（x2，y2），则，∴x2=1，y2=e∴k2=e．由题意知，切线l1的斜率，∴切线l1的方程为，设l1与曲线y=f（x）的切点为（x1，y1），∴，∴，，又y1=lnx1﹣a（x1﹣1），消去y1，a后整理得，令，则，∴m（x）在（0，1）上单调递减，在（1，+∞）上单调递增，若x1∈（0，1），∵，，∴，而，在单调递减，∴．若x1∈（1，+∞），∵m（x）在（1，+∞）上单调递增，且m（e）=0，∴x1=e，∴综上，a=0或．【作业2】．（2017•黄山二模）已知函数f（x）=（ax2+x﹣1）e x+f'（0）．（1）讨论函数f（x）的单调性；（2）若g（x）=e﹣x f（x）+lnx，h（x）=e x，过O（0，0）分别作曲线y=g（x）与y=h（x）的切线l1，l2，且l1与l2关于x轴对称，求证：﹣＜a ＜﹣．四．求公切线的方程【例6】．（2018•安阳一模）已知函数，g（x）=3elnx，其中e为自然对数的底数．（Ⅰ）讨论函数f（x）的单调性．（Ⅱ）试判断曲线y=f（x）与y=g（x）是否存在公共点并且在公共点处有公切线．若存在，求出公切线l的方程；若不存在，请说明理由．【解答】解：（Ⅰ）由，得，令f′（x）=0，得．当且x≠0时，f′（x）＜0；当时，f′（x）＞0．∴f（x）在（﹣∞，0）上单调递减，在上单调递减，在上单调递增；（Ⅱ）假设曲线y=f（x）与y=g（x）存在公共点且在公共点处有公切线，且切点横坐标为x＞0，则，即，其中（2）式即．记h（x）=4x3﹣3e2x﹣e3，x∈（0，+∞），则h'（x）=3（2x+e）（2x﹣e），得h（x ）在上单调递减，在上单调递增，又h（0）=﹣e3，，h（e）=0，故方程h（x0）=0在（0，+∞）上有唯一实数根x=e，经验证也满足（1）式．于是，f（x0）=g（x）=3e，f′（x）=g'（x）=3，曲线y=g（x）与y=g（x）的公切线l的方程为y﹣3e=3（x﹣e），即y=3x．【作业3】．已知函数f （x）=lnx，g（x）=2﹣（x＞0）（1）试判断当f（x）与g（x）的大小关系；（2）试判断曲线 y=f（x）和 y=g（x）是否存在公切线，若存在，求出公切线方程，若不存在，说明理由；（3）试比较（1+1×2）（1+2×3）…（1+2012×2013）与 e4021的大小，并写出判断过程．五.与公切线有关的参数取值范围问题【例7】．已知函数f（x）=blnx，g（x）=ax2﹣x（a∈R）．（Ⅰ）若曲线f（x）与g（x）在公共点A（1，0）处有相同的切线，求实数a、b的值；（Ⅱ）当b=1时，若曲线f（x）与g（x）在公共点P处有相同的切线，求证：点P唯一；（Ⅲ）若a＞0，b=1，且曲线f（x）与g（x）总存在公切线，求正实数a的最小值．【解答】解：（Ⅰ）f′（x）=，g'（x）=2ax﹣1．∵曲线f（x）与g（x）在公共点A（1，0）处有相同的切线，∴，解得a=b=1．（Ⅱ）设P（x0，y），则由题设有lnx=ax2﹣x…①，又在点P有共同的切线，∴f′（x0）=g′（x），∴，∴a=，代入①得lnx0=x，设h（x）=lnx ﹣+x，则h′（x）=+（x＞0），则h′（x）＞0，∴h（x）在（0，+∞）上单调递增，所以 h（x）=0最多只有1个实根，从而，结合（1）可知，满足题设的点P只能是P（1，0）．（Ⅲ）当a＞0，b=1时，f（x）=lnx，f′（x）=，f（x）在点（t，lnt）处的切线方程为y﹣lnt=（x﹣t），即y=x+lnx﹣1．与y=ax2﹣x，联立得ax2﹣（1+）x﹣lnt+1=0．∵曲线f（x）与g（x）总存在公切线，∴关于t（t＞0）的方程△=+4a（lnt﹣1）=0，即=4a（1﹣lnt）（*）总有解．若t＞e，则1﹣lnt＜0，而＞0，显然（*）不成立，所以 0＜t＜e，从而，方程（*）可化为4a=．令H（t）=（0＜t＜e），则H′（t）=．∴当0＜t＜1时，h'（t）＜0；当1＜t＜e时，h'（t）＞0，即 h（t）在（0，1）上单调递减，在（1，e）上单调递增．∴h（t）在（0，e）上的最小值为h（1）=4，∴要使方程（*）有解，只须4a≥4，即a≥1．∴正实数a的最小值为1．【例8】．（2017•韶关模拟）.已知函数f（x）=ae x（a≠0），g（x）=x2（Ⅰ）若曲线c1：y=f（x）与曲线c2：y=g（x）存在公切线，求a最大值．（Ⅱ）当a=1时，F（x）=f（x）﹣bg（x）﹣cx﹣1，且F（2）=0，若F（x）在（0，2）内有零点，求实数b的取值范围．【解答】解：（Ⅰ）设公切线l与c1切于点（x1，a）与c2切于点（x2，），∵f′（x）=ae x，g′（x）=2x，∴，由①知x2≠0，①代入②：=2x2，即x2=2x1﹣2，由①知a=，设g（x）=，g′（x）=，令g′（x）=0，得x=2；当x＜2时g′（x）＞0，g（x）递增．当x＞2时，g′（x）＜0，g（x）递减．∴x=2时，g（x）max =g（2）=，∴amax=．（Ⅱ）F（x）=f（x）﹣bg（x）﹣cx﹣1=e x﹣bx2﹣cx﹣1，∵F（2）=0=F（0），又F（x）在（0，2）内有零点，∴F（x）在（0，2）至少有两个极值点，即F′（x）=e x﹣2bx﹣c在（0，2）内至少有两个零点．∵F″（x）=e x﹣2b，F（2）=e2﹣4b﹣2c﹣1=0，c=，①当b≤时，在（0，2）上，e x＞e0=1≥2b，F″（x）＞0，∴F″（x）在（0，2）上单调增，F′（x）没有两个零点．②当b≥时，在（0，2）上，e x＜e2≤2b，∴F″（x）＜0，∴F″（x）在（0，2）上单调减，F′（x）没有两个零点；③当＜b＜时，令F″（x）=0，得x=ln2b，因当x＞ln2b时，F″（x）＞0，x＜ln2b时，F″（x）＜0，∴F″（x）在（0，ln2b）递减，（ln2b，2）递增，所以x=ln2b时，∴F′（x）最小=F′（ln2b）=4b﹣2bln2b﹣+，设G（b）=F′（ln2b）=4b﹣2bln2b﹣+，令G′（b）=2﹣2ln2b=0，得2b=e，即b=，当b＜时G′（b）＞0；当b＞时，G′（b）＜0，当b=时，G（b）最大=G（）=e+﹣＜0，∴G（b）=f′（ln2b）＜0恒成立，因F′（x）=e x﹣2bx﹣c在（0，2）内有两个零点，∴，解得：＜b ＜，综上所述，b 的取值范围（，）．【作业4】．已知函数f（x）=a（x ﹣）﹣blnx（a，b∈R），g（x）=x2．（1）若a=1，曲线y=f（x）在点（1，f（1））处的切线与y轴垂直，求b的值；（2）若b=2，试探究函数f（x）与g（x）在其公共点处是否有公切线，若存在，研究a的个数；若不存在，请说明理由．六．公切线的条数问题【例9】．已知函数f（x）=lnx，g（x）=e x．（1）确定方程f（x）=实数根的个数；（2）我们把与两条曲线都相切的直线叫作这两条曲线的公切线，试确定曲线y=f （x），y=g（x）公切线的条数，并证明你的结论．【解答】解：（1）由题意得lnx==1+，即lnx﹣1=．分别作出y=lnx﹣1和y=的函数图象，由图象可知：y=lnx﹣1和y=的函数图象有两个交点，∴方程f（x）=有两个实根；（2）解：曲线y=f（x），y=g（x）公切线的条数是2，证明如下：设公切线与f（x）=lnx，g（x）=e x的切点分别为（m，lnm），（n，e n），m≠n，∵f′（x）=，g′（x）=e x，∴，化简得（m﹣1）lnm=m+1，当m=1时，（m﹣1）lnm=m+1不成立；当m≠1时，（m﹣1）lnm=m+1化为lnm=，由（1）可知，方程lnm=有两个实根，∴曲线y=f（x），y=g（x）公切线的条数是2条．【作业5】．已知函数f（x）=x2+2（1﹣a）x﹣4a，g（x）=﹣（a+1）2，则f （x）和g（x）图象的公切线条数的可能值是．【作业1解答】解：（1）f′（x）=（2x+1）（x﹣1）2=0，x=﹣或1，∴x=﹣是h（x）的零点；∵g′（x）=k﹣，k＜0，g′（x）＜0，g（x）在[1，+∞）上单调递减，g（x）的最大值为g（1）=k+1．k＜﹣1，g（1）＜0，g（x）在[1，+∞）上无零点；k=﹣1，g（1）=0，g（x）在[1，+∞）上有1个零点；﹣1＜k＜0，g（1）＞0，g（e1﹣k）=ke1﹣k+k＜0，g（x）在[1，+∞）上有1个零点；综上所述，k＜﹣1时，h（x）有1个零点；﹣1≤k＜0时，h（x）有两个零点；（2）设切点（t，f（t）），f′（x）=6x2﹣6x，∴切线斜率f′（t）=6t2﹣6t，∴切线方程为y﹣f（t）=（6t2﹣6t）（x﹣t），∵切线过P（a，﹣4），∴﹣4﹣f（t）=（6t2﹣6t）（a﹣t），∴4t3﹣3t2﹣6t2a+6ta﹣5=0①由题意，方程①有3个不同的解．令H（t）=4t3﹣3t2﹣6t2a+6ta﹣5，则H′（t）=12t2﹣6t﹣12at+6a=0．t=或a．a=时，H′（t）≥0，H（t）在定义域内单调递增，H（t）不可能有两个零点，方程①不可能有两个解，不满足题意；a时，在（﹣），（a，+∞）上，H′（t）＞0，函数单调递增，在（，a）上，H′（t）＜0，函数单调递减，H（t）的极大值为H（），极小值为H （a）；a时，在（﹣∞，a），（，+∞）上，H′（t）＞0，函数单调递增，在（a，）上，H′（t）＜0，函数单调递减，H（t）的极大值为H（a），极小值为H （）；要使方程①有三个不同解，则H（）H（a）＜0，即（2a﹣7）（a+1）（2a2﹣5a+5）＞0，∴a＞或a＜﹣1．【作业2解答】解：由已知得f'（x）=[ax2+（2a+1）x]e x，f'（0）=0，所以f （x）=（ax2+x﹣1）e x．（1）f'（x）=[ax2+（2a+1）x]e x=[x（ax+2a+1）]e x．①若a＞0，当或x＞0时，f'（x）＞0；当时，f'（x）＜0，所以f（x）的单调递增区间为；单调递减区间为．②若a=0，f（x）=（x﹣1）e x，f'（x）=xe x，当x＞0时，f'（x）＞0；当x＜0时，f'（x）＜0，所以f（x）的单调递增区间为（0，+∞）；单调递减区间为（﹣∞，0）．③若，当或x＜0时，f'（x）＜0；当时，f'（x）＞0，所以f（x）的单调递增区间为；单调递减区间为．④若，故f（x）的单调递减区间为（﹣∞，+∞）．⑤若，当或x＞0时，f'（x）＜0；当时，f'（x）＞0，所以f（x）的单调递增区间为；单调递减区间为．当a＞0时，f（x）的单调递增区间为；单调递减区间为．当a=0时，f（x）的单调递增区间为（0，+∞）；单调递减区间为（﹣∞，0）．，当时，f（x）的单调递增区间为；单调递减区间为．当时，f（x）的单调递减区间为（﹣∞，+∞）；当时，f（x）单调递增区间为；单调递减区间为，（0，+∞）；（2）证明：g（x）=e﹣x f（x）+lnx=﹣e﹣x（ax2+x﹣1）e x+lnx=ax2+x﹣1+lnx，设l2的方程为y=k2x，切点为（x2，y2），则，所以x2=1，y2=e，k2=e．由题意知k1=﹣k2=﹣e，所以l1的方程为y=﹣ex，设l1与y=g（x）的切点为（x1，y1），则．又，即，令，在定义域上，u'（x）＞0，所以（0，+∞）上，u（x）是单调递增函数，又，所以，即，令，则，所以，故．【作业3解答】解：（1）证明：设F（x）=f（x）﹣g（x），则F′（x）=﹣，由F'（x）=0，得x=3，当0＜x＜3时，F'（x）＜0，当x＞3时F'（x）＞0，可得F（x）在区间（0，3）单调递减，在区间（3，+∞）单调递增，所以F（x）取得最小值为F（3）=ln3﹣1＞0，∴F（x）＞0，即f（x）＞g（x）；（2）假设曲线f（x）与g（x）有公切线，切点分别为P（x0，lnx）和Q（x1，2﹣）．因为f′（x）=，g′（x）=，所以分别以P（x0，lnx）和Q（x1，2﹣）为切线的切线方程为y=+lnx﹣1，y=+2﹣．令，即2lnx1+﹣（3+ln3）=0．令h（x）=2lnx1+﹣（3+ln3）．所以由h′（x）=﹣=0，得x1=3．显然，当0＜x1＜3时，h'（x）＜0，当x1＞3时，h'（x）＞0，所以h（x）min=ln3﹣1＞0，所以方程2lnx1+﹣（3+ln3）=0无解，故二者没有公切线．所以曲线y=f（x）和y=g（x）不存在公切线；（3）（1+1×2）（1+2×3）•…•（1+2012×2013）＞e4021．理由：由（1）可得lnx＞2﹣（x＞0），可令x=1+n（n+1），可得ln（1+n（n+1））＞2﹣＞2﹣=2﹣3（﹣），则ln（1+1×2）+ln（1+2×3）+…+ln（1+2012×2013）＞2×2012﹣3（1﹣+﹣+…+﹣）=4024﹣3+＞4021．即有（1+1×2）（1+2×3）…（1+2012×2013）＞e4021．【作业4解答】解：（Ⅰ）∵f（x）=x﹣﹣blnx，∴f′（x）=1+﹣，由于曲线y=f（x）在点（1，f（1））处的切线垂直于y轴，故该切线斜率为0，即f′（1）=0，即1+1﹣b=0，∴b=2；（2）假设f（x），g（x）的图象在其公共点（x0，y）处存在公切线，由f（x）=a（x﹣）﹣2lnx，得f′（x）=，g′（x）=2x，由f′（x0）=g′（x），得=2x，即2x3﹣ax2+2x﹣a=0，即（x02+1）（2x﹣a）=0，则x=，又函数的定义域为（0，+∞），当a≤0时，x0=≤0，则f（x），g（x）的图象在其公共点（x，y）处不存在公切线；当a＞0时，令f（）=g（），﹣2ln﹣2=，即=ln，令h（x）=﹣ln（x＞0），h′（x）=x﹣=，则h（x）在（0，2）递减，（2，+∞）递增．且h（2）=﹣＜0，且当x→0时，h（x）→+∞；当x→+∞时，h（x）→+∞，∴h（x）在（0，+∞）有两个零点，∴方程=ln在（0，+∞）解的个数为2．综上：当a≤0时，函数f（x）与g（x）的图象在其公共点处不存在公切线；当a＞0时，函数f（x）与g（x）的图象在其公共点处存在公切线，a的值有2个．在导数的练习中，常见这一类题型：已知含有的一个不等式，以及的一些其他性质，让解不等式或者比较大小。
用导数求切线方程的四种类型
用导数求切线方程的四种类型用导数求切线方程是导数的重要应用之一。
求曲线的切线方程的关键在于求出切点P(x,y)及斜率。
设P(x,y)是曲线y=f(x)上的一点，则以P的切点的切线方程为：y-y=f'(x)(x-x)。
若曲线y=f(x)在点P(x,f(x))的切线平行于y轴（即导数不存在）时，由切线定义知，切线方程为x=x。
下面例析四种常见的类型及解法。
类型一：已知切点，求曲线的切线方程这类题较为简单，只需求出曲线的导数f'(x)，并代入点斜式方程即可。
例如，曲线y=x^3-3x^2+1在点(1,-1)处的切线方程为y-(-1)=-3(x-1)，即y=-3x+2.类型二：已知斜率，求曲线的切线方程这类题可利用斜率求出切点，再用点斜式方程加以解决。
例如，与直线2x-y+4=0平行的抛物线y=x^2的切线方程为2x-y-1=0.类型三：已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法。
例如，求过曲线y=x^3-2x上的点(1,-1)的切线方程。
设想P(x,y)为切点，则切线的斜率为y'|(x=x)=3x^2-2.故所求切线方程为y-(1-2)=(3-2)(x-1)，或5x+4y-1=0.类型四：已知两曲线的交点，求切线方程这类题一般需先求出两曲线在交点处的导数，再代入点斜式方程加以解决。
例如，已知曲线y=x^3-x和y=2x-x^2的交点为(1,0)，求它们在该点的切线方程。
两曲线在交点处的导数分别为1和-1.故所求切线方程为y-(0)=1(x-1)，或y-(0)=-1(x-1)，即y=x-1或y=-x+1.类型四：已知过曲线外一点，求切线方程对于这类问题，我们可以先设定切点，再求解切点，使用待定切点法来解决。
例4：求过点(2,0)且与曲线$y=x/(1+x^2)$相切的直线方程。
解：设P(x,y)为切点，则切线的斜率为$y'=\frac{1-x^2}{(1+x^2)^2}$。
考点49 利用导数求切线方程(讲解)(解析版)
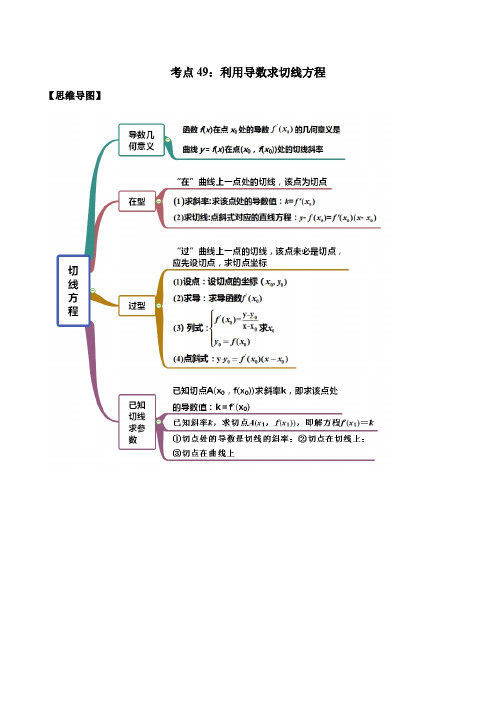
考点49：利用导数求切线方程【思维导图】【常见考法】考点一：求切线的斜率或倾斜角1．曲线1x y xe -=在点（1,1）处切线的斜率等于 . 【答案】2【解析】由1x y xe -=，得，故，故切线的斜率为.2．点P在曲线y =α为曲线在点P 处的切线的倾斜角，则α的取值范围为 . 【答案】2,3ππ⎡⎫⎪⎢⎣⎭【解析】根据题意可知：''1xy e ==+⎝⎭ 则()()()221111'111x xxx e y e e e ⎫+-⎪=-=-⎪+++⎝⎭令()1,0,11x t t e =∈+所以)()2',0,1y t t t =-∈可知)'y ⎡∈⎣ 曲线在点P 处的切线的斜率范围为)⎡⎣，所以)tan α⎡∈⎣故2,3παπ⎡⎫∈⎪⎢⎣⎭3．已知函数()()21,.f x g x xx==若直线l 与曲线()f x ，()g x 都相切，则直线l的斜率为 . 【答案】4-【解析】设直线l 的斜率为k ，则()21'k f x x ==-，解得x =，切点为⎛⎝；且()'2kg x x ==，解得2kx =，切点为2,24k k ⎛⎫⎪⎝⎭； 因为l 与曲线()f x ，()g x 都相切，所以2k k +=，解得4k =-．考法二：在某点处求切线方程1．设曲线3ln(1)y x x =-+ 在点(0,0)处的切线方程_________________. 【答案】20x y -=【解析】由题意，函数3ln(1)y x x =-+的导数为131y x '=-+， 可得曲线3ln(1)y x x =-+在点(0,0)处的切线斜率为312-=，即切线的斜率为2， 则曲线在点(0,0)处的切线方程为02(0)y x -=-，即为2y x =，即20x y -=． 故答案为：20x y -=．2．函数3()2ln 2f x x x =-+的图象在1x =处的切线方程为______________________. 【答案】20x y -+=【解析】由题3(1)12ln123f =-+=,又22'()3f x x x=-,故3()2ln 2f x x x =-+在(1,3)处的斜率为2'(1)311f =-=,故在(1,3)处的切线方程为31(1)20y x x y -=⨯-⇒-+= 故答案为：20x y -+= 3．已知函数()2()1xf x x x e =++，则()f x 在(0, (0))f 处的切线方程为 .【答案】210x y -+=【解析】因为()2()32x f x e x x '=++，所以(0)2f '=，又因为(0)1f =，所以切点为(0)1，， 所以曲线()f x 在(0, (0))f 处的切线方程为210x y -+=.4．已知()()221f x x xf '=+，则曲线()y f x =在点()()00f ，处的切线方程为 .【答案】40x y +=【解析】由题：()()221f x x xf =+'，所以()()'221f x x f +'=，()()'1221f f =+'，所以()'12f =-，所以()24f x x x =-，()24f x x '=-，()00f =，()04f '=-所以切线方程为40x y +=.5．设a 为实数，函数()()322f x x ax a x =++-的导函数是fx ，且fx 是偶函数，则曲线()y f x =在原点处的切线方程为 . 【答案】2y x =-【解析】由()()322f x x ax a x =++-所以()()2'322f x x ax a =++-，又()f x '是偶函数，所以20a =，即0a =所以()2'32f x x =-则()'02f =-，所以曲线()y f x =在原点处的切线方程为2y x =-考法三：过某点求切线方程1．曲线ln y x =过点(0,1)-的切线方程为_________． 【答案】10x y --= 【解析】由题, 1'y x=,设切点为()00,ln x x ,则在切点处的切线斜率为01x ,又切线过点(0,1)-,故0000ln (1)11x x x x --=⇒=.故切点为()1,0. 故切线方程为()101101x y y x -=---=⇒.故答案为：10x y --= 2．求函数()32f x x x x =-+的图象经过原点的切线方程为 . 【答案】0x y -=【解析】由函数()32f x x x x =-+，则()2321f x x x '=-+，所以()01f '=，所以函数()32f x x x x =-+的图象经过原点的切线方程为()010y x -=-，即0x y -=.3．若过原点的直线l 与曲线2ln y x =+相切，则切点的横坐标为 . 【答案】1e【解析】设切点坐标为()00,2ln x x +，由1y x'=，切线方程为00012ln ()y x x x x --=-， 原点坐标代入切线方程，得02ln 1x +=，解得01ex =.4．已知函数()3f x x x =-，则曲线()y f x =过点()1,0的切线条数为 .【答案】2【解析】设切点坐标 3000(,)P x x x -,由()3f x x x =-，得2()31x f x '=-，∴切线斜率2031k x =-，所以过3000(,)P x x x -的切线方程为320000(31)()y x x x x x -+=--，即2300(31)2y x x x =--，切线过点()1,0，故32002310x x -+=，令()32000231h x x x =-+,则()200066h x x x '=-，由()00h x '=，解得00x =或01x =，当0(,0),(2,)x ∈-∞+∞时，()00h x '>，当0(0,2)x ∈时，()00h x '<，所以()0h x 的极大值极小值分别为 h (0)10=>，(1)0h =， 故其图像与x 轴交点2个，也就是切线条数为2.考法四：已知切线求参数1．已知函数()()e xf x x a =+的图象在1x =和1x =-处的切线相互垂直，则a = .【答案】-1 【解析】因为'()(1)xf x x a e =++ ，所以1'(1)(2)'(1)af a e f aee，-=+-==，由题意有(1)'(1)1f f -=- ，所以1a =-.2．已知在曲线()21ax f x x =+在点()()1,1f 处切线的斜率为1，则实数a 的值为 .【答案】43【解析】当0x >时，()()2221ax axf x x +'=+，()11f '=，即314a=，得43a =.. 3．已知函数()ln f x x x ax =+，过点()1,1P 可作两条直线与()f x 的图象相切，则a 的取值范围是 。
用导数求切线方程的四种类型
添加标题
添加标题
添加标题
导数大于0表示函数在对应区间内 单调递增
导数小于0表示函数在对应区间内 单调递减
导数在几何上表导数等于0时，函数可能存在拐点或极值点 导数小于0时，函数在对应区间内单调递减
导数等于切线斜率 导数可以求出切线的斜率
导数在求切线方程中起到关 键作用
添加标题
添加标题
切线与该点处的切线垂直
添加标题
添加标题
切线方程的求解需要用到切点处的 坐标和斜率
确定函数表达式 确定导数表达式 计算导数值 代入切点坐标
代入切点坐标求斜率要细心 切线斜率与函数值大小无关 切线方程的形式要正确 切线方程与函数解析式不同
切线方程的书写格式要正确 切线斜率的计算要准确 切点坐标的选取要合理 切线方程的求解方法要规范
切线斜率：通 过将切点坐标 代入导函数中，
求得斜率为 f'(x0)
切线方程：利 用点斜式方程 y-y0=f'(x0)(xx0)，得到切线
方程
确定函数在某点的导数 利用导数求出该点的切线斜率 根据切线斜率和已知点写出切线方程 验证切线方程是否符合题意
切点是曲线上某一点，在该点处函 数的导数存在
切点处函数值必须为零
汇报人：XX
导数与切线斜率的关系是密 切相关的
切点是曲线上某 一点，在该点处 曲线的切线存在
切点处的导数值 即为切线的斜率
切点坐标由曲线 方程和切线斜率 共同确定
切点是唯一确定 的，但切线方程 可能有多种形式
确定函数表达 式
求导函数
代入切点坐标
计算切线斜率
切点坐标：已 知曲线上的一 个点，记为(x0,
y0)
定义：切线方 程是表示切点 与曲线在某一 点的切线关系
利用导数求切线方程
3
题型二：求曲线过一点的切线方程 例：已知曲线C：f (x) x3 x 2 ，求经
过点 P(1, 2) 的曲线C的切线方程。
思考（1）判断P点 所处的位置？ （2）从图像探究， 过该点有几条切线， 如何印证你的探究
答案：2x-y=0或x+4y-9=0
点P是曲线 y x2 ln x上任意一点，则点P 到直线 y x 2 的最小距离是多少?
T 切线
P
o
x
3.基本初等函数的导数公式
原函数 f(x)=c(c为常数) f(x)=xα(α∈Q*)
f(x)=sinx f(x)=cosx
导函数 f′(x)=__0
f′(x)=___α_x_α_-1
f′(x)=_c_o__s_x f′(x)=__-s_i_n_x_
原函数
导函数
f(x)=ax(a>0,且a≠1) f(x)=ex
答案：
求曲线上的点到直线的最小距离。
• 练习：
1.求y xex 2x 1在(0，0)处的切线
3x y 1 0
2.曲线y x2 ax b在(0，b)处的切线方程是
x y 1 0，求a,b
a 1,b 1
已知切线方程为y ex,曲线为f (x) ex ,
求切点坐意义
函数 y f (x) 在x x0 处的导数就是函数
y f (x) 的图像在点 (x0 , f (x0 )) 处的切线的 斜率，即
k f (x0 )
一.曲线的切线
请看当点Q沿着曲线逐渐向点P接近时，割线PQ
绕着点P逐渐转动的情况.
y
y=f(x)
割
线 Q
解：f ' (x) 6x2 3 k f '(1) 3 y 1 3(x 1)3x y 4 0
用导数求切线方程的四种类型
用导数求切线方程的四种类型在微积分中，切线是曲线上某一点的切线。
通过使用导数，我们可以求解给定曲线上某一点的切线方程。
在本文中，我们将探讨四种使用导数求解切线方程的常见类型。
1. 曲线方程已知的情况首先，我们考虑的是当曲线方程已知时求解切线方程的情况。
假设我们有一个曲线y=f(x)，其中f(x)是一个可导函数。
要求解曲线上某一点(x1,y1)处的切线方程，我们可以执行以下步骤：1.计算函数f(x)在点(x1,y1)处的导数f′(x1)。
2.使用点斜式或一般式等方程形式得到切线方程。
点斜式切线方程的一般形式为y−y1=m(x−x1)，其中m是斜率。
一般式切线方程的一般形式为ax+by=c，其中a,b,c是常数。
2. 给定两个点的情况其次，我们考虑的是当曲线上两个点已知时求解切线方程的情况。
与上一种情况不同，我们不知道曲线的具体方程，但我们已知曲线上的两个点(x1,y1)和(x2,y2)。
为了求解这种情况下的切线方程，我们可以按照以下步骤进行：1.使用点斜式求解斜率。
2.写出点斜式的一般方程形式y−y1=m(x−x1)。
3.将另一个点(x2,y2)替代初始点(x1,y1)。
4.解方程得出切线方程。
3. 已知切线方程的情况接下来，我们讨论已知切线方程的情况。
假设我们已经知道了曲线上某一点处的切线方程，我们的目标是求解曲线方程。
我们可以按照以下步骤进行操作：1.确定切线方程的斜率m。
2.使用导数的定义f′(x)=m来设置方程。
3.解方程以获得曲线方程。
4. 求解切线与坐标轴的交点最后，我们研究切线与坐标轴相交的情况。
为了求解切线与x轴和y轴的交点，我们可以按照以下步骤进行：1.求解切线与x轴的交点：将y值设为0，然后解方程得到x坐标的值。
2.求解切线与y轴的交点：将x值设为0，然后解方程得到y坐标的值。
通过上述四种类型的方法，我们可以使用导数来求解切线方程。
这些方法在解决微积分问题以及实际问题中的应用非常广泛。
导数的切线方程
导数的切线方程
导数作为微积分中的重要概念，在物理学、工程学、经济学等领域都具有广泛应用。
本文将重点介绍导数的切线方程。
首先，需要明确什么是导数。
导数是一个函数在某一点处的变化率或斜率，可以用以下公式表示：
f'(x) = lim (h → 0) [f(x+h) - f(x)]/h
其中f(x)表示函数的值，f(x+h)表示函数在x+h处的值，h为趋近于0的极小值。
得到导数后，就可以计算出函数在该点的切线斜率。
切线斜率即为导数值，可以用点斜式或一般式来表示切线方程。
点斜式公式为y - y0 = k(x - x0)，其中(x0, y0)为切点，k为切线斜率。
一般式公式为Ax + By + C = 0，其中A、B、C为常数，表示切线的一般性质。
接下来，我们以一个具体例子来说明如何求解切线方程。
假设我们有函数f(x) = x^2 + 2x + 1，求出该函数在x=2处的切线方程。
首先，求出导数f'(x) = 2x + 2，在x=2处导数为6。
其次，确定切点，即x=2处的函数值为f(2) = 9。
最后，将切点和导数代入点斜式公式中，得到切线方程y - 9 = 6(x - 2)或y = 6x - 3。
至此，我们成功求出了函数f(x)在x=2处的切线方程。
总的来说，导数作为微积分的基础概念，其应用广泛，特别是在计算机图像处理、机器学习等领域都有着重要作用。
了解导数的切线方程，能够帮助我们更好地理解函数、优化算法等。
导数法求双曲线切线方程的三种题型
导数法求双曲线切线方程的三种题型双曲线是数学中的一种曲线，它的方程可以通过导数法求解切线方程。
在求解双曲线切线方程时，我们可以遇到三种不同的题型，分别是直角双曲线、平方差双曲线和标准双曲线。
下面将逐一介绍这三种题型的求解方法。
1. 直角双曲线的切线方程对于直角双曲线的切线方程的求解，步骤如下：1. 先将直角双曲线的方程表示为标准方程，即$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$。
2. 求出曲线上任意一点 $(x_0, y_0)$ 的导数 $y'$。
3. 代入切点 $(x_0, y_0)$ 的坐标，求出导数的值 $y'(x_0)$。
4. 利用点斜式或一般式，得到切线方程。
2. 平方差双曲线的切线方程平方差双曲线的切线方程的求解过程如下：1. 先将平方差双曲线的方程表示为标准方程，即$\frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1$。
2. 求出曲线上任意一点 $(x_0, y_0)$ 的导数 $y'$。
3. 代入切点 $(x_0, y_0)$ 的坐标，求出导数的值 $y'(x_0)$。
4. 利用点斜式或一般式，得到切线方程。
3. 标准双曲线的切线方程标准双曲线的切线方程的求解过程如下：1. 标准双曲线的方程为 $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$。
2. 求出曲线上任意一点 $(x_0, y_0)$ 的导数 $y'$。
3. 代入切点 $(x_0, y_0)$ 的坐标，求出导数的值 $y'(x_0)$。
4. 利用点斜式或一般式，得到切线方程。
这三种题型的求解方法都是利用导数法来求解切线方程，但具体求解步骤可能会有所不同。
以上就是求解双曲线切线方程的三种题型的基本方法。
对于更复杂的情况，可能需要借助其他数学知识和技巧来进行求解。
希望这份文档能对你有所帮助！。
专题一：用导数求切线方程的四种类
用导数求切线方程的四种类型求曲线的切线方程是导数的重要应用之一，用导数求切线方程的关键在于求出切点00()P x y ，与斜率，其求法为：设00()P x y ，是曲线()y f x =上的一点，则以P 的切点的切线方程为：000()()y y f x x x '-=-．若曲线()y f x =在点00(())P x f x ，的切线平行于y 轴（即导数不存在）时，由切线定义知，切线方程为0x x =．下面例析四种常见的类型与解法． 类型一：已知切点，求曲线的切线方程此类题较为简单，只须求出曲线的导数()f x '，并代入点斜式方程即可．例1 曲线3231y x x =-+在点(11)-，处的切线方程为（ ） Ａ．34y x =- Ｂ．32y x =-+ Ｃ．43y x =-+ Ｄ．45y x =- 1解：由2()36f x x x '=-则在点(11)-，处斜率(1)3k f '==-，故所求的切线方程为(1)3(1)y x --=--，即32y x =-+，因而选Ｂ．练习：1．设f ′(x 0)＝0，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线( ) A ．不存在 B ．与x 轴平行或重合 C ．与x 轴垂直 D ．与x 轴斜交答案 B 2.已知函数y ＝f (x )的图像如右图所示，则f ′(x A )与f ′(x B )的大小关系是( )A ．f ′(x A )>f ′(xB ) B ．f ′(x A )<f ′(x B )C ．f ′(x A )＝f ′(x B )D ．不能确定 答案 B2．曲线y ＝－2x 2＋1在点(0,1)处的切线的斜率是( )A ．－4B ．0C ．4D ．不存在答案 B10．已知曲线y ＝2x 3上一点A (1,2)，则A 处的切线斜率等于( )A ．2B ．4C ．6＋6·Δx ＋2·(Δx )2D ．6答案 D4．函数y ＝sin 2x 的图像在⎝ ⎛⎭⎪⎫π6，14处的切线的斜率是( )A. 3B.33C.12D.32答案 D分析 将函数y ＝sin 2x 看作是由函数y ＝u 2，u ＝sin x 复合而成的．解析 ∵y ′＝2sin x cos x ， ∴y ′|x ＝π6＝2sin π6cos π6＝322．曲线y ＝13x 3－2在点(－1，－73)处切线的倾斜角为( )A ．30°B ．45°C ．135°D ．60°答案 B6．y ＝x 3的切线倾斜角的围为________． 答案 [0，π2)解析 k ＝y ′＝3x 2≥0.8．设点P 是曲线y ＝x 3－3x ＋23上的任意一点，点P 处切线倾斜角为α，则角α的取值围是( )A.⎣⎢⎡⎭⎪⎫23π，π B.⎝ ⎛⎦⎥⎤π2，56π C.⎣⎢⎡⎭⎪⎫0，π2∪⎝ ⎛⎭⎪⎫56π，πD.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π答案 D解析 由y ′＝3x 2－3，易知y ′≥－3，即tan α≥－ 3. ∴0≤α<π2或23π≤α<π.14．已知曲线C ：y ＝x 3，求在曲线C 上横坐标为1的点处的切线方程．解析 将x ＝1代入曲线C 的方程得y ＝1， ∴切点P (1,1)．∵y ′＝lim Δx →0Δy Δx ＝lim Δx →0x ＋Δx 3－x 3Δx＝lim Δx →03x 2Δx ＋3x Δx2＋Δx3Δx＝lim Δx →0[3x 2＋3xΔx ＋(Δx )2]＝3x 2，∴y ′|x ＝1＝3.∴过P 点的切线方程为y －1＝3(x －1)， 即3x －y －2＝0.14．求曲线y ＝sin x 在点A (π6，12)处的切线方程．解析 ∵y ＝sin x ，∴y ′＝cos x . ∴y ′|x ＝π6＝cos π6＝32，k ＝32.∴切线方程为y －12＝32(x －π6)．化简得63x －12y ＋6－3π＝0. 6．曲线y ＝xx －2在点(1，－1)处的切线方程为( )A ．y ＝x －2B ．y ＝－3x ＋2C ．y ＝2x －3D ．y ＝－2x ＋1答案 D例3 求曲线y ＝1x 2－3x 在点(4，12)处的切线方程．[思路分析] 将函数变形为y ＝(x 2－3x )－12，将其看做是由函数y ＝u －12、u ＝x 2－3x 复合而成．[解析] ∵y ＝1x 2－3x＝(x 2－3x )－12， ∴y ′＝－12(x 2－3x )－32·(x 2－3x )′＝－12(x 2－3x )－32·(2x －3)．∴曲线y ＝1x 2－3x在点(4，12)处的切线斜率为 k ＝y ′|x ＝4＝－12(42－3×4)－32·(2×4－3)＝－516.∴曲线在点(4，12)处的切线方程为y －12＝－516(x －4)，即5x ＋16y －28＝0. 探究3 此题不要将函数y ＝1x 2－3x看做是由y ＝1u ，u ＝v ，v ＝x 2－3x 三个函数复合而成的，这样求导就麻烦了．思考题 3 (1)曲线y ＝3x 2＋1在点(1,2)处的切线方程为__________________．[答案] 3x －2y ＋1＝0(2)y ＝11－x 2的水平切线方程是________．[解析] 令y ′＝0，得x ＝0，∴y ＝1.12．求曲线y ＝2x －x 3在点(－1，－1)处的切线的方程与此切线与x 轴、y 轴所围成的平面图形的面积．答案 x ＋y ＋2＝0；28．曲线y ＝e 12 x在点(4，e 2)处的切线与坐标轴所围三角形的面积为( )A.92e 2 B ．4e 2 C ．2e 2 D ．e 2答案 D解析 ∵y ′＝12·e 12 x，∴切线的斜率k ＝y ′|x ＝4＝12e 2.∴切线方程为y －e 2＝12e 2(x －4)．∴横纵截距分别为2，－e 2，∴S ＝e 2，应选D.11．已知函数y ＝f (x )的图像在点M (1，f (1))处的切线方程是y ＝12x＋2，则f (1)＋f ′(1)＝________.答案 3解析 f ′(1)＝12，f (1)＝12×1＋2＝52，∴f (1)＋f ′(1)＝3.5．如图是函数f (x )与f (x )在点P 处切线的图像，则f (2)＋f ′(2)＝________.答案 98解析 由题图知，切线方程为x 4＋y4.5＝1，f (2)＝4.5·(1－24)＝94，f ′(2)＝－4.54＝－98.∴f (2)＋f ′(2)＝94－98＝98.类型二：已知斜率，求曲线的切线方程此类题可利用斜率求出切点，再用点斜式方程加以解决． 例2 与直线240x y -+=的平行的抛物线2y x =的切线方程是（ ）Ａ．230x y -+= Ｂ．230x y --= Ｃ．210x y -+= Ｄ．210x y --=2 解：设00()P x y ，为切点，则切点的斜率为0022x xy x ='==|．01x =∴．由此得到切点(11)，．故切线方程为12(1)y x -=-，即210x y --=，应选Ｄ．评注：此题所给的曲线是抛物线，故也可利用∆法加以解决，即设切线方程为2y x b =+，代入2y x =，得220x x b --=，又因为0∆=，得1b =-，应选Ｄ．练习：3．曲线y ＝x 3在点P 处的切线斜率为3，则点P 的坐标为( ) A ．(－2，－8) B ．(1,1)，(－1，－1) C ．(2,8) D ．(－12，－18)答案 B13．若曲线y ＝2x 3上某点切线的斜率等于6，求此点的坐标． 解析 ∵y ′|x ＝x 0＝lim Δx →02x 0＋Δx3－2x 30Δx＝6x 20，∴6x 20＝6.∴x 0＝±1.故(1,2)，(－1，－2)为所求． 3．已知曲线y ＝x 24－3ln x 的一条切线的斜率为12，则切点的横坐标为( )A ．3B ．2C ．1 D.12答案 A解析 y ′＝12x －31x ，由12x －3x ＝12.得x ＝3或x ＝－2.由于x >0，所以x ＝3.3．已知曲线y ＝f (x )在点P (x 0，f (x 0))处的切线方程为2x ＋y ＋1＝0，那么( )A ．f ′(x 0)＝0B ．f ′(x 0)<0C ．f ′(x 0)>0D ．f ′(x 0)不能确定答案 B5．如果曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为x ＋2y －3＝0，那么( )A ．f ′(x 0)>0B ．f ′(x 0)<0C ．f ′(x 0)＝0D ．f ′(x 0)不存在答案 B7．在曲线y ＝x 2上切线的倾斜角为π4的点是( )A ．(0,0)B ．(2,4)C ．(14，116)D ．(12，14)答案 D2．若曲线y ＝x 4的一条切线l 与直线x ＋4y －8＝0垂直，则l 的方程为( )A ．4x －y －3＝0B ．x ＋4y －5＝0C ．4x －y ＋3＝0D ．x ＋4y ＋3＝0答案 A解析 ∵l 与直线x ＋4y －8＝0垂直， ∴l 的斜率为4.∵y ′＝4x 3，∴由切线l 的斜率是4，得4x 3＝4，∴x ＝1. ∴切点坐标为(1,1)．∴切线方程为y －1＝4(x －1)， 即4x －y －3＝0.应选A.11．已知P (－1,1)，Q (2,4)是曲线y ＝x 2上的两点，则与直线PQ 平行的曲线y ＝x 2的切线方程是________．答案 4x －4y －1＝0解析 k ＝4－12－－1＝1，又y ′＝2x ，令2x ＝1，得x ＝12，进而y ＝14，∴切线方程为y －14＝1·(x －12)，即4x －4y －1＝0.13．如果曲线y ＝x 2＋x －3的某一条切线与直线y ＝3x ＋4平行，求切点坐标与切线方程．答案 切点坐标为(1，－1)，切线方程为3x －y －4＝0 13．曲线y ＝x 3＋3x 2＋6x －10的切线中，斜率最小的切线方程为______________．答案 3x －y －11＝0解析 y ′＝3x 2＋6x ＋6＝3(x ＋1)2＋3≥3， 当且仅当x ＝－1时取等号，当x ＝－1，时y ＝－14. ∴切线方程为y ＋14＝3(x ＋1)，即3x －y －11＝0.9．设直线y ＝12x ＋b 是曲线y ＝ln x (x >0)的一条切线，则实数b的值为________．答案 ln2－14．设曲线y ＝ax 2在点(1，a )处的切线与直线2x －y －6＝0平行，则a 等于( )A ．1 B.12 C ．－12D ．－1答案 A14．设曲线y ＝e ax 在点(0,1)处的切线与直线x ＋2y ＋1＝0垂直，则a ＝________.答案 2解析 由题意得y ′＝a e ax ，y ′|x ＝0＝a e a ×0＝2，a ＝2. 10．函数f (x )＝a sin ax (a ∈R )的图像过点P (2π，0)，并且在点P 处的切线斜率为4，则f (x )的最小正周期为( )A ．2πB ．π C.π2 D.π4答案 B解析 f ′(x )＝a 2cos ax ，∴f ′(2π)＝a 2cos2πa . 又a sin2πa ＝0，∴2πa ＝k π，k ∈Z . ∴f ′(2π)＝a 2cos k π＝4，∴a ＝±2. ∴T ＝2π|a |＝π.6．曲线y ＝ln(2x －1)上的点到直线2x －y ＋3＝0的最短距离是( )A. 5 B ．2 5 C ．3 5 D ．0 答案 A解析 y ′＝22x －1＝2，∴x ＝1.∴切点坐标为(1,0)．由点到直线的距离公式，得d ＝|2×1－0＋3|22＋12＝ 5. 19．曲线y ＝x (x ＋1)(2－x )有两条平行于y ＝x 的切线，则两切线之间的距离为________．答案 16272解析 y ＝x (x ＋1)(2－x )＝－x 3＋x 2＋2x ，y ′＝－3x 2＋2x ＋2，令－3x 2＋2x ＋2＝1，得x 1＝1或x 2＝－13.∴两个切点分别为(1,2)和(－13，－1427)．切线方程为x －y ＋1＝0和x －y －527＝0.∴d ＝|1＋527|2＝16227.类型三：已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法．6．以下说确的是( )A ．曲线的切线和曲线有交点，这点一定是切点B ．过曲线上一点作曲线的切线，这点一定是切点C ．若f ′(x 0)不存在，则曲线y ＝f (x )在点(x 0，f (x 0))处无切线D ．若曲线y ＝f (x )在点(x 0，f (x 0))处有切线，则f ′(x 0)不一定存在答案 D例3 求过曲线32y x x =-上的点(11)-，的切线方程．3解：设想00()P x y ，为切点，则切线的斜率为02032x xy x ='=-|．∴切线方程为2000(32)()y y x x x -=--．320000(2)(32)()y x x x x x --=--．又知切线过点(11)-，，把它代入上述方程，得3200001(2)(32)(1)x x x x ---=--．解得01x =，或012x =-．故所求切线方程为(12)(32)(1)y x --=--，或13112842y x ⎛⎫⎛⎫⎛⎫--+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，即20x y --=，或5410x y +-=．评注：可以发现直线5410x y +-=并不以(11)-，为切点，实际上是经过了点(11)-，且以1728⎛⎫- ⎪⎝⎭，为切点的直线．这说明过曲线上一点的切线，该点未必是切点，解决此类问题可用待定切点法． 练习：类型四：已知过曲线外一点，求切线方程此类题可先设切点，再求切点，即用待定切点法来求解．例4 求过点(20)，且与曲线1y x=相切的直线方程．4解：设00()P x y ，为切点，则切线的斜率为0201x xy x ='=-|．∴切线方程为00201()y y x x x -=--，即020011()y x x x x -=--． 又已知切线过点(20)，，把它代入上述方程，得02011(2)x x x -=--． 解得000111x y x ===，，即20x y +-=． 评注：点(20)，实际上是曲线外的一点，但在解答过程中却无需判断它的确切位置，充分反映出待定切点法的高效性例5 已知函数33y x x =-，过点(016)A ，作曲线()y f x =的切线，求此切线方程．5解：曲线方程为33y x x =-，点(016)A ，不在曲线上． 设切点为00()M x y ，，则点M的坐标满足30003y x x =-．因200()3(1)f x x '=-，故切线的方程为20003(1)()y y x x x -=--．点(016)A ，在切线上，则有32000016(3)3(1)(0)x x x x --=--． 化简得308x =-，解得02x =-．所以，切点为(22)M --，，切线方程为9160x y -+=．评注：此类题的解题思路是，先判断点A 是否在曲线上，若点A 在曲线上，化为类型一或类型三；若点A 不在曲线上，应先设出切点并求出切点．练习：17．已知曲线方程为y ＝x 2，求过A (3,5)点且与曲线相切的直线方程．解析 解法一 设过A (3,5)与曲线y ＝x 2相切的直线方程为y －5＝k (x －3)，即y ＝kx ＋5－3k .由⎩⎪⎨⎪⎧y ＝kx ＋5－3k y ＝x 2，得x 2－kx ＋3k －5＝0.Δ＝k 2－4(3k －5)＝0，整理得(k －2)(k －10)＝0. ∴k ＝2或k ＝10. 所求的直线方程为2x －y －1＝0,10x －y －25＝0.解法二设切点P的坐标为(x0，y0)，由y＝x2，得y′＝2x.∴y′|x＝x0＝2x0.由已知kPA＝2x0，即5－y03－x0＝2x0.又y0＝2x0，代入上式整理，得x0＝1或x0＝5.18．已知曲线S：y＝3x－x3与点P(2,2)，则过点P可向S引切线，其切线条数为( )A．0 B．1C．2 D．3答案 D解析显然P不在S上，设切点为(x0，y0)，由y′＝3－3x2，得y′|x＝x0＝3－3x20.切线方程为y－(3x0－x30)＝(3－3x20)(x－x0)．∵P(2,2)在切线上，∴2－(3x0－x30)＝(3－3x20)(2－x0)，即x30－3x20＋2＝0.∴(x0－1)(x20－2x0－2)＝0.由x0－1＝0，得x0＝1.由x20－2x0－2＝0，得x0＝1± 3.∵有三个切点，∴由P向S作切线可以作3条．综合练习：10．已知f(x)＝x2＋2xf′(1)，则f′(0)等于( )A．0 B．－4C．－2 D．2答案 B解析 f ′(x )＝2x ＋2f ′(1)，令x ＝1，得f ′(1)＝2＋2f ′(1)，∴f ′(1)＝－2. ∴f ′(0)＝2f ′(1)＝－4.12．设函数f (x )＝g (x )＋x 2，曲线y ＝g (x )在点(1，g (1))处的切线方程为y ＝2x ＋1，则曲线y ＝f (x )在点(1，f (1))处的切线的斜率为( )A ．4B ．－14C ．2D ．－12答案 A解析 依题意得f ′(x )＝g ′(x )＋2x ，f ′(1)＝g ′(1)＋2＝4，选A.15．(1)求过曲线y ＝e x 上点P (1，e)且与曲线在该点处的切线垂直的直线方程；(2)曲线y ＝15x 5上一点M 处的切线与直线y ＝－x ＋3垂直，求此切线方程．解析 (1)∵y ′＝e x ，∴曲线在点P (1，e)处的切线斜率是y ′|x ＝1＝e. ∴过点P 且与切线垂直的直线的斜率为k ＝－1e .∴所求直线方程为y －e ＝－1e(x －1)，(2)∵切线与y ＝－x ＋3垂直，∴切线斜率为1. 又y ′＝x 4，令x 4＝1，∴x ＝±1.∴切线方程为5x －5y －4＝0或5x －5y ＋4＝0.4．y ＝ax 2＋1的图像与直线y ＝x 相切，则a ＝( ) A.18 B.14 C.12 D ．1答案 B解析 由已知{ y ＝ax 2＋1，y ＝x 有唯一解，即x ＝ax 2＋1，ax 2－x ＋1＝0有唯一解， ∴Δ＝1－4a ＝0，∴a ＝14.15．点P 在曲线y ＝f (x )＝x 2＋1上，且曲线在点P 处的切线与曲线y ＝－2x 2－1相切，求点P 的坐标．解析 设P (x 0，y 0)，则y 0＝x 20＋1.f ′(x 0)＝lim Δx →0x 0＋Δx2＋1－x 20＋1Δx＝2x 0.所以过点P 的切线方程为y －y 0＝2x 0(x －x 0)，即y ＝2x 0x ＋1－x 20.而此直线与曲线y ＝－2x 2－1相切，所以切线与曲线y ＝－2x 2－1只有一个公共点． 由{ y ＝2x 0x ＋1－x 20，y ＝－2x 2－1，得即Δ＝4x 20－8(2－x 20)＝0.解得x 0＝±233，y 0＝73.所以点P 的坐标为(233，73)或(－233，73)．17．若直线y ＝kx 与曲线y ＝x 3－3x 2＋2x 相切，求k 的值． 解析 设切点坐标为(x 0，y 0)，y ′|x ＝x 0＝3x 20－6x 0＋2＝k .若x 0＝0，则k ＝2.若x 0≠0，由y 0＝kx 0，得k ＝y 0x 0.∴3x 20－6x 0＋2＝y 0x 0，即3x 20－6x 0＋2＝x 30－3x 20＋2x 0x 0.解之，得x 0＝32. ∴k ＝3×(32)2－6×32＋2＝－14.综上，k ＝2或k ＝－14.16．已知函数f (x )＝2x 3＋ax 与g (x )＝bx 2＋c 的图像都过点P (2,0)，且在点P 处有公共切线，求f (x )、g (x )的表达式．解析 ∵f (x )＝2x 3＋ax 的图像过点P (2,0)， ∴a ＝－8.∴f (x )＝2x 3－8x .∴f ′(x )＝6x 2－8. 对于g (x )＝bx 2＋c 的图像过点P (2,0)，则4b ＋c ＝0. 又g ′(x )＝2bx ，∴g ′(2)＝4b ＝f ′(2)＝16. ∴b ＝4.∴c ＝－16. ∴g (x )＝4x 2－16. 综上可知，f (x )＝2x 3－8x ，g (x )＝4x 2－16.1．已知直线l 1为曲线y ＝x 2＋x －2在点(1,0)处的切线，l 2为该曲线的另一条切线，且l 1⊥l 2.(1)求直线l 1，l 2的方程；(2)求由直线l 1，l 2和x 轴所围成的三角形的面积．分析 (1)求曲线在某点处的切线方程的步骤：先求曲线在这点处的导数，这点对应的导数值即为过此点切线的斜率，再用点斜式写出直线方程；(2)求面积用S ＝12a ·h 即可完成．解析 (1)因为y ′＝2x ＋1，则直线l 1的斜率k 1＝2×1＋1＝3，则直线l 1的方程为y ＝3x －3，设直线l 2过曲线y ＝x 2＋x －2上的点B (x0,y0)，因为l 1⊥l 2。
导数法求对数函数切线方程的三种题型
导数法求对数函数切线方程的三种题型
引言
本文将介绍三种常见的题型，通过导数法求解对数函数的切线方程。
对数函数是数学中常见的一类函数，求解其切线方程是数学研究中的重要内容之一。
问题1：已知对数函数的函数式求切线方程
当已知对数函数的函数式，求对应点上的切线方程时，可以通过以下步骤来进行求解：
1. 求对数函数的导数；
2. 计算给定点的横坐标和纵坐标；
3. 代入导数公式，求得切线方程的斜率；
4. 使用切线方程的一般式，将斜率和给定点代入，得到切线方程。
问题2：已知对数函数的切点求切线方程
当已知对数函数的切点，求对应切点上的切线方程时，可以按照以下步骤来进行求解：
1. 求切点处的导数值；
2. 使用切线方程的一般式，将切点的斜率和坐标代入，得到切线方程。
问题3：已知对数函数的切线方程求函数式
当已知对数函数的切线方程，求对应对数函数的函数式时，可以通过以下步骤来进行求解：
1. 对给定的切线方程，提取出切线的斜率和截距；
2. 求解对数函数的导数，得到导数公式；
3. 将切线的斜率代入导数公式，得到方程的解；
4. 根据解得到的方程，确定对数函数的函数式。
结论
通过导数法求解对数函数的切线方程是一种常见且实用的方法。
掌握了三种题型的求解步骤，可以更好地解决相关问题。
但需要注
意的是，在使用导数法求解切线方程时，要注意计算的准确性和步
骤的合理性。
参考资料：
- 曹智勇，高等数学，北京：高等教育出版社，2006年。
- 杨学凤，高等数学，北京：高等教育出版社，2007年。
专题一：用导数求切线方程的四种类
用导数求切线方程的四种类型求曲线的切线方程是导数的重要应用之一，用导数求切线方程的关键在于求出切点00()P x y ，及斜率，其求法为：设00()P x y ，是曲线()y f x =上的一点，则以P 的切点的切线方程为：000()()y y f x x x '-=-．若曲线()y f x =在点00(())P x f x ，的切线平行于y 轴（即导数不存在）时，由切线定义知，切线方程为0x x =．下面例析四种常见的类型及解法． 类型一：已知切点，求曲线的切线方程此类题较为简单，只须求出曲线的导数()f x '，并代入点斜式方程即可．例1 曲线3231y x x =-+在点(11)-，处的切线方程为（ ） Ａ．34y x =- Ｂ．32y x =-+ Ｃ．43y x =-+ Ｄ．45y x =- 1解：由2()36f x x x '=-则在点(11)-，处斜率(1)3k f '==-，故所求的切线方程为(1)3(1)y x --=--，即32y x =-+，因而选Ｂ．练习：1．设f ′(x 0)＝0，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线( ) A ．不存在 B ．与x 轴平行或重合 C ．与x 轴垂直 D ．与x 轴斜交答案 B 2.已知函数y ＝f (x )的图像如右图所示，则f ′(x A )与f ′(x B )的大小关系是( )A ．f ′(x A )>f ′(xB ) B ．f ′(x A )<f ′(x B )C ．f ′(x A )＝f ′(x B )D ．不能确定 答案 B2．曲线y ＝－2x 2＋1在点(0,1)处的切线的斜率是( )A ．－4B ．0C ．4D ．不存在答案 B10．已知曲线y ＝2x 3上一点A (1,2)，则A 处的切线斜率等于( )A ．2B ．4C ．6＋6·Δx ＋2·(Δx )2D ．6答案 D4．函数y ＝sin 2x 的图像在⎝ ⎛⎭⎪⎫π6，14处的切线的斜率是( )A. 3B.33C.12D.32答案 D分析 将函数y ＝sin 2x 看作是由函数y ＝u 2，u ＝sin x 复合而成的．解析 ∵y ′＝2sin x cos x ， ∴y ′|x ＝π6＝2sin π6cos π6＝322．曲线y ＝13x 3－2在点(－1，－73)处切线的倾斜角为( )A ．30°B ．45°C ．135°D ．60°答案 B6．y ＝x 3的切线倾斜角的围为________． 答案 [0，π2)解析 k ＝y ′＝3x 2≥0.8．设点P 是曲线y ＝x 3－3x ＋23上的任意一点，点P 处切线倾斜角为α，则角α的取值围是( )A.⎣⎢⎡⎭⎪⎫23π，π B.⎝ ⎛⎦⎥⎤π2，56π C.⎣⎢⎡⎭⎪⎫0，π2∪⎝ ⎛⎭⎪⎫56π，πD.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π答案 D解析 由y ′＝3x 2－3，易知y ′≥－3，即tan α≥－ 3. ∴0≤α<π2或23π≤α<π.14．已知曲线C ：y ＝x 3，求在曲线C 上横坐标为1的点处的切线方程．解析 将x ＝1代入曲线C 的方程得y ＝1， ∴切点P (1,1)．∵y ′＝lim Δx →0Δy Δx ＝lim Δx →0x ＋Δx 3－x 3Δx＝lim Δx →03x 2Δx ＋3x Δx2＋Δx3Δx＝lim Δx →0[3x 2＋3xΔx ＋(Δx )2]＝3x 2，∴y ′|x ＝1＝3.∴过P 点的切线方程为y －1＝3(x －1)， 即3x －y －2＝0.14．求曲线y ＝sin x 在点A (π6，12)处的切线方程．解析 ∵y ＝sin x ，∴y ′＝cos x . ∴y ′|x ＝π6＝cos π6＝32，k ＝32.∴切线方程为y －12＝32(x －π6)．化简得63x －12y ＋6－3π＝0. 6．曲线y ＝xx －2在点(1，－1)处的切线方程为( )A ．y ＝x －2B ．y ＝－3x ＋2C ．y ＝2x －3D ．y ＝－2x ＋1答案 D例3 求曲线y ＝1x 2－3x 在点(4，12)处的切线方程．【思路分析】 将函数变形为y ＝(x 2－3x )－12，将其看做是由函数y ＝u －12、u ＝x 2－3x 复合而成．【解析】 ∵y ＝1x 2－3x＝(x 2－3x )－12， ∴y ′＝－12(x 2－3x )－32·(x 2－3x )′＝－12(x 2－3x )－32·(2x －3)．∴曲线y ＝1x 2－3x在点(4，12)处的切线斜率为 k ＝y ′|x ＝4＝－12(42－3×4)－32·(2×4－3)＝－516.∴曲线在点(4，12)处的切线方程为y －12＝－516(x －4)，即5x ＋16y －28＝0. 探究3 本题不要将函数y ＝1x 2－3x看做是由y ＝1u ，u ＝v ，v ＝x 2－3x 三个函数复合而成的，这样求导就麻烦了．思考题 3 (1)曲线y ＝3x 2＋1在点(1,2)处的切线方程为__________________．【答案】 3x －2y ＋1＝0(2)y ＝11－x 2的水平切线方程是________．【解析】 令y ′＝0，得x ＝0，∴y ＝1.12．求曲线y ＝2x －x 3在点(－1，－1)处的切线的方程及此切线与x 轴、y 轴所围成的平面图形的面积．答案 x ＋y ＋2＝0；28．曲线y ＝e 12 x在点(4，e 2)处的切线与坐标轴所围三角形的面积为( )A.92e 2 B ．4e 2 C ．2e 2 D ．e 2答案 D解析 ∵y ′＝12·e 12 x，∴切线的斜率k ＝y ′|x ＝4＝12e 2.∴切线方程为y －e 2＝12e 2(x －4)．∴横纵截距分别为2，－e 2，∴S ＝e 2，故选D.11．已知函数y ＝f (x )的图像在点M (1，f (1))处的切线方程是y ＝12x＋2，则f (1)＋f ′(1)＝________.答案 3解析 f ′(1)＝12，f (1)＝12×1＋2＝52，∴f (1)＋f ′(1)＝3.5．如图是函数f (x )及f (x )在点P 处切线的图像，则f (2)＋f ′(2)＝________.答案 98解析 由题图知，切线方程为x 4＋y4.5＝1，f (2)＝4.5·(1－24)＝94，f ′(2)＝－4.54＝－98.∴f (2)＋f ′(2)＝94－98＝98.类型二：已知斜率，求曲线的切线方程此类题可利用斜率求出切点，再用点斜式方程加以解决． 例2 与直线240x y -+=的平行的抛物线2y x =的切线方程是（ ）Ａ．230x y -+= Ｂ．230x y --= Ｃ．210x y -+= Ｄ．210x y --=2 解：设00()P x y ，为切点，则切点的斜率为0022x xy x ='==|．01x =∴．由此得到切点(11)，．故切线方程为12(1)y x -=-，即210x y --=，故选Ｄ．评注：此题所给的曲线是抛物线，故也可利用∆法加以解决，即设切线方程为2y x b =+，代入2y x =，得220x x b --=，又因为0∆=，得1b =-，故选Ｄ．练习：3．曲线y ＝x 3在点P 处的切线斜率为3，则点P 的坐标为( ) A ．(－2，－8) B ．(1,1)，(－1，－1) C ．(2,8) D ．(－12，－18)答案 B13．若曲线y ＝2x 3上某点切线的斜率等于6，求此点的坐标． 解析 ∵y ′|x ＝x 0＝lim Δx →02x 0＋Δx3－2x 30Δx＝6x 20，∴6x 20＝6.∴x 0＝±1.故(1,2)，(－1，－2)为所求． 3．已知曲线y ＝x 24－3ln x 的一条切线的斜率为12，则切点的横坐标为( )A ．3B ．2C ．1 D.12答案 A解析 y ′＝12x －31x ，由12x －3x ＝12.得x ＝3或x ＝－2.由于x >0，所以x ＝3.3．已知曲线y ＝f (x )在点P (x 0，f (x 0))处的切线方程为2x ＋y ＋1＝0，那么( )A ．f ′(x 0)＝0B ．f ′(x 0)<0C ．f ′(x 0)>0D ．f ′(x 0)不能确定答案 B5．如果曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为x ＋2y －3＝0，那么( )A ．f ′(x 0)>0B ．f ′(x 0)<0C ．f ′(x 0)＝0D ．f ′(x 0)不存在答案 B7．在曲线y ＝x 2上切线的倾斜角为π4的点是( )A ．(0,0)B ．(2,4)C ．(14，116)D ．(12，14)答案 D2．若曲线y ＝x 4的一条切线l 与直线x ＋4y －8＝0垂直，则l 的方程为( )A ．4x －y －3＝0B ．x ＋4y －5＝0C ．4x －y ＋3＝0D ．x ＋4y ＋3＝0答案 A解析 ∵l 与直线x ＋4y －8＝0垂直， ∴l 的斜率为4.∵y ′＝4x 3，∴由切线l 的斜率是4，得4x 3＝4，∴x ＝1. ∴切点坐标为(1,1)．∴切线方程为y －1＝4(x －1)， 即4x －y －3＝0.故选A.11．已知P (－1,1)，Q (2,4)是曲线y ＝x 2上的两点，则与直线PQ 平行的曲线y ＝x 2的切线方程是________．答案 4x －4y －1＝0解析 k ＝4－12－－1＝1，又y ′＝2x ，令2x ＝1，得x ＝12，进而y ＝14，∴切线方程为y －14＝1·(x －12)，即4x －4y －1＝0.13．如果曲线y ＝x 2＋x －3的某一条切线与直线y ＝3x ＋4平行，求切点坐标与切线方程．答案 切点坐标为(1，－1)，切线方程为3x －y －4＝0 13．曲线y ＝x 3＋3x 2＋6x －10的切线中，斜率最小的切线方程为______________．答案 3x －y －11＝0解析 y ′＝3x 2＋6x ＋6＝3(x ＋1)2＋3≥3， 当且仅当x ＝－1时取等号，当x ＝－1，时y ＝－14. ∴切线方程为y ＋14＝3(x ＋1)，即3x －y －11＝0.9．设直线y ＝12x ＋b 是曲线y ＝ln x (x >0)的一条切线，则实数b的值为________．答案 ln2－14．设曲线y ＝ax 2在点(1，a )处的切线与直线2x －y －6＝0平行，则a 等于( )A ．1 B.12 C ．－12D ．－1答案 A14．设曲线y ＝e ax 在点(0,1)处的切线与直线x ＋2y ＋1＝0垂直，则a ＝________.答案 2解析 由题意得y ′＝a e ax ，y ′|x ＝0＝a e a ×0＝2，a ＝2. 10．函数f (x )＝a sin ax (a ∈R )的图像过点P (2π，0)，并且在点P 处的切线斜率为4，则f (x )的最小正周期为( )A ．2πB ．π C.π2 D.π4答案 B解析 f ′(x )＝a 2cos ax ，∴f ′(2π)＝a 2cos2πa . 又a sin2πa ＝0，∴2πa ＝k π，k ∈Z . ∴f ′(2π)＝a 2cos k π＝4，∴a ＝±2. ∴T ＝2π|a |＝π.6．曲线y ＝ln(2x －1)上的点到直线2x －y ＋3＝0的最短距离是( )A. 5 B ．2 5 C ．3 5 D ．0 答案 A解析 y ′＝22x －1＝2，∴x ＝1.∴切点坐标为(1,0)．由点到直线的距离公式，得d ＝|2×1－0＋3|22＋12＝ 5. 19．曲线y ＝x (x ＋1)(2－x )有两条平行于y ＝x 的切线，则两切线之间的距离为________．答案 16272解析 y ＝x (x ＋1)(2－x )＝－x 3＋x 2＋2x ，y ′＝－3x 2＋2x ＋2，令－3x 2＋2x ＋2＝1，得x 1＝1或x 2＝－13.∴两个切点分别为(1,2)和(－13，－1427)．切线方程为x －y ＋1＝0和x －y －527＝0.∴d ＝|1＋527|2＝16227.类型三：已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法．6．下列说确的是( )A ．曲线的切线和曲线有交点，这点一定是切点B ．过曲线上一点作曲线的切线，这点一定是切点C ．若f ′(x 0)不存在，则曲线y ＝f (x )在点(x 0，f (x 0))处无切线D ．若曲线y ＝f (x )在点(x 0，f (x 0))处有切线，则f ′(x 0)不一定存在答案 D例3 求过曲线32y x x =-上的点(11)-，的切线方程．3解：设想00()P x y ，为切点，则切线的斜率为02032x xy x ='=-|．∴切线方程为2000(32)()y y x x x -=--．320000(2)(32)()y x x x x x --=--．又知切线过点(11)-，，把它代入上述方程，得3200001(2)(32)(1)x x x x ---=--．解得01x =，或012x =-．故所求切线方程为(12)(32)(1)y x --=--，或13112842y x ⎛⎫⎛⎫⎛⎫--+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，即20x y --=，或5410x y +-=．评注：可以发现直线5410x y +-=并不以(11)-，为切点，实际上是经过了点(11)-，且以1728⎛⎫- ⎪⎝⎭，为切点的直线．这说明过曲线上一点的切线，该点未必是切点，解决此类问题可用待定切点法． 练习：类型四：已知过曲线外一点，求切线方程此类题可先设切点，再求切点，即用待定切点法来求解．例4 求过点(20)，且与曲线1y x=相切的直线方程．4解：设00()P x y ，为切点，则切线的斜率为0201x xy x ='=-|．∴切线方程为00201()y y x x x -=--，即020011()y x x x x -=--． 又已知切线过点(20)，，把它代入上述方程，得02011(2)x x x -=--． 解得000111x y x ===，，即20x y +-=． 评注：点(20)，实际上是曲线外的一点，但在解答过程中却无需判断它的确切位置，充分反映出待定切点法的高效性例5 已知函数33y x x =-，过点(016)A ，作曲线()y f x =的切线，求此切线方程．5解：曲线方程为33y x x =-，点(016)A ，不在曲线上． 设切点为00()M x y ，，则点M的坐标满足30003y x x =-．因200()3(1)f x x '=-，故切线的方程为20003(1)()y y x x x -=--．点(016)A ，在切线上，则有32000016(3)3(1)(0)x x x x --=--． 化简得308x =-，解得02x =-．所以，切点为(22)M --，，切线方程为9160x y -+=．评注：此类题的解题思路是，先判断点A 是否在曲线上，若点A 在曲线上，化为类型一或类型三；若点A 不在曲线上，应先设出切点并求出切点．练习：17．已知曲线方程为y ＝x 2，求过A (3,5)点且与曲线相切的直线方程．解析 解法一 设过A (3,5)与曲线y ＝x 2相切的直线方程为y －5＝k (x －3)，即y ＝kx ＋5－3k .由⎩⎪⎨⎪⎧y ＝kx ＋5－3k y ＝x 2，得x 2－kx ＋3k －5＝0.Δ＝k 2－4(3k －5)＝0，整理得(k －2)(k －10)＝0. ∴k ＝2或k ＝10. 所求的直线方程为2x －y －1＝0,10x －y －25＝0.解法二设切点P的坐标为(x0，y0)，由y＝x2，得y′＝2x.∴y′|x＝x0＝2x0.由已知kPA＝2x0，即5－y03－x0＝2x0.又y0＝2x0，代入上式整理，得x0＝1或x0＝5.18．已知曲线S：y＝3x－x3及点P(2,2)，则过点P可向S引切线，其切线条数为( )A．0 B．1C．2 D．3答案 D解析显然P不在S上，设切点为(x0，y0)，由y′＝3－3x2，得y′|x＝x0＝3－3x20.切线方程为y－(3x0－x30)＝(3－3x20)(x－x0)．∵P(2,2)在切线上，∴2－(3x0－x30)＝(3－3x20)(2－x0)，即x30－3x20＋2＝0.∴(x0－1)(x20－2x0－2)＝0.由x0－1＝0，得x0＝1.由x20－2x0－2＝0，得x0＝1± 3.∵有三个切点，∴由P向S作切线可以作3条．综合练习：10．已知f(x)＝x2＋2xf′(1)，则f′(0)等于( )A．0 B．－4C．－2 D．2答案 B解析 f ′(x )＝2x ＋2f ′(1)，令x ＝1，得f ′(1)＝2＋2f ′(1)，∴f ′(1)＝－2. ∴f ′(0)＝2f ′(1)＝－4.12．设函数f (x )＝g (x )＋x 2，曲线y ＝g (x )在点(1，g (1))处的切线方程为y ＝2x ＋1，则曲线y ＝f (x )在点(1，f (1))处的切线的斜率为( )A ．4B ．－14C ．2D ．－12答案 A解析 依题意得f ′(x )＝g ′(x )＋2x ，f ′(1)＝g ′(1)＋2＝4，选A.15．(1)求过曲线y ＝e x 上点P (1，e)且与曲线在该点处的切线垂直的直线方程；(2)曲线y ＝15x 5上一点M 处的切线与直线y ＝－x ＋3垂直，求此切线方程．解析 (1)∵y ′＝e x ，∴曲线在点P (1，e)处的切线斜率是y ′|x ＝1＝e. ∴过点P 且与切线垂直的直线的斜率为k ＝－1e .∴所求直线方程为y －e ＝－1e(x －1)，(2)∵切线与y ＝－x ＋3垂直，∴切线斜率为1. 又y ′＝x 4，令x 4＝1，∴x ＝±1.∴切线方程为5x －5y －4＝0或5x －5y ＋4＝0.4．y ＝ax 2＋1的图像与直线y ＝x 相切，则a ＝( ) A.18 B.14 C.12 D ．1答案 B解析 由已知{ y ＝ax 2＋1，y ＝x 有唯一解，即x ＝ax 2＋1，ax 2－x ＋1＝0有唯一解， ∴Δ＝1－4a ＝0，∴a ＝14.15．点P 在曲线y ＝f (x )＝x 2＋1上，且曲线在点P 处的切线与曲线y ＝－2x 2－1相切，求点P 的坐标．解析 设P (x 0，y 0)，则y 0＝x 20＋1.f ′(x 0)＝lim Δx →0x 0＋Δx2＋1－x 20＋1Δx＝2x 0.所以过点P 的切线方程为y －y 0＝2x 0(x －x 0)，即y ＝2x 0x ＋1－x 20.而此直线与曲线y ＝－2x 2－1相切，所以切线与曲线y ＝－2x 2－1只有一个公共点． 由{ y ＝2x 0x ＋1－x 20，y ＝－2x 2－1，得即Δ＝4x 20－8(2－x 20)＝0.解得x 0＝±233，y 0＝73.所以点P 的坐标为(233，73)或(－233，73)．17．若直线y ＝kx 与曲线y ＝x 3－3x 2＋2x 相切，求k 的值． 解析 设切点坐标为(x 0，y 0)，y ′|x ＝x 0＝3x 20－6x 0＋2＝k .若x 0＝0，则k ＝2.若x 0≠0，由y 0＝kx 0，得k ＝y 0x 0.∴3x 20－6x 0＋2＝y 0x 0，即3x 20－6x 0＋2＝x 30－3x 20＋2x 0x 0.解之，得x 0＝32. ∴k ＝3×(32)2－6×32＋2＝－14.综上，k ＝2或k ＝－14.16．已知函数f (x )＝2x 3＋ax 与g (x )＝bx 2＋c 的图像都过点P (2,0)，且在点P 处有公共切线，求f (x )、g (x )的表达式．解析 ∵f (x )＝2x 3＋ax 的图像过点P (2,0)， ∴a ＝－8.∴f (x )＝2x 3－8x .∴f ′(x )＝6x 2－8. 对于g (x )＝bx 2＋c 的图像过点P (2,0)，则4b ＋c ＝0. 又g ′(x )＝2bx ，∴g ′(2)＝4b ＝f ′(2)＝16. ∴b ＝4.∴c ＝－16. ∴g (x )＝4x 2－16. 综上可知，f (x )＝2x 3－8x ，g (x )＝4x 2－16.1．已知直线l 1为曲线y ＝x 2＋x －2在点(1,0)处的切线，l 2为该曲线的另一条切线，且l 1⊥l 2.(1)求直线l 1，l 2的方程；(2)求由直线l 1，l 2和x 轴所围成的三角形的面积．分析 (1)求曲线在某点处的切线方程的步骤：先求曲线在这点处的导数，这点对应的导数值即为过此点切线的斜率，再用点斜式写出直线方程；(2)求面积用S ＝12a ·h 即可完成．解析 (1)因为y ′＝2x ＋1，则直线l 1的斜率k 1＝2×1＋1＝3，则直线l 1的方程为y ＝3x －3，设直线l 2过曲线y ＝x 2＋x －2上的点B (x0,y0)，因为l 1⊥l 2。
用导数求切线方程
用导数求切线方程
“用导数求切线方程”是指利用导数的性质，通过求函数某一点处的导数，来求得该点处函数的切线方程。
首先，我们回顾下梯形法则：函数f(x)在某一点处的导数f'(x)就是函数在该点上的切线斜率。
可以看出，如果能够求出函数某一点处的导数，就已经可以知道这个点处函数的切线。
其次，我们来看看如何用导数求切线方程。
假设函数f(x)在点A(x0,y0)处有定义，要求点A处函数的切线方程，只需要依据梯形法则，先计算出函数f(x)在点A处的导数f'(x0)，然后根据梯形法则，可以知道点A处函数的切线斜率为f'(x0)。
接下来，根据直线的斜截式：y=kx+b，我们可以知道点A处函数的切线方程为：y-y0=f'(x0)(x-x0)，其中，
k=f'(x0)，b=y0-f'(x0)x0。
最后，由于我们已经知道点A处函数的切线斜率
f'(x0)以及点A的横纵坐标，所以我们就可以得到点A处函数的切线方程：y-y0=f'(x0)(x-x0)。
综上所述，用导数求切线方程的步骤是：首先，使用梯形法则求出函数在某一点处的导数；然后，根据直线的斜截式，得到函数在该点处的切线方程；最后，根据函数
在该点处的导数及横纵坐标，求得该点处函数的切线方程。
专题一用导数求切线方程四种类
用导数求切线方程的四种种类求曲线的切线方程是导数的重要应用之一，用导数求切线方程的要点在于求出切点P(x，y)及斜率，其求法为：设P(x，y)是曲线yf(x)上的一点，则以P的切点的切线方程为：yy0f(x)(x x)．若曲线f(x)在点P(x0，f(x0))的切线平行于y轴（即导数不存在）时，由切线定义知，切线方程为xx．下边例析四种常有的种类及解法．种类一：已知切点，求曲线的切线方程此类题较为简单，只须求出曲线的导数f(x)，并代入点斜式方程即可．例1曲线yx33x21在点(1，1)处的切线方程为（）Ａ．y3x 4Ｂ．y3x 2Ｃ．y4x3Ｄ．y4x51解：由f(x)3x26x则在点(1，1)处斜率k f(1)3，故所求的切线方程为y(1)3(x1)，即y3x2，因此选Ｂ．练习：1．设f′(x0)＝0，则曲线A．不存在C．与x轴垂直y＝f(x)在点(x0，f(x0))处的切线(B．与x轴平行或重合D．与x轴斜交)答案B2.已知函数y＝f(x)的图像如右图所示，则f′(xA )与f′(xB)的大小关系是()A．f′(x A)>f′(x B)B．f′(x A)<f′(x B)C．f′(x A)＝f′(x B)D．不可以确立答案B2．曲线y＝－2x2＋1在点(0,1)处的切线的斜率是()A．－4B．0C．4D．不存在答案B10．已知曲线y＝2x3上一点A(1,2)，则A处的切线斜率等于()A．2B．42D．6C．6＋6·Δx＋2·(Δx)答案D4．函数y＝sin2x的图像在π1处的切线的斜率是() 6，4答案D剖析将函数y＝sin2x看作是由函数y＝u2，u＝sinx复合而成的．分析∵y′＝2sinxcosx，πππ3∴y′|x ＝6＝2sincos＝2661在点7)处切线的倾斜角为()2．曲线y＝x3－2(－1，－33A．30°B．45°C．135°D．60°答案B6．y＝x3的切线倾斜角的范围为________．π答案[0，2)分析k＝y′＝3x2≥0.8．设点P是曲线y＝x3－ 3x＋23上的随意一点，点P处切线倾斜角为α，则角α的取值范围是()∪5π，π26∪π，π3π答案D分析由y′＝3x2－3，易知y′≥－3，即tanα≥－3.20≤α<2或3π≤α<π.14．已知曲线C：y＝x3，求在曲线C上横坐标为1的点处的切线方程．分析将x＝1代入曲线C的方程得y＝1，∴切点P(1,1)．Δy x＋Δx3－x3∵y′＝lim＝limΔxΔxΔx→0Δx→0πlim3x2Δx＋3xΔx2＋Δx3ΔxΔx→0lim[3x2＋3xΔx＋(Δx)2]＝3x2，Δx→0y′|x＝1＝3.∴过P点的切线方程为y－1＝3(x－1)，即3x－y－2＝0.114．求曲线y＝sinx在点A(6，2)处的切线方程．分析∵y＝sinx，∴y′＝cosx.ππ331y′|x＝6＝cos6＝2，k＝2.3π∴切线方程为y－2＝2(x－6)．化简得6 3x－12y＋6－3π＝0.x6．曲线y＝x－2在点(1，－1)处的切线方程为()A．y＝x－2B．y＝－3x＋2C．y＝2x－3D．y＝－2x＋1答案D例3求曲线y＝1在点(4，1)处的切线方程．x2－3x2【思路剖析】将函数变形为y＝(x2－3x)－12，将其看做是由函数y＝u－12、u＝x2－3x复合而成．【分析】∵y＝1＝(x2－3x)－1，x2－3x2∴y′＝－1(x2－3x)－3·(x2－3x)′22＝－1(x2－3x)－3·(2x－3)．2211∴曲线y＝在点(4，)处的切线斜率为x2－3x21 (4235k＝y′|x＝4＝－－3×4)－·(2×4－3)＝－.22161∴曲线在点(4，2)处的切线方程为15y－2＝－16(x－4)，即5x＋16y－28＝0.研究3本题不要将函数y＝1看做是由y＝1，u＝v，vx2－3xu＝x2－3x三个函数复合而成的，这样求导就麻烦了．思虑题3(1)曲线y＝3x2＋1在点(1,2)处的切线方程为__________________．【答案】3x－2y＋1＝01的水平切线方程是________．(2)y＝1－x2【分析】令y′＝0，得x＝0，∴y＝1.12．求曲线y＝2x－x3在点(－1，－1)处的切线的方程及此切线与x轴、y轴所围成的平面图形的面积．答案x＋y＋2＝0；21x8．曲线y＝e2在点(4，e2)处的切线与坐标轴所围三角形的面积为()e2B．4e2C．2e2D．e2答案D11x分析∵y′＝·e2，2∴切线的斜率k＝y′|x＝4＝12e2.1∴切线方程为y－e2＝2e2(x－4)．∴横纵截距分别为2，－e2，∴S＝e2，应选D.111．已知函数y＝f(x)的图像在点M(1，f(1))处的切线方程是y＝2x＋2，则f(1)＋f′(1)＝________.答案3分析f′(1)＝1，f(1)＝1×1＋2＝5，∴f(1)＋f′(1)＝3.2225．如图是函数f(x)及f(x)在点P处切线的图像，则f(2)＋f′(2)＝________.9 答案 28分析由题图知，切线方程为4x ＋错误!＝1，9f(2)＝·(1－4)＝4，f′(2)＝－错误!＝－错误!.9 9 9∴f(2)＋f′(2)＝4－8＝8.种类二：已知斜率，求曲线的切线方程此类题可利用斜率求出切点，再用点斜式方程加以解决．例2与直线2x y40的平行的抛物线y x 2的切线方程是（） Ａ．2xy30Ｂ．2xy30Ｃ．2xy10Ｄ．2xy1 02解：设P(x0，y0)为切点，则切点的斜率为y|xx 0 2x 0 2．∴x 0 1．由此获得切点(11)，．故切线方程为y12(x 1)，即2x y1 0，应选Ｄ． 评注：本题所给的曲线是抛物线，故也可利用法加以解决，即设切线方程为y2x b，代入y x2，得x22xb0，又因为0，得b1，应选Ｄ．练习：3．曲线y＝x3在点P处的切线斜率为3，则点P的坐标为() A．(－2，－8)B．(1,1)，(－1，－1)C．(2,8)11 D．(－，－)28答案B13．若曲线y＝2x3上某点切线的斜率等于6，求此点的坐标．2x0＋Δx3－2x30分析∵y′|x＝x0＝lim＝6x 20，Δx→06x20＝6.∴x0＝±1故.(1,2)，(－1，－2)为所求．3．已知曲线y＝x2－3lnx的一条切线的斜率为1，则切点的横坐42标为()A．3B．2C．1答案A分析1x－31131 y′＝x，由x－＝.22x2得x＝3或x＝－2.因为x>0，因此x＝3.3．已知曲线y＝f(x)在点P(x0，f(x0))处的切线方程为2x＋y＋1＝0，那么() A．f′(x0)＝0B．f′(x0)<0C．f′(x0)>0D．f′(x0)不可以确立答案B5．假如曲线y＝f(x)在点(x0，f(x0))处的切线方程为x＋2y－3＝0，那么()A．f′(x0)>0B．f′(x0)<0C．f′(x0)＝0D．f′(x0)不存在答案B7．在曲线y＝x2π上切线的倾斜角为的点是()4A．(0,0)B．(2,4)11)11)C．(，16D．(，424答案D2．若曲线y＝x4的一条切线l与直线x＋4y－8＝0垂直，则l的方程为()A．4x－y－3＝0B．x＋4y－5＝0C．4x－y＋3＝0D．x＋4y＋3＝0答案A分析∵l与直线x＋4y－8＝0垂直，∴l的斜率为4.∵y′＝4x3，∴由切线l的斜率是4，得4x3＝4，∴x＝1.∴切点坐标为(1,1)．∴切线方程为y－1＝4(x－1)，即4x－y－3＝0.应选A.11．已知P(－1,1)，Q(2,4)是曲线y＝x2上的两点，则与直线PQ平行的曲线y＝x2的切线方程是________．答案4x－4y－1＝04－1分析k＝2－－1＝1，又y′＝2x，令2x＝1，得1x＝2，从而1y＝4，∴切线方程为y－14＝1·(x－12)，即4x－4y－1＝0.13．假如曲线y＝x2＋x－3的某一条切线与直线y＝3x＋4平行，求切点坐标与切线方程．答案切点坐标为(1，－1)，切线方程为3x－y－4＝013．曲线y＝x3＋3x2＋6x－10的切线中，斜率最小的切线方程为______________．答案3x－y－11＝0分析y′＝3x2＋6x＋6＝3(x＋1)2＋3≥3，当且仅当x＝－1时取等号，当x＝－1，时y＝－14.∴切线方程为y＋14＝3(x＋1)，即3x －y－11＝0.19．设直线y＝2x＋b是曲线y＝lnx(x>0)的一条切线，则实数b的值为________．答案ln2－14．设曲线y＝ax2在点(1，a)处的切线与直线2x－y－6＝0平行，则a等于()A．11C．－2D．－1答案A14．设曲线y＝e ax在点(0,1)处的切线与直线x＋2y＋1＝0垂直，则a＝________.答案2分析由题意得y′＝ae ax，y′|x ＝＝ae a×0＝2，a＝2.10．函数f(x)＝asinax(a∈R)的图像过点P(2π，0)，而且在点P处的切线斜率为4，则f(x)的最小正周期为()A．2πB．π答案B分析22πa. f′(x)＝acosax，∴f′(2＝π)acos2又asin2πa＝0，∴2πa＝kπ，k∈Z.f′(2＝π)a2coskπ＝4，∴a＝±2.2π∴T＝|a|＝π.6．曲线y＝ln(2x－1)上的点到直线2x－y＋3＝0的最短距离是() B．25C．3 5D．0答案A2分析y′＝2x－1＝2，∴x＝1.∴切点坐标为(1,0)．由点到直线的距离公式，得d＝|2×1－0＋3|＝5.22＋1219．曲线y＝x(x＋1)(2－x)有两条平行于y＝x的切线，则两切线之间的距离为________．16答案272分析y＝x(x＋1)(2－x)＝－x3＋x2＋2x，y′＝－3x2＋2x＋2，令－3x2＋2x＋2＝1，得1x1＝1或x2＝－3.114∴两个切点分别为(1,2)和(－3，－27)．切线方程为x－y＋1＝0和x－y－275＝0.5|1＋|2d＝2＝27.27种类三：已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法．6．以下说法正确的选项是()A．曲线的切线和曲线有交点，这点必定是切点B．过曲线上一点作曲线的切线，这点必定是切点C．若f′(x0)不存在，则曲线y＝f(x)在点(x0，f(x0))处无切线D．若曲线y＝f(x)在点(x0，f(x0))处有切线，则f′(x0)不必定存在答案D例3求过曲线yx32x上的点(1，1)的切线方程．3解：假想P(x0，y0)为切点，则切线的斜率为y|x x03x022．∴切线方程为yy0(3x22)(x x)．y(x32x)(3x22)(xx0)．又知切线过点(1，1)，把它代入上述方程，得1(x032x)(3x22)(1x)．解得1．x1，或x02故所求切线方程为y (12)(32)(x1)，或y1132x1，842即xy20，或5x4y10．评注：能够发现直线 5x 4y 10其实不以(1，1)为切点，其实是经过了点(1，1)且以 1 7为切点的直线．这说明过曲线上一点的切线，， 2 8该点未必是切点，解决此类问题可用待定切点法． 练习：种类四：已知过曲线外一点，求切线方程此类题可先设切点，再求切点，即用待定切点法来求解．例4求过点(2，0)且与曲线y1相切的直线方程． x4解：设P(x0，y0)为切点，则切线的斜率为 y|xx 0 1．x 20 ∴切线方程为yy 0 1(x x 0) ，即 y 1 1(xx 0) ．x 0 2 x 0 x0 2又已知切线过点(2，0)，把它代入上述方程，得 1 1x0 2(2x 0)．x0 解得x 01，y 0 1 1，即xy20．x 0评注：点(2，0)其实是曲线外的一点，但在解答过程中却无需判 断它确实切地点，充足反应出待定切点法的高效性例5 已知函数yx 33x ，过点A(016)， 作曲线yf(x)的切线，求此切线方程．5解：曲线方程为yx 33x ，点A(016)，不在曲线上．设切点为M(x 0，y 0)，则点M 的坐标知足y 0x033x 0．因f(x 0)3(x2 1)，故切线的方程为yy 03(x21)(x x0)．点A(016)，在切线上，则有16(x 0 3 3x 0) 3(x0 2 1)(0x 0)．化简得x 038，解得x0 2．因此，切点为M(2，2)，切线方程为9x y 160．评注：此类题的解题思路是，先判断点A能否在曲线上，若点A在曲线上，化为种类一或种类三；若点A不在曲线上，应先设出切点并求出切点．练习：17．已知曲线方程为y＝x2，求过A(3,5)点且与曲线相切的直线方程．分析解法一设过A(3,5)与曲线y＝x2相切的直线方程为y－5k(x－3)，即y＝kx＋5－3k.y＝kx＋5－3k由y＝x2，得x2－kx＋3k－5＝0.k2－4(3k－5)＝0，整理得(k－2)(k－10)＝0.k＝2或k ＝10.所求的直线方程为2x－y－1＝0,10x－y－25＝0.解法二设切点P的坐标为(x0，y0)，由y＝x2，得y′＝2x.y′|x＝x0＝2x0.5－y0＝2x0.又y0＝2x0，代入上式整理，得x0＝1或x0＝由已知kPA＝2x0，即3－x05.18．已知曲线S：y＝3x－x3及点P(2,2)，则过点P可向S引切线，其切线条数为()A．0B．1 C．2D．3答案D分析明显P不在S上，设切点为(x0，y0)，由y′＝3－3x2，得y′|x＝x0＝3－3x20.切线方程为y－(3x0－x30)＝(3－3x20)(x－x0)．P(2,2)在切线上，2－(3x0－x30)＝(3－3x20)(2－x0)，即x30－3x20＋2＝0.(x0－1)(x20－2x0－2)＝0.由x0－1＝0，得x0＝1.由x20－2x0－2＝0，得x0＝1±3.∵有三个切点，∴由P向S作切线能够作3条．综合练习：10．已知f(x)＝x2＋2xf′(1)，则f′(0)等于()A．0B．－4C．－2D．2答案B分析f′(x)＝2x＋2f′(1)，令x＝1，得f′(1)＝2＋2f′(1)，∴f′(1)＝－2.f′(0)＝2f′(1)＝－4.12．设函数f(x)＝g(x)＋x2，曲线y＝g(x)在点(1，g(1))处的切线方程为y＝2x＋1，则曲线y＝f(x)在点(1，f(1))处的切线的斜率为()1A．4B．－41C．2D．－2答案A分析依题意得f′(x)＝g′(x)＋2x，f′(1)＝g′(1)＋2＝4，选A.15．(1)求过曲线y＝e x上点P(1，e)且与曲线在该点处的切线垂直的直线方程；(2)曲线y＝15x5上一点M处的切线与直线y＝－x＋3垂直，求此切线方程．分析(1)∵y′＝e x，∴曲线在点P(1，e)处的切线斜率是y′|x＝1＝e.1∴过点P且与切线垂直的直线的斜率为k＝－e.1∴所求直线方程为y－e＝－e(x－1)，即x＋ey－e2－1＝0.(2)∵切线与y＝－x＋3垂直，∴切线斜率为 1.又y′＝x4，令x4＝1，∴x＝±1.∴切线方程为5x－5y－4＝0或5x－5y＋4＝0.4．y＝ax2＋1的图像与直线y＝x相切，则a＝()D．1答案B分析由已知{y ＝ax 2＋1，y ＝x 有独一解，即x ＝ax 2＋1，ax 2－x ＋1＝0有独一解，1∴Δ＝1－4a ＝0，∴a ＝4.15．点P 在曲线y ＝f(x)＝x 2＋1上，且曲线在点P 处的切线与曲线y ＝－2x 2－1相切，求点P 的坐标．分析 设P(x 00 2 ＋1. 00，y)，则y ＝x0 x 0＋Δx 2＋1－ x 02＋1 ＝2x 0. f′(x)＝lim ΔxΔx→0因此过点P 的切线方程为y －y0＝2x0(x －x0)，即y ＝2xx ＋1－x 2.00而此直线与曲线y ＝－2x 2－1相切，因此切线与曲线y ＝－2x 2－1只有一个公共点．由{ y ＝2x 02 2 0 y ＝－2x －1， 得x ＋1－x ，2 22x ＋2x0x ＋2－x0＝0.2 2即＝4x 0－8(2－x)＝0.±23 7解得x 0＝ 3 ，y0＝.3因此点P 的坐标为(23，7 )或(－ 2 3 3，7 )．3 3 3 17．若直线y ＝kx 与曲线y ＝x 3－3x 2＋2x 相切，求k 的值．分析 设切点坐标为(x 0 0 0 20 0，y)，y′|x＝x ＝3x －6x ＋2＝k.若x 0 0 0 0y0 .＝0，则k ＝2.若x ≠0，由y ＝kx ，得k ＝ x ∴3x 02－6x 0＋2＝y，x0即3x0203203x－3x＋2x000－6x＋2＝x0.解之，得x＝2.3231∴k＝3×(－6×＋2＝－4.2)2综上，k＝2或k＝－1.416．已知函数f(x)＝2x3＋ax与g(x)＝bx2＋c的图像都过点P(2,0)，且在点P处有公共切线，求f(x)、g(x)的表达式．分析∵f(x)＝2x3＋ax的图像过点P(2,0)，a＝－8.∴f(x)＝2x3－8x.∴f′(x)＝6x2－8.关于g(x)＝bx2＋c的图像过点P(2,0)，则4b＋c ＝0.又g′(x)＝2bx，∴g′(2)＝4b＝f′(2)＝16.b＝4.∴c＝－16.∴g(x)＝4x2－16.综上可知，f(x)＝2x3－8x，g(x)＝4x2－16.1．已知直线l1为曲线y＝x2＋x－2在点(1,0)处的切线，l2为该曲线的另一条切线，且l1⊥l2.(1)求直线l1，l2的方程；(2)求由直线l1，l2和x轴所围成的三角形的面积．剖析(1)求曲线在某点处的切线方程的步骤：先求曲线在这点处的导数，这点对应的导数值即为过此点切线的斜率，再用点斜式写出1直线方程；(2)求面积用S＝2a·h即可达成．分析(1)因为y′＝2x＋1，则直线l1的斜率k1＝2×1＋1＝3，则直线l1的方程为y＝3x－3，设直线l2过曲线y＝x2＋x－2上的点B(x0,y0)，因为l1⊥l2。
利用导数求抛物线切线方程的三种问题类型
利用导数求抛物线切线方程的三种问题类型问题类型一：已知抛物线上一点求切线方程已知抛物线方程为 $y=ax^2+bx+c$，且已知抛物线上一点为$(x_1, y_1)$，求该点处的切线方程。
解题步骤如下：1. 求出抛物线方程的导数 $\frac{dy}{dx}$。
2. 将已知点 $(x_1, y_1)$ 代入导数 $\frac{dy}{dx}$ 中，求出切线的斜率 $k$。
3. 使用点斜式来表示切线方程，即 $y-y_1=k(x-x_1)$。
问题类型二：已知切线斜率求切线方程已知抛物线方程为$y=ax^2+bx+c$，且已知切线的斜率为$k$，求切线方程。
解题步骤如下：1. 求出抛物线方程的导数 $\frac{dy}{dx}$。
2. 将切线的斜率 $k$ 代入导数 $\frac{dy}{dx}$ 中，得到一个方程。
3. 解方程，求出该方程对应的横坐标 $x$。
4. 将求得的横坐标 $x$ 代入抛物线方程中，求出纵坐标 $y$。
5. 使用点斜式来表示切线方程，即 $y-y=k(x-x_1)$，其中 $(x_1, y_1)$ 为切点坐标。
问题类型三：已知抛物线与切线重合求切点坐标已知抛物线方程为$y=ax^2+bx+c$，且已知抛物线与切线重合，求切点的坐标。
解题步骤如下：1. 求出抛物线方程的导数 $\frac{dy}{dx}$。
2. 将导数$\frac{dy}{dx}$ 与抛物线方程相等，得到一个方程。
3. 解方程，求出该方程对应的横坐标 $x$。
4. 将求得的横坐标 $x$ 代入抛物线方程中，求出纵坐标 $y$。
5. 切点的坐标为 $(x, y)$。
以上是利用导数求抛物线切线方程的三种问题类型及解题步骤。
希望对你有所帮助！。
用导数求切线方程的四种类型[精选.]
![用导数求切线方程的四种类型[精选.]](https://img.taocdn.com/s3/m/61a637510740be1e650e9aff.png)
用导数求切线方程的四种类型浙江 曾安雄求曲线的切线方程是导数的重要应用之一，用导数求切线方程的关键在于求出切点00()P x y ，及斜率，其求法为：设00()P x y ，是曲线()y f x =上的一点，则以P 的切点的切线方程为：000()()y y f x x x '-=-．若曲线()y f x =在点00(())P x f x ，的切线平行于y 轴（即导数不存在）时，由切线定义知，切线方程为0x x =．下面例析四种常见的类型及解法． 类型一：已知切点，求曲线的切线方程此类题较为简单，只须求出曲线的导数()f x '，并代入点斜式方程即可．例1 曲线3231y x x =-+在点(11)-，处的切线方程为（ ）Ａ．34y x =- Ｂ．32y x =-+ Ｃ．43y x =-+Ｄ．45y x =-解：由2()36f x x x '=-则在点(11)-，处斜率(1)3k f '==-，故所求的切线方程为(1)3(1)y x --=--，即32y x =-+，因而选Ｂ．类型二：已知斜率，求曲线的切线方程此类题可利用斜率求出切点，再用点斜式方程加以解决． 例2 与直线240x y -+=的平行的抛物线2y x =的切线方程是（ ）Ａ．230x y -+= Ｂ．230x y --= Ｃ．210x y -+=Ｄ．210x y --=解：设00()P x y ，为切点，则切点的斜率为0022x xy x ='==|．01x =∴．由此得到切点(11)，．故切线方程为12(1)y x -=-，即210x y --=，故选Ｄ．评注：此题所给的曲线是抛物线，故也可利用∆法加以解决，即设切线方程为2y x b =+，代入2y x =，得220x x b --=，又因为0∆=，得1b =-，故选Ｄ．类型三：已知过曲线上一点，求切线方程过曲线上一点的切线，该点未必是切点，故应先设切点，再求切点，即用待定切点法．例3求过曲线32y x x =-上的点(11)-，的切线方程． 解：设想00()P x y ，为切点，则切线的斜率为02032x xy x ='=-|． ∴切线方程为2000(32)()y y x x x -=--．320000(2)(32)()y x x x x x --=--．又知切线过点(11)-，，把它代入上述方程，得3200001(2)(32)(1)x x x x ---=--．解得01x =，或012x =-．故所求切线方程为(12)(32)(1)y x --=--，或13112842y x ⎛⎫⎛⎫⎛⎫--+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，即20x y --=，或5410x y +-=．评注：可以发现直线5410x y +-=并不以(11)-，为切点，实际上是经过了点(11)-，且以1728⎛⎫- ⎪⎝⎭，为切点的直线．这说明过曲线上一点的切线，该点未必是切点，解决此类问题可用待定切点法．类型四：已知过曲线外一点，求切线方程此类题可先设切点，再求切点，即用待定切点法来求解．例4 求过点(20)，且与曲线1y x=相切的直线方程．解：设00()P x y ，为切点，则切线的斜率为0201x xy x ='=-|．∴切线方程为00201()y y x x x -=--，即020011()y x x x x -=--． 又已知切线过点(20)，，把它代入上述方程，得02011(2)x x x -=--． 解得000111x y x ===，，即20x y +-=．评注：点(20)，实际上是曲线外的一点，但在解答过程中却无需判断它的确切位置，充分反映出待定切点法的高效性．例5 已知函数33y x x =-，过点(016)A ，作曲线()y f x =的切线，求此切线方程．解：曲线方程为33y x x =-，点(016)A ，不在曲线上．设切点为00()M x y ，， 则点M 的坐标满足30003y x x =-．因200()3(1)f x x '=-，故切线的方程为20003(1)()y y x x x -=--．点(016)A ，在切线上，则有32000016(3)3(1)(0)x x x x --=--．化简得308x =-，解得02x =-．所以，切点为(22)M --，，切线方程为9160x y -+=．评注：此类题的解题思路是，先判断点A 是否在曲线上，若点A 在曲线上，化为类型一或类型三；若点A 不在曲线上，应先设出切点并求出切点．在初中数学中，曲线的切线没有一般的定义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
切线方程的求法
●基础知识总结和逻辑关系
一、 函数的单调性
求可导函数单调区间的一般步骤和方法:
1) 确定函数的()f x 的定义区间；
2) 求'()f x ，令'()0f x =，解此方程，求出它在定义区间内的一切实根；
3) 把函数()f x 的无定义点的横坐标和上面的各实数根按由小到大的顺序排列起来，
然后用这些点把函数()f x 的定义区间分成若干个小区间；
4) 确定'()f x 在各个区间内的符号，由'()f x 的符号判定函数()f x 在每个相应小区
间内的单调性.
二、 函数的极值
求函数的极值的三个基本步骤
1) 求导数'()f x ；
2) 求方程'()0f x =的所有实数根；
3) 检验'()f x 在方程'()0f x =的根左右的符号，如果是左正右负（左负右正），则()
f x 在这个根处取得极大（小）值.
三、 求函数最值
1) 求函数()f x 在区间(,)a b 上的极值；
2) 将极值与区间端点函数值(),()f a f b 比较，其中最大的一个就是最大值，最小的一个就
是最小值.
四利用导数证明不等式
1） 利用导数得出函数单调性来证明不等式
我们知道函数在某个区间上的导数值大于（或小于）0时，则该函数在该区间上单调递增（或递减）.因而在证明不等式时，根据不等式的特点，有时可以构造函数，用导数证明该函数的单调性,然后再用函数单调性达到证明不等式的目的.即把证明不等式转化为证明函数的单调性.具体有如下几种形式：
① 直接构造函数，然后用导数证明该函数的增减性；再利用函数在它的同一单调递增（减）
区间，自变量越大，函数值越大（小），来证明不等式成立.
② 把不等式变形后再构造函数,然后利用导数证明该函数的单调性，达到证明不等式的目
的.
2） 利用导数求出函数的最值（或值域）后，再证明不等式.
导数的另一个作用是求函数的最值. 因而在证明不等式时，根据不等式的特点，有时可以构造函数，用导数求出该函数的最值；由当该函数取最大（或最小）值时不等式都成立，可得该不等式恒成立.从而把证明不等式问题转化为函数求最值问题.
●解题方法总结和题型归类
1导数的几何意义及切线方程的求法
1）曲线y ＝f (x )“在”点P (x 0，y 0)处的切线与“过”点P (x 0，y 0)的切线的区别： 曲线y ＝f (x )在点P (x 0，y 0)处的切线是指P 为切点，若切线斜率存在时，切线斜率为k ＝f ′(x 0)，是唯一的一条切线；曲线y ＝f (x )过点P (x 0，y 0)的切线，是指切线经过P 点，点P 可以是切点，也可以不是切点，而且这样的直线可能有多条．
2）解决方案：解这类问题的关键就是抓住切点.看准题目所求的是“在曲线上某点处的切线方程”还是“过某点的切线方程”，然后求某点处的斜率，用点斜式写出切线方程.
【题】求过曲线cos y x =上点1
(,)32
P π且与在这点的切线垂直的直线方程.
【答案】：22032
x π--+= 【难度】*
【点评】
【题】已知曲线3:2C y x x =+，按下列条件求切线方程：
（1）切线过曲线C 上一点(1,3)；
（2）切线过曲线C 外一点(1,2)；
（3）切线的斜率为2.
【答案】：（1）520x y --=或11410x y -+=
（2）20x y -=或354270x y --=
（3）20x y -=
【难度】**
【点评】求切线方程要讨论过点是否为切点，（1）如果是切点，利用000()()y y f x x x '-=-求出切线方程。
（2）不是切点，①设出切点11(,)M x y ，②写出过切点的切线方程111()()y y f x x x '-=-，③将点00(,)P x y 带入，求出x1，④讲x1的值带入，
11
1()()y y f x x x '-=-可得到切线方程。
【题】曲线313y x x =+在点4(1,)3
处的切线与坐标轴围成的三角形面积为( )
A. 19
B. 29
C. 13
D. 23
【答案】：A
【难度】**
【题】.点P 在曲线323
y x x =-+上移动，设点P 处切线的倾斜角为α，则角α的取值范围是（）
A. [0,]2π
B. 3[0,)[,)24πππ
C. 3[,)4
ππ D. 3(,]24
ππ 【答案】: B
【难度】**
【题】已知曲线33y x x =-，分别求满足下述条件的的切线方程。
（1）在点(0,0)P 处；
（2）过点(0,16)M -；
（3）过点(2,2)N 。
【答案】：（1）3y x =-
（2）9160x y --=
（3）2y =
【难度】**
【题】.设P 为曲线2:23C y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围是[0,]4
π
，则点P 横坐标的取值范围是( ) A. 1[1,]2
-- B. [1,0]- C. [0,1] D. 1[,1]2
【答案】: A
【难度】**
【题】设()f x 是偶函数,若曲线()y f x =在点(1,(1))f 处的切线
的斜率为1,则该曲线在(1,(1))f --处的切线的斜
率为_________.
【答案】：1-
【难度】*
【题】设P 是函数ln y x =图像上的动点，则点P 到直线y x =的距离的最小值为________.
【答案】：2
【难度】**
【题】设函数2()f x x ax b =++，()()x g x e cx d =+，若曲线
()y f x =和曲线()y g x =都过点(0,2)P ，
且在点P 处有相同的切线42y x =+，求a ，b ，c ，d 的值.
【答案】：a =4,b =2,c =2,d =2
【难度】**
【题】已知函数3()f x x =的切线的斜率等于3，则切线有
( )
A. 1条
B. 2条
C. 3条
D.不确定
【答案】: B
【难度】**
【题】设函数()ln f x x =，当120x x <<，下列结论正确的是
( )
A. 12112()()1f x f x x x x ->-
B. 12212
()()1f x f x x x x ->- C. 12112
()()1f x f x x x x +<+ D. 以上都不对 【答案】: A
【难度】**
【题】若函数3211()(1)(2)332
f x x f x f x ''=+-+，则()f x 在点(0,(0))f 处切线的倾斜角为( )
A. 4π
B. 3π
C. 23π
D. 34
π 【答案】: D
【难度】***
【题】求曲线ln y x =在点(,1)M e 处的切线的斜率和切线的方程。
【答案】：1y x e
= 【难度】**
【题】（1）求曲线32y x x =-在点(1,1)A -处的切线方程
（2）求过曲线32y x x =-上的点(1,1)A -处的切线方程
【答案】:(1)20x y --=,
(2) 20x y --=或5410x y +-=
【难度】***
【题】在32()3610f x x x x =++-的切线中，斜率最小的切线方程为( )
A. 3110x y +-=
B. 360x y -+=
C. 3110x y --=
D. 3110x y --=
【答案】: D
【难度】**
【题】已知直线1y kx =+与曲线3y x ax b =++相切于点(1,3)，则b 的值为（）
A .3
B .3-
C .5
D .5-
【答案】:A
【难度】**
【题】曲线3231y x x =-+在点(1,1)-处的切线方程为（）
A. 34y x =-
B. 32y x =-+
C. 43y x =-+
D. 45y x =-
【答案】: B
【难度】** 【题】已知曲线2
3ln 4
x y x =-的一条切线的斜率为12，则切点的横坐标为( )
A. 3
B. 2
C. 1
D. 12
【答案】: A
【难度】**
【题】与直线240x y -+=的平行的抛物线2y x =的切线方程是( )
A. 230x y -+=
B. 230x y --=
C.210x y -+=
D. 210x y --=
【答案】: D
【难度】**
【题】求过点(2,0)且与曲线1y x
=相切的直线方程. 【答案】:20x y +-=
【难度】**
【题】已知函数2,1()(2),1
ax bx c x f x f x x ⎧++≥-=⎨--<-⎩其图像在点(1,(1))
f 处的切线方程为2+1y =x ，则它在点(3,(3))f --处的切线方程为()
A. 23y x =--
B. 23y x =-+
C. 23y x =-
D. 23y x =+
【答案】: A
【难度】***。