电磁场原理习题与解答(第4章)
电磁场与电磁波(第四版)习题解答
电磁场与电磁波(第四版）习题解答第1章习题习题1．1给定三个矢量A 、B 和C 如下:23x y z =+-A e e e ．4y z=-+B e e ，52x z =-C e e ,解:(1）22323)12(3)A x y z e e e A a e e e A+-===+-++- （2）2641x y z A B e e e -=+-==(3)(23)(4)11x y z y z A B e e e e e •=+-•-+=-（4）arccos135.5A B AB θ•===︒ (５)1711cos -=⋅=⋅⋅==B B A A B B A A A A AB Bθ(６）12341310502xy zx Y Z e e e A C e e e ⨯=-=---- (７)0418520502xy zx Y Z e e e B C e e e ⨯=-=++-()(23)(8520)42x Y Z x Y Z A B C e e e e e e •⨯=+-•++=-123104041xy zx Y Z e e e A B e e e ⨯=-=---- ()(104)(52)42x Y Z x Z A B C e e e e e ⨯•=---•-=-(8）()10142405502x y zx Y Z e e e A B C e e e ⨯⨯=---=-+-()1235544118520xy zx Y Z e e e A B C e e e ⨯⨯=-=-- 习题1．4给定两矢量 234x y z =+-A e e e 和 456x y z =-+B e e e ,求它们之间的夹角和 A 在 Ｂ上的分量。
解：29)4(32222=-++=A776)5(4222=+-+=B31)654()432(-=+-⋅-+=⋅z y x z y x e e e e e e B A则A 与B之间的夹角为131772931cos =⎪⎪⎭⎫ ⎝⎛⋅-=⎪⎪⎪⎭⎫⎝⎛⋅⋅=ar BA B A arcis ABθ A 在B上的分量为532.37731cos -=-=⋅=⋅⋅⋅==B B A BA B A A A A AB Bθ习题1.９用球坐标表示的场225rr =E e ， (1）求在直角坐标中点(3,4,5)--处的E 和x E ；(2）求在直角坐标中点(3,4,5)--处E 与矢量22x y z =-+B e e e 构成的夹角。
电磁场与电磁波第四章习题及参考答案
第四章 习题4-1、 电量为nC 500的点电荷，在磁场)(ˆ2.1T zB =中运动，经过点)5,4,3(速度为 s m y x/ˆ2000ˆ500+ 。
求电荷在该点所受的磁场力。
解：根据洛仑兹力公式B v q F⨯=N x y z y x 4491012ˆ103ˆ2.1ˆ)ˆ2000ˆ500(10500---⨯+⨯-=⨯+⨯⨯= N y x4103)ˆˆ4(-⨯-= 4-2、真空中边长为a 的正方形导线回路，电流为I ，求回路中心的磁场。
解：设垂直于纸面向下的方向为z 方向。
长为a 的线电流I 在平分线上距离为a/2的点上的磁感应强度为aIzB πμ2ˆ01= 因而，边长为a 的正方形导线回路在中心点上的磁感应强度为aIz B B πμ24ˆ401==题4-2图 题4-3图4-3、真空中边长为a 的正三角形导线回路，电流为I ，求回路中心的磁场.解：设垂直于纸面向下的方向为z 方向。
由例4-1知，长为a 的线电流I 在平分线上距离为b 的点上的磁感应强度为2201)2(ˆa b a bIz B +=πμ所以220)2(3ˆa b a bIz B +=πμ ，其中)6(2πtg a b =4-4、真空中导线绕成的回路形状如图所示，电流为I 。
求半圆中心处的磁场。
(c)题4-4 图解：设垂直于纸面向内的方向为z 方向。
由例4-2知，半径为a 的半圆中心处的磁场为aIz B 4ˆ01μ= （1）因为在载流长直导线的延长线上磁场为零，因此aIz B 4ˆ0μ= （2）由例4-1知，本题半无限长的载流长直导线在距离为a 处的磁场为aIz B πμ4ˆ02= 因此本题磁场为半圆环的磁场与两半无限长的直导线的磁场之和)2(4ˆ0+-=ππμaIz B （3）本题磁场为电流方向相反的两不同半径的半圆环的磁场之和，即)11(4ˆ0ba I zB -=μ 4-5、 在真空中将一个半径为a 的导线圆环沿直径对折，使这两半圆成一直角。
《电磁场与电磁波》课后习题解答(全)
（3）
【习题3.4】
解：（1）在区域中，传导电流密度为0，即J=0
将 表示为复数形式，有
由复数形式的麦克斯韦方程，可得电场的复数形式
所以，电场的瞬时值形式为
（2） 处的表面电流密度
（3） 处的表面电荷密度
（4） 处的位移电流密度
【习题3.5】
解：传导电流密度 （A/ ）
位移电流密度
【习题3.6】
（2）内导体表面的电流密度
（3）
所以，在 中的位移电流
【习题2.13】
解：（1）将 表示为复数形式:
则由时谐形式的麦克斯韦方程可得：
而磁场的瞬时表达式为
（2）z=0处导体表面的电流密度为
z=d处导体表面的电流密度为
【习题2.14】
已知正弦电磁场的电场瞬时值为
式中
试求：（1）电场的复矢量；
（2）磁场的复矢量和瞬时值。
由安培环路定律： ，按照上图所示线路积分有
等式左边
等号右边为闭合回路穿过的总电流
所以
写成矢量式为
将 代入得
【习题3.18】
解：当 时， ，
当 时， ，
这表明 和 是理想导电壁得表面，不存在电场的切向分量 和磁场的法向分量 。
在 表面，法线
所以
在 表面，法线
所以
【习题3.19】
证明：考虑极化后的麦克斯韦第一方程
（1）
和 （2）
若采用库仑规范，即 （3）
对（1）式两边取散度，有
将（2）、（3）式代入，得
故电流连续性也是满足的。
【习题4.3】解：
【习题4.4】
证明：因为 即
故 满足连续性方程。
另外， 满足洛仑兹条件。
电磁场与电磁波课后习题及答案四章习题解答
如题图所示为一长方形截面的导体槽，槽可视为无限长，其上有一块与槽相绝缘的盖板，槽的电位为零，上边盖板的电位为，求槽内的电位函数。
解根据题意，电位满足的边界条件为①②③根据条件①和②，电位的通解应取为题图由条件③，有两边同乘以，并从0到对积分，得到故得到槽内的电位分布两平行无限大导体平面，距离为，其间有一极薄的导体片由到。
上板和薄片保持电位，下板保持零电位，求板间电位的解。
设在薄片平面上，从到，电位线性变化，。
题图解应用叠加原理，设板间的电位为其中，为不存在薄片的平行无限大导体平面间（电压为）的电位，即；是两个电位为零的平行导体板间有导体薄片时的电位，其边界条件为：①②③根据条件①和②，可设的通解为由条件③有两边同乘以，并从0到对积分，得到故得到求在上题的解中，除开一项外，其他所有项对电场总储能的贡献。
并按定出边缘电容。
解在导体板（）上，相应于的电荷面密度则导体板上（沿方向单位长）相应的总电荷相应的电场储能为其边缘电容为如题图所示的导体槽，底面保持电位，其余两面电位为零，求槽内的电位的解。
解根据题意，电位满足的边界条件为①题图②③根据条件①和②，电位的通解应取为由条件③，有两边同乘以，并从0到对积分，得到故得到槽内的电位分布为一长、宽、高分别为、、的长方体表面保持零电位，体积内填充密度为的电荷。
求体积内的电位。
解在体积内，电位满足泊松方程（1）长方体表面上，电位满足边界条件。
由此设电位的通解为代入泊松方程（1），可得由此可得或（2）由式（2），可得故如题图所示的一对无限大接地平行导体板，板间有一与轴平行的线电荷，其位置为。
求板间的电位函数。
解由于在处有一与轴平行的线电荷，以为界将场空间分割为和两个区域，则这两个区域中的电位和都满足拉普拉斯方程。
而在的分界面上，可利用函数将线电荷表示成电荷面密度。
电位的边界条件为题图①②③由条件①和②，可设电位函数的通解为由条件③，有（1）（2）由式（1），可得（3）将式（2）两边同乘以，并从到对积分，有（4）由式（3）和（4）解得故如题图所示的矩形导体槽的电位为零，槽中有一与槽平行的线电荷。
电磁场与电磁波：第四章作业答案
由于轴对称性，两板间的磁场只有 分量，且在以 轴为中心、 为半径的圆周 上处处相等。于是由
可得
所以
（2）损耗功率瞬时值 为
平均损耗功率 为
（3）进入电容器的平均功率为
由此可见有
根据边界条件，在导线表面上电场的切向分量连续，即 。因此，在导线表面外侧的电场的切向分量为
又利用高斯定理，容易求得导线表面外侧的电场的法向分量为
故导线表面外侧的电场为
利用安培环路定理，可求得导线表面外侧的磁场为
故导线表面外侧的坡印廷矢量为
由内导体表面每单位长度进入其内部的功率
式中 是内导体单位长度的电阻。由此可见，由导线表面进入其内部的功率等于导体内的焦耳热损耗功率。
解坡印廷矢量的瞬时值为
故平均坡印廷矢量为
4.15在半径为 、电导率为 的无限长直圆柱导线中，沿轴向通以均匀分布的恒定电流 ，且导线表面上有均匀分布的电荷面密度 。
（1）导线表面外侧的坡印廷矢量 ；
（2）证明：由导线表面进入其内部的功率等于导线内的焦耳热损耗功率。
解：（1）当导线的电导率 为有限值时，导线内部存在沿电流方向的电场
4.9自由空间中的电磁场为
式中 。求：
（1）瞬时坡印廷矢量；
（2）平均坡印廷矢量；
（3）任一时刻流入如题4.9图所示的平行六面体（长 、横截面积为 ）中的净功率。
解（1）瞬时坡印廷矢量
（2）平均坡印廷矢量
（3）任一时刻流入如题4.9图所示的平行六面体中的净功率为
4.10已知某电磁场的复矢量为
式中 ， 为真空中的光速， 是波长。求：（1） 、 、 各点处的瞬时坡印廷矢量；（2）以上各点处的平均坡印廷矢量。
4.16由半径为 的两圆形导体平板构成一平行板电容器，间距为 ，两板间充满介电常数为 、电导率为 的媒质，如题4.16题所示。设两板间外加缓变电压 ，略去边缘效应，试求：
高等电磁场理论习题解答（作业）
⾼等电磁场理论习题解答（作业）第⼀章基本电磁理论1-1 利⽤Fourier 变换, 由时域形式的Maxwell ⽅程导出其频域形式。
（作1-2—1-3）解：付⽒变换和付⽒逆变换分别为：dt e t f F t j ?∞∞-=ωω)()(ωωπωd e F t f tj ?∞∞--=)(21)( 麦⽒⽅程：t D J H ??+=??ρρρtB E ??-=??ρρ0=??B ρρ=??D ρ对第⼀个⽅程进⾏付⽒变换：),(),(),ωωωr H dt e t r H dt e t r H t j tj ρρρρρρ??=??=??=∞∞-∞∞-（左端),(),(),(),(]),(),[ωωωωωωωr D j r J dte t r D j r J dt e t t r D t r J t j tj ρρρρρρρρρρρρ+=+=??+=??∞∞-∞∞-（右端（时谐电磁场） =??∴),(ωr H ρρ),(),(ωωωr D j r J ρρρρ+同理可得：()()ωωω,,r B j r H ??ρρ-=??()0,=??ωr B ρ()()ωρω,,r r D ?ρ?=??上⾯四式即为麦式⽅程的频域形式。
1-2 设各向异性介质的介电常数为=300420270εε当外加电场强度为 (1) 01E x e E =；(2)02E y e E =；(3) 03E z e E =；(4) )2(04y x E e e E +=；(5))2(05y x E e e E +=求出产⽣的电通密度。
（作1-6）解：()),(,t r E t r D ?Θ?=ε=333231232221131211εεεεεεεεεz y x D D D 即z y x E E E 将E 分别代⼊，得：=??=??????????027003000420270000111E E D D D z y x εε )?2?7(001y x E D +=ε?=??=??????????042003000420270000322E E D D D z y x εε )?4?2(002y x E D +=ε? ????=??=??????????300003000420270000333E E D D D z y x εε z E D ?3003ε=? ??==010110230004202700000444E E E D D D z y x εε )?10?11(004y x E D +=ε? ==08160230004202700000555E E E D D D z y x εε )?8?16(005y x E D +=ε? 1-3 设各向异性介质的介电常数为=4222422240εε试求：(1) 当外加电场强度)(0z y x E e e e E ++=时，产⽣的电通密度D ；(2) 若要求产⽣的电通密度004E x εe D =，需要的外加电场强度E 。
电磁场三四章习题 ppt课件
习题3．如图所示，分界面左侧为磁导率μ→∞的 无限大导磁媒质，右侧媒质的磁导率为μ0，其中有一无 限长直导线平行于媒质的分界面，且与一矩形线圈共 面。
求：导线与矩形线圈的互感。
μ→∞ μ0
c
d ab
电磁场三四章习题
5
I ⊙ I
1m μ0
1m
μFE
电磁场三四章习题
2
精品资料
• 你怎么称呼老师？ • 如果老师最后没有总结一节课的重点的难点，你
是否会为老师的教学方法需要改进？ • 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭 • “不怕太阳晒，也不怕那风雨狂，只怕先生骂我
笨，没有学问无颜见爹娘 ……” • “太阳当空照，花儿对我笑，小鸟说早早早……”
第三四章复习题
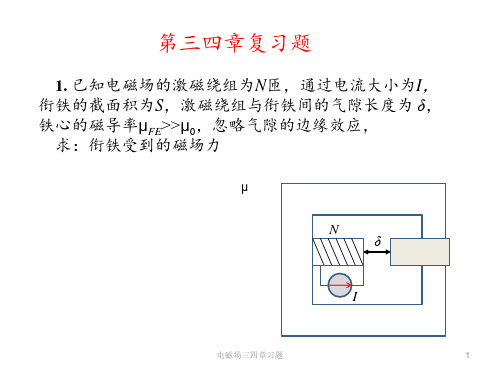
1. 已知电磁场的激磁绕组为N匝，通过电流大小为I，
衔铁的截面积为S，激磁绕组与衔铁间的气隙长度为 δ， 铁心的磁导率μFE>>μ0，忽略气隙的边缘效应，
求：衔铁受到的磁场力
μ
N δ
I
电磁场三四章习题
1
习题2.无限大铁磁平面( μFE>>μ0)上有一对平行的 长直载流直导线，导线半径R=1mm，如图所示。求单位 长度载流导线对的自感。
《电磁场与电磁波》习题参考答案
况下，电场和磁场可以独立进行分析。（ √ ）
12、静电场和恒定磁场都是矢量场，在本质上也是相同的。（ × ）
13、静电场是有源无旋场，恒定磁场是有旋无源场。（ √ ） 14、位移电流是一种假设，因此它不能象真实电流一样产生磁效应。（
×）
15、法拉第电磁感应定律反映了变化的磁场可以产生变化的电场。（ √ ） 16、物质被磁化问题和磁化物质产生的宏观磁效应问题是不
D.有限差分法
6、对于静电场问题，仅满足给定的泊松方程和边界条件，
而形式上不同的两个解是不等价的。（ × ）
7、研究物质空间内的电场时，仅用电场强度一个场变量不能完全反映物 质内发生的静电现象。（ √ ）
8、泊松方程和拉普拉斯方程都适用于有源区域。（ × ）
9、静电场的边值问题，在每一类的边界条件下，泊松方程或拉普拉斯方 程的解都是唯一的。（ √ ）
是（ D ）。
A．镜像电荷是否对称
B．电位所满足的方程是否未改变
C．边界条件是否保持不变 D．同时选择B和C
5、静电场边值问题的求解，可归结为在给定边界条件下，对拉普拉斯
方程的求解，若边界形状为圆柱体，则宜适用( B )。
A.直角坐标中的分离变量法
B.圆柱坐标中的分离变量法
C.球坐标中的分离变量法
两个基本方程：
3、写出麦克斯韦方程组，并简述其物理意义。
答：麦克斯韦方程组的积分形式：
麦克斯韦方程组的微分形式：
每个方程的物理意义： (a) 安培环路定理，其物理意义为分布电流和时变电场均为磁
场的源。 (b) 法拉第电磁感应定律，表示时变磁场产生时变电场，即动
磁生电。 (c) 磁场高斯定理，表明磁场的无散性和磁通连续性。 (d)高斯定理，表示电荷为激发电场的源。
电磁场与电池波第四章 习题答案1
4.3 若半径为 a、电流为 I 的无线长圆柱导体置于空气中，已知导体的磁导率为 μ0 ，求导体 内、外的磁场强度 H 和磁通密度 B。 解： （1）导体内：0 ≤ ρ <a 由安培环路定理， H • dl = I
l
∫
K
K
'
Iρ2 I 2 I = 2 .πρ = 2 a πa
'
所以， H1. 2πρ =
4.5 在下面的矢量中，哪些可能是磁通密度 B？如果是，与它相应的电流密度 J 为多少？ （1） F = aρ 解: ∇. F =
→ →
→
→
ρ
所以 F 不是磁通密度
→
1 ∂ 1 . ( ρ Fρ ) = .2 ρ =2 ≠ 0 ρ ∂ρ ρ
→
（2） F =- ax y+ a y x 解： ∇ . F = −
→
→
∂y ∂x + =0 所以 F 是磁通密度 ∂x ∂y
→ →
ax → → ∂ ∇ × B = μ0 J = ∂x −y
（3） F = ax x - a y y
→
→
ay ∂ ∂y x
→
az → ∂ =2 a z ∂z 0
→
所以
J=
2
→
μ0
az
→
∇ . F =0
→
F 是磁通密度
→
a x → → ∂ ∇ × B = μ0 J = ∂x x
由折射定律得
tan θ1 μ1 = tan θ 2 μ 2
所以 tan θ 2 =
μ2 tan θ1 μ1
θ 2 = 0.107 0
B2 = 0.13 × 10 −2 T
电磁场与电磁波第三版答案第四章
《电磁场与电磁波》——习题详解第四章 静态场的解4-1 一个点电荷 Q 与无穷大导体平面相距为 d ,如果把它移动到无穷远处,需要 作多少功? 解: 用镜像法, 相当于两个电荷关于 y = 0 平面向相反方向离开,当 Q 移到 y 处时,受到 的电场力为:y Qdy y xdF= Q2 4πε 0 (2 y ) 2-Q 此时移动 d y 需对电荷做功图 4-1dw = Fd y =移到无穷远处做的总功为:Q2 16πε 0 y 2dyW = dw = Fd y =d∫∫∞∫∞ dQ216πε 0 y 2dy=Q2 16πε 0 d当用外力将电荷 Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以在整个过程中,外力作的总功为Q2 8πε 0 d也可以用静电能计算,在移动以前,系统的静电能等于两个点电荷之间的相互 作用能:W=1 1 1 1 Q Q Q2 + (Q) q11 + q2 2 = Q = 2 2 2 4π ε 0 (2d ) 2 4π ε 0 (2d ) 8π ε 0 d移动点电荷到无穷远以后,系统的静电能为零.因此,在这个过程中,外力作 功等于系统静电能的增量,即外力作功为Q2 8πε 0 d.43习题四4-2 一个点电荷放在直角导体内部(如图 4-2),求出所有镜像电荷的位置和大小y-q r2 d r3O r1 r4rq ax -qq图 4-2 解:假设如图所示三个镜像电荷,则空间电荷分布为φ (r ) =v1 1 1 1 ( + ) 4πε 0 r1 r2 r3 r4q经检验:在 y = 0 平面上 φ ( r ) = 0 ,在 x = 0 平面上vφ (r ) = 0所以上述解为原问题的解.因此求得镜像电荷的位置和大小如图 4-2 所示,即vq 2 = q 位置 ( a, d ) , q3 = q 位置 ( a, d ) , q 4 = q 位置 (a, d )4-3 证明:一个点电荷 q 和一个带有电荷 Q ,半径为 R 的导体球之间的作用力为Rq Q + D q DRq F= 2 4π ε 0 D 2 (D R 2 ) 2 其中 D 是 q 到球心的距离 ( D > R ) . 证明:使用镜像法分析.由于导体球不接地,本身又带电 Q ,必须在导体球内 加上两个镜像电荷来等效导体球对外的影响.在距离球心 b = R / D 处,镜像电荷2为 q′ = Rq / D ;在球心处,镜像电荷为 q2 = Q q′ = Q + Rq / D .点电荷 q 受导 体球的作用力就等于球内两个镜像电荷对 q 的作用力,即44《电磁场与电磁波》——习题详解F= q2 q′ D 2 + ( D b) 2 4π ε 0 q Rq Rq Q + D q D = + R2 2 4π ε 0 D 2 2 (D ) D Rq Q + D DRq = 2 4π ε 0 D 2 (D R 2 ) 2 q4-4 两个点电荷 + Q 和 Q 位于一个半径为 a 的接地导体球的直径的延长线上, 分 别距离球心 D 和 D . (1) (2) 证明:镜像电荷构成一电偶极子,位于球心,偶极矩为 2a Q / D . 令 Q 和 D 分别趋于无穷,同时保持 Q / D 不变,计算球外的电场. 使用导体球面的镜像法和叠加原理分析.在球内加上两个镜像电荷:2 2 3 2解:(1)一个是 Q 在球面上的镜像电荷, 1 = aQ / D , q 距离球心 b1 = a / D ; 第二个是 Q 在球面上的镜像电荷, q2 = aQ / D ,距离球心 b2 = a / D .当距离较大时,镜像2电荷间的距离很小,等效为一个电偶极子,电偶极矩为p = q 1 (b1 b2 ) =(2) 2a 3Q D2球外任意点的电场等于四个点电荷产生的电场的叠加.设 + Q 和 Q 位于2坐标 z 轴上,当 Q 和 D 分别趋于无穷,同时保持 Q / D 不变时,由 + Q 和 Q 在空 间产生的电场相当于均匀平板电容器的电场,是一个均匀场,均匀场的大小为v 2Q / 4π ε 0 D 2 ,方向在 ez ,由镜像电荷产生的电场可以由电偶极子的公式计算.v E=p 4π ε 0 r3v v (er 2 cos θ + eθ sin θ )45习题四=4-5 2 a 3Q v v (er 2 cos θ + eθ sin θ ) 3 2 4π ε 0 r D接地无限大导体平板上有一个半径为 a 的半球形突起,在点 (0,0, d ) 处有一个 点电荷 q (如图 4-3),求导体上方的电z dq a bq2 -bq3-dq1 图 4-3位. 解:计算导体上方的电位时,要保持导 体平板部分和半球部分的电位都为零.先找平 面导体的镜像电荷 q1 = q ,位于 (0,0, d ) 处.再找球面镜像电荷 q2 = aq / d ,位于(0,0, b) 处,b = a 2 / d .当叠加这两个镜像电荷和原电荷共同产生的电位时,在导体平面上位于 (0,0,b) 处. 和球面上都不为零, 应当在球内再加上一个镜像电荷 q3 = aq / d , 这时,三个镜像电荷和原电荷共同产生的电位在导体平面和球面上都为零,而且三 个镜像电荷在要计算的区域以外. 导体上方的电位为四个点电荷电位的叠加,即=其中 q q1 q2 q3 + + + 4π ε 0 R r1 r2 r3 1R = [ x 2 + y 2 + ( z d ) 2 ]1 2 r1 = [ x 2 + y 2 + ( z + d ) 2 ]1 2 r2 = [ x 2 + y 2 + ( z b) 2 ]1 2 r3 = [ x 2 + y 2 + ( z + b) 2 ]1 24-6 求截面为矩形的无限长区域( 0 < x < a , 0 < y < b )的电位,其四壁的电位 为 ( x,0) = ( x, b) = 0 ,46《电磁场与电磁波》——习题详解 (0, y ) = 0U 0 y b , ( a, y ) = y U 0 (1 ), b 0 < y ≤ b/ 2 b/ 2 < y < b解:法一:由边界条件 ( x,0) = ( x, b) = 0 知,方程的基本解在 y 方向应该 为周期函数,且仅仅取正弦函数,即Yn = sin k n y(k n =nπ ) b在 x 方向,考虑到是有限区域,选取双曲正弦函数和双曲余弦函数,使用边界 (0, y ) = 0 条件,得出仅仅选取双曲正弦函数,即X n = sh nπ x b将基本解进行线性组合,得 = ∑ Cn shn =1∞nπ x nπ y sin b b待定常数由 x = a 处的边界条件确定,即 (a, y ) = ∑ Cn shn =1∞nπ a nπ y sin b b使用正弦函数的正交归一性质,有b nπ a C n sh = 2 b∫ (a, y) sin0bnπ y dy bb/2∫b/2 02 U0 y U b nπ y by nπ y nπ y sin d y = 0 cos sin b b b nπ b nπ b 0=U0 b b nπ b2 nπ cos sin 2 2nπ 2 nπ 2∫y nπ y U 0 1 sin dy b b/2 bb47习题四b 2 b nπ y U b nπ y by nπ y 0 = U 0 cos cos sin nπ b b / 2 b nπ b nπ b bb/2b nπ U 0 b nπ = U 0 sin + cos nπ cos 2 b nπ 2 nπ +化简以后得2U 0 b2 U b b nπ cos nπ 0 cos 2 b nπ b nπ 2b nπ a = C n sh b 2∫ (a, y) sin0bnπ y b nπ d y = 2U 0 2 2 sin b 2 nπ求出系数,代入电位表达式,得nπ 4U 2 sin nπ y sh nπ x = ∑ 2 02 nπ a b b n =1 n π sh b 4-7 一个截面如图 4-4 所示的长槽,向 y 方向无限延伸,两侧的电位是零,槽内∞siny → ∞ , → 0 ,底部的电位为 ( x,0) = U 0求槽内的电位. 解:法一:令 ( x, y ) = X ( x)Y ( y ) = 0 , 因边界条件y =0 =0 = U0 (0, y ) = (a, y ) = 0a图 4-4x所以 X(x) = Acos K x x + B sin K x xQ X ( x) = X (a) = 0求得A = 0 , Kx =nπ a( n = 1,2,3L )X ( x) = Bn sinnπ x ( n = 1,2,3L ) a48《电磁场与电磁波》——习题详解由 Kx + Ky = 0 得 所以 Y ( y ) = C n enπ y a22K y = K x K y = ± j22nπ a( n = 1,2,3L )+ Dn e nπ y a nyπ a nyπ a ( x, y ) =∑n =1 ∞∞(C n e+ Dn e )Bn sinnπ x a=∑n =1 ′ (C n enyπ a′ + Dn e nyπ a) sinnπ x a′ 由边界条件 ( x,+∞) = 0 可得 C n = 0所以 ( x, y ) =∑n =1∞′ Dn enπ y asinnπ x a再由边界条件 ( x,0) = U 0 代入可得∑n =1∞′ Dn e nπ 0 asinnπ x= a∑ D′ sinn n =1∞nπ x = U0 a再两边同乘以 sinmπ x ,并从 0 到 a 积分得 a 4U 0 2U 0 ′ Dn = (1 cos mπ ) = mπ mπ 0 所以槽内电位为∞m = 1,3,5L m = 2,4,6L ( x, y ) =4U 0 myπ mπ e a sin x mπ a m =1, 3, 5....∑=∑n =1∞( 2 n 1) yπ 4U 0 (2n 1)π a x e sin a (2n 1)π法二:由于在 x = 0 和 x = a 两个边界的电位为零,故在 x 方向选取周期解, 且仅仅取正弦函数,即X n = sin k n xnπ kn = a 49习题四在 y 方向,区域包含无穷远处,故选取指数函数,在 y → ∞ 时,电位趋于零,所以 选取Yn = e kn y由基本解的叠加构成电位的表示式为nπ x nπa y e = C n sin a n =1∑∞待定系数由 y = 0 的边界条件确定.在电位表示式中,令 y = 0 ,得U 0 = ∑ Cn sinn =1∞nπ x aCna = 2∫a0U 0 sinaU 0 nπ x dx = (1 cos nπ ) nπ a当 n 为奇数时, Cn =4U 0 ,当 n 为偶数时, Cn = 0 .最后,电位的解为 nπnπ y a=4-84U nπ x ∑,5 nπ0 sin a e n =1, 3∞若上题的底部的电位为 ( x,0) = U 0 sin重新求槽内的电位3π x a解:同上题,在 x 方向选取正弦函数,即 X n = sin k n x , k n = 向选取 Yn = e kn y nπ ,在 y 方 a .由基本解的叠加构成电位的表示式为 = ∑ Cn sinn =1∞nπ x e anπ y a将 y = 0 的电位代入,得 U 0 sinnπ x 3π x ∞ = ∑ Cn sin a a n =1其余系数 Cn = 0 , 应用正弦级数展开的惟一性, 可以得到 n = 3 时,C3 = U 0 ,50《电磁场与电磁波》——习题详解所以 = U 0 sin4-93π x e a3π y a一个矩形导体槽由两部分构成, 如图 4-5 所示, 两个导体板的电位分别是 U 0 和 零,求槽内的电位. 解: 将原问题的电位看成是两个电位的叠加. 一个电位与平行板电容器的电位相同(上板电位为 U 0 ,下板电位为零 ),另一个电位为 U ,即=U0 y +U a y = 0 ,U = 0 y = a ,U = 0 a a 2y其中,U 满足拉普拉斯方程,其边界条件为 = U0 =0x图 4-5x = 0 时, U0 U 0 a y, U0 y= U = (0, y ) U a 0 y, a a < y<a 2 a 0< y< 2x → ∞ 时,电位 U 应该趋于零. U 的形式解为 nπ y e U = ∑ Cn sin a n =1待定系数用 x = 0 的条件确定.∞ ∞ nπ x aU (0, y ) = ∑ Cn sinn =1nπ y anπ y dy aa/2a C = 2 n∫a 0U (0, y ) sin∫a/2 02 U0 y U 0 a nπ y nπ y a nπ y sin dy = y cos sin a a a nπ a nπ a 051习题四U = 0 a a 2 nπ a 2 nπ cos + sin 2 2nπ 2 nπ a∫y nπ y a nπ y U 0 1 sin d y = U 0 cos a a/2 nπ a aaa/2 aU 0 a a 2 nπ y ay nπ y cos sin a nπ a nπ nπ U0 a sin + 2 a nπ 2a/2= U 0a nπnπ cos nπ cos 2 +化简后,得到U a a U0 a2 nπ cos nπ 0 cos 2 a nπ 2 a nπ U a nπ y nπ d y = 0 cos a nπ 2a C = 2 n∫a0U (0, y ) sin只有偶数项系数不为零.将系数求出,代入电位的表达式,得=4-10∞ U0 y 2U 0 nπ nπ y + ∑ cos sin e a a 2 n = 2 , 4 ,L nπnπ x a将一个半径为 a 的无限长导体管平分成两半,两部分之间互相绝缘,上半(0 < φ < π ) 接电压 U 0 ,下半 (π < φ < 2π ) 电位为零,如图 4-6,求管内的电位. 解:圆柱坐标的通解为 (r , φ ) = ( A0φ + B0 )(C0 ln r + D0 ) + ∑ r n ( An cos nφ + Bn sin nφ )n =1∞+ ∑ r n (Cn cos nφ + Dn sin nφ )n =1∞由于柱内电位在 r = 0 点为有限值,通解中不能有 ln r 和 rn项,即有52《电磁场与电磁波》——习题详解Cn = 0 , Dn = 0 , C0 = 0 (n = 1,2, L)柱内电位是角度的周期函数, A0 = 0 .因此,该题的通 解取为 r = U0 φx (r , φ ) = B0 D0 + ∑ r ( An cos nφ + Bn sin nφ )n n =1∞ =0图 4-6各项系数用 r = a 处的边界条件来定. (a, φ ) = B0 D0 + ∑ a n ( An cos nφ + Bn sin nφ ) = n =1∞ U0, 0 < φ < π 0, π < φ < 2πB 0 D0 =a n An =U 1 2π (a, φ ) d φ = 0 2π 0 2∫1π1∫ ∫0 (a, φ ) cos nφ d φ = 02π2πa n Bn =柱内的电位为π0 (a, φ ) sin nφ d φ =U0 (1 cos nπ ) nπ2U U (r , φ ) = 0 + 0 2 π4-111r ∑5L n a sin nφ n =1, 3,∞n半径为无穷长的圆柱面上,有密度为 ρ S = ρ S 0 cos φ 的面电荷,求圆柱面内, 外的电位. 解:由于面电荷是余弦分布,所以柱内,外的电位也是角度的偶函数.柱外的电位不应有 r 项,柱内电位不应有 r 是角度的周期函数.故柱内电位选为nn项.柱内,外的电位也不应有对数项,且1 = A0 + ∑ r n An cos nφn =1∞柱外电位选为 2 = C0 + ∑ r nCn cos nφn =1∞53习题四假定无穷远处的电位为零,定出系数 C0 = 0 . 在界面 r = a 上, 1 = 2 , ε0∞ 2 + ε0 1 = ρ S 0 cos φ r r∞即A0 + ∑ a n An cos nφ = ∑ a nCn cos nφn =1 n =1 ε0 ∑ na n 1Cn cos nφ + ε0 ∑ na n 1 An cos nφ = ρ S 0 cos φn =1 n =1∞∞解之得A0 = 0 , A1 =ρS 0 a2 ρS 0 , C1 = 2ε 2ε 0(n > 1)An = 0 , Cn = 0最后的电位为 ρS0 2ε r cos φ , = 2 0 a ρ S 0 cos φ , 2ε 0 r 3-12r<a r>a将一个半径为 a 的导体球置于均匀电场 E0 中,求球外的电位,电场. 解:采用球坐标系求解,设均匀电场沿正 z 方向,并设原点为电位零点(如图v4-7) . 因 球 面 是 等 位 面 , 所 以 在 r = a 处 , = 0 ; 在 r → ∞ 处 , 电 位 应 是 = E0 r cos θ ,球坐标中电位通解具有如下形式: (r ,θ ) = ∑ ( An r n + Bn r n 1 ) Pn (cos θ )n =0∞用无穷远处的边界条件 r → ∞ 及 = E0 r cos θ ,得到 A1 = E0 ,其余An = 0 .再使用球面上 ( r = a ) 的边界条件54《电磁场与电磁波》——习题详解∞ (a,θ ) = E0 a cos θ + ∑ Bn a n 1 Pn (cos θ ) = 0n =0上式可以改写为E0 a cos θ = ∑ Bn a n 1 Pn (cos θ )n =0∞因为勒让德多项式是完备的,即将任意的函数展开成勒让德多项式的系数是 惟 一 的 , 比 较 上 式 左 右 两 边 , 并 注 意 P (cos θ ) = cos θ , 得 E0 a = B1a 12,即B1 = E0 a 3 ,其余的 Bn = 0 .故导体球外电位为 = 1 电场强度为a3 E0 r cos θ r3 rE0θz图 4-7Er = 2a 3 = E0 1 + 3 cos θ r r a = E0 1 3 sin θ r rθ 3Eθ = 4-13将半径为 a , 介电常数为 ε 的无限长介质圆柱放置于均匀电场 E0 中, E0 沿 设vvx 方向,柱的轴沿 z 轴,柱外为空气,如图 4-8,求任意点的电位,电场.解: 选取原点为电位参考点, 1 表示柱内电位, 2 表示柱外电位. r → ∞ 用 在 处,电位 2 = E0 r cos φ因几何结构和场分布关于 y = 0 平面对称, 故电位表 示式中不应有 φ 的正弦项.令rE0φε ε0图 4-8x1 = A0 + ∑ ( An r n + Bn r n ) cos nφn =1∞55习题四∞ 2 = C0 + ∑ (Cn r n + Dn r n ) cos nφn =1因在原点处电位为零,定出 A0 = 0 , Bn = 0 .用无穷远处边界条件 r → ∞ 及 2 = E0 r cos φ ,定出 C1 = E0 ,其余 Cn = 0 .这样,柱内,外电位简化为 1 = ∑ An r n cos nφn =1∞ 2 = C1r cos φ + ∑ Dn r n cos nφn =1∞再用介质柱和空气界面 ( r = a ) 的边界条件 1 = 2 及 ε 1 = ε 0 2 ,得 r r∞ ∞ n n ∑ An a cos nφ = E0 a cos φ + ∑ Dn a cos nφ n =1 n =1 ∞ ∞ ∑ εnAn a n 1 cos nφ = ε 0 E0 cos φ ∑ ε 0 nDn a n 1 cos nφ n =1 n =1 比较左右 n = 1 的系数,得A1 解之得D1 D1 = E0 , ε A1 + ε 0 2 = ε 0 E0 2 a aA1 = 2ε 0 ε ε0 E0 , D1 = E0 a 2 ε + ε0 ε + ε0比较系数方程左右 n > 1 的各项,得An Dn D = 0 , ε An + ε 0 2n = 0 2n a a n由此解出 An = Dn = 0 .最终得到圆柱内,外的电位分别是1 = E02ε 0 r cos φ , ε + ε0ε ε0 a2 2 = E0 r cos φ + E0 cos φ ε + ε0 r56《电磁场与电磁波》——习题详解电场强度分别为v v 2ε 0 v 2ε 0 E1 = 1 = er E0 cos φ eφ E0 sin φ ε + ε0 ε + ε0v v ε ε 0 a2 v ε ε 0 a2 1 + E0 cos φ eφ 1 E2 = 2 = er ε + ε r 2 E0 sin φ ε + ε0 r2 0 4-14 在均匀电场中,设置一个半径为 a 的介质球,若电场的方向沿 z 轴,求介质 球内,外的电位,电场(介质球的介电常数为 ε ,球外为空气). 解:设球内,外电位解的形式分别为1 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ ) ,n =0 ∞∞ 2 = ∑ (Cn r n + Dn r n 1 ) Pn (cos nθ )n =0在 选取球心处为电位的参考点, 则球内电位的系数中 A0 = 0 ,Bn = 0 . r → ∞ 处,电位 2 = E0 r cos θ ,则球外电位系数 Cn 中,仅仅 C1 不为零,即 C1 = E0 , 其余为零.因此,球内,外解的形式分别简化为1 = ∑ An r n Pn (cos nθ ) ,n =0∞ 2 = E0 r cos θ + ∑ Dn r n 1 Pn (cos nθ )n =0∞再用介质球面 ( r = a ) 的边界条件 1 = 2 及 ε1 = ε 0 2 ,得 r r∞ ∞ n An a Pn (cos nθ ) = E 0 a cos θ + Dn a n 1 Pn (cos nθ ) n =1 n =1 ∞ ∞ εnA a n 1 P (cos nθ ) = ε E cos θ ε 0 (n + 1) Dn a n 2 Pn (cos nθ ) n n 0 0 n =1 n =1 ∑ ∑∑∑比较上式的系数,可以知道,除了 n = 1 以外,系数 An , Dn 均为零,且A1a = E0 a + D1a 2 , ε A1 = ε 0 E0 2ε 0 D1a 357习题四由此,解出系数A1 = 3ε 0 ε ε0 E0 , D1 = E0 a 3 ε + 2ε 0 ε + 2ε 0 3ε 0 r cos θ , ε + 2ε 0最后得到电位,电场1 = E0 2 = E0 r cos θ + E0v v E1 = 1 = erε ε 0 a3 cos θ ε + 2ε 0 r 23ε 0 v 3ε 0 E0 cos θ eθ E0 sin θ ε + 2ε 0 ε + 2ε 0v ε ε 0 a3 ε ε 0 a3 v v 1 + 2 E0 cos θ eθ 1 E2 = 2 = er ε + 2ε r 3 E0 sin θ ε + 2ε 0 r 3 0 4-15 已知球面 ( r = a ) 上的电位为 = U 0 cos θ ,求球外的电位. 解:设球外电位解的形式为 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ )n =0∞在无穷远处,应该满足自然边界条件,即电位趋于零.这样确定系数 An = 0 ,球外 电位的形式解简化为 = ∑ Bn r n 1 Pn (cos nθ )n =0∞使用球面 ( r = a ) 的边界条件,有U 0 cos θ = ∑ Bn a n 1 Pn (cos nθ )n =0∞由于勒让德多项式 Pn (cos nθ ) 是线性无关的,考虑到 P (cos θ ) = cos θ ,比较上式 1 左右的系数,得到 B1 = U 0 a , Bn = 02(n = 0,2,3,L) .所以,球外的电位分布为58《电磁场与电磁波》——习题详解 = U04-16a2 cos θ r2求无限长矩形区域 (0 < x < a,0 < y < b) 第一类边值问题的格林函数(即矩形 槽的四周电位为零,槽内有一与槽平行的单位线源,求槽内电位,如图 4-9). 解:这个问题的格林函数满足的方程为 2G 2G 1 + 2 = δ( x x′) δ( y y′) 2 x y ε0格林函数的边界条件是,在矩形区域的四周为零,即 x = 0 或 x = a , G = 0 ,y = 0 或 b = 0 , G = 0 .用分离变量法求这个问题的格林函数.考虑到格林函数在x = 0 , x = a 时的边界条件,将格林函数表示为y b(x',y')G = ∑Ψ n ( y ) sinn =1∞nπ x a将其代入格林函数方程,得a x 2 nπ 2 nπ x 1 = δ( x x′) δ( y y′) Ψ n ( y ) sin 图 4-9 ∑ y 2 a ε0 a n =1 nπ x 上式左右乘以 sin , 并在 0 < x < a 区间积分, 利用正弦函数的正交性和 δ 函数 a∞的积分性质,得函数Ψ n ( y ) 满足的微分方程为2 d2 nπ x ′ 2 nπ sin δ( y y ′) Ψn ( y ) = 2 a ε 0a dy a 在确定函数Ψ n ( y ) 时,将原来的区域分为两个区域,并注意到边界条件,设nπ An sh a (b y ), Ψ n ( y) = nπ Bn sh y, a 在 y = y′ 处,电位连续,即y > y′ y < y′An shnπ nπ (b y′) = Bn sh y′ a a59习题四对于函数Ψ n ( y ) 满足的微分方程,在点源附近积分,得∫y′+ 0 y′0d2 nπ Ψn ( y ) d y 2 dy a 2∫y′+ 0 y′0Ψ0 ( y ) d y = nπ x 2 sin ε 0a a因为电位连续,故上式左边第二项的积分为零,从而有d d nπ x′ 2 sin Ψ n ( y) Ψ n ( y) = dy dy a ε 0a y = y′ y = y′ + 代入函数Ψ n ( y ) 的形式,得nπ nπ nπ nπ x′ nπ 2 (b y′) sin An ch Bn ch y′ = a a a a ε 0a a将上式与 An shnπ nπ (b y′) = Bn sh y′ 相互联立求解,得 a a nπ 2 1 An = sh y′ , nπ ε 0 sh nπ b a a nπ 2 1 Bn = sh (b y′) nπ ε 0 sh nπ b a asin最后得到矩形区域的格林函数为nπ x ′ n π x nπ nπ sin y ≤ y′ sh a (b y′) sh a y, 2 a a = G= nπ ∑ nπ nπ b ε 0π n =1 sh y′ sh (b y ), y ≥ y′ n sh a a a 4-17 推导无限长圆柱区域内(半径为 a )第一类边值问题的格林函数. 解:使用镜像法及其格林函数的定义计算.在半径为 a 的导体圆柱内部离轴 线 r ′ 处,放置一个线密度为 1 单位,与导体圆柱平行的无穷长线电荷,并且维持导∞体柱面的电位为零,求出柱内的电位,这个电位就是柱内的格林函数.当原电荷位 于 r 处,需要在 r ′ 的镜像位置 r ′′ 处,加一个线密度为 1 的线电荷.此时,圆柱内 的电位是v v G (r , r ′) =1 2π εln1 1 1 ln +C R1 2π ε R2R1 和 R2 分别是从 r ′ 和 r ′′ 到 r 的距离(如图 4-10),C 是常数.由柱面上的电位为零,60《电磁场与电磁波》——习题详解可以定出这个常数的值.最后得到柱内的格林函数为v v G (r , r ′) =1 2π εlnR2 r ′ R1 a yrR1 r'R2 r'' x =0 = U0图 4-10 4-18d图 4-11x两个无限大导体平板间距离为 d ,其间有体密度 ρ =ρ 0 x / d 的电荷,极板的电位如图 4-11 所求,用格林函数法求极板之间的电位. 解:先用直接积分法求解.电位仅仅是 x 的函数,故其满足如下方程:ρ x d2 ρ = = 0 2 dx ε0 ε 0d对以上方程积分得ρ x2 ρ x3 d = C1 0 , = C2 + C1 x 0 dx 2ε 0 d 6ε 0 d由 x = 0 及 = 0 , 可 定 出 系 数 C2 = 0 ; 由 x = d 及 = U 0 , 可 定 出 系 数C1 =U 0 ρ0d + ,从而,得到电容器内的电位为 d 6ε 0 =ρ0 x3 6ε 0 dU ρ d + 0 + 0 x d 6ε 0 再用格林函数法求解.这个问题的格林函数为 d x′ x < x′ ε d x, 0 G ( x, x′) = x′ (d x), x > x′ ε 0d 为了计算方便,将这个问题分解为两个:一个是平板电容器内有电荷,而两极板的61习题四电位为零,即奇次边界条件,记电位 1 ;另一个是无电荷分布,极板的电位维持原 来的电位,记电位 2 .用格林函数法计算奇次边界条件时的电位 1 :1 = ρ ( x ′)G ( x, x ′) d x ′0∫d= ρ ( x ′)G ( x, x ′) d x ′ + ρ ( x ′)G ( x, x ′) d x ′0 x∫x∫d=∫x 0ρ 0 x ′ x ′(d x) d x′ + d ε 0d∫d xρ 0 x ′ (d x ′) x d x′ d ε 0dρ 0 (d x) x 3 ρ 0 x 1 2 2 1 (d x )d + (d 3 x 3 ) = + 2 2 3 ε 0d 2 3 ε 0d =ρ0 3 ρ0d x + x 6ε 0 d 2 6ε 0至于电位 2 ,容易得出 2 = (U 0 / d ) x .故所求电位为 = 1 + 2 = 4-192ρ0 2 U 0 ρ0d x + d + 6ε x 6ε 0 d 0 分析复变函数 w = z 能够表示的静电场. 解: w = u + j v = z = ( x + j y ) = x y + j 2 xy2 2 2 2u = x 2 y 2 , v = 2 xy实部的等值线是双曲线 x y = C1 ;虚部的等值线也是双曲线,其方程为2 22 xy = C2 .因此,这个函数能够表示极板形状为双曲线的导体附近的静电场.如果用虚部表示电位函数,在 x = 0 或 y = 0 处,电位为零,可以表示接地的直角导体拐 角附近的静电场. 4-20 分析复变函数 w = arccos z 能够表示哪些情形的静电场.62《电磁场与电磁波》——习题详解解: z = x + j y = cos(u + j v) = cos u ch v j sin u sh vx = cos u ch v , y = sin u sh vx2 y2 x2 y2 + 2 = 1, 2 =1 ch 2 v sh v cos 2 u sin u可见,虚部的等值线是一簇椭圆,实部的等值线是一簇双曲线.当用虚部表示 电位时,能够表示两个共焦点的椭圆柱体之间的场;当用实部表示电位时,能够表 示两个共焦点的双曲线柱体之间的场. 4-21 用有限差分法求图 4-12 所示区域中各个节点的电位. 解:1 4 1 2 = (1 + 4 + 100) 4 1 3 = (1 + 4 ) 4 1 4 = ( 2 + 3 ) 41 = ( 2 + 3 + 100)解这一方程组,得到1 = 2 = 37.5 V , 3 = 4 = 12.5 V100V 1 0V 3 4 2 0V0V 图 4-1263。
电磁场与电磁波(第四版)课后答案 第四章习题
∫Байду номын сангаас
2π / ω
0
r 2650 cos (ωt − kz )dt = ez 1325 W / m 2
2
（3）任一时刻流入长为1m横截面积为0.25平方米的 平行六面体中的净功率。 r r r r r r P = − ∫ S en dS = − S ( −ez ) |z =0 + S ez |z =1 × 0.25
试求（1）瞬时坡印廷矢量 （2）平均坡印廷矢量 （3）任一时刻流入长为1m横截面积为0.25平方米的 平行六面体中的净功率。 解：（1）瞬时坡印廷矢量 r r r r S = E × H = ez 2650 cos 2 (ωt − kz ) W / m 2 （2）平均坡印廷矢量
r r ω S av = ez 2π
式中
k0 =
2π
µ0
A/ m
λ0
试求（1）
c λ0 λ0 各点处的瞬时坡印廷矢量 z = 0, , 8 4
=
ω
C为真空的光速，λ0是波长。
（2）以上各点处的平均坡印廷矢量 解：（1）E和H的瞬时矢量为
r r r ex jE0 sin ( k0 z ) e jωt = −ex E0 sin ( k0 z ) sin (ωt ) V / m E ( z , t ) = Re r r ε0 r ε0 jωt H ( z , t ) = Re e y E0 cos ( k0 z ) e = ey E0 cos ( k0 z ) cos (ωt ) µ0 µ0 A/ m
s
= 2650 × 0.25 cos 2 (ωt ) − cos 2 (ωt − 0.42 ) = −270.2sin ( 2ωt − 0.42 )W
电磁学第四章习题答案
第四章 习题一(磁场)1、一根载有电流I 的无限长直导线，在A 处弯成半径为R 的圆形，由于导线外有绝缘层，在A 处两导线并不短路，则在圆心处磁感应强度B的大小为( C )(A) I (μ0＋1)／(2πR) (B) μ0πI ／(2πR) (C) μ0I(1＋π)／(2πR) (D) μ0I(1＋π)／(4πR)2、载有电流为I 的无限长导线，弯成如图形状，其中一段是半径为a 的半圆，则圆心处的磁感应强度B的大小为( D )(A) μ0I ／(4a ) + μ0I ／(4πa )(B))8/(2)4/()4/(a I a I a I o o o πμπμμ++(C) ∞(D))4/(2)4/()4/(a I a I a I o o o πμπμμ+-3、如图，电流I 均匀地自下而上通过宽度为a 的 无限长导体薄平板，求薄平板所在平面上距板的一 边为d 的P 点的磁感应强度。
解：该薄板可以看成是由许多无限长的细直载流 导线组成的，每一条载流线的电流为dI =Idx /a ， 根据无限长直载流线磁场公式，它们在P 点产 生的磁感应强度的大小为xdxa πI μx πdI μdB 2200==，B d 的方向⊗ ∴ dad a πI μx dx a πI μdB B a d d ad d+===⎰⎰++ln 2200，B 的方向⊗PB4、电流均匀地自下而上通过宽为2a 的无限长导体薄平板，电流为I ，通过板的中线并与板面垂直的平面上有一点P ，P 到板的垂直距离为x ，设板厚可略去不计，求P 点磁感应强度B 。
解：面电流线密度a I j 2/=在离轴线y 处取一宽为dy 的窄条，其电流为dy a Ijdy dI 2==, 22y x r +=P 点B d的方向如图所示。
r πdI μdB 20=220044yx dy a πI μr dy a πI μ+== 22cos sin yx x rx φθ+===，22sin cos yx y ry φθ+===2204cos y x ydya πI μθdB dB x +==，2204sin y x xdy a πI μθdB dB y+== 04220=+==⎰⎰--a a aa x x yx ydya πI μdB Bxaa πI μx y a πI μy x dy aπIx μdB B aa aa aa y y arctan 2arctan 4400220==+==---⎰⎰ y y y x x e x a aπIμe B e B B ⎪⎭⎫ ⎝⎛=+=arctan 205、求上题当a →∞，但维持aIj 2=(单位宽度上的电流，叫做电流线密度)为一常量时P 点的磁感应强度。
电磁场与电磁波(第4版)习题第4章
word 版本.第4章 时变电磁场部分习题解答4.1 证明：在无源的真空中，以下矢量函数满足波动方程222210c t∂∇-=∂EE ，其中2001c με=，0E 为常数。
（1）0cos()x E t z cωω=-E e ；（2）0sin()cos()x E z t cωω=E e ；（3）0cos()y E t z cωω=+E e解 （1）222002cos()cos()x x E t z E t z c z cωωωω∂∇=∇-=-=∂E e e20()cos()x E t z c cωωω--e2220022cos()cos()x x E t z E t z t t c cωωωωω∂∂=-=--∂∂E e e 故22220022211()cos()[cos()]0x x E t z E t z c t c c c cωωωωωω∂∇-=-----=∂E E e e即矢量函数0cos()x E t z c ωω=-E e 满足波动方程222210c t ∂∇-=∂E E 。
（2）222002[sin()cos()][sin()cos()]x x E z t E z t c z cωωωω∂∇=∇==∂E e e20()sin()cos()x E z t c cωωω-e2220022[sin()cos()][sin()cos()]x x E z t E z t t t c cωωωωω∂∂==-∂∂E e e 故22220022211()sin()cos()[sin()cos()]0x x E z t E z t c t c c c cωωωωωω∂∇-=---=∂E E e e即矢量函数0sin()cos()x E z t c ωω=E e 满足波动方程222210c t∂∇-=∂E E 。
（3）222002cos()cos()y y E t z E t z c z cωωωω∂∇=∇+=+=∂E e e20()cos()y E t z c cωωω-+e2220022cos()cos()y x E t z E t z t t c cωωωωω∂∂=+=-+∂∂E e e 故22220022211()cos()[cos()]0y y E t z E t z c t c c c cωωωωωω∂∇-=-+--+=∂E E e e4－4即矢量函数0cos()y E t z c ωω=+E e 满足波动方程222210c t∂∇-=∂EE 。
电磁场课后答案4
kr =
衰减常数：
ωμσ
2
案
为 300 米。 试求电场强度的振幅为 1 微伏/米时离海面的距离， 并写出这个位置上的E， H之表示式。
=
ki =
复数波阻抗为：
网
平面电磁波在海平面处的场强表示式为： E = x 0 1000 e
2π × 10 6 × 4π × 10 −7 × 1 = 2 （弧度/米） 2
4.1 写出ω,k,f,T,λ单位。 答：ω (rad/s), k (rad/m) ,f (Hz) , T (s), λ (m) 4.2 激光器输出波长为 6.328 × 10-7m，计算它的f,T,k。 答： f =
c
λ
=
3 × 10 8 1 = 4.741 × 1014 Hz ， T = = 2.11 × 10 −15 s ， −7 f 6.328 × 10
ωt + 30 o = 180 o 或 ωt +
π
co
)
μ0 ，
m
解： k = ω
ε r ε 0 μ 0 = 2ω μ 0 ε 0 =
2 × 2π × 150 × 10 6 = 2π 3 × 10 8
(m )
−1
答： f = f 0 ， λ = 0.5λ0 ， k = 2k 0 ， v = 0.5v0 。
解之得：z = 10.35（米） 距海水 10.35 米处 E、H 之表示式为：
2 z = 9 × ln 10
E = x 0 1000e −2 z e j (ωt −2 z )
= x 0 1000e − 20.7 e j (ωt −1180 )
o
= x 0 10 3 e − 20.7 e j (ωt −100 )
电磁学第四章答案解析全
第四章 习题2、平行板电容器（面积为S,间距为d ）中间两层的厚度各为d 1和d 2（d 1+d 2=d ），介电常数各为1ε和2ε的电介质。
试求：（1）电容C ；（2）当金属板上带电密度为0σ±时，两层介质的分界面上的极化电荷密度'σ；（3）极板间电势差U;（4）两层介质中的电位移D ； 解：（1）这个电容器可看成是厚度为d 1和d 2的两个电容器的串联：12210212121d d SC C C C C εεεεε+=+=（2）分界处第一层介质的极化电荷面密度（设与d 1接触的金属板带正电）1111011111εσεεεσ)(E )(P n P '-=-=-=⋅=分界处第二层介质的极化电荷面密度：21222022211εσεεεσ)(E )(P n P '--=--=-=⋅=所以， 21021211εεσεεσσσ+-=+=)('''若与d 1接触的金属板带负电，则21021211εεσεεσσσ+--=+=)('''（3）2101221202010102211εεσεεεεσεεσ)d d (d d d E d E U +=+=+= （4）01101σεε==E D ，02202σεε==E D4、平行板电容器两极板相距3.Ocm ，其间放有一层02.=ε的介电质，位置与厚度如图所示，已知极板上面电荷密度为21101098m /c .-⨯=σ，略去边缘效应，求: (1)极板间各处的P 、E 和D 的值; (2)极板间各处的电势(设正极板处00=U );(3)画出E-x ，D-x ，U-x 曲线;解：（1）由高斯定理利用对称性，可给出二极板内：2111098m /c .D e -⨯==σ（各区域均相同），在0与1之间01==P ,r ε，m /V DE 20101⨯==ε在1与2之间210000010454112m /c .D)(E )(P ,r r r -⨯=-=-==εεεεεεε，m /V D E r500==εε 在2与3之间，01==P ,r ε，m /V DE 20101⨯==ε（2）0=A V ：0-1区：,x dx E V xD 100=⋅=⎰1-2区：),x x (dx E V xx 1501-=⋅=⎰)x x x ,.x x )x x (V 2111505010050≤≤+=+-=2-3区：),x x (dx E V xx 2100021-=⋅=⎰∆)x x x (,.x ).x (,x x x x x )x x (V 3212221501000050100505010010010050≤≤-=-=+-=-++=题4图6、一平行板电容器两极板相距为d,其间充满了两种介质，介电常数为1ε的介质所占的面积为S 1, 介电常数为2ε的介质所占的面积为S 2。
《电磁场与电磁波》（第四版）习题集：第4章时变电磁场
《电磁场与电磁波》（第四版）习题集：第4章时变电磁场第4章时变电磁场在时变的情况下，电场和磁场相互激励，在空间形成电磁波，时变电磁场的能量以电磁波的形式进行传播。
电磁场的波动方程描述了电磁场的波动性，本章首先对电磁场的波动方程进行讨论。
在时变电磁场的情况下，也可以引入辅助位函数来描述电磁场，使一些复杂问题的分析求解过程得以简化。
本章对时变电磁场的位函数及其微分方程进行了讨论。
电磁能量一如其它能量服从能量守恒原理，本章将讨论电磁场的能流和表征电磁场能量守恒关系的坡印廷定理。
本章在最后讨论了随时间按正弦函数变化的时变电磁场，这种时变电磁场称为时谐电磁场或正弦电磁场。
4. 1 波动方程由麦克斯韦方程可以建立电磁场的波动方程，揭示了时变电磁场的运动规律，即电磁场的波动性。
下面建立无源空间中电磁场的波动方程。
在无源空间中，电流密度和电荷密度处处为零，即0ρ=、0=J 。
在线性、各向同性的均匀媒质中，E 和H 满足的麦克斯韦方程为t ε=?EH （4.1.1） tμ=-?HE （4.1.2） 0?=H （4.1.3） 0?=E （4.1.4）对式（4.1.2）两边取旋度，有()()tμ=-E H 将式（4.1.1）代入上式，得到22()0t με+=?EE利用矢量恒等式2()()=??-?E E E 和式（4.1.4），可得到2220tμε??-=?EE （4.1.5）此式即为无源区域中电场强度矢量E 满足的波动方程。
同理可得到无源区域中磁场强度矢量H 满足的波动方程为2220tμε??-=?H H （4.1.6）无源区域中的E 或H 可以通过求解式（4.1.5）或式（4.1.6）的波动方程得到。
在直角坐标系中，波动方程可以分解为三个标量方程，每个方程中只含有一个场分量。
例如，式（4.1.5）可以分解为222222220x x x xE E E E x y z tμε++-= （4.1.7） 222222220yyyyE E E E x y z t με++-= （4.1.8）222222220z z z zE E E E x y z t με++-= （4.1.9）在其它坐标系中分解得到的三个标量方程都具有复杂的形式。
(完整版)电工基础四版习题册答案第四章磁场与电磁感应
电工基础四版习题册答案第四章磁场与电磁感8.如图4-1所示, 导体ad的磁感应强度B的方向为N极穿出纸面,导体的电流方向是_由a→b__.二.判断题1.每个磁体都有两个磁极,一个叫N极,另一个叫S极,若把磁体分成两端,则一段为N极,另一段叫S 极.( × )2.磁场的方向总是由N极指向S极.(×)3.地球是一个大磁体.( √)4.磁场总是由电流产生的.(×)5.由于磁感线能想象地描述磁场的强弱和方向,所以它存在于磁极周围的空间里.( × )三.选择题1.在条形磁铁中,磁性最强的部位在(B )A.中间B. 两极 c.整体2.磁感线上任意点的( B )方向,就是该点的磁场方向.A.指向N极的B.切线 c.直线3.关于电流的磁场,正确说法是(C )A.直线电流的磁场只分布在垂直与导线的某一平面上B.直线电流的刺伤是一些同心圆,距离导线越远,磁感线越密.C. 直线电流,环形电流的磁场方向都可用安培定则判断.四.综合分析题1.有两位同学,各自在铁棒上绕一些导线制成电磁铁,照后按照从右段流入,从左段流出的顺序通入电流.甲同学制成的电磁铁,左端是N极,右端是S极;而乙同学制成的电磁铁,恰好左端是S 极,右端是N极.那么,它们各自是怎样绕导线的?请用简图表示出来.2.判断图4-2中各小磁针的偏转方向.§4—2磁场的主要物理量一.填空题1.描述磁场在空间某一范围内分布情况的物理量称为磁通，用符号表示，单位为____Wb________;描述磁场中各点磁场强弱和方向的物理量称为磁感应强度，用符号 B 表示，单位为特斯拉（T）。
在均匀磁场中,两者的关系可用公式Φ=B S表示。
2.用来表示媒介质导磁性的物理量叫磁导率，用符号 u 表示,单位是B.顺磁物质、顺磁物质、铁磁物质C.顺磁物质、铁磁物质、铁磁物质2.下列与磁导率无关的量是( B ).A.磁感应强度B.磁场强度C.磁通四、问答题1.试总结磁感线的特点.答：①磁通越密磁场越强，磁力线越疏磁场越弱。
电磁学答案第四章
H4 = 0
w4 = 0
W4 = 0
单位长度总能量:
W = W1 + W2 + W3 + W4 2 c μ 0 I 4c ln 3c 4 + 4c 2 b 2 b 4 μ0 I 2 μ0 I 2 b b = + ln + 2 2 2 16π 4π a 16π ( c b )
2
2 c 4c ln 3c 4 + 4c 2 b 2 b 4 b μ0 I 2 1 b = 1.7 × 10 5 J + ln + = 2 2 2 4π 4 a 4 (c b )
μr
(103) ? ! 4.9 6.4 7.8 8.8 8.6 6.1 3.8 2.1
memo
最大
⑶ 最大磁导率: 0.011 N/A2
P. 289 4-42, 【解】:
H = i 2π r
D
原磁化方向
I
i = 2π rH
最大值
i ≥ π DH C 103 = π × 0.8 × 10 3 × 2 × 4π = 0.4A
B~H曲线
H(A/m) 0 100 200 300 400 500 600
⑵ 磁导率: H (A/m) 1 2 3 4 5 6 7 8 9 0 33 50 61 72 93 155 290 600
μr μ0 B (Wb/m2) (10-3N/A2) 0 ? ! 0.2 6.1 0.4 8.0 0.6 9.8 0.8 11.1 1.0 10.8 1.2 7.7 1.4 4.8 1.6 2.7
1.0 498 2 × + × 10 3 4π × 10 7 796 1 = 2.09 × 10 3 =
P. 290 4-50, 【解】: ⑴ 气隙中
电磁场与电磁波课后习题及答案四章习题解答
电磁场与电磁波课后习题及答案四章习题解答(共20页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2四章习题解答如题图所示为一长方形截面的导体槽，槽可视为无限长，其上有一块与槽相绝缘的盖板，槽的电位为零，上边盖板的电位为0U ，求槽内的电位函数。
解 根据题意，电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ= ③ 0(,)x b U ϕ=根据条件①和②，电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③，有01sinh()sin()n n n b n x U A a aππ∞==∑ 两边同乘以sin()n xaπ，并从0到a 对x 积分，得到 002sin()d sinh()an U n xA x a n b a aππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩， 故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑ 两平行无限大导体平面，距离为b ，其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ，下板保持零电位，求板间电位的解。
设在薄片平面上，从0=y 到d y =，电位线性变化，0(0,)y U y d ϕ=。
题图3解 应用叠加原理，设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中，1(,)x y ϕ为不存在薄片的平行无限大导体平面间（电压为0U ）的电位，即10(,)x y U y ϕ=；2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位，其边界条件为：① 22(,0)(,)0x x b ϕϕ==② 2(,)0()x y x ϕ=→∞③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩ 根据条件①和②，可设2(,)x y ϕ的通解为 21(,)sin()e n x b n n n y x y A b ππϕ∞-==∑ 由条件③有 00100(0)sin()()n n U U y y d n y bA U U b y y d y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑ 两边同乘以sin()n yb π，并从0到b 对y 积分，得到 0002211(1)sin()d ()sin()d d bn dU U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ 故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b bππππ∞-=+∑ 求在上题的解中，除开0U y b 一项外，其他所有项对电场总储能的贡献。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章习题答案4-4 设磁矢量位的参考点为无穷远处，计算一段长为2m 的直线电流I 在其中垂线上距线电流1m 的磁矢量位值。
解：选圆柱坐标，在z '处取元电流段z e I l I'dz d ＝，元电流段 产生的元磁矢量位为z 0e R4z Id A d πμ'=整个线电流产生的磁矢量位：C e R z Id 4A z 2l 2l 0+'=⎰-//πμ 其中 22z R '+=ρ，电流有限分布，参考点选在无穷远处，所以积分常数C 为零。
()()z e 2l 2l 2l 2l 2I e z z Id 4A 22220z 2l 2l 220 ////ln //++-++='+'=⎰-ρρπμρπμ将 l =2 ，1=ρ 带入上式，得z 0e 222I A11π-+=ln μ4.5解：由恒定磁场的基本方程，磁感应强度一定要满足0B ∇=，因此，此方程可以作为判断一个矢量是否为磁感应强度B的条件。
4-6 相距为d 的平行无限大平面电流，两个平面分别在2d z -=和2d z =且平行与xO y 平面。
相应的面电流密度分别为x e k 和y e k,求由两个无限大平面分割出来的三个空间区域的磁感应强度。
解：由例题4-7结果，分别求出面电流x e k 和y e k产生的磁场，然后应用叠加原理，x e k产生的磁场为：ρy图4-4⎪⎪⎩⎪⎪⎨⎧-<->-2d z e 2K 2d z e 2K B y 0y 01,,)()(μμ＝ y e k产生的磁场为⎪⎩⎪⎨⎧><-2),(22),(2002d z e K d z e K B x xμμ＝ 由叠加原理知：⎪⎪⎪⎩⎪⎪⎪⎨⎧>+-<<-+--<-=2),(222,)(22),(2000d z e e K d z d e e K d z e e K B xy x y x yμμμ4-7 参见教材例4.84-8 如题图4-8所示，同轴电缆通以电流I ，求各处的磁感应强度。
解：选圆柱坐标，应用安培环路定律：in 0I l d B lμ=⎰∙当10R <<ρ时：内导体上的电流密度：z21e R I J π= I R B e d e B l d B l 2120202ππρμπραρφφπ===∙∙⎰⎰ φπρμπρμe R I B R I B 2102102,2==∴当21R R <<ρ时I B l d B l02μπρ==⎰∙题图4-8φπρμπρμe I B IB 2,200==∴当 32R R <<ρ时外导体上的电流密度：()z2223e R R IJ -=π I R R R B l d B l )1(222232220---==⎰∙ρμπρ φρπρμρπρμe R R R I B R R R I B )(2)(,)(2)(2223223022232230--=--=∴ 当ρ<3R 时0=⎰∙ll d B0=∴B4-9略4-10有内半径为1R ，外半径为2R ，厚度为h ，磁导率为μ（)0μμ>>的圆环形铁芯，其上均匀绕有N 匝线圈，线圈中电流为I ，如题4-10所示。
求铁芯中的磁感应强度和铁芯截面上的磁通以及线圈的磁链。
解：由于磁场为轴对称场，建立圆柱坐标系 φρe )(∙=B B 用安培环路定理可得：φφρπρρe I μN B NI H I N H NIl H π2e 22πd l ===⇒=∴∙∙⎰ 122R 1R m ln 2d 2d 2d 2d R R h I N μh I N h I N e h e I N s d B m πρπρμρπρμρπρμφφ==Φ===Φ⎰∙∙由于每匝交链的磁通都相等122122m R R h N I R R h I N N ln2L ln2m πμψπμΦψ====,题4.10图12222R R h I N I W ln4L 21m πμ==4-11 在无限大磁媒质分界面上，有一无限长直线电流I ，如题图4-11所示。
求两种媒质中的磁感应强度和磁场强度。
解：由分界面衔接条件 2121 0)(B B B B e n==-∙选用圆柱坐标，利用安培环路定理有：()φμμρμμμμμμe IB B IB B l d B l d B l H l l21212122112211l πd 21+===⎪⎪⎭⎫⎝⎛+=+=∴⎰⎰⎰∙∙∙()φμμρμe I μB H 111 212π+== ， ()φμμρμe I μB H 222211π+==4-14、如题图4-14所示，有内半径为1R ，外半径为2R ，厚度为h ，磁导率为μ（)0μμ>>的圆环形铁芯，其上均匀绕有N 匝线圈，求线圈的自感。
若将铁芯割掉一小段，形成空气隙，空气隙对应的圆心角为α∆，求线圈的自感。
解：铁心被切去一小段后，形成空气隙，由安培环路定理得：IN l d H l d H NIl H l l=+⇒=⎰⎰⎰∙∙∙2121l dB B B B B e n===-∙21210)( I N B l d B l d B l l =⎥⎦⎤⎢⎣⎡∆-+∆=+∙∙⎰⎰ραπμαρμμμ)(211020121[]φρα∆πμα∆μμμe I N B)(2 00-+=∴[]120000)(2d )(2R R I N h h I N NN 2R R m m 21ln α∆πμα∆μμμρα∆πμα∆μμμΦψ-+=-+==⎰1202122mR R h μμN R R hN Ilnln α∆μμπμα∆πμα∆μμμψ)(2)(2L 0000-+=-+==2m L 21I W =题图 4-14题图 4-114-15解：选圆柱坐标，电流与z 轴重合，图4-15（a ）、（b ）所示无限长直导线中电流I 在距导线ρ处的磁感应强度为φπρμe 20I B =直线m n 的方程为：（两点式）()a bd-=ρ2z ()φφρρρe d 2e d z d a b ds -== 该磁场在（a ）中的三角形线框产生的磁通和磁链为：()())ln (2I d 2I d 222I d 0ba a0ba a0m m ab a a b b d a bda bds B s +-=-=-==Φ=ψ⎰⎰⎰++∙πμρρπρμρρπρμ)b ln (2M 0m aa ab b d I +-=ψ=πμ 同理，磁场在（b ）中的三角形线框产生的磁通和磁链为：⎥⎦⎤⎢⎣⎡-+⋅+=-+⋅==Φ=ψ⎰⎰+∙b a b a b a b d b d b a B ba aln )(2I d )(2I s d 00Sm m πμρρπρμ⎥⎦⎤⎢⎣⎡-+⋅+==b a b a ln b)(a b 2d IM 0mπμψ（b ）（a ） 图4-15N(a+b ,d /2)ozP(ρ,z )4-18解：由于是均匀磁化， 0M 为常数。
在圆柱内部磁化电流面密度为：0e M M J z m =⨯∇=⨯∇=磁化体密度为： n m e M K⨯=其中 n e为表面的法向方向。
在圆柱的两个端面，其外法向方向分别为z e±，代入上式可知端面上0K m =，不存在磁化电流线密度。
在圆柱的侧面ρe e n=，故侧面上的磁化电流线密度为：φρe M e e M K 0z 0m =⨯=由此可见，要求永久磁化圆柱沿轴线的磁场，就是求磁化电流线密度 φe M K 0m= 在空间沿轴各处的磁感应强度。
圆柱上的磁化电流可以视为若干个小圆环电流，每个小圆环电流为'dz M dz'K dI 0m m ==式中 'dz 是小圆环的宽度，每个小圆环在轴线上某点均产生磁感应强度。
利用圆环电流在其中心轴线一点的磁感应强度的表达式，可利用 m dI 在轴线上产生沿轴线方向的磁感应强度为232202023222m 0])'z z (a [2'dz M a ])'z z (a [2a dI dB -+=-+=μμ}])l z (a [z l ])l z (a [z -l {2M ])'z z (a [2'dz M a l l B 21222122002322020-+++-+=-+-=⎰μμ 磁感应强度的方向沿 z e的方向MB H e }])l z (a [z l ])l z (a [z -l {2M B 0z 2122212200-=-+++-+=μμ 当 l z l -≤≤ 时z 0z 212221220e M e }])l z (a [z l ])l z (a [z -l {2M H --+++-+=当 l z >或l z -< 时，0M =z 212221220e }])l z (a [z l ])l z (a [z -l {2M H -+++-+=4-19解：选择1I 和2I 的参考方向，使1I 产生的磁通与2I 成右手螺旋关系，使2I 产生的磁通与1I 成右手螺旋关系，则互感系数为正值；选择1I 和2I 的参考方向，使1I 产生的磁通与2I 成左手螺旋关系，使2I 产生的磁通与1I 成左手螺旋关系，则互感系数为负值。
4-20解：由对称性分析知,A仅为圆柱坐标系中ρ的函数，且只有φ分量当a ≤ρ时 0A 1=⨯∇⨯∇()z 1z 1A 10A 000A e e e e φφφρφρρρρρρρρ∂∂==⨯∇∂∂1/1/)(()()0A 1A 000A 11z1=⎥⎦⎤⎢⎣⎡∂∂∂∂-=∂∂=⨯∇⨯∇∂∂φφφφρφρρρρρρρρρρe e e e 1/1/)(解得 ρρφ21C A +=1C同理 a >ρ时 ， 0A 2=⨯∇⨯∇解得 ρρφ42C A +=3C当0→ρ时，1A 为有限值；∞→ρ时，2A为有限值，所以0C 0C 32==,由边界条件 a 2a 1A A ===ρρ|| aC a C 41=⇒(1)K A A =∂∂-∂∂==a 12a 1111ρρρμρμ|| 即：K 0a 2a 1μρρρρ=∂∂-∂∂==||A A K aC C 0241μ=+⇒ （2）联立求解（1）（2）得 2KC 01μ=， 2Ka C 204μ=⎪⎪⎩⎪⎪⎨⎧=φφρμρμe 2Ka e K 21A 200 )a ()a 0(>≤<ρρ⎩⎨⎧=⨯∇=0e K A B 0ρμ)a ()a 0(>≤<ρρ。